Quantum Calculations On Hydrogen Bonds In Certain Water Clusters Show Cooperative Effects

Abstract

Water molecules in clefts and small clusters are in a significantly different environment than in bulk water. We have carried out ab initio calculations that demonstrate this in a series of clusters, showing that cooperative effects must be taken into account in the treatment of hydrogen bonds and water clusters in such bounded systems. Hydrogen bonds between water molecules in simulations are treated most frequently by using point charge water potentials, such as TIP3P or SPC, sometimes with a polarizable extension. These produce excellent results in bulk water, for which they are calibrated. Clefts are different from bulk; it is necessary to look at smaller systems, and investigate the effect of limited numbers of neighbors. We start with a study of isolated clusters of water with varying numbers of neighbors of a hydrogen bonded pair of water molecules. The cluster as a whole is in vacuum. The clusters are defined so as to provide the possible arrangements of nearest neighbors of a central hydrogen bonded pair of water molecules. We then scan the length and angles of the central hydrogen bond of the clusters, using density functional theory, for each possible arrangement of donor and acceptor hydrogen bonds on the central hydrogen bonding pair; the potential of interaction of two water molecules varies with the number of donor and of acceptor neighbors. This also involves changes in charge on the water molecules as a function of bond length, and changes in energy and length as a function of number of neighboring donor and acceptor molecules. Energy varies by approximately 6 k_BT near room temperature from the highest to the lowest energy when bond length alone is varied, enough to seriously affect simulations.

INTRODUCTION

The simulation of systems containing water, whether by molecular dynamics (MD) or Monte Carlo (MC), requires an interaction potential for the water molecules. Of the several successful point charge water models in the literature, it appears that TIP3P (plus TIP4P, TIP5P)^1-5 (more recently TIP4P-Ew) and SPC and SPC/E (and some of their descendents)^6,7 are most popular. There are some polarizable versions of these (e.g., Polarizable SPC, or PSPC ⁸), but these are more complex, and difficult to use in simulations. For water clusters excellent results can be obtained with the TTM2-F potential^9-11, which is, however, also difficult to use in an MD simulation. The simpler versions allow much faster simulations that include explicit water. These models are built from point charges on or near the oxygen and hydrogens, plus van der Waals terms. They are insensitive to their surroundings; the same charges are used in all cases (Gaussian03 now allows some variation, but this has not been much used yet.). A new potential, based on quantum calculations with fitting to water has very recently been proposed¹², and it appears that it may be better than the point charge models, although it has yet to be applied. Relatively early studies pointing out types of cooperativity include a study of water trimers, in which non-additivity was calculated¹³. Several other studies demonstrated the non-additive properties of specific, sometimes optimized, small rings or linear clusters. There are a number of studies of larger polyhedral water clusters as well: 20-mers were studied by Kuo et al¹⁴ Hexamers were evaluated by Tissandier et al¹⁵, while Tsai and Jordan considered cubic clusters of size 8, 12, 16, and 20¹⁶ Anick studied more general polyhedral water clusters, finding cooperative effects in energy and bond length for equilibrium clusters that extended to next nearest neighbors^17,18. Hodges et al¹⁹ compared ab initio results to two potentials (ASP-W2 and ASP-W4, which do not appear to be widely used at present) for some small clusters. A related study of trimers, tetramers, and pentamers estimated that omitting cooperative effects would lead to errors exceeding 20% for clusters larger than pentamers (although these were not explicitly calculated)²⁰ Ojamae and Hermansson²¹ calculated frequencies and binding energies for water chains, as well as one ring structure and a pentamer. Chen and Gordon broke down the interactions into several energy components (electrostatic, exchange, polarization, and charge transfer), in a paper largely concerned with techniques of calculation²². In general, these papers use optimized clusters, without studying the dependence of energy on bond length and angles. They do, however, find the dependence of optimized bond length and energy on geometry and bond topology. There is also experimental evidence for cooperativity in hydrogen bonding from IR spectra. Going beyond Zundel’s work, Luck et al²³ have shown shifts in IR spectra for hydrogen bonding to bases, principally demonstrating anti-cooperativity. New potentials²⁴, or steps toward new potentials²⁵, continue to appear. Typically these are based on quantum calculations, whether Empirical Valence Band or, more commonly, density functional, calculations. Some compare several density functional or alternate methods, principally for accuracy in describing water^26-28.

Point charge models do a very satisfactory job of reproducing the properties of bulk water, for which the parameters of the model are calibrated^4,5,8,29,30. It is less certain that they do a satisfactory job of reproducing the properties of water in cases in which the water-molecule interactions cannot be averaged as in bulk. Polarizable models are not useful for small clusters as they are calibrated for the average electric field in bulk water, which can be very different in a small cluster. Other difficulties often arise when new properties, such as phase changes, are being simulated. We are particularly concerned with clefts in proteins in this context. The importance of water in such clefts is suggested by recent work by Anishkin and Sukharev³¹ and by Beckstein and Sansom³², in which water in an ion channel cleft shows behavior that is perhaps surprising, as it leaves a “vapor phase” with a water surface inside a hydrophobic part of a protein. Here, a small number of water-water interactions with a near vacuum surface might be a reasonably correct representation of the system. Accurate description of such systems requires inclusion of cooperative interactions among the water molecules of the cluster, which in turn needs explicit representation of the forms of hydrogen bonding among the molecules. Point charge models, by their definition, do not change when the surroundings change. Only with Car-Parinello quantum MD (CPMD) is it possible to take such effects into account, or to allow a proton to transfer to another molecule. However, CPMD requires such large computer resources that it cannot simulate systems over about 200 atoms. Proton transfer is required for a wide range of important biological processes. A procedure equivalent to Car-Parinello has been used for the species H₅O₂⁺ and H₃O₂^-33. The study of cooperative interactions in water clusters is of sufficient interest that work continues to appear on this subject; the eventual result will be a potential that is simple enough to use in a simulation, but still includes the cooperative effects.

Calibration of a hydrogen bond potential will be aided by spectroscopy. In order to reach this goal, it will be necessary to study not only clusters, whether optimized or not, but to move to studies as a function of distance and angle. Our procedure is a step towards a usable hydrogen bond model. We also show how the energy of several types of donor and acceptor arrangements varies with bond distance and angle.

Surfaces are another type of system in which these effects are important, and surfaces bounding aqueous solutions in turn are important for most of biology. Hydrogen bonds in high electric fields require still more detailed treatment³⁴, but even at low fields calculations of surfaces give results that are not always in agreement with experiment. Experimental results may show that the H-bond network at a surface fails to survive intact. In fact there is a quite large literature on water at various types of surfaces, especially metal surfaces, showing water that has increased (usually) density, and other rearrangements, sometimes in the first layer only, sometimes for as much as three layers. In some cases, as with brushite, there are two separate arrangements of water at the surface³⁵. Even simulations using traditional potentials show differences in composition of surface layers, compared to bulk³⁶. Our earlier work on MC simulations of water in pores, which included high electric fields and polarizable potentials, also showed changes in ordering and density ^37-39. Somewhat similar results were obtained by Guidoni et al ⁴⁰. Other groups have shown various effects at surfaces, including biologically interesting surfaces. Experimentally, for example, α-hemolysin, a large bacterial channel, changes its permeability with pH, apparently because, when the channel is charged, water is strongly hydrogen bonded to the channel wall⁴¹. Experimental evidence exists for unusual behavior of water near surfaces, and standard simulations do not always adequately reproduce the experimental behavior. The importance of the solvent environment for the stabilization and conformation of peptide function is emphasized in a recent simulation study by Johnston et al of three different environments of channel forming peptides ⁴². In this study classical potentials are used, but the structure of the peptides depends strongly on the solvation. Changing the potential is equivalent to changing the solvent, as the solvent is included in the simulation in the form of its potential. The changes we discuss here may be more subtle than those of that simulation, but still make a significant difference. Earlier work by Scheiner and coworkers also considered many aspects of hydrogen bonding, including proton transfer along water wires (not as simulation). Much of this was reviewed by Scheiner in the context of kinetic isotope effects⁴³. He has also considered cationic oligomers of water⁴⁴. Most relevant is a study primarily directed at methyl substitution, in which the electron density was calculated, and the Mulliken electrical charges on atoms obtained and related to the hydrogen bonds ⁴⁵. Much of this work was aimed at answering somewhat similar questions to those we address here, although the use of Mulliken charges suggests that the quantitative results may be of limited accuracy. We are concerned with the relation of neighboring water molecule hydrogen bond donor and acceptor molecules to the energy, charge, and other properties of the hydrogen bonds. The problem does not appear to have been previously treated from this point of view. Cooperativity or non-pairwise additivity in clusters has been shown to be important for other properties, including simulations of the liquid state⁴⁶, and infrared spectra⁴⁷ It is of interest to note that Kirchner⁴⁶ has demonstrated that B3LYP does as well as MP2, provided a good basis set is used, and does better (or less badly), if a smaller basis set is used.

In recent work we found that the hydrogen bonds of a system of four acetic acid molecules and six waters had rather simple and surprising bond-length vs electron density, and bond length vs energy, relations ⁴⁸. This time we seek to understand more than the charge density at the bond critical point (bcp) that is defined in the Atoms in Molecules (AIM) method of Bader⁴⁹. We previously focused primarily on the bond properties that could be described in terms of the electron density, and did not examine the variation in the bond energy, our first property of interest.

We have tested clusters consisting of water molecule pairs with zero to six neighbors, using density functional calculations. The central hydrogen bond in each pair has a certain set of properties (energy, charge, bond length, electron density in the bond). Furthermore, the charge distribution on the atoms of the water molecules, and the dipole moments, are of interest in themselves. These properties of the bond and of the molecules also change as additional water molecules hydrogen bond to the original pair.

We have studied all 36 possible sets of neighbors as a function of oxygen-oxygen distance of the two central molecules to determine these properties with reasonable accuracy (when two donors, or two acceptors, appear on a single central molecule, they are counted as part of a single set, since they are equivalent by symmetry; otherwise there would be 2⁶, or 64, sets. The correct count of 36 is given in the Methods section). There are significant differences in the equilibrium bond distance, and even larger differences in the energy of the hydrogen bond. The energy differences would matter greatly in MD or MC simulations. Short hydrogen bonds are stronger, and have some covalent character; then the hydrogen bonded pair shows a slightly polar character, in that a small charge is transferred between donor and acceptor molecules. The fact that shorter bonds are stronger is not a new finding; there is a substantial literature referring to short strong hydrogen bonds (SSHBs)^50-52. They have also been studied experimentally. Here, we have studied H-bond properties using several tools: AIM, (Bader⁴⁹), Natural Bond Orbitals (NBO⁵³), and the energy and geometry of the bonds. In addition to non-additivity of energy, intermolecular charge transfer (something not normally considered for neutral clusters), bond length and intramolecular charge distribution depend on the same factors.

METHODS

1. Clusters

The clusters were set up with a central pair, donor and acceptor, of water molecules, with a hydrogen atom from one along the line connecting the two oxygen atoms. The O_a – O_d – H_d (sub-a: acceptor, sub-d: donor) angle is approximately 3.4°, with the H_d being the hydrogen distant from the acceptor. This pair was optimized under the following constraints:

1. all four OH covalent bonds were the same length

2. the two intramolecular HOH angles were equal (105.4°)

3. the dihedral angle defined by the acceptor water oxygen and the three atoms of the donor molecule was set equal to zero.

This pair, optimized with constraints i) to iii), formed the template for the neighbor pairs, which were added to form the other clusters. The same OH bond distance, and water molecule angles were used; there could be a maximum of six “neighbors”, two donors and two acceptors each, with the central pair forming each other’s first donor or acceptor. Each “neighbor” was aligned with respect to one of the original molecules at a distance and angle that was appropriate to an isolated pair, using the constrained optimized results.

2. Cluster definition

The clusters were defined by the number of donor and acceptor hydrogen bonds formed by each of the two central water molecules. The donor of the central hydrogen bond can donate one more hydrogen bond, and have up to two acceptor bonds. The acceptor of the central bond can be the donor for 0, 1, or 2 bonds, and the acceptor for 1 or 2 (the first bond from the other water in the pair counts as 1, so zero is not possible). Thus, an isolated pair can be designated 1001, where the first 1 indicates the number of donor hydrogen bonds of the donor (there being only the one donor hydrogen bond in the water pair). There is a zero in the second place, as there are no acceptor hydrogen bonds on that oxygen (no other water molecules are available to be the donors). 3. Similarly, the acceptor of the pair is not a donor to any acceptor, so the third digit is zero. The fourth digit is one, as the acceptor of the pair accepts the one central hydrogen bond, and only that one. Added “neighbor” molecules can be donors or acceptors, and the four digit index is adjusted accordingly. For example, the four digit index 1221 means that the donor water oxygen donates only the single hydrogen bond to the other central water (1^st digit), but it accepts two from other water molecules (2^nd digit); the acceptor molecule donates two to other water molecules (3^rd digit), but has only the one accepted hydrogen bond (4^th digit).

This notation is another way to see that there are a total of 36 possible sets, as mentioned previously (the first and last digits can be 1 or 2, the two middle digits 0, 1, or 2, for a total of 2 × 3 × 3 × 2 = 36 possibilities). A similar notation has been introduced by Ohno et al⁴⁷.

Clusters of two types, constrained and unconstrained, are used in the calculation. We define the two types of cluster in Table I, Figure 1, and the succeeding paragraph. In the end, we found little difference in the two types of cluster, but it was necessary to prove this by explicit calculation.

TABLE I.

Z-matrix showing bond lengths, angles, and dihedrals for the 2222 cluster; atom labels are as shown in Fig. 1, below this Table. Values of distances, angles, and dihedrals are below the Table.

A: Initial pair Z-matrix:
water		Z-Matrix
1	Acceptor of central hydrogen bond	O1
		H2	O1	R1
		H3	O1	R1	H2	a1
5	Donor of central hydrogen bond	O13	O1	oo	H3	a3	H2	d3
		H14	O13	R1	O1	a2	H3	d2
		H15	O13	R1	H14	a1	O1	d4
B: Other water clusters:
1	Acceptor of central hydrogen bond	O1
		H2	O1	R1
		H3	O1	R1	H2	a1
2	Neighbor: acceptor for 1st water	O4	O1	Oo	H2	a2	H3	d4
		H5	O4	r1	O1	a3	H2	-d2
		H6	O4	r1	H5	a1	O1	d3
3	Neighbor: acceptor for 1st water	O7	O1	Oo	H3	a2	H2	d4
		H8	O7	r1	O1	a3	H3	-d2
		H9	O7	r1	H8	a1	O1	d3
4	Neighbor: donor for 1st water	O10	O1	Oo	H2	a3	H3	d3
		H11	O10	r1	O1	a2	H2	d2
		H12	O10	r1	H11	a1	O1	d4
5	Donor of central hydrogen bond1	O13	O1	Oo*	H3	a3*	H2	d3*
		H14	O13	r1	O1	a2*	H3	d2*
		H15	O13	r1	H14	a1	O1	d4*
6	Neighbor: acceptor for 5th water	O16	O13	Oo	H15	a2	H14	d4
		H17	O16	r1	O13	a3	H15	-d2
		H18	O16	r1	H17	a1	O13	d3
7	Neighbor: donor for 5th water	O19	O13	Oo	H14	a3	H15	d3
		H20	O19	r1	O13	a2	H14	d2
		H21	O19	r1	H20	a1	O13	d4
8	Neighbor: donor for 5th water	O22	O13	Oo	H15	a3	H14	d3
		H23	O22	r1	O13	a2	H15	d2
		H24	O22	r1	O23	a1	O13	d4

Results of constrained optimization:

r₁, a₁ – water internal parameters

oo, a₂, a₃, d₂, d₃, d₄– hydrogen bond geometry parameters

All values: r₁=0.96413002, a₁=105.40080101, oo=2.90045756, a₃=1 14.12081154, d₃=125.98640241, a₂=108.80066074, d₂=1 19.34653902, d₄=0.

Use the results of Table IA to create the remaining clusters. For the maximum cluster, with each central molecule having 2 donors and 2 acceptors, the parameters are given by the Z-matrix:

Fig. 1.

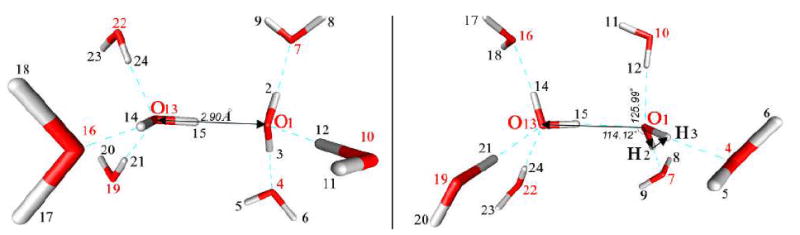
A 2222 cluster (maximum number of neighbors). The O – O distance is shown as 2.90 Å, and the HO---O (HO from the acceptor molecule, latter O is the central donor oxygen) angle as 114.12°. The dihedral angle formed by the central acceptor water plus the central donor oxygen is 125.99°. The remainder of the geometry is given in Table I.

DEFINITION OF A Z-MATRIX

The Z-matrix gives the positions, angles, and dihedrals of the atoms in the system in terms of the positions of atoms defined on lines above that for the atom being defined. The first column gives the atom being defined, the second another atom, the third the distance between them, the fourth another atom defined earlier, the fifth the angle formed by those three atoms, the sixth another atom defined earlier, the seventh and last the dihedral formed by those four atoms. The first three rows are incomplete, as insufficient atoms have been previously defined. The first three atoms are the “anchor” that sets the positions of all others.

Fig. 1 shows a 2222 cluster with the constrained values for certain angles and distances. The internal coordinates in the cluster are prepared by placing them in a Z-matrix, as shown in Table I. The Z-matrix contains the results of the operations described above in Section 1, and in this Section. These values were used as the input to the calculation.

1) Variables that were scanned are marked by asterisks

Fig. 1 illustrates the 2222 cluster, and it and Table I give the initial values of the principal distances and angles. The constrained cluster was very close to the unconstrained cluster in all parameters: unconstrained bond lengths ranged from 0.9611 to 0.9699 Å, constrained value 0.9641 Å for all four O-H covalent bonds. The “unconstrained pair” was defined by taking the initial central pair, freezing all oxygens (2 to 8 oxygens), and optimizing the hydrogens only. These conditions produced the very limited ranges of distance and angle that are defined as unconstrained here. Bond angles were 105.21 to 105.61. (unconstrained), 105.40 (constrained); the dihedral defined as d4 above was frozen at zero for the unconstrained as well as the constrained dimer, but is in any case <1°. Variables were scanned with and without the constraints. This gives O – O distance 2.90056 Å vs. 2.90046 Å (constrained). The angle defined by the two donors and the H covalently bonded on the acceptor (a₃ above) was 114.08° vs 114.12° (constrained). The dihedral given by the two oxygens and the two hydrogens on the acceptor molecule (d₃ above) was 126.1° vs 126.0° on the constrained pair. Other results were also very close: Energy, -152.96350 H vs. -152.96306 H (constrained) (We use energy units of Hartrees (H), or millihartrees (10^-3 H, written mH) throughout this paper. 1 mH ≈ k_BT, where k_B = Boltzmann’s constant, T = temperature (K)), at approximately 300 K, where most simulations of biological interest are done. Electron density at bond critical point is 0.02464 vs. 0.02430 (constrained). Thus, the constraints are unlikely to have a serious effect on any conclusions, to better than 1%.

Although the unconstrained clusters were computed, the constrained values offer a reproducible set of conditions among all clusters, allowing more valid comparison. A wider range of values were found when the oxygens were not frozen, including cases in which some of the clusters were not completely stable. In the majority of the cases, the clusters changed little. However, that is not the point of this work, and we do not consider the fully optimized clusters further.

2). Clusters other than minimal (1001) and maximal (2222)

The remaining 34 clusters were generated by starting with the 2222 cluster and deleting molecules, so that the remaining molecules had the same coordinates as in the 2222 cluster. The deleted molecules were replaced by ghost atoms, keeping their orbitals in the calculation. This is further discussed under BSSE below.

Scans

The variables that were scanned were those marked by asterisks in Table IB, in the central donor rows: O – O distance, two angles, and three dihedrals. In all scans, only one variable at a time was scanned, with all others held constant at their optimized (for the isolated pair) values. The results showed that only O – O distance made a major difference. Cross terms were not investigated. The central oxygen-oxygen distance was scanned at 0.1 Å intervals, and the energy and other properties redetermined as a single point calculation at each position.

3). The O – O distance at the energy minimum was further defined by an additional scan of 40 points at 0.01 Å intervals; the minimum of the 0.1 Å scan was included in the range, although the range was not always centered exactly on the minimum. These energy values were also used for the computation of forces (see below). Scans were similarly performed on the O – H – O angle and on certain values of three dihedral angles, as shown in Fig. 1, which shows the 2222 cluster. Angles and dihedrals gave relatively small effects (<0.8 mH, exceeding 0.5 mH only near the end of the range) as a function of neighbors and of angles, as long as the angles did not grow beyond the level that continued to be hydrogen bonded. The angle and dihedral effects were small, over the range that was investigated, ±10°. For a₃, the effect was at maximum less than 0.00035H, around 1/3 k_BT (T=300 K), and no regularity was found. However, changes in a2 sometimes produced larger energy differences, sometimes double that of a2, making it marginally large enough to be of importance in simulations at room temperature; results will be given below. Similarly, each of the three dihedral angles was tested at five points, the optimized value, and that value ±5° and ±10°. Only d4, of the dihedrals defined here, exceeded the 0.0005 H threshold, and is included specifically in the results. The other two dihedrals did not quite reach 0.0003 H at 10°, and are omitted. In this manner, the entire plot of O—O distance vs. energy was generated (with the best H-bond angles, omitting second order corrections), as well as the other properties, as a function of distance, and of angles and dihedral angles.

4). Calculation method

Density functional calculations were done using B3LYP/6-311++G**. The Gaussian03 package⁵⁴ was used for all calculations. The charges on the hydrogens and oxygens were determined using NBO from Gaussian03⁵³; Atoms in Molecules (AIM) calculations were carried out for certain clusters, as a check on the other methods of determining charge.

The hydrogen bond energy is calculated as follows:

$${\mathrm{E}}_{\mathrm{WW}}(\mathrm{R})=\mathrm{E}(\mathrm{bond})-{\mathrm{E}}_{3.9}=\mathrm{E}(\mathrm{cluster})-(6{\mathrm{V}}_{\mathrm{c}}(\mathrm{pairs})+6{\mathrm{V}}_{\mathrm{vdW}}(\mathrm{pairs}))-{\mathrm{E}}_{3.9}$$ (1)

V_c is defined as the Coulomb energy between non-bonded pairs of molecules, with hydrogen bonds counted as bonds, V_vdW is the corresponding van der Waals energy. E_3.9 is the energy of the pair at O – O distance of 3.9 Å, at which distance the hydrogen bond is considered to have disappeared, making the hydrogen bond energy equal to zero. Therefore, the E_WW (R) defined by equation (1) is the difference in water-water interaction energy of the hydrogen-bonded central pair of molecules at an oxygen –oxygen distance R, from the energy at 3.9 Å. and V_vdW is the total van-der-Waals energy of all nonbonded water pairs, calculated using TIP3P-model potential parameters. Because the contribution of van der Waals energy is so small (<2%), it makes little difference if the values are somewhat approximate for this term. Although the distances between pairs of molecules hydrogen bonded to either one of the two central molecules is constant, the charges change slightly with distance between central molecules, so the energy pair terms, even between molecules at a constant distance and orientation with respect to each other, will change as well. Eqn 1 also makes these corrections. The corrections for the Coulomb energy of pairs hydrogen bonded to different water molecules, as the distance changes between the central water molecules, amounts to several mH. The corrections accompanying charge changes on water molecules both bonded to the same central water molecule, thus at constant distance from each other, are much smaller, less than 0.5 mH.

The van der Waals terms, as estimated from the TIP3P parameters, follow a similar pattern, and are very small. Molecules that are bonded to the same central water, and which therefore remain at constant distance as the central water-water distance changes, have constant van der Waals interactions with each other as the central pair separates; these interactions will be removed by subtracting E_3.9. The van der Waals correction between molecules on opposite sides of the cluster is already small at closest approach, and diminishes from there. However, these corrections are included in the computation; the TIP3P accuracy is adequate for the small correction terms. The net energy from eqn 1 subtracts the energy of all interactions with pairs other than the central pair. The energy shown as the hydrogen bond energy is thus the total interaction energy in the cluster less the energy of the pairwise interactions not involving the pair of molecules forming the hydrogen bond of interest. Any self-energy terms for water molecules are independent of distance for a given class of molecules, so subtracting E_3.9 removes this contribution for each cluster. As a result, the differences in energy with distance between the central oxygens are meaningful for the central hydrogen bond.

Wiberg bond indices found using NBO are the sum of squares of off-diagonal density matrix elements between atoms. They function as a nominal bond order. The Wiberg indices give a measure of the bond interaction between two atoms; for our purposes it shows the extent of bond overlap associated with the central hydrogen bond—the bond is not purely electrostatic.

5). Basis Set Superposition Error (BSSE) and ghost atoms

Because the hydrogen bond energy is determined as a small difference between two large energies, the BSSE is still >10% of the hydrogen bond itself (both constrained and unconstrained for a single pair). Therefore, in calculating with neighbors, all calculations start from the 2222 configuration, and preparation of smaller clusters is accomplished by deletion of the neighbor molecules, leaving ghost atoms; hence, all orbitals remain. Therefore, the BSSE is also subtracted, and no further correction is needed for this, making all results comparable. To estimate the actual value, the following calculation can be used: The energy of the 1001 cluster is computed, with all the remainder of the 2222 cluster replaced by ghost atoms. The sum of the energies of the cluster with each of the 1001 water molecules separately replaced by ghost atoms is subtracted. The difference is - 0.0077417 H. This is compared with the same calculation on 1001 without the ghost atoms of the remainder of 2222—that is, just two water molecules, in the same geometry. The water molecules that are removed from 1001 then have exactly the same energy as that of a single water molecule. Subtracting the 2 independent water molecules from the isolated 1001 pair gives -0.0092697 H. The difference, 0.0014720 H, would be the BSSE, were it not removed by using the ghost atoms. In all cases, the constrained values were used for water geometry, so that the results are consistent.

6) Atoms in Molecules (AIM)^49,55 and Natural Bond Orbitals (NBO⁵³)

AIM has been used to obtain the properties of the bond (principally bond critical point (bcp), and electron density at the bcp). Other properties, such as the Laplacian, were not as informative, and are not discussed further. Software used for the purpose was obtained from the Bureau fur Innovative Software⁵⁶.

7) Force

The force along the hydrogen bond at the energy minimum for each case is determined by fitting a parabola to the 11 energy values consisting of the energy minimum, and five points at 0.01 Å intervals on either side, for a total distance of 0.05 Å on each side of the minimum. The derivatives could then be determined analytically from the parabolas, with the 2^nd derivative giving the Hooke’s Law constant.

8) Dipole moments and charges

The dipole moments of the central water pair were calculated for each of the 64 clusters (although 24 of them are almost redundant by symmetry, slight shifts in angle of a nearest neighbor break the symmetry. This may make a small contribution, in principle, so all 64 were calculated—the shift is not large enough for further discussion, the maximum value being 0.05 D). Charges on the central water atoms, from Gaussian03, were used in the calculations. The dipoles are computed from the integrated wave function from Gaussian03, and the charges are found using NBO.

RESULTS AND DISCUSSION

The results are best expressed in figures showing the energy and other properties that were calculated. Figure 2 has the key finding, concerning energy, determined from eqn 1:

Fig. 2.

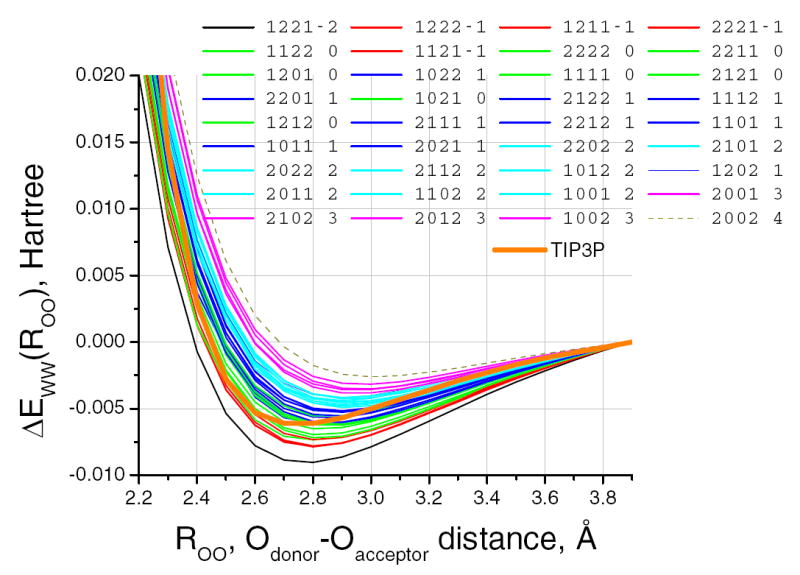
All 36 energy-(O – O) distance curves for the total set of neighbor types (four-digit number-see text) are shown. Colors represent neighbor indices: The final single digit numbers=K₁ - K₂ - K₃ + K₄ = K_N, where K_i (i= 1,2,3,4) is the number of neighbors in the corresponding 4 digit index; call K_N the net index. Curves with the same K_N values group together (same color means same K_N). The energy values increase monotonically with K_N; K_N= -2 (black) is lowest energy, +4 (dotted) weakest, with each color change at an increase of 1 in K_N. The heavy yellow curve shows the TIP3P model result, with no dependence on neighbors, and a somewhat different shape of potential-distance curve from the quantum calculations for any set of neighbors. E_WW (R) for all clusters is set to zero at 3.9 Å, as defined in eqn 1.

The slope of the curves in Fig. 2 differs; therefore, the forces on the molecules differ. This is one key to understanding why, and how, these would behave differently in a MD simulation. Note that the correlation is, to first order, with the index K_N, not individual structures. We group the curves by K_N value, as the total range is approximately 6mH, while no single K_N spreads energy at the minimum over 1 mH (although it is close). Taking the energy for a given K_N as the average, we will always be within 0.5mH. We shall see below that charge transfer is similarly correlated. This is therefore a step toward a potential for hydrogen bonds as a function of neighbor bonds, in which K_N is the key index. The TIP3P result is good on average, in bulk, but would not reproduce the particular behavior—energy, forces—in a system with a limited number of nearest neighbors. It is necessarily the case that the same would be true of any point charge model. A polarizable model would do little better, in that it depends on the electric field, which in turn varies drastically (by a factor of close to three) in a local cluster. Thus, it differs from the bulk average for which such potentials are parameterized, making it not useful to compare the results from such a potential. Therefore, in simulations involving limited size clusters, we see strong evidence that the relation of energy as well as force to numbers of neighbors of each type should be included in the water potential. In this study, only water is considered as a neighboring species, but in proteins there are carbonyls, carboxylates, amines, and other groups as well. While these have been calibrated for TIP3P water with the OPLS potentials, cooperative effects would still not be represented. The variation of hydrogen bonds in differing conditions might be as great as that of water with different numbers of water neighbors.

The energies at the minima in Fig. 2 cover a range equivalent to approximately 6 k_BT near room temperature. In MD, the force as well as the energy matters. For the TIP3P curve, in the range of 2.8 to around 3.2 Å, where the bonds have their greatest effect (counting the number in that range as well as the energy) force is about 0.0067 H Å^-1, while for the others it ranges from approximately 0.004 to 0.008 H Å^-1, to 0.010 for the 1221 cluster) meaning that the water molecules could move more or less rapidly than the average. The angle dependences are much weaker, as noted in the methods section. However, one angle, a2, and one dihedral, d4, produce energies differing by slightly over ±0.5 mH, making them just large enough to take into consideration (while it might seem arbitrary to set a threshold of 0.5 mH, it is necessary to set some threshold at a reasonable value. If the other angle and dihedrals were included, they would produce similar results, but with a little more scatter and a little less significance. We characterize the angles by an equation of the form:

$$\mathrm{E}(\mathrm{D})={\mathrm{C}}_1\mathrm{D}+{\mathrm{C}}_2{\mathrm{D}}^2$$ (2)

where in this case D can be either an angle or a dihedral. The equation was fitted to the five points (D=-10°, -5°, 0, 5°, 10°, with 0° being the value at the minimum), for each of the clusters. The plots are C₁ vs C₂ (normalized by the average value of the plot). Again, we see that K_N is a valuable parameter in classifying the points, but the energy differences here are much smaller (roughly by an order of magnitude).

The properties of the hydrogen bonds, whether determined as bond order, electron density at the bond critical point, energy, or the index K_N, all have a similar relation to O – O distance, as shown in Fig. 4. There are several ways to show how the bond distance, energy, electron density, and bond length are related; the key point is that the relation is dependent on the arrangement of neighbors of the hydrogen bonded pair of water.

Fig. 4.

Properties of the clusters as a function of the O – O distance of the central pair at the energy minimum; the minimum covers 0.23 Å, from the shortest to longest bonds, while the energy varies by approximately 6 mH, or about 6 k_BT near room temperature:

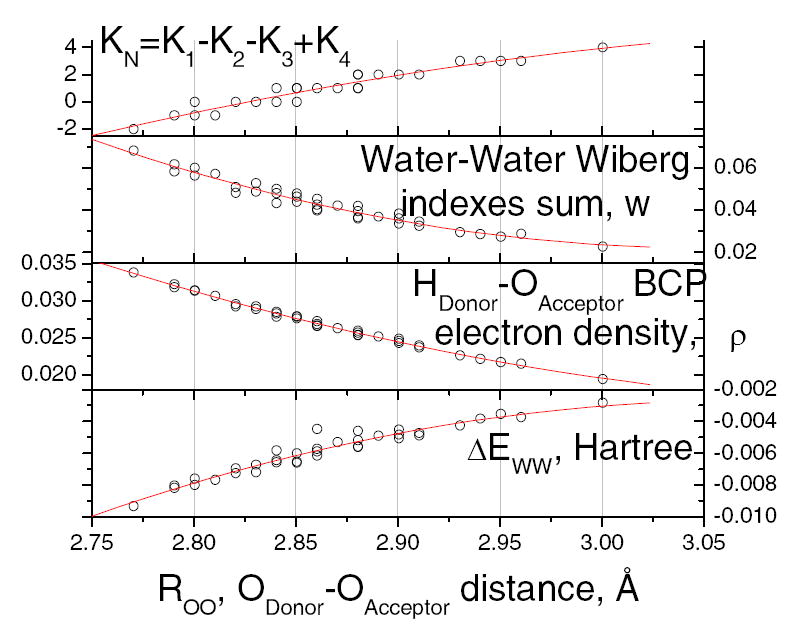
1. K_N = K₁ – K₂ – K₃ + K₄, the net index; the other properties appear to correlate with this index more closely than with the individual indices.
2. the sum of Wiberg bond indices for all pairs of the central pair atoms (sum of 3 × 3 = 9 indices, with 3 atoms on each molecule)
3. the electron density at the bcp for the hydrogen bond (calculated from AIM).
4. The energy of the system relative to that at central O – O separation of 3.9 Å. For the parabolic fits to these results, see eqns. 3a-c and 3e, with two other quantities represented by eqns 3d and 3f. Note the correlation with K_N in particular carries through to all the properties; the K_N values can be read from the figure for the other three properties shown (extend a vertical line down from a). There are four cases in which there is overlap of K_N values at the same bond distance, and the other properties tend to overlap at these distances also.

Eqn. 3 gives six such relations. All are fitted parabolas. Define R_d = R_OO – 2.9 Å, (2.9 Å is the equilibrium distance for the 1001 cluster) where R_OO is the oxygen – oxygen distance of the central pair, for each of the single point calculations in the scan. Then we can express: 1) the hydrogen bond energy at the minimum, relative to the energy at 3.9 Å, ΔE_WW (3.9 Å=full separation, as shown in Fig. 2) 2) the electron density at the bcp ρ (from AIM), 3) w, the sum of the Wiberg indices for the six atoms of the two central molecules 4) theWiberg index for the central hydrogen bond alone, w1, 5) the net index K_N, and 6) the Hooke’s Law force constant F at the minimum distance determined within 0.5 Å of the energy minimum,

$$\begin{array}{ll}\mathrm{\Delta }{\mathrm{E}}_{\mathrm{WW}}=-0.00474+0.2418{\mathrm{R}}_{\mathrm{d}}-0.06967{\mathrm{R}}_{\mathrm{d}}^2(\mathrm{Hartrees})& (3\mathrm{a})\\ \text{ρ}=0.02444-0.0585{\mathrm{R}}_{\mathrm{d}}+0.0977{\mathrm{R}}_{\mathrm{d}}^2& (3\mathrm{b})\\ \mathrm{w}=0.03502-0.17074{\mathrm{R}}_{\mathrm{d}}+0.55466{\mathrm{R}}_{\mathrm{d}}^2& (3\mathrm{c})\\ \mathrm{w}1=0.0238-0.13417{\mathrm{R}}_{\mathrm{d}}+0.45388{\mathrm{R}}_{\mathrm{d}}^2& (3\mathrm{d})\\ {\mathrm{K}}_{\mathrm{N}}=1.97106+23.69411{\mathrm{R}}_{\mathrm{d}}-38.72767{\mathrm{R}}_{\mathrm{d}}^2& (3\mathrm{e})\\ \mathrm{F}=0.04271-0.16497{\mathrm{R}}_{\mathrm{d}}+0.11094{\mathrm{R}}_{\mathrm{d}}^2(\mathrm{Hartrees}/{\AA }^2)& (3\mathrm{f})\end{array}$$

Since there is little interaction between atoms that are neighbors but are not covalently bonded, the index values are small; however, they are appreciably different from zero, and the w1 index suggests some significant bond overlap for the hydrogen bond. The other quantities are given in Fig. 4. R_d is at most ±0.13 Å, but the curvature is nevertheless appreciable. The Wiberg bond index for the hydrogen bond is roughly 2/3 of the sum of these indices for the 9 pairs of atoms at all separations. Fig. 4 suggests also the limited level of scatter in the relations.

Charge transfer between the central water molecules also occurs. Fig. 5 shows the charge on the central donor molecule as the central pair and its associated neighbors are separated, for each group of possible neighbors. In this plot, the clusters are shown according to their first two (donor) indices. This is a result that cannot be reproduced by any of the standard point charge models, for which the charges are fixed, with net charge zero. The charge includes transfer to neighbors on the same side of the cluster, which is responsible for the non-zero value of the charge at large separations. The sum of the charges on the donor side, and on the acceptor side, does go to zero as required at large separations.

Fig. 5.

a) Charge on the central donor molecule (for definition of charge see eqns. 4, with the text below) for all 36 clusters, grouped by donor molecule indices. Acceptor molecule indices for each curve are not shown, because they group tightly enough that they are not important. Note that the charge on the molecule when the two half clusters have separated at large distance is approximately 0.013 to 0.014 charges for an increment of one in X, and about -0.010 to - 0.012 for an increment of 1 in W. The charge on the central molecule does not go to zero at infinite separation (except fortuitously, for the 21 YZ clusters), because of charge transfer within the half cluster. The charge transferred for short bonds is much greater, which is not a surprise. Even at large distance, the difference between having the central molecule being a donor twice and never an acceptor (20YZ), and being an acceptor twice and donor only the one time required by definition (12YZ), is >0.03 electronic charges, which is appreciable.

b) Charge on the half clusters : This time, the charge must go to zero at large distances. The curves appear to cross, because of conflicting effects of donor and acceptors. However, the lowest curve (largest negative charge) again goes with the 20YZ (double donor, no acceptor) cluster, the least negative is the 12YZ cluster. The difference in charge at 2. 9Å is >0.01 e, large enough to be important.

Forces are calculated as Hooke’s Law constants from the parabolic fit near the energy minimum, and are also well ordered by the index K_N; the strongest bond, and the shortest, has K_N=-2 (i.e., the 1221 cluster), with K_N=-1 grouped close behind, and a reasonably well ordered progression on to +4 (2002 cluster). The ordering is not perfect, with three clusters, with indices 22xx, having slightly larger constants than the equation gives.

What is surprising is the range of the Hooke’s Law constants, from 0.0068 H Å^-2 (1221) for the strongest, down to 0.0028 H Å^-2 for the weakest (2002). As the force constants control motion in a simulation, this is a matter of some importance.

Finally, we have the dipole moments, shown in Table II. The charges on the central donor, in Fig. 5, obtained from NBO calculations, show a clear relation to the donor half of the cluster, and a much weaker relation to the acceptor half; only at short distances is the Y, Z dependence sufficient that there is appreciable difference in charge. The charge on the donor water of the central pair in a cluster can be described, at a central oxygen-oxygen distance of 2.9 Å, by eqn. 4a:

TABLE II.

Contribution of each molecule to the dipole moment of the cluster, above that of the isolated molecule, for each type of calculation; first and second row, donor to the acceptor, third, acceptor to the acceptor, fourth, donors to the donor, fifth and sixth, acceptors to the donor. Only the magnitude of the vector contribution is given. Columns are in the order given in the text, with unmodified TIP3P not shown.

Molecule As in caption	No Ghost atoms	Ghost atoms	Ghost atoms OH reoptimized	Modified TIP3P OH reoptimized
1	0.611	0.717	0.724	0.002
2	0.611	0.717	0.724	0.002
3	0.588	0.668	0.667	0.004
4	0.582	0.710	0.716	0.002
5	0.634	0.730	0.738	0.005
6	0.634	0.730	0.738	0.005

$$\mathrm{Q}=\sum \mathrm{i}{\mathrm{\delta }\mathrm{Q}}_{\mathrm{i}}$$ (4a)

with

$$\mathrm{\delta }\mathrm{Q}=-0.0127+0.0013(\mathrm{W}-1)-0.0020\mathrm{X}-0.0024\mathrm{Y}+0.0008(\mathrm{Z}-1)$$ (4b)

These quantities are defined as follows:

1. The δQ_i of eqn. 4a is determined from the charge transfer from the donor member of the central dimer to the (up to) four neighbors of that molecule. The resulting charge on the donor water is Q, and is the quantity shown in Fig. 5a.

The δQ of eqn 4b is the charge transfer between the two members of the central dimer. This is the same as the total charge transfer between the donor half of the cluster and the acceptor half. This is also the charge transfer Q shown in Fig 5b

2) Dipoles

Dipoles are computed by integrating the wave function, hence by a method nominally independent of the computation of the charge (of course the two are related, but one is not found directly from another). We are primarily concerned here, not with the total dipole moment, but with the difference in the dipole due to the cooperative effects we are studying. Therefore, define

$$\mathrm{\delta }\mathrm{\mu }={\mathrm{\mu }}_{\mathrm{cluster}}-({\mathrm{\mu }}_{\mathrm{dimer}}+{\sum }_{\mathrm{n}}{\mathrm{\mu }}_{\mathrm{n}})$$ (5)

In other words, δμ is the vector difference between what the cluster would have for a dipole moment if there were no cooperative interactions, and what it actually has. The values are calculated as vectors, and then averaged over all 64 possible clusters. The isolated molecule contributions are subtracted in δμ.

Table II shows the interesting result that the magnitude of the vector contribution of an added water molecule is roughly the same for all the possible water molecules that can be added to the central pair, on average. The computation has been done for the following cases: 1) Add water “physically” (i.e., when the water is not present, the wave functions are not left behind) using constrained clusters 2) Use ghost atoms when the neighbor water is not present, again using constrained clusters. This removes BSSE. 3) Relax the constraint to the extent of reoptimizing the OH distance in the central hydrogen bond, and use ghost atoms again. 4) Use TIP3P, which should make the cooperative effect zero. This is not shown in the Table; the actual values were about 10^-6, too small to show in the Table. That value gives the error, including round-off error, in the suite of programs used to get these values, and served as a check 5) Modified TIP3P, with the central OH bond optimized. These results were of the order of 10^-3, and are shown.

The average is computed by determining δμ for each cluster

$$\mathrm{\delta }\mathrm{\mu }={\sum }_{\mathrm{i}}^6{\mathrm{k}}_{\mathrm{i}}{\mathbf{x}}_{\mathbf{i}}$$ (6)

where the k_i are 0 or 1, depending on whether the molecule to which it refers is present or absent, the x_i are the vector contributions of each water molecule. The result is fitted to allow the total cluster to have the correct value of δμ, giving the magnitudes of the x_i. The result is averaged over all 64 clusters (each k_i has two values, hence there are 2⁶ total values). It is this average that is shown in Table II

Clearly, the dipoles are somewhat affected by BSSE, so the correction should be included. Also, the symmetry of the donors on the acceptor, and of the two acceptors on the donor, is as expected (doing them separately both takes account of the possibility that the slight asymmetry of the angles may matter—evidently, it does not—and acts as a check on the calculation). Were any of the differences in these cases large, it would have shown an error. The differences are of the order of 10^-5, which shows that the angle asymmetry can be neglected, and that no error in the program can be found from this part of the calculation. What is especially important in this set of results is the fact that all the molecules make a similar contribution, suggesting that the non-linear effects, although much too large to ignore, will not be too difficult to include in a fairly simple set of parameters in a new potential.

Consequences for molecular dynamics simulations

For MD simulations, these relations suggest a major readjustment in treatment of water in limited clusters. The extent to which such clusters are a good description of water molecules bounded as, for example, in proteins, remains to be demonstrated, as the clusters we have studied exist in vacuum. However, it would be surprising if water in small bounded cavities behaved like bulk water; it is possible that certain groups, especially carboxyl or hydroxyl, could partially replace water. Other groups, such as amines, or charged groups, might produce results even more different from bulk water than vacuum does. The OPLS³ potentials are designed for proteins with TIP3P water, but again cooperative effects are not included in any point charge model. The differences will include deciding whether the water is likely to remain bound or will change positions rapidly, and whether the hydrogen bonds form a barrier to solutes, or permit passage. Temperature dependence will also be altered, as will the work done in moving a solute through the water. Further work is required to make it possible to use potentials consonant with these results in a simulation. In particular, methods for tracking the number and type of nearest neighbors are being developed. In addition a consistent set of potentials for other atom types in molecules (with biomolecules of special interest) must be worked out. We have not mentioned charged clusters at all here. However, work is underway to study these, as well as to keep track of individual atoms, in order to make possible the simulation of proton transfer. When the entire system of potentials and other software is complete, it should be possible to simulate a system containing hydrogen bonds accurately, with the cooperative effects, and include in the simulation the exchange of protons, whether or not the species are charged.

CONCLUSIONS

Hydrogen bonds have been found to have significantly different bonding strength from that in bulk water in a type of small cluster that emphasizes the role of cooperative effects involving nearest neighbors. Energy, bond length, electron density at the bond critical point, force constants, dipole moments, and Wiberg bond indices are strongly correlated with the number and type of nearest neighbors. Forces that differ from those in bulk water would have significant effects on the results of MD simulations. Since the clusters were in vacuum, further work will be required to extend these results to proteins with small clusters of water in clefts or cavities. However, it is now clear that it is dangerous to ignore cooperative effects in simulations using point charge potentials under non-bulk conditions.

Fig. 3.

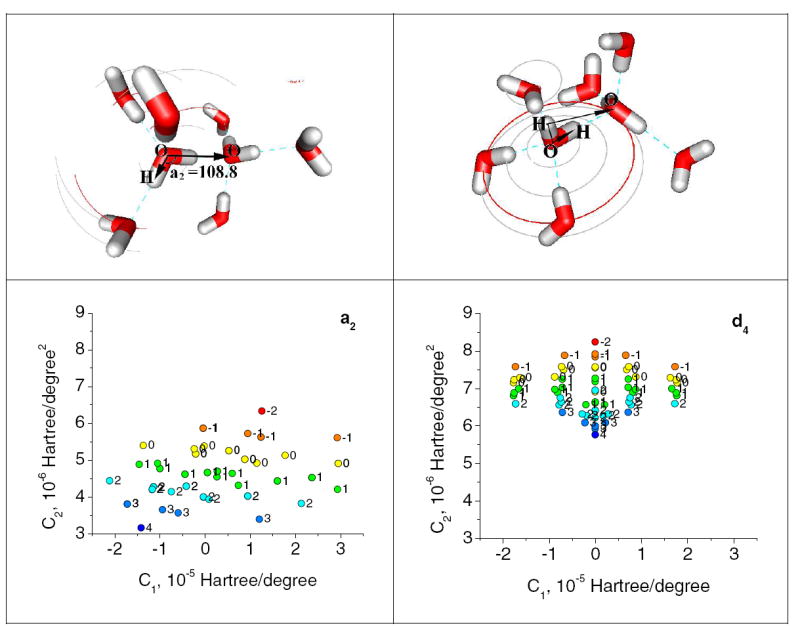
Angle a2 and Dihedral d4: The values of angle a2 and d4 shown as C₁ vs C₂ of eqn. 2. The top panels show a2 and d4 pictorially; the red arcs show how the oxygen atoms move, gray arcs the corresponding hydrogen atoms, when the angle or dihedral is scanned. The atoms that move do so as a rigid body. Those that do not move do not have arcs. The initial (zero) value of the O_a-O_d-H_d (sub-a= acceptor, sub-d=donor) angle D is 108.8°, of the dihedral is 0°. The points in the lower plots are shown in color according to K_N, and labeled with the K_N value. The energy scale of the two figures has been set up identically so that it is clear that the C₂ value, which provides the larger contribution to the energy, is larger for the dihedral (to get energy, multiply by (angle)², hence, at 10°, 100). We do not have an explanation for the fairly even spacing of the dihedral C1 values. The most obvious regularity shows that the smaller the K_N value, the larger the C₂ value.