Virtual Colonoscopy Screening with Ultra Low-Dose CT and Less-Stressful Bowel Preparation

Abstract

Computed tomography colonography (CTC) or CT-based virtual colonoscopy (VC) is an emerging tool for detection of colonic polyps. Compared to the conventional fiber-optic colonoscopy, VC has demonstrated the potential to become a mass screening modality in terms of safety, cost, and patient compliance. However, current CTC delivers excessive X-ray radiation to the patient during data acquisition. The radiation is a major concern for screening application of CTC. In this work, we performed a simulation study to demonstrate a possible ultra low-dose CT technique for VC. The ultra low-dose abdominal CT images were simulated by adding noise to the sinograms of the patient CTC images acquired with normal dose scans at 100 mAs levels. The simulated noisy sinogram or projection data were first processed by a Karhunen-Loève domain penalized weighted least-squares (KL-PWLS) restoration method and then reconstructed by a filtered backprojection algorithm for the ultra low-dose CT images. The patient-specific virtual colon lumen was constructed and navigated by a VC system after electronic colon cleansing of the orally-tagged residue stool and fluid. By the KL-PWLS noise reduction, the colon lumen can successfully be constructed and the colonic polyp can be detected in an ultra low-dose level below 50 mAs. Polyp detection can be found more easily by the KL-PWLS noise reduction compared to the results using the conventional noise filters, such as Hanning filter. These promising results indicate the feasibility of an ultra low-dose CTC pipeline for colon screening with less-stressful bowel preparation by fecal tagging with oral contrast.

I. Introduction

Colorectal carcinoma is the third most commonly diagnosed cancer and the second leading cause of death from cancer in the United States [1][2]. According to the American Cancer Society statistics (http://www.cancer.org/docroot/home/index.asp), it is estimated that 147,500 new cases will be diagnosed this year with 57,100 dying from the disease. Most colon cancers (more than 90%) arise from polyps over a 5 to 15 year period of malignant transformation, early detection and removal of the polyps can significantly reduce the risk of death. The American Cancer Society has recommended a colon examination every three to five years for people of age over 50. As of 2007, 41.8 millions of the 70.1 million average-risk adults of age 50 or older need colon screening, but less than 50% (20.9 millions) have been screened by any manner and only 13.5 millions have undergone the preferred “total colonic examination” with fiber-optic colonoscopy (OC). Patients are usually reluctant to take the OC procedure because it is invasive, time consuming, and expensive. The cancer is usually diagnosed at an advanced stage, after the patient has developed symptoms, explaining its high mortality rate.

Computed tomography colonography (CTC) or CT-based virtual colonoscopy (VC) is an emerging tool for colon polyp detection [3][4]. Since the introduction of reimbursed CTC screening at University of Wisconsin Medical Center, the number of patients screened by colonoscopy (OC or VC) has been more than doubled [5]. Although CTC is minimally or non-invasive and less stressful to the patient, CTC is not totally risk-free. The radiation in forms of X-ray exposure to the patient during CT scan could lead to adverse health effects in a later time of the patient’s life. By a recent survey, CT procedures account for as much as 60% of manmade radiation exposure to Americans due to its increasing use in diagnosis, treatment planning and follow-up examinations [6]-[8]. Sixty-two million CT scans are performed a year in the US, including at least four millions for children. This manmade radiation exposure could be a potential link to the increase of 1.5 to 2% cancer causes [9]. Minimizing the radiation risk to the patient, while maintaining satisfactory CT image quality, becomes urgent for colon screening with CTC.

Dose reduction for CT imaging can be achieved by acquiring projection data with low-mAs protocols. With a low-mAs acquisition protocol, noise due to fewer X-ray photons will degrade the CT image quality. In the past years, research effort on both hardware optimization and noise filtering on acquired data has made noticeable progress from normal dose scans (over 100 mAs levels) down to low-dose CTC scans as low as 50 mAs level [4]. Further decreasing the mAs level for ultra low-dose CTC scans (lower than 50 mAs) may induce streak artifacts in the reconstructed images if oral contrast solutions are used to tag the stool and colonic fluid because the contrast solutions absorb a noticeable amount of X-rays [10]. Therefore, more sophisticated noise treatment than a simple low-pass noise filtering is necessary. Several strategies based on local characteristic of projection data [11][12] have been proposed to reduce noise acquired with low mAs protocols. Recently a statistics-based framework of sinogram restoration followed by filtered backprojection (FBP) image reconstruction has shown promising results for ultra low-dose CT [13]-[18]. This framework is based on noise modeling of the projection data, where the noise modeling is similar to that of a statistical iterative image reconstruction approach. Difference between this sinogram restoration framework and the iterative image reconstruction approach is that the penalty or the smoothing constraint in the sinogram restoration framework is in the sinogram space while the penalty for the iterative image reconstruction approach is in the image domain. In our previous work [15], we have shown a similar performance between a statistics-based sinogram restoration strategy and a statistical iterative reconstruction algorithm in terms of image quality and detectability in low-contrast environment, where both methods seek the same solution of minimizing the penalized weighted least-squares (PWLS) cost function of the data distribution which was simulated from anthropomorphic digital phantoms. However, the iterative image reconstruction algorithm consumed a great computing power for volumetric CT and might not be practical for clinical use. For example, the reconstruction time for a routine clinical study consisting of several hundred slice images of 512×512 array size is at the order of hours by a currently available fastest PC platform. The sinogram restoration strategy is much more efficient (with more than ten fold reduction of computing time) and has the potential to be utilized in real-time clinical situations.

In this work, we performed a simulation study using patient CTC images to demonstrate a possible ultra low-dose CT technique for VC screening purpose. The ultra low-dose projection data or sinograms were simulated from the patient volumetric CTC images based on the noise properties of clinical CT projection data [14][19][20] and had a noise level equivalent or less than 50 mAs of a clinical low-dose scanning protocol. The simulated ultra low-dose sinograms were first processed by the statistics-based Karhunen-Loève domain PWLS (KL-PWLS) restoration strategy [13][15] and then the restored sinograms were reconstructed by a standard FBP algorithm (i.e., by the use of the ramp filter which was apodized with a rectangular window whose cutoff was at 100% Nyquist frequency). Promising results were obtained, demonstrating the feasibility of an ultra low-dose CTC pipeline for colon screening with less-stressful bowel preparation by fecal tagging with oral contrast.

II. Methods

A. Statistics-Based Sinogram Restoration for Ultra Low-Dose CT

The KL-PWLS restoration strategy [13][15] is a statistics-based algorithm that aims to estimate the ideal sinogram by minimizing the PWLS objective function in the KL domain,

$${\Phi }_l\left({\tilde{q}}_l\right)={({\tilde{y}}_l-{\tilde{q}}_l)}^{\prime }{\tilde{\Sigma }}_l^{-1}({\tilde{y}}_l-{\tilde{q}}_l)+(\beta ∕d_l)\tilde{R}\left({\tilde{q}}_l\right)$$ (1)

where l = 1,2,3, ${\tilde{y}}_l$ and ${\tilde{q}}_l$ are the l-th KL principal components of the noisy sinogram p and the ideal sinogram $\stackrel{‒}{p}$ (to be estimated) respectively, and ${\tilde{\Sigma }}_l$ is the diagonal variance matrix of ${\tilde{y}}_l$. Symbol ’ denotes the transpose operation. Notation d_l indicates the eigenvalue of the l-th KL component, β is a smoothing parameter which controls the degree of agreement between the estimated and the measured data via the penalty term $\tilde{R}\left({\tilde{q}}_l\right)$ which usually has a quadratic form of

$$\tilde{R}\left({\tilde{q}}_l\right)={{\tilde{q}}_l}^{\prime }\tilde{R}{\tilde{q}}_l=\frac{1}{2}\sum _i\sum _{m\in N_l}{w}_{im}{({\tilde{q}}_{i,l}-{\tilde{q}}_{m,l})}^2$$ (2)

where N_i indicates the nearest or first-order neighbors of the i-th pixel in each KL component along the bin (or x-) and view (or y-) directions (after the KL transform was applied along the direction of rotation or z-direction) in the sinogram domain and parameter w_im is equal to 1 for the first-order neighbors. This objective function (1) models the first and second statistical moments (i.e., the mean and variance) of the sinogram data and needs the knowledge on the relationship between the mean and variance. In our previous work [20], a non-linear relationship between the mean and variance was found, i.e., equation (3) below, which reflects the non-stationary noise property of low-dose CT and specifies the weights or the diagonal elements in matrix ${\tilde{\Sigma }}_l$ in the PWLS criterion. It is noted that the first and second moments play the essential role for noise modeling and treatment. The minimization of the cost function (1) can be computationally efficient. Furthermore, the decomposition by KL transform reduces the correlation between the components in the projection space, hence realizing better estimation potential than data matching via equation (1) in raw sinogram space.

In this work, three slices of the simulated ultra low-dose three-dimensional (3D) sinogram data were selected to perform the KL transform, i.e., one slice above and one slice below the concerned slice along the z-direction in the sinogram domain. The KL transform matrix A can be obtained from the selected neighboring slices of the sinogram data through the covariance matrix K_t of 3×3 size according to K_t A’ = A’D, where matrix A’ is the transpose of matrix A, D is the diagonal matrix of 3×3 size with elements being the eigenvalues of the KL components. The obtained KL transform matrix A is also of 3×3 size and represents the eigenvectors of the KL components. The KL transform models the correlation among neighboring slices of the sinogram data (i.e., along the axial direction of the helical scans) and, therefore, provides a data-adaptive penalty role. The goal of minimizing the objective function is to find an optimal solution based on the data statistics and data correlation. After the KL transform, the chosen neighboring slices of the sinogram data were decomposed to three independent KL principal components. Each KL component is associated with a KL eigenvalue, which reflects a corresponding signal-to-noise ratio (SNR) of the KL component. A larger KL eigenvalue corresponds to a higher SNR, and this information provides a mechanism to control the smoothing strength at different KL components via the penalty. By setting the smoothing parameter inversely proportional to the eigenvalue at each KL component, i.e., β / d_l, the KL component with lower SNR (small eigenvalue) will be smoothed more during the PWLS restoration [13][15][18].

The minimization of the cost function (1) can be performed by many numerical means [21]. In this study, it was minimized efficiently by the Gaussian-Seidel updating strategy [15]. After each of the three KL components was processed by the PWLS criterion in the KL domain, the inverse KL transform was applied to the three processed KL components to obtain an estimate of the concerned slice of the ideal sinogram data or recover the true line integrals of the attenuating object. Each slice of the 3D sinogram data was processed sequentially by the KL-PWLS strategy before CT image reconstruction in this study, although parallel computation of all the slices can be performed by a computer cluster or multiple CPUs.

The restored 3D sinogram was reconstructed by a standard FBP algorithm slice-by-slice in 2D fan-beam geometry. In order to avoid the non-uniform noise propagation problem in fan-beam geometry, the intersecting area of fan-beam strip and square image pixel was used as the weight, rather than a bi-linear interpolation, in the backprojection step in the FBP algorithm [22]. The non-uniform noise propagation problem in fan-beam CT is believed to be caused by the distance-dependent factor 1/L² in fan-beam FBP reconstruction [23][24]. The “cause” implies that the same CT data noise property in parallel geometry and different focal length fan-beam geometries could generate different noise distributions in the corresponding FBP and fan-beam FBP reconstructed images, resulting in variable regional quantitative measures across the field-of-view (FOV) [25]. The spatially-variant area weighting term in the image reconstruction formula plays the role in canceling out the non-uniform propagation effect due to the distance-dependent factor 1/L² in the fan-beam FBP reconstruction, thus the non-uniform propagation effect during image reconstruction will be compensated across the FOV.

Similarly to the cutoff frequency in the conventional low-pass filtration during FBP image reconstruction, there is also a free parameter β in the presented KL-PWLS method which controls the trade-off of the noise level and the structure preservation in the standard FBP reconstructed images. In this study, the choice of β was made by visual judgment based on an error-and-trial fashion [15], which is somewhat empirical.

The quality of CT images from the KL-PWLS sinogram restoration followed by the standard FBP reconstruction is generally superior to the results from the conventional FBP reconstruction with low-pass filters [15]-[17]. Comparison studies between the KL-PWLS noise reduction and low-pass Hanning noise filtration for single-slice helical CT have shown that the KL-PWLS strategy outperforms the Hanning filtration in terms of noise-resolution tradeoff and lesion detectability in low-contrast environment.

B. Simulation of Low-Dose CT Sinograms

Ultra low-dose CT sinograms of the patient abdomen were simulated from a corresponding patient CTC volume image acquired by a GE 16-slice CT scanner at a routine normal dose level, i.e., acquired by a protocol with a mAs value around 100 (or 200 mA at a rotation speed of 0.5 seconds per rotation) and a pitch value of 1.375:1 in helical mode. The other acquisition parameters include 120 kVp, 1.25 slice thickness, and 32×32 cm² FOV. The CT volume image of size 512×512×413 was reconstructed using the STANDARD filter after weighting and interpolation from the 3D spiral data.

The sinograms (or line integrals) of the patient abdominal CTC volume image were calculated by re-projection in a slice-by-slice fashion. The simulated sinograms from all the image slices mimic the experimental sinogram data in Radon space after system calibration, which includes interpolation of spiral-sampled projection data from multi-detector bands, data conditioning via the logarithm transformation, uniformity calibration on detector cells’ responses, etc. Although simulating the transmission raw data is feasible to accurately model the statistics of the interaction of X-ray radiation with matter in the object and at the detector, the system calibration from the transmission raw data to the sinograms in Radon space remains a challenge for CT sinogram simulation. In this study, we focus on the noise problem in low-dose situations, and will not address the challenge problem. The geometry used to simulate the sinograms in Radon space was a 2D fan-beam configuration, which is similar to the commercial (GE) CT scanner. The number of detector cells per view is 888. A total of 984 views spans evenly on a circular orbit of 360°. The detector arrays in each band are on an arc concentric to the X-ray source with a distance of 949.075 mm. The distance from the rotation center to the X-ray source is 541 mm. The detector cell spacing is 1.0239 mm.

Each of the 888 line integrals at each of the 984 view angles was calculated based on the Siddon’s ray-tracing technique [26] between the X-ray source point and the center of the detector cell. The intersecting length of the ray with a square image pixel was used as the weight of the pixel’s contribution to the line integral. The re-projected sinogram size was 888×984×413. Lower dose data can be simulated by adding corresponding noise levels [27]. It has been shown that a lower dose scan can be simulated by adding Gaussian noise with a variance dependent on the mAs level of the normal scan [23][28]. In our previous experimental studies [14][19][20], the noise in CT sinogram (i.e., the line integrals of the attenuation coefficient map after logarithmic transform) was shown to have a signal-dependent variance. The variance of projection datum or line integral ${\stackrel{‒}{p}}_i$ at detector cell i, ${\sigma }_{p_i}^2$, can be estimated by

$${\sigma }_{p_i}^2=f_i\exp ({\stackrel{‒}{p}}_i∕\eta )$$ (3)

where η is a scaling factor and f_i represents a scanner-specific adjustable parameter adaptive to each detector cell across the FOV and considers mainly the bowtie filtration effect for different incident photon numbers toward different detector cells. If the line integrals $\left\{{\stackrel{‒}{y}}_l\right\}$ are calculated from the physical attenuation coefficient map, η =1. If the line integrals are calculated from the CT image with intensity values in units of CT numbers or Hounsfield units (HU), η is the scaling factor relating to the line integral from the attenuation map and the line integral from the CT numbers. The scanner-specific adaptive parameter f_i can be determined at a specific mAs level by repeated scans. Given a sinogram acquired at a high mAs level, a lower mAs sinogram may be simulated by adding Gaussian noise with a corresponding curve of {f_i} across the FOV.

It shall be noted that as mAs value decreases, the noise of sinogram will be less likely following Gaussian (or normal) distribution. From the experimental studies reported in [20], the percentage of sinogram data that passes the normality test drops from 94% at 100 mAs to 91% at 17 mAs, although the mean-variance relationship still holds even at 17 mAs level. When mAs level goes very low such that photon starvation occurs, the model of compound Poisson noise of X-ray photon energy integration plus Gaussian noise of electronic background in the transmission (or raw data) space [29][30] may provide a better data simulation in such situation. However, how will this model in the transmission space be altered in the Radon space remains an open question. By the repeated phantom scans at 17 mAs level, the probability distribution function (PDF) fits visually well to the Gaussian distribution (better than other functions, such as Poisson and Gamma). The probability of receiving a zero photon number for a random variable of Poisson distribution (i.e., the raw data) in the transmission space is very small (approximately at the order of 4.5×10^-5). In fitting the relationship (3) by repeated scans, the electronic background noise has been implicitly considered into the adaptive parameter {f_i}. By explicitly adding the background noise term into equation (3) via the Taylor expansion, the adaptive parameter form may be altered but the mean $\left\{{\stackrel{‒}{y}}_l\right\}$ and variance $\left\{{\sigma }_{p_i}^2\right\}$ are the same, so the fitted adaptive parameter curve would not change much. Based on the above observations, a Gaussian functional PDF would be acceptable for mAs greater than 17 under the condition that a non-linear mean-variance relationship (3) is held. Given the determined relationship (3) from repeated phantom experiments, a lower mAs sinogram was simulated from the line integrals of a higher mAs CT image as follows.

The higher mAs patient CTC images were obtained at normal dose (100 mAs) from the commercial GE scanner. The re-projected line integrals of the patient CTC images reflect a corresponding high mAs level sinogram. By selecting a lower mAs curve {f_i} across the 888 detector cells or at each projection view, a corresponding low mAs sinogram was simulated. Each datum in the low mAs sinogram was a sample from a Gaussian random number generator [21] with the mean being the corresponding line integral of the high mAs image and the variance being determined by the corresponding relationship (3). Figure 1 shows the curve of {f_i} at 50 mAs level by repeated scans of an anthropomorphic torso phantom using the GE CT scanner [20]. Figure 2(a) shows a typical re-projected sinogram from the image slice of Figure 4(a) of the 100 mAs CT volume image. Figure 2(c) shows the simulated low-dose sinogram from the high mAs sinogram of Figure 4(a) using the 50 mAs curve {f_i} via the mean-variance relation (1). The computed variance map using the 50 mAs curve {f_i} and the mean distribution of Figure 4(a) is shown by Figure 2(b), which reflects a strong signal dependence. The dependence is clearly seen in Figure 3(b) which is the horizontal profile drawn from the center of Figure 2(b). Figure 3(a) is the horizontal profile drawn from the center of Figure 2(a) and Figure 3(c) is the horizontal profile drawn from the center of Figure 2(c). The added noise is noticeably high.

Figure 1.

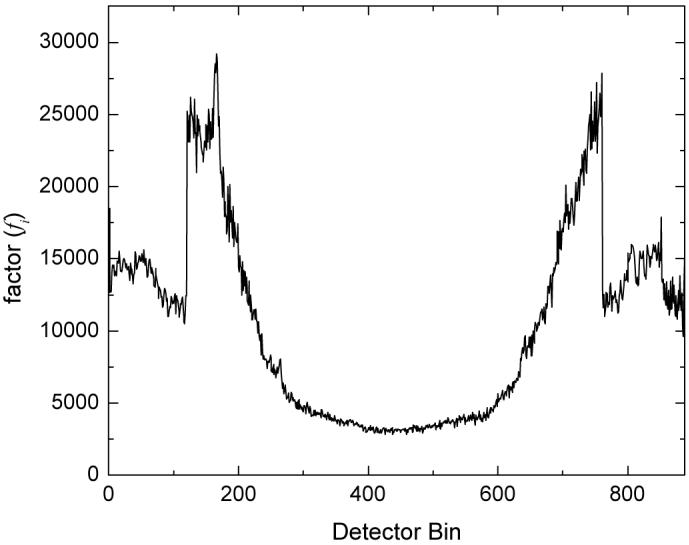
Plot of f_i used for simulation of the low-dose CT sinogram.

Figure 2.

A typical simulated sinogram from an image slice. Picture (a) shows the re-projected sinogram from the high mAs CT image slice of Figure 4(a). Picture (b) shows the variance map at 50 mAs level for the mean map of Figure 2(a). Picture (c) shows the low-dose sinogram by adding non-stationary Gaussian noise with variance at 50 mAs level. Picture (d) shows the restored sinogram by the presented KL-PWLS algorithm. The displays are in the full range from zero to maximum pixel intensity respectively.

Figure 4.

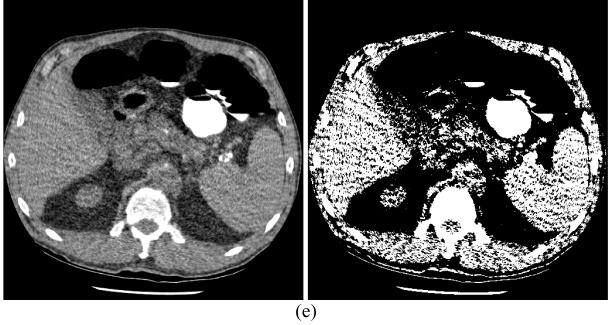
Illustration of one slice of the volume image: (a) from the normal dose scan (the arrow indicates the position of the polyp); (b) from standard FBP reconstruction of the re-projected normal dose projection data (i.e., Figure 2(a)); (c) from standard FBP reconstruction of the simulated ultra low-dose projection data (i.e., Figure 2(c)); (d) from conventional FBP reconstruction of the simulated ultra low-dose projection data, where the Hanning window had a cutoff at 80% Nyquist frequency; and (e) from standard FBP reconstruction of the simulated ultra low-dose projection data after the KL-PWLS sinogram noise reduction was applied. The displays are in the full range from zero to maximum voxel intensity respectively.

Figure 3.

Horizontal profiles drawn through the centers of the pictures in Figure 2, respectively. Picture (a) shows the horizontal profile drawn through the center of Figure 2(a). Picture (b) shows the horizontal profile drawn through the center of Figure 2(b). Picture (c) shows the horizontal profile drawn through the center of Figure 2(c). Picture (d) shows horizontal profile drawn through the center of Figure 2(d).

It shall be noted that the re-projected sinogram of Figure 2(a) will not reproduce the 100 mAs level of noise present in the original scan. The original images, e.g., Figure 4(a), were generated through some steps of weighting, interpolation, filtering and backprojection, all of which affect the statistical noise in the images. In particular, the filtering step on commercial scanners is highly optimized for image quality, trading off noise and resolution performance and controlling aliasing via the shape of the window, the roll-off of the ramp filter, and the filter cutoff frequency. The re-projection by the Siddon ray-tracing strategy [26] will further alter the noise characteristics by introducing high frequency artifacts. Therefore, adding in Gaussian noise with variance at 50 mAs level upon the re-projected sinogram may not generate an equivalent noisy sinogram at the exact 50 mAs level. The noise level would be less than 50 mAs. In addition, the simulated noise characteristics of the ultra low-dose sinogram may not mimic exactly the real-scanned sinogram at the corresponding mAs level because of the imperfect modeling of the re-projection as stated above. To mitigate this deficiency, we shall set up a reference for comparison purposes between previously well-established method and the presented algorithm. In doing so, we applied (i) the standard FBP algorithm (where the ramp filter was apodized with a rectangular window whose cutoff was at 100% percentage of the Nyquist frequency) which indicates a reference from the same sinogram data by laboratory reconstruction method, not the optimized commercial reconstruction algorithm; and (ii) the conventional FBP algorithm (i.e., the ramp filter was apodized with a Hanning window whose cutoff was optimized at a percentage of the Nyquist frequency) which indicates the best results that the conventional FBP can achieve. From the reconstructed ultra low-dose CT images, two post-reconstruction operations are needed for VC application and are presented below.

C. Electronic Colon Cleansing by Partial Volume Image Segmentation

The reconstructed ultra low-dose CT images contained tagged residue stool and fluid inside the colon lumen. The tagging was carried out by ingesting oral contrast solutions during a period of one or two days prior to the CT scan and is necessary in order to differentiate the stool and colonic fluid from the colon wall. The enhanced image intensity of the tagged materials is the result of absorbing more X-rays and, therefore, a higher mAs value is needed compared to CTC without stool tagging. The tagged colonic materials were virtually removed from the CT images by an electronic colon cleansing (ECC) technique [31], which is based on a partial volume (PV) segmentation algorithm [32]. The PV image segmentation algorithm determines the tissue mixture percentages inside each voxel and therefore considers accurately the PV effect upon the colon wall due to the enhanced image intensity of the tagged materials. The segmentation algorithm models the image data statistics and seeks the maximum a posterior (MAP) solution [31][32]. The MAP solution was computed by the expectation-maximization (EM) algorithm [33]. The output of the ECC was a PV layer which covers the colon mucosa. For hollow organs, such as colon, most clinical abnormalities occur on the mucosa, e.g., colonic polyp. Therefore, any change on the mucosa reflects very useful clinical information. Within the PV layer enclosure, the colon lumen was cleansed by a region-growing strategy. The MAP-EM PV image segmentation-based ECC technique has shown advantages in improving the detection of colonic polyps [32].

D. Construction of Colon Lumen Models for VC

The cleansed colon lumen was fed into the V3D-Colon Module developed by Viatronix Inc. (Stony Brook, NY), where the virtual colon model of the patient was constructed. The V3D-Colon Module simulates the navigation procedure of the clinical OC and provides a volume-rendered 3D endoscopic view at each location on a centerline of the virtual colon model. During the fly-through navigation along the centerline, the user has the control on the navigation speed and the view angle to facilitate colon polyp detection [3][4][10].

III. Results

A patient CTC dataset of size 512×512×413 was selected to test the above described ultra low-dose CTC pipeline for colon screening. A colon polyp of size 5 mm is centered at slice number 323 and indicated by an arrow in Figure 4(a). The polyp is covered by the tagged colonic fluid. Electronic colon cleansing of the tagged colonic materials is needed for 3D endoscopic view during flythrough navigation. All 413 slices of the CTC volume image were chosen to generate the line integrals or projection data. Each image slice generated a corresponding 2D sinogram of fan-beam geometry.

After all the 2D sinograms were computed by re-projection from the 413 image slices respectively, a signal-dependent Gaussian noise was added to the re-projected data according to the sinogram noise model of equation (3), simulating low-mAs acquisition protocols. The original CTC image was acquired at a normal dose level of 100 mAs and re-projected to simulate the ultra low-dose sinogram. The noise was added by imposing a variance distribution at 50 mAs level upon the re-projected data. By considering the “noise” propagated from the original 100 mAs scan, the simulated noisy sinogram would have a noise level equivalent to or lower than 50 mAs. A typical simulated 2D sinogram from an image slice of the CTC volume image is shown in Figure 2.

To show the simulation accuracy, the re-projected normal dose sinogram of Figure 2(a) was reconstructed by the standard FBP algorithm (where the ramp filter was apodized with a rectangular window whose cutoff was at the Nyquist frequency) and the result is shown by Figure 4(b). To visualize the similarity between the original image of Figure 4(a) and the reconstructed image of Figure 4(b) from the re-projected data of Figure 2(a), two different window displays (40/400 HU and 35/10 HU) are shown in Figure 5(a) and 5(b), respectively. This similarity reflects a satisfactory simulation of the sinogram and reconstruction of the simulated data.

Figure 5.

Illustration of two different window displays of the reconstructed images of Figure 4: (a) from the normal dose scan; (b) from the standard FBP reconstruction of the re-projected normal dose projection data; (c) from the standard FBP reconstruction of the simulated ultra low-dose projection data; (d) from the conventional FBP reconstruction of the simulated ultra low-dose projection data, where the Hanning filter had an optimized cutoff at 80% Nyquist frequency; and (e) from the standard FBP reconstruction of the simulated ultra low-dose projection data after KL-PWLS sinogram noise reduction was applied. Left column shows the displays at window setting of 40/400 HU (this is the default window setting for pelvic CT images in clinic). Right column shows the displays at window setting of 35/10 HU (i.e., displays at a narrower window).

The simulated noisy 3D sinogram (e.g., Figure 2(c)) was first reconstructed by the standard FBP algorithm to set a reference for comparison purpose. Figure 4(c) shows the reconstructed image slice from the corresponding noisy 2D sinogram of Figure 2(c). It can be observed that the polyp is degraded by excessive noise. For comparison purpose, a conventional FBP reconstruction of the simulated noisy 3D sinogram was also performed by carefully tuning the low-pass Hanning filter at an adequate cutoff frequency for a visually best result among the frequency range from 25% to 100% Nyquist frequency. The Hanning filter was the ramp filter apodized by a Hanning window with an adequate cutoff frequency. The reconstructed image slice from the corresponding noisy 2D sinogram of Figure 2(c) is shown by Figure 4(d). Some improvement is seen by the optimized low-pass Hanning filter. This can be seen from the different window displays of Figure 5(c) and 5(d). The low-pass linear Hanning filter suppressed noise with compromise of losing details. It also altered the image texture toward radial streaks across the FOV. This might be due to the use of spatially-invariant linear filter for reduction of the spatially-variant low-dose CT noise.

Then the noisy 3D sinogram was processed by the KL-PWLS restoration strategy, followed by the standard FBP algorithm for image reconstruction. A 2D sinogram or a slice of the restored 3D sinogram is shown by Figure 2(d), which is at the slice corresponding to the noisy 2D sinogram of Figure 2(c). Major features were satisfactorily restored. This can be seen from the profiles in Figure 3. The FBP reconstructed image slice from the corresponding restored 2D sinogram of Figure 2(d) is shown in Figure 4(e). It can be observed that the KL-PWLS sinogram restoration produces a better image quality than that of the Hanning filter, in terms of noise suppression and edge feature preservation. From the different window displays of Figure 5(d) and 5(e), it can be seen that more isolated noise spots near the borders of the objects (e.g., the colon and lungs) are removed by the KL-PWLS noise reduction strategy than by the low-pass Hanning noise filtration. Compared to the normal dose reconstruction of Figure 5(b), both Figure 5(d) and Figure 5(e) show some different image textures from that of Figure 5(b). The KL-PWLS noise filter produces some local texture patterns. This may be due to its use of the quadratic penalty on nearby pixels. The difference between the spatially-invariant Hanning filter and the spatially-variant KL-PWLS noise treatment was further revealed by 3D endoscopic views using the commercial V3D Colon-Module as follows.

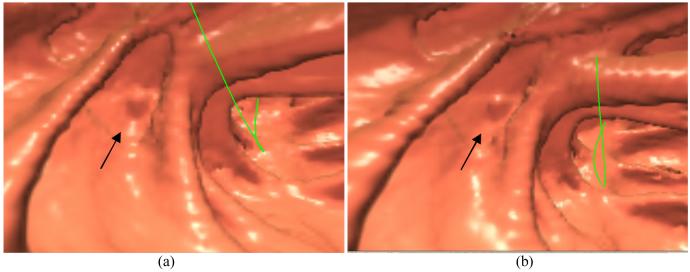
All the reconstructed 3D images after the ramp filter (i.e., the standard FBP result), the Hanning filter (i.e., the conventional FBP result) and the KL-PWLS noise treatment respectively were further processed through the ECC pipeline and then fed into the V3D-Colon Module for both the construction of their corresponding virtual colon models and the navigation inside the constructed virtual models. Due to excessive noise presented in the images, the whole virtual colon model of the ramp filter result could not be constructed by the V3D-Colon Module. The output was several separated colon segments. The whole virtual colon models from the Hanning filtered and the KL-PWLS treated results were successfully constructed and navigated by the V3D-Colon Module. The most visually-appealing endoscopic views from which the polyp can be observed are shown in Figure 6. It can be seen that detection of the polyp in the colon model from the KL-PWLS treated result is easier than that from the Hanning filtered result.

Figure 6.

Endoscopic view of a polyp of 5 mm size: (a) from the result after noise reduction by the Hanning filter; (b) from the result after the KL-PWLS sinogram restoration. The arrows indicate the position of the polyp. The green line is the central line for guided navigation inside the colon lumen, which is provided by the VC software and facilitates the navigation procedure. Both pictures show the most visually-appealing views.

IV. Discussion and Conclusion

The KL transform provides a unique means to consider correlations among acquired data [13][15][18]. In this work, the KL transform was applied among neighboring slices of a 3D sinogram which was simulated from a patient CTC volume image by a slice-by-slice fashion in fan-beam geometry. For a routine clinical CT scan with helical acquisition mode, it is preferred to apply the KL transform directly on the 3D spiral-sampled sinogram data before interpolating the 3D data into 2D sinogram slices. The KL transform shall be directly applied to 3D helical CT sinogram of cone-beam geometry of flat-panel or multi-row detectors.

In this work, the sinogram data of normal dose scans were simulated from reconstructed CT images based on Siddon’s ray-tracing method [21] because we were not able to access the raw data of the commercial CT scanner. The noise properties in the re-projected sinogram may not be the same as the original measurements due to the filtration as well as the back-projection during the image reconstruction process in the commercial CT scanner. A more robust way for the data simulation would be to add noise on the measured projection of normal dose scans. This would be possible if the raw data from the commercial CT scanner were available. To avoid the obstacle, the reconstructed CT image was chosen as a digital phantom with moderate noise survived from the filtration by the commercial scanner. The low-dose CT sinograms were then simulated by adding additional noise on the re-projected normal dose CT sinogram.

The PWLS criterion used in this paper is based on noise properties of the low-dose CT sinogram after the logarithm operation and necessary calibration process. The noise properties are reflected by the non-linear relationship (3) between the mean and variance, which is based on the Poisson model in the transmission space, where the electronic background noise was not explicitly considered and was implicitly included in the adaptive factor via the fitting by repeated experimental scans. Alternatively, the electronic background noise could be included explicitly in equation (3) via the Taylor expansion [34], i.e.,

$${\sigma }_{p_i}^2=f_i\exp ({\stackrel{‒}{p}}_i∕\eta )[1+{\sigma }_e^2{f}_i\exp ({\stackrel{‒}{p}}_i∕\eta )]$$ (4)

where ${\sigma }_e^2$ indicates the electronic noise variance of Gaussian distribution. This is a theoretical investigation under progress.

Minimizing the cost function (1) is computationally efficient since the cost function is in quadratic form. The time used to de-noise the whole sinogram of size 888×984×413 was 200 seconds on a PC with 2.4 GHz CPU. Alternatively, the cost function for sinogram restoration algorithm can be constructed based on noise modeling of measurement of detector counts in the transmission space. For example, Whiting et al. [29] investigated a model of compound Poisson noise in the X-ray counts plus Gaussian noise in the electronic background for the measurement of CT projection. While approximating the compound Poisson by the classic discrete Poisson has shown no noticeable difference between these two Poisson functions [35], modeling the detector counts in the transmission space by both the compound Poisson and the classic discrete Poisson distributions may have the benefit of considering other physics factors during X-ray detection, such as photon scattering, count starvation, difference in spectral sensitivity of the X-ray detector channels, and non-linear response of the detector channel at low energy. Comparison study of these two cost functions will be an interesting topic and worth of investigation.

In the present work, we mainly focus on software-based approaches to reduce noise in low-dose CT. Dose reduction can also be achieved through hardware optimization. For example, current high-end CT provides automatic exposure control features in which mAs levels will be adjusted at different views and z-axis positions with the aim to avoid under- or over- exposure [36]. Others include dynamic collimation and bowtie optimizations. The KL-PWLS strategy can be applicable to process the data of the optimized hardware technologies.

In summary, we have performed a simulation study to demonstrate a possible strategy for VC screening with ultra low-dose CT scans (i.e., at 50 mAs level or lower) and less-stressful bowel preparation by fecal tagging with oral contrast. Without noise suppression mechanism, the whole virtual colon model could not be constructed using the commercial V3D-Colon Module, which is dedicated to VC navigation mimicking the OC procedure. With an adequate noise reduction mechanism, the virtual colon model can be successfully constructed. The KL-PWLS noise reduction was shown to preserve more border details on the polyp than the Hanning filter. This is confirmed by the endoscopic views on the polyp using the V3D-Colon Module navigation system. This preliminary study indicates that an ultra low-dose CT-based VC is possible by the use of an adequate noise reduction strategy, such as the presented KL-PWLS sinogram restoration. It is expected that an ultra low-dose CT based VC could minimize the radiation risk and improve the compliance of colon screening recommendation and therefore reduce the mortality of colon cancers. Further studies are needed which include (1) generating a large number (e.g., greater than 500) of ultra low-dose CT scans of the patient CTC data (with the 5 mm polyp) and performing a polyp detection task using receiver operating characteristic merit and (2) performing the polyp detection task on a large number of patient ultra low-dose CTC scans with various polyp size and shapes.