Mimicking the Self-Organized Microstructure of Tooth Enamel

Abstract

Under near-physiological pH, temperature, and ionic strength, amelogenin (Amel) accelerates hydroxyapatite (HAP) nucleation kinetics, decreasing the induction time in a concentration-dependent manner. Hierarchically organized apatite microstructures are achieved by self-assembly involving nucleated nanocrystallites and Amel oligomers and nanospheres at low supersaturations and protein concentrations in a slow and well-controlled constant composition (CC) system. The CC method allows the capture of an intermediate structure, the nanorod, following the formation of the critical nuclei at the earliest nucleation stages of calcium phosphate crystallization. The nanorod building blocks form spontaneously by synergistic interactions between flexible Amel protein assemblies and rigid calcium phosphate nanocrystallites. These intermediate structures further assemble by a self-epitaxial growth mechanism to form the final hierarchically organized microstructures that are compositionally and morphologically similar to natural enamel. This in vitro observation provides direct evidence that Amel promotes apatite crystallization and organization. We interpret our observations to propose that in vivo Amel may maximally exert an influence on the structural control of developing enamel crystals at the earliest nucleation stages.

Introduction

Structural composite materials in nature show complex hierarchical organization involving building blocks from nanometer to macroscopic length scales.¹ Enamel tissue is a complex example of such a composite, because it is highly organized with parallel arranged nanorods that are tightly packed in a species-specific manner by extracellular matrix protein modulation.^2-4 It has been suggested that the predominant enamel matrix protein, amelogenin (Amel), self-assembles to form supramolecular nanospheres that facilitate the organization of inorganic nanostructures in developing enamel crystals.^5,6 In vitro preparation of materials that resemble enamel is more difficult, even at the lowest level of hierarchical organization, because it involves two dissimilar organic and inorganic nanophases.⁷ Extensive investigations of apatite crystallization have attempted to mimic the formation of enamel-like microstructures in the presence of Amel^8,9 and other organic additives such as gels, surfactant/polymers, and protein/peptide systems.^10-14 Others have examined applications of external fields¹⁵ and the use of various hydrothermal conditions, including extreme temperature, pressure, and pH.^16-18 However, these in vitro studies have not focused on the initial contact between mineral nuclei and organic additives that drive the earliest nucleation events responsible for subsequent directed assembly, yielding the complex morphologies and mineral phases found in enamel. Moreover, the relatively high supersaturations used in these studies inevitably obscure the events that would take place in a slow crystallization process. High supersaturations increase the possibility of structural mismatch between mineral and organic substrate, inducing the formation of less ordered mineralized structures.¹⁹

It has been suggested that cooperative assembly and interactions between forming crystals and assembling protein/peptide is pivotal to biomineralization systems such as silica, calcite, and apatite.^20-24 Some clues about the synergistic self-assembly occurring at initial nucleation stages have been provided by our recent studies of the promotion of octacalcium phosphate (OCP) nucleation by Amel in a slow and controlled constant composition (CC) crystallization system.²⁵ Elongated hydroxyapatite (HAP) microstructures were formed in OCP supersaturated solutions only at relatively low supersaturations.²⁵ This suggests that organic nanophases exert control over crystal nucleation at the very earliest CC crystallization stages. To date, virtually nothing has been known about the crystallization pathway from solvated ions through nuclei to the final apatitic mineral phase, nor has the potential existence of anticipated intermediate stable phases been explored. We have further developed this CC crystallization technique that is uniquely suited for monitoring the earliest nucleation stages for calcium phosphate crystallization under precisely defined thermodynamic driving forces and near-physiological conditions. This newly developed CC method, sensitive to ion concentration changes at the nanomolar level, yields reproducible measured induction periods for HAP and other apatites having different stoichiometries and enables nucleation and growth reactions to be investigated at very low thermodynamic driving forces, an essential requirement for probing the earliest nucleation events. Moreover, since concentrations remain constant, the stoichiometries of the phases formed can be determined with a sensitivity unachievable using other crystallization methods. Herein, we report that, in a solution closer to the physiological microenvironment and having HAP stoichiometry at low supersaturation (σ_HAP = 15.1, ionic strength = 0.15 M, 37 °C, and pH 7.40), Amel kinetically promotes HAP nucleation by decreasing the induction time in a concentration-dependent manner. An intermediate structure is successfully captured following the formation of the critical nuclei at the earliest nucleation stages: the nanorod building blocks formed by synergistic interactions between the flexible Amel protein assemblies and the rigid calcium phosphate nanocrystallites. These intermediate structures further assemble to form the final hierarchically organized microstructures. Self-organized microstructures, compositionally and morphologically similar to natural enamel, are achieved in a slow and precisely controlled CC crystallization system without the use of extreme hydrothermal conditions.

Experimental Section

Amel Protein Purification and Aspartic Acid-Rich Peptide Synthesis

The recombinant porcine Amel rP172 for this study was purified and prepared as described previously.^25,26 The 27-mer aspartic acid-rich peptide with serine spacers was synthesized by the sequential addition of Fmoc amino acids based on a standard procedure as previously described,²⁷ and the condensed formula for the peptide with serine spacers is (DDDS)₆ DDD (D = aspartic acid and S = serine).²⁸

HAP Crystallization by Constant Composition

Constant composition (CC) is a quantitative nucleation and crystal growth method where induction times and growth rates can be measured systematically as a function of the parameters controlling apatite crystallization, especially for monitoring a slow reaction at very low driving forces.²⁹ As a macroscopic crystallization technique, CC overcomes the problems associated with changing solution composition during crystallization and the chemical potentials of the solution species that are maintained constant during the reaction.²⁹ In this study, HAP crystallization experiments were performed at 37.0 ± 0.1 °C and the constancy of concentrations during the experiments was verified as described previously.²⁵ The reaction solutions were purged with nitrogen gas saturated with water vapor at 37 ± 0.1 °C. The relative supersaturation σ and supersaturation ratio S are given by eq 1:

$$\sigma =S-1={\left(\frac{\mathrm{IAP}}{K_{\mathrm{sp}}}\right)}^{1/\upsilon }-1$$ (1)

in which υ (=18) is the number of ions in a formula unit of the HAP phase and IAP and K_sp are the ionic activity and thermodynamic solubility product (5.52 × 10⁻¹¹⁸ mol¹⁸ L⁻¹⁸ at 37 °C),³⁰ respectively. Solution speciation calculations were made by using the extended Debye–Hückel equation proposed by Davies.³¹ Supersaturated reaction solution ([CaCl₂] = 1.80 mmol L⁻¹, [KH₂PO₄] = 1.08 mmol L⁻¹, [KOH] = 0.907 mmol L⁻¹, and [NaCl] = 0.142 mol L⁻¹ for σ_HAP = 15.1 at pH 7.400) was prepared by the slow mixing of calcium chloride (0.020 mol L⁻¹) and potassium dihydrogen phosphate (0.020 mol L⁻¹) with sodium chloride to maintain the ionic strength I = 0.150 mol L⁻¹. Amel proteins were added to supersaturated reaction solutions to achieve concentrations ranging from 0.5 to 5.0 μg mL⁻¹. The lowering of the pH in all crystallization experiments was monitored by a pH electrode (Orion 91-01) coupled with a single-junction Ag/AgCl reference electrode (Orion 90-01). The output of the potentiometer (Orion 720A) was constantly compared with a preset value, and a difference in hydrogen ion activities, or error signal (±0.05 mv), activated motor-driven titrant burets, for the simultaneous addition of two titrant solutions having HAP stoichiometries, thereby maintaining constant activity of all ionic species in the reaction solution.

Concentrations of titrant I containing calcium chloride and sodium chloride are given by eqs 2 and 3, respectively.

$$T_{{\mathrm{CaCl}}_2}=2W_{{\mathrm{CaCl}}_2}+5C_{\mathrm{eff}}$$ (2)

$$T_{\mathrm{NaCl}}=2W_{\mathrm{NaCl}}-10C_{\mathrm{eff}}$$ (3)

Titrant II contained potassium dihydrogen phosphate and potassium hydroxide with concentrations given by eqs 4 and 5, respectively.

$$T_{{\mathrm{KH}}_2{\mathrm{PO}}_4}=2W_{{\mathrm{KH}}_2{\mathrm{PO}}_4}+3C_{\mathrm{eff}}$$ (4)

$$T_{\mathrm{KOH}}=2W_{\mathrm{KOH}}+7C_{\mathrm{eff}}$$ (5)

In eqs 2-5, T and W are the titrant and supersaturated reaction solution concentrations, respectively, and C_eff (0.180 mmol L⁻¹ in this study) is the effective concentration of added titrants with respect to HAP.

Morphological and Structural Characterizations

Crystallites were collected from the solution by filtration at the end of experiments, and samples under vacuum were sputter-coated with a thin carbon deposit and then examined by field-emission scanning electron microscopy (SEM, Hitachi S-4000) at 20 keV. High-resolution transmission electron microscopy (HRTEM) and diffraction pattern investigations for nucleated crystallites were carried out using a JEOL TEM 2010 instrument at an accelerating voltage of 200 keV.

Results

Nucleation Kinetics of HAP in the Presence of Amel

In the present study, the influence of Amel at various concentrations on in vitro HAP nucleation was investigated in calcium phosphate metastable supersaturated solutions having HAP stoichiometry. During an initial induction period, solution concentrations remained unchanged and the volume of added titrant was essentially zero, confirming the absence of mineral nucleation. At the onset of nucleation, the reduction in solution pH accompanying deprotonation of acidic phosphate ions associated with the formation of HAP initiated titrant addition. The delay (induction) time for nucleation in pure supersaturated solutions was 778 ± 30 min (n = 3). However, in the presence of 0.5, 1.25, or 5.0 μg mL⁻¹ Amel, the induction times decreased to 705 ± 25 (n = 3), 398 ± 20 (n = 3), and 255 ± 20 (n = 3) min, respectively (Figure 1). In contrast, the addition of 0.15 μg mL⁻¹ aspartic acid-rich peptide with serine (S) insertion after each triplet of aspartic acids (DDD) in 27-mer peptide sequences (DDDS) markedly inhibited nucleation by prolonging the induction time to 913 ± 25 (n = 3) min, consistent with the known inhibitory roles in both calcium phosphate^13,32 and calcium oxalate crystallization systems.²⁸

Figure 1.

pH curves for HAP crystallization (free drift experiments, no titrant addition) in the absence and presence of Amel. Amel dramatically accelerates the nucleation by decreasing the induction time in a concentration-dependent manner (σ_HAP = 15.1, pH 7.400, and 37 °C). The polyaspartate, DDDS, served as a control.

In Vitro Formation of the Self-Organized Microstructures

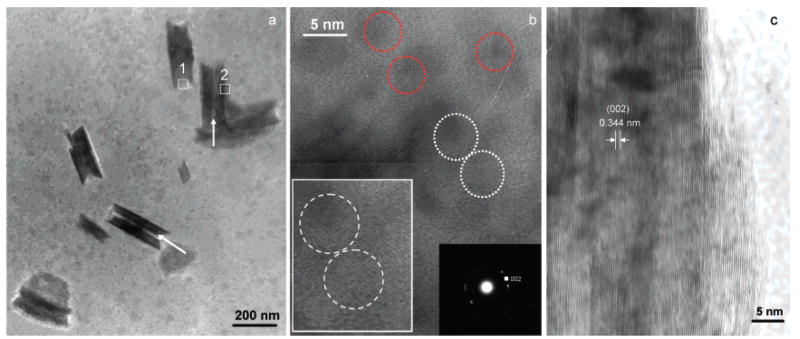
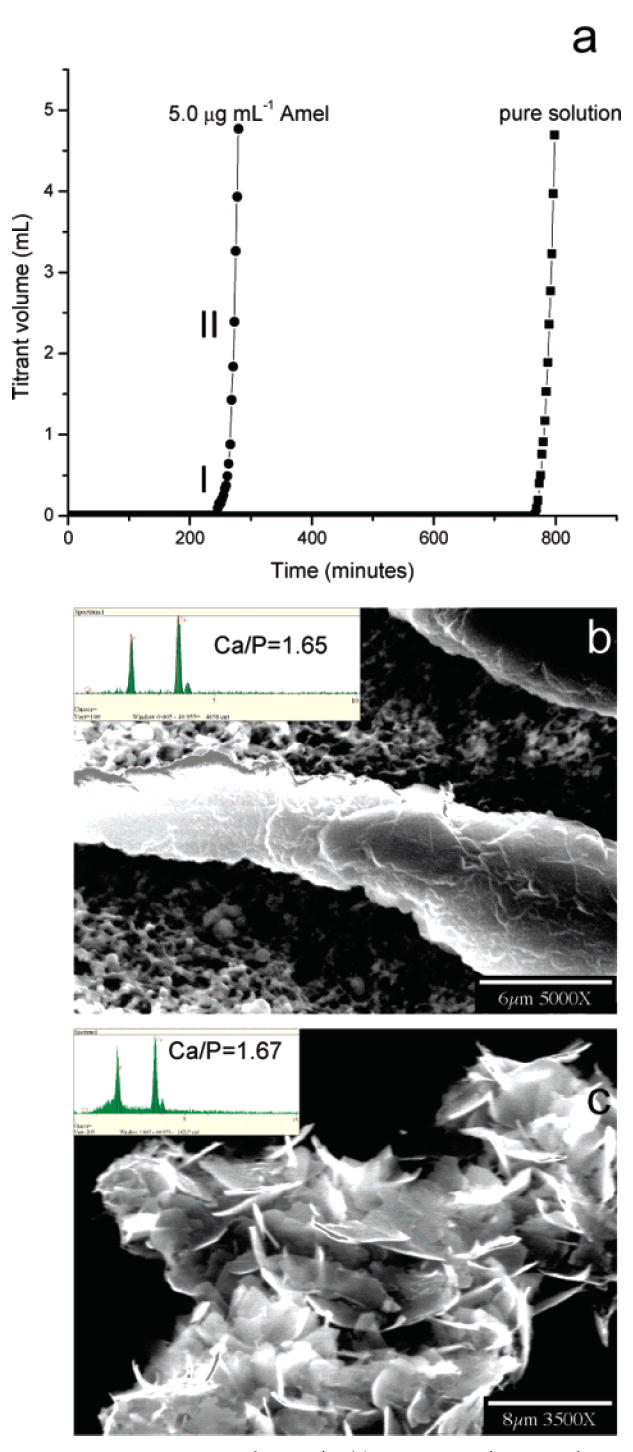
Following the 255 min initial induction period in the presence of 5.0 μg mL⁻¹ Amel (Figure 1), the pH slowly decreased by approximately 0.01 in about 10–15 min (corresponding to stage I of the CC curve in Figure 4a). This was followed by a more rapid pH reduction to <7.35 (stage II, Figure 4a). High-resolution TEM of collected precipitated solids after stage I showed that, in the presence of 5.0 μg mL⁻¹ Amel, the first detectable crystallites were uniform-sized nanorods (about 50 nm wide, i.e., diameter, and 250 nm long) (Figure 2a). Many nanorods were aligned as parallel, yet separated, dimers as shown by the arrows (Figure 2a), while others had already fused into larger nanorods. In less mineralized areas (rectangle 1, Figure 2a), nanorod assemblies consisted of ~3–5 nm nanocrystallites as indicated by dotted circles in Figure 2b, and selected-area electron diffraction (SAED) patterns corresponded to the (002) plane of HAP (inset, Figure 2b). Some nanocrystals were initially randomly oriented as shown by red dotted circles in Figure 2b, whereas adjacent 3–4 nm particles aggregated, adopting parallel oriented structures in three dimensions as shown by two white dotted circles and an inset of enlarged white dotted circles in Figure 2b. By oriented nanorod aggregation, in the more mineralized areas (rectangle 2, Figure 2a), the primary nanoparticles were also aligned with respect to each other, subsequently forming larger clusters with parallel crystallographic axes (Figure 2c). The measured lattice spacing of ~0.344 nm corresponds to the (002) HAP lattice plane (Figure 2c). After stage II (Figure 4a), the pH rapidly decreased and highly ordered extended solids were created. Analytical TEM investigations of these solids showed that organized elongated crystals were formed with a higher aspect ratio, 30–50 μm in length and 5–10 μm in width (Figure 3 and Figure 4b). The SAED pattern also confirmed preferential alignment of the HAP crystallographic c-axes along the long axes of the elongated microstructures shown by the arrow in Figure 3.

Figure 4.

CC HAP crystal growth. (a) Representative CC plots of titrant addition as a function of time for HAP crystal growth in the absence and presence of 5.0 μg mL⁻¹ Amel. SEM images of (b) an ordered and thickened crystal induced by 5.0 μg mL⁻¹ Amel and (c) randomly aggregated HAP crystallites in the absence of Amel collected from the bulk solution by filtration following the long induction periods. The Inset in (b) is the EDS of the elongated crystals showing a HAP Ca/P ratio of 1.65 ± 0.08 (n = 5, number of crystals) (σ_HAP = 15.1, pH 7.400, and 37 °C).

Figure 2.

TEM images of nucleated nanorods collected at stage I in the presence of 5.0 μg mL⁻¹ Amel. (a) Low magnification TEM image of nanorods. (b) HRTEM image taken from rectangle 1 in (a), revealing that the less mineralized area of the nanorods consists of nanocrystallites ~3–5 nm in diameter (indicated by dotted circles). The SAED pattern corresponds to the (002) plane of HAP (right inset, (b)). Some adjacent 3–4 nm particles aggregated, and their structures adopted parallel orientations in three dimensions as shown by two white dotted circles and their enlargement (left inset, (b)). (c) HRTEM image taken from rectangle 2 of the more mineralized areas in (a). The measured lattice spacing ~0.344 nm corresponds to the (002) HAP lattice plane.

Figure 3.

TEM characterization of one part of a ribbon collected after stage II (Figures 1 and 4) in a free drift nucleation experiment in the presence of 5.0 μg mL⁻¹ Amel. The inserted SAED pattern confirmed that the ribbonlike structure was HAP. The long arrow indicates the long axis direction of the elongated microstructures.

When the nucleation barrier was overcome, the second crystal growth stage began. Figure 4a shows a typical CC crystal nucleation and growth curve following the long induction time. This pH lowering triggered the simultaneous addition of two titrant solutions to maintain constant activities of all reaction solution species. A more rapid titrant addition reflected the exponential growth of crystals on the nuclei formed in the heterogeneous nucleation stage (Figure 4a). Thicker apatite crystals were grown in the presence of 5.0 μg mL⁻¹ Amel, but they retained their elongated morphology (Figure 4b). Energy-dispersive spectrometry (EDS) revealed a Ca/P molar ratio of 1.65 ± 0.08 (n = 5, number of crystals), consistent with HAP (inset in Figure 4b). In the absence of Amel, HAP crystallites were randomly aggregated with different orientations (Figure 4c) via the interaction between crystalline surfaces with unfavorable surface charges.¹⁷

Discussion

Self-Assembly of Nucleated Nanocrystallite–Amel Nanosphere Mixtures

Our proposed in vitro model schematically presented in Figure 5 is based on the experimental evidence and reported theoretical analysis, and it involves a stepwise mesoscale transformation mechanism: self-assembly of nucleated apatite nanocrystallite–Amel nanosphere mixtures. Controlled aggregation of primary composite nanoparticles takes place at relatively low supersaturations to form nanorods, which may, as secondary building blocks, further self-assemble into organized elongated microstructures. However, it is unfortunately difficult to acquire independent evidence to suggest that all nanorods converted to elongated mineral ribbons by the end of the experiments. This has been due in part to the limitations of existing experimental approaches for monitoring in situ and time-resolved particle evolution of nuclei. In the absence of Amel, the apatite nanocrystallites (critical nuclei) grow uncontrollably and aggregate randomly. The nanorod, the intermediate phase, was not detected by TEM observations of collected precipitated solids after stage I and II. A low concentration of Amel (5.0 μg mL⁻¹) dissolved in solutions with similar ionic concentrations to those of the HAP crystallization solutions results in the formation of larger 60–80 nm assemblies from the monomer (R_H 2.4 nm) and smaller nanospheres (R_H 9.8 nm) characterized by dynamic light scattering (DLS).²⁵ These DLS measurements were conducted at pH 6.8, and the Amel assemblies’ sizes are usually larger at pH 7.4.³³ Wiedemann-Bidlack et al. have suggested a very similar assembly with increasing pH from 7.2 to 7.7.³⁴ The hydrophilic C-terminal “tails” of Amel nanospheres may serve as nucleation sites to selectively bind with Ca²⁺ or calcium phosphate nuclei. Acidic and basic residues at the C-termius that also promote the adsorption of both calcium and phosphate ions therefore may aid in producing, locally, a high degree of supersaturation to induce the formation of primary organic–inorganic composite nanoparticles.¹⁹ Moradian-Oldak et al. have proposed that the hydrophilic C-terminal of Amel can be exposed on the surfaces of the nanospheres, creating structured domains with which apatite can preferentially interact.³⁵ This has been confirmed by solid-state nuclear magnetic resonance³⁶ and molecular dynamics simulation studies³⁷ of Amel–HAP interaction through the hydrophilic COOH-terminal region of Amel.³⁸ The notion that Amel nanospheres have their negatively charged domains exposed to their surfaces was experimentally supported by recent streaming potential measurements.³⁹ Beniash et al. have demonstrated that the C-terminal domain is essential for HAP organization into parallel arrays in the presence of the full-length and higher concentration (1 mg mL⁻¹) Amel.²⁴ Thus, under our experimental conditions, the presence of structured Amel nanospheres will promote nucleation and nanoparticle assembly of apatite to induce nanorod formation. It has been suggested that nanorods may emerge from a supersaturated solution containing inorganic nanoparticles (nuclei) if each nanoparticle “docks” with a neighbor, such that the two are fully aligned and subsequently fuse to form oriented arrangements, a process termed “oriented attachment”.^40,41 The detailed mechanism of oriented attachment remains unclear, but the process appears to occur for many material and biomineralization systems. The most frequent products of oriented attachment are rods and wires.⁴² The introduction of an organic molecule that selectively adheres to a particular crystal facet can selectively slow the growth of that face relative to others, leading to the formation of rod-shaped nanocrystals.⁴² Kinetic shape control through selective adhesion has been suggested by the strongest interaction of Amel with the (010) face, followed by the (001) face, and weakly with the (100) face of OCP crystals.⁴³ This may well account for the initial elongated growth of OCP crystals. Moreover, linear arrays of spherical substructures have been also detected in the enamel extracellular matrix in vivo.^44,45 Fusion of enamel crystallites in the early stages of mineral formation has been proposed to explain the unusual long crystals formed in mature enamel.⁴⁶ A most recent molecular dynamics simulation study showed that the carboxyl groups mainly contribute to the adsorption of leucine-rich Amel protein (LRAP) at the HAP (001) face.³⁷ It was suggested that two carboxyl oxygen atoms behaved like a “claw” to grasp the calcium cations occupying the outmost layer of the HAP (001) face in the c-axis. This Coulombic interaction dominated the adsorption between LRAP and HAP; LRAP has many such “claws” in the molecule fusing the HAP nanorods together to form larger and elongated microstructures.³⁷ This simulation might provide an explanation for the elongation of growing HAP crystallites in the presence of Amel. Alternatively, a self-epitaxial nucleation-mediated assembly mechanism would explain the parallel twinned HAP nanorods that further assemble into the well-aligned and elongated microstructures.^19,47-49 The self-aligned HAP aggregates are formed when emerging daughter HAP crystallites grow epitaxially at the actual surface of parent HAP crystallites at relatively low supersaturations through slow surface integration kinetics.^19,47 Self-epitaxial nucleation and growth normally occurs at relatively low supersaturations, resulting in small-angle mismatch. At high supersaturations, it is very possible to form wide-angle self-epitaxial branching.¹⁹ Thus, perfect alignment and strong bonding between HAP nanorods depend on the supersaturation at the surface of the growing crystals.^19,47 Heterogeneous crystallization may follow completely different mechanisms across the continuum of driving forces. Therefore, it is necessary to carefully select the driving forces (supersaturations) for in vitro biomimetic mineralization studies.

Figure 5.

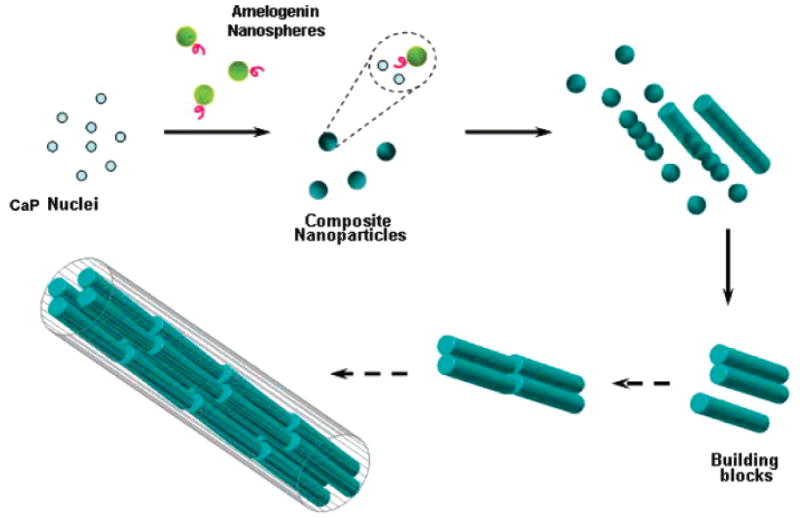
Mechanism illustration of in vitro hierarchically organized microstructure formation by self-assembly of nucleated apatite nanocrystallite–Amel nanosphere mixtures based on experimental evidence (solid arrows) and theoretical analysis (dotted arrows). See text for details.

In this study, we have emphasized the earliest stage of crystallization, referred to as nucleation, that usually dictates the remainder of the growth process, and the crystallization pathway from solvated ions to an intermediate nanorod phase prior to the final apatitic mineral phase. Technically, nucleation is the initial appearance of a new phase (here, the emergence of tiny crystal nuclei) during a first-order phase transition, in which small nuclei forming in a supersaturated solution must overcome a nucleation barrier before reaching a critical size, the so-called critical nucleus.^50,51 According to classical nucleation theory (CNT),⁵¹ the total free energy of a crystallite that forms in a supersaturated solution contains two terms: The first is a “bulk” term that expresses the fact that the solid is more stable than the supersaturated fluid (this term is negative and proportional to the volume of the crystallite). The second is a “surface” term that takes into account the free-energy cost of creating a solid–liquid interface. This term is positive and proportional to the surface area of the crystallite.⁵¹ According to CNT, the total (Gibbs) free-energy cost to form a spherical crystallite with radius r is⁵¹

$$\mathrm{\Delta }G=\frac{4}{3\mathrm{\Omega }}\pi r^3\mathrm{\Delta }\mu +4\pi r^2\gamma$$ (6)

where Ω is the volume per growth unit, Δμ (<0) is the difference in chemical potential between the solid and the liquid, and γ is the solid–liquid interfacial free energy. The function ΔG goes through a maximum at r = 2γΩ/|Δμ|, and the height of the nucleation barrier is^47,51,52

$$\mathrm{\Delta }G=\frac{16\pi {\gamma }^3{\mathrm{\Omega }}^2}{3\mathrm{\Delta }{\mu }^2}=\frac{16\pi {\gamma }^3{\mathrm{\Omega }}^2}{3{(\mathit{kT})}^2{[\ln (1+\sigma )]}^2}$$ (7)

where k is Boltzmann’s constant, T is the absolute temperature, and σ is the relative supersaturation of the solution. In the presence of organic additives/substrates, the nucleation barrier is reduced to^19,52

$$\mathrm{\Delta }{G}^{\ast }=\mathrm{\Delta }\mathit{Gf}(m)(0\le f(m)\le 1)$$ (8)

where f(m) is the interfacial correlation factor describing the lowering of the nucleation barrier due to the presence of the organic additive. The technical difficulties involved in directly evaluating the crystal nucleation rate have led to other approaches to initial crystallization events, and one of the most common ways to characterize the kinetics of nucleation is to measure the induction period (t_s) prior to nucleation at different supersaturations. The induction period can be expressed as eq 9: ^19,52

$$\ln t_{\mathrm{s}}=\frac{\kappa f(m)}{{[\ln (1+\sigma )]}^2}-\ln \{V{(R^{\mathrm{s}})}^2{N}^{0}f″(m){[f(m)]}^{1/2}B\}$$ (9)

where κ [= 16πγ³Ω²/3(kT)³] remains constant under a given set of conditions. V is the volume of the system, R^s and N⁰ are the radius of curvature and the density of the additives/substrates, respectively, and B is a kinetic constant. In the Amel/HAP nucleation system, since Amel serves as “seeds” or organic substrates for HAP nucleation, the change of its concentration is equivalent to changing N⁰ in eq 9, leading to significantly shorter induction times (Figure 1) with a consequent promotion of nucleation. Recently, Tarasevich et al. also reported a promoting influence of low concentration of Amel (rM179) on OCP nucleation.⁵³ However, relatively high supersaturations were used to induce the formation of less ordered mineralized structures.⁵³ According to eq 9, the plot of ln(t_s) against 1/[ln(1 + σ)]² will result in a straight line whose slope is determined by κ and f(m).^47,52 Obviously, for a given system (constant κ and B), the slope of the straight line will be dependent on f(m). It has been shown that f(m), describing the interfacial correlation between minerals and additives/substrates, will increase with supersaturation.^47,52 This implies that an increase of supersaturation will drive the organic substrates/biominerals from an interfacial structural matched state (f(m) → 0) to a state of greater mismatch (f(m) → 1); the substrate exerts almost no influence on the nucleation barrier. It follows that a good structural synergy between biominerals and additive molecules/substrates will promote an ordered biomineral structure and this will occur only at low supersaturations.^47,52 Our previous studies²⁵ showed that, in an OCP supersaturated solution with a high supersaturation, the induction times in the absence and presence of Amel show no significant change; less ordered structures were formed when compared to those at a lower supersaturation. Interestingly, the structures are more ordered in the presence of Amel when compared to the control without Amel at higher supersaturations.²⁵ This observation may constitute direct evidence that, at higher supersaturations, the less ordered structures that are formed can be explained by supersaturation-driven interfacial structural mismatch;^25,52 on the other hand, some nuclei without strong interactions with Amel may form too rapidly to have opportunities for further organization. Therefore, we intentionally chose a relatively low supersaturation in this HAP crystallization system to acquire a slow and well-controlled mineralization by magnifying the Amel additive/template effect on the nucleation/growth at relatively low protein concentrations.

Small crystal nuclei form spontaneously in supersaturated solutions, but unless their size exceeds a critical value, they will redissolve rather than grow because a small crystallite has a large surface to volume ratio.^50,51 However, as Amel is introduced into the supersaturated solutions, these nuclei ~3–5 nm in diameter either are attached to surrounding negatively charged Amel^36,37,39 or flocculate to form aggregates. The interactions of nanoparticles with polymers/proteins are mediated by the ligands attached to the nanoparticles; thus, the ligands markedly influence particle spatial distribution and rearrangement.⁵⁴ In addition to lowering the nucleation barrier, Amel nanospheres will reduce random Brownian motion-driven particle collisions and stabilize these nanoparticles. Jiggling of nanoparticles by Brownian motion may also allow adjacent particles to rotate to find the low-energy configuration represented by a coherent particle–particle interface.⁵⁵ Zhu et al. demonstrated, by molecular dynamics simulation, the rotation of particles within aggregates to achieve parallel orientations, and this may also be driven by short-range interactions between adjacent surfaces.⁵⁶ Nanoparticles aggregate via oriented attachment to achieve parallel orientations to form nanorods, and finally these nanorods self-assemble into elongated microstructures by the self-epitaxial nucleation and growth mechanism.¹⁹ In the light of the foregoing analysis, it is very important to form the intermediate secondary nanorod phase in a slow crystallizing system, because small nanoparticles, prior to reaching critical sizes, are not stable in supersaturated solutions and readily redissolve. Theoretically, if crystals grow via atom by atom, a certain number of defects for extended solids is inevitable even at equilibrium; however, when this same number of atoms is partitioned into nanometer-sized crystals, then, on average, each nanorod need not contain any interior defects or etched active pits on its surfaces.⁵⁷ Thus, they are stabilized to resist dissolution. Moreover, by way of oriented aggregation and self-epitaxial assembly to form the parallel-aligned twinned nanorods, the surface energy is reduced substantially because the interface is eliminated.^58,59

Structural Comparison of In Vitro Nucleated Apatite and Natural Enamel

Consistent with the size of these nanorods, measurements of human enamel crystallites in their mature stage are 26.3 ± 2.2 nm in thickness, 68. 3 ± 13.4 nm in width, and 100–1000 nm in length.^60,61 Gao et al. have suggested that the size of the mineral particles, typically tens to hundreds of nanometers, is not arbitrary.⁶² Rather, it seems to give tooth enamel remarkable characteristics: as the mineral size falls below a critical length scale around 20–50 nm, (a) the strength of a perfect mineral crystal is maintained and (b) the biomaterials become insensitive to dissolution at the nanoscale. It has been found that CC demineralization reactions of tooth enamel may be inhibited or even suppressed due to the absence of active pits on the crystallite surfaces of the nanorods with similar sizes around 50 nm in width and 200 nm in length (Figure S1 in the Supporting Information). This phenomenon actually involves particle-size-dependent critical conditions of energetic control at the molecular level and can be explained by a unique dissolution model involving size considerations at the nanoscale [R(r) ≈ R_∞(1 − r*/r) and r* = γω/|kT ln(1 + σ)|, where r is the pit radius that is confined by crystallite size and r* is the critical radius for the formation of a two-dimensional pit/dissolution step. R_∞ is the velocity of dissolution steps at r → ∞. ω is the molecular volume, γ is the step free energy per unit step height, and σ is the relative undersaturation of the solution.].^63,64 It has been shown that only pits which are larger than critical sizes (r*) provide the active dissolution sites that contribute to dissolution.^62,63 When r is closer to r*, there is no fast movement of its stepwave and the macroscopic dissolution rate is markedly reduced, approaching zero, despite the sustained driving force (Figure S2 in the Supporting Information). Clearly, this dissolution termination is a kinetic phenomenon and cannot be attributed to reaction retardation as a result of surface modification by additives. Not surprisingly, sizes of the nanorods formed via bottom-up (CC solution synthesis in the presence of Amel) and top-down (CC dissolution of bulk enamel discs) kinetic methods converge at the same nanoscale. Elongated structures formed by the in vitro CC crystallization method resemble incomplete native enamel structures. This difference possibly arises from natural biomineralization as a total consequence of (i) cell compartment confinement (Tomes’ process), (ii) the influence of combined genetic and niche factors, (iii) the modulation and modification by other enamel (non-Amel) proteins and small molecules,⁶⁵ (iv) the spatiotemporal control of ionic transports by Ca²⁺ and PO₄³⁻ ionic transporters, and (v) the difference between Amel concentrations in vitro and in vivo.⁶⁶ Can ameloblasts and their gene products control the local physiological concentrations of secreted Amel during different developing stages to promote or inhibit crystallization?

Conclusions

Because of differences in the solution conditions used in our CC crystallization system and the physiological microenvironment in the enamel extracellular matrix, it is difficult to directly relate our in vitro results to in vivo enamel formation. However, this study has taken an important initial step toward a further understanding of an isolated factor, namely how Amel controls HAP nucleation and postnucleation growth at the earliest stages of mineralization. Hierarchical self-assembly, a nucleation-growth pathway, gives rise to a remarkably high degree of cooperativity (a state of greater interfacial structural match between inorganic and organic nanophases, and self-epitaxial alignment between inorganic nanorods at lower driving forces). We clearly demonstrate, that under cooperative kinetic control, self-assembly of nucleated nanoparticle–Amel nanospheres/oligomer mixtures plays an explicit role in guiding nanoparticles toward nanorods. Kinetic formation of nanorods as the secondary building blocks may be not arbitrary; they will most likely remain relatively stable to form larger structures by the self-epitaxial assembly mechanism during the slow crystallization process. Nanostructure optimization in a complex biocomposite, such as tooth enamel, will be expected to show a remarkable degree of self-preservation in the fluctuating physiological milieu.⁶⁴ In association with organic matrix, most nanorods may result from growth conditions in which some particles remain stable at a critical size, while others continue to grow into ordered extended microstructures and finally to mature products.

Supplementary Material

SM. Supporting Information Available.

Materials and methods for CC dissolution kinetics of tooth enamel; SEM images of enamel demineralization at different dissolution stages; and CC curve of tooth enamel dissolution. This material is available free of charge via the Internet at http://pubs.acs.org.