Theory and Inference for Regression Models with Missing Responses and Covariates

Summary

In this paper, we carry out an in-depth theoretical investigation for inference with missing response and covariate data for general regression models. We assume that the missing data are Missing at Random (MAR) or Missing Completely at Random (MCAR) throughout. Previous theoretical investigations in the literature have focused only on missing covariates or missing responses, but not both. Here, we consider theoretical properties of the estimates under three different estimation settings: complete case analysis (CC), a complete response analysis (CR) that involves an analysis of those subjects with only completely observed responses, and the all case analysis (AC), which is an analysis based on all of the cases. Under each scenario, we derive general expressions for the likelihood and devise estimation schemes based on the EM algorithm. We carry out a theoretical investigation of the three estimation methods in the normal linear model and analytically characterize the loss of information for each method, as well as derive and compare the asymptotic variances for each method assuming the missing data are MAR or MCAR. In addition, a theoretical investigation of bias for the CC method is also carried out. A simulation study and real dataset are given to illustrate the methodology.

1 Introduction

Missing data arise in nearly every type of application in the statistical sciences. Over the past 30 years, there has been an enormous literature on likelihood-based methods of estimation and inference for a wide variety of missing data problems, including missing covariate data in linear models, generalized linear models, generalized linear mixed models, and survival models, as well as missing response data for models of longitudinal data. Since the literature is too vast to list here, we refer the reader to three review articles that discuss various methods for handling missing data: Little (1992), Horton and Laird (1999), and Ibrahim, Chen, Lipsitz, and Herring (2005). There has also been some literature for likelihood-based methods for establishing identifiability and asymptotic properties of estimators in missing covariate problems including Robins and Rotnitzky (1995), Lipsitz, Ibrahim, and Zhao (1999), Herring and Ibrahim (2001), and Chen, Ibrahim, and Shao (2004). There also has been some work on models for longitudinal data with nonignorable responses, including Baker and Laird (1988), Ibrahim, Chen, and Lipsitz (2001), and Tang, Little, and Raghunathan (2003). There has been some work done on maximum likelihood estimation in the presence of ignorable or nonignorable missing response and/or covariate data in longitudinal models, including Stubbendick and Ibrahim (2003, 2006) and Chen and Ibrahim (2006). However, there has been almost no literature examining theoretical properties of estimators in the presence of both MAR responses and covariates in regression models. This type of missing data problem presents many new challenges in estimation and theory that do not arise in missing covariate problems or missing response problems alone.

We refer to a regression problem with missing covariates and responses as a “missing (x, y) problem” throughout. An important issue in a missing (x, y) problem is the contribution to the information matrix of the cases with missing responses alone, the contributions of the cases with missing covariates alone, and the contributions of the cases with missing covariates and responses. In particular, we consider theoretical properties of the estimates under three different estimation settings: complete case analysis (CC), a complete response analysis (CR) that involves an analysis of those subjects with only completely observed responses, and the all case analysis (AC), which is an analysis based on all of the cases. Under each scenario, we derive general expressions for the likelihood and devise estimation schemes based on the EM algorithm. We compare the three estimation methods in the normal linear model and characterize the loss of information for each method as well as derive and compare the asymptotic variances for each method assuming the missing data are MAR. For the linear model, we show that AC analysis has more information than the CR and CC analyses in the sense that the Fisher information for the AC analysis has a greater determinant and trace compared to the Fisher information matrices for the CR and CC analyses, and the CR analysis yields a Fisher information with a greater determinant and trace compared to the Fisher information matrix for the CC analysis. Moreover, we show that the asymptotic variances of the estimates for the CC analyses are larger than the other two methods (CR or AC), and the asymptotic variances for some estimates in the AC analysis are larger than that of the corresponding estimates based on a CR analysis. We also carry out a theoretical investigation of bias for the CC method and analytically show that CC estimates under certain settings are biased.

The rest of this paper is organized as follows. In Section 2, we consider the basic data structure for a regression model with MAR response and/or covariate data. In Section 3, we consider the three analysis methods: CC, CR, and AC. For each method, we give the likelihood function corresponding to the method. Section 4 gets into the heart of the theory and properties of estimators for the three methods and several results are given characterizing the behavior of the Fisher information matrix and asymptotic variances for each method for the normal linear model with missing (x, y). Section 5 examines bias issues for MAR response and covariate data. Section 6 presents a simulation study and real dataset illustrating the theoretical results derived in Section 4. A brief discussion is given in Section 7. In the Appendix A, we devise the computational schemes based on the EM algorithm for obtaining the maximum likelihood estimates (MLE’s), and derive E and M-steps of the EM algorithm as well as the observed information matrix based on the observed data using Louis’s method for the missing (x, y) problem.

2 Model and Data Structure

2.1 Model

Suppose that {(x_i, y_i), i = 1, 2,…, n} are independent observations, where y_i is the response variable, and x_i = (x_i1, … , x_ip)′ is a p × 1 random vector of covariates. We specify the joint distribution of (x_i, y_i) by specifying the conditional distribution of y_i given x_i, denoted [y_i | x_i], and the marginal distribution of x_i, denoted [x_i].

We let

$$f({\mathit{x}}_i|\mathit{\alpha })$$

denote the joint density for the marginal distribution [x_i], where where α is the vector of model parameters for i = 1, 2, … , n. Assume that the distribution function for [y_i | x_i] is of the form

$$f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })=f(y_i|{\mathit{x}}_i^{\prime }\mathit{\beta },\mathit{\zeta }),$$ (2.1)

where β = (β₁, β₂,…, β_p)′ denotes the p × 1 random vector of regression coefficients, and ζ is the column vector of nuisance parameters. In (2.1), we assume that the distribution [y_i | x_i] depends on x_i and β only through x′β. If an intercept is included in the model, x_i and β are modified accordingly.

The generalized linear model (GLM) is a special case of (2.1). In the GLM, the conditional density of [y_i|x_i] is given by

$$f(y_i|x_i,\mathit{\beta },\tau )=\text{exp}\{a_i^{-1}\tau (y_i{\theta }_i-b({\theta }_i))+c(y_i,\tau )\},i=1,2,\dots ,n,$$ (2.2)

where θ_i = θ(η_i) is the canonical parameter, ${\eta }_i={\mathit{x}}_i^{\prime }\mathit{\beta }$, and τ is a dispersion parameter. The functions b and c determine a particular family in the class, such as the binomial, normal, Poisson, etc. The functions a_i(τ) are commonly of the form $a_i(\tau )={\tau }^{-1}{w}_i^{-1}$, where the w_i’s are known weights. Thus, (2.1) reduces to the GLM with

$$f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\zeta })=\text{exp}\{a_i\tau (y_i\theta ({\mathit{x}}_i^{\prime }\mathit{\beta })-b(\theta ({\mathit{x}}_i^{\prime }\mathit{\beta })))+c(y_i,\tau )\}$$

and ζ = τ.

2.2 Missing Data Structures

We consider a general setting in which y_i and some components of x_i may be missing. Let M_i = {1 ≤ l ≤ p : x_il is missing}, which denotes the set of indices for the i^th missing covariates. We also let Ω = {1,2,…,p} denote the whole index space for x_i. Table 1 gives the general data structure and characterizations of the various missing data patterns in the missing (x, y) problem.

Table 1.

The Data Structure with Various Missing Patterns

Pattern (Block)	Response	Covariates
	yi	xi
B1	observed	observed (Mi = θ)
B2	Observed	partially or all missing (Mi ≠ θ or Mi = Ω)
B3	missing	observed (Mi = θ)
B4	missing	only partially missing (Mi ≠ θ and Mi ≠ Ω)
B5	missing	completely missing (Mi = Ω)

We denote each pattern above by B_j, j = 1,…, 5, and refer to B_j as the j^th pattern or j^th block. B₁ denotes the portion of the data with both y_i and x_i completely observed. In B₂, y_i is observed while each x_i is at least partially missing or completely missing. In B₃, y_i is missing and x_i is completely observed, in B₄, y_i is missing but at least partial x_i is observed, and both y_i and x_i are completely missing in B₅.

Based on the data structure given in Table 1, we use y_i if the i^th response is observed and y_i,mis if the i_th response variable is missing. Also, we write ${\mathit{x}}_i=({\mathit{x}}_{i,\mathit{\text{obs}}}^{\prime },{\mathit{x}}_{i,\mathit{\text{mis}}}^{\prime })\prime$ where ${\mathit{x}}_{i,\mathit{\text{mis}}}^{\prime }=(x_{il},l\in M_i)$ and x_i,obs is the observed portion of x_i.

3 Three Analysis Methods

In this section, we assume that the missing response and the missing covariates are missing at random (MAR). Under the MAR assumption, we only need to model [y_i, x_i]. We give the forms of the observed data log-likelihood functions under three analysis methods: complete case (CC) analysis, complete response (CR) analysis, and all case (AC) analysis.

3.1 Complete Case (CC) Analysis

Because standard techniques for regression models require full response and covariate information, one simple way to avoid the problem of missing data is to analyze only those subjects who are completely observed. This method is known as a complete case (CC) analysis.

Based on the data structure displayed in Table 1, the CC analysis uses the portion of data given in Block B₁. Thus, the likelihood function under this method is given by

$$L_{cc}(\mathit{\theta })={\displaystyle \prod _{i:y_i\text{observed},M_i=\mathrm{\theta }}}f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })f({\mathit{x}}_i|\mathit{\alpha }),$$ (3.1)

where θ = (β, ϕ, α), and the log-likelihood function is given by

$$l_{cc}(\mathit{\theta })={\displaystyle \sum _{i:y_i\text{observed},M_i=\mathrm{\theta }}}[\text{log}f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })+\text{log}f({\mathit{x}}_i|\mathit{\alpha })].$$ (3.2)

3.2 Complete Response (CR) Analysis

The complete response cases (CR) analysis is to analyze only those subjects whose responses are completely observed. Thus, in the CR analysis, we only include the portion of data given in Blocks B₁ and B₂ of Table 1. The likelihood function under CR is given by

$$L_{cr}(\mathit{\theta })=L_{cc}{\displaystyle \prod _{i:y_i\text{observed},M_i\ne \mathrm{\theta }}}\left[{\displaystyle \int f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })}f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}|\mathit{\alpha })d{\mathit{x}}_{i,\mathit{\text{mis}}}\right],$$ (3.3)

and the log-likelihood function is given by

$$l_{cr}(\mathit{\theta })=l_{cc}+{\displaystyle \sum _{i:y_i\text{observed},M_i\ne \mathrm{\theta }}}\text{log}\left[{\displaystyle \int f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })}f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}|\mathit{\alpha })d{\mathit{x}}_{i,\mathit{\text{mis}}}\right].$$ (3.4)

3.3 All Case (AC) Analysis

The all cases (AC) analysis uses the whole data. The likelihood function is given by

$$\begin{array}{c}{L}_{ac}(\mathit{\theta })=L_{cr}\left[{\displaystyle \prod _{i:y_i\text{missing},M_i=\mathrm{\theta }}{\displaystyle \int f(y_{i,\mathit{\text{mis}}}|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })f({\mathit{x}}_i|\mathit{\alpha })d{\mathit{y}}_{i,\mathit{\text{mis}}}}}\right]\hfill \\ \times \left[{\displaystyle \prod _{i:y_i\text{missing},M_i\ne \mathrm{\theta },M_i\ne \mathrm{\Omega }}{\displaystyle \int {\displaystyle \int f(y_{i,\mathit{\text{mis}}}|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}|\mathit{\alpha })d{\mathit{y}}_{i,\mathit{\text{mis}}}d{\mathit{x}}_{i,\mathit{\text{mis}}}}}}\right]\hfill \\ \times \left[{\displaystyle \prod _{i:y_i\text{missing},M_i=\mathrm{\Omega }}{\displaystyle \int {\displaystyle \int f(y_{i,\mathit{\text{mis}}}|{\mathit{x}}_{i,\mathit{\text{mis}}},\mathit{\beta },\mathit{\varphi })f({\mathit{x}}_{i,\mathit{\text{mis}}}|\mathit{\alpha })d{\mathit{y}}_{i,\mathit{\text{mis}}}d{\mathit{x}}_{i,\mathit{\text{mis}}}}}}\right].\hfill \end{array}$$ (3.5)

Since

$${\displaystyle \int f(y_{i,\mathit{\text{mis}}}|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })d{\mathit{y}}_{i,\mathit{\text{mis}}}=1\text{and}{\displaystyle \int f({\mathit{x}}_{i,\mathit{\text{mis}}}|\mathit{\alpha })d{\mathit{x}}_{i,\mathit{\text{mis}}}=1,}}$$

the likelihood function L_ac(θ) reduces to

$$\begin{array}{ccc}{L}_{ac}(\mathit{\theta })\hfill & =\hfill & L_{cr}\left[{\displaystyle \prod _{i:y_i\text{missing},M_i=\mathrm{\theta }}f({\mathit{x}}_i|\mathit{\alpha })}\right]\hfill \\ \hfill & \hfill & \times \left[{\displaystyle \prod _{i:y_i\text{missing},M_i\ne \mathrm{\theta },M_i\ne \mathrm{\Omega }}{\displaystyle \int f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}|\mathit{\alpha })}d{\mathit{x}}_{i,\mathit{\text{mis}}}}\right].\hfill \end{array}$$ (3.6)

Thus, the portion of the data given in Block B₅ of Table 1 does not make any contribution to the likelihood function even under the AC analysis under the MAR assumption.

Using (3.6), the log-likelihood function is given by

$$\begin{array}{cc}{l}_{ac}(\mathit{\theta })=\hfill & l_{cr}+\left[{\displaystyle \sum _{i:y_i\text{missing},M_i=\mathrm{\theta }}\text{log}f({\mathit{x}}_i|\mathit{\alpha })}\right]\hfill \\ \hfill & +\left[{\displaystyle \sum _{i:y_i\text{missing},M_i\ne \mathrm{\theta },M_i\ne \mathrm{\Omega }}\text{log}{\displaystyle \int f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}|\mathit{\alpha })}d{\mathit{x}}_{i,\mathit{\text{mis}}}}\right].\hfill \end{array}$$ (3.7)

4 Theoretical Comparisons Between CC, CR, and AC for the Normal Linear Regression Model

In this section, we characterize the properties of the three analysis methods by examining the Fisher information matrix under each method and determining information loss (gain) for each method as well as comparing the asymptotic variances for each method. This comparison allows us to examine the efficiency of each method. To facilitate comparisons in this section, we assume that the missing data are MCAR, since closed-form analytic results for the Fisher information are available in the (x, y) missing problem only under MCAR.

4.1 Simple Linear Regression Model with Missing Responses and Covariates

We first consider a simple normal regression model with a single covariate and unit variances. In this case, we have

$$f(y_i|x_i,\mathit{\beta },\alpha )=\frac{1}{\sqrt{2\mathrm{\pi }}}\text{exp}\left\{-\frac{{(y_i-{\beta }_0-{\beta }_1{x}_i)}^2}{2}\right\}\text{and}f(x_i|\alpha )=\frac{1}{\sqrt{2\mathrm{\pi }}}\text{exp}\left\{-\frac{{(x_i-\alpha )}^2}{2}\right\}.$$ (4.1)

Write θ = (β′, α)′. Let n_j = #(B_j) be the cardinality of B_j for j = 1, 2, 3 and n = n₁ + n₂ + n₃. For the CC analysis, we have

$$l_{cc}(\mathit{\theta })={\displaystyle \sum _{i:y_i\text{observed},M_i=\mathrm{\theta }}\left[-\text{log}(2\mathrm{\pi })-\frac{{(y_i-{\beta }_0-{\beta }_1{x}_i)}^2}{2}-\frac{{(x_i-\alpha )}^2}{2}\right]}$$

and the Fisher information matrix is given by

$$I_{cc}(\mathit{\theta })=-E\left[\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\prime }}{l}_{cc}(\mathit{\theta })\right]=E\left[{\displaystyle \sum _{i\in B_1}\left(\begin{array}{ccc}\hfill 1\hfill & \hfill x_i\hfill & \hfill 0\hfill \\ \hfill x_i\hfill & \hfill x_i^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)}\right]=n_1\left(\begin{array}{ccc}\hfill 1\hfill & \hfill \alpha \hfill & \hfill 0\hfill \\ \hfill \alpha \hfill & \hfill 1+{\alpha }^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).$$ (4.2)

For the CR analysis, we have

$$l_{cr}(\mathit{\theta })=l_{cc}(\mathit{\theta })+{\displaystyle \sum _{i\in B_2}\left\{-\text{log}\sqrt{2\mathrm{\pi }}-\frac{1}{2}\text{log}(1+{\beta }_1^2)-\frac{1}{2(1+{\beta }_1^2)}{(y_i-{\beta }_0-{\beta }_1\alpha )}^2\right\}.}$$

After some messy algebra, we obtain the Fisher information matrix given by

$$\begin{array}{c}{I}_{cr}(\mathit{\theta })=-E\left[\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\prime }}{l}_{cr}(\mathit{\theta })\right]\hfill \\ =n_1\left(\begin{array}{ccc}\hfill 1\hfill & \hfill \alpha \hfill & \hfill 0\hfill \\ \hfill \alpha \hfill & \hfill 1+{\alpha }^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)+n_2\left(\begin{array}{ccc}\hfill \frac{1}{1+{\beta }_1^2}\hfill & \hfill \frac{\alpha }{1+{\beta }_1^2}\hfill & \hfill \frac{{\beta }_1}{1+{\beta }_1^2}\hfill \\ \hfill \frac{\alpha }{1+{\beta }_1^2}\hfill & \hfill \frac{{\alpha }^2}{1+{\beta }_1^2}+\frac{2{\beta }_1^2}{{(1+{\beta }_1^2)}^2}\hfill & \hfill \frac{\alpha {\beta }_1}{1+{\beta }_1^2}\hfill \\ \hfill \frac{{\beta }_1}{1+{\beta }_1^2}\hfill & \hfill \frac{\alpha {\beta }_1}{1+{\beta }_1^2}\hfill & \hfill \frac{{\beta }_1^2}{1+{\beta }_1^2}\hfill \end{array}\right).\end{array}$$ (4.3)

For the AC analysis, the log-likelihood function is given by

$$l_{ac}(\mathit{\theta })=l_{cr}(\mathit{\theta })+{\displaystyle \sum _{i:y_i\text{missing},M_i=\mathrm{\theta }}\text{log}f(x_i|\alpha )}=l_{cr}(\mathit{\theta })+{\displaystyle \sum _{i\in B_3}\left[-\text{log}\sqrt{2\mathrm{\pi }}-\frac{1}{2}{(x_i-\alpha )}^2\right]}.$$

The corresponding Fisher information matrix is given by

$$\begin{array}{c}{I}_{ac}(\mathit{\theta })=-E\left[\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\prime }}{l}_{ac}(\mathit{\theta })\right]\hfill \\ \hfill =n_1\left(\begin{array}{ccc}\hfill 1\hfill & \hfill \alpha \hfill & \hfill 0\hfill \\ \hfill \alpha \hfill & \hfill 1+{\alpha }^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)+n_2\left(\begin{array}{ccc}\hfill \frac{1}{1+{\beta }_1^2}\hfill & \hfill \frac{\alpha }{1+{\beta }_1^2}\hfill & \hfill \frac{{\beta }_1}{1+{\beta }_1^2}\hfill \\ \hfill \frac{\alpha }{1+{\beta }_1^2}\hfill & \hfill \frac{{\alpha }^2}{1+{\beta }_1^2}+\frac{2{\beta }_1^2}{{(1+{\beta }_1^2)}^2}\hfill & \hfill \frac{\alpha {\beta }_1}{1+{\beta }_1^2}\hfill \\ \hfill \frac{{\beta }_1}{1+{\beta }_1^2}\hfill & \hfill \frac{\alpha {\beta }_1}{1+{\beta }_1^2}\hfill & \hfill \frac{{\beta }_1^2}{1+{\beta }_1^2}\hfill \end{array}\right)+n_3\left(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).\hfill \end{array}$$ (4.4)

Using (4.2), we have

$$\mathit{\text{det}}(I_{cc})=n_1^3,\mathit{\text{tr}}(I_{cc})=n_1(3+{\alpha }^2),\text{and}{I}_{cc}^{-1}=\frac{1}{n_1}\left(\begin{array}{ccc}\hfill 1+{\alpha }^2\hfill & \hfill -\alpha \hfill & \hfill 0\hfill \\ \hfill -\alpha \hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right).$$ (4.5)

Observe that

$$I_{cr}(\mathit{\theta })=\left(\begin{array}{ccc}\hfill n_1\hfill & \hfill n_1\alpha \hfill & \hfill 0\hfill \\ \hfill n_1\alpha \hfill & \hfill n_1+n_1{\alpha }^2+\frac{2n_2{\beta }_1^2}{{(1+{\beta }_1^2)}^2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill n_1\hfill \end{array}\right)+\frac{n_2}{1+{\beta }_1^2}\left(\begin{array}{c}\hfill 1\hfill \\ \hfill \alpha \hfill \\ \hfill {\beta }_1\hfill \end{array}\right)(\begin{array}{ccc}\hfill 1\hfill & \hfill \alpha \hfill & \hfill {\beta }_1\hfill \end{array})\stackrel{\mathit{\text{def}}}{=}A+u{u}^{\prime },$$

where

$$A=\left(\begin{array}{ccc}\hfill n_1\hfill & \hfill n_1\alpha \hfill & \hfill 0\hfill \\ \hfill n_1\alpha \hfill & \hfill n_1+n_1{\alpha }^2+\frac{2n_2{\beta }_1^2}{{(1+{\beta }_1^2)}^2}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill n_1\hfill \end{array}\right)$$

and $\mathit{u}=\sqrt{\frac{n_2}{1+{\beta }_1^2}}(\begin{array}{ccc}\hfill 1\hfill & \hfill \alpha \hfill & \hfill {\beta }_1{)}^{\prime }\hfill \end{array}$. After some algebra, we have

$$A^{-1}=\frac{1}{n_1\left[1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}\right]}\left(\begin{array}{ccc}\hfill 1+{\alpha }^2+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}\hfill & \hfill -\alpha \hfill & \hfill 0\hfill \\ \hfill -\alpha \hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}\hfill \end{array}\right).$$

Note that u′A⁻¹u = n₂/n₁. Thus, we have

$$\begin{array}{cc}\mathit{\text{det}}(I_{cr})\hfill & =\mathit{\text{det}}(A)(1+{\mathit{u}}^{\prime }{A}^{-1}\mathit{u})=n_1^3\left[1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}\right]\left(1+\frac{n_2}{n_1}\right)\hfill \\ \hfill & =n_1^3+n_1^2{n}_2+\frac{2n_1{n}_2{\beta }_1^2(n_1+n_2)}{{(1+{\beta }_1^2)}^2}=\mathit{\text{det}}(I_{cc})+n_1^2{n}_2+\frac{2n_1{n}_2{\beta }_1^2(n_1+n_2)}{{(1+{\beta }_1^2)}^2},\hfill \end{array}$$ (4.6)

the trace of I_cr is given by

$$\mathit{\text{tr}}(I_{cr})=\mathit{\text{tr}}(I_{cc})+n_2\left[1+\frac{{\alpha }^2}{1+{\beta }_1^2}+\frac{2{\beta }_1^2}{{(1+{\beta }_1^2)}^2}\right],$$ (4.7)

and the inverse matrix of I_cr is given by

$$\begin{array}{cc}{I}_{cr}^{-1}(\mathit{\theta })\hfill & =A^{-1}-\frac{1}{1+{\mathit{u}}^{\prime }{A}^{-1}\mathit{u}}{A}^{-1}\mathit{u}{\mathit{u}}^{\prime }{A}^{-1}=A^{-1}-\frac{1}{1+n_2/n_1}{A}^{-1}\mathit{u}{\mathit{u}}^{\prime }{A}^{-1}\hfill \\ \hfill & =A^{-1}-\frac{n_2}{n_1(n_1+n_2)(1+{\beta }_1^2)}\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill {\beta }_1\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill {\beta }_1\hfill & \hfill 0\hfill & \hfill {\beta }_1^2\hfill \end{array}\right)\hfill \\ \hfill & =\frac{1}{n_1}\left(\begin{array}{ccc}\hfill 1+\frac{{\alpha }^2}{1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}}-\frac{n_2}{(n_1+n_2)(1+{\beta }_1^2)}\hfill & \hfill -\frac{\alpha }{1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}}\hfill & \hfill -\frac{n_2{\beta }_1}{(n_1+n_2)(1+{\beta }_1^2)}\hfill \\ \hfill -\frac{\alpha }{1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}}\hfill & \hfill \frac{1}{1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}}\hfill & \hfill 0\hfill \\ \hfill -\frac{n_2{\beta }_1}{(n_1+n_2)(1+{\beta }_1^2)}\hfill & \hfill 0\hfill & \hfill 1-\frac{n_2}{n_1+n_2}\frac{{\beta }_1^2}{1+{\beta }_1^2}\hfill \end{array}\right).\hfill \end{array}$$ (4.8)

Similarly, we can write

$$I_{ac}(\mathit{\theta })=I_{cr}+\mathit{\upsilon }{\mathit{\upsilon }}^{\prime },$$

where $\mathit{\upsilon }=\sqrt{n_3}(\begin{array}{ccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}{)}^{\prime }$. We have

$$\begin{array}{cc}\mathit{\text{det}}(I_{ac})\hfill & =\mathit{\text{det}}(I_{cr})(1+{\mathit{\upsilon }}^{\prime }{I}_{cr}^{-1}\mathit{\upsilon })=\mathit{\text{det}}(I_{cr})+\mathit{\text{det}}(I_{cr}){\mathit{\upsilon }}^{\prime }{I}_{cr}^{-1}\mathit{\upsilon }\hfill \\ \hfill & =\mathit{\text{det}}(I_{cr})+n_3\left[n_1+\frac{2n_2{\beta }_1^2}{{(1+{\beta }_1^2)}^2}\right]\left[n_1+\frac{n_2}{1+{\beta }_1^2}\right],\hfill \end{array}$$ (4.9)

the trace of I_ac is given by

$$\mathit{\text{tr}}(I_{ac})=\mathit{\text{tr}}(I_{cr})+n_3,$$ (4.10)

and the inverse matrix of I_ac is given by

$$\begin{array}{cc} \hfill & I_{ac}^{-1}(\mathit{\theta })=I_{cr}^{-1}-\frac{1}{1+{\mathit{\upsilon }}^{\prime }{I}_{cr}^{-1}\mathit{\upsilon }}{I}_{cr}^{-1}\mathit{\upsilon }{\mathit{\upsilon }}^{\prime }{I}_{cr}^{-1}\hfill \\ =\hfill & I_{cr}^{-1}-\frac{b*}{n_1}\left(\begin{array}{ccc}\hfill n_2{\beta }_1^2\hfill & \hfill 0\hfill & \hfill -n_2{\beta }_1[n_1(1+{\beta }_1^2)+n_2]\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill -n_2{\beta }_1[n_1(1+{\beta }_1^2)+n_2]\hfill & \hfill 0\hfill & \hfill {[n_1(1+{\beta }_1^2)+n_2]}^2\hfill \end{array}\right)\hfill \\ =\hfill & \frac{1}{n_1}\left(\begin{array}{ccc}\hfill 1+\frac{{\alpha }^2}{1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}}-\frac{n_2}{(n_1+n_2)(1+{\beta }_1^2)}-b^{*}{n}_2{\beta }_1^2\hfill & \hfill -\frac{\alpha }{1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}}\hfill & \hfill -\frac{n_2{\beta }_1}{(n_1+n_2)(1+{\beta }_1^2)}+b^{*}{n}_2{\beta }_1{b}_1^{*}\hfill \\ \hfill -\frac{\alpha }{1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}}\hfill & \hfill \frac{1}{1+\frac{2n_2{\beta }_1^2}{n_1{(1+{\beta }_1^2)}^2}}\hfill & \hfill 0\hfill \\ \hfill -\frac{n_2{\beta }_1}{(n_1+n_2)(1+{\beta }_1^2)}+b^{*}{n}_2{\beta }_1{b}_1^{*}\hfill & \hfill 0\hfill & \hfill 1-\frac{n_2}{n_1+n_2}\frac{{\beta }_1^2}{1+{\beta }_1^2}-b^{*}{b_1^{*}}^2\hfill \end{array}\right),\hfill \end{array}$$ (4.11)

where $b^{*}=\frac{n_3}{(n_1+n_2)(1+{\beta }_1^2)[n_2{n}_3+n_1(n_1+n_2+n_3)(1+{\beta }_1^2)]}\text{and}{b}_1^{*}=n_1(1+{\beta }_1^2)+n_2$.

Using (4.5) — (4.11), we are led to the following results.

Result 4.1

Based on either the determinant or the trace of Fisher information matrix, AC yields most gain in information over both CR and CC, and CR gains more information than CC. Specifically, we have

$$\begin{array}{c}\hfill \text{det}(I_{ac})-\text{det}(I_{cr})=n_3\left[n_1+\frac{2n_2{\beta }_1^2}{{(1+{\beta }_1^2)}^2}\right]\left[n_1+\frac{n_2}{1+{\beta }_1^2}\right]>0,\hfill \\ \hfill \text{det}(I_{cr})-\text{det}(I_{cc})=n_1^2{n}_2+\frac{2n_1{n}_2{\beta }_1^2(n_1+n_2)}{{(1+{\beta }_1^2)}^2}>0,\hfill \\ \hfill \mathit{\text{tr}}(I_{ac})-\mathit{\text{tr}}(I_{cr})=n_3>0,\hfill \end{array}$$

and

$$\mathit{\text{tr}}(I_{cr})-\mathit{\text{tr}}(I_{cc})=n_2\left[1+\frac{{\alpha }^2}{1+{\beta }_1^2}+\frac{2{\beta }_1^2}{{(1+{\beta }_1^2)}^2}\right].$$

The inverse of the Fisher information gives the asymptotic variance and covariance matrix of the MLE’s under each analysis method. Now, let Var $({\hat{\beta }}_j,.)$ and Var (α̂.) denote the asymptotic variances under each of CC, CR, AC. Then, we have the following results.

Result 4.2

(i) CR leads to smaller asymptotic variances for all parameters than CC. Specifically, we have

$$\begin{array}{cc}\mathit{\text{Var}}({\hat{\beta }}_{0,cc})-\mathit{\text{Var}}({\hat{\beta }}_{0,cr})\hfill & =\frac{2n_2{\alpha }^2{\beta }_1^2}{n_1[{(1+{\beta }_1^2)}^2+2n_2{\beta }_1^2]}+\frac{n_2}{n_1(n_1+n_2)(1+{\beta }_1^2)}>0,\hfill \\ \mathit{\text{Var}}({\hat{\beta }}_{1,cc})-\mathit{\text{Var}}({\hat{\beta }}_{1,cr})\hfill & =\frac{2n_2{\beta }_1^2}{n_1[n_1{(1+{\beta }_1^2)}^2+2n_2{\beta }_1^2]}>0,\hfill \\ \hfill \mathit{\text{Var}}({\hat{\alpha }}_{cc})-\mathit{\text{Var}}({\hat{\alpha }}_{cr})& =\frac{n_1{n}_2{\beta }_1^2}{n_1(n_1+n_2)(1+{\beta }_1^2)}>0.\hfill \end{array}$$

(ii) AC improves the asymptotic variances for β₀ and α over CR, but not for β₁. Specifically, we have

$$\begin{array}{cc}\mathit{\text{Var}}({\hat{\beta }}_{0,cr})-\mathit{\text{Var}}({\hat{\beta }}_{0,ac})\hfill & =b^{*}{n}_2{\beta }_1^2>0,\hfill \\ \mathit{\text{Var}}({\hat{\beta }}_{1,cr})-\mathit{\text{Var}}({\hat{\beta }}_{1,ac})\hfill & =0,\hfill \\ \hfill \mathit{\text{Var}}({\hat{\alpha }}_{cr})-\text{Var}({\hat{\alpha }}_{ac})& =b^{*}{b_1^{*}}^2>0,\hfill \end{array}$$

where b^* and $b_1^{*}$ are given in (4.11).

From Result 4.2, the additional information from Block B₃ does improve the standard errors of ${\hat{\beta }}_0$ and α̂. Surprisingly, the information from Block B₃ does not help improve the standard error of ${\hat{\beta }}_1$.

4.2 Multiple Linear Regression Model with Missing Responses and Covariates

To further examine the theoretical relationship among these three analysis methods, we consider a multiple normal linear regression model with p ≥ 2. For illustrative purposes, it suffices to consider two missing covariates. Specifically, we assume that x_i,p−1 and x_i,p have at least one missing value and x_i1, x_i2, and x_i,p−2 are observed in all cases as we have shown in Section 3.3 that the cases in Block 5 do not make any contribution to the log-likelihood function l_ac(θ). For notational convenience, we let z_i1 = (1, x_i1,…,x_i,p−2)′. We further assume

$$\begin{array}{c}\hfill y_i|{\mathit{x}}_i,\mathit{\beta }~N(({\mathit{z}}_{i1}^{\prime },x_{i,p-1},x_{ip}{)}^{\prime }({\mathit{\beta }}_0,{\beta }_1,{\beta }_2),{\sigma }^2),\hfill \\ \hfill x_{i,p-1}|x_i^{(\mathit{\text{obs}})},{\mathit{\alpha }}_1~N({\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_1,{\tau }_1^2),\hfill \end{array}$$

where α₁ = (α₁₀, α₁₁,…,α_1,p−2)′, and

$$x_{ip}|x_i^{(\mathit{\text{obs}})},x_{i,p-1},{\mathit{\alpha }}_2~N(({\mathit{z}}_{i1}^{\prime },x_{i,p-1})({\mathit{\alpha }}_{21},{\alpha }_{22}),{\tau }_2^2),$$

where α₂₁ = (α₂₀, α₂₁,…, α_2,p−2)′. We assume all variances ${\sigma }^2,{\tau }_1^2,\text{and}{\tau }_2^2$ are known. For ease of exploration, we choose ${\sigma }^2={\tau }_1^2={\tau }_2^2=1$.

In this setting, we need to consider the cases from Blocks 1 to 4.

For Blocks 2 and 4, we assume $B_2={\displaystyle {\cup }_{k=2}^4{B}_{2k}}\text{and}{B}_4={\displaystyle {\cup }_{k=2}^3{B}_{4k}}$, where

$$\begin{array}{c}{B}_{j1}=\{i:\text{both}{x}_{i,p-1}\text{and}{x}_{ip}\text{are observed}\},\hfill \\ B_{j2}=\{i:x_{i,p-1}\text{is missing and}{x}_{ip}\text{is observed}\},\hfill \\ B_{j3}=\{i:x_{i,p-1}\text{is observed and}{x}_{ip}\text{is missing}\}\hfill \end{array}$$

for j = 2, 4, and B₂₄ = {i : both x_i,p−1 and x_ip are missing}. We further let n_jk = #(B_jk) be the cardinality of B_jk for j = 2, 4. Then we have $n_2={\displaystyle {\sum }_{k=2}^4{n}_{2k}}\text{and}{n}_4={\displaystyle {\sum }_{k=2}^3{n}_{4k}}$.

Define $A_j={\displaystyle {\sum }_{i\in B_j}{\mathit{z}}_{i1}{\mathit{z}}_{i1}^{\prime }}$, where j = 1, 22, 23, 24, 3, 42, 43, and $\mathit{\theta }=({\mathit{\beta }}_0^{\prime },{\beta }_1,{\beta }_2,{\mathit{\alpha }}_1^{\prime },{\mathit{\alpha }}_{21}^{\mathit{\prime }},{\alpha }_{22})\prime$. For the CC analysis, we have

$$\begin{array}{cc}{l}_{cc}(\mathit{\theta })={\displaystyle \sum _{i:y_i\text{observed},M_i=\mathrm{\theta }}}\hfill & [-\frac{3}{2}\text{log}(2\mathrm{\pi })-\frac{{(y_i-{\mathit{z}}_{i1}^{\prime }{\beta }_0-{\beta }_1{x}_{i,p-1}-{\beta }_2{x}_{ip})}^2}{2}\hfill \\ \hfill & -\frac{{(x_{i,p-1}-{\mathit{z}}_{i1}{\mathit{\alpha }}_1)}^2}{2}-\frac{{(x_{ip}-z_{i1}{\mathit{\alpha }}_{21}-x_{i,p-1}{\alpha }_{22})}^2}{2}]\hfill \end{array}$$

and the Fisher information matrix is given by

$$I_{cc}(\mathit{\theta })=(\begin{array}{cccccc}\hfill A_1\hfill & \hfill A_1{\mathit{\alpha }}_1\hfill & \hfill A_1{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill {\mathit{\alpha }}_1^{\prime }{A}_1\hfill & \hfill n_1+{\mathit{\alpha }}_1^{\prime }{A}_1{\mathit{\alpha }}_1\hfill & \hfill n_1{\alpha }_{22}+{\mathit{\alpha }}_1^{\prime }{A}_1{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill 0\hfill \\ \hfill {\tilde{\mathit{\alpha }}}_{12}^{\prime }{A}_1\hfill & \hfill n_1{\alpha }_{22}+{\mathit{\alpha }}_1^{\prime }{A}_1{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill n_1(1+{\alpha }_{22}^2)+{\tilde{\mathit{\alpha }}}_{12}^{\prime }{A}_1{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill 0\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill A_1\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill A_1\hfill & \hfill A_1{\mathit{\alpha }}_1\hfill \\ \hfill \mathbf{0}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \mathbf{0}\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{A}_1\hfill & \hfill n_1+{\mathit{\alpha }}_1^{\prime }{A}_1{\mathit{\alpha }}_1\hfill \end{array}),$$

where ${\tilde{\mathit{\alpha }}}_{12}={\mathit{\alpha }}_{21}+{\mathit{\alpha }}_1{\alpha }_{22}$.

For the CR analysis, we have

$$\begin{array}{c}{l}_{cr}(\mathit{\theta })=l_{cc}(\mathit{\theta })\hfill \\ \hfill +{\displaystyle \sum _{i:y_i\text{observed},M_i\ne \mathrm{\theta }}\text{log}\left[{\displaystyle \int f(y_i|{\mathit{x}}_i,\mathit{\beta })}f(x_{i,p}|{\mathit{z}}_{i1},x_{i,p-1},{\mathit{\alpha }}_2)f(x_{i,p-1}|{\mathit{z}}_{i1},{\mathit{\alpha }}_1)d{x}_{i,\mathit{\text{mis}}}\right]}\hfill \\ =l_{cc}(\mathit{\theta })+l_{cc,1}(\mathit{\theta })+l_{cc,2}(\mathit{\theta }),\hfill \end{array}$$

where

$$\begin{array}{cc} \hfill & l_{cc,1}(\mathit{\theta })\hfill \\ =\hfill & {\displaystyle \sum _{i\in B_{22}}\{-\text{log}(2\mathrm{\pi })-\frac{\text{log}(1+{\beta }_1^2+{\alpha }_{22}^2)}{2}-[{({\alpha }_{22}(y_i-{\mathit{z}}_{i1}^{\prime }{\mathit{\beta }}_0-x_{ip}{\beta }_2)-{\beta }_1(x_{ip}-{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_{21}))}^2}\hfill \\ \hfill & \hfill +{(y_i-{\mathit{z}}_{i1}^{\prime }{\mathit{\beta }}_0-{\beta }_1{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_1-x_{ip}{\beta }_2)}^2+{(x_{ip}-{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_{21}-{\alpha }_{22}{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_1)}^2]/2(1+{\beta }_1^2+{\alpha }_{22}^2)\}\end{array}$$

and

$$\begin{array}{cc} \hfill & l_{cc,2}(\mathit{\theta })\hfill \\ =\hfill & {\displaystyle \sum _{i\in B_{23}}\{-\text{log}(2\mathrm{\pi })-\frac{1}{2}\text{log}(1+{\beta }_2^2)-\frac{[{(y_i-{\mathit{z}}_{i1}^{\prime }{\mathit{\beta }}_0-x_{i,p-1}{\beta }_1-{\beta }_2({\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_{21}+x_{i,p-1}{\alpha }_{22})]}^2}{2(1+{\beta }_2^2)}}\hfill \\ \hfill & -\frac{{(x_{i,p-1}-{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_1)}^2}{2}\}+{\displaystyle \sum _{i\in B_{24}}\{-\frac{1}{2}\text{log}(2\mathrm{\pi })-\frac{1}{2}\text{log}({({\beta }_1+{\beta }_2{\alpha }_{22})}^2+1+{\beta }_2^2)}\hfill \\ \hfill & -\frac{[{(y_i-{\mathit{z}}_{i1}^{\prime }{\mathit{\beta }}_0-{\beta }_2{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_1-({\beta }_1+{\beta }_2{\alpha }_{22}){\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_1]}^2}{2({({\beta }_1+{\beta }_2{\alpha }_{22})}^2+1+{\beta }_2^2)}\}.\hfill \end{array}$$

After some messy algebra, we obtain the Fisher information matrix given by

$$I_{cr}(\mathit{\theta })=-E\left[\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\prime }}{l}_{cr}(\mathit{\theta })\right]=I_{cr}(\mathit{\theta })+I_{cr,1}(\mathit{\theta })+n_{22}{I}_{cr,2}(\mathit{\theta })+n_{23}{I}_{cr,3}+n_{24}{I}_{cr,4},$$

where

$$I_{cr,1}(\mathit{\theta })=\left(\begin{array}{cccccc}\hfill M_1\hfill & \hfill M_1{\mathit{\alpha }}_1\hfill & \hfill M_1{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill M_2\hfill & \hfill M_3\hfill & \hfill M_3{\mathit{\alpha }}_1\hfill \\ \hfill {\mathit{\alpha }}_1^{\prime }{M}_1\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_1{\mathit{\alpha }}_1\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_1{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_2\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_3\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_3{\mathit{\alpha }}_1\hfill \\ \hfill {\tilde{\mathit{\alpha }}}_{12}^{\prime }{M}_1\hfill & \hfill {\tilde{\mathit{\alpha }}}_{12}^{\prime }{M}_1{\mathit{\alpha }}_1\hfill & \hfill {\tilde{\mathit{\alpha }}}_{12}^{\prime }{M}_1{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill {\tilde{\mathit{\alpha }}}_{12}^{\prime }{M}_2\hfill & \hfill {\tilde{\mathit{\alpha }}}_{12}^{\prime }{M}_3\hfill & \hfill {\tilde{\mathit{\alpha }}}_{12}^{\prime }{M}_3{\mathit{\alpha }}_1\hfill \\ \hfill M_2\hfill & \hfill M_2{\mathit{\alpha }}_1\hfill & \hfill M_2{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill M_6\hfill & \hfill M_4\hfill & \hfill M_4{\mathit{\alpha }}_1\hfill \\ \hfill M_3\hfill & \hfill M_3{\mathit{\alpha }}_1\hfill & \hfill M_3{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill M_4\hfill & \hfill M_5\hfill & \hfill M_5{\mathit{\alpha }}_1\hfill \\ \hfill {\mathit{\alpha }}_1^{\prime }{M}_3\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_3{\mathit{\alpha }}_1\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_3{\tilde{\mathit{\alpha }}}_{12}\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_4\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_5\hfill & \hfill {\mathit{\alpha }}_1^{\prime }{M}_5{\mathit{\alpha }}_1\hfill \end{array}\right),$$

$$I_{cr,2}(\mathit{\theta })=\left(\begin{array}{cccccc}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \frac{{\alpha }_{22}^2}{{\upsilon }_{22}}+\frac{2{\beta }_1^2}{{\upsilon }_{22}^2}\hfill & \hfill \frac{{\alpha }_{22}(1+{\alpha }_{22}^2)}{{\upsilon }_{22}}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill -\frac{{\alpha }_{22}{\beta }_1}{{\upsilon }_{22}}+\frac{2{\alpha }_{22}{\beta }_1}{{\upsilon }_{22}^2}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \frac{{\alpha }_{22}(1+{\alpha }_{22}^2)}{{\upsilon }_{22}}\hfill & \hfill \frac{{(1+{\alpha }_{22}^2)}^2}{{\upsilon }_{22}}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \frac{{\beta }_1(1-{\alpha }_{22}^2)}{{\upsilon }_{22}}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill -\frac{{\alpha }_{22}{\beta }_1}{{\upsilon }_{22}}+\frac{2{\alpha }_{22}{\beta }_1}{{\upsilon }_{22}^2}\hfill & \hfill \frac{{\beta }_1(1-{\alpha }_{22}^2)}{{\upsilon }_{22}}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \frac{{\beta }_1^2}{{\upsilon }_{22}}+\frac{2{\alpha }_{22}^2}{{\upsilon }_{22}^2}\hfill \end{array}\right),$$

$$I_{cr,3}(\mathit{\theta })=\left(\begin{array}{cccccc}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \frac{1}{{\upsilon }_{23}}\hfill & \hfill \frac{{\alpha }_{22}}{{\upsilon }_{23}}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \frac{{\beta }_2}{{\upsilon }_{23}}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \frac{{\alpha }_{22}}{{\upsilon }_{23}}\hfill & \hfill \frac{{\alpha }_{22}^2}{{\upsilon }_{23}}+\frac{2{\beta }_2^2}{{\upsilon }_{23}^2}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \frac{{\beta }_2{\alpha }_{22}}{{\upsilon }_{23}}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \frac{{\beta }_2}{{\upsilon }_{23}}\hfill & \hfill \frac{{\beta }_2{\alpha }_{22}}{{\upsilon }_{23}}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \frac{{\beta }_2^2}{{\upsilon }_{23}}\hfill \end{array}\right),$$

$$I_{cr,4}(\mathit{\theta })=\left(\begin{array}{cccccc}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \frac{2{({\beta }_1+{\beta }_2{\alpha }_{22})}^2}{{\upsilon }_{24}^2}\hfill & \hfill \frac{2({\beta }_1+{\beta }_2{\alpha }_{22}){\upsilon }_{25}}{{\upsilon }_{24}^2}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \frac{2{\beta }_2{({\beta }_1+{\beta }_2{\alpha }_{22})}^2}{{\upsilon }_{24}^2}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \frac{2({\beta }_1+{\beta }_2{\alpha }_{22}){\upsilon }_{25}}{{\upsilon }_{24}^2}\hfill & \hfill \frac{2{\upsilon }_{25}^2}{{\upsilon }_{24}^2}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \frac{2{\beta }_2({\beta }_1+{\beta }_2{\alpha }_{22}){\upsilon }_{25}}{{\upsilon }_{24}^2}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \frac{2{\beta }_2{({\beta }_1+{\beta }_2{\alpha }_{22})}^2}{{\upsilon }_{24}^2}\hfill & \hfill \frac{2{\beta }_2({\beta }_1+{\beta }_2{\alpha }_{22}){\upsilon }_{25}}{{\upsilon }_{24}^2}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \frac{2{\beta }_2^2{({\beta }_1+{\beta }_2{\alpha }_{22})}^2}{{\upsilon }_{24}^2}\hfill \end{array}\right),$$

${\upsilon }_{22}=1+{\beta }_1^2+{\alpha }_{22}^2,{\upsilon }_{23}=1+{\beta }_2^2,{\upsilon }_{24}={({\beta }_1+{\beta }_2{\alpha }_{22})}^2+1+{\beta }_2^2,{\upsilon }_{25}={\beta }_2+({\beta }_1+{\beta }_2{\alpha }_{22}){\alpha }_{22},M_1=\frac{1+{\alpha }_{22}^2}{{\upsilon }_{22}}{A}_{22}+\frac{1}{{\upsilon }_{23}}{A}_{23}+\frac{1}{{\upsilon }_{24}}{A}_{24},M_2=\frac{{\beta }_1}{{\upsilon }_{22}}{A}_{22}+\frac{{\beta }_1+{\beta }_2{\alpha }_{22}}{{\upsilon }_{24}}{A}_{24},M_3=-\frac{{\beta }_1{\alpha }_{22}}{{\upsilon }_{22}}{A}_{22}+\frac{{\beta }_2}{{\upsilon }_{23}}{A}_{23}+\frac{{\beta }_2}{{\upsilon }_{24}}{A}_{24},M_4=\frac{{\alpha }_{22}}{{\upsilon }_{22}}{A}_{22}+\frac{{\beta }_2({\beta }_1+{\beta }_2{\alpha }_{22})}{{\upsilon }_{24}}{A}_{24},M_5=\frac{1+{\beta }_1^2}{{\upsilon }_{22}}{A}_{22}+\frac{{\beta }_2^2}{{\upsilon }_{23}}{A}_{23}+\frac{{\beta }_2^2}{{\upsilon }_{24}}{A}_{24},\text{and}{M}_6=\frac{{\beta }_1^2+{\alpha }_{22}^2}{{\upsilon }_{22}}{A}_{22}+A_{23}+\frac{{({\beta }_1+{\beta }_2{\alpha }_{22})}^2}{{\upsilon }_{24}}{A}_{24}$.

For the AC analysis, the log-likelihood function is given by

$$\begin{array}{cc} \hfill & l_{ac}(\mathit{\theta })\hfill \\ =\hfill & l_{cr}(\mathit{\theta })+{\displaystyle \sum _{i\in B_3}\left\{-\text{log}(2\mathrm{\pi })-\frac{{({\mathit{x}}_{i,p-1}-{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_1)}^2}{2}-\frac{{(x_{ip}-{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_{21}-x_{i,p-1}{\alpha }_{22})}^2}{2}\right\}}\hfill \\ \hfill & +{\displaystyle \sum _{i\in B42}\left\{-\frac{\text{log}(2\mathrm{\pi })}{2}-\frac{1}{2}\text{log}(1+{\alpha }_{22}^2)-\frac{{(x_{ip}-{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_{21}-{\alpha }_{22}^2{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_1)}^2}{2(1+{\alpha }_{22}^2)}\right\}+}\hfill \\ \hfill & +{\displaystyle \sum _{i\in B43}\left\{-\frac{1}{2}\text{log}(2\mathrm{\pi })-\frac{1}{2}{(x_{i,p-1}-{\mathit{z}}_{i1}^{\prime }{\mathit{\alpha }}_1)}^2\right\}}\hfill \end{array}$$

The corresponding Fisher information matrix is given by

$$\begin{array}{c}{I}_{ac}(\mathit{\theta })=I_{cr}(\mathit{\theta })\hfill \\ +\left(\begin{array}{cccc}\hfill {\mathbf{0}}_{(p+1)\times (p+1)}\hfill & \hfill {\mathbf{0}}_{(p+1)\times (p-1)}\hfill & \hfill {\mathbf{0}}_{(p+1)\times (p-1)}\hfill & \hfill 0\hfill \\ \hfill {\mathbf{0}}_{(p-1)\times (p+1)}\hfill & \hfill A_3+\frac{{\alpha }_{22}^2}{{\upsilon }_{42}}{A}_{42}+A_{43}\hfill & \hfill \frac{{\alpha }_{22}}{{\upsilon }_{42}}{A}_{42}\hfill & \hfill \frac{{\alpha }_{22}}{{\upsilon }_{42}}{A}_{42}{\mathit{\alpha }}_1\hfill \\ \hfill {\mathbf{0}}_{(p-1)\times (p+1)}\hfill & \hfill \frac{{\alpha }_{22}}{{\upsilon }_{42}}{A}_{42}\hfill & \hfill A_3+\frac{1}{{\upsilon }_{42}}{A}_{42}\hfill & \hfill A_3{\mathit{\alpha }}_1+\frac{1}{{\upsilon }_{42}}{A}_{42}{\mathit{\alpha }}_1\hfill \\ \hfill {\mathbf{0}}_{1\times (p+1)}\hfill & \hfill \frac{{\alpha }_{22}}{{\upsilon }_{42}}{\mathit{\alpha }}_1^{\prime }{A}_{42}\hfill & \hfill {\alpha }_1^{\prime }{A}_3+\frac{1}{{\upsilon }_{42}}{\mathit{\alpha }}_1^{\prime }{A}_{42}\hfill & \hfill i_{22}\hfill \end{array}\right),\hfill \end{array}$$ (4.12)

where ${\upsilon }_{42}=1+{\alpha }_{22}^2\text{and}{i}_{22}=n_3+{\mathit{\alpha }}_1^{\prime }{A}_3{\mathit{\alpha }}_1+n_{42}\frac{2{\alpha }_{22}^2}{{\upsilon }_{42}^2}+\frac{1}{{\upsilon }_{42}}{\mathit{\alpha }}_1^{\prime }{A}_{42}{\mathit{\alpha }}_1$.

For ease of exploration, we choose p=2, in other words, the completely observed covariates only include the intercept.

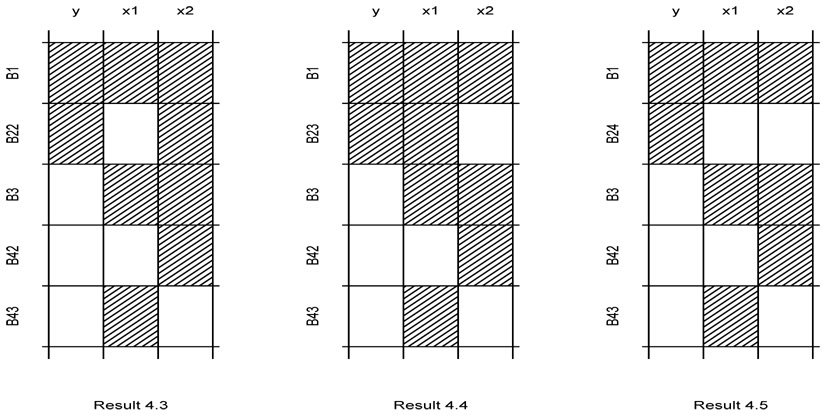
Result 4.3

(i) When n₂₃ = n₂₄ = 0, CR leads to smaller asymptotic variances for β₁ and β₂ than CC. Specifically, we have

$$\begin{array}{cc} \hfill & \mathit{\text{Var}}({\hat{\beta }}_{1,cc})-\mathit{\text{Var}}({\hat{\beta }}_{1,cr})\hfill \\ =\hfill & \frac{2n_{22}{\beta }_1^2[{\upsilon }_{42}(n_1+n_{22})(n_1{\upsilon }_{42}^2+2n_{22}{\alpha }_{22}^2)+n_1^2{\upsilon }_{42}^2{\beta }_1^2+n_1{n}_{22}(1+{\alpha }_{22}^4){\beta }_1^2]}{d_{11}}>0,\hfill \\ \hfill & \mathit{\text{Var}}({\hat{\beta }}_{2,cc})-\mathit{\text{Var}}({\hat{\beta }}_{2,cr})\hfill \\ =\hfill & \frac{4n_{22}^3{\alpha }_{22}^2{\beta }_1^2+n_1^2{n}_{22}{\upsilon }_{22}^2+2n_1{n}_{22}{\upsilon }_{22}{\alpha }_{22}^2{\beta }_1^2(n_1+n_{22})+2n_1{n}_{22}^2({\alpha }_{22}^2+{\beta }_1^2+3{\alpha }_{22}^2{\beta }_1^2)}{d_{11}}>0,\hfill \end{array}$$

where $d_{11}=n_1^2(n_1+n_{22}){\upsilon }_{22}[n_1{\upsilon }_{22}^2+2n_{22}({\beta }_1^2+{\alpha }_{22}^2+{\beta }_1^2{\alpha }_{22}^2)]+2n_1{n}_{22}^2{\beta }_1^2{\alpha }_{22}^2(3n_1+2n_{22})$.

(ii) When n₂₃ = n₂₄ = 0, AC leads to smaller asymptotic variances for β₁ and β₂ than CR. Specifically, we have

$$\begin{array}{c}\hfill \mathit{\text{Var}}({\hat{\beta }}_{1,cr})-\mathit{\text{Var}}({\hat{\beta }}_{1,ac})=\frac{4n_1{n}_{22}^2{\alpha }_{22}^2{\beta }_1^6(n_3{\upsilon }_{42}^2+2n_{42}{\alpha }_{22}^2){[{\upsilon }_{42}(n_1+n_{22})+n_1{\beta }_1^2]}^2}{d_{13}}>0,\hfill \\ \hfill \mathit{\text{Var}}({\hat{\beta }}_{2,cr})-\mathit{\text{Var}}({\hat{\beta }}_{2,ac})=\frac{n_1{n}_{22}^2{\beta }_1^2(n_3{\upsilon }_{42}^2+2n_{42}{\alpha }_{22}^2){[2n_{22}{\beta }_1^2-n_1{\alpha }_{22}^4+n_1{(1+{\beta }_1^2)}^2]}^2}{d_{13}}>0,\hfill \end{array}$$

where $d_{13}=d_{11}\{2n_3{n}_{22}^2{\upsilon }_{42}^4{\beta }_1^2+2n_{22}{\upsilon }_{42}^2{\alpha }_{22}^2(n_{22}+n_{42})(2n_{22}{\beta }_1^2+n_1{\upsilon }_{42})+n_1^3{\upsilon }_{42}^2{\upsilon }_{22}^3+n_1{n}_{22}{\upsilon }_{42}[n_3{\upsilon }_{42}^4+2{\upsilon }_{42}{\beta }_1^2(2n_3{\upsilon }_{42}^2+n_{22}+{\alpha }_{22}^2(n_{22}{\upsilon }_{42}+5n_{22}+4n_{42}))+{\upsilon }_{42}^2{\beta }_1^4(3n_3+2n_{22})+6{\beta }_1^4{\alpha }_{22}^2{n}_{42}]+n_1^2{\upsilon }_{22}[n_3{\upsilon }_{42}^2{\upsilon }_{22}^2+2n_{42}{\alpha }_{22}^2{\upsilon }_{22}^2+n_{22}{\upsilon }_{42}^2({\upsilon }_{22}^2+2{\beta }_1^2+2{\alpha }_{22}^2+2{\alpha }_{22}^2{\beta }_1^2)]\}$.

Result 4.4

(i) When n₂₂ = n₂₄ = 0, CR leads to smaller asymptotic variances for β₁ and β₂ than CC. Specifically, we have

$$\begin{array}{c}\hfill \mathit{\text{Var}}({\hat{\beta }}_{1,cc})-\mathit{\text{Var}}({\hat{\beta }}_{1,cr})=\frac{n_1{n}_{23}{\upsilon }_{23}^2+2n_{23}{\beta }_2^2[n_{23}+(n_1+n_{23}){\upsilon }_{23}{\alpha }_{22}^2]}{n_1(n_1+n_{23}){\upsilon }_{23}(2n_{23}{\beta }_2^2+n_1{\upsilon }_{23}^2)}>0,\hfill \\ \hfill \mathit{\text{Var}}({\hat{\beta }}_{2,cc})-\mathit{\text{Var}}({\hat{\beta }}_{2,cr})=\frac{2n_{23}{\beta }_2^2}{n_1(2n_{23}{\beta }_2^2+n_1{\upsilon }_{23}^2)}>0.\hfill \end{array}$$

(ii) When n₂₂ = n₂₄ = 0, AC improves the asymptotic variances for β₁ over CR, but not for β₁. Specifically, we have

$$\begin{array}{c}\hfill \mathit{\text{Var}}({\hat{\beta }}_{1,cr})-\mathit{\text{Var}}({\hat{\beta }}_{1,ac})=\frac{n_{23}^2({\upsilon }_{42}^2{n}_3+2{\alpha }_{22}^2{n}_{42}){\beta }_2^2}{d_{23}}>0,\hfill \\ \hfill \mathit{\text{Var}}({\hat{\beta }}_{2,cr})-\mathit{\text{Var}}({\hat{\beta }}_{2,ac})=0,\hfill \end{array}$$

where $d_{23}=n_1(n_1+n_{23}){\upsilon }_{23}[n_1(n_1+n_{23}){\upsilon }_{23}{\upsilon }_{42}^2+(2n_{42}{\alpha }_{22}^2+n_3{\upsilon }_{42}^2)(n_1{\upsilon }_{23}+n_{23})]$.

Result 4.5

(i) When n₂₂ = n₂₃ = 0, CR leads to smaller asymptotic variances for β than CC. Specifically, we have

$$\begin{array}{c}\hfill \mathit{\text{Var}}({\hat{\beta }}_{1,cc})-\mathit{\text{Var}}({\hat{\beta }}_{1,cr})=\frac{2n_{24}{\beta }_1^2}{d_{31}}>0,\hfill \\ \hfill \mathit{\text{Var}}({\hat{\beta }}_{2,cc})-\mathit{\text{Var}}({\hat{\beta }}_{2,cr})=\frac{2n_{24}{\beta }_2^2}{d_{31}}>0,\hfill \end{array}$$

where $d_{31}=2n_1{n}_{24}[{\beta }_1^2{\upsilon }_{23}+2{\upsilon }_{23}{\beta }_1{\beta }_2{\alpha }_{22}+{\beta }_2^2+{\beta }_2^2{\alpha }_{22}^2{\upsilon }_{23}]+n_1^2{\upsilon }_{24}^2$.

(ii) When n₂₂ = n₂₃ = 0, AC leads to smaller asymptotic variances for β than CR. Specifically, we have

$$\begin{array}{c}\hfill \mathit{\text{Var}}({\hat{\beta }}_{1,cr})-\mathit{\text{Var}}({\hat{\beta }}_{1,ac})=\frac{4n_{24}^2{\beta }_1^2{\beta }_2^2{({\beta }_1+{\alpha }_{22}{\beta }_2)}^2(2{\alpha }_{22}^2{n}_{42}+n_3{\upsilon }_{42}^2)}{d_{33}}>0,\hfill \\ \hfill \mathit{\text{Var}}({\hat{\beta }}_{2,cr})-\mathit{\text{Var}}({\hat{\beta }}_{2,ac})=\frac{4n_{24}^2{\beta }_2^4{({\beta }_1+{\alpha }_{22}{\beta }_2)}^2(2{\alpha }_{22}^2{n}_{42}+n_3{\upsilon }_{42}^2)}{d_{33}}>0,\hfill \end{array}$$

where $d_{33}=d_{31}[2n_{24}{({\beta }_1+{\beta }_2{\alpha }_{22})}^2(n_3{\upsilon }_{42}^2+n_1{\upsilon }_{23}{\upsilon }_{42}^2+2n_{42}{\alpha }_{22}^2)+{\upsilon }_{42}^2(n_1+n_3)(2n_{24}{\beta }_2^2+n_1{\upsilon }_{24}^2)+2n_{42}{\alpha }_{22}^2(2n_{24}{\beta }_2^2+n_1{\upsilon }_{24}^2)]$.

Remark 1

The information in Block B₄₃ does not improve the asymptotic variances of the estimates of β₁ and β₂ in all of the three situations considered here.

Remark 2

When n₂₃ = n₂₄ = 0 (Result 4.3), the differences of the asymptotic variances for β₁ and β₂ do not depend on β₂ comparing CR to CC and AC to CR.

Remark 3

When n₂₂ = n₂₄ = 0 (Result 4.4), the differences of the asymptotic variances for β₁ and β₂ do not depend on β₁ comparing CR to CC and AC to CR.

Remark 4

When n₂₂ = n₂₃ = 0 (Result 4.5), the ratios of the asymptotic variances improvement of β₁ versus β₂ equal to ${\beta }_1^2/{\beta }_2^2$ for CR versus CC and AC versus CR, i.e.

$$\frac{\text{Var}({\hat{\beta }}_{1,cc})-\text{Var}({\hat{\beta }}_{1,cr})}{\text{Var}({\hat{\beta }}_{2,cc})-\text{Var}({\hat{\beta }}_{2,cr})}=\frac{\text{Var}({\hat{\beta }}_{1,cr})-\text{Var}({\hat{\beta }}_{1,ac})}{\text{Var}({\hat{\beta }}_{2,cr})-\text{Var}({\hat{\beta }}_{2,ac})}=\frac{{\beta }_1^2}{{\beta }_2^2}$$

Remark 5

When n₂₃ = n₂₄ = 0, the differences of the asymptotic variances of β₁ are monotone decreasing function of n₁ for CR versus CC and AC versus CR. Other monotonic properties are listed in Table 2.

Table 2.

Monotonic Properties for CR versus CC and AC versus CR

Missing Pattern	Parameter	n1	n22	n23	n24
	$\text{Var}({\hat{\beta }}_{1,cc})-\text{Var}({\hat{\beta }}_{1,cr})$	NM	NM
Result 4.3	$\text{Var}({\hat{\beta }}_{2,cc})-\text{Var}({\hat{\beta }}_{2,cr})$	NM	NM
n23 = n24 = 0	$\text{Var}({\hat{\beta }}_{1,cr})-\text{Var}({\hat{\beta }}_{1,ac})$	NM	NM
	$\text{Var}({\hat{\beta }}_{2,cr})-\text{Var}({\hat{\beta }}_{2,ac})$	NM	NM
	$\text{Var}({\hat{\beta }}_{1,cc})-\text{Var}({\hat{\beta }}_{1,cr})$	↘		NM
Result 4.4	$\text{Var}({\hat{\beta }}_{2,cc})-\text{Var}({\hat{\beta }}_{2,cr})$	↘		↗
n22 = n24 = 0	$\text{Var}({\hat{\beta }}_{1,cr})-\text{Var}({\hat{\beta }}_{1,ac})$	↘		↗
	$\text{Var}({\hat{\beta }}_{2,cr})-\text{Var}({\hat{\beta }}_{2,ac})=0$
	$\text{Var}({\hat{\beta }}_{1,cc})-\text{Var}({\hat{\beta }}_{1,cr})$	↘			↗
Result 4.5	$\text{Var}({\hat{\beta }}_{2,cc})-\text{Var}({\hat{\beta }}_{2,cr})$	↘			↗
n22 = n23 = 0	$\text{Var}({\hat{\beta }}_{1,cr})-\text{Var}({\hat{\beta }}_{1,ac})$	↘			↗
	$\text{Var}({\hat{\beta }}_{2,cr})-\text{Var}({\hat{\beta }}_{2,ac})$	↘			↗

5 Analysis of Bias

In this section, we examine bias in the CC situation when the missing data are MAR. For inference with only missing response data, Little and Rubin (2002, page 43.) note without proof that when the data are MAR, the CC estimates are not biased when the missing data mechanism depends only on the covariates and not the response. The estimates, however, are biased if the missing data mechanism depends on the response. We now examine this bias issue in the missing (x, y) problem, where missingness is MAR.

Based on the data structure given in Table 1, define missing data indicators ${\mathit{r}}_i=(r_{iy,}{\mathit{r}}_{ix}^{\prime })\prime$ as

$$r_{iy}=\{\begin{array}{cc}1\hfill & \text{if}{y}_i\text{is observed}\hfill \\ 0\hfill & \text{if}{y}_i\text{is missing}\hfill \end{array}$$

and

$$r_{ix,j}=\{\begin{array}{cc}1\hfill & \text{if the}{j}^{th}\text{component of}{\mathit{x}}_i\text{is observed},\hfill \\ 0\hfill & \text{if the}{j}^{th}\text{component of}{\mathit{x}}_i\text{is missing},\hfill \end{array}$$

for j = 1, 2,…,p.

Let f(r_i|ϕ, y_i, x_i denote the distribution of r_i, which may possibly depend on y_i and x_i, where ϕ is the vector of parameters in the r_i model. Under the MAR assumption, following models for r_i are possible:

$$f({\mathit{r}}_i|\mathit{\varphi },y_i,{\mathit{x}}_i)=f({\mathit{r}}_i|\mathit{\varphi }),$$ (5.1)

$$f({\mathit{r}}_i|\mathit{\varphi },y_i,{\mathit{x}}_i)=f(r_{ix}|{\mathit{\varphi }}_1)f({\mathit{r}}_{iy}|{\mathit{\varphi }}_2,{\mathit{r}}_{ix}○{\mathit{x}}_i),$$ (5.2)

where ○ denotes the direct product, or

$$f({\mathit{r}}_i|\mathit{\varphi },y_i,{\mathit{x}}_i)=f(r_{iy}|{\mathit{\varphi }}_1)f({\mathit{r}}_{ix}|{\mathit{\varphi }}_2,r_{iy}{y}_i).$$ (5.3)

Note that the model specified by (5.1) defines MCAR and some other versions of the MAR models can be considered as well.

Because standard techniques for regression models require full response and covariate information, one simple way to avoid the problem of missing data is to analyze only those subjects who are completely observed. This method is known as a complete case (CC) analysis.

Based on the data structure displayed in Table 1, the CC analysis uses the portion of data given in Block B₁. Thus, the likelihood function under this method is given by

$$L_{cc}(\mathit{\theta })={\displaystyle \prod _{i:\text{both}{y}_i\text{and}{x}_i\text{observed}}f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha })f({\mathit{r}}_i|\mathit{\varphi },y_i,{\mathit{x}}_i),}$$ (5.4)

where θ = (β,α,ϕ), and the log-likelihood function is given by

$$l_{cc}(\mathit{\theta })={\displaystyle \sum _{i:\text{both}{y}_i\text{and}{x}_i\text{observed}}[\text{log}f(y_i|x_i,\mathit{\beta })+\text{log}f({\mathit{x}}_i|\mathit{\alpha })+\text{log}f({\mathit{r}}_i|\mathit{\varphi },y_i,{\mathit{x}}_i)]}.$$ (5.5)

Under CC, we will make conditional inference given r_i = 1, where 1 = (1, 1,…,1)′. More specifically, we need to consider conditional distribution [y_i, x_i|r_i = 1] in examining biasness of the MLE’s and in deriving the Fisher information matrix. We assume throughout that ϕ is distinct from β and α.

Under the model given by (5.1), we have

$$f(y_i,{\mathit{x}}_i|\mathit{\beta },\mathit{\alpha },\mathit{\varphi },{\mathit{r}}_i=\mathbf{1})=\frac{f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha })f({\mathit{r}}_i|\mathit{\varphi })}{{\displaystyle \int f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha })f({\mathit{r}}_i|\mathit{\varphi })d{\mathit{x}}_{i}d{y}_i}}=f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha }).$$

Thus, under MCAR, the conditional distribution of (y_i, x_i) given r_i = 1 is the same as the unconditional distribution and hence, the MLE’s of β and α are unbiased or asymptotically consistent under certain usual regularity conditions.

Under MAR with the model given by (5.2) for r_i, we have

$$\begin{array}{cc}f(y_i,{\mathit{x}}_i|\mathit{\beta },\mathit{\alpha },\mathit{\varphi },{\mathit{r}}_i=\mathbf{1})\hfill & =\frac{f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha })f({\mathit{r}}_{ix}=\mathbf{1}|{\mathit{\varphi }}_1)f(r_{iy}=1|{\mathit{\varphi }}_2,{\mathit{x}}_i)}{{\displaystyle \int f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha })f({\mathit{r}}_{ix}=\mathbf{1}|{\mathit{\varphi }}_1)f(r_{iy}=1|{\mathit{\varphi }}_2,{\mathit{x}}_i)d{y}_{i}d{\mathit{x}}_i}}\hfill \\ \hfill & =f(y_i|{\mathit{x}}_i,\mathit{\beta })\times \frac{f({\mathit{x}}_i|\mathit{\alpha })f(r_{iy}=1|{\mathit{\varphi }}_2,{\mathit{x}}_i)}{{\displaystyle \int f({\mathit{x}}_i|\mathit{\alpha })f(r_{iy}=1|{\mathit{\varphi }}_2,{\mathit{x}}_i)d{\mathit{x}}_i}}.\hfill \end{array}$$ (5.6)

From (5.6), it is easy to see that the MLE of β is unbiased or asymptotically consistent, but the MLE of α may not be in this case.

Under the MAR with the model given by (5.3) for r_i, we obtain

$$\begin{array}{cc}f(y_i,{\mathit{x}}_i|\mathit{\beta },\mathit{\alpha },\mathit{\varphi },{\mathit{r}}_i=\mathbf{1})\hfill & =\frac{f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha })f(r_{iy}=1|{\mathit{\varphi }}_1)f({\mathit{r}}_{ix}=\mathbf{1}|{\mathit{\varphi }}_2,y_i)}{{\displaystyle \int f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha })f(r_{iy}=1|{\mathit{\varphi }}_1)f({\mathit{r}}_{ix}=\mathbf{1}|{\mathit{\varphi }}_2,y_i)d{y}_{i}d{\mathit{x}}_i}}\hfill \\ \hfill & =\frac{f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha })f({\mathit{r}}_{ix}=\mathbf{1}|{\mathit{\varphi }}_2,y_i)}{{\displaystyle \int f(y_i|{\mathit{x}}_i,\mathit{\beta })f({\mathit{x}}_i|\mathit{\alpha })f({\mathit{r}}_{ix}=\mathbf{1}|{\mathit{\varphi }}_2,y_i)d{y}_{i}d{\mathit{x}}_i}}.\hfill \end{array}$$ (5.7)

In this case, the MLE’s for both β and α are likely to be biased.

To obtain the closed form analytical results for (5.6) and (5.7), we consider the simple normal regression model given by (4.1). For notational simplicity, we assume that both y_i and x_i are observed for i = 1, 2,…,m. Let y_obs = (y₁, y₂,…, y_m)′, $X_{\mathit{\text{obs}}}^{\prime }=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill \dots \hfill & \hfill 1\hfill \\ \hfill x_1\hfill & \hfill x_2\hfill & \hfill \dots \hfill & \hfill x_m\hfill \end{array}\right)$, and r_obs = (1, 1,…,1)′. Then, the MLE of β is given by ${\hat{\mathit{\beta }}}_{cc}={(X_{\mathit{\text{obs}}}^{\prime }{X}_{\mathit{\text{obs}}})}^{-1}{X}_{\mathit{\text{obs}}}^{\prime }{\mathit{y}}_{\mathit{\text{obs}}}$ and the MLE of α is ${\hat{\alpha }}_{cc}=\frac{1}{m}{\displaystyle {\sum }_{i=1}^m{x}_i}$.

In (5.6), we assume $f(r_{iy}=1|{\mathit{\varphi }}_2,x_i)=\frac{\text{exp}({\varphi }_{20}+{\varphi }_{21}{x}_i)}{1+\text{exp}({\varphi }_{20}+{\varphi }_{21}{x}_i)}$. Then, (5.6) implies

$$f(y_i|\mathit{\beta },\alpha ,\mathit{\varphi },x_i,{\mathit{r}}_i=\mathbf{1})=f(y_i|x_i,\mathit{\beta })=\frac{1}{\sqrt{2\mathrm{\pi }}}\text{exp}\left\{-\frac{{(y_i-{\beta }_0-{\beta }_1{x}_i)}^2}{2}\right\}$$

and

$$f(x_i|\alpha ,\mathit{\varphi },{\mathit{r}}_i=\mathbf{1})=\frac{\text{exp}\{-{(x_i-\alpha )}^2/2\}\left[\frac{\text{exp}({\varphi }_{20}+{\varphi }_{21}{x}_i)}{1+\text{exp}({\varphi }_{20}+{\varphi }_{21}{x}_i)}\right]}{{\displaystyle \int \text{exp}\{-{(x_i-\alpha )}^2/2\}\left[\frac{\text{exp}({\varphi }_{20}+{\varphi }_{21}{x}_i)}{1+\text{exp}({\varphi }_{20}+{\varphi }_{21}{x}_i)}\right]d{x}_i}}.$$ (5.8)

Thus, we have

$$E[{\hat{\mathit{\beta }}}_{cc}|{\mathit{r}}_{\mathit{\text{obs}}}]=E\{E{[(X_{\mathit{\text{obs}}}^{\prime }{X}_{\mathit{\text{obs}}})}^{-1}{X}_{\mathit{\text{obs}}}^{\prime }{\mathit{y}}_{\mathit{\text{obs}}}|X_{\mathit{\text{obs}}}]|{\mathit{r}}_{\mathit{\text{obs}}}\}=E\{{(X_{\mathit{\text{obs}}}^{\prime }{X}_{\mathit{\text{obs}}})}^{-1}{X}_{\mathit{\text{obs}}}^{\prime }{X}_{\mathit{\text{obs}}}\mathit{\beta }|{\mathit{r}}_{\mathit{\text{obs}}}\}=\mathit{\beta },$$

which is unbiased. However,

$$E[{\hat{\alpha }}_{cc}|{\mathit{r}}_{\mathit{\text{obs}}}]\ne \alpha ,$$

which may be biased. Also, an analytical derivation of the Fisher information matrix is not possible as the conditional distribution of x_i given r_i = 1 involves an analytically intractable integral.

Under MAR given by (5.3), we assume a logistic regression model for r_ix, i.e.,

$$f(r_{ix}=1|{\mathit{\varphi }}_2,r_{iy}{y}_i)=\frac{\text{exp}({\varphi }_{20}+{\varphi }_{21}{r}_{iy}{y}_i)}{1+\text{exp}({\varphi }_{20}+{\varphi }_{21}{r}_{iy}{y}_i)}.$$

From (5.7), we obtain

$$f(y_i|\mathit{\beta },\alpha ,\mathit{\varphi },x_i,{\mathit{r}}_i=\mathbf{1})=\frac{\text{exp}\left\{-\frac{{(y_i-{\beta }_0-{\beta }_1{x}_i)}^2}{2}\right\}\left[\frac{\text{exp}({\varphi }_{20}+{\varphi }_{21}{y}_i)}{1+\text{exp}({\varphi }_{20}+{\varphi }_{21}{y}_i)}\right]}{{\displaystyle \int \text{exp}\left\{-\frac{{(y_i-{\beta }_0-{\beta }_1{x}_i)}^2}{2}\right\}\left[\frac{\text{exp}({\varphi }_{20}+{\varphi }_{21}{y}_i)}{1+\text{exp}({\varphi }_{20}+{\varphi }_{21}{y}_i)}\right]d{y}_i}}.$$

Thus, E[y_i|β, α, ϕ, x_i, r_i = 1] ≠ β₀ + β₁x_i. In this case, both ${\hat{\mathit{\beta }}}_{cc}$ and ${\hat{\alpha }}_{cc}$ may be biased. Again, an analytical derivation of the Fisher information matrix is not possible.

6 Simulation Studies and a Real Data Example

In this section, we present two detailed simulation studies and a real data example, demonstrating the various properties of the CC, CR, and AC methodology for analyzing MCAR and MAR response and/or covariate data in linear regression and logistic regression. In particular, we study efficiency and bias in the estimates for the three methods for these two types of regression models.

6.1 Simulation Study I: Normal Linear Regression Model with MCAR Response and Covariate Data

We consider a multiple linear regression model with an intercept, a completely observed covariate and two missing covariates. 5000 replicates with n = 500 subjects are considered. The response model is y_i ~ N(β₀ + β₁z_i1 + β₂x_i1 + β₃x_i2, 1), where z_i is simulated from Unif(0, 1), x_i1 is simulated from N(α₁₀ + α₁₁z_i1, 1), x_i2 is simulated from N(α₂₀ + α₂₁z_i1 + α₂₂x_i1, 1), and y_i, x_i1 and x_i2 are missing for some subjects. In each simulation, the sizes for each missing pattern, n₁₁, n₂, n₂₃, n₂₄, n₃, n₄₂, n₄₃ and n₅, were varied in order to evaluate the various properties of the CC, CR, and AC methods. To better study the differences of the asymptotic variances of the estimates of the regression coefficients using the three methods, we calculated the variances in two ways: plugging in the true parameter values as well as plugging in the maximum likelihood estimates into the Fisher information matrix.

Table 3 gives the simulation results of the linear regression model with the variances evaluated at the true parameter values. We note here that the variance estimates decrease monotonically based on the three methods, CC, CR, and AC. In particular, Result 4.3 and Result 4.4 hold and Remark 1 – Remark 3 hold, but not Remark 4. We note that Remark 1 is only true for the regression coefficients of the missing covariates but not of the completely observed covariates. The information in Block B₄₃ does improve the asymptotic variances of regression coefficients of the z_i0 = 1 and z_i1 when the AC method is used.

Table 3.

Variance Comparison with True Parameters Plugged-in for Linear Regression

(n1, n22, n23, n24, n3, n42, n43, n5)	Para	CC (VCC)	CR (VCC-VCR)	AC (VCR-VAC)
(50, 200, 0, 0, 100, 100, 50, 0)	β0 = 1.0	1.224 ×10−1	6.111 ×10−2	1.451 ×10−2
	β1 = 1.0	2.895 ×10−1	1.420 ×10−1	3.481 ×10−2
	β2 = 2.0	1.000 ×10−1	6.419 ×10−2	1.117 ×10−3
	β3 = 3.0	2.000 ×10−2	1.336 ×10−2	8.718 ×10−6
(50, 200, 0, 0, 100, 100, 50, 0)	β0 = 1.0	1.224 ×10−1	6.111 ×10−2	1.451 ×10−2
	β1 = 1.0	2.895 ×10−1	1.420 ×10−1	3.481 ×10−2
	β2 = 2.0	1.000 ×10−1	6.419 ×10−2	1.117 ×10−3
	β3 = 2.5	2.000 ×10−2	1.336 ×10−2	8.718 ×10−6
(50, 200, 0, 0, 100, 100, 20, 30)	β0 = 1.0	1.224 ×10−1	6.111 ×10−2	1.424 ×10−2
	β1 = 1.0	2.895 ×10−1	1.420 ×10−1	3.412 ×10−2
	β2 = 2.0	1.000 ×10−1	6.419 ×10−2	1.117 ×10−3
	β3 = 3.0	2.000 ×10−2	1.336 ×10−2	8.718 ×10−6
(50, 0, 200, 0, 100, 100, 50, 0)	β0 = 1.0	1.224 ×10−1	1.660 ×10−2	8.930 ×10−3
	β1 = 1.0	2.895 ×10−1	3.001 ×10−2	2.380 ×10−2
	β2 = 2.0	1.000 ×10−1	3.509 ×10−2	1.749 ×10−3
	β3 = 3.0	2.000 ×10−2	8.372 ×10−3	0
(50, 0, 200, 0, 100, 100, 50, 0)	β0 = 1.0	1.224 ×10−1	1.660 ×10−2	8.930 ×10−3
	β1 = 1.0	2.895 ×10−1	3.001 ×10−2	2.380 ×10−2
	β2 = 1.5	1.000 ×10−1	3.509 ×10−2	1.749 ×10−3
	β3 = 3.0	2.000 ×10−2	8.372 ×10−3	0
(50, 0, 200, 0, 100, 100, 20, 30)	β0 = 1.0	1.224 ×10−1	1.660 ×10−2	8.921 ×10−3
	β1 = 1.0	2.895 ×10−1	3.001 ×10−2	2.378 ×10−2
	β2 = 2.0	1.000 ×10−1	3.509 ×10−2	1.749 ×10−3
	β3 = 3.0	2.000 ×10−2	8.372 ×10−3	0
(50, 0, 0, 200, 100, 100, 50, 0)	β0 = 1.0	1.224 ×10−1	7.183 ×10−3	2.314 ×10−3
	β1 = 1.0	2.895 ×10−1	1.057 ×10−2	4.814 ×10−2
	β2 = 2.0	1.000 ×10−1	1.439 ×10−2	8.327 ×10−3
	β3 = 3.0	2.000 ×10−2	5.173 ×10−3	1.090 ×10−3
(50, 0, 0, 200, 100, 100, 50, 0)	β0 = 1.0	1.224 ×10−1	1.116 ×10−2	3.274 ×10−3
	β1 = 1.0	2.895 ×10−1	1.476 ×10−2	9.621 ×10−2
	β2 = 2.0	1.000 ×10−1	2.191 ×10−2	1.112 ×10−3
	β3 = 2.0	2.000 ×10−2	7.754 ×10−3	1.264 ×10−3
(50, 0, 0, 200, 100, 100, 20, 30)	β0 = 1.0	1.224 ×10−1	7.183 ×10−3	2.206 ×10−3
	β1 = 1.0	2.895 ×10−1	1.057 ×10−2	4.519 ×10−3
	β2 = 2.0	1.000 ×10−1	1.439 ×10−2	8.327 ×10−3
	β3 = 3.0	2.000 ×10−2	5.173 ×10−3	1.090 ×10−3

Table 4 gives the simulation results of the linear regression model with the variances evaluated at the maximum likelihood estimates (MLE’s). The results show the gain in using the AC method over CR method, and using CR method over CC method. When when n₂₂ = 200 and n₂₃ = n₂₄ = 0, the gain on the asymptotic variance of β₃ is small compared to the AC to CR method and the difference of the empirical variances is slight.

Table 4.

Variance Comparison with MLE’s Plugged in for Linear Regression

(n1, n22, n23n3, n42, n43, n5)		CC				CR				AC
	Para	MLE	Sim:Vcc	Vcc	95% CP	MLE	Sim:Vcc–Sim:Vcr	Vcc–Vcr	95% CP	MLE	Sim:Vcr–Sim:Vac	Vcr–Vac	95% CP
(50, 200, 0, 0, 100, 100, 50, 0)	β0 = 1.0	0.988	0.130	0.124	97.2	0.994	6.922 ×10−2	6.214 ×10−2	97.4	0.992	1.448 ×10−2	1.490 ×10−2	96.8
	β1 = 1.0	1.011	0.305	0.292	97.2	0.995	1.500 ×10−1	1.442 ×10−1	97.4	0.994	4.252 ×10−2	3.566 ×10−2	97.5
	β2 = 2.0	2.003	0.112	0.100	97.0	1.987	7.352 ×10−2	6.392 ×10−2	96.7	1.981	1.383 ×10−3	1.101 ×10−3	96.6
	β3 = 3.0	3.000	0.022	0.020	97.1	3.006	1.483 ×10−2	1.332 ×10−2	97.7	3.009	< 1.0 × 10−4	< 1.0 × 10−4	98.0
(50, 200, 0, 0, 100, 100, 50, 0)	β0 = 1.0	0.988	0.130	0.124	97.2	0.994	6.922 ×10−2	6.214 ×10−2	97.4	0.992	1.448 ×10−2	1.490 ×10−2	96.8
	β1 = 1.0	1.011	0.305	0.292	97.2	0.995	1.500 ×10−1	1.442 ×10−1	97.4	0.994	4.252 ×10−2	3.566 ×10−2	97.5
	β2 = 2.0	2.003	0.112	0.100	97.0	1.987	7.352 ×10−2	6.392 ×10−2	96.7	1.981	1.383 ×10−3	1.101 ×10−3	96.6
	β3 = 3.0	2.500	0.022	0.020	97.1	2.506	1.483 ×10−2	1.332 ×10−2	97.7	2.509	< 1.0 × 10−4	< 1.0 × 10−4	98.0
(50, 200, 0, 0, 100, 100, 50, 0)	β0 = 1.0	0.988	0.130	0.124	97.2	0.994	6.922 ×10−2	6.214 ×10−2	97.4	0.992	1.405 ×10−2	1.461 ×10−2	96.8
	β1 = 1.0	1.011	0.305	0.292	97.2	0.995	1.500 ×10−1	1.442 ×10−1	97.4	0.994	4.117 ×10−2	3.495 ×10−2	97.4
	β2 = 2.0	2.003	0.112	0.100	97.0	1.987	7.352 ×10−2	6.392 ×10−2	96.7	1.981	1.383 ×10−3	1.100 ×10−3	96.6
	β3 = 3.0	3.000	0.022	0.020	97.1	3.006	1.483 ×10−2	1.332 ×10−2	97.7	3.009	< 1.0 × 10−4	< 1.0 × 10−4	98.0
(50, 0, 200, 0, 100, 100, 50, 0)	β0 = 1.0	0.988	0.130	0.124	97.3	0.987	1.939 ×10−2	1.686 ×10−2	97.4	0.991	8.583 ×10−3	9.371 ×10−3	97.2
	β1 = 1.0	1.011	0.305	0.292	97.3	1.010	4.199 ×10−2	3.087 ×10−2	97.7	1.008	2.295 ×10−2	2.459 ×10−2	97.9
	β2 = 2.0	2.003	0.112	0.100	97.0	2.003	4.255 ×10−2	3.509 ×10−2	97.3	2.005	3.047 ×10−3	1.784 ×10−3	97.4
	β3 = 3.0	3.000	0.022	0.020	97.1	3.000	1.017 ×10−2	8.376 ×10−3	97.1	2.999	< 1.0 × 10−4	< 1.0 × 10−4	97.0
(50, 0, 200, 0, 100, 100, 50, 0)	β0 = 1.0	0.988	0.130	0.124	97.3	0.987	1.939 ×10−2	1.686 ×10−2	97.4	0.991	8.583 ×10−3	9.371 ×10−3	97.2
	β1 = 1.0	1.011	0.305	0.292	97.3	1.010	4.199 ×10−2	3.087 ×10−2	97.7	1.008	2.295 ×10−2	2.459 ×10−2	97.9
	β2 = 1.5	1.503	0.112	0.100	97.0	1.503	4.255 ×10−2	3.509 ×10−2	97.3	1.503	3.047 ×10−3	1.784 ×10−3	97.4
	β3 = 3.0	3.000	0.022	0.020	97.1	3.000	1.017 ×10−2	8.376 ×10−3	97.1	2.999	< 1.0 × 10−4	< 1.0 × 10−4	97.0
(50, 0, 200, 0, 100, 100, 20, 30)	β0 = 1.0	0.988	0.130	0.124	97.3	0.987	1.939 ×10−2	1.686 ×10−2	97.4	0.991	8.625 ×10−3	9.341 ×10−3	97.2
	β1 = 1.0	1.011	0.305	0.292	97.3	1.010	4.199 ×10−2	3.087 ×10−2	97.7	1.008	2.305 ×10−2	2.456 ×10−2	97.9
	β2 = 2.0	2.003	0.112	0.100	97.0	2.003	4.255 ×10−2	3.509 ×10−2	97.3	2.005	3.046 ×10−3	1.784 ×10−3	97.4
	β3 = 3.0	3.000	0.022	0.020	97.1	3.000	1.017 ×10−2	8.376 ×10−3	97.1	2.999	< 1.0 × 10−4	< 1.0 × 10−4	97.0
(50, 0, 200, 0, 100, 100, 50, 0)	β0 = 1.0	0.988	0.130	0.124	97.2	0.983	2.849 ×10−3	6.160 ×10−3	96.9	0.987	3.209 ×10−3	3.779 ×10−3	96.9
	β1 = 1.0	1.011	0.305	0.292	97.2	1.005	5.615 ×10−3	8.373 ×10−3	97.4	1.008	8.295 ×10−3	8.444 ×10−3	97.5
	β2 = 2.0	2.003	0.112	0.100	97.0	1.998	2.241 ×10−4	1.448 ×10−2	95.9	2.001	1.159 ×10−4	8.268 ×10−3	95.1
	β3 = 3.0	3.000	0.022	0.020	97.1	3.003	1.849 ×10−4	5.171 ×10−3	94.9	3.001	< 1.0 × 10−4	1.088 ×10−3	94.0
(50, 0, 200, 0, 100, 100, 50, 0)	β0 = 1.0	0.988	0.130	0.124	97.2	0.983	5.208 ×10−3	1.032 ×10−2	96.6	0.988	5.290 ×10−3	4.636 ×10−3	96.8
	β1 = 1.0	1.011	0.305	0.292	97.2	1.004	9.803 ×10−3	1.305 ×10−2	97.4	1.007	1.362 ×10−2	1.395 ×10−2	97.5
	β2 = 2.0	2.003	0.112	0.100	97.0	1.996	5.067 ×10−4	2.205 ×10−2	95.3	2.000	2.442 ×10−4	1.101 ×10−2	93.6
	β3 = 2.0	2.000	0.022	0.020	97.1	2.004	2.720 ×10−4	7.745 ×10−3	93.1	2.001	1.257 ×10−4	1.264 ×10−3	91.9
(50, 0, 200, 0, 100, 100, 50, 0)	β0 = 1.0	0.988	0.130	0.124	97.2	0.983	2.849 ×10−3	6.160 ×10−3	97.4	0.987	2.939 ×10−3	3.632 ×10−3	96.9
	β1 = 1.0	1.011	0.305	0.292	97.2	1.005	5.615 ×10−3	8.373 ×10−3	97.7	1.008	7.312 ×10−3	8.101 ×10−3	97.6
	β2 = 2.0	2.003	0.112	0.100	97.0	1.998	2.241 ×10−4	1.448 ×10−2	97.3	2.001	9.505 ×10−5	8.266 ×10−3	95.1
	β3 = 3.0	3.000	0.022	0.020	97.1	3.003	1.849 ×10−4	5.171 ×10−3	97.1	3.001	< 1.0 × 10−4	1.088 ×10−3	93.9

Sim:V_cc, Sim:V_cr and Sim:V_ac are the simulated variances of CC, CR and AC methods. V_cc, V_cr and V_ac are the variances of CC, CR and AC methods using the formula derived in Section 4 with MLE’s plug-in. 95% CP is the 95% coverage probability.

6.2 Simulation Study II: Logistic Regression Model with MAR Response and Covariate Data

A simulation with 1000 replicates was conducted to numerically compare the CC, CR and AC methods in a logistic regression model. The estimates using the full data (FD) before missing are also provided as a benchmark of other methods. In each simulation, we generated 500 binary samples from a logistic regression model logit(P(y_i = 1)) = β₀ + β₁z_i1 + β₂x_i1, where z_i1 was simulated from Unif(0, 1) and x_i1 was simulated from a Bernoulli distribution with the success probability modeled as logit(P(x_i1 = 1)) = α₀ + α₁z_i1. The covariate z_i1 is completely observed for all subjects, and x_i1 and the response y_i are missing at random (MAR) for some subjects. The missing mechanisms for y_i and x_i1 are logit(P(r_iy = 1)) = ϕ₂₀ + ϕ₂₁z_i1 and logit(P(r_ix = 1)) = ϕ₁₀ + ϕ₁₁z_i1 + ϕ₁₂r_iyy_i, where r_iy = 1 or r_ix = 1 if y_i or x_i1 is observed, 0 otherwise. On average, 31.4% samples have completely observed covariate and response, 34.8% have missing covariate but observed response, 15.0% have observed covariate but missing response, and 18.8% have missing covariate and missing response.

Table 5 gives the simulation results of the logistic regression model. The AC method provides estimates with higher precision (smaller standard error) and lower mean square error (MSE) than the CR method for all the parameters. Both the CR and AC methods are uniformly better than the CC method in terms of bias, simulated standard error and MSE.

Table 5.

Simulation for Logistic Regression Model

Method		β0 = −1.8	β1 = 1.0	β2 = 2.0	α0 = −0.5	α1 = 2.0
CC	Bias	0.224	0.483	0.059	0.104	0.273
	SE	0.450	0.723	0.408	0.351	0.672
	SSE	0.466	0.720	0.419	0.351	0.680
	CP%	99.5	99.6	97.8	98.8	98.4
	MSE	0.484	1.268	0.355	0.257	1.000
CR	Bias	−0.036	−0.008	0.059	−0.017	0.056
	SE	0.378	0.544	0.437	0.372	0.687
	SSE	0.408	0.527	0.419	0.339	0.650
	CP%	97.9	98.7	97.9	98.7	97.7
	MSE	0.333	0.555	0.355	0.230	0.847
AC	Bias	−0.035	−0.007	0.055	−0.019	0.051
	SE	0.377	0.528	0.417	0.262	0.539
	SSE	0.402	0.516	0.415	0.250	0.533
	CP%	97.7	98.3	97.6	98.5	97.7
	MSE	0.324	0.533	0.347	0.126	0.571
FD	Bias	−0.020	0.006	0.023	−0.011	0.016
	SE	0.245	0.366	0.223	0.186	0.344
	SSE	0.247	0.364	0.225	0.181	0.337
	CP%	97.4	97.5	97.4	97.4	98.0
	MSE	0.123	0.264	0.102	0.065	0.227

$\text{Bias}=\hat{\beta }-{\beta }_{\mathit{\text{true}}}$, SE is the mean of the standard error calculated by Louis’s formula, SSE is the simulated standard error, CP is the coverage probability, MSE = Bias² + SSE² is the mean square error.

6.3 Analysis of Small Cell Lung Cancer Data

We consider a real dataset to compare the three analysis methods in terms of bias and efficiency. We consider a lung cancer dataset from a recent phase III clinical trial (Socinski et al., 2002) of non-small-cell lung cancer (NSCLC), which is the leading cause of cancer-related mortality. In the year 2001, among approximately 170,000 patients newly diagnosed, more than 90% died from NSCLC and approximately 35% of all new cases were stage IIIB/IV (malignant pleural effusion) the disease. A randomized, two-armed, multi-center trial was initiated in 1998 with the aim to determine the optimal duration of chemotherapy by comparing four cycles of therapy versus continuous therapy in advanced NSCLC. Patients were randomized to two treatment arms: four cycles of carboplatin at an area under the curve of 6 and paclitaxel 200 mg/m² every 21 days (arm A), or continuous treatment with carboplatin/paclitaxel until progression (arm B). At progression, all patients on both arms received second-line weekly paclitaxel at 80 mg/m². One of the primary endpoints was quality of life (QOL). There were n = 230 patients in this dataset. The response variable considered in this analysis is the quality of life (QOL) factg score. The covariates included in the model were treatment (trt, 0=arm A, 1=arm B), gender (0=female, 1=male), Histology (hist, 0=Non-Squamous, 1=Squamous), age at entry in years, highest grade toxicity (recorded by cycle) (apex, 0 if highest grade toxicity =0 and 1 if highest grade toxicity > 0), and recovery status (recov, 0 if recovered and 1 otherwise). For these six covariates, apex and recov had missing information and trt, gender, hist, and age were completely observed for all cases. In this population, 63% of the patients were male, and the age at entry ranged from 32 to 82 with a mean of 62. The missing data fractions were 28% in apex, 54% in recov, and 35% in factg. There was a total missing data fraction of 74% on apex, recov, and factg.

We use a linear regression to model the response variable, factg, as

$${\text{factg}}_i={\beta }_0+{\beta }_1{\text{trt}}_i+{\beta }_2{\text{gender}}_i+{\beta }_3{\text{hist}}_i+{\beta }_4{\text{age}}_i++{\beta }_5{\text{apex}}_i+{\beta }_6{\text{recov}}_i+{\epsilon }_i.$$

We consider two models for the missing covariates recov and apex as follows.

Model M1

$$\begin{array}{c}\hfill \text{logit}({\text{apex}}_{\mathrm{\text{i}}}=1)={\alpha }_{10}+{\alpha }_{11}{\text{trt}}_{\mathrm{\text{i}}}+{\alpha }_{12}{\text{gender}}_{\mathrm{\text{i}}}+{\alpha }_{13}{\text{hist}}_{\mathrm{\text{i}}}+{\alpha }_{14}{\text{age}}_{\mathrm{\text{i}}},\hfill \\ \hfill \text{logit}({\text{recov}}_{\mathrm{\text{i}}}=1|{\text{apex}}_{\mathrm{\text{i}}}=1)={\alpha }_{20}+{\alpha }_{21}{\text{trt}}_{\mathrm{\text{i}}}+{\alpha }_{22}{\text{gender}}_{\mathrm{\text{i}}}+{\alpha }_{23}{\text{hist}}_{\mathrm{\text{i}}}+{\alpha }_{24}{\text{age}}_{\mathrm{\text{i}}}+{\alpha }_{25}{\text{apex}}_{\mathrm{\text{i}}}.\hfill \end{array}$$

Model M2

$$\begin{array}{c}\hfill \text{logit}({\text{recov}}_{\mathrm{\text{i}}}=1)={\alpha }_{10}+{\alpha }_{11}{\text{trt}}_{\mathrm{\text{i}}}+{\alpha }_{12}{\text{gender}}_{\mathrm{\text{i}}}+{\alpha }_{13}{\text{hist}}_{\mathrm{\text{i}}}+{\alpha }_{14}{\text{age}}_{\mathrm{\text{i}}},\hfill \\ \hfill \text{logit}({\text{apex}}_{\mathrm{\text{i}}}=1|{\text{recov}}_{\mathrm{\text{i}}})={\alpha }_{20}+{\alpha }_{21}{\text{trt}}_{\mathrm{\text{i}}}+{\alpha }_{22}{\text{gender}}_{\mathrm{\text{i}}}+{\alpha }_{23}{\text{hist}}_{\mathrm{\text{i}}}+{\alpha }_{24}{\text{age}}_{\mathrm{\text{i}}}+{\alpha }_{25}{\text{recov}}_{\mathrm{\text{i}}}.\hfill \end{array}$$

Table 6 shows the results for the CC, CR and AC methods discussed in Section 4. We assume that the missing data are MAR so that a missing data mechanism need not be considered in the estimation scheme for β. As shown in the table, the overall conclusions are the same for the CR and AC methods, as these two methods yield similar p-values for the various regression coefficients. significance level. However, the CR and AC methods yield more significant p-values than the CC analysis, especially for the age effect. Table 6 also shows that the estimates of β and the standard errors of the estimated regression coefficients are quite similar for model M1 and model M2, indicating robustness of estimates to the the choice of covariate distribution. The EM algorithm was implemented for computing all maximum likelihood estimates. The convergence criterion for the EM algorithm was that the squared distance between the k^th and (k + 10)^th iterations was less than 10⁻⁷. The EM algorithm required 25 iterations to converge under both model M1 and model M2.

Table 6.

Lung Cancer Data Analysis

		Model M1			Model M2
Method	Effect	Estimate	SE	P-value	Estimate	SE	P-value
CC	Intercept	79.008	3.536	< 0.001	79.008	3.536	< 0.001
	trt	−2.366	3.222	0.463	−2.366	3.222	0.463
	gender	−3.033	3.431	0.377	−3.033	3.431	0.377
	hist	3.011	3.694	0.415	3.011	3.694	0.415
	age	3.049	1.587	0.055	3.049	1.587	0.055
	apex	4.825	5.004	0.335	4.825	5.004	0.335
	recov	−0.485	3.421	0.887	−0.485	3.421	0.887
	${\sigma }_{\mathit{\text{MLE}}}^2$	147.896	27.230	< 0.001	147.896	27.230	< 0.001
CR	Intercept	81.565	2.912	< 0.001	81.573	2.910	< 0.001
	trt	0.743	2.543	0.770	0.730	2.540	0.774
	gender	−6.048	2.580	0.019	−6.034	2.576	0.019
	hist	2.003	3.076	0.515	2.007	3.076	0.514
	age	3.640	1.244	0.003	3.641	1.244	0.003
	apex	3.473	6.088	0.568	3.433	6.078	0.572
	recov	−4.676	4.319	0.279	−4.700	4.317	0.276
	${\sigma }_{\mathit{\text{MLE}}}^2$	210.197	25.511	< 0.001	210.183	25.525	< 0.001
AC	Intercept	81.533	2.768	< 0.001	81.535	2.762	< 0.001
	trt	0.905	2.556	0.723	0.905	2.550	0.723
	gender	−5.778	2.516	0.021	−5.777	2.508	0.021
	hist	2.067	3.064	0.500	2.074	3.057	0.497
	age	3.527	1.234	0.004	3.532	1.232	0.004
	apex	3.227	6.168	0.601	3.199	6.154	0.603
	recov	−5.326	4.362	0.222	−5.343	4.348	0.219
	${\sigma }_{\mathit{\text{MLE}}}^2$	208.812	25.667	< 0.001	208.436	25.573	< 0.001

Although we have assumed that data are MAR and a missing data mechanism need not be modeled, it is of some interest if we could determine the best fitting MAR missing data mechanism, so that we could at least (though somewhat ad-hoc) determine whether the missing data are MAR or MCAR. Towards this goal, we posited several different MAR and MCAR missing data mechanisms, and using the complete cases to fit these models as logistic regression in SAS. We then computed the log-likelihood statistic to determine the best fitting missing data mechanism. We considered 5 missing data mechanism, two of them are MCAR, and the other three are MAR. Let r_i,factg, r_i,apex, and r_i,recov denote the missing data indicators for factg, apex, and recov, respectively. To determine the final log-likelihood statistic value, we added the three contributions from the three parts of the binary regression models for r_i,factg, r_i,apex, and r_i,recov. Two MCAR models are [r_i,factg][r_i,apex][r_i,recov] (MCAR1) and [r_i,factg|r_i,apex, r_i,recov][r_i,apex][r_i,recov|r_i,apex] (MCAR2), where, for example, [r_i,factg] denotes a logistic regression model with intercept only and [r_i,factg|r_i,apex, r_i,recov] is a logistic regression model with intercept and covariates r_i,apex and r_i,recov. Let x_i,obs = (trt_i, gender_i, hist_i, age_i). Three MAR models include [r_i,factg|x_i,obs, apex_ir_i,apex, recov_ir_i,recov] [r_i,apex|x_i,obs][r_i,recov|x_i,obs, apex_ir_i,apex] (MAR1), [r_i,factg|x_i,obs, r_i,apex, r_i,recov][r_i,apex|x_i,obs] [r_i,recov|x_i,obs, r_i,apex] (MAR2), and [r_i,factg|trt_i, gender_i, r_i,apex, r_i,recov][r_i,apex|trt_i, gender_i] [r_i,recov|trt_i, gender_i, r_i,apex] (MAR3). For the lung cancer data, the log-likelihood statistics, −2 log(likelihood), are 889.4, 873.5, 868.5, 856.6, and 860.5 under models MCAR1, MCAR2, MAR1, MAR2, and MAR3, respectively. We see from these results that the best fitting model is MAR2 as the missing data mechanism suggesting that the missing data are missing at random.

7 Discussion

We have given several results regarding bias and efficiency of estimates in missing (x, y) regression problems, and have shown that the AC analysis provides the most efficient estimates and the least biased estimates in the MAR setting. The results derived in Section 4, Section 5, and Section 6 are new and important and shed light on the bias and efficiency of estimates in regression problems with MCAR or MAR responses and/or covariates. In Section 4.1 and 4.2, the variances are assumed to be known. This assumption can be relaxed. The asymptotic variance and covariance matrix of the MLE’s under each analysis method for the simple linear regression model with unknown variances is derived in Appendix B. With the known variances, as shown in Result 4.2, the AC analysis does not improve the efficiency of the MLE for β₁ over the CR analysis. When the variances are unknown, it is interesting to see, from Appendix B, that the AC analysis improves the efficiency of the MLE for ²₁ over both the CC and CR analsyese. Thus, the AC analysis becomes even more important in this case. However, the derivation of the asymptotic variance and covariance matrix of the MLE’s under each analysis method for the multiple linear regression model with unknown variances becomes very lengthy and hence, detailed derivations are omitted for brevity.

Finally, we mention that we have assumed throughout that jointly, (x_i, y_i) are iid. This is by far the most common approach in regression settings with missing covariate and/or response data. We note here, however, that since inference typically focuses on the parameters of [y_i|x_i], the y_i’s conditional on the x_i’s are not iid, but rather only independent. This development is still quite general since is covers settings such as the linear model and generalized linear models with MAR covariate and/or response data. Future work involves examination of the proposed methods for dependent responses, including dynamic linear models, models for longitudinal data, and generalized linear mixed models. Such theoretical investigations are currently being examined. The initial investigation taken here is the first of its kind, and should lead to fruitful results for other types of models.

Figure 1. Missing Patterns.

Note: Blank block stands for missing, marked block stands for observed.

Appendix A

Computational Development

We describe the model fitting and computational procedures for each of the analysis methods. For CC, the MLE of θ can be obtained by standard statistical software such as SAS. Here, we consider only for AC as the computation of the MLE’s under CR is similar to and even easier than AC.

We first consider the case where all x_i,mis’s are categorical. In this case, we use the EM algorithm via the method of weights proposed by Ibrahim (1990). Let θ^(t) = (β^(t), ϕ^(t), α^(t)) denote the value of θ at the t^th iteration of EM algorithm.

The E-step at the (t + 1)^st iteration can be written as

$$\begin{array}{ccc}Q(\mathit{\theta }|{\mathit{\theta }}^{(t)})\hfill & =\hfill & {\displaystyle \sum _{i:y_i\text{observed},M_i=\mathrm{\theta }}[\text{log}f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })+\text{log}f({\mathit{x}}_i|\mathit{\alpha })]}\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{i:y_i\text{observed},M_i\ne \mathrm{\theta }}{\displaystyle \sum _{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\left[\text{log}f(y_i|{\mathit{x}}_i,(j),\mathit{\beta },\mathit{\varphi })+\text{log}f({\mathit{x}}_i(j)|\mathit{\alpha })\right]}}\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{i:y_i\text{missing},M_i=\mathrm{\theta }}\text{log}f({\mathit{x}}_i|\mathit{\alpha })}\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{i:y_i\text{missing},M_i\ne \mathrm{\theta },M_i\ne \mathrm{\Omega }}{\displaystyle \sum _{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\text{log}f({\mathit{x}}_i(j)|\mathit{\alpha })}}\hfill \\ \hfill & =\hfill & Q^{(1)}(\mathit{\beta },\mathit{\varphi }|{\mathit{\theta }}^{(t)})+Q^{(2)}(\mathit{\alpha }|{\mathit{\theta }}^{(t)}),\hfill \end{array}$$ (A.1)

where ${\mathit{x}}_i(j)=({\mathit{x}}_{i,\mathit{\text{obs}}}^{\prime },{\mathit{x}}_{i,\mathit{\text{mis}}}^{\prime }(j))\prime$,

$$\begin{array}{ccc}{Q}^{(1)}(\mathit{\beta },\mathit{\varphi }|{\mathit{\theta }}^{(t)})\hfill & =\hfill & {\displaystyle \sum _{i:y_i\text{observed},M_i=\mathrm{\theta }}\text{log}f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })}\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{i:y_i\text{observed},M_i\ne \mathrm{\theta }}{\displaystyle \sum _{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\text{log}f(y_i|{\mathit{x}}_i(j),\mathit{\beta },\mathit{\varphi })}}\hfill \end{array}$$ (A.2)

and

$$\begin{array}{cc}{Q}^{(2)}(\mathit{\alpha }|{\mathit{\theta }}^{(t)})=\hfill & {\displaystyle \sum _{i:y_i\text{observed or missing},M_i=\mathrm{\theta }}\text{log}f({\mathit{x}}_i|\mathit{\alpha })}\hfill \\ \hfill & +{\displaystyle \sum _{i:y_i\text{observed},M_i\ne \mathrm{\theta }}{\displaystyle \sum _{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\text{log}f({\mathit{x}}_i(j)|\mathit{\alpha })}}\hfill \\ \hfill & +{\displaystyle \sum _{i:y_i\text{missing},M_i\ne \mathrm{\theta },M_i\ne \mathrm{\Omega }}{\displaystyle \sum _{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\text{log}f({\mathit{x}}_i(j)|\mathit{\alpha }).}}\hfill \end{array}$$ (A.3)

The inner sum extends over all of the possible values of the missing components of the covariate vector, with j indexing the distinct covariate patterns for subject i.

The weights, w_ij,(t), are the conditional probabilities corresponding to [x_i,mis|x_i,obs, y_i θ] or [x_i,mis|x_i,obs, α] and are given by

$$\begin{array}{cc} \hfill & w_{ij,(t)}=f({\mathit{x}}_{i,\mathit{\text{mis}}}(j)|{\mathit{x}}_{i,\mathit{\text{obs}}},y_i,{\mathit{\theta }}^{(t)})\hfill \\ =\hfill & \frac{f(y_i|{\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}(j),{\mathit{\beta }}^{(t)},{\mathit{\varphi }}^{(t)})f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}(j)|{\mathit{\alpha }}^{(t)})}{{\displaystyle {\sum }_{x_{i,\mathit{\text{mis}}}(j)}f}(y_i|{\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}(j),{\mathit{\beta }}^{(t)},{\mathit{\varphi }}^{(t)})f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}(j)|{\mathit{\alpha }}^{(t)})}\hfill \end{array}$$

or

$$w_{ij,(t)}=f({\mathit{x}}_{i,\mathit{\text{mis}}}(j)|{\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{\alpha }}^{(t)})=\frac{f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}(j)|{\mathit{\alpha }}^{(t)})}{{\displaystyle {\sum }_{x_{i,\mathit{\text{mis}}}(j)}f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}(j)|{\mathit{\alpha }}^{(t)})}}.$$

The M-step at the (t + 1)^st iteration proceeds as follows. We first compute

$$\underset{\mathit{\beta },\mathit{\varphi }}{({\mathit{\beta }}^{(t+1)},{\mathit{\varphi }}^{(t+1)})=\text{arg max}{Q}^{(1)}(\mathit{\beta },\mathit{\varphi }|{\mathit{\theta }}^{(t)})}$$

and

$$\underset{\mathit{\alpha }}{{\mathit{\alpha }}^{(t+1)}=\text{arg max}{Q}^{(2)}(\mathit{\alpha }|{\mathit{\theta }}^{(t)})}.$$

When we use the saturated model for x_i,mis, we have α = (α_(j)), where α_(j) denotes the probability of the j^th missing pattern. In this case, we update

$${\alpha }_{(j)}^{(t+1)}=\frac{{\displaystyle {\sum }_{i=1}^n{w}_{ij,(t)}}}{n}$$

where when x_i is completely observed, w_ij,(t) = 1 if x_i(j) = x_i and w_ij,(t) = 0 if x_i(j) ≠ x_i.

Let θ̂ denote the estimate of θ at EM convergence. We use Louis’s method (Louis, 1982) to compute the estimated observed information matrix of θ based on the observed data. Write the matrix of second derivatives of Q(θ|θ^(t)) as

$$\ddot{Q}(\mathit{\theta }|{\mathit{\theta }}^{(t)})=\left(\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial \mathrm{\gamma }\partial {\mathrm{\gamma }}^{\prime }}{Q}^{(1)}(\mathit{\beta },\mathit{\varphi }|{\mathit{\theta }}^{(t)})\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{{\partial }^2}{\partial \mathit{\alpha }\partial {\mathit{\alpha }}^{\prime }}{Q}^{(2)}(\mathit{\alpha }|{\mathit{\theta }}^{(t)})\hfill \end{array}\right),$$

where γ = (β′, ϕ′)′,

$$\begin{array}{cc}\frac{{\partial }^2}{\partial \mathrm{\gamma }\partial {\mathrm{\gamma }}^{\prime }}{Q}^{(1)}(\mathit{\beta },\mathit{\varphi }|{\mathit{\theta }}^{(t)})=\hfill & {\displaystyle \sum _{i:y_i\text{observed},M_i=\mathrm{\theta }}\frac{{\partial }^2}{\partial \mathrm{\gamma }\partial {\mathrm{\gamma }}^{\prime }}\text{log}f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })}\hfill \\ \hfill & +{\displaystyle \sum _{i:y_i\text{observed},M_i\ne \mathrm{\theta }}\frac{{\partial }^2}{\partial \mathrm{\gamma }\partial {\mathrm{\gamma }}^{\prime }}{\displaystyle \sum _{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\text{log}f(y_i|{\mathit{x}}_i(j),\mathit{\beta },\mathit{\varphi }),}}\hfill \end{array}$$

and

$$\begin{array}{cc}\frac{{\partial }^2}{\partial \mathit{\alpha }\partial {\mathit{\alpha }}^{\prime }}{Q}^{(2)}(\mathit{\alpha }|{\mathit{\theta }}^{(t)})=\hfill & {\displaystyle \sum _{i:y_i\text{observed or missing},M_i=\mathrm{\theta }}\frac{\partial }{{\partial }^2\mathit{\alpha }\partial {\mathit{\alpha }}^{\prime }}\text{log}f({\mathit{x}}_i|\mathit{\alpha })}\hfill \\ \hfill & +{\displaystyle \sum _{i:y_i\text{observed},M_i\ne \mathrm{\theta }}{\displaystyle \sum _{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\frac{{\partial }^2}{\partial \mathit{\alpha }\partial {\mathit{\alpha }}^{\prime }}\text{log}f({\mathit{x}}_i(j)|\mathit{\alpha })}}\hfill \\ \hfill & +{\displaystyle \sum _{i:y_i\text{missing},M_i\ne \mathrm{\theta },M_i\ne \mathrm{\Omega }}{\displaystyle \sum _{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\frac{{\partial }^2}{\partial \mathit{\alpha }\partial {\mathit{\alpha }}^{\prime }}\text{log}f({\mathit{x}}_i(j)|\mathit{\alpha }).}}\hfill \end{array}$$

Write the gradient vector of Q_i(θ|θ^(t)) for the i^th observation as

$$\begin{array}{cc} \hfill & {\dot{Q}}_i(\mathit{\theta }|{\mathit{\theta }}^{(t)})\hfill \\ =\hfill & \{\begin{array}{cc}\frac{\partial }{\partial \mathit{\theta }}\text{log}[f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })f({\mathit{x}}_i|\mathit{\alpha })]\hfill & \text{if}{y}_i\text{observed},M_i=\mathrm{\theta }\hfill \\ {\displaystyle {\sum }_{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\frac{\partial }{\partial \mathit{\theta }}\text{log}[f(y_i|{\mathit{x}}_i(j),\mathit{\beta },\mathit{\varphi })f({\mathit{x}}_i(j)|\mathit{\alpha })]}\hfill & \text{if}{y}_i\text{observed},M_i\ne \mathrm{\theta }\hfill \\ \frac{\partial }{\partial \mathit{\theta }}\text{log}f({\mathit{x}}_i|\mathit{\alpha })\hfill & \text{if}{y}_i\text{missing},M_i=\mathrm{\theta }\hfill \\ {\displaystyle {\sum }_{{\mathit{x}}_{i,\mathit{\text{mis}}}(j)}{w}_{ij,(t)}\frac{\partial }{\partial \mathit{\theta }}\text{log}f({\mathit{x}}_i(j)|\mathit{\alpha })}\hfill & \text{if}{y}_i\text{missing},M_i\ne \mathrm{\theta },M_i\ne \mathrm{\Omega }.\hfill \end{array}\hfill \end{array}$$

In addition, write the complete data score vector S_i(θ|x_i, y_i) as

$$S_i(\mathit{\theta }|{\mathit{x}}_i,y_i)=\{\begin{array}{cc}\frac{\partial }{\partial \mathit{\theta }}\text{log}[f(y_i|{\mathit{x}}_i,\mathit{\beta },\mathit{\varphi })f({\mathit{x}}_i|\mathit{\alpha })]\hfill & \text{if}{y}_i\text{observed}\hfill \\ \frac{\partial }{\partial \mathit{\theta }}\text{log}f({\mathit{x}}_i|\mathit{\alpha })\hfill & \text{if}{y}_i\text{missing}.\hfill \end{array}$$

Then, the estimated observed information matrix of θ̂ is given by

$$\begin{array}{cc}I(\hat{\mathit{\theta }})=\hfill & -\ddot{Q}(\hat{\mathit{\theta }}|\hat{\mathit{\theta }})\hfill \\ \hfill & -\left\{\left[{\displaystyle \sum _{i:M_i\ne \mathrm{\theta }}{\displaystyle \sum _{{\mathit{x}}_{i,\mathit{\text{mis}}(j)}}{w}_{ij,(t)}{S}_i(\hat{\mathit{\theta }}|{\mathit{x}}_i(j),y_i)S_i(\hat{\mathit{\theta }}|{\mathit{x}}_i(j),y_i{)}^{\prime }}}\right]-{\displaystyle \sum _{i:M_i\ne \mathrm{\theta }}{\dot{Q}}_i(\hat{\mathit{\theta }}|\hat{\mathit{\theta }}){\dot{Q}}_i(\hat{\mathit{\theta }}|\hat{\mathit{\theta }}{)}^{\prime }}\right\},\hfill \end{array}$$ (A.4)

where the weights, w_ij,(t), are computed at EM convergence. Thus, the estimate of the asymptotic covariance matrix of θ̂ is [I (θ̂)]⁻¹.

When missing covariates are continuous or mixed Continuous and categorical, a Monte Carlo EM (MCEM) algorithm is required. The implementation of the MCEM is similar to the EM algorithm for the categorical missing covariates, and is developed in detail in Ibrahim, Lipsitz and Chen (1999), and Ibrahim, Chen, and Lipsitz (1999). Specifically, we replace the weight average in (A.2), (A.3) and (A.4) by a Monte Carlo average. For example, in the E-Step, for missing covariates in the Block B₂, we take an MCMC sample of size $m_i^{(t)},{\mathit{x}}_{i,\mathit{\text{mis}}}^{(t1)},{\mathit{x}}_{i,\mathit{\text{mis}}}^{(t2)},\dots ,{\mathit{x}}_{i,\mathit{\text{mis}}}^{(t{m}^{(t)})},$ from

$$f(x_{i,\mathit{\text{mis}}}|x_{i,\mathit{\text{obs}}},y_i,{\mathit{\theta }}^{(t)})\mathrm{\propto }f(y_i|{\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}},{\mathit{\beta }}^{(t)},{\mathit{\varphi }}^{(t)})f({\mathit{x}}_{i,\mathit{\text{obs}}},{\mathit{x}}_{i,\mathit{\text{mis}}}|{\mathit{\alpha }}^{(t)}).$$

Then, we compute

$$\begin{array}{cc}{Q}^{(1)}(\mathit{\beta },\mathit{\varphi }|{\mathit{\theta }}^{(t)})=\hfill & {\displaystyle \sum _{i:y_i\text{observed},M_i=\mathrm{\theta }}\text{log}f(y_i|{\mathit{x}}_i},\mathit{\beta },\mathit{\varphi })\hfill \\ \hfill & +{\displaystyle \sum _{i:y_i\text{observed},M_i\ne \mathrm{\theta }}\frac{1}{m^{(t)}}{\displaystyle \sum _{l=1}^{m^{(t)}}\text{log}f(y_i|{\mathit{x}}_i^{(tl)},\mathit{\beta },\mathit{\varphi }),}}\hfill \end{array}$$

${\mathit{x}}_i^{(tl)}=({\mathit{x}}_{i,\mathit{\text{obs}}}^{\prime },{\mathit{x}}_{i,\mathit{\text{mis}}}^{(tl{)}^{\prime }}{)}^{\prime }$. We then take m^(t+1) = m^(t) + Δm, where Δm > 0. In such a way, the MCEM algorithm requires much less computational time, as a large m^(t) is not needed in early iterations of the algorithm.

Appendix B

Simple Linear Regression Model with Unknown Variances

We consider a simple normal regression model with a single covariate and unknown variances here. In this case, we have

$$f(y_i|x_i,\mathit{\beta },\sigma )=\frac{1}{\sqrt{2\mathrm{\pi }{\sigma }^2}}\text{exp}\left\{-\frac{{(y_i-{\beta }_0-{\beta }_1{x}_i)}^2}{2{\sigma }^2}\right\}\text{and}f(x_i|\alpha ,\tau )=\frac{1}{\sqrt{2\mathrm{\pi }{\tau }^2}}\text{exp}\left\{-\frac{{(x_i-\alpha )}^2}{2{\tau }^2}\right\}.$$

Write θ = (β′, σ², α, τ²)′. Let n_j = #(B_j) be the cardinality of B_j for j = 1, 2, 3 and n = n₁ + n₂ + n₃. For the CC analysis, we have

$$l_{cc}(\mathit{\theta })={\displaystyle \sum _{i:y_i\text{observed},M_i=\mathrm{\theta }}\left[-\text{log}(2\mathrm{\pi }\sqrt{{\sigma }^2{\tau }^2})-\frac{{(y_i-{\beta }_0-{\beta }_1{x}_i)}^2}{2{\sigma }^2}-\frac{{(x_i-\alpha )}^2}{2{\tau }^2}\right]}$$

and the Fisher information matrix is given by

$$I_{cc}(\mathit{\theta })=-E\left[\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\prime }}{l}_{cc}(\mathit{\theta })\right]=n_1\left(\begin{array}{ccccc}\hfill 1/{\sigma }^2\hfill & \hfill \alpha /{\sigma }^2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \alpha /{\sigma }^2\hfill & \hfill ({\tau }^2+{\alpha }^2)/{\sigma }^2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1/(2{\sigma }^4)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1/{\tau }^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1/(2{\tau }^4)\hfill \end{array}\right).$$

For the CR analysis, we have

$$l_{cr}(\mathit{\theta })=l_{cc}(\mathit{\theta })+{\displaystyle \sum _{i\in B_2}\left\{-\text{log}\sqrt{2\mathrm{\pi }}-\frac{\text{log}(\upsilon )}{2}-\frac{{(y_i-{\beta }_0-{\beta }_1\alpha )}^2}{2\upsilon }\right\}},$$

where $\upsilon ={\sigma }^2+{\beta }_1^2{\tau }^2$. After some messy algebra, we obtain the Fisher information matrix given by

$$I_{cr}(\mathit{\theta })=-E\left[\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\prime }}{l}_{cr}(\mathit{\theta })\right]=I_{cc}(\mathit{\theta })+\frac{n_2}{{\upsilon }^2}\left(\begin{array}{ccccc}\hfill \upsilon \hfill & \hfill \alpha \upsilon \hfill & \hfill 0\hfill & \hfill {\beta }_1\upsilon \hfill & \hfill 0\hfill \\ \hfill \alpha \upsilon \hfill & \hfill {\alpha }^2\upsilon +2{\beta }_1^2{\tau }^4\hfill & \hfill {\beta }_1{\tau }^2\hfill & \hfill \alpha {\beta }_1\upsilon \hfill & \hfill {\beta }_1^3{\tau }^2\hfill \\ \hfill 0\hfill & \hfill {\beta }_1{\tau }^2\hfill & \hfill 1/2\hfill & \hfill 0\hfill & \hfill {\beta }_1^2/2\hfill \\ \hfill {\beta }_1\upsilon \hfill & \hfill \alpha {\beta }_1\upsilon \hfill & \hfill 0\hfill & \hfill {\beta }_1^2\upsilon \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\beta }_1^3{\tau }^2\hfill & \hfill {\beta }_1^2/2\hfill & \hfill 0\hfill & \hfill {\beta }_1^4\hfill \end{array}\right).$$

For the AC analysis, the log-likelihood function is given by

$$l_{ac}(\mathit{\theta })=l_{cr}(\mathit{\theta })+{\displaystyle \sum _{i:y_i\text{missing},M_i=\mathrm{\theta }}\text{log}f(x_i|\alpha )}=l_{cr}(\mathit{\theta })+{\displaystyle \sum _{i\in B_3}\left[-\text{log}\sqrt{2\mathrm{\pi }{\tau }^2}-\frac{{(x_i-\alpha )}^2}{2{\tau }^2}\right].}$$

The corresponding Fisher information matrix is given by

$$I_{ac}(\mathit{\theta })=-E\left[\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^{\prime }}{l}_{ac}(\mathit{\theta })\right]=I_{cr}(\mathit{\theta })+n_3\left(\begin{array}{ccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1/{\tau }^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1/(2{\tau }^4)\hfill \end{array}\right).$$

Based on either the determinant or the trace of Fisher information matrix, AC yields most gain in information over both CR and CC, and CR gains more information than CC. Specifically, we have

$$\begin{array}{cc} \hfill & \text{det}(I_{ac})-\text{det}(I_{cr})\hfill \\ =\hfill & \frac{n_1{n}_3}{4{\upsilon }^5{\sigma }^8{\tau }^4}[n_1^2{\upsilon }^5(2n_1+3n_2+n_3)+n_1{n}_2{\sigma }^2{\upsilon }^4(n_1+2n_2+2n_3)+n_2{\sigma }^2{\upsilon }^3(n_2{n}_3{\sigma }^2+n_1{n}_2{\beta }_1^2{\tau }^2\hfill \\ \hfill & +n_1{n}_3{\beta }_1^2{\tau }^2)+n_2^2{\beta }_1^2{\sigma }^2{\tau }^2{\upsilon }^2(n_3{\sigma }^2+2n_1{\beta }_1^2{\tau }^2)+n_2^2{\beta }_1^4{\sigma }^2{\tau }^4\upsilon (n_2{\sigma }^2+n_1{\beta }_1^2{\tau }^2)+n_2^3{\beta }_1^6{\sigma }^4{\tau }^6]\hfill \\ >\hfill & 0,\hfill \end{array}$$

$$\begin{array}{cc} \hfill & \text{det}(I_{cr})-\text{det}(I_{cc})\hfill \\ =\hfill & \frac{n_1^2{n}_2}{4{\upsilon }^4{\sigma }^8{\tau }^4}\left[n_1{\upsilon }^4(2n_1+n_2)+n_1{\beta }_1^4{\tau }^4{\upsilon }^2(n_1+n_2)+n_2{\beta }_1^4{\sigma }^2{\tau }^4(n_1+n_2)(\upsilon +{\beta }_1^2{\tau }^2)\right]>0,\hfill \end{array}$$

$$\mathit{\text{tr}}(I_{ac})-\mathit{\text{tr}}(I_{cr})=\frac{n_3(1+2{\tau }^2)}{2{\tau }^4}>0,$$

and

$$\mathit{\text{tr}}(I_{cr})-\mathit{\text{tr}}(I_{cc})=\frac{n_2}{2{\upsilon }^2}\left[2\upsilon (1+{\beta }_1^2+{\alpha }^2)+4{\beta }_1^2{\tau }^4+2{\beta }_1^4+1\right]>0.$$

CR leads to smaller asymptotic variances for all parameters than CC. Specifically, we have

$$\begin{array}{ccc}\hfill \text{Var}({\hat{\beta }}_{1,cc})-\text{Var}({\hat{\beta }}_{1,cr})& =\hfill & 2n_2{\beta }_1^2{\sigma }^4(n_2{\beta }_1^4{\tau }^4+n_1{\upsilon }^2)/a_1>0,\hfill \\ \hfill \text{Var}({\hat{\sigma }}_{cc}^2)-\text{Var}({\hat{\sigma }}_{cr}^2)& =\hfill & 2n_2{\sigma }^8(n_2{\beta }_1^4{\tau }^4+n_1{\upsilon }^2)/a_1>0,\hfill \\ \hfill \text{Var}({\hat{\alpha }}_{cc})-\text{Var}({\hat{\alpha }}_{cr})& =\hfill & n_2{\beta }_1^2{\tau }^4/n_1(n_1+n_2)\upsilon >0,\hfill \\ \hfill \text{Var}({\hat{\tau }}_{cc}^2)-\text{Var}({\hat{\tau }}_{cr}^2)& =\hfill & 2n_2{\beta }_1^4{\tau }^8[2n_1{\upsilon }^2+n_2{\sigma }^2(\upsilon +{\beta }_1^2{\tau }^2)]/a_1>0,\hfill \end{array}$$

where $a_1=n_1(n_1^2{\upsilon }^4+n_2^2{\beta }_1^4{\sigma }^2{\tau }^4(\upsilon +{\beta }_1^2{\tau }^2)+n_1{n}_2{\upsilon }^2({\upsilon }^2+{\beta }_1^4{\tau }^4))$.

In addition, AC improves the asymptotic variances over CR. Specifically, we have

$$\begin{array}{ccc}\hfill \text{Var}({\hat{\beta }}_{1,cr})-\text{Var}({\hat{\beta }}_{1,ac})& =\hfill & 2{\upsilon }^4{n}_2^2{n}_3{\beta }_1^6{\sigma }^4{\tau }^4/a_2{a}_3>0,\hfill \\ \hfill \text{Var}({\hat{\sigma }}_{cr}^2)-\text{Var}({\hat{\sigma }}_{ac}^2)& =\hfill & 2{\upsilon }^4{n}_2^2{n}_3{\beta }_1^4{\sigma }^8{\tau }^4/a_2{a}_3>0,\hfill \\ \hfill \text{Var}({\hat{\alpha }}_{cr})-\text{Var}({\hat{\alpha }}_{ac})& =\hfill & n_3{\tau }^2(n_2{\sigma }^2+n_1\upsilon )/n_1(n_1+n_2)(n_2{n}_3{\sigma }^2+n_1(n_1+n_2+n_3)\upsilon )\upsilon >0,\hfill \\ \hfill \text{Var}({\hat{\tau }}_{cr}^2)-\text{Var}({\hat{\tau }}_{ac}^2)& =\hfill & 2n_3{\tau }^4{\upsilon }^4{[n_1{\upsilon }^2+n_2{\sigma }^2(\upsilon +{\beta }_1^2{\tau }^2)]}^2/a_2{a}_3>0,\hfill \end{array}$$

where $a_2={\upsilon }^4{n}_1(n_1+n_2)+n_2{\beta }_1^4{\sigma }^4\upsilon (n_1\upsilon +n_2{\sigma }^2)+n_2^2{\beta }_1^6{\sigma }^2{\tau }^6,\text{and}{a}_3=n_1(n_1+n_2+n_3){\upsilon }^4+n_2{\sigma }^2(\upsilon +{\beta }_1^2{\tau }^2)(n_3{\upsilon }^2+n_2{\beta }_1^4{\tau }^4)+n_1{n}_2{\beta }_1^4{\tau }^4{\upsilon }^2$.