Stochastic probability landscape model for switching efficiency, robustness, and differential threshold for induction of genetic circuit in phage λ

Abstract

The genetic switch of phage lambda provides a paradigm for studying developmental biology and cell fate. Although there have been numerous experimental and theoretical studies, the mechanisms for switching efficiency, stability and robustness, maintenance of lysogenic state, and the induction lytic state are not fully understood. In this paper, a new method is adopted to account for the full stochasticity typical in small copy events and the exact steady state probability landscape of the genetic circuit of the switch network is computed. The stability and sensitivity of phage λ switch and its robustness against perturbations derived from our model for wild type and mutants are consistent with experimental data. Our study has revealed likely mechanism of the phage switch network that was previously unknown.

I. INTRODUCTION

The gene regulatory circuit in phage λ controls the switch between the maintenance of the lysogenic state and the induction of the lytic state. The components and chemical reactions of the circuit have been fully identified, and corresponding binding/kinetic constants have been measured [1]. As a paradigm for understanding cell development, it has been the focus of many experimental [2], [3] and theoretical [4]–[11] studies. Of central importance is to understand the regulation mechanism of the switch, its systems stability against perturbation, and its robustness against genetic mutations. For example, an important question is how the nutritional conditions or DNA damage signal due to UV radiation affect the fate of phage and host cells.

A. Phage λ switch

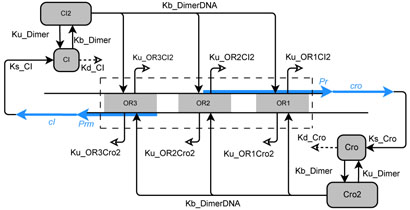
The switch of phage λ is composed of three operators (named OR1, OR2 and OR3) and two promoters (Pr and Prm). Promoter Pr overlaps with OR1 and OR2, and can initialize the transcription of protein Cro, which activates a series of gene expression and leads to the lytic state. Promoter Prm overlaps with OR3 and can initialize the transcription of another gene CI, which can repress the induction of the lytic state through the repression of Cro expression. Protein CI and Cro form dimers, which bind to any of the three operator sites with different affinities. CI dimers have the highest affinity for OR1, and the lowest affinity for OR3. In contrast, Cro dimers have the highest affinity for OR3, and lower affinities for OR2 and OR1. The state of the phage λ is determined by the relative concentration of CI and Cro dimers in the living cells. Higher concentration of CI keeps the phage λ in the dormant lysogenic state, and higher concentration of Cro flips the switch irreversibly from lysogenic state to lytic state, and in the end kills the host cell and releases more virus to infect other bacterial cells. The topological structure of the phage λ switch is shown in Fig 1, and the descriptions of all kinetic constants are listed in Table I.

Fig. 1.

The topological structure of the phage λ switch. Reactions, including binding and unbinding, synthesis and degradation, dimerization,are labeled as arrows, along with labels for the corresponding kinetic constants.

TABLE I.

Kinetic constants of Phage λ switch.

Label	Value	Description
Kb_DimerDNA	0.021 /sec	binding rate of dimers to DNA
Ku_OR1CI2	0.04 /sec	unbinding rate of CI dimer from OR1
Ku_OR2CI2	1.026 /sec	unbinding rate of CI dimer from OR2
Ku_OR3CI2	5.197 /sec	unbinding rate of CI dimer from OR3
Ku_OR1Cro2	0.09 /sec	unbinding rate of Cro dimer from OR1
Ku_OR2Cro2	0.613 /sec	unbinding rate of Cro dimer from OR2
Ku_OR3Cro2	0.009 /sec	unbinding rate of Cro dimer from OR3
Kb_Dimer	0.05 /M · sec	rate of dimerising
Ku_Dimer	0.5 /sec	dissociation rate of dimers
Ks_CI	0.0077 /sec	synthesis rate of CI
Ks_Cro	0.0534 /sec	synthesis rate of Cro
Kd_CI	0.0007 /sec	degradation rate of CI monomer
Kd_Cro	0.0025 /sec	degradation rate of Cro monomer

B. Prior theoretical studies

Shea and Ackers first developed a statistical-thermodynamic model of phage λ, and studied several key molecular processes. [4]. Arkin et al. modeled the whole phage λ lysis-lysogeny genetic circuit using the stochastic simulation algorithm [12] and studied the dynamical behaviors of the system [5]. The studies of several mutant by Little et al reveal additional experimental insight: it was found that the switch circuitry is quite robust, with the mutants exhibiting qualitatively the same behavior as that of the wild-type, albeit at different levels of gene expression [2]. Aurell et al. adopted a deterministic ODE model to study the stability of phage λ switch, and modeled the switch to lysis as a first exit problem [6]. Zhu et al. developed a model that considers the stochastic effects by introducing a random noise term, and their calculations are in excellent agreement with Little's experiment results [8].

C. Our study

As the copy numbers of CI and Cro dimers range roughly from 50 to 200 per cell [5], [13], [14], stochasticity intrinsic in such small copy events cannot be neglected, as they may play important roles in phage λ switch. In this study, we model the λ switch with full stochasticity. Our model includes explicitly the dimerization processes of Cro and CI dimer. We compute the exact steady state probability landscape over all possible microstates of the phage λ switch for both wild type and several mutants. We compare our results with experimental data, and infer the underlying mechanism of the λ-phage network.

II. METHODS

A. Molecular species of the model

We considered a total of 14 molecular species: three empty operator sites (OR1, OR2 and OR3), operator sites bound by CI dimer (ROR1, ROR2 and ROR3), and bound by Cro dimer (COR1, COR2 and COR3), protein monomer (CI and Cro), protein dimer (CI2 and Cro2), and a buffer. As this phage λ model is an open system, i.e., there exist synthesis and degradation reactions, a buffer is introduced to limit the state space for computational purpose [15]. The buffer size of 50 used in this study, namely, the maximum copy number of net molecules synthesized in the system, can model the λ phage rather realistically.

B. Reactions and kinetic parameters

All ten biochemical reactions in this model are reversible. There are a total of 13 kinetic parameters, and their values are listed in Table I.

Protein binding to operators

We assume CI and Cro proteins have equal rate to access the operators on DNA. Association rate constant k_a = 2.57 × 10⁷/M·sec is derived using the experimentally measured protein diffusion coefficient 10⁻⁷cm²/s [16]. We use the rate constant Kb_DimerDNA = k_a/A·V = 0.021/sec, where A = 6.023 × 10²³ is the Avo-gadro's number and V = 2 × 10⁻¹⁵l is roughly the volume of E. coli cell. Dissociation rate constant is $k_d=\frac{k_a}{k_{eq}},$ where $k_{eq}=e^{\frac{-\Delta G}{R\cdot T}}$, ΔG is the Gibbs free energy, R is the universal gas constant and T = 310.15 Kelvin, which is the absolute temperature at which the experiments were performed, i.e., 37 Celsius. The binding free energies of CI repressor to the operators are taken from Koblan and Ackers [17], and that of Cro comes from [18]

Protein synthesis

We regard the time required for protein synthesis is dictated by the transcription process, including transcript initiation and elongation. The rate limiting step in transcript initiation is taken to be the closed- to open-complex isomerization reaction [19]. The rate of transcript initiation reaction $RNAP+P\stackrel{K_B}{\leftrightarrow }RNAP\ast P_c\stackrel{K_f}{\to }RNAP\ast P_c$ is 9.46 × 10⁵ and 6.7 × 10⁶/M·sec for CI and Cro protein, respectively [20]–[22]. Transcription elongation rate is selected as an average rate of = 30nt/sec [5]. An average ten copies of proteins are assumed to be produced per transcript for all genes [4], [5].

Protein degradation and dimerization

CI and Cro degradation rates and dimerization rate come from [5].

C. Algorithms

The algorithms used in this study has been described in detail elsewhere [15]. Briefly, we study the stochastic properties of the network by first enumerating all possible microscopic states of the system under a given initial condition, following the topology of the phage λ switch network (Fig. 1). We then compute the transition coefficients between different states according to reaction kinetics and the copy numbers of reactants. With the state-transition matrix A filled with computed transition coefficients, we compute the exact steady state probability landscape and analyze the properties of the network [15]. We use the ARPACK program [23] to compute the steady state probability landscape by finding the normalized eigenvector of matrix M with eigenvalue 1, where M = I+AΔt. Marginal probabilities for copy number combinations of each Cro and CI dimer are then computed, which collective gives the steady state probability landscape projected on the axes of the Cro and the CI concentrations.

D. Computing CI and Cro levels

We compute the steady state protein concentration of CI and Cro monomer from the landscape as: $C_m={\displaystyle \sum s\in }\chi c_m^{s}Prob(s),m\in \{CI,Cro\},$ where χ is the state space, s is a microstate in χ, $c_m^s$ is the copy number of molecular species m in state s, and Prob(s) is the probability of s in the steady state probability distribution.

III. RESULTS

A. Probability landscape of lysogenic, lytic and saddle transition states

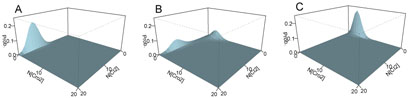
An example of the landscape of the steady state probabilities of all CI and Cro copy number combinations is shown in Fig 2. To probe how changes in CI synthesis affect the qualitative behavior of λ phage, we compute the different probability landscape under different CI synthesis rate.

Fig. 2.

Lysogenic and lytic states and CI synthesis rate. (A) Lysogenic state, Ks_CI=0.045/sec, (B) The switching state, Ks CI=0.0245/sec, (C) Lytic state, Ks_CI=0.0077/sec. X and Y axes are copy numbers of CI and Cro dimers; and Z axes is the marginal probability.

To identify conditions under which the system stays in the lysogenic state, we decrease the CI synthesis rate by ten-fold from 0.077 /sec to 0.0077 /sec. When the CI synthesis rate is greater than 0.03 per sec, the system stay in the lysogenic state and is far from switching to lytic state. Fig. 2A shows the landscape of lysogenic state when CI synthesis rate is 0.045 per sec, where the level of CI protein is much higher than that of Cro protein. We found that the system starts to transit to a lytic state when the CI synthesis rate is decreased to 0.0245 per sec. The landscape at this synthesis rate appears to be saddle-shaped (Fig. 2B). When the system switches from lysogenic to lytic state, the lysogenic peak (high CI, low Cro) gradually decreases, and the lytic peak (low CI and high Cro) increases when the CI synthesis rate decreases. At the CI synthesis rate of 0.0077 per sec, the systems is in the lytic state (Fig 2C), i.e., the system will eventually disable and kill the host cell.

B. Landscape of mutant λ phage

We have also computed the steady state probability landscape of mutant λ phages whose experimental results are available [2]. As the three operators in wild type are arranged in the order of 321 (Fig. 1), mutant λ phage can be constituted where the operators are substituted into the patterns of 121, 323, and 123. At the CI synthesis rate of Ks CI=0.03/sec for the lysogenic state and Ks CI=0.0077/sec for the lytic state, the relative CI level in lysogen and Cro level in lysis compared to the wild type phage in percentages are shown in Table II and Table III, respectively. The results by Little and Zhu et al. [8] are also listed. Overall, our results show similar patterns as the experimental data, although there is quantitative difference for mutant 121 in lysogenic state.

TABLE II.

Comparison to Little's and Zhu et al's results [8], [9]. The CI synthesis used for the lysogen is Ks_CI=0.03/sec.

phage	Zhu et al's	J. Little's	our results
Wile-type	100%	100%	100%
1-2-1	20%	25-30%	62.6%
3-2-3	70%	60-75%	74.1%

TABLE III.

Comparison to Zhu et al's results [8], [9], with Ks_CI=0.0077/sec for lysis.

phage	Zhu et al's	our results
Wile-type	100%	100%
1-2-1	100%	87%
3-2-3	70%	51%

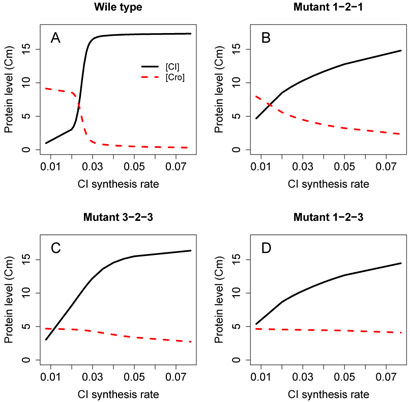
The CI and Cro levels in wild type and mutant 121, 323 and 123 at additional CI synthesis rates between 0.0077/sec and 0.077/sec have been further computed. The results are summarized in Fig. 3, where each point represents CI or Cro concentration computed from a calculated landscape similar to that in Fig. 2.

Fig. 3.

CI and Cro dimer levels at different CI synthesis rate. CI levels are plotted in solid lines, and Cro levels in dashed lines. The protein dimer levels are relative values, their computations are described in Section II (D).

IV. CONCLUSIONS

A. Wild type phage has stable and optimized switching efficiency

Fig. 3A shows the CI and Cro levels over different CI synthesis rate for the wild type phage. We observe a very robust and efficient switch over the range of CI synthesis rate from 0.077 to 0.0077 per sec. While the CI synthesis rate may fluctuate wildly between 0.077 and 0.03 per sec, the CI level is maintained at almost identical level. At the same time, Cro is strongly repressed. This demonstrate that the state of lysogen of phage lambda switch is very stable despite possible large fluctuation in CI level.

However, when the CI synthesis rate goes down from 0.03 to 0.02 per sec, a relatively small change compared to the range of 0.077 – 0.0077 per sec, the switch is efficiently flipped from the lysogenic state to the lytic state. That is, when the switch receives a true signal beyond random fluctuation, CI and Cro do not maintain the stable levels of the lysogenic state. Instead, CI level decreases and Cro level increases dramatically, and the phage lambda is switched to the lytic state. The levels of CI and Cro now attain a different set of stable levels with a higher Cro level. These results show that the wild-type phage lambda switch possesses the property of a good switch of stability and switching efficiency.

Our results show that all other mutants, including 121, 323, and 123, have different switching behavior. The level of CI in mutant 121 and 123 is not robust against small fluctuation of CI synthesis rate: The level of CI does not remain at a stable level, and decreases continuously when the CI synthesis rate decreases. This is accompanied by continuous increase of the Cro level in mutant 121. Our results indicates an increased level of spontaneous induction of phage lambda, and the switching behavior of these mutants is not efficient. Little et al. observed that mutant 323 lysogenizes with a reduced frequency [2]. This mutant has th elowest CI level at low CI synthesis rate. Our result is consistent with the experimental observation.

B. Difference of threshold behavior for UV induction

We observed that all three mutants have lower CI levels in lysogenic state. As Cro synthesis is not suppressed at the same level as the wild type, it is reasonable to expect that these mutants can be induced to lytic state by a lower dose of UV than that of the wild type. This is again consistent with Little's results of “hair-trigger variants” [2].

Our results also suggest a mechanism by which the CI levels in all three mutants are lower than that of wild type. In mutant 121 and 123, CI self-repression becomes a dominant limiting factor to CI levels. We find that Ku_OR3CI2=5.197 in the wild type, but Ku_OR3CI2=0.04 in the mutants 121 and 123, as it takes the value of Ku_OR1CI2 in the wild type. This indicates that CI expression is repressed more severely in the mutants 121 and 123 than in the wild type in the lysogenic state, where the CI level is higher than the Cro level. The case of mutant 323 is different, as CI level is still mainly repressed by Cro. However, since OR1 at the righthand side is replaced by an OR3, CI cannot repress Cro effectively. As a result, the Cro level is elevated compare to that of the wild type. More production of Cro represses the level of CI.

Little et al. observed that the mutant 323 is different from the other two mutants, in which some isolated derivatives of mutant 323 can only be induced by a dose of 10J/m² UV, which is the dose of induction for wild type phage, while the other two mutants are both induced by a lower dose of UV irradiation. It was thought that mutant 323 can evolve to modulate its sensitivity to UV induction [2]. Our results suggest that mutant 323 has a pattern more similar to that of the wild type, and is more robust against random fluctuation in changes of CI synthesis rate than the other two mutants. The origin of this differential UV dosage can be accounted for by the differential affinity configuration of CI and Cro to the operator sites. Our conclusion is different from previous study in which the relative affinities to different operator sites are thought to be unimportant [2].

C. Summary conclusion

In this study, we have applied a novel method to study the full stochastic probability landscape of the genetic circuits of the switch in λ-phage. Profiles of the wild type and mutant phage λ switches behavior at different CI synthesis rate indicate that compared to mutants, wild type phage is stable against random fluctuations, at the same time switches efficiently between the lysogenic and the lytic state when true signals are received.

Our study provide a novel approach to investigate the behavior of molecular networks. Unlike previous experimental studies where system with fixed parameters are used, our study can probe the behavior of the genetic circuits over a wide range of experimental conditions e.g., different CI synthesis rates. Unlike previous theoretical studies, stochasticity is fully accounted for in our model, and our approach is especially suited for studying critical events with small copy numbers. Our approach works for small networks, but will require careful model simplification for larger network. Our current study does not incorporate DNA loop, which will be subject for further studies.