Detecting Remote Homologues Using Scoring Matrices Calculated from the Estimation of Amino Acid Substitution Rates of Beta-Barrel Membrane Proteins

Abstract

Beta-barrel membrane proteins (MP) are found in Gram-negative bacteria, mitochondria and chloroplasts. They play important roles in metabolism of bacteria, where they are involved in transport of solutes in and out of the cell. Beta-barrel proteins may also act as proteases, lipases and may be important for cell-cell adhesion. Currently, there are about 30 non-redundant solved structures of β-barrels. Although the number of b-barrel folds is fairly small, it is possible to expand the amount of available structural information by homology modeling using existing structures as templates. The scope of structure prediction may be widened by finding remote homologues of the existing structures. To improve the sensitivity of the database searches and the quality of sequence alignments, we first study evolutionary history of transmembrane segments of 7 β-barrel membrane proteins by estimating substitution rates with a Bayesian Monte Carlo approach. Next, we calculate amino acid substitution matrices, beta-barrel Transmembrane scoring Matrices (bbTM), specifically tuned for TM regions, which can be used to detect remote homologues. We then test bbTM matrices by comparing their performance with membrane-protein derived scoring matrices PHAT and SLIM. Our results demonstrate that bbTM matrices have higher selectivity towards transmembrane β-barrel proteins and may be used with higher confidence in database searches for remote homologues of this class of proteins.

I. INTRODUCTION

Sequence analysis of homologous proteins showed that certain amino acid substitutions occur more frequently than others due to physical, chemical or structural reasons, which prompted the use of scoring matrices as a punctuation system. The classic PAM (Percentage of Acceptable point Mutations) matrices [1] were based on robustly accurate alignments of closely related proteins, from which target frequencies for any desired evolutionary distance were extrapolated using a time-reversible Markov model [2, 3]. BLOSUM (BLOcks of Amino Acid SUbstitution Matrix) matrices [4] avoid such extrapolation by estimating target frequencies directly from different evolutionary distances by using the ungapped segments of multiple sequence alignments. BLOSUM62 is the default matrix for the popular database search BLAST, while FASTA is usually used with BLOSUM50 matrix. An update of PAM matrices based on the same counting approach that PAM and BLOSUM, using a much larger database is the Jones-Taylor-Thornton (JTT) amino acid substitution matrix [5], widely used in phylogenetic analysis [5-7].

The quality of the results obtained with BLAST searches against protein databases depends strongly on the choice of the scoring matrix and these commonly used matrices are not exempt from problems. For example, the counting methods behind their calculations present two main problems: the systematic underestimation of substitution in certain branches of a phylogeny, and the inefficiency in using all the information contained in the amino acid residue sequences [8].

Assuming that the counting methods would be sufficient, BLOSUM and PAM have been derived from globular proteins that have a particular “standard” amino acid composition. The compositional adjustment of amino acid scoring matrices has been proposed from different approaches for other globular proteins with a non-conventional amino acid composition [9-12]. The same adjustment is required for membrane proteins based on their different structural features, different amino acid composition, and residue exchangeabilities [13], as a consequence of a different environment in which they are found, e.g., the lipid bilayer.

Currently, two different types of membrane proteins based on their secondary structure can be distinguished: alpha helical and β-barrel membrane proteins, which account for a significant share of proteins in a typical genome of a respective organism [14]. These proteins play central roles in many cellular processes, such as cell signaling and transport. In this study, we focus on β-barrel membrane proteins, which are found in the outer membrane of Gram-negative bacteria, as well as in mitochondria and chloroplasts [15]. There is only a handful of structures of β-barrels currently solved. Finding remote homologues of the existing structures may widen the scope of structure prediction and facilitate functional annotations of microbial genomes. To this end, it is important to increase the ability of searching algorithms to detect related membrane proteins with high confidence. One of the approaches is to develop a scoring matrix specifically tailored for a given class of proteins. Several scoring matrices were developed for α-helical membrane proteins, e.g., PHAT [16] and SLIM [17] scoring matrices. PHAT matrices were built from predicted hydrophobic and transmembrane regions of the Block database following the BLOSUM method. SLIM non-symmetric score matrices were derived from two competing stochastic models for aligned amino acid pairs: an asymmetric null model and an alternative model (following different strategies to estimate the parameters). There were no attempts to develop matrices specific for β-barrel membrane proteins.

To fill this gap, we first studied evolutionary history of transmembrane segments of β-barrel membrane proteins by estimating amino acid substitution rates with a Bayesian Monte Carlo approach. This approach has advantages over counting methods and standard position specific weight matrix generated by PSI-BLAST. First, it avoids the problem of systematic underestimation of certain substitutions, as a phylogenetic tree is explicitly built for rate estimation, whereas method such as PSI-BLAST treats every retrieved sequence with equal weight. In addition, matrices such as PAM and BLOSUM have implicit parameters whose values were determined from the precomputed analysis of large quantities of sequences, while the information of β-barrel membrane proteins has limited or no influence. Markovian evolutionary models are parametric models and do not have pre-specified parameter values. Based on the estimated substitution rates, we next built a series of scoring matrices named beta-barrel Transmembrane Matrices (bbTM) specific for transmembrane regions of β-barrels. Finally, we tested bbTM matrices for detection of remote homologues of β-barrel MP and compared their performance with scoring matrices PHAT and SLIM.

II. METHODS

We selected a dataset of 7 non-homologous β-barrel membrane proteins with available X-ray structure (1A0S, 1BXW, 1FEP, 1I78, 1KMO, 1NQE, 1QJ8, 2OMF). For each protein sequence, we performed a BLAST search against NCBI NR database and selected homologous sequences with 20-90% sequence identity (e-value <10⁻¹⁰) in such a way that the identity was based on the sequence of transmembrane fragments, and not more than two gaps were allowed in the alignment of every individual transmembrane fragment. We then built a phylogenetic tree of the selected sequences using a maximum likelihood method [6]. Next, a Bayesian Markov Monte Carlo simulation was carried out to estimate amino acid substitution rates in the aligned sequences, following the approach developed by Tseng and Liang [18].

A. Calculation of amino acid substitution rates with Bayesian Markov Monte Carlo simulation

Given the sequence divergence (branch lengths) of a calculated phylogenetic tree using a Maximum Likelihood method, and given a set of homologous sequences, the probability of observing all residues in the given sequence is given by (1).

To estimate the Q matrix, a continuous time Markov

$$P(S|T,Q)=P(x_1,\dots ,x_s|T,Q)={\displaystyle \prod _{h=1}^{x}p(x_h|T,Q)}$$ 1

model for residue substitutions is implemented using a Bayesian approach, where the prior distribution π(Q) is employed to encode the past knowledge of amino acid substitution rates for proteins. The instantaneous substitution rate Q = {q_ij} is described by a posterior distribution π(Q|S,T), which summarizes the information contained in the given sequences S and in the optimal tree topology T. After integrating the prior information and the likelihood function, the posterior distribution π(Q|S,T) can be estimated up to a constant. Therefore, our goal is to estimate the posterior means of rates in Q as summarizing indices (2)

$${\text{E}}_{\pi }(\text{Q})=\int \text{Q}.\pi (Q|S,T)dQ$$ 2

For this study, we used both uniform uninformative priors and the priors obtained from BLOSUM62, which gave similar results. Next, a Markov chain was run to generate samples drawn from the target distribution π(Q|S,T). Starting from a rate sample Q_t at time t, a new rate matrix Q_t+1 using the proposal function T(Q_t, Q_t+1) was generated. The proposed new matrix Q_t+1 will be either accepted or rejected, depending on the outcome of the acceptance rule r(Q_t, Q_t+1). This is achieved by using the Metropolis-Hastings acceptance ratio r(Q_t, Q_t+1) to either accept or reject Q_t+1 depending on whether the following inequalities hold:

$$u\le r(Q_t,Q_{t+1})=\min \{1,\frac{\pi (Q_{t+1}|S,T).T(Q_{t+1},Q_t)}{\pi (Q_t|S,T).T(Q_t,Q_{t+1})}\}$$ 3

where u is a random number drawn from the uniform distribution U[0,1]. With the assumption that the underlying Markov process is ergodic, irreducible, and aperiodic [19], a Markov chain will reach the stationary state.

B. Calculation of scoring matrices

We derived residue similarity scoring matrices from the estimated amino acid substitution rates in each of the 7 protein sequences from the dataset described above. This was done by calculating the similarity score b_ij(t) between residues i and j from the substitution rates at different evolutionary times, t_e (e=1, 2… 300) obtained from the rate matrix Q. In this study, we used the scoring matrix at time t=1 because it demonstrated the best performance in the database searches. Finally, the matrices obtained from the protein data set were averaged into a beta-barrel Transmembrane Matrix (bbTM), which was further used for database searches and analysis.

C. Blast searches and databases

We performed BLASTP searches with bbTM, PHAT and SLIM matrices using transmembrane segments of a set of β-barrel membrane proteins with known structure as a query sequence (1T16, 1THQ, 2F1C, 2F1T, 2O4V) in order to evaluate the performance of each matrix. Default BLAST parameters were used for searching the following protein databases: (a) PROFtmb [20] containing 2,150 protein sequences of predicted bacterial β-barrel membrane proteins; (b) a randomized version of PROFtmb, where each sequence was randomly shuffled; (c) a parsed version of SWISSPROT database consisting of 258,573 sequences of globular soluble proteins from bacteria and eukaryota.

III. RESULTS

A. Amino acid substitution rates in bbTM, PHAT and SLIM matrices

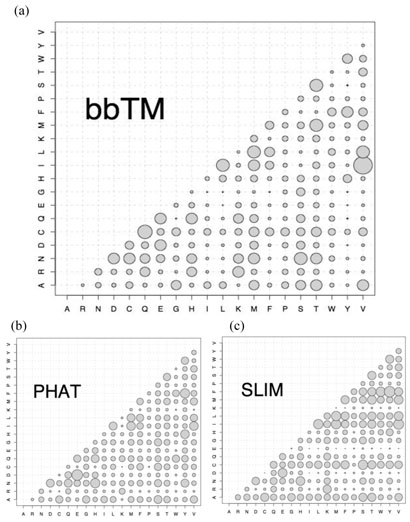
We calculated amino acid substitution rates for PHAT and SLIM matrices and presented them as bubble plots together with bbTM substitution rates (Fig. 1). Here, the higher the substitution rate between two amino acids in the analyzed sequences, the bigger the corresponding bubble. The substitution patterns are clearly different in all three matrices.

Fig. 1.

Amino acid substitution rates in a) bbTM, b) PHAT and c) SLIM matrices.

The highest rate of amino acid exchange in bbTM matrix is observed for pairs I↔V, N↔S, I↔L, L↔M, M↔T, L↔V, and S↔T and represents an exchange of amino acid residues with similar physico-chemical properties (Fig. 1a). PHAT matrix, on the other hand, contains a larger number of fast exchanging pairs of polar amino acids such as D↔E, H↔N/Y, and H/N↔Q together with aromatic pair F↔Y and hydrophobic pairs I↔V/M (Fig. 1b). SLIM matrix contains a slightly different set of quickly exchanging pairs that includes F↔Y, I↔L/V, F↔W, I/L↔M, C↔S, H↔N, and D↔E (Fig. 1c).

B. Performance of bbTM matrices in BLAST searches of databases

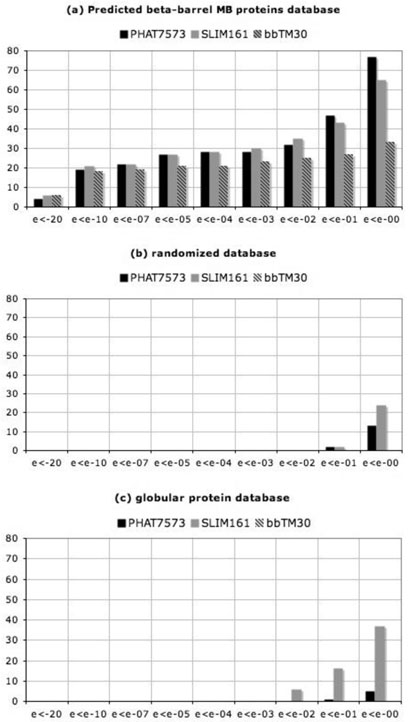
To assess the performance of bbTM matrix in BLAST searches, we compared in a cumulative fashion the number of hits obtained from searches in different databases using bbTM, PHAT and SLIM scoring matrices. The results of BLAST searches for retrieved sequences within different ranges of e-values are summarized in Fig. 2. PHAT and SLIM matrices consistently retrieved a larger number of hits in BLAST searches against the predicted membrane protein database. The number of retrieved sequences was similar for all three matrices at lower e-values, but differed significantly in the range of e-values between 0.1 and 1.0 (Fig. 2a), where retrieved hits have no statistical significance.

Fig. 2.

Results of BLAST searches with bbTM, PHAT and SLIM matrices: a) against a predicted database of β-barrel membrane proteins; b) the same database but with every sequence randomly shuffled; and c) a database of globular proteins from bacteria and eukaryota.

The advantage of using bbTM and its high specificity for transmembrane β-barrel sequences is best demonstrated by the results of searches against the databases containing only sequences of globular proteins or shuffled (randomized) sequences of predicted β-barrels.

For example, when the BLAST searches with TM segments were performed against the globular protein database, PHAT and SLIM matrices retrieved 5 and 37 sequences, respectively, with e-values ranging from 10⁻² to 1.0, while no sequences were retrieved by bbTM scoring matrices at any range of e-values (Fig. 2c). Similarly, BLAST searches of randomized database with PHAT and SLIM yielded 13 and 24 hits, respectively. Again, searches with bbTM matrix found no hits at any range of e-values (Fig. 2b). As the reduction of false positive becomes a critical issue when genome-wide search for β-barrel membrane protein is carried out, existing matrices such as PHAT and SLIM are not suitable for studying β-barrel membrane proteins, as they will lead to a large number of proteins mislabeled as β-barrel membrane proteins. Our results indicate that bbTM matrices have higher selectivity towards transmembrane β-barrel proteins and may be used with confidence in database searches for remote homologues of β-barrel membrane proteins.

IV. CONCLUSIONS

We have estimated amino acid substitution rates for the transmembrane segments of β-barrel membrane proteins. We found that they are different from soluble proteins and α-helical membrane proteins represented by other scoring matrices (Figure 1). Despite of the fact that β-barrel membrane proteins share a low sequence identity, the substitution rates estimated from very different β-barrel membrane proteins share a strong common pattern.

It is challenging to evaluate the specificity and sensitivity of a given matrix, as the hits retrieved by a BLAST search cannot be guaranteed to be membrane proteins. A good indicator is the use of a shuffled randomized database as a target database: the number of hits obtained from this database can be considered as false positives, which provides a measure of the quality of the scoring matrix. In addition, we selected a database of non-membrane proteins from the SWISSPROT database, excluding every sequence with any reference to the word “membrane”. A large number of hits against this database is a clear indicator of the loss of specificity of the searches, which are the cases for PHAT and SLIM matrices. Our bbTM matrix generates no hits, indicating an excellent specificity.

We expect that the scoring matrix bbTM derived from the estimated substitution rates can be used for detection of remote homologues of known structures through BLAST searches. This will allow the structures of a large number of β-barrel membrane proteins to be modeled.