Generalized ensemble methods for de novo structure prediction

Abstract

Current methods for predicting protein structure depend on two interrelated components: (i) an energy function that should have a low value near the correct structure and (ii) a method for searching through different conformations of the polypeptide chain. Identification of the most efficient search methods is essential if we are to be able to apply such methods broadly and with confidence. In addition, efficient search methods provide a rigorous test of existing energy functions, which are generally knowledge-based and contain different terms added together with arbitrary weights. Here, we test different search methods with one of the most accurate and predictive energy functions, namely Rosetta the knowledge-based force-field from Baker's group [Simons K, Kooperberg C, Huang E, Baker D (1997) J Mol Biol 268:209–225]. We use an implementation of a generalized ensemble search method to scale relevant parts of the energy function. This method, known as Hamiltonian Replica Exchange Monte Carlo, outperforms the original Monte Carlo Simulated Annealing used in the Rosetta package in terms of sampling low-energy states. It also outperforms another widely used generalized ensemble search method known as Temperature Replica Exchange Monte Carlo. Our results reveal clear deficiencies in the low-resolution Rosetta energy function in that the lowest energy structures are not necessarily the most native-like. By using a set of nonnative low-energy structures found by our extensive sampling, we discovered that the long-range and short-range backbone hydrogen-bonding energy terms of the Rosetta energy discriminate between the nonnative and native-like structures significantly better than the low-resolution score used in Rosetta.

Predicting the functional 3-dimensional structure (the native state) of a protein from its amino acid sequences is of central importance to structural and functional biology and has enormous applications in alleviating human disease. Even if the structures of all proteins were known, we would still not be able to answer questions related to diseases directly caused by protein misfolding, such as certain types of cancer and Alzheimer's and Parkinson disease. For this we would need to understand the physical basis of the energy terms that make the native state so special. Such understanding of the energetics of the system would also lead to more efficient and comprehensive drug design. Structure prediction depends on solving two problems: (i) describing the energy function with sufficient accuracy and (ii) searching the conformational space sufficiently well. These problems are particularly severe for proteins of biologically relevant lengths (>150 aa).

In this work we focus on conformational sampling, which has been recognized as the critical step in high-resolution structure prediction (1–3). Most widely used standard methods for de novo structure prediction are based on the variants of the Monte Carlo method (4–6) and are unable to explore low-energy regions efficiently because of the ruggedness of the potential energy surface. To overcome these problems, a number of generalized ensemble Monte Carlo methods have been developed (7–10). These methods strive to search energy space better by computing the density of states, sampling expanded ranges of temperatures, or computing other physical quantities affecting transitions between the states during the search. In particular, advanced methods such as Temperature Replica Exchange Monte Carlo (TREM) (8) and Hamiltonian Replica Exchange Monte Carlo (HREM) (10), have been shown to outperform standard Monte Carlo in terms of sampling for both simplified and all-atom force fields of small proteins (8, 10, 11).

For longer proteins, the computational cost and ruggedness of the all-atom energy function makes solving this problem particularly challenging as evidenced by the modest success of full-atom refinement (12–14). For this reason, there are multiscale approaches that start with low-resolution or reduced-model energy functions and then use all-atom energy functions on a few selected conformations [often relying on additional steps such as use of sequence homologs (2) or clustering (3, 4)] been developed (4, 6, 12, 13). These approaches often fail to generate low-resolution models within the “radius of convergence” (rmsd <3 Å) of the native state necessary for the success of subsequent full-atom refinement (2).

In this work, we test whether enhanced conformational sampling of low-resolution models can improve structure prediction. Specifically, we apply generalized Monte Carlo methods to one of the most powerfully predictive de novo protein potential energy functions, the low-resolution Rosetta force field (1). We compare the performance of two of the best-performing search methods, Temperature Replica Exchange Monte Carlo and Hamiltonian Replica Exchange Monte Carlo, with the four-stage Monte Carlo Simulated Annealing protocol used in the original Rosetta algorithm. We show that for a representative set of 40 proteins containing α, β, α+β, and α/β folds both the HREM and, to a lesser degree, TREM methods enhance sampling of low-energy states as compared with the original Rosetta method. More importantly, we are able to use the nonnative-like low-energy structures sampled by generalized ensemble methods to suggest improvements of the low-resolution scoring function used in Rosetta. Our analysis of energy landscapes and structure clusters shows that HREM outperforms other search methods, not only in terms of finding more low-energy states, but also in sampling a more diverse set of compact structures for use in optimization of energy functions.

Results and Discussion

Four Stages of the Rosetta Scoring Function.

Rosetta's low-resolution Monte Carlo method (known here as ROSETTA) employs a hierarchical protocol consisting of four sequential searches that involve swapping fragments of length 9 and then 3 residues. Each stage employs a different scoring function. These four different energy-scoring functions involve (i) replacement of the extended chain (score0), (ii) buildup of the secondary structure (score1), (iii) alternation of high (score2) and low (score5) sheet weights, and (iv) low-resolution centroid refinement (score3) (15). Finally, structures are selected according to another low-resolution centroid refinement score (score4). Each subsequent scoring function used in ROSETTA adds new terms, while leaving many energy contributions unchanged; this provides significant overlap of the energy values of conformations sampled by different scoring functions. In addition, the cumulative nature of the energy functions used consecutively in ROSETTA allows one to represent each scoring function as a scaled variant of the full energy function (score3). Additional information about specific energy contributions and scaling parameters for each energy component used by ROSETTA is provided in Materials and Methods. Our observation of overlap between scoring functions used in ROSETTA lead us to introduce a new HREM implementation for Rosetta. Overlap provides a number of similar Hamiltonians that are related by a scale. In our implementation of HREM, we assign each replica to one of the four scoring functions, and attempt exchanges between the replicas. We find that HREM's “low-effective-temperature” replicas (replicas that use the full, nonscaled energy potential) sample lower energies than those sampled by the final stage of the low-resolution protocol in ROSETTA. Moreover, the overlap between the distributions of conformations sampled by four different scoring functions is increased by our HREM scheme [supporting information (SI) Fig. S1].

Low-Energy and Low-rmsd Conformational Sampling.

To study energy landscape features of each of the three search methods, we examined energy values and rmsd value of conformations sampled during 20,000 runs starting from an extended state. Fig. 1 shows results for 40 sequences of different lengths (55–208 aa) and belonging to the four different structural classes α, β, α/β, and α+β. Analyzing the low energies sampled (Fig. 1A) we found that the HREM search method generally outperforms other search methods in terms of sampling low-energy states on all sequences. In particular, performance differences between the generalized ensemble methods, HREM and TREM, and ROSETTA (the lowest energy, the energy level below which 10% of the structures lie, and the lowest energy among the five highly populated clusters) become more marked as the length of the protein increases and seems to be larger for β-folds. In comparison with ROSETTA, HREM (consistently) and TREM (often) gave rise to significant improvement in terms of lower energy values. This did not always lead to the improvement in rmsd because of false minima in the energy landscapes (Fig. 1B).

Fig. 1.

Energy and rmsd differences for HREM and TREM as compared to ROSETTA. (A) Showing the difference in energy value between conformations sampled during 20,000 independent runs by HREM and TREM and those conformations independently generated by ROSETTA for 40 selected proteins from the four structural classes of SCOP (55–208 aa). In each case we show differences for (i) the lowest energy values (min), (ii) the cutoff energy value for the 90th percentile of low-energy structures (p90, best 10% of structures), and (iii) the lowest energy values from the five largest clusters (Cbest). In all cases, HREM gets lower energy values than ROSETTA (energy differences <0), whereas TREM is better than ROSETTA in just 50% of the cases. (B) Showing the difference in C_α root mean square deviation (rmsd) values between same conformations. In each case we show differences for (i) the rmsd for the lowest energy structure (min), (ii) the mean rmsd for the 90th percentile of low-energy structures (p90), and (iii) the cluster centroid rmsd from five largest clusters (Cbest).

Energy Landscapes Sampled by ROSETTA and HREM.

To gain additional insight into the energy landscape encountered during the search for a given protein, we examined the 2-dimensional distribution of conformations as a function of the low-resolution Rosetta's score (score4), on the y axis and the C_α rmsd or C_α global distance test total score [GDT_TS (16)] to the native state, on the x axis. We used the density of states to reveal the free energy of the underlying landscape when folding with HREM and ROSETTA for all 40 proteins. Particular insight comes from comparing results obtained starting from an extended and the native state: both starting states have converged to a similar structure in the lower-energy range for most proteins. However, simulations from the native state showing location of the near-native states (rmsd < 3 Å) usually reveal a false region of attraction with rmsd from 3.5 to 17.4 Å (average value, 8.7 ± 4.5 Å) having energies 54.0 ± 23.8 kT lower than the near-native conformations (energy differences range from 14.4 to 135.3 kT). Longer proteins (>90 aa) tend to be at the upper end of this range for both rmsd and energy differences. By contrast, shorter proteins tend to have energy landscapes with a flat, false lowest-energy region: many states with a wide range of rmsd values have almost the same low energy value, which are lower than the energy values of the near-native states.

Fig. 2 shows typical energy landscapes sampled from the extended and the native state by HREM and ROSETTA. ROSETTA tends to sample only a local part of the energy landscape, whereas HREM samples much more extensively. Nevertheless, because of false regions of attraction, HREM simulations from an extended state do not sample near-native conformations of interest (rmsd < 3 Å). Together with the analysis presented in the previous section, these results show that the low-resolution energy function in Rosetta cannot reliably recognize near-native states.

Fig. 2.

Shown are distributions of conformations (blue to red for low to high density, a measure of the underlying free energy) generated by HREM and ROSETTA as a function of the low-resolution Rosetta score (score4) and the fit to the native structure as measured by either the C_α root mean square deviation (rmsd) or the C_α Global Distance Test Total Score (GDT_TS). A total of 20,000 structures were generated for each method starting from (i) an extended state or (ii) the native state of the all-β protein, 1e43a1 (Alpha Amylase, C-terminal β-sheet domain from Bacillus licheniformis) containing 90 aa). Clearly, HREM generates a much better sampling of conformations than ROSETTA.

Differences in Top Cluster Centers for ROSETTA and HREM.

In principle, an accurate energy function should always recognize near-native conformations and discriminate them from nonnative conformations. In practice, there are scoring function inaccuracies and structural clustering must be used by de novo structure prediction methods to identify native-like structures (2, 4, 13). This makes two assumptions: (i) that the native conformation should have more structural neighbors than any other conformation because of the loss in configurational entropy on folding; and (ii) that this near-native energy basin is detected by the knowledge-based scoring functions used in Rosetta in that the basin results from the long-range hydrophobic interactions associated with native globular proteins (17). In our work, we used the “LEADER”clustering algorithm extensively tested with the Rosetta protocol in the Critical Assessment of Structure Prediction (CASP) competition (2, 12, 13, 18). We clustered 5,000 lowest-energy structures of the 20,000 lowest-energy conformations found in independent runs by each method. As seen in Fig. 3, HREM finds more diverse and larger clusters than TREM or ROSETTA. It is worth noting that agreement within HREM clusters is stronger than for TREM or ROSETTA (see Tables S4 and S5). A possible explanation for these observations, also supported by the energy landscape analysis in the previous section, is that HREM samples a more diverse set of highly populated low-energy basins of conformations. This indicates that the basins associated with false local minima are highly populated and thus represent conformations against which the scoring functions should be improved.

Fig. 3.

Differences in top 5 clusters sampled by ROSETTA, HREM, and TREM. (A) Shown is how the average rmsd of the top five clusters depends on protein length. (B) Shown is how the average cluster size (for the top five largest clusters) depends on protein length. In both cases we present data for the entire set of 40 proteins for the tree methods: ROSETTA, HREM, and TREM. Superior performance of HREM is clear for both measures.

Deficiencies of the Rosetta Low-Resolution Scoring Function.

To further understand how the individual energy terms of the Rosetta energy function discriminate near-native states from incorrect low-energy states, we examined two sets of 1,000 low-rmsd states and one set of 1,000 low-energy (score4) states generated by all three methods for each of the 40 proteins in our dataset. The first set of low-rmsd states (low-rmsd_nat, mean rmsd 3.98 Å) was generated by sampling from the native state (structures closer than 1.0 Å were removed to prevent possible artifacts in recognition by an energy function parameterized on high-resolution crystal structures), the second set of low-rmsd states (low-rmsd_ext, mean rmsd 8.56 Å) and the set of low score4 energy states (low-score4_ext, mean rmsd 13.12 Å) were generated by sampling from an extended state. With its much greater efficiency, HREM contributed most (85%) to the set of low-energy structures found by starting with an extended state. Because these low-scoring decoys were produced by rigorously sampling the energy function, they represent a challenging set of local minima of Rosetta's low-resolution energy function.

We calculated two independent statistical measures that capture the ability of the scoring function to discriminate the native-like conformations from nonnative-like: (i) the Z score of the rmsd values of native-like conformations; and (ii) the Pearson correlation coefficient between rmsd and score. In Table 1, we give these values for the following discrimination tasks: (i) discriminate low-rmsd_nat from low-score4_ext, and (ii) discriminate low-rmsd_ext from low-score4_ext for the original low-resolution score (score4) as well as a selected set of Rosetta's low-resolution energy score terms that were identified as having most discriminatory power. We analyze each of the four structural classes separately, in addition to a combined analysis for all proteins in our dataset. As seen (Table 1), good native-like average Z scores (Z < −1.0), and higher Pearson's correlation coefficients (r > 0.3), indicate the enhanced discrimination power of the hydrogen bond backbone–backbone scores for both tasks for all structural classes.

Table 1.

Native-like average Z score (top portion of the table), Pearson's correlation coefficient between rmsd and energy score (bottom portion of the table), for low-rmsd_nat vs. low-score4_ext and low-rmsd_ext vs. low-score4_ext discrimination

	Low-rmsdnat vs. low-score4ext discrimination				Low-rmsdext vs. low-score4ext discrimination
	score4	hb_srbb	hb_lrbb	rama	score4	hb_srbb	hb_lrbb	rama
Zα	9.21 ± 6.45	−0.61 ± 3.40	−0.90 ± 1.76	−0.58 ± 2.43	10.19 ± 5.60	−1.08 ± 1.97	0.97 ± 0.95	−0.38 ± 0.39
Zβ	8.44 ± 8.06	−0.48 ± 1.86	−1.41 ± 2.38	−0.78 ± 1.53	10.18 ± 4.84	−0.64 ± 1.08	1.52 ± 0.91	−0.21 ± 0.74
Zα/β	7.80 ± 4.23	−0.19 ± 1.37	−2.37 ± 3.26	−1.05 ± 2.63	8.53 ± 4.16	−0.21 ± 0.88	1.26 ± 0.79	−0.16 ± 0.48
Zα+β	6.10 ± 6.74	−0.23 ± 2.10	−1.12 ± 2.26	−1.12 ± 1.41	9.44 ± 5.61	−0.69 ± 1.45	0.88 ± 0.98	−0.28 ± 0.46
Zall	8.19 ± 6.87	−0.38 ± 2.17	−1.44 ± 2.42	−0.87 ± 1.97	9.92 ± 5.45	−0.64 ± 1.36	1.13 ± 0.90	−0.23 ± 0.52
rα	−0.76 ± 0.16	0.07 ± 0.63	0.26 ± 0.46	0.40 ± 0.52	−0.72 ± 0.15	0.26 ± 0.32	−0.31 ± 0.29	0.17 ± 0.18
rβ	−0.51 ± 0.53	0.15 ± 0.57	0.18 ± 0.29	0.26 ± 0.42	−0.73 ± 0.17	0.16 ± 0.30	−0.46 ± 0.21	0.03 ± 0.28
rα/β	−0.56 ± 0.26	0.05 ± 0.36	0.33 ± 0.34	0.21 ± 0.62	−0.60 ± 0.18	0.07 ± 0.25	−0.38 ± 0.22	0.03 ± 0.20
rα+β	−0.34 ± 0.52	0.07 ± 0.42	0.21 ± 0.29	0.32 ± 0.34	−0.65 ± 0.24	0.17 ± 0.32	−0.29 ± 0.32	0.14 ± 0.21
rall	−0.52 ± 0.42	0.08 ± 0.47	0.24 ± 0.33	0.28 ± 0.47	−0.67 ± 0.19	0.16 ± 0.29	−0.35 ± 0.27	0.08 ± 0.23

Mean and standard deviation are provided.

For discrimination between perturbed native states (low-rmsd_nat) and incorrectly scored low-energy states (low-score4_ext), the “long-range” hydrogen bond term (hb_lrbb), where donor and acceptor of a backbone–backbone hydrogen bond separated by at least 5 amino acids along the sequence, is more successful. For the more challenging discrimination between near-native states sampled during ab initio folding (low-rmsd_ext) and incorrectly scored low-energy states (low-score4_ext), the “short-range” backbone–backbone hydrogen bond term (hb_srbb), where donor and acceptor of a hydrogen bond is 4 or fewer amino acids apart along the sequence, is more successful. Although this holds for all protein folds, it is less marked for α/β proteins; in our dataset these folds have longer lengths and larger rmsd values for both near-native and low-energy sets. Enhanced discrimination is also shown by the Ramachandran score (rama).

We observed that low-rmsd_nat conformations differed from the low-rmsd_ext conformations in having more favorable long-range hydrogen bonds for β, α+β, and α/β folds (mean Z score is −1.53 ± 1.33) and lower Ramachandran energies for β-folds (Z score is −1.58 ± 0.79) as well as having less favorable short-range hydrogen bonds for β-folds (Z score is 1.30 ± 1.76) and higher contact order for all folds (mean Z score is 1.27 ± 1.36). Thus, the low-rmsd_ext decoys are less native-like and have fewer nonlocal interactions resulting in less favorable long-range and more favorable short-range hydrogen bonds; this suggests that, as folding from an extended state proceeds to form more long-range interactions, the discriminatory power of hydrogen bonds shifts from short-range to long-range.

Fig. 4 shows how the long-range and short-range hydrogen bonding backbone–backbone potential transforms the original low-resolution Rosetta energy (score4) landscape assigning lower energies to closer-to-native (low-rmsd) conformations. This is shown separately for all of the proteins in each of the four fold classes: α, β, α+β, and α/β. In Fig. 4A, we show low-rmsd_nat set (start from the native state) and low-score4_ext set (start from an extended state) discrimination by the original low-resolution energy (score4) and by long-range hydrogen bond score (hb_lrbb). In Fig. 4B, we show a more difficult discrimination test for the low-rmsd_ext and low-score4_ext decoys (both start from an extended state). Decoys in low-rmsd_ext set are less native-like than those in the low-rmsd_nat set and are thus harder to distinguish from the low-score4_ext decoys. In Fig. 4B, we see that the score4 energy function is unable to distinguish structures with low rmsd values. In fact, the structures with the lowest score4 energies are generally >10 Å from the native structure; there is a distinct pattern of anticorrelation with the energy becoming more favorable as the rmsd increases. A different energy term, the short-range backbone–backbone hydrogen bond energy (hb_srbb) shown on Fig. 4B Right is generally able to reverse this anticorrelation, but the energy of the low-rmsd decoys is now about the same as that of the decoys with higher rmsd. These results indicate that with efficient search methods such as HREM the discrimination power of low-resolution energy functions can be improved. A promising methodology to improve the discrimination power further is to use efficient methods like HREM to locate decoys that are energy minima; this is then followed by optimization of the energy function against these decoys. This paradigm, pioneered in 1996 (19–20), proved important in the formulation of Rosetta (1) and will likely be as important for future improvement of methods for structure prediction.

Fig. 4.

Discrimination between native-like and nonnative-like conformations. (A) Comparing the ability of the low-resolution Rosetta scoring function (score4) and the long-range hydrogen-bonding backbone–backbone potential (hb_lrbb) to discriminate between native-like low-rmsd_nat (starting from the native state) and nonnative low-score4_ext (starting from an extended state) conformations. Colors used for each fold class are as follows: all-α, bright and dark red; all-β, bright and dark green; α/β, bright and dark orange; and α+β, bright and dark purple. The darker color is always used for the near-native decoys (low rmsd). Note how the hb_lrbb score is better at discrimination than score4 is. (B) Comparing the discrimination ability of the low-resolution Rosetta scoring function (score4) and the short-range hydrogen-bonding backbone–backbone potential (hb_srbb) to discriminate between native-like low-rmsd_ext and nonnative low-score4_ext conformations (both starting from an extended state). The hb_srbb score generally raises the energy of the nonnative-like conformations (low-score4_ext, high rmsd) relative to the near-native conformations (low-rmsd_ext); this makes the lower edge of the distribution slope toward rather than away from the native state.

An orientation-dependent hydrogen-bonding energy term was first added to Rosetta energy force field to enhance discrimination between native-like and nonnative conformations just before and during full-atom refinement (21). This energy is a linear combination of four terms that are parameterized by using a set of high-resolution protein crystal structures: (i) distance-dependent energy term derived from the distribution of distances between the hydrogen and acceptor atoms (distances range from 1.4 to 2.6 Å), (ii) angular energy measuring angle at the hydrogen atom, (iii) angular energy measuring angle at the acceptor atom, and (iv) dihedral angle term corresponding to rotation around the acceptor–acceptor base bond in the case of an sp² hybridized acceptor (21). It has also been shown that this knowledge-based hydrogen-bonding potential in Rosetta is consistent with the quantum mechanical calculations unlike molecular mechanics force fields, including CHARM27, OPLS-AA, and MM3–2000 (22). Recently a modified version of Rosetta's hydrogen bonding potential was successfully used for protein structure refinement of homology models (23). That study showed that the modified Rosetta's hydrogen bonding potential in combination with two other statistical potentials can discriminate near-native models (obtained by using temperature replica exchange molecular dynamics) with an accuracy comparable to Rosetta's full-atom score (23). In our work, we show that backbone–backbone hydrogen-bonding energy terms significantly enhance discrimination of near-native and misfolded native-like states for ab initio protocol.

Conclusion

In this work we have shown that development of search methods that more efficiently sample local minima is important for two reasons: (i) better protein structure prediction and (ii) better optimization of the energy function. We have found that Hamiltonian Replica Exchange Monte Carlo method is the most promising search method for de novo protein structure prediction with low-resolution force fields; it outperforms Temperature Replica Exchange Monte Carlo and the original Rosetta Monte Carlo method. A better set of local minima provides a more challenging decoy set against which the energy function can be optimized. Thus, our results reveal some of the deficiencies of the existing energy terms in Rosetta, including the presence of false local minima and a general flatness of the energy landscape near the native states. Only through better understanding of these deficiencies, as revealed by our very powerful search method, will we be able to develop better energy functions and representations.

We used an implementation of HREM that utilizes the four scoring functions from the existing Rosetta protocol; in future work we will investigate other implementations of HREM that will scale individual energy contributions of different energy terms. Our results confirm that the Hamiltonian Replica Exchange Monte Carlo method and its variants are promising and deserve further study.

Materials and Methods

Protein Dataset Used.

To evaluate and compare the algorithms, a set of 40 nonhomologous folds was selected from the Structural Classification of Proteins (SCOP) (24) structural domain database (ranging in length from 55 to 208 aa). Protein families in the test set span four SCOP class categories: all α, all β, α/β, α+β and are of different protein sequence lengths to ensure the generality of the reported results. We generated six independent sets of 20,000 decoys for each protein sequence for each search method starting from the completely extended state and starting from the native state.

The Rosetta Energy Function.

All of the search methods developed and implemented were tested for Rosetta's low-resolution protein structure representation and scoring functions. Rosetta is a protein structure prediction program developed in Baker's group and made freely available to academic community (1). Rosetta incorporates (i) a low-resolution representation of a protein that uses the main chain atoms and a side-chain centroid and (ii) a high-resolution representation that uses all atoms. The low-resolution Rosetta energy function includes the van der Waals hard sphere repulsion (vdw), environment (env), pair (pair), C_β packing density (cb), secondary structure packing [helix–helix pairing (hh), helix-strand pairing (hs), strand-strand pairing (ss), strand pair distance/register (rsigma) and strand arrangement into sheets (sheet)], radius of gyration (rg) energetic contributions, contact order (co), and Ramachandran torsion angle filters (rama) (2, 14). Additional hydrogen bonding (short- (hb_srbb) and long-range (hb_lrbb) backbone–backbone hydrogen bond) energy terms are added right before (score6) and used during full-atom refinement (score12). All of the energy scoring components of Rosetta's energy score are described in details elsewhere (15).

TREM.

Standard (8) implementation of Temperature Replica Exchange Monte Carlo (TREM) is used here. Eight replicas run at related exponentially distributed temperatures (β_i: 1.40, 1.95, 2.72, 3.79, 5.29, 7.38, 10.31, and 14.39 kT) to ensure efficiency of the exchanges, underwent four different stages of Monte Carlo interrupted by the attempted exchanges after each stage (see Additional Methods Description. TREM in the SI). These specific temperature settings were optimized in a number of short preliminary runs. Following the general criterion for choosing the exchange frequency between replicas by integrating autocorrelation time of the higher temperature simulation (25), exchanges between replicas were attempted after every 2,000 steps.

HREM.

Hamiltonian Replica Exchange Monte Carlo uses several related Hamiltonians for different replicas, where only some of the terms of the potential energy function, U(X), are modified across replicas through scaling parameters λ_i (10). Similarly to TREM, exchanges between pairs of replicas are attempted with a certain frequency, allowing it to overcome interactions responsible for the ruggedness of the landscape to be weakened. Unlike regular TREM that scales with the square root of total degrees of freedom in the number of replicas required to guarantee optimal overlap, HREM scales as a square root of only relevant subsystem degrees of freedom and is therefore preferable for large systems. The key difference between the standard implementation of HREM (10) in our work, is that λ_i is a vector of weights and not a scalar:

where

The weights are:

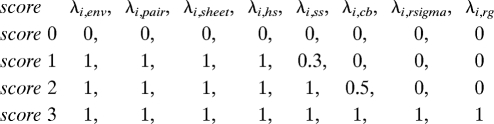
for i ∈ (0, 1, 2, 3). In order for HREM to be effective, energy Hamiltonians should only differ in a limited number of energy components. Four different low-resolution scores of Rosetta low-energy function satisfy this condition with the following sets of Rosetta scaling parameters:

To satisfy the condition of the detailed balance, the probability of attempted pairwise exchanges between replicas follows the equation:

where

The exchange frequency between replicas was chosen by integrating the autocorrelation time of the highest “effective temperature” (score0) simulation (25); exchanges between replicas were tried after every 2,000 Monte Carlo steps. The inverse temperature, β, was set to 2.0 kT as in ROSETTA.