Abstract
The knowledge of a pharmacophore, or the 3D arrangement of features in the biologically active molecule that is responsible for its pharmacological activity, can help in the search and design of a new or better drug acting upon the same or related target. In this paper we describe two new algorithms based on the frequent clique detection in the molecular graphs. The first algorithm mines all frequent cliques that are present in at least one of the conformers of each (or a portion of all) molecules. The second algorithm exploits the similarities among the different conformers of the same molecule and achieves an order of magnitude performance speedup compared to the first algorithm. Both algorithms are guaranteed to find all common pharmacophores in the dataset, which is confirmed by the validation on the set of molecules for which pharmacophores have been determined experimentally. In addition, these algorithms are able to scale to datasets with arbitrarily large number of conformers per molecule and identify multiple ligand binding modes or multiple binding sites of the target.
1 Introduction
The concept of a pharmacophore is widely used in modern drug design and it is generally defined as the 3D arrangement of certain features in the ligand that are responsible for its activity against a particular protein target.1,2 The importance of the pharmacophore stems from the fact that once it has been identified, it can be used to rationally design new ligands that contain it and thus have a greater chance of producing the desired pharmacological effect.
The pharmacophore can be relatively easily identified if the 3D structure structure is available for several ligands bound to the same binding site of the same protein by aligning the features of all the ligands and finding their largest common arrangement, referred to as the common pharmacophore (CP). The underlying assumption behind such an approach is that the structurally conserved characteristics of a set of active ligands are responsible for their biological activity against the specific protein target.1,2 However, the number of ligands for which the 3D structure has been determined represents a very small fraction of all the binding data currently available. In most cases such as in high-throughput screening assays,3 the actual 3D geometry of the binding conformation is not known and only the activity is provided. In order to identify a common pharmacophore in a set of ligands for which exact 3D structures are not known, one can usually enumerate all possible low-energy conformations of all ligands, identify a potential binding conformation for each ligand and then align those binding conformations to find the largest common arrangement of features. However, the identification of the binding conformation is not an easy task. It can be further complicated by the fact that different ligands may have different binding modes or bind to different sites of the target.4
A number of methods and associated programs have been developed for identifying a common pharmacophore using the information from the active ligands. One of the earliest programs for CP identification is DISCO,5 which tries to align conformers of different ligands to the one rigid conformation of the reference ligand. Catalyst/HipHop6 uses a pruned exhaustive search method by building a pharmacophore model starting with the smallest arrangements of features until no larger CP exists. GASP7 uses a genetic algorithm to align flexible molecules to the most rigid one in the set. The more recent PHASE8 program uses a tree-based partitioning technique to find all k-point pharmacophores in the active ligands. A recursive distance partitioning (RDP)9 and Gibbs sampling10 algorithms have also been employed recently in the identification of a common pharmacophore.
In this paper we take an entirely different approach for identifying a common pharmacophore that is based on frequent graph mining. We model each conformation by a graph, referred to as the conformer graph, whose vertices are the pharmacophore points and the edges are the binned distances between the points. Our method then mines these graphs to find all vertex- and edge-labeled cliques (i.e., fully-connected subgraphs) that are present in at least one conformer graph of each ligand (or a large fraction of them). Each of these cliques represents a set of pharmacophore points whose pairwise distances are conserved and thus, they correspond to a common pharmacophore.
Even though in recent years a number of efficient algorithms have been developed for frequent subgraph mining such as FSG,11 gSpan,12 FFSM,13 and CLAN,14 these algorithms cannot be used to find the frequent cliques needed in order to identify the common pharmacophore. This is because the notion of the frequency utilized in the above algorithms is entirely different from that required for common pharmacophore identification. The existing methods define the frequency in terms of the entire set of conformations, whereas in the case of the common pharmacophore the frequency is defined in terms of ligands. In addition, the existing algorithms are designed to solve different problems. FSG, gSpan, and FFSM find all frequent subgraphs instead of only the cliques, thus spending a large amount of time finding unnecessary subgraphs, whereas CLAN is designed to find frequent cliques in graphs that have only labels on the vertices but not on the edges. Labeled edges are critical for finding the common pharmacophore as they are used to capture the distance between each pair of pharmacophore points.
In this paper we present two algorithms for mining the graphs corresponding to low-energy conformations of a set of active ligands for the same protein target. These algorithms, referred to as multiple conformer miner (MCM) and unified conformer miner (UCM), are designed to find the frequently occurring cliques suitable for solving the common pharmacophore identification problem. The MCM algorithm is modeled after existing clique-mining methods, mines the conformer graphs using a depth-first approach, operates on edge-labeled graphs, and correctly determines the frequency of a common pharmacophore based on its embeddings in the pharmacophore graphs of the various ligands. The UCM algorithm improves the computational complexity of MCM by leveraging the fact that there is a high degree of structural similarity among subsets of the 3D conformations of each molecule. The computational requirements of both methods are relatively small as the they do not perform any explicit structural alignments. Moreover, by assigning multiple labels to each edge (corresponding to overlapping distance bins), our methods provide a flexible framework which allows the identification of common pharmacophores even when their overall structure is somewhat variable. The experimental evaluation of these methods on a number of synthetic datasets and datasets with known pharmacophores shows that they have very low computational requirements and that they can identify the known common pharmacophores. In addition, the UCM’s exploitation of the structural similarity of conformers improves performance by an order of magnitude.
2 Methods
2.1 Definitions and Notations
Each labeled and undirected graph G is represented as a tuple G = {V,E,L,ℒ}, where V is a set of vertices or nodes, E ⊆ V × V is a set of undirected edges of G, L is a set of disjoint vertex and edge labels, and ℒ : V ∪ E→L is a function that maps the vertices and edges to their corresponding labels. A graph is represented by its |V| × |V| adjacency matrix M in which each off-diagonal element Mi,j contains the label of the edge (υi, υj) and each diagonal element Mi,i contains the label of the vertex υi,
Two graphs G1 = {V1, E1, L, ℒ1} and G2 = {V2, E2, L, ℒ2} are considered isomorphic if |V1| = |V2|, |E1| = |E2| and there exists a bijection f: V1 → V2 such that ∀υ ∈ V1, ℒ1(υ) = ℒ2 (f(υ)) and ∀(υ,u) ∈ E1, ℒ1((υ,u)) = ℒ2((f(υ),f(u))) (i.e., there is a one-to-one correspondence of the vertices and edges between the two graphs). Graph G′ = {V′,E′} is called a subgraph of G = {V, E}, denoted by G′ ⊆ G, if V′ ⊆ V and E′ ⊆ E. If there exists a subgraph g′ of a graph G that is isomorphic to a graph g, then g′ is called an embedding of g in graph G. If a graph G contains at least one embedding of a graph g, then g is said to be supported by G.
A clique is a fully connected graph, i.e., for each pair of vertices in V there exist an edge in E. The size of a clique is defined by the number of vertices it contains, i.e., |V|. A clique with n vertices is called an n-clique. As a result, the number of edges in the n-clique is n × (n − 1)/2. For example, Fig. 1 contains two graphs G1 and G2. G1 is a clique because every node is connected to all other in the graph. On the other hand, graph G2 is not a clique because it lacks an edge between nodes υ3 and υ5. Looking at Fig. 1, one can see that the set of vertices υ1, υ2, and υ5 and the edges connecting them in the graph G2 are isomorphic to the graph G1, which is a clique, because they have the identically labeled vertices and edges. Thus, the set of vertices υ1, υ2, and υ5 and the connecting edges are the embedding of the clique G1 in the graph G2.
Figure 1.
Example of graphs. G1 is a clique, G2 is not a clique.
2.2 Canonical Representation of Cliques
Almost all graphs can be represented in more than one way depending on the order of vertices and edges in the representative string. This fact can significantly reduce the performance of most graph mining algorithms that will try to find the embeddings of the same graph multiple times due to multiple available representations. In order to avoid such redundancy, one needs to use a canonical graph labeling. Canonical label is the unique code of a given graph.15,16 The canonical code of a graph G (denoted by can(G)) should be the same regardless of its representation as long as the topological structure of the graph and its vertex and edge labels remain the same.
The canonical code that we use is based on the minimum adjacency matrix code.11,13 This code is constructed by taking an adjacency matrix and rewriting it in one line by concatenating all its rows. The minimum adjacency matrix code is the lexicographically minimum code among all possible adjacency matrix codes for a given graph. This canonical code has a prefix preservation property, i.e., for each graph G there exists a subgraph GS⊆G such that the canonical code of the GS is a prefix of the G’s canonical code. In this study, we used a modified version of a minimum adjacency matrix code to represent the cliques to have all node labels in the code be in lexicographic order. The code is simply a string consisting of node labels followed by the edge labels to each preceding node in the clique in order. For example, the clique represented by graph G1 in Fig. 1 can have several codes: ABaCba ≺ ACbBaa ≺ BAaCab ≺ BCaAab ≺ CAbBaa ≺ CBaAba. However, since the code ABaCba lexicographically precedes all other codes, it is the canonical code for that clique. Now, consider a clique formed by vertices υ2, υ3, and υ4 and the connecting edges in graph G2 in Fig. 1. This clique can also be represented by several codes, two of which, viz. AAaCbc and AAaCcb, have the same alphabetical order of the node labels. However, since AAaCbc ≺ AAaCcb, the AAaCbc is the canonical code for that clique.
2.3 Graph Representation of Conformations
Each molecular conformation is represented as a graph, where pharmacophore points are the vertices and edges are the inter-point distances. From here on we will use the terms pharmacophore points and vertices as well as inter-point distances and edges interchangeably.
For each graph G = {V, E, L, ℒ}, there are two sets of labels in L = LV ∪ LE: one for vertices (LV) and another one for edges (LE). The labels of the vertices are used to capture the type of the pharmacophore points and they are user-defined. In the current study we used a total of six vertex labels corresponding to the following types of pharmacophore points: P (positive ionizable atom), N (negative ionizable atom), A (hydrogen-bond acceptor), D (hydrogen-bond donor), R (aromatic ring centroids), and H (hydrophobic).
The labels of the edges are used to capture the distance between the pair of pharmacophore points associated with the vertices. In our graph model, the actual distances are discretized into a finite number of bins. Specifically, the distance range between [dmin, dmax] is discretized into l equal-size intervals with the corresponding labels 0, …, l−1. Based on the actual distance between a pair of pharmacophore points, each edge can be assigned up to two labels. The first label corresponds to the bin that its distance falls in. The second label is designed to maximize the identification of common pharmacophores due to the above distance binning. In particular, if the actual length of an edge is within δ (where δ ≤ 0.5) of the bin size from a bin boundary, then the label corresponding to the adjacent left or right bin is also assigned to that edge. The parameters dmin, dmax, l, and δ are user-defined. Also, any distances that fall outside the [dmin, dmax] range are ignored and they are treated to represent vertices that are either too close to actually represent different pharmacophore points (e.g., same atom was assigned more than one label) or they are too far away to be meaningful pharmacophore points.
The multiple label assignment guarantees that all frequent cliques in which the variation of the distances between any pairs of vertices does not exceed 2δof the bin size will be discovered even if the corresponding distances in different molecules are assigned different labels. For example, if the bin size l = 1Å and δ = 0.25, then all of the distances differing by up to 2 × δ × l = 0.5Å will be assigned at least one common label. Selecting a smaller value of δ will decrease the runtime but will only find very high-quality (low RMSD values) pharmacophores; selecting a larger value will find looser pharmacophores at the expense of more computational requirement. For example, selecting δ = 0.5 will always assign two labels to every edge and the algorithm will be guaranteed to find all cliques in which identical inter-point distances differ by no more than the bin size l.
2.4 Problem Definition
Let
 = {
= {
 1,…,
1,…,
 n] be a set of sets of graphs, one for each of the active molecules {ℳ1,…, ℳn}. Each
n] be a set of sets of graphs, one for each of the active molecules {ℳ1,…, ℳn}. Each
 i is a set of graphs {Gi1,…,Gimi} for each of the mi conformations of the molecule ℳi. For a given clique C, the support of a clique in the
i is a set of graphs {Gi1,…,Gimi} for each of the mi conformations of the molecule ℳi. For a given clique C, the support of a clique in the
 is defined as sup(C) = |
is defined as sup(C) = |
 |, where
|, where
 ⊆ {ℳ1,…, ℳn} is a set of molecules that each have at least one conformer graph G that supports C. Thus, provided the above, the common pharmacophore identification problem is defined as follows: Given
⊆ {ℳ1,…, ℳn} is a set of molecules that each have at least one conformer graph G that supports C. Thus, provided the above, the common pharmacophore identification problem is defined as follows: Given
 and the minimum support fraction σ, find all cliques in
and the minimum support fraction σ, find all cliques in
 whose support is ≥ σ · |
whose support is ≥ σ · |
 |. Setting σ to 100% restricts the search to only pharmacophores supported by all molecules. On the other hand, allowing σ to be less than 100% allows to find pharmacophores supported by only a portion of molecules which is required in cases when multiple binding sites, multiple binding modes or noisy data is a possibility.
|. Setting σ to 100% restricts the search to only pharmacophores supported by all molecules. On the other hand, allowing σ to be less than 100% allows to find pharmacophores supported by only a portion of molecules which is required in cases when multiple binding sites, multiple binding modes or noisy data is a possibility.
2.5 Algorithms
In this section we describe the two proposed algorithms for common pharmacophore identification using frequent clique mining in the graphs representing low-energy conformations of the active molecules, or ligands. The MCM algorithm is based on existing clique-mining methods and mines the conformer graphs using a depth-first approach and operating on edge-labeled graphs, and correctly determines the frequency of a common pharmacophore based on its embeddings in the pharmacophore graphs of the various ligands. The UCM algorithm improves the computational complexity of MCM by capitalizing on the fact that there is a high degree of structural similarity among the 3D conformations of a molecule. Both algorithms produce identical results and differ only in the execution time.
2.5.1 Multiple Conformer Miner Algorithm
The MCM algorithm described in this section uses a depth-first approach to discover all frequent cliques. During each step, it generates a new candidate n + 1-clique by growing the size of the current frequent n-clique via addition of a single new vertex and n new edges. All added edges are taken from the set of all frequent 2-cliques generated at the beginning of the algorithm. The clique is grown in such a way that the canonical code of the current clique is a prefix of the candidate clique. The latter ensures that the same clique is not enumerated multiple times. After the candidate generation step, the clique is enumerated (i.e., the embeddings of the clique are mined) and, if found frequent, reported and used for further growth.
MCM algorithm uses a simple adjacency matrix M to store each conformer separately for each molecule. When a two-bin assignment is used, the two different labels (differing by 1) corresponding to the distance between the same two vertices are stored in Mi,j and Mj,i. If a single-bin assignment is selected, then all off-diagonal elements in the lower triangular matrix are assigned −1, i.e., ∀j < i : Mi,j = −1. Sample adjacency matrices for conformers depicted in Fig. 2 are presented in Fig. 3a (for visualization purposes, the numeric edge labels were replaced with alphabetical ones to avoid confusion with conformer IDs used by the unified conformer matrix described in the following section).
Figure 2.
Three graphs representing three conformations of the same molecule. The edge labels represent two-bin assignment of the distances.
Figure 3.
Representations of graphs in Fig. 2: a) adjacency matrices for each conformer and b) unified conformational matrix.
The embeddings of the cliques are stored in a set
 = {
= {
 ℳ1,…,
ℳ1,…,
 ℳn} whose members are the molecular structures representing each molecule ℳi containing at least one conformer graph supporting the clique. Each molecular structure
ℳn} whose members are the molecular structures representing each molecule ℳi containing at least one conformer graph supporting the clique. Each molecular structure
 ℳi consists of two members: molecule ID and a set of conformer structures {
ℳi consists of two members: molecule ID and a set of conformer structures {

 1,…,
1,…,

 n}. Each conformer structure
n}. Each conformer structure

 i contains a conformer ID and a set of embeddings {
i contains a conformer ID and a set of embeddings {
 εl,…,
εl,…,
 εn. Each embedding
εn. Each embedding
 εi is a list of vertices (i.e., vertex IDs) in that conformer that have the appropriate vertex labels and edges. For the simplicity of the pseudocode, we omit the IDs of the molecules and conformers in the
εi is a list of vertices (i.e., vertex IDs) in that conformer that have the appropriate vertex labels and edges. For the simplicity of the pseudocode, we omit the IDs of the molecules and conformers in the
 ℳi and
ℳi and

 i and treat them simply as sets of conformers and embeddings, respectively.
i and treat them simply as sets of conformers and embeddings, respectively.
The MCM algorithm consists of three main programs: The FIND_FREQ_CLIQUES (Program 1) that is the entry point of the algorithm, GROW_CLIQUE (Program 2) that recursively finds frequent cliques larger than the currently discovered one, and MCM_ENUMERATE (Program 3) that finds the embeddings of a particular clique.
Program 1.
FIND_FREQ_CLIQUES(
 )
)
Program 2.
GROW_CLIQUE(f,
 )
)
| 1: | record f,

|
| 2: | ℂ ← {c| |c| = |f| + 1 AND |
∀ 2-clique ⊂ c, 2-clique ∈
 2 AND 2 AND |
|
| can(f) is a prefix of can(c)} | |
| 3: | Prune geometrically impossible cliques |
| 4: | for each c ∈ ℂ do |
| 5: |
 c ← ENUMERATE(f, c ← ENUMERATE(f,
 , c) , c) |
| 6: | if sup(c) ≥ σ · |
 | | |
| 7: | then GROW_CLIQUE(c,
 c) c) |
Program 3.
MCM_ENUMERATE(f,
 , c)
, c)
| 1: |
 ′ ← {} ′ ← {} |
| 2: | l ← ℒ (Vc − Vf) |
| 3: | ℬ ← ℒ (Ec − Ef) |
| 4: |
for each molecule ℳ with embeddings
 ℳ ∈ ℳ ∈
 do do
|
| 5: |
 ← {υ ∈ Vℳ |ℒ (υ) = l} ← {υ ∈ Vℳ |ℒ (υ) = l} |
| 6: |
 ′ℳ ← {} ′ℳ ← {} |
| 7: | for each conformer
 with embeddings with embeddings
  ∈ ∈
 ℳ do ℳ do
|
| 8: |
 ′ ′ ← {} ← {} |
| 9: | for each embedding
 ε ∈ ε ∈
  do do
|
| 10: |
 e ← e ←
 – –
 ε ε
|
| 11: |
 ′ε ← {} ′ε ← {} |
| 12: | for each υ ∈
 e do e do
|
| 13: | for i ← 1 to|
 ε| do ε| do
|
| 14: | u ←
 εi εi
|
| 15: | if ∃(υ,u) ∈ Gℳc,ℒ (υ,u) = ℬI |
| 16: | then i ← i + 1 |
| 17: | else break |
| 18: | if i >|
 ε| ε| |
| 19: | then
 ′ε ← ′ε ←
 ′ε ∪ { ′ε ∪ {
 ε ∪ υ} ε ∪ υ} |
| 20: |
 ′ ′ ← ←
 ′ ′ ∪ { ∪ {
 ′ε} ′ε} |
| 21: |
 ′ℳ ← ′ℳ ←
 ′ℳ ∪ { ′ℳ ∪ {
 ′ ′ } } |
| 22: |
 ′ ← ′ ←
 ′ ∪ { ′ ∪ {
 ′ℳ} ′ℳ} |
| 23: | if |
 ′|+ # remaining mol. in ′|+ # remaining mol. in
 < σ · | < σ · |
 | | |
| 24: | then return {} |
| 25: |
return
 ′ ′ |
The FIND_FREQ_CLIQUES starts by enumerating all 2-cliques in the graphs contained in
 and storing the embeddings of those 2-node cliques that are determined to be frequent. For each of these cliques, the GROW_CLIQUE function is called to find all cliques of size larger than two that have a canonical code of the passed 2-clique as their prefix.
and storing the embeddings of those 2-node cliques that are determined to be frequent. For each of these cliques, the GROW_CLIQUE function is called to find all cliques of size larger than two that have a canonical code of the passed 2-clique as their prefix.
GROW_CLIQUE records the pharmacophore and its embeddings that are passed to it as an argument. Recording can be restricted by user to, for example, only 4-point pharmacophores or larger. On line 2, all candidate cliques of size 1 vertex larger than the one passed to it and for which all subcliques of size 2 are frequent and for whose canonical code the canonical code of the passed clique is a prefix are generated. A pruning step on line 3 removes all cliques in which any three vertices and the edges between them fail the triangular inequality. Each candidate clique is then enumerated and, if found to be frequent (i.e., the support for the clique, or the size of the set of em-beddings
 c of the clique c is not less than the minimum support), used for generation of larger candidate cliques with a recursive call to GROW_CLIQUE. In other words, the algorithm performs a depth-first search of all present frequent cliques by growing the currently discovered frequent clique by an intelligent addition of a single vertex in each of the recursive calls.
c of the clique c is not less than the minimum support), used for generation of larger candidate cliques with a recursive call to GROW_CLIQUE. In other words, the algorithm performs a depth-first search of all present frequent cliques by growing the currently discovered frequent clique by an intelligent addition of a single vertex in each of the recursive calls.
The pseudocode for enumeration program MCM_ENUMERATE is presented in Program 3. This program takes three arguments: the canonical code of the new clique to be enumerated f, a set of the current clique embeddings
 , and the canonical code c of the current clique for which embeddings are supplied in
, and the canonical code c of the current clique for which embeddings are supplied in
 . Note, that since the clique is growing only by one vertex after it is confirmed to be frequent, the difference between the f and c is a single vertex and the number of edges equal to the number of vertices in c. The program starts with creating an empty set of embeddings
. Note, that since the clique is growing only by one vertex after it is confirmed to be frequent, the difference between the f and c is a single vertex and the number of edges equal to the number of vertices in c. The program starts with creating an empty set of embeddings
 ′ for the new clique f, and determining the label l of the new node added to c and obtaining a list of labels ℬ of the edges from all nodes in c to the new node in order (lines 1–3). After that, a loop through all molecules in the
′ for the new clique f, and determining the label l of the new node added to c and obtaining a list of labels ℬ of the edges from all nodes in c to the new node in order (lines 1–3). After that, a loop through all molecules in the
 is initiated. In each loop, a set of vertices
is initiated. In each loop, a set of vertices
 of the molecule with the labels identical to that of the new node, or a set of candidate vertices, is created (line 5).
of the molecule with the labels identical to that of the new node, or a set of candidate vertices, is created (line 5).
In the main loop (lines 4–24), every conformer of the molecule that has at least one embedding of c, and each embedding is visited. Since the vertices participating in the current embedding cannot be candidate vertices, a new set of candidate vertices
 e is created by removing the vertices in the current embedding from the candidate vertices set
e is created by removing the vertices in the current embedding from the candidate vertices set
 . Then, for each candidate vertex in
. Then, for each candidate vertex in
 e, the edge labels to all other vertices in the clique c are looked up in the adjacency matrices of the corresponding conformers and checked against the labels in the new edge labels set ℬ (lines 12–17). If all corresponding edge labels are found, the embedding is added to the set of new embeddings
e, the edge labels to all other vertices in the clique c are looked up in the adjacency matrices of the corresponding conformers and checked against the labels in the new edge labels set ℬ (lines 12–17). If all corresponding edge labels are found, the embedding is added to the set of new embeddings
 ′ε (line 19). On lines 20–22, the sets of embeddings
′ε (line 19). On lines 20–22, the sets of embeddings
 ′ε, conformers
′ε, conformers
 ′
′ , and molecules
, and molecules
 ′ℳ containing embeddings are added to the sets of conformers
′ℳ containing embeddings are added to the sets of conformers
 ′
′ molecules
molecules
 ′ℳ and new clique embedding set
′ℳ and new clique embedding set
 ′, respectively. After processing each molecule with embeddings, the algorithm checks if the needed minimum support (the minimum number of molecules) can be achieved given the size of the current embedding set
′, respectively. After processing each molecule with embeddings, the algorithm checks if the needed minimum support (the minimum number of molecules) can be achieved given the size of the current embedding set
 ′ and the number of molecules remaining unprocessed in
′ and the number of molecules remaining unprocessed in
 . If the required minimum support cannot be achieved, the program terminates by returning the empty embedding set (lines 23–24). Finally, the program returns the set of new clique embeddings
. If the required minimum support cannot be achieved, the program terminates by returning the empty embedding set (lines 23–24). Finally, the program returns the set of new clique embeddings
 ′.
′.
Notice that in the cases when the pharmacophore being enumerated consists of four or more pharmacophore points, the 3D arrangements that are mirror images of each other (and, therefore, not superimposable) will be indistinguishable. Thus, for all 4-point and larger pharmacophores, the algorithm checks (just before the line 19) if the last point is located above or below the plane formed by the three immediately preceding points and saves the vertices in one of two separate embeddings. Therefore, the algorithm returns two sets of embeddings instead of one for all 4-point or larger pharmacophores (for the sake of simplicity this was omitted in the Program 3). Even though these extra computations may seem to increase the runtime of the algorithm, this is not necessarily the case as it will in most cases prune infrequent pharmacophores much earlier. Indeed, the MCM algorithm runtime for the dataset described in the Section 3.1 decreased by 33% after this additional step was added.
2.5.2 Unified Conformer Miner Algorithm
A unique characteristic of frequent clique discovery in the context of the common pharmacophore identification problem is that there is a high degree of overlap between the graphs corresponding to the multiple conformations of the same molecule. Specifically, all the graphs in the set
 ℳi, i.e., all conformers of the same molecule ℳi, have exactly the same number and types of vertex labels and our analysis showed that 40–60% of the edges between pharmacophore points are conserved among the confermations of the same molecule. This degree of conservation stems from the facts that (i) some of the edges represent chemical bonds between underlying atoms that do not vary during conformer generation using molecular mechanics force fields and (ii) parts of the molecule may belong to a rigid part of the molecule.
ℳi, i.e., all conformers of the same molecule ℳi, have exactly the same number and types of vertex labels and our analysis showed that 40–60% of the edges between pharmacophore points are conserved among the confermations of the same molecule. This degree of conservation stems from the facts that (i) some of the edges represent chemical bonds between underlying atoms that do not vary during conformer generation using molecular mechanics force fields and (ii) parts of the molecule may belong to a rigid part of the molecule.
To take advantage of these overlaps and reduce the amount of time required to solve the common pharmacophore identification problem we developed the unified conformer miner (UCM) algorithm. The UCM algorithm uses a new data structure, referred to as the unified conformational matrix, to compactly store the information about all conformers of the same molecule. The unified conformational matrix M is the matrix of size n×n, where n is the number of pharmacophore points in the molecule, with the lower-left off-diagonal elements being unused. Each diagonal element Mi,j, contains the label of the corresponding vertex υi. The difference from the adjacency matrix used by the MCM algorithm is in the contents of the upper-right off-diagonal elements. Each off-diagonal element Mi,j (i < j) is a map with the edge labels serving as the keys and the sets of conformers (namely, conformer IDs) of a molecule that support this distance between vertices υi and υj serving as the mapped values. The unified conformational matrix for the molecule represented by three conformers depicted in Fig. 2 is shown in Fig. 3b. One can see from Fig. 2 that distance a between vertices υ1 and υ2 is supported by conformations 1 and 2. Thus, the map in the matrix element M1,2 has the following entry: a ≺ {1,2}. Another significant improvement of the unified conformational matrix is the replacement of all sets that contain all conformers' IDs with a single-element set {−1}. This should significantly improve the performance of the clique enumeration as well as reduce the storage requirements since about 40% to 60% of the distances between the same two vertices do not vary among the conformers, leading to a large number of the sets of conformers being identical and containing all conformer IDs for the molecule. For example, one can see from Fig. 2 that the distance b between vertices υ1 and υ2 is supported by all conformations. Thus, one of the elements in the map stored in matrix element M1,2 is b ≺ {−1}.
UCM algorithm also consists of three programs. The pseudocode of the first two programs is almost identical to FIND_FREQ_CLIQUES and GROW_CLIQUE from the MCM algorithm, with only modification being that the elements of the maps in the unified conformational matrices that are infrequent (i.e., not used in any of the frequent 2-cliques) are completely removed after discovering all frequent 2-cliques in the FIND_FREQ_CLIQUES to improve the performance of the rest of the algorithm. Due to the differences in the structure of the set
 and in the way the embeddings of the cliques are being enumerated and stored in the two algorithms, the enumeration code in the UCM_ENUMERATE (Program 4) is significantly different from that used in the MCM algorithm.
and in the way the embeddings of the cliques are being enumerated and stored in the two algorithms, the enumeration code in the UCM_ENUMERATE (Program 4) is significantly different from that used in the MCM algorithm.
Program 4.
UCM_ENUMERATE(f,
 , c)
, c)
| 1: |
 ′ ← {} ′ ← {} |
| 2: | l ← ℒ (Vc – Vf) |
| 3: | ℬ ← ℒ(Ec – Ef) |
| 4: |
for each molecule ℳ with embeddings
 ℳ ∈ ℳ ∈
 do do
|
| 5: |
 ← {υ ∈ Vℳ| ℒ (υ) = l} ← {υ ∈ Vℳ| ℒ (υ) = l} |
| 6: |
 ′ℳ ← {} ′ℳ ← {} |
| 7: | for each key-value pair (εvert, εconf) ∈
 ℳ do ℳ do
|
| 8: |
 e ← e ←
 – εvert – εvert
|
| 9: | for each υ ∈
 e do e do
|
| 10: |
 ← εconf ← εconf
|
| 11: | for i ← 1 to |εvert| |
| 12: | u ← Equation |
| 13: | if ∃( υ, u) ∈
 ℳ, ℒ (υ,u) = ℬi ℳ, ℒ (υ,u) = ℬi
|
| 14: | if Mℳ [υ][u][ℬi] = {−1} |
| 15: | then continue |
| 16: | else
 ← ←
 & cap Mℳ[υ][u][ℬi] & cap Mℳ[υ][u][ℬi] |
| 17: | else |
| 18: |
 ← {} ← {} |
| 19: | break |
| 20: | if
 = 0 = 0 |
| 21: | then break |
| 22: | i ← i + 1 |
| 23: | if
 ≠ 0 ≠ 0 |
| 24: | εvert′ ← {εvert ∪ υ} |
| 25: | εconf′ ←

|
| 26: |
 ′ℳ ← ′ℳ ←
 ′ℳ ∪(εvert′, εconf′) ′ℳ ∪(εvert′, εconf′) |
| 27: |
 ′ ← ′ ←
 ′ ∪ ′ ∪
 ′ℳ ′ℳ
|
| 28: | if |
 ′| + # remaining mol. in ′| + # remaining mol. in
 < σ · | < σ · |
 | | |
| 29: | then return {} |
| 30: |
return
 ′ ′ |
The embeddings in the UCM are also stored in a set
 of molecular structures
of molecular structures
 ℳ with two members, one of which is the molecule ID. However, the second element in the structure is now a set of pairs (εvert, εconf), where εvert is the list of vertices representing the embedding of a clique in the molecule and εconf is the set of conformer IDs that contain the embedding with these vertices. In the following algorithm descriptions we have omitted the assignment of molecule and conformer IDs for simplicity.
ℳ with two members, one of which is the molecule ID. However, the second element in the structure is now a set of pairs (εvert, εconf), where εvert is the list of vertices representing the embedding of a clique in the molecule and εconf is the set of conformer IDs that contain the embedding with these vertices. In the following algorithm descriptions we have omitted the assignment of molecule and conformer IDs for simplicity.
In each iteration of the main loop of the UCM_ENUMERATE, after selecting an initial set of candidate vertices on line 5, the algorithm visits every vertices-conformers pair (εvert εconf) in
 ℳ, the set of embeddings in the molecule ℳ. Since the εvert is a set of vertices that represent the embedding of the clique c, they cannot be candidate vertices for extension and must be removed from the set of vertices
ℳ, the set of embeddings in the molecule ℳ. Since the εvert is a set of vertices that represent the embedding of the clique c, they cannot be candidate vertices for extension and must be removed from the set of vertices
 (line 8). The loop on lines 9–26 goes through every vertex in the candidate set and computes the intersection of the set of conformers εconf that support current embedding with the sets of conformers for each distance in ℬ between the candidate vertex and each vertex in the current embedding εvert of the frequent clique c. If the set of conformations of molecule ℳ supporting a particular distance ℬi between two vertices υ and u contains a single element −1 (line 14), which means that all conformations support that edge, then no intersection needs to be calculated as it will not change. Otherwise, the set of conformations
(line 8). The loop on lines 9–26 goes through every vertex in the candidate set and computes the intersection of the set of conformers εconf that support current embedding with the sets of conformers for each distance in ℬ between the candidate vertex and each vertex in the current embedding εvert of the frequent clique c. If the set of conformations of molecule ℳ supporting a particular distance ℬi between two vertices υ and u contains a single element −1 (line 14), which means that all conformations support that edge, then no intersection needs to be calculated as it will not change. Otherwise, the set of conformations
 that support the frequent clique c and all new edges processed so far is updated by taking its intersection with the set of conformations supporting the edge being currently processed (line 16). Note, that since each new edge in the f must be supported by at least one conformation, whenever it is found that the edge is not supported, the set
that support the frequent clique c and all new edges processed so far is updated by taking its intersection with the set of conformations supporting the edge being currently processed (line 16). Note, that since each new edge in the f must be supported by at least one conformation, whenever it is found that the edge is not supported, the set
 is emptied and the loop is terminated (lines 17–19). If the intersection is not an empty set after processing all edges from a vertex in the candidate set to all vertices in the current clique, then an embedding for clique f in the molecule ℳ is added to the
is emptied and the loop is terminated (lines 17–19). If the intersection is not an empty set after processing all edges from a vertex in the candidate set to all vertices in the current clique, then an embedding for clique f in the molecule ℳ is added to the
 ′ℳ (lines 24–26). If the set of the embeddings
′ℳ (lines 24–26). If the set of the embeddings
 ′ℳ is not empty, i.e., if there is at least one conformer that contains an embedding of clique f, then
′ℳ is not empty, i.e., if there is at least one conformer that contains an embedding of clique f, then
 ′ℳ is added to the new clique embedding set
′ℳ is added to the new clique embedding set
 ′. Just as in MCM enumeration, the possibility to achieve the minimum support is checked after processing each molecule and empty set is returned immediately (lines 28–29) if minimum support cannot be reached given the size of the current set of embeddings
′. Just as in MCM enumeration, the possibility to achieve the minimum support is checked after processing each molecule and empty set is returned immediately (lines 28–29) if minimum support cannot be reached given the size of the current set of embeddings
 ′ and the number of remaining unprocessed molecules in
′ and the number of remaining unprocessed molecules in
 .
.
Like the MCM algorithm, UCM checks if the last point of the 4-point or larger pharmacophore being enumerated is above or below the plane formed by the three preceding points (just before the line 24) to distinguish between mirror images of the pharmacophores possessing the same clique code. Therefore, it will return two instead of one embedding set for the pharmacophores of size 4 points or larger.
3 Results and Discussion
We have experimentally evaluated the performance of our common pharmacophore identification algorithms using various datasets. The purpose of these evaluations is the validation of the exhaustiveness, correctness, scalability, and ability to handle difficult situations such as multiple binding modes or errors in the data. All calculations have been performed on Linux workstation with Xeon 2.3 GHz processor.
3.1 Comparison to Other Computational Methods
To compare the common pharmacophores identified by the proposed frequent clique mining approach to those identified by some recent computational methods, we have obtained 196 conformers for the five highly similar molecules presented in Fig. 4 from the authors of the RDP algorithm.9 The same molecules were used in another study17 as well as in PHASE8 User's Guide. The CP identification in this dataset is complicated due to very high similarity of the molecules that leads to a large number of overlapping features in all conformers. It was reported that the identification of exclusively 5-point CPs9 took about 160 s for the PHASE and 12 s for the RDP programs on a Linux workstation with a 3.4 GHz Intel Xeon processor.
Figure 4.
The five molecules used for pharmacophore identification study (obtained from9).
Since the authors9 have limited the types of pharmacophore sites to only hydrogen bond acceptors (A) and aromatic rings (R), we have also modified our program to use only those two types. In addition, we also used a distance of 2 Å as the minimum distance between pharmacophore points to be considered in the same pharmacophore to avoid having two pharmacophore sites produced by the same atom or atoms of the same group.
The results for 5-point pharmacophores (i.e., cliques of size five) obtained using σ set to 100% for σ set to 0.0, 0.1, 0.25, and 0.5 are presented in Table 1. In each run (except for a single-bin distance assignment), the algorithms identified four sets of pharmacophores consisting of the following sets of pharmacophore points (vertex labels): AAAAR, AAARR, AARRR, and ARRRR. A pharmacophore set AARRR, for example, means that it consists of two hydrogen bond acceptors and three aromatic rings. The difference between the members of each set has to do with the distances between the pharmacophore points (edge labels). One can see that the total number of pharmacophores identified grows quickly as δ increases because more intersite distances are assigned more than one label. For example, the dual distance label assignment (δ = 0.5) with a single spacial arrangement of 5 pharmacophore points (with 10 inter-point distances) generates up to 210 = 1024 potential distinct pharmacophores. Therefore, even in the case when some conformers share the exact same configuration of the pharmacophore points, the dual labeling will still produce up to 1024 5-point pharmacophores.
Table 1.
The number of identified pharmacophores and runtime with different multiple-bin labeling parameter δ for a set of 196 conformers of the molecules in Fig. 4.
| Runtime (s)
|
Number of unique pharmacophores3 | ||
|---|---|---|---|
| δ | MCM | UCM | |
| 0.0 | 0.5 | 0.1 | 1 |
| 0.1 | 1.2 | 0.4 | 14 |
| 0.25 | 3.1 | 1.0 | 108 |
| 0.5 | 60.8 | 16.1 | 3,645 |
Unique pharmacophores are defined here as those with identical sets of embeddings (identical conformers and vertices) regardless of the clique code.
A large number of reported pharmacophores requires some pharmacophore scoring in order to separate high-quality pharmacophores with a large number points from very loose pharmacophores with only few pharmacophore points. Such scoring can be obtained by computing the RMSD of aligned pharmacophore points in conformers as well as other values such as molecular (and/or conformer) support, rarity of the pharmacophore point types, size of the pharmacophore, etc. In this paper we chose to concentrate on the algorithms and not to implement any pharmacophore scoring.
The program finished the pharmacophore identification and enumeration with minimal multiple-bin assignment into neighboring bins (δ = 0.1) in less than 2 seconds. The same process took 61 and 16 seconds using MCM and UCM, respectively, when always-two-bin assignment was used (δ = 0.5). These runtimes cannot be directly compared to those reported in9 due to a different processor speed and the fact that even though one may select to output only pharmacophores of a particular size n, still all of the frequent pharmacophores with sizes 2 to n−1 need to be discovered before proceeding to size n. Thus, the runtime may be longer for our program when run with parameters similar to those in.9 On the other hand, we feel that it is advantageous to report all pharmacophores starting with a particular size instead of only of a particular size because in most cases the user will not know the size of the pharmacophore being identified in advance and instead would like to identify the largest one(s) available.
3.2 Comparison with Experimental Results
To evaluate the ability of the proposed frequent clique mining algorithms to identify correct common pharmacophores, we performed the common pharmacophore identification for the dopamine D2 and D4 receptor antagonists for which experimental binding affinity data was used in a 3D QSAR pharmacophore modeling.18
The structures of the studied molecules have been arranged into three sets each having a different pharmacophore. Each of the three pharmacophores consists of two aromatic rings, ammonium nitrogen and a site-point in the N—H direction in different geometrical configuration. Since our program does not have a definition for a site-point in the N—H direction, we have concentrated on identifying the other three features in the conformers.
The structures of all conformers were generated using OpenEye’s Omega19 software for conformer generation with an upper threshold of 20 kcal/mol and maximum of 1000 conformations. A range of 20 kcal/mol is probably the minimum needed to cover most of the conformational space of the molecule because the actual binding conformation may lie within 5–40 kcal/mol20,21 from the lowest-energy (least strained) conformation when computed in vacuum without a solvation correction. In order to select the most diverse conformations, Omega uses a minimum RMSD value between two conformers (default is 0.8 Å) below which the conformers are considered duplicates. Some of the pharmacophore elucidation programs limit the number of generated conformers, which in turn can significantly limit the searched conformational space resulting in a set of conformers none of which are close to the binding conformations. For example, HipHop is limited to 255 conformations, while DISCO is limited to about 80 conformations per molecule. Our program, on the other hand, can consider an arbitrary number of conformations.
After generating conformations for each molecule in the dopamine D2 and D4 receptor antagonists, the first set (compounds 1–11) contained only 63 conformations, second set (compounds 12–22) contained 657 conformations, and the third set (compounds 23–32) contained 779 conformations. One can see that since the first set contains much fewer conformers per molecule, it contains the least flexible structures. This fact can be easily observed from the chemical structures of the compounds (see18). The most flexible molecule in set 1 (compound 8) contained only 17 conformations. In contrast, sets 2 and 3 contained much more flexible molecules with up to 258 (compound 24) conformers per molecule.
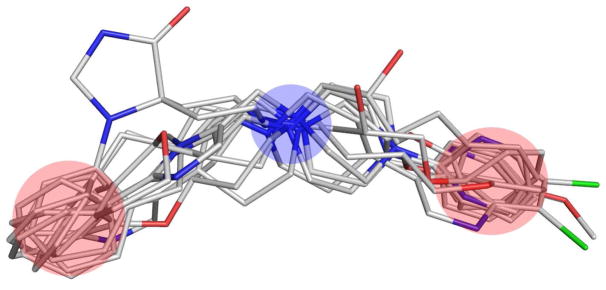
For all three sets we ran our programs with a support fraction σ of 100% to find pharmacophores supported by all conformations. In each of the three cases we were able to find different variations of the same pharmacophore (differing only due to the assignment to different distance bins) as described in.18 The total number of 3-point pharmacophores for each of the three sets was 12, 18, and 38 respectively. The alignments of all molecules in each set and the corresponding pharmacophores are shown in Figs. 5–7. The alignments were performed using the discovered pharmacophore points with PyMOL.22
Figure 5.
The pharmacophore model for the compounds in set 1 (red regions indicate aromatic ring sites R and blue ones indicate the ammonium nitrogen that can be P or D).
Figure 7.
The pharmacophore model for the compounds in set 3 (red regions indicate aromatic ring sites R and blue ones indicate the ammonium nitrogen that can be P or D).
3.3 Identification of Different Binding Modes
Sometimes one needs to identify pharmacophores that are not supported by all molecules in the dataset. For example, different molecules can have different binding modes or the target may have more than one binding site with different ligands binding to different binding sites. To illustrate how our proposed method can be used in such scenarios, we have selected the same set of 12 molecules used in,10 which is composed of 6 molecules that are more selective towards D2 receptors (compound IDs 2, 3, 8, 9, and 10), and 6 molecules that are more selective towards D4 receptors (compounds 12, 13, 15, 18, 19, and 21), all taken from the same study18 described in the previous section.
The resulting set of 12 molecules had a total of 417 conformers. The program was run with a minimum support of 50%, which allows it to find pharmacophores that are present in at least 50% of the molecules. The two different pharmacophores (albeit with different combinations of distance labels due to multiple-bin assignment) identified by the program and each supported by a different half of molecules are identical to the ones depicted in Figs. 5 and 6. One can see that the frequent clique-discovery approach can be used for such difficult cases as multiple binding modes/sites. In contrast, some of the programs, particularly HipHop, are known to fail in such situations.10
Figure 6.
The pharmacophore model for the compounds in set 2 (red regions indicate aromatic ring sites R and blue ones indicate the ammonium nitrogen that can be P or D).
3.4 Scalability and Parameter Sensitivity Study
To assess the scalability of our methods for finding common pharmacophores in a large number of structurally diverse molecules as well as sensitivity to several variable parameters (minimum support σ, multiple-bin labeling parameter δ, maximum number of hydrophobic groups in a pharmacophore), we selected three concentration-response bioassays from PubChem23 that contained over 200 confirmed active compounds. Conformers for each these compounds were generated using the Omega program with upper strain energy limit of 20 kcal/mol and a maximum number of conformers per molecule of 5000. The limit on the number of hydrophobic groups in the pharmacophore to zero or one to avoid pharmacophores consisting mostly of hydrophobic sites.
The results of the pharmacophore identification runs are presented in Tables 2–4. The following parameters have been used for our algorithms: distance bin size = 1 Å, minimum inter-point distance = 2 Å, maximum inter-point distance = 13 Å, maximum pharmacophore size = unlimited. The resulting number of conformers for randomly selected subsets of molecules of different size is given in parentheses in the first column in Tables 2–4.
Table 2.
Runtimes (in sec) for compounds from PubChem AID 1030 assay with various support values, multiple-bin labeling parameter and number of molecules/conformers.
| MCM | UCM | |||||
|---|---|---|---|---|---|---|
| Min. Support σ (%)
|
||||||
| # mol (conf) | 90 | 70 | 50 | 90 | 70 | 50 |
| δ = 0.5, no hydrophobic groups | ||||||
| 50 (5,789) | 0.2 | 1.2 | 11.9 | 0.1 | 0.2 | 1.2 |
| 100 (14,340) | 0.4 | 2.6 | 16.7 | 0.1 | 0.3 | 1.3 |
| 200(27,711) | 2.3 | 10.2 | 57.4 | 0.7 | 1.7 | 5.8 |
| δ = 0.5, up to 1 hydrophobic group | ||||||
| 50 (5,789) | 0.8 | 5.8 | 51.1 | 0.2 | 0.7 | 6.3 |
| 100 (14,340) | 1.9 | 12.1 | 72.9 | 0.6 | 1.5 | 6.9 |
| 200(27,711) | 5.8 | 32.7 | 218.4 | 1.8 | 4.7 | 21.6 |
| δ = 0.25, up to 1 hydrophobic group | ||||||
| 50 (5,789) | 0.6 | 2.6 | 13.1 | 0.2 | 0.4 | 1.4 |
| 100 (14,340) | 1.4 | 4.8 | 26.5 | 0.4 | 0.8 | 2.5 |
| 200(27,711) | 4.2 | 12.2 | 66.7 | 1.3 | 2.6 | 7.4 |
Table 4.
Runtimes (in sec) for compounds from PubChem AID 652 assay with various support values, multiple-bin labeling parameter and number of molecules/conformers.
| MCM | UCM | |||||
|---|---|---|---|---|---|---|
| Min. Support σ (%)
|
||||||
| # mol (conf) | 90 | 70 | 50 | 90 | 70 | 50 |
| δ = 0.5, no hydrophobic groups | ||||||
| 50 (8,369) | 3.8 | 95.7 | 631 | 0.3 | 8.3 | 63.5 |
| 100 (17,465) | 7.1 | 142.1 | 729 | 0.6 | 12.1 | 66.8 |
| 200 (40,169) | 9.3 | 149.0 | 1137 | 1.0 | 13.6 | 96.0 |
| δ = 0.5, up to 1 hydrophobic group | ||||||
| 50 (8,369) | 12.6 | 310.9 | 1712 | 1.0 | 27.6 | 186.8 |
| 100 (17,465) | 19.5 | 456.2 | 2133 | 1.8 | 40.8 | 213.0 |
| 200 (40,169) | 22.9 | 558.7 | 3387 | 2.6 | 51.9 | 334.9 |
| δ = 0.25, up to 1 hydrophobic group | ||||||
| 50 (8,369) | 4.4 | 53.6 | 324 | 0.4 | 4.6 | 30.1 |
| 100 (17,465) | 7.8 | 80.7 | 466 | 0.8 | 7.0 | 43.7 |
| 200 (40,169) | 12.5 | 111.3 | 768 | 1.6 | 10.4 | 72.2 |
The results suggest that the runtime of both the MCM and the UCM algorithms scales almost linearly with the input size in terms of the number of molecules and/or conformers. Since the molecules in the PubChem AID 1030 assay are slightly more rigid (fewer conformers per molecule), the runtimes for that dataset are smaller. On the other hand, the longer runtimes for the PubChem AID 652 assay could have been merely caused by a less favorable order of the molecules in the dataset. As expected, the decrease of the minimum support value significantly increases the runtime as much more pharmacophores can be identified that are supported by a smaller number of molecules. The inclusion of the hydrophobic pharmacophore points also significantly increases the runtime as hydrophobic groups represent the majority of the points in the molecules. However, the results of our experiments indicate that the runtime stops increasing after allowing just two or three hydrophobic groups (depending on the σ) for all datasets in this section. Moreover, when the restriction on the number of hydrophobic groups in the pharmacophore was removed, the runtimes remained the same for σ= 90%, and increased only by a factor of 1.5 and 3.0 for σ= 70% and σ = 50%, respectively when compared to the runtimes with a maximum of one hydrophobic group.
When comparing the performance of MCM and UCM, it can be seen that the latter outperforms the former by up to 14 times and on average runs about 10 times faster. The results in Tables 2–4 indicate that UCM performs significantly better than MCM especially with lower minimum support values, which is important for situations where a lot of noise is present in the input data. This indicates that significant computational benefits can be obtained by exploiting the shared information among the conformational graphs of each molecule.
4 Conclusions
This paper presents two algorithms based on frequent clique discovery that are designed to identify the common pharmacophore from a set of experimentally determined active molecules. We show that both algorithms are efficient and guarantee to find all common cliques where the variation of the distance between any pair of identical points in the pharmacophore in different molecules does not exceed the size of the distance bin. Current approach can be applied to situations with arbitrarily large number of conformers per molecule and was shown to work for situations with multiple binding sites or binding modes. We also show that the exploitation of the structural similarities among the conformers of the same molecule by the UCM algorithm improves the performance by up to 14 times.
Table 3.
Runtimes (in sec) for compounds from PubChem AID 468 assay with various support values, multiple-bin labeling parameter and number of molecules/conformers.
| MCM | UCM | |||||
|---|---|---|---|---|---|---|
| Min. Support σ (%)
|
||||||
| # mol (conf) | 90 | 70 | 50 | 90 | 70 | 50 |
| δ = 0.5, no hydrophobic groups | ||||||
| 50(11,906) | 0.5 | 9.2 | 169 | 0.1 | 0.8 | 12.8 |
| 100(23,011) | 1.1 | 19.1 | 294 | 0.2 | 1.4 | 20.7 |
| 200 (39,857) | 2.6 | 41.5 | 566 | 0.5 | 3.2 | 39.6 |
| δ = 0.5, up to 1 hydrophobic group | ||||||
| 50(11,906) | 4.4 | 43.7 | 602 | 0.7 | 4.2 | 62.1 |
| 100(23,011) | 7.1 | 93.8 | 1056 | 1.1 | 7.7 | 99.2 |
| 200 (39,857) | 13.8 | 201.0 | 2021 | 1.9 | 17.6 | 183.4 |
| δ = 0.25, up to 1 hydrophobic group | ||||||
| 50(11,906) | 1.8 | 18.8 | 131 | 0.4 | 1.7 | 13.2 |
| 100(23,011) | 3,7. | 33.9 | 233 | 0.7 | 2.8 | 21.1 |
| 200 (39,857) | 5.6 | 65.5 | 456 | 0.9 | 5.1 | 40.3 |
Acknowledgments
This work was supported by NSF ACI-0133464, IIS-0431135, NIH R01 LM008713A, and by the Digital Technology Center at the University of Minnesota.
References
- 1.Güner OF, editor. Pharmacophore Perception, Development, and Use in Drug Design. International University Line; LaJolla, CA: 2000. [Google Scholar]
- 2.Langer T, Hoffmann RD, editors. Pharmacophores and Pharmacophore Searches. Wiley-VCH; Weinheim: 2006. [Google Scholar]
- 3.Eglen RM, Schneider G, Böhm H-J. High-Thoughput Screening and Virtual Screening: Entry Points to Drug Discovery. In: Böhm H-J, Schneider G, editors. Virtual Screening for Bioactive Molecules. Wiley-VCH; Weinheim: 2000. pp. 1–14. [Google Scholar]
- 4.VanDrie JH. Future Directions in Pharmacophore Discovery. In: Güner OF, editor. Pharmacophore Perception, Development, and Use in Drug Design. International University Line; La Jolla, CA: 1999. pp. 515–530. [Google Scholar]
- 5.Martin YC, Bures MG, Danaher EA, De-Lazzer J, Lico I, Pavlik PA. A fast new approach to pharmacophore mapping and its application to dopaminergic and benzodiazepine agonists. J Comput-Aided Mol Des. 1993;7:83–102. doi: 10.1007/BF00141577. [DOI] [PubMed] [Google Scholar]
- 6.Barnum D, Greene J, Smellie A, Sprague P. Identification of Common Functional Configurations Among Molecules. J Chem Inf Comput Sci. 1996;36:563–571. doi: 10.1021/ci950273r. [DOI] [PubMed] [Google Scholar]
- 7.Jones G, Willett P, Glen RC. A genetic algorithm for flexible molecular overlay and pharmacophore elucidation. J Comput-Aided Mol Des. 1995;9:532–549. doi: 10.1007/BF00124324. [DOI] [PubMed] [Google Scholar]
- 8.Dixon SL, Smondyrev AM, Knoll EH, Rao SN, Shaw DE, Friesner RA. PHASE: a new engine for pharmacophore perception, 3D QSAR model development, and 3D database screening: 1. Methodology and preliminary results. J Comput-Aided Mol Des. 2006;20:647–671. doi: 10.1007/s10822-006-9087-6. [DOI] [PubMed] [Google Scholar]
- 9.Zhu F, Agrafiotis DK. Recursive Distance Partitioning Algorithm for Common Pharmacophore Identification. J Chem Inf Model. 2007;47:1619–1625. doi: 10.1021/ci7000583. [DOI] [PubMed] [Google Scholar]
- 10.Feng J, Sanil A, Young SS. PharmID: Pharmacophore Identification Using Gibbs Sampling. J Chem Inf Model. 2006;46:1352–1359. doi: 10.1021/ci050427v. [DOI] [PubMed] [Google Scholar]
- 11.Kuramochi M, Karypis G. Frequent Subgraph Discovery. Proceedings of the IEEE International Conference on Data Mining (ICDM’01); San Jose, California, USA. November 29 – December 2, 2001; IEEE Computer Society; 2001. [Google Scholar]
- 12.Yan X, Han J. gSpan: Graph-Based Substructure Pattern Mining. Proceedings of the 2nd IEEE International Conference on Data Mining (ICDM’02); Maebashi City, Japan. December 9–12, 2002; IEEE Computer Society; 2002. [Google Scholar]
- 13.Huan J, Wang W, Prins J. Efficient Mining of Frequent Subgraph in the Presence of Isomorphism. Proceedings of the 3rd IEEE International Conference on Data Mining (ICDM’03); Melbourne, Florida, USA. December 19–22, 2003; IEEE Computer Society; 2003. [Google Scholar]
- 14.Wang J, Zeng Z, Zhou L. CLAN: An Algorithm for Mining Closed Cliques from Large Dense Graph Databases. In: Liu L, Reuter A, Whang K, Zhang J, editors. Proceedings of the 22nd International Conference on Data Engineering (ICDE 2006); Atlanta, GA, USA. April 3–8, 2006; IEEE Computer Society; 2006. [Google Scholar]
- 15.Read RC, Corneil DG. The graph isomorphism desease. J Graph Theory. 1977;1:339–363. [Google Scholar]
- 16.Fortin S. The graph isomorphism problem. Department of Computer Science, University of Alberta; 1996. Technical Report TR96-20. [Google Scholar]
- 17.Krovat EM, Langer T. Non-peptide Angiotensin II Receptor Antagonists: Chemical Feature Based Pharmacophore Identification. J Med Chem. 2003;46:716–726. doi: 10.1021/jm021032v. [DOI] [PubMed] [Google Scholar]
- 18.Boström J, Böhm M, Gundertofte K, Klebe G. A 3D QSAR Study on a Set of Dopamine D4 Receptor Antagonists. J Chem Inf Comput Sci. 2003;43:1020–1027. doi: 10.1021/ci034004+. [DOI] [PubMed] [Google Scholar]
- 19.OpenEye Scientific Software. [accessed Sept 2, 2008];Omega. http://www.eyesopen.com/products/applications/omega.html.
- 20.Nicklaus MC, Wang S, Driscoll JS, Milne GWA. Conformational Changes of Small Molecules Binding to Proteins. Bioorg Med Chem. 1995;3:411–428. doi: 10.1016/0968-0896(95)00031-b. [DOI] [PubMed] [Google Scholar]
- 21.Diller DJ, Merz KM. Can We Separate Active from Inactive Conformations? J Comput-Aided Mol Des. 2002;16:105–112. doi: 10.1023/a:1016320106741. [DOI] [PubMed] [Google Scholar]
- 22.The PyMOL Molecular Graphics System. DeLano Scientific; San Carlos, CA: [Google Scholar]
- 23. [accessed Sept 2, 2008];The PubChem Database. http://pubchem.ncbi.nlm.nih.gov.