Bounding Sample Size Projections for the Area Under a ROC Curve

Abstract

Studies of diagnostic tests are often designed with the goal of estimating the area under the receiver operating characteristic curve (AUC) because the AUC is a natural summary of a test’s overall diagnostic ability. However, sample size projections dealing with AUCs are very sensitive to assumptions about the variance of the empirical AUC estimator, which dependens on two correlation parameters. While these correlation parameters can be estimated from available data, in practice it is hard to find reliable estimates before the study is conducted. Here we derive achievable bounds on the projected sample size that are free of these two correlation parameters. The lower bound is the smallest sample size that would yield the desired level of precision for some model, while the upper bound is the smallest sample size that would yield the desired level of precision for all models. These bounds are important reference points when designing a single or multi-arm study; they are the absolute minimum and maximum sample size that would ever be required. When the study design includes multiple readers or interpreters of the test, we derive bounds pertaining to the average reader AUC and the ‘pooled’ or overall AUC for the population of readers. These upper bounds for multireader studies are not too conservative when several readers are involved.

1 Introduction

Receiver operating characteristic (ROC) curves assess the ability of a diagnostic test to discriminate between two populations. See Pepe and Zhou et. al. for a comprehensive description of methods for diagnostic tests [25, 33]. The area under the ROC curve (AUC) is the probability that a randomly selected observation from one population scores less on the test than a randomly selected observation from the other population. If the AUC is one (or zero) then the test discriminates perfectly, but if the AUC is one-half then the test has no discriminative ability whatsoever. The AUC is an easily understood metric that summarizes the test’s overall diagnostic ability. Studies that seek to assess the ability of a diagnostic test are typically designed to estimate the AUC within a fixed margin of error [9, 10, 20, 23, 24, 13].

The AUC estimator of choice is the empirical (scaled Mann-Whitney-U) estimator because it is a consistent and efficient estimator under very general conditions [9, 15]. Its variance depends on the true AUC and two additional correlation parameters, both of which can be estimated nonparametrically from the data at hand [17, 9, 1]. However, at the design stage, there is seldom any data available to estimate these parameters. Investigators may have an idea of what the AUC might be, but they seldom have a reliable guess for the correlation parameters. Unfortunately these correlation parameters play an important role in determining the variance, making the subsequent sample size projections quite sensitive to the initial inputs.

However, it is possible to determine the maximum and minimum sample size required to achieve a certain level of efficiency, over all models, without having to specify the correlation parameters. To derive these bounds, we use the fact that the maximum and minimum variance of the empirical AUC estimate, over all models, depends only on the true AUC and the sample size. Specification of the two key correlation parameters is, in this sense, eliminated. The minimum sample size will yield the desired level of precision for some model, while the maximum will yield the desired level of precision for all models. These bounds are useful for determining the sensitivity of sample size projections to modeling assumptions and for determining the extent of resources that may be needed for a given study.

We then extend these bounds to complex designs involving multiple tests and multiple readers of each test. These situations require specification of the correlation structure between the tests and readers. We examine the bounds in relation to projections obtained according to the standard ANOVA approach for multi-reader studies. This approach is based on a random effects ANOVA model for each reader’s empirical AUC, which does account for correlation between readers. These methods apply, in principle, to any large sample situation under certain conditions (see [31, 21, 28]). However, the ANOVA approach is highly sensitive to assumptions about the components of variance and may yield projections greater than the upper bound. We illustrate this behavior and discuss when these bounds are themselves sufficient projections.

Section §2 is background and establishes notation. Sample size projections for estimating a single AUC are in §4 and projections for estimating the difference between two AUCs are in §5. Extensions to designs involving multiple readers are also considered. Closing comments are in section §7.

2 Background

A sample of test outcomes from the ‘non-diseased’ or normal population will be represented by random variables X₁, X₂, … , X_m with cumulative distribution function F. Likewise, represent the test outcomes from the ‘diseased’ or abnormal population as Y₁, Y₂, … , Y_n with CDF G. Denote the AUC as θ = P(X < Y) [1]. The empirical estimator of the AUC, θ̂, is

$$\widehat{\theta }=\frac{1}{\mathit{mn}}\sum _{i=1}^{\mathit{m}}\sum _{j=1}^{\mathit{n}}{Z}_{\mathit{ij}}$$ (1)

where $Z_{\mathit{ij}}=I(X_i<Y_j)+\frac{1}{2}I(X_i=Y_j)$ and I(·) is an indicator function. If CDFs F and G are continuous then E[θ̂] = θ and

$$\mathit{V\; ar}[\widehat{\theta }]=\frac{\theta (1-\theta )}{\mathit{mn}}(1+(n-1){\rho }_y+(m-1){\rho }_x)$$ (2)

where ρ_y = [P (X < min(Y_i, Y_j)) − θ²]/θ(1 − θ) and ρ_x = [P (max(X_i, X_j) < Y) − θ²]/θ(1 − θ) are the correlation coefficients between two indicators variables based on the same y (or x) observation. The major contributors to the varaince are ρ_y/m and ρ_x/n; the first term is O(1/mn). Both ρ_y and ρ_x take different forms depending on the underlying model, but both can be estimated non-parametrically if data are available [17, 9, 1].

Ties reduce the variance of θ̂ [26]. Assume that F and G have common discontinuities (the only ones that allow ties of importance), finite in number and denoted by ξ_k, k = 1, … , K. Define p_k = P(X_i = ξ_k) and q_k = P(Y_j = ξ_k) then $E[\widehat{\theta }]={\theta }^{\ast }=P(X<Y)+\frac{1}{2}P(X=Y)$ and the variance of θ̂ is now

$$\mathrm{V\; ar}[\widehat{\theta }]=\frac{{\theta }^{\ast }(1-{\theta }^{\ast })}{\mathit{mn}}\left(1+(n-1){\rho }_y^{\ast }+(m-1){\rho }_x^{\ast }\right)-\frac{1}{12\mathit{mn}}\sum _k{p}_k{q}_k[(n-1)q_k+(m-1)p_k+3]$$ (3)

where ${\rho }_y^{\ast }$ and ${\rho }_x^{\ast }$ are now the corresponding correlation coefficients. The correction term is often negligible, but can, under certain circumstances, be of the same order of magnitude as the initial term in the variance [15, p. 20].

In the sections that follow, we will use the fact that the empirical AUC estimator, θ̂, and difference between two such estimators for different tests, say θ̂_A − θ̂_B, are both approximately normally distributed in large samples [15, 16]. Hence, an approximate (1 − α)100% confidence interval for θ is

$$\widehat{\theta }\pm Z_{\alpha /2}\sqrt{V\left(\widehat{\theta }\right)}$$ (4)

where V (θ̂) is given by (2). Likewise a hypothesis test of H₀ : θ = θ₀ versus H₁ : θ = θ₁ > θ₀ based on the test statistic $(\widehat{\theta }-{\theta }_0)/\sqrt{V_0(\widehat{\theta })}$ has Type II error probability:

$$\beta =\mathrm{\Phi }\left[Z_{\alpha /2}\frac{\sqrt{V_0(\widehat{\theta })}}{\sqrt{V_1(\widehat{\theta })}}+\frac{{\theta }_0-{\theta }_1}{\sqrt{V_1(\widehat{\theta })}}\right]$$ (5)

Here we ignored the lower tail of the test, which contributes very little in any case. Equations (4) and (5) readily generalize when the object of inference is θ_A − θ_B and they are often used for sample size projections with the understanding that misspecification of ρ_y and ρ_x can be costly [5, 12].

Although ρ_y and ρ_x are often intractable, there are two important exceptions where an analytical form for V (θ̂) can be obtained [2, 8]. The first is the ‘biexponential’ model where X_i ~ Exponential(λ_x) and Y_j ~ Exponential(λ_y). Direct calculation yields P (max(X_i, X_j) < Y) = 2θ²/(1 + θ) and P (X < min(Y_i, Y_j)) = θ/(2 − θ) with correlation parameters ρ_x = θ/(1 + θ) and ρ_y = (1 − θ)/(2 − θ) [2, 9]. Because the correlation parameters depend on the AUC in a simple fashion, this model is routinely used for sample size calculations [9, 23]. However this can (and often does) lead to sample sizes that are too small for many applications [20, 32].

The second noteworthy case is an equal variance ‘binormal’ model where a Taylor series expansion of the AUC variance is free of correlation parameters. The binormal assumption is that some monotonic transformation, say h(·), can be found such that $h(X_i)\sim N({\mu }_x,{\sigma }_x^2)$ and $h(Y_j)\sim N({\mu }_y,{\sigma }_y^2)$ [18, 19, 6, 30]. Without loss of generality let μ_x < μ_y. The area under that ROC curve is $P(X<Y)=P(h(X)<h(Y))={\theta }_{\mathit{nor}}=\mathrm{\Phi }[({\mu }_y-{\mu }_x)/\sqrt{{\sigma }_x^2+{\sigma }_y^2]}$where Φ[·] is the standard normal CDF. θ_nor is a monotone increasing function of $\delta =({\mu }_y-{\mu }_x)/\sqrt{{\sigma }_x^2+{\sigma }_y^2}$ and inference on δ leads to inference on θ by a simple transformation [27, 7, 24]. A Taylor series argument yields the following approximation for the standard error when σ_x = σ_y,

$$\mathit{V\; ar}\left[{\widehat{\theta }}_{\mathit{nor}}\right]\approx \left(0.0099\times \exp \left\{-A^2/2\right\}\right)\times \left(\frac{5A^2+8}{n}+\frac{A^2+8}{m}\right)$$ (6)

where A = 1.414×Φ⁻¹[θ] [20, 23]. We will use these two cases for comparison against the sample size bounds.

3 Bounding the Variance of the Empirical AUC Estimator

When F and G are both continuous, Birnbaum and Klose [4] show that

$$\frac{\theta (1-\theta )}{\mathit{mn}}{B}_i\left(m,n,\theta \right)\le \mathit{V\; ar}\left[\widehat{\theta }\right]\le \frac{\theta (1-\theta )}{\mathit{mn}}\max (m,n)=\frac{\theta (1-\theta )}{\min (m,n)}$$ (7)

where i = 1 if $\frac{\min (m,n)-1}{\max (m,n)-1}\le 2\min (\theta ,1-\theta )$, i = 2 otherwise, and

$$B_1\left(m,n,\theta \right)=\left[\min (m,n)-\frac{{(\min (m,n)-1)}^2}{12(\max (m,n)-1)\theta (1-\theta )}\right]$$ (8)

$$B_2\left(m,n,\theta \right)=\left[1-\left(m+n-2\right)\frac{\min (\theta ,1-\theta )}{\max (\theta ,1-\theta )}+\frac{4}{3\max (\theta ,1-\theta )}\sqrt{2\min (\theta ,1-\theta )(m-1)(n-1)}\right]$$ (9)

These bounds are achievable when the underlying distributions are continuous. The confidence interval, $\widehat{\theta }\pm Z_{\alpha /2}\sqrt{\theta (1-\theta )/\min (m,n)}$ is robust in that it maintains at least (1 − α)100% coverage probability under model failure (see [3]). We will make use of the fact that (7) implies

$$B_i(m,n,\theta )\le (1+(n-1){\rho }_y+(m-1){\rho }_x)\le \max (m,n)$$ (10)

where i = 1, 2 depending on (min(m, n) − 1)/(max(m, n) − 1) as noted above. The middle term of (10) is the inflation factor that corrects the variance for the dependence between indicator variables.

When ties are present, equation (3) indicates that the upper bound on the variance still holds. In fact, Lemma 5.1 of Lehmann [14] shows that these bounds extend immediately by simply subtracting $\frac{1}{12\mathit{mn}}{\sum }_k{p}_k{q}_k[(n-1)q_k+(m-1)p_k+3]$ from each of the upper and lower bounds and replacing θ with θ*. Note that this correction term, which requires specification of the probability mass on points of common discontinuities, is often quite small. Hence ignoring ties, which we do for the remainder of this paper, is at worse conservative.

Now consider two distinct diagnostic tests, A and B. For test ‘A’, let X_A1, X_A2, … , X_Am and Y_A1, Y_A2, … , Y_An have CDFs F_A and G_A respectively. The AUC is θ_A = P(X_A < Y_A) and the variance of θ̂_A depends on ρ_Ay and ρ_Ax, the cluster correlations under modality ‘A’. Let a similar notational structure exist for test ‘B’. The difference in AUCs, θ_A − θ_B, is of interest. The variance of the estimated difference is

$$\mathit{V\; ar}\left[{\widehat{\theta }}_A-{\widehat{\theta }}_B\right]=\mathit{V\; ar}\left[{\widehat{\theta }}_A\right]+\mathit{V\; ar}\left[{\widehat{\theta }}_B\right]-2\rho \sqrt{\mathit{V\; ar}\left[{\widehat{\theta }}_A\right]\mathit{V\; ar}\left[{\widehat{\theta }}_B\right]}$$ (11)

where ρ = Corr[θ̂_A, θ̂_B]. If different participants are evaluated on each modality then ρ = 0. However, we gain efficiency by evaluating the same cases under both modalities because ρ is now positive. Hanley and McNeil provide a useful discussion and tabulation of ρ [10]. Assuming ρ is fixed and nonnegative, equation (11) can be bounded by substituting the upper and lower bounds for the variance as follows:

$$\mathit{V\; ar}\left[{\widehat{\theta }}_A-{\widehat{\theta }}_B\right]<\frac{{\theta }_A(1-{\theta }_A)+{\theta }_B(1-{\theta }_B)}{\min (m,n)}-\frac{2\rho \sqrt{{\theta }_A(1-{\theta }_A)B_i(m,n,{\theta }_A){\theta }_B(1-{\theta }_B)B_i(m,n,{\theta }_B)}}{\mathit{mn}}$$ (12)

$$\mathit{V\; ar}\left[{\widehat{\theta }}_A-{\widehat{\theta }}_B\right]>\frac{{\theta }_A(1-{\theta }_A)B_i(m,n,{\theta }_A)+{\theta }_B(1-{\theta }_B)B_i(m,n,{\theta }_B)}{\mathit{mn}}-\frac{2\rho \sqrt{{\theta }_A(1-{\theta }_A){\theta }_B(1-{\theta }_B)}}{\min (m,n)}$$ (13)

where i = 1 if $\frac{\min (m,n)-1}{\max (m,n)-1}\le 2\min (\theta ,1-\theta )$, i = 2 otherwise. Define the lower bound to be zero whenever the RHS of (13) is negative. These bounds are achievable only when ρ = 0. Nevertheless, they are useful reference points.

If the cluster correlations are the same across modalities (i.e., ρ_Ax = ρ_Bx = ρ_x and ρ_Ay = ρ_By = ρ_y), then a set of tighter, achievable bounds exist. Factoring out the now common over-dispersion term (1 + (n − 1)ρ_y + (m − 1)ρ_x) in equation (11) and bounding by (10) yields

$$\mathit{V\; ar}\left[{\widehat{\theta }}_A-{\widehat{\theta }}_B\right]\le \frac{1}{\min (m,n)}\left[{\theta }_A(1-{\theta }_A)+{\theta }_B(1-{\theta }_B)-2\rho \sqrt{{\theta }_A(1-{\theta }_A){\theta }_B(1-{\theta }_B)}\right]$$ (14)

$$\mathit{V\; ar}\left[{\widehat{\theta }}_A-{\widehat{\theta }}_B\right]\ge \frac{\max (B_i(m,n,{\theta }_A),B_i(m,n,{\theta }_B))}{\mathit{mn}}\times \left[{\theta }_A(1-{\theta }_A)+{\theta }_B(1-{\theta }_B)-2\rho \sqrt{{\theta }_A(1-{\theta }_A){\theta }_B(1-{\theta }_B)}\right]$$ (15)

The maximum of the B_i’s is required in the first term of the RHS of equation (15) because (10) must hold for both modalities. These bounds are achievable, but hold only when the cluster correlations are equal across modalities. Upper bounds (12) and (14) are equal when ρ = 0.

4 Sample Size Projections for a Single AUC

To bound the projected sample size, we substitute the maximum and minimum variance from (7) for V (θ̂) in (4) and (5) and solve. The idea is to find the smallest sample size that will meet the statistical planning criteria in every model, call it n_max and the smallest sample size that will meet the statistical criteria for some model, call it n_min. Any projected sample size must then be less than or equal to n_max and greater than or equal to n_min. These limits reveal the range of potential sample sizes, which we can use to address the projection’s sensitivity to violations of assumptions.

Substituting the maximum variance for V (θ̂) yields the smallest sample size that achieves a (1 − α)100% CI of at most length L in every model. This upper bound for projected sample sizes is,

$$n_{\mathit{max}}=\min (m,n)=4{\left(Z_{\alpha /2}\right)}^2\frac{\theta (1-\theta )}{L^2}$$ (16)

The smaller of the normal and abnormal groups must be at least n_max to guarantee that a (1 − α)100% CI will have length L or less. There is no model under which n_max would result in a (1 − α)100% CI with length greater than L.

Substituting the minimum variance for V (θ̂) yields the smallest sample size that could possibly achieve a (1 − α)100% CI of length L. The lower bound for projected sample sizes is the solution to

$$\frac{\mathit{nm}}{B_i(m,n,\theta )}=4{(Z_{\alpha /2})}^2\frac{\theta (1-\theta )}{L^2}$$ (17)

where i = 1, 2 depending on (min(m, n) − 1)/(max(m, n) − 1) as noted eariler. This equation must be solved numerically for n_min. A useful device is to fix the ratio of group sizes, say k, so that m = kn and then solve for n. Here k = m/n is the ratio of normals to abnormals; typically k > 1. The solution, n_min, is the smallest sample size that could possibly yield a (1 − α)100% CI of length L. There is some model for which n_min would result in a (1 − α)100% CI with length L.

The same logic applies for power calcualtions: just substitute the maximum and minimum variance from (7) for V (θ̂) in (5). Numerical solutions are again needed to solve for n_min, but an analytical expression exists for n_max:

$$n_{\mathit{max}}=\min (m,n)=\frac{{\left(Z_{\beta }\sqrt{{\theta }_1(1-{\theta }_1)}+Z_{\alpha /2}\sqrt{{\theta }_0(1-{\theta }_0)}\right)}^2}{{({\theta }_1-{\theta }_0)}^2}$$ (18)

The smaller of the normal and abnormal groups must be at least n_max to guarantee at least (1 − β) power to detect θ₁ under any model. With n_min, there is at least one model under which there is (1 − β) power to detect θ₁. Simply put, at least n_min observations will be required to achieve (1 − β) power, but up to n_max observations may be needed.

EXAMPLE 1a: An investigator guesses that the AUC for a new diagnostic assay will be 85% and he would like to estimate that AUC within a margin of error of 5% (i.e., L = 0.1) from a 95%CI. Equal numbers of disease and non-diseased participants will be recruited. The maximum projection is 196 participants in both groups and the lower projection is at least 101 participants per group. (Here, i = 2 and B₂(101, 101, 0.85) = 51.62 so that the LHS of (17) is 197.61, which is the closest to 195.91=RHS without going below). Under the equal variance binormal model we project 151 participants per group and under the biexponential model we need 117 per group. The biexponential model appears quite optimistic. The maximum projections require 30% more participants than the binormal and 68% more than the biexponential.

EXAMPLE 1b: An investigator wants to test the hypothesis that the accuracy of a new diagnostic assay is 0.8. She believes recent improvements will increase the accuracy to 0.9 and she wants to have 80% power to detect this difference with 5% Type I error. If the ratio of normals to abnormals is 1:1 (i.e., k=1), then she requires at least 58 abnormal participants, but no more than 108. The binormal model suggests 81 abnormal and the biexponential models suggests 66. But if 2 normals are enrolled for every abnormal (i.e., k=2), then the binormal models suggests only 66 abnormal and the biexponential only 57. Now the projection bounds indicate that at least 39 abnormals are required, but no more than 108 are needed. Remember that the maximum bound depends only on the smaller of the two groups. (Here, i = 2 for all cases. When k = 1, B₂(58, 58, 0.8) = 22.06, $\sqrt{V(0.8)}=0.0393$, B₂(58, 58, 0.9) = 17.73, $\sqrt{V(0.9)}=0.0264$; when k = 2, B₂(78, 39, 0.8) = 29.27, B₂(78, 39, 0.9) = 24.06, $\sqrt{V(0.8)}=0.0392$ and $\sqrt{V(0.9)}=0.0267$. Substituting these into (5) gives 1 − β ≈ 0.807 in both cases.)

4.1 Multiple Readers and their Average AUC

Sometimes the outcome of a diagnostic test must be interpreted by a ‘reader’. For example, X-rays and MRI scans require the interpretaion of a reader. But two readers may score the same test result, in this case an image, differently. This disagreement ultimately results in different ROC curves for each reader and introduces a source of variability that is not due to the diagnostic test itself. (This framework also applies to multicenter trials when the outcome of an ‘objective’ diagnostic test for the same case may vary as it is evaluated at each site.) The primary interest in a multireader design such as this is no longer each reader’s AUC, but instead the average reader AUC.

A sample of test outcomes for the r^th reader (r = 1, … , R readers) will be represented as X_r1, X_r2, … , X_rm and Y_r1, Y_r2, … , Y_rn with CDFs F_r and G_r. Each reader’s AUC is θ_r = P(X_r < Y_r). Its empirical estimate is ${\widehat{\theta }}_r=\frac{1}{\mathit{mn}}{\sum }_{i=1}^m{\sum }_{j=1}^n{Z}_{\mathit{rij}}$ where Z_rij = I(X_ri < Y_rj), i = 1, … , m, j = 1, … , n and the variance of θ̂_r depends on θ_r, ρ _ry and ρ_rx.

In the design stage, it is not unreasonable to assume that readers are exchangeable in the sense that they have the same true accuracy and cluster correlation parameters. That is, θ_r = θ, ρ_ry = ρ_y and ρ_rx = ρ_x for all r. Then, the obvious empirical estimate of θ is, $\widehat{\theta }.=\frac{1}{R}{\sum }_{r=1}^R{\widehat{\theta }}_r$ and V ar [θ̂_r] does not depend on r by assumption. Then

$$\mathit{V\; ar}\left[\widehat{\theta }.\right]=\frac{1}{R^2}\mathit{Cov}\left[\sum _{r=1}^R{\widehat{\theta }}_r,\sum _{s=1}^R{\widehat{\theta }}_s\right]=\mathit{V\; ar}\left[\widehat{\theta }\right]\left[\frac{1}{R}+\frac{R-1}{R}{\rho }_{\mathit{dr},\mathit{sm}}\right]$$ (19)

where ρ_dr,sm is the correlation between different readers on the same modality (typically ρ_dr,sm > 0). Note that V ar [θ̂] is the term we have been bounding and estimating under different models.

Equation (19) shows that including multiple readers deflates the variance by [1/R + ρ_dr,sm(R − 1)/R]. Therefore, accounting for multiple readers amounts to nothing more than deflating the projected sample sizes (and bounds) by the same factor. That is, the new upper bound is $n_{\mathit{max}}^{\prime }=n_{\mathit{max}}\times [1/R+{\rho }_{\mathit{dr},\mathit{sm}}(R-1)/R]$ and the new lower bound is $n_{\mathit{min}}^{\prime }=n_{\mathit{min}}\times [1/R+{\rho }_{\mathit{dr},\mathit{sm}}(R-1)/R]$. Likewise for projections under the binormal and biexponential models. For example, with 4 readers and ρ_dr,sm = 0.3, the projections are reduced by a factor of 0.475. In example 1a, this means the maximum reduces to 94, the lower to 48, the binormal to 72, and biexponential to 56. The same applies for the power projections in example 1b.

4.2 Efficiency Considerations

The loss in efficiency incurred when using the maximum sample size projection depends on the true underlying model. The maximum potential increase in sample size, over all models, is (n_max/n_min − 1)100%. In example 1a, the potential increase in sample size is 94.1%. However, this maximum is only achieved if the true underling model happens to yield the smallest possible variance for the empirical AUC estimator. This is unlikely. A more realistic approach is to compare the maximum sample size to that obtained under the two most commonly assumed models: the biexponential and binormal. In example 1a, we saw that the increase in sample size was 68% and 30%.

To illustrate, we assume k = m/n ≥ 1, which is most common in practice and compare the sample sizes required to provide a confidence interval of length L. The ratios of projected sample sizes for the maximum versus binormal and maximum versus biexponential are

$$\frac{n_{\mathit{max}}}{n_{\mathit{nor}}}=\frac{\theta (1-\theta )}{\left(0.0099\times \exp \left\{-A^2/2\right\}\right)\times \left(5A^2+8+\frac{A^2+8}{k}\right)}$$ (20)

and

$$\frac{n_{\mathit{max}}}{n_{\mathit{exp}}}=\frac{k}{\frac{1-\theta }{2-\theta }+k\frac{\theta }{1+\theta }}$$ (21)

For the biexponential model we use an approximation to the variance to obtain a closed form expression for the sample size ratio. Namely V ar [θ̂] ≈ θ(1 − θ)(ρ_y + kρ_x)/nk, which just assumes that 1/kn² is zero.

Figure 1 displays these ratios as a function of the area under the curve, θ ∈ [0.5, 1], and k ∈ {1, 2, 3}. For large values of the AUC the sample size ratio for the binormal model approaches infinity. This is an artifact of the Taylor series approximation; under both models the variance of the AUC estimator converges to zero as θ approaches 1, but the binormal convergence is (exponentially) faster. Hence the appearance of greatly increased efficiency at extremely high AUCs. The figure indicates that if the underlying model is exponential then the maximum sample size represents an increase ranging from 50%-100% when k=1. Under the equal variance binormal model the smallest sample size ratio is approximately 1.3. It is known that the biexponential model tends to give sample sizes that are too small [20, 32] and Figure 1 indicates that those sample size projections can be quite optimistic (i.e., half of the maximum possible). However, using a binormal model that assumes equal variance may not be much better.

Figure 1.

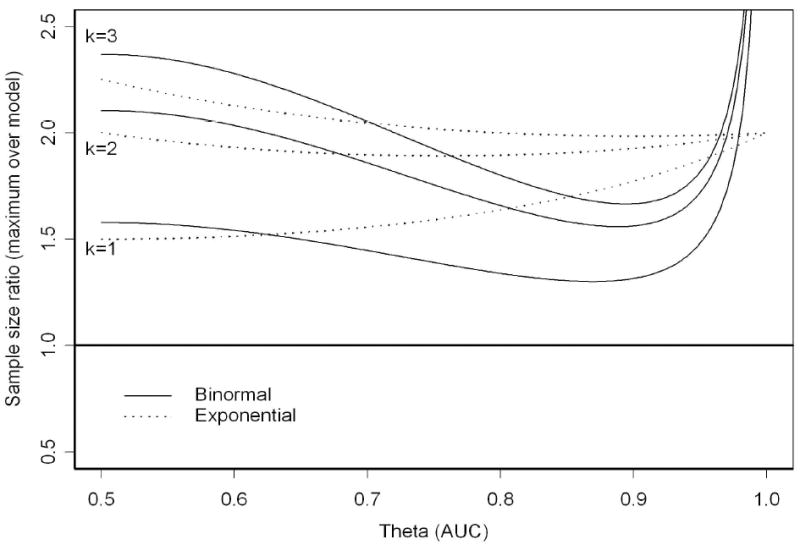
Sample Size Ratios

While the inclusion of multiple readers does not change these considerations, the resulting standard errors will be much smaller and consideration of their absolute magnitude is very important. Table 1 provides some examples of standard errors for comparison. The absolute loss in efficiency is quite small and the difference can be mediated by adding readers.

Table 1.

Comparison of Multireader Standard Errors on θ̂_A

ρdr,sm = 0.33			Multireader Standard Errors of θ̂A
θA	raters	(m, n)	Lower Bound	Exponential	Binormal	Upper Bound
0.70	3	(50,100)	0.0306	0.0320	0.0340	0.0482
		(100,100)	0.0269	0.0274	0.0283	0.0341
		(200,300)	0.0169	0.0172	0.0181	0.0241
0.70	6	(50,100)	0.0274	0.0286	0.0304	0.0431
		(100,100)	0.0240	0.0245	0.0253	0.0305
		(200,300)	0.0151	0.0153	0.0162	0.0215
0.70	9	(50,100)	0.0262	0.0273	0.0291	0.0412
		(100,100)	0.0230	0.0234	0.0242	0.0291
		(200,300)	0.0144	0.0147	0.0155	0.0206
0.80	3	(50,100)	0.0257	0.0264	0.0303	0.0421
		(100,100)	0.0222	0.0233	0.0257	0.0298
		(200,300)	0.0140	0.0143	0.0162	0.0210
0.80	6	(50,100)	0.0230	0.0236	0.0270	0.0376
		(100,100)	0.0199	0.0208	0.0230	0.0266
		(200,300)	0.0125	0.0128	0.0145	0.0188
0.80	9	(50,100)	0.0220	0.0225	0.0259	0.0360
		(100,100)	0.0190	0.0199	0.0220	0.0254
		(200,300)	0.0120	0.0123	0.0139	0.0180
0.90	3	(50,100)	0.0175	0.0182	0.0223	0.0316
		(100,100)	0.0149	0.0168	0.0195	0.0223
		(200,300)	0.0094	0.0101	0.0121	0.0158
0.90	6	(50,100)	0.0156	0.0162	0.0199	0.0282
		(100,100)	0.0133	0.0150	0.0174	0.0199
		(200,300)	0.0084	0.0090	0.0108	0.0141
0.90	9	(50,100)	0.0149	0.0155	0.0191	0.0270
		(100,100)	0.0127	0.0144	0.0166	0.0191
		(200,300)	0.0081	0.0086	0.0103	0.0135

5 Sample Size Projections for Comparing Two AUCs

The goal of many studies is to compare the accuracy of two tests by comparing their AUCs. The approach for this case is similar to that already outlined concerning a single AUC; we substitute for V ar[θ̂ _A − θ̂_B] its bounds in the two-sample versions of equations (4) and (5) to derive the bounds on the projected sample size. The only caveat is that there are two sets of bounds to choose from: The strict (and sometimes unachievable) bounds or the (achievable) bounds that assume equal cluster correlations across modalities. We assume throughout the same ratio of abnormal to normals for each modality (e.g., when both tests are run on each subject or when both tests drawn from the same global population).

Most of these calculations must be done numerically, substituting the bounds for the actual variance. However, if we are willing to assume equal cluster correlations, the upper bound on the projected sample size for a CI is

$$n_{\mathit{max}}=\min (m,n)=4\frac{{\left(Z_{\alpha /2}\right)}^2}{L^2}\left[{\theta }_A(1-{\theta }_A)+{\theta }_B(1-{\theta }_B)-2\rho \sqrt{{\theta }_A(1-{\theta }_A){\theta }_B(1-{\theta }_B)}\right]$$ (22)

Thus, a minimum of n_max observations in each groups will gaurantee a (1 − α)100% CI of length L as long as cluster correlations are equal across modalities. Likewise the sample size that provides 1 − β power for a α-sized hypothesis test of H₀ : Δ₀ = θ_A0 − θ_B0 versus H₁ : Δ₁ = θ_A1 − θ_B1 is given by the solution to

$$\beta =\mathrm{\Phi }\left[Z_{\alpha /2}\frac{\sqrt{V_0}}{\sqrt{V_1}}+\frac{{\mathrm{\Delta }}_0-{\mathrm{\Delta }}_1}{\sqrt{V_1}}\right]$$ (23)

where V_i = V ar[θ̂_Ai − θ̂_Bi]. The upper bound on the sample size projection is the solution to this equation when V_i is replaced with (12) (or (14) if we are willing to assume equal correlations), while the lower bound is the solution when V_i replaced with (13) (or (15) if we are willing to assume equal correlations). The binormal or biexponential models can also be used calculate V_i via equations (11) and (2).

EXAMPLE 2a: Two assays are to be compared. Equal numbers of normal and abnormal participants are available (i.e., k=1) and each participant will undergo both assays (say with ρ = 0.3). An investigator guesses that the AUCs for assays A and B are 0.7 and 0.8 and would like a 95% CI on their difference to have a margin of error of 0.075 (i.e., length of 0.15). The maximum sample size is 209 abnormals or 178 if equal cluster correlations can be assumed. The minimum sample size is 76 abnormals or 111 if equal cluster correlations can be assumed. Projections under the biexponential and binormal model give 113 and 127 abnormals, respectively. Compared with the bounds these projections appear optimistic.

EXAMPLE 2b: Same situation as example 2a, but the investigator wishes to conduct a hypothesis test against the null hypothesis that the two assays have equal accuracy of 0.7. With 80% power and 5% type I error, the maximum sample size is 260 abnormals or 223 if equal cluster correlations can be assumed. The minimum sample size is 101 abnormals or 139 if equal cluster correlations can be assumed. Projections under the biexponential and binormal model give 143 and 156, respectively. Here as well the binormal and biexponential models appear optimistic.

A practical approach to balancing efficiency and robustness concerns might be to choose the sample size given from the lower upper bound (i.e., assume equal cluster correlations) or to select the midpoint of the sample size range (143 in example 2a and 181 in example 2b).

5.1 Multiple Readers and the Average Difference in AUCs

The arguments of §4.1 apply here directly. The empirical difference in average reader AUCs is ${\widehat{\theta }}_{A.}-{\widehat{\theta }}_{B.}=\frac{1}{R}{\sum }_{r=1}^R({\widehat{\theta }}_{\mathit{Ar}}-{\widehat{\theta }}_{\mathit{Br}})=\frac{1}{R}{\sum }_{r=1}^R{\widehat{\theta }}_{\mathit{dr}.}$ Note the V ar [θ̂_dr] does not depend on r because of our common accuracy and common cluster correlation assumption. Then we have

$$\begin{array}{ll}\mathit{V\; ar}\left[{\widehat{\theta }}_A.-{\widehat{\theta }}_B.\right]& =\frac{1}{R^2}\mathit{Cov}\left[\sum _{r=1}^R{\widehat{\theta }}_{\mathit{dr}},\sum _{s=1}^R{\widehat{\theta }}_{\mathit{ds}}\right]\\ & =\frac{1}{R}\left[\mathit{V\; ar}\left[{\widehat{\theta }}_{\mathit{dr}}\right]+(R-1)\mathit{Corr}\left[{\widehat{\theta }}_{\mathit{dr}},{\widehat{\theta }}_{\mathit{ds}}\right]\sqrt{\mathit{V\; ar}\left[{\widehat{\theta }}_{\mathit{dr}}\right]\mathit{V\; ar}\left[{\widehat{\theta }}_{\mathit{ds}}\right]}\right]\\ & =\mathit{V\; ar}\left[{\widehat{\theta }}_A-{\widehat{\theta }}_B\right]\left[\frac{1}{R}+\frac{R-1}{R}{\rho }_{\mathit{dr},\mathit{diff}}\right]\end{array}$$ (24)

Here ρ_dr,diff represents the correlation between different readers on the difference in AUC estimates. That is, it is the correlation of the empirical AUC differences among the readers. Also, the quantity ρ from §5 will now be denoted by ρ_sr,dm (the correlation between the same reader on different modalities). Just like before, accounting for multiple readers amounts to nothing more than deflating the projected sample sizes and bounds. That is, the new upper bound is $n_{\mathit{max}}^{\prime }=n_{\mathit{max}}\times [1/R+{\rho }_{\mathit{dr},\mathit{diff}}(R-1)/R]$ and the new lower bound is $n_{\mathit{min}}^{\prime }=n_{\mathit{min}}\times [1/R+{\rho }_{\mathit{dr},\mathit{diff}}(R-1)/R]$. Likewise for projections under the binormal and biexponential models.

5.2 Relationship to other Multireader Projections

Multireader designs typically specify three different correlation parameters: ρ₁ (ρ_sr,dm in our notation), the correlation between AUCs estimated by the same reader but in two different modalities; ρ₂ (ρ_dr,sm in our notation), the correlation between AUCs estimated by different readers in the same modality; and ρ₃ (ρ_dr,dm in our notation) is the correlation between AUCs estimated by different readers in different modalities [21, 28]. So far, we have only encountered ρ_sr,dm and ρ_dr,diff, but all are related. Expanding Cov[θ̂_dr, θ̂_ds] shows

$${\rho }_{\mathit{dr},\mathit{diff}}=\frac{\left[\mathit{V\; ar}\left({\widehat{\theta }}_{\mathit{Ar}}\right)+\mathit{V\; ar}\left({\widehat{\theta }}_{\mathit{Br}}\right)\right]{\rho }_{\mathit{dr},\mathit{sm}}-2{\rho }_{\mathit{dr},\mathit{dm}}\sqrt{\mathit{V\; ar}\left({\widehat{\theta }}_{\mathit{Ar}}\right)\mathit{V\; ar}\left({\widehat{\theta }}_{\mathit{Br}}\right)}}{\mathit{V\; ar}\left({\widehat{\theta }}_{\mathit{Ar}}\right)+\mathit{V\; ar}\left({\widehat{\theta }}_{\mathit{Br}}\right)-2{\rho }_{\mathit{sr},\mathit{dm}}\sqrt{\mathit{V\; ar}\left({\widehat{\theta }}_{\mathit{Ar}}\right)\mathit{V\; ar}\left({\widehat{\theta }}_{\mathit{Br}}\right)}}$$ (25)

This relationship depends on both group sample sizes, (m, n), through V ar(θ̂), although this expression is O_p(1). When the true variances are in doubt (as is often the case) this relationship cannot be calculated. However, the biexponential model can be used to calculate the variances for comparison purposes.

Traditional approaches to multireader studies are based on a random effects ANOVA model that works with the reader specific AUC estimates (see [31, 21, 28]). While these ANOVA models may apply in principle to any large sample situation, they fail to incorporate distributional assumptions that enter through the variance. Not unexpectedly, these projections are highly sensitive to assumptions about the components of variance. Obuchowski [21] shows that the ANOVA variance for the difference between two AUC estimates is

$$\mathit{V\; ar}\left({\widehat{\theta }}_A.-{\widehat{\theta }}_B.\right)=\frac{2}{R}\left[{\sigma }_b^2(1-{\rho }_b)+\frac{{\sigma }_w^2}{J}+{\sigma }_c^2\left[1-{\rho }_1+(R-1)({\rho }_2-{\rho }_3)\right]\right]$$ (26)

where ${\sigma }_b^2$ is the between reader variability; ${\sigma }_w^2$ is the within reader variability; ${\sigma }_c^2$ is variability due to cases; ρ_b is the correlation between AUCs estimated by a set of readers under two different modalities; the correlation parameters ρ₁, ρ₂, ρ₃, discussed earlier; and J is the number of replications (almost always J = 1). Technically, this ANOVA variance is unconstrained and can produce standard errors much larger (or smaller) than even the absolute upper (or lower) bound established earlier. However one vetted set of estimates from the radiology literature is: ${\sigma }_b^2=0.00104$, ${\sigma }_w^2=0.0001$, ρ_b = 0.82, ρ₁ = 0.44, ρ₂ = 0.33, ρ₃ = 0.29 [21]. The last component of variance ${\sigma }_c^2$ is estimated as (V ar [θ̂_A ] + V ar [θ̂_B ])/2 assuming an biexponential model [21].

For illustrative purposes, table 2 displays multireader standard errors under the ANOVA model with the components of variance identified above and our bounds, under a variety of conditions and sample sizes with five readers. The ANOVA standard errors under this set of variance components fairs well for moderate sample sizes. They are close to the sharp lower bound for smaller sample sizes and in some cases exceed the upper bounds (see table 2). Of course, small changes in the assumptions about the variance components (e.g., say ${\sigma }_w^2=0.001$ or ${\sigma }_b^2=0.0001$) often cause relatively large changes in the ANOVA standard errors. While these results are not generalizable, they most likely represent the best case scenario for the ANOVA method (because we have chosen vetted estimates of the variance components from the literature etc.). The point is that even if the variance components and correlations are chosen wisely, the standard errors could still be too large or too small.

Table 2.

Comparison of Multireader Standard Errors of θ̂_A − θ̂_B with 5 readers and σ_b² = 0.00104, σ_w² = 0.00012;

ρ1 = 0.44, ρ2 = 0.33, ρ3 = 0.29				Multireader Standard Errors of θ̂A − θ̂B for 5 Readers
θA	θB	(m, n)	ρdr,diff	Lower Bound	LB**	ANOVA	UB**	Upper Bound
0.60	0.50	(50,100)	0.072	0.0000	0.0243	0.0284	0.0376	0.0454
		(100,100)	0.072	0.0168	0.0217	0.0242	0.0266	0.0299
		(400,500)	0.072	0.0067	0.0102	0.0148	0.0133	0.0153
0.60	0.55	(50,100)	0.072	0.0000	0.0242	0.0282	0.0375	0.0453
		(100,100)	0.072	0.0167	0.0216	0.0241	0.0265	0.0298
		(400,500)	0.072	0.0067	0.0101	0.0148	0.0133	0.0153
0.75	0.70	(50,100)	0.073	0.0000	0.0216	0.0246	0.0339	0.0412
		(100,100)	0.072	0.0132	0.0189	0.0219	0.0240	0.0274
		(400,500)	0.073	0.0050	0.0089	0.0139	0.0120	0.0140
0.85	0.80	(50,100)	0.077	0.0000	0.0178	0.0207	0.0291	0.0356
		(100,100)	0.075	0.0087	0.0153	0.0191	0.0205	0.0239
		(400,500)	0.076	0.0027	0.0072	0.0130	0.0103	0.0122
0.90	0.80	(50,100)	0.100	0.0000	0.0174	0.0195	0.0284	0.0346
		(100,100)	0.094	0.0081	0.0149	0.0182	0.0199	0.0233
		(400,500)	0.096	0.0025	0.0070	0.0127	0.0100	0.0119
0.90	0.85	(50,100)	0.082	0.0000	0.0151	0.0183	0.0256	0.0315
		(100,100)	0.080	0.0054	0.0129	0.0173	0.0180	0.0213
		(400,500)	0.081	0.0000	0.0061	0.0124	0.0090	0.0108

^**Indicates bound assumes equal correlation across modalitites.

6 Considerations for Pooled AUCs

It might be of interest to assess the accuracy of the entire population of readers, taken as a single unit. In this case, we are interested in how the group of readers performs as a whole and so the focus is on the AUC that results from pooling data across all readers. This is interesting when there is little variability from reader to reader e.g., when the ‘readers’ are actually an objective test, such as a blood test preformed at different centers.

A sample of test outcomes for the r^th reader (r = 1, … , R readers), under modality A, will be represented as X_Ar1, X_Ar2, … , X_Arm and Y_Ar1, Y_Ar2, … , Y_Arn with CDFs F_Ar and G_Ar respectively and AUC θ_Ar = P(X_Ar < Y_Ar). An additional level is added to account for the population of readers. For outcomes from the ‘non-diseased’ population let F_Ar(X) = F_A(X; α_r) be the reader specific CDF where α_r has CDF H_A(α_r). Then the individual scores, X_A, have CDF $F_A(X)={\int }_{-\infty }^X\int f_A(z;{\alpha }_r){\mathit{dH}}_A({\alpha }_r)\mathit{dz}$. The key insight here is that this model considers all of the X’s as being generated from a single population of ‘non-diseased’ scores comprised from all readers. The one caveat is the this model assumes that all readers operate on the same scoring scale, while the analysis of average reader AUCs in the previous section does not.

For the ‘diseased’ population, we have Y_Ar with CDF G_Ar(Y) = G_A(Y ; β_r) where β_r has CDF W_A(β_r). Because H_A(α_r) and G_Ar(Y) = G_A(Y ; β_r) are not necessarily equal, reader variability may differ depending on the population being scored, even though the readers remain constant. The resulting convolution is $G_A(Y)={\int }_{-\infty }^Y\int g_A(z;{\beta }_r)d{W}_A({\beta }_r)\mathit{dz}$. The AUC for modality A is θ_A = P(X_Ak < Y_Al) (without reader subscript). As expected, the population AUC is a weighted average of the reader specific AUCs, but the weights don’t add to one (see the appendix for details and an example).

The pooled AUC is estimated by ${\widehat{\theta }}_A={\sum }_{k=1}^{\mathit{Rm}}{\sum }_{l=1}^{\mathit{Rn}}{Z}_{\mathit{Akl}}/R^2\mathit{mn}$ where Z_Akl = I(X_Ak < Y_Al) makes no distinction between readers. The variance of θ̂_A follows from (2). Now the bounds on sample size projections for comparing two AUCs (see §5) apply here by simply replacing m and n with mR and nR respectively. This is easily adapted to designs that are not fully factorial by replacing mR by Σ_rm_i and nR by Σ_rn_i, where r indexes the readers and m_i and n_i represent the number of non-diseased and diseased cases evaluated by rater i.

7 Comments

This paper outlines a method for bounding the projected sample sizes in studies that seek to estimate or compare the area under ROC curves. These bounds provide an important benchmark for assessing the sensitivity of projections to underling assumptions. The potential efficiency loss from designing a study with the maximum sample size projection must be balanced against the potential for not achieving the desired statistical objective. In multireader studies, this efficiency loss can be offset by adding readers. In other situations, the midpoint of the sample size range may represent an acceptable balance between efficiency and robustness. Small studies or studies collecting an unequal number of disease and non-diseased cases could substantially benefit from making some sort of distributional assumption, if that assumption is indeed correct. However, in multireader studies, the absolute efficiency difference is often quite small (because the standard errors themselves are already very small), so there appears to be little advantage to making these distributional assumptions. Overall, these bounds provide a nice complement to any model based approach.

A Appendix

The population AUC, θ, that is derived from pooling data across readers is a weighted average of the reader specific AUCs, θ_r(α_r, β_r).

$$\begin{array}{ll}\theta & ={\int }_{S}G(S)f(S)\mathit{dS}\\ & ={\int }_S{\int }_{-\infty }^S{\int }_{{\beta }_r}g(Y_S;{\beta }_r)w({\beta }_r)d{\beta }_{r}d{Y}_S{\int }_{{\alpha }_r}f(S;{\alpha }_r)h({\alpha }_r)d{\alpha }_r\mathit{dS}\\ & ={\int }_{{\alpha }_r}h({\alpha }_r){\int }_S{\int }_{-\infty }^S{\int }_{{\beta }_r}g(Y_S;{\beta }_r)w({\beta }_r)d{\beta }_{r}d{Y}_{S}f(S;{\alpha }_r)\mathit{dSd}{\alpha }_r\\ & ={\int }_{{\alpha }_r}{\int }_{{\beta }_r}h({\alpha }_r)w({\beta }_r){\int }_S{\int }_{-\infty }^{S}g(Y_S;{\beta }_r)d{Y}_{S}f(S;{\alpha }_r)\mathit{dSd}{\alpha }_{r}d{\beta }_r\\ & ={\int }_{{\alpha }_r}{\int }_{{\beta }_r}h({\alpha }_r)w({\beta }_r){\theta }_r({\alpha }_r,{\beta }_r)d{\alpha }_{r}d{\beta }_r\end{array}$$

While ∫_αr h(α_r)dα_r = ∫_βr, w(β_r)dβ_r = 1, in general, ∫_αr ∫_βr h(α_r) w(β_r)dα_rdβ_r ≠ 1. Hence θ is a weighted average of the reader specific AUCs, but the weights do not necessarily add to one. This allows θ to take values beyond the range of the reader specific AUCs. A similar situation is encountered in Sukhatme [29].

For an example of this model structure, consider the r^th reader under a Binormal model. We have that $X_{\mathit{ri}}|{\mu }_{\mathit{xr}}\sim N({\mu }_{\mathit{xr}},{\sigma }_x^2)$ and $Y_{\mathit{rj}}|{\mu }_{\mathit{yr}}\sim N({\mu }_{\mathit{yr}},{\sigma }_y^2)$. Variability in the population of readers is characterized by ${\mu }_{\mathit{xr}}\sim N({\mu }_x,{\tau }_x^2)$ and ${\mu }_{\mathit{yr}}\sim N({\mu }_y,{\tau }_y^2)$, resulting in a model that implies $X_k\sim N({\mu }_x,{\sigma }_x^2+{\tau }_x^2)$ where k = 1, … , Rm and $Y_l\sim N({\mu }_y,{\sigma }_y^2+{\tau }_y^2)$ where l = 1, … , Rn. The accuracy for this group of readers is

$$P(X_k<Y_l)=\mathrm{\Phi }\left[\frac{{\mu }_y-{\mu }_x}{\sqrt{({\sigma }_y^2+{\tau }_y^2)+({\sigma }_x^2+{\tau }_x^2)}}\right]$$

Thus the accuracy of the group may be significantly less than any individual reader depending on the magnitude of $({\tau }_x^2+{\tau }_y^2)$.