Dropwise condensation

Abstract

Dropwise condensation of water vapor from a naturally cooling, hot water reservoir onto a hydrophobic polymer film and a silanized glass slide was studied by direct observation and simulations. The observed drop growth kinetics suggest that smallest drops grow principally by the diffusion of water adsorbed on the substrate to the drop perimeter, while drops larger than 50 μm in diameter grow principally by direct deposition from the vapor onto the drop surface. Drop coalescence plays a critical role in determining the drop size distribution, and stimulates the nucleation of new, small drops on the substrates. Simulations of drop growth incorporating these growth mechanisms provide a good description of the observed drop size distribution. Because of the large role played by coalescence, details of individual drop growth make little difference to the final drop size distribution. The rate of condensation per unit substrate area is especially high for the smallest drops, and may help account for the high heat transfer rates associated with dropwise condensation relative to filmwise condensation in heat exchange applications.

1. Introduction

Many everyday interactions between water vapor and relatively cool, hydrophobic surfaces produce intriguing patterns of condensed drops with a variety of sizes. Breathing on contaminated glass surfaces, or surfaces given hydrophobic surface treatments, can produce a fog of tiny drops, giving the glass a frosted appearance. In contrast, breathing on very clean (hydrophilic) glass produces a thin film of water, leaving the glass transparent. These “breath figures” have long been used to test the cleanliness and uniformity of glass surfaces.¹ The contrasting behavior of hydrophilic and hydrophobic glass illustrates the important role of substrate properties (here, contact angle) on the behavior of condensed water.

Drop nucleation and coalescence are everyday phenomena. Figure 1a shows a high density of relatively uniform drops formed on the inner surface of a coffee cup lid after brief exposure to vapor. With prolonged exposure, growing drops contact and coalesce to produce an intricate pattern of relatively uniform large drops and much smaller drops in between, as shown in Fig. 1b. Similar patterns appear on plastic wrap used to cover containers with warm leftovers in the refrigerator or (later) reheated in a microwave oven (Fig. 1c). When viewed after removal, the surface is “alive” with activity: the dynamic process of drop coalescence continues vigorously long after heating has ceased and the liquid gradually cools.

Fig. 1.

Water drops condensed on a plastic coffee cup lid imaged (a) soon after the drops become visible and (b) after many cycles of coalescence and growth. (c) Similar water drops condensed on Saran® over water heated in a microwave.

Drop nucleation, growth, and condensation have important practical consequences. Significantly, heat transfer rates in dropwise condensation can be much higher than in filmwise condensation.^2,3 Thus dropwise condensation is often preferred to filmwise condensation in heat exchangers.^4,5 The more general problem of liquid drops interactions on surfaces is of interest for inkjet printing, pesticide application, and spray coating. The rhythmic growth and coalescence of water drops have also been used to construct micro-scale engines⁶ and to pattern sub-micron masks.^7-9

Drop growth and coalescence are affected by surface orientation and composition, vapor and surface temperatures, humidity, and vapor flow rate. Considerable work has focused on flowing moist air or steam directed against cool surfaces including silanized glass,^10-13 and polyethylene.¹⁴ Experiments with non-flowing vapor are less common.² Condensation in particular is strongly affected by the presence of non-condensable gases.

Substantial effort has also been directed to numerical simulations of drop growth and coalescence. However, the wide range of size and time scales involved can strain computational resources. Typically, one populates a computational grid with randomly placed drops and increases their size according to an empirical growth law. When adjacent drops touch, a new drop is formed at the common center of mass.^5,15,16 More complex simulations account for the continuous nucleation of drops,^17-19 sometimes with dynamical lattice rescaling.²⁰ To maintain computational tractability, simulations with more complex growth laws often limit the number of nucleation sites^21,22 or the duration of the simulation.²³

In this work we examine a naturally cooling system, with hydrophobic surfaces near room temperature (silanized glass and a commercial plastic wrap, polyvinylidene chloride) suspended over a vessel of initially hot, slowly cooling water in the presence of the ambient atmosphere. Our goal in part is to provide understanding of condensation relating to the commonplace observation of condensation over covered, cooling liquids, such as those observed in everyday life (covered hot drinks and containers in the kitchen). Under these conditions, drop growth is considerable slower than in most steady-state experiments, allowing for some phenomenon (e.g., coalescence-induced nucleation, vapor depletion around individual drops) that either do not occur under steady-state conditions, or occur too rapidly for convenient characterization. Cooling “stretches the time scale” of our measurements.

We focus on growth and coalescence from the time the drops become visible in our apparatus (radius ∼ 2 μm) through many generations of nucleation and coalescence, but before the drops grow large enough to fall from the surface. Measurements of the drop growth kinetics suggest that the smallest drops grow principally by the accretion of water molecules diffusing along the surface, while drops larger than 50 μm in diameter grow principally by the accretion of water vapor directly from the surrounding atmosphere. The resulting drop size distributions are strongly bimodal, with large drops and many much smaller drops, but few drops of intermediate size. We present indirect evidence that the atmosphere surrounding larger drops is somewhat depleted in water vapor relative to points farther away, and that this depletion hinders the nucleation of new drops on the adjacent surface. Implications for heat transfer are discussed.

To help clarify the mechanisms responsible for the resulting patterns of drop growth, we compare experimental drop size distributions with distributions computed from numerical simulations. These simulations incorporate the two growth mechanisms described above (accretion from the surface and from the atmosphere) with fluxes appropriate to the vapor above a cooling water bath. Coalescence is treated by replacing pairs of touching drops with a new drop of the same total volume, located at their mutual center of mass. A wide range of initial nucleation densities and subsequent nucleation rates are probed. Given modest initial and subsequent nucleation densities, the resulting drop-size distributions are amazingly insensitive to further increases in the nucleation densities. We attribute this insensitivity to the important role of coalescence in determining the drop-size distribution after many cycles of growth and coalescence.

2. Experiment

The condensation surface was generally a commercial grade polyvinylidene chloride (PVDC) film, more commonly known as Saran®, nominally 30 μm thick. For comparison, more strongly hydrophobic surfaces were prepared by treating glass slides with octadecyltrichlorosilane (OTS). Edge-on photographs of condensed drops showed contact angles of θ_water ≈ 60° for water on Saran® and θ_water ≈ 100° for water on OTS-coated glass. The film or glass was fastened with double-sided tape across a 5-cm hole in a clear plastic sheet (sample holder). To avoid wrinkles, the Saran® film was affixed under tension. A fresh surface was used for each experiment.

The condensation chamber was a 400-ml glass beaker filled with approximately four cm of water (∼130 ml). The beaker was preheated by rinsing with water at the desired temperature, filled with water at that temperature, covered, and mounted on a microscope stage. The cover was then replaced by the sample holder. Most experiments used water which was initially at the boiling point (∼97° C at our elevation), but lower initial temperatures were also employed. Drops were imaged from above while illuminated indirectly from below so that the drop edges were dark. All experiments were stopped before the pendant drops grew large enough to detach from the surface.

A digital still camera with a resolution of 1280 × 1024 pixels was used to image largescale patterns for measurements of drop size distributions. A microscope equipped with a CCD video camera with a resolution of 710 × 480 pixels at 30 frames per second was employed to monitor the growth of individual drops. Size scales were calibrated by imaging a TEM grid with known periodicity. The smallest measurable drops were ∼2 μm in radius.

Drop size distributions were determined with ImageJ — an image analysis package available from the US National Institute of Health. The software first identified the dark drop edges and then calculated the position and area of each drop in the image. Drop areas were converted to radii assuming circular geometries. Distribution functions were generated by binning these measurements into appropriate intervals.

Computer simulations of drop growth and coalescence were implemented in the C programming language and run on a Windows workstation. Simulations were initiated by positioning 0.5-μm drops randomly along the surface. Subsequent drop growth was modeled by assuming two sources of water, one proportional to the drop perimeter (i.e., accretion of adsorbed water molecules from the surrounding substrate surface) and another proportional to the drop surface area (i.e., accretion vapor from the gas phase). When the edges of two drops touched, a new drop was formed with the combined volume of the two coalescing drops, positioned at the center-of-mass of the pair. Details of the simulation are found in Appendix I.

2. Results

Initial Drop Densities

On substrates suspended over hot water, initial drop nucleation is very rapid. When they grow large enough to touch and coalesce, the number of these “first generation” drops begins to decrease. Log-log plots of experimental measurements of first generation drop densities are shown as a function of time in Fig. 2. The initial drop densities are close to 10⁶ cm^-2 for all but the lowest initial water temperatures. This corresponds to initial average drop separations of about 10 μm. Over 30° C water, the initial density is 10⁴-10⁵ cm^-2 and gradually increases before subsequently falling. This behavior reflects the relatively slow nucleation and growth expected at low water vapor pressures.^{5,15,16,18,24,25} At higher water temperatures, our time resolution was not sufficient to resolve this initial increase in drop density.

Fig. 2.

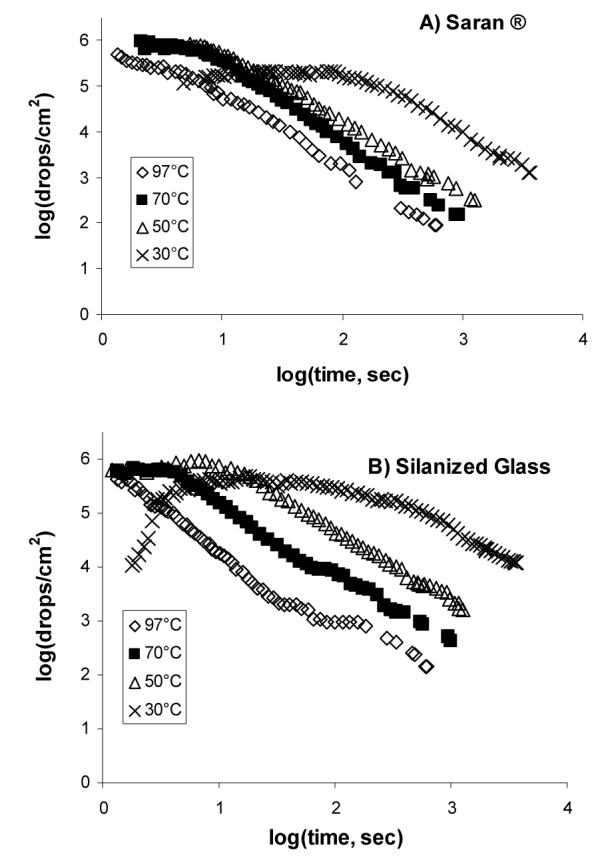
Densities of surviving, first generation drops on (a) Saran® and (b) OTS-treated glass, during condensation over water at four different temperatures. The decrease at longer time is due to coalescence.

The measured initial drop densities in Fig. 2 (10⁴-10⁶ cm^-2) are comparable to other published values of ∼10⁴-10⁸ cm^-2. Although some have observed higher nucleation densities at higher interfacial contact angles,²⁶ we observe no significant differences between Saran® (θ_water ≈ 60°) and silanized glass (θ_water ≈ 100°). Somewhat higher nucleation densities appear at higher water bath temperatures, consistent with previous work.¹⁴

After initial nucleation, the drop density remains nearly constant until the drops grow large enough to touch and coalesce. When initial nucleation is complete, the nucleation of new drops is hindered until the onset of coalescence, as discussed below. Since drop growth is faster at higher water vapor pressures, coalescence begins earlier at the higher bath temperatures, and at the highest temperature coalescence had already begun by the time the first images were acquired. After the onset of coalescence, the drop densities begin to fall in a power-law fashion. The power-law exponent for the decay of first generation drop density (the slope of the linear region of the log-log plot) for silanized glass varies smoothly from -1.2 at 30 °C to -1.7 at 97 °C. The power-law exponents on Saran® show a similar decrease, dropping from -1.0 at 30 °C to -1.3 at 97 °C.

Drop coalescence and nucleation

After the initial burst of nucleation, subsequent drop nucleation is hindered. Until the existing drops grow large enough to touch and coalesce, new drops are not observed. A series of video still frames showing a typical series of coalescence events in a mature stage of drop evolution is shown in Fig. 3. In this sequence of images, the four marked drops in Fig. 3a are the first to coalesce.

Fig. 3.

Video images of water drops on Saran® over water initially at 97°C. (a) Drops prior to coalescence; the drops to coalesce are marked with x’s. The arrow identifies a drop-free region where drops will be observed later. Time t = 0 corresponds to the acquisition of this image. (b) The same region during coalescence. (c) The next image, where drops to coalesce are marked with x’s. (d) The same region during coalescence and (e) after coalescence. (f) The same region seconds later, after newly nucleated drops become visible following coalescence. Some of these drops appear in the region marked in (a), which was drop-free prior to the coalescence events.

The image in Fig. 3b, acquired 33 ms after the image in Fig. 3a, appears to be double exposed because of the interleaving feature of the CCD camera. Each video image is composed of two interleaved images, one acquired 16.7 ms after the other; the first and second partial images are displayed in alternating lines. Interleaving allows motion to be displayed more smoothly. However, when the image changes significantly between the acquisition of the two interleaved images, the superimposed images show the drop positions at different times, as in Figs. 3b and 3d. Since such images were frequently observed, the duration of coalescence must often be shorter than the time between partial images, that is, less than 16.7 ms.

Images acquired before and after coalescence events (e.g., Figs. 3b and 3d) confirm that coalescing drops are centered at the center of mass of the original drops. Larger combined drops sometimes take a few seconds to achieve circularity, as in Figs. 3b and 3e, suggesting that the edges of the drops are weakly pinned by frictional forces.²⁶ However, these forces are not sufficient to alter the center-of-mass position or to distort the final, circular shape of the new drop (Fig. 3f).

After a coalescence event, small drops nucleate in nearby open spaces on the substrate. New drops continue to appear for a few seconds, after which time no new drops appear until another pair of nearby drops coalesce. For instance, the drop-free region marked by the arrow in Fig. 3a was formed 3.3 s before this image was acquired; this area remains free of new drops until 1.1 s after the coalescence event of Fig. 3b. The resulting new drops appear in Fig. 3f, acquired 2.4 s after coalescence. These new drops are observed both in areas exposed by the coalescence and in nearby exposed areas that have been free of drops for several seconds. Both are triggered by the coalescence event. Extrapolating drop size measurements back to zero for these newly nucleated drops suggests that nucleation takes place on time scales of less than 1 s after coalescence. Variations in nucleation time would help account for the small but significant variations in the size of newly formed drops (Fig. 3f).

As discussed below, we believe that the water vapor pressure along the substrate surface hinders nucleation of new drops prior to a coalescence event. The vapor pressure required for nucleation and initial drop growth is significantly higher than the equilibrium vapor pressure near the larger drops. For drops less than about 100 nm in radius, the high surface tension of water and high surface curvature significantly increases the equilibrium vapor pressure (Laplace pressure). Thus small drops can evaporate at water vapor pressures that cause large drops to grow. However, coalescence produces a transient increase in the vapor concentration along the surface, thereby triggering the dramatic nucleation and growth of new drops. The apparent delay in drop nucleation is attributed to the time required for the formation of stable (sufficiently large) drop nuclei.

In Fig. 3f, new drops rarely appear within 50 μm of pre-existing large drops, although new drops frequently are closer to each other. Normally nucleation within a band 20-50 μm wide around pre-existing drops is rare. This is consistent with the local depletion of diffusing water molecules near pre-existing drops both on the surface and in the gas phase. A similar effect reduces growth rates of closely-spaced drops and is described below. Significantly, nucleation-free zones around drops of deionized water placed on Saran® before initial exposure to water vapor are narrower, often only 10 μm wide. Prior to vapor exposure, the concentration of adsorbed water is quite low. Initial nucleation apparently occurs before diffusion can establish larger (> 10 μm) depletion zones around pre-existing drops.

The average densities of new drops after coalescence events range from 0.7 to 1.4 × 10⁵ drops/cm², corresponding to average drop separations of 25-40 μm. These nucleation densities are an order of magnitude lower than the initial nucleation densities, but the average drop separation is comparable to the width of the nucleation-free zones. The nucleation densities associated with coalescence events remain constant over the course of an experiment. However, lowering the temperature of the source water reduces the nucleation density associated with coalescence. At the lowest source temperature in this work (30 °C), almost no new drops appear after the initial burst of nucleation. Of course, source temperature decrease during the duration of the cooling experiment has exactly the same effect eventually terminating drop nucleation.

Coalescence has a profound effect on the distribution of drop sizes. Figure 4 shows a drop size distribution acquired from images taken with a still camera after many generations of coalescence and nucleation. In order to sample a large area, a relatively low magnification was used, so drops of less than about 0.2 mm radius were not be measured. Also displayed is a drop-size distribution from a computer simulation of drop growth and coalescence performed under comparable conditions. (Drops smaller than 0.2 mm are omitted from the simulated drop size distribution.) Two distinct peaks are observed. The peak at large radii is composed principally of survivors from the first generation of drops, nucleated at the beginning of the experiment. This first peak shifts to larger sizes with increasing time. The peak at smaller radii is composed of drops nucleated much later; although many of these smaller drops have experienced many coalescence events, they have never coalesced with a first generation drop. No evidence for additional, distinct drop populations is observed, either experimentally or in simulations. The agreement between experiment and the model is satisfying.

Fig. 4.

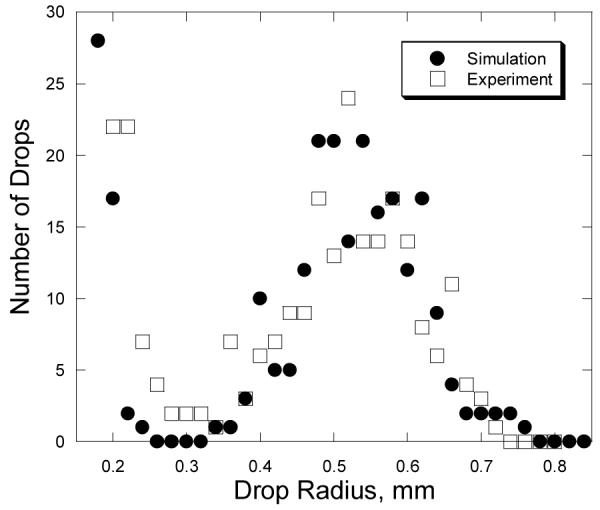
Drop size distributions from experiment (after 3000 s) and simulation (2300 simulation cycles) for drops condensed on Saran® over water with an initial temperature of 97 °C.

The average sizes of drops in the two populations of Fig. 4 evolve quite differently, as shown in Fig. 5, both experimentally and in our model. The mean radius of the small drop population grows very slowly after 2000 s. The small drop population apparently approaches a steady state: drops lost to the large drop population by coalescence are replaced by new nucleation and growth. In contrast, the mean radius of the large drop population continues to grow throughout the experiment—for at least 3000 s. This growth is driven in part by coalescence with other first generation survivors: as the number of drops in the large drop population decreases (See Fig. 2.), the average size of the remaining drops can only increase. This growth is supplemented by vapor adsorption and by coalescence with drops from the small drop population.

Fig. 5.

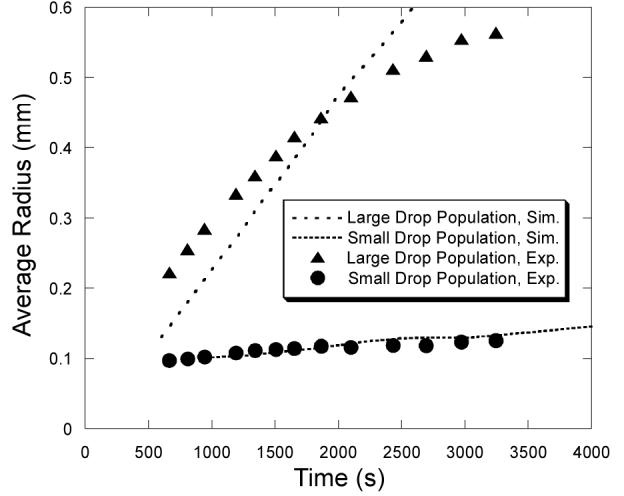
Average drop sizes for the two drop populations in Fig. 4, from experiment (dots) and from simulation (lines).

As seen n Fig. 5, the simulations account for the growth of the small drop population quite well, and qualitatively account for the growth of the large drop population. However, they fail to reproduce the sublinear increase (i.e., the functional dependence) in the average radius of the large drop population at long times. Our simulations consistently show linear growth in this population at all times. Given the good description of single-drop growth rates and coalescence rates in our model, the difference is most likely due to our treatment of nucleation.

To assess the sensitivity of our simulation to model parameters, the average size of first generation drops after 6000 cycles were compared over a range of assumed vapor fluxes and nucleation rates. The first generation drop radius varies linearly with the magnitude of the vapor flux over the probed range, as expected. Changes in the initial drop density have little effect on the average first generation drop radius. When subsequent nucleation is allowed in any open area, varying the initial drop density from one to 10⁶ drops/cm² has no significant effect. When subsequent nucleation is allowed only near coalescing drops, the initial nucleation density has some effect, but only at initial drop densities below 2 × 10⁴ drops/cm². Similar simulations in which the density of drops nucleated after initial nucleation is varied through a similar range show at most factor-of-two variations in the average size of first generation drops. This insensitivity to initial conditions is consistent with the results of previous modeling efforts.^5,15,17-19 It is also helps explain why our drop size distributions at long times are remarkably insensitive to many experimental variables.

Nucleation-free zones

The complex interaction between drops, substrates, and the surrounding atmosphere hinders nucleation in a thin band around existing drops. To investigate this effect, it is convenient to employ a system with a much larger nucleation-free zone. Williams and Blanc²⁷ reported 1-2 mm wide nucleation-free zones around drops formed when vapor condenses on a grain of salt. Figure 6 shows a Saran® surface with a drop of saturated salt solution on the left and a drop of pure water on the right—both placed on the surface before exposure to water vapor. When the Saran® is inverted over a hot water bath, white regions appear where small drops condense. Consistent with the results of Williams and Blanc, the salt water drop on the left shows a large, 3-5 mm wide nucleation-free zone. The nucleation-free zone around the pure water drop on the right cannot be observed at this magnification.

Fig. 6.

Drops of saturated salt solution (left) and deionized water (right) on Saran® suspended over a water bath with an initial temperature of 28 °C. Fine drops have condensed over much of the Saran® (bright region), except for a 3-5 mm band (droplet free) around the drop of saturated salt water (dark region).

The dramatic difference in the sizes of the nucleation-free zones in Fig. 6 is clearly associated with drop composition and not substrate composition. The effect of water vapor pressure was probed by repeating the experiment at different water bath temperatures. Measurements of the nucleation-free zone around the salt water drop as a function of the temperature difference between the bath and the substrate appear in Fig. 7. As the temperature difference increases, the width of the nucleation-free zones decreases dramatically. This is the opposite of what one would expect if the nucleation-free zone was associated with a ring (or “foot”) of adsorbed water around the base of the drop.

Fig. 7.

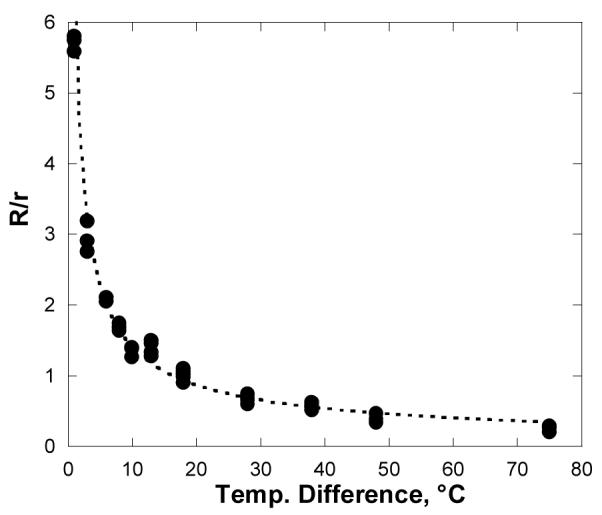
The ratio between the width of the dark region, R (nucleation-free zone), and the radius r of a drop of saturated salt solution, as a function of temperature difference. As in Fig. 6, the drops were suspended on Saran® over a warm water bath. The dotted line shows an empirical least square fit of a power law to the data: R/r ∼ 7(ΔT)^-0.7.

The large nucleation-free zone around the salt water drop is due to the lower equilibrium vapor pressure of water over concentrated salt solutions. The vapor pressure over a saturated NaCl solution at 100 °C is about 77% of the vapor pressure of pure water at the same temperature. When suspended over a hot water bath, the relatively low evaporation rate from the salt solution is associated with a relatively high net flux of vapor to the drop. In the absence of convection, this net flux is accommodated by diffusion, which requires a concentration gradient in the vapor near the surface. Thus the water vapor pressure is reduced near the salt water drop. In Fig. 6, this depletion is sufficient to prevent nucleation within 3-5 mm of the drop. As the vapor concentration near the drop is increased (by increasing the temperature of the water bath), the thickness of the depleted layer decreases, decreasing the width of the nucleation-free zone.

In the case of the pure water drop, the relatively high vapor pressure of pure water is associated with a relatively low net flux of water vapor to the drop. This results in a relatively small concentration gradient in the surrounding atmosphere and a much narrower nucleation-free zone. At water bath temperatures of 30-50 °C, the measured nucleation-free zones around pure water drops placed on the substrate before exposure to vapor were all in the 20-50 μm range. At higher water bath temperatures, the nucleation-free zones were too narrow for reliable measurement.

Surface Coverage

One statistic of interest in dropwise condensation is the fraction of the surface covered by drops. Surface coverage (droplet area/substrate area) increases as drops grow and nucleate, and decreases as drops coalesce. In both experiments on Saran® and simulations at a contact angle of 60°, surface coverages of 75-80% are typical. Surface coverages on silanized glass are somewhat less, typically about 60%. Using Monte Carlo techniques, Tanemura²⁸ has shown that random packing of uniform disks (drops) yields surfaces coverages up to 55%. Coverages greater than 55% require a distribution of drop sizes. Just before the onset of coalescence, when the dispersion of our drop radii is still small, our simulations yield surface coverages of about 55%, consistent with this geometric limit.

Drop Growth

Video measurements of the growth of individual drops show that the radial growth rate (dr/dt) between coalescence events is a strong function of drop size, where small drops grow more quickly than large drops. We were surprised to find that the growth rates for small drops in the earlier stages of an experiment are very close to the growth rates of drops of the same size observed later in the experiment, when the bath temperature is lower. Nevertheless, increasing the initial temperature of the water bath increases the drop growth rates. This apparently contradictory behavior may be related to the fact that both the vapor source and the condensation surface are allowed to cool.

To quantify the growth rates, drop size measurements were made from sequential images. Growth rates were then calculated from the slope of the best fit line through sets of seven consecutive points. In order to measure only single-drop (or intrinsic) growth rates, rates were calculated only between coalescence events.

Average growth rates dr/dt vs. drop radius r for Saran® are plotted in Fig. 8a, and for OTS-coated glass in Fig. 8b. On both substrates, the growth rate is highest for the smallest drops and falls asymptotically to a constant (nonzero) value with increasing drop size. Similar behavior has been reported for water condensing on polyethylene,¹⁴ although in that case the studied drops were large (> 25 μm) and thus probed the slower regime of drop growth. Under the conditions of this work, drop growth on the OTS-coated glass is somewhat slower than on Saran®. The dashed lines are fits to a model presented below.

Fig. 8.

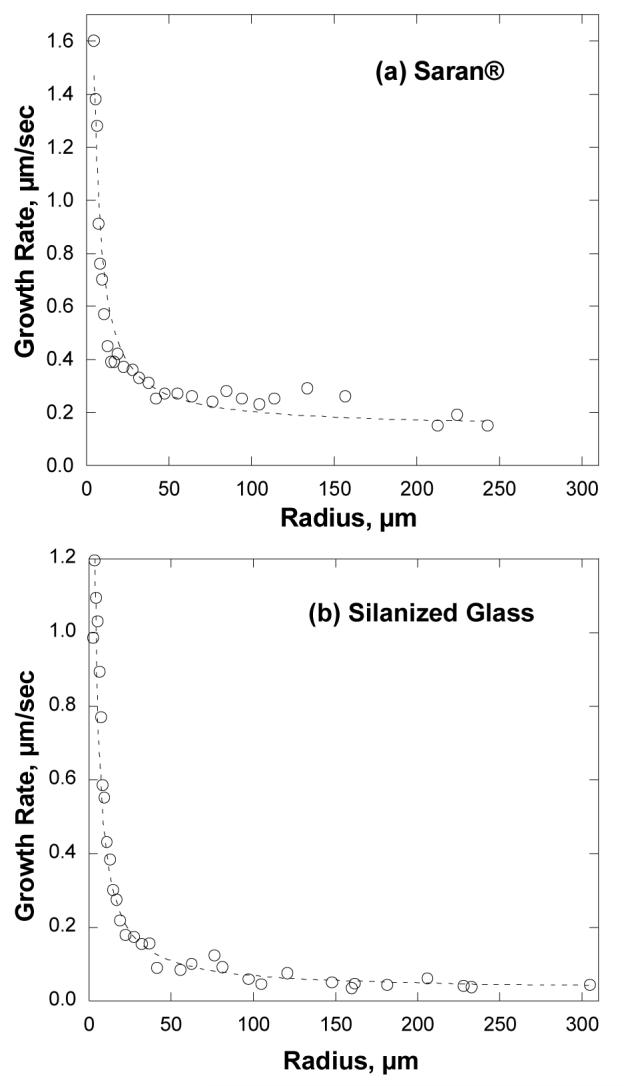
Droplet growth rates dr/dt as a function of drop radius r over a water bath initially at 97 °C for (a) Saran® and (b) OTS-treated glass. The curves represent least squares fits of Eq. (4) to the data.

In general, growth rates are not significantly affected by nearby drops. The principal exceptions are very small drops close to much larger drops, which often grow more slowly, due to the local depletion of adsorbed water or vapor. Figure 9 shows the radius of three small drops, labeled R, S, and T in the inset, as a function of time. Drops S and T are 17 and 13 μm from the nearest large drop, respectively, while Drop R is about 50 μm from the nearest large drop. Drop R grew 20% faster than Drops S and T, i.e., those closest to large drops. Adsorbed water diffusing between large and small drops has a higher probability of encountering the larger drop than the smaller drop, resulting in slower growth for the smaller drop. Thus “the rich get richer” at a faster rate. Multiple measurements of this effect suggest that diffusive transport of adsorbed water on Saran® is limited to 20-50 μm. This limit may be associated with a short average residence time for water molecules on this hydrophobic surface.

Fig 9.

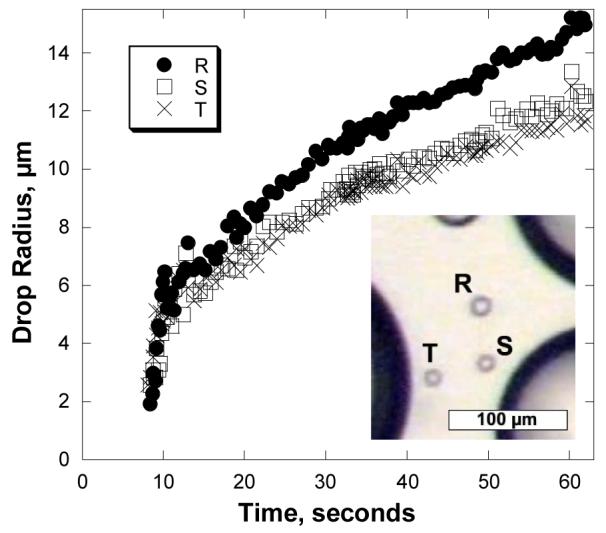
Growth of three small drops over 50 °C water. The inset shows an image of the drop geometry. Drop R is about 50 μm from the nearest large drop, and Drops S and T are less than 20 μm from the nearest large drops. Time t = 0 corresponds to the coalescence event responsible for the nucleation of the three small drops.

5. Discussion

Drop Growth

Drop growth has frequently been described by a power law in time:^29-31

$$r\left(t\right)=a{(t-t_0)}^{\mu }$$ (1)

where a drop nucleated at time t₀ is observed at time t. McCormick et al. reported μ = 0.5 for water condensing on copper.² For water on silanized glass or silicon, μ = 1/3 or μ = 0.23, respectively, were found.^10,16,26 In prolonged experiments at constant water vapor pressure and temperature, the condensation rate approaches steady state conditions and μ tends to 1/3.³² Thus μ can be a function of time.²⁹ Ichikawa found that for water on silanized glass in supersaturated vapor, μ = 2/3 soon after nucleation, rose to μ = 1/2 and then fell to μ = 1/3 as the drop grew (steady state behavior).⁶

In principle, one expects μ = 0.5 when growth is dominated by diffusion of water from the surrounding substrate to the perimeter of the drop. Assuming the drop volume V increases at a rate proportion to the perimeter, and thus in proportion to the radius r yields

$$\frac{dV}{dt}=2\pi r\frac{dr}{dt}\propto r$$ (2)

Integrating this expression yields r ∝ t^1/2, yielding μ = 0.5. Growth proportional to the drop perimeter is favored for the smallest drops, which have high perimeter-to-area ratios. Conversely, larger drops have low perimeter-to-area ratios, and the accretion of vapor along the drop surface (due to direct collisions between gas phase water and the drop surface) becomes dominant. Then the drop volume increases in proportion to r²:

$$\frac{dV}{dt}=4\pi r^2\frac{dr}{dt}\propto r^2$$ (3)

Integrating this expression yields r ∝ t, or μ = 1. Drop growth between these limits would be described by 0.5 < μ < 1.

To compare the data of Fig. 8 with our simulations, we express the growth rate dr/dt as a function of r. In the small drop limit, where we expect growth from the drop perimeter to dominate, dr/dt is proportional to r^-1. In the large drop limit, growth from the drop area dominates and dr/dt is constant. The growth rates in Fig. 8 are well described by the sum of the two limiting expressions:

$$dr∕dt=k_1{r}^{-1}+k_2$$ (4)

The dotted lines in Fig. 8 are least-squares fits of Eq. (4) to the data. Although these two sets of measurements were performed on different substrates, both are well described by Eq. 4. The dominant growth mechanism changes from perimeter accretion to surface accretion as drops reach a radius of about 25 μm for the Saran and about 50 μm for the OTS-coated glass.

Surface coverage

Previous computer simulations of the growth of first generation drops which did not consider formation of new drops have found that surface coverage saturates at about 55%.^5,15,33 Our simulations reproduce this result prior to the onset of coalescence. A coverage of 55% corresponds to the maximum average random packing density for uniform discs on a surface.²⁸ Higher surface coverages are possible with a distribution of disk sizes. Immediately prior to the onset of coalescence, the drop-size distribution is relatively narrow, and the maximum surface coverage is close to the ideal value for uniform disks.

As condensation proceeds, the drop size distribution broadens tremendously and higher coverages are possible. Experimental saturation coverages of about 60% have been reported for water on silanized glass¹⁶ and 64-72% for water on copper promoted with benzyl mercaptan.² The maximum surface coverage generally decreases with increasing contact angle. On silicon treated with varying amounts of silane, surface coverages of 55% were found at a contact angle of 90° and reached 95% at a contact angle of 10°.²⁶ Computer simulations show similar trends, with a surface coverage of about 80% at a contact angle of 90°.¹⁷ Our experimental surface coverage of 75-80% on Saran® is consistent with our simulations, assuming the measured contact angle of 60°. This surface coverage is very close to that for partially silanated silicon at a contact angle of 60°.²⁶ On silanized glass (contact angle ∼100°) we found maximum coverages of about 60%, which is similar to the 50% coverage reported for partially silanated silicon at a contact angle of 90°,²⁶ and equal to a previous measurement on silanized glass.¹⁶

Initial Nucleation

The surfaces of the polymer film and silane-coated glass were quite smooth and uniform, so the density of nucleation sites (perhaps adhering dust or surface flaws) are expected to be fairly low. The initial nucleation densities observed in this study, typically 10⁶ drops/cm², are quite high consistent with homogeneous nucleation along the surface. A few cases of clear heterogeneous nucleation were observed—where drops nucleated at the same location before growing and merging with a larger drop. Such heterogeneous nucleation appears to be rare. That said, we cannot rule out heterogeneous nucleation if the average distance between nucleation sites is smaller than the resolution of our images. Simulations employing fixed, active sites for nucleation were indistinguishable from simulations assuming random, homogeneous nucleation as long as the density of nucleation sites was larger than 10⁴ cm^-2.

Simulation

Our simulations successfully reproduce the main features of our experimental observations in Figs. 4 and 5. However, the simulation parameters can be varied over a wide range without significantly altering the results. This consistent with previous simulation work, where drop growth was adequately represented despite a wide variety of assumptions and simplifications.^5,15,17-19 The drop growth mechanism appears to be very robust, probably because large drops grow mostly by coalescence with other drops.

Implications for Heat Transfer

Under certain conditions, dropwise condensation provides for much higher heat transfer rates than filmwise condensation.^2,3 Although a drop has a larger surface area than a film occupying the same surface area, this difference is relatively small. At a contact angle of 60°, the ratio of drop surface area to the substrate area occupied by the drop is 1.33. However, the fraction of the surface covered by drops is only about 75%. In this case, the total drop surface area is equal to that of a surface film.

In principle, the especially rapid growth of small drops can have a much greater effect on heat transfer rates. These drops grow mostly by vapor accretion along the perimeter, so that vapor deposited onto the substrate surface between drops can be incorporated into growing drops. Since growth from the perimeter increases with the inverse of the radius, the contribution of these smallest drops to the condensation rate is out of proportion to the small area they occupy on the substrate. Figure 10 shows the measured condensation rate in μm³/s per unit area physically occupied by the drop on the substrate, in μm², as a function of drop radius. The condensation rate per unit surface area is by far the greatest for the smallest drops, and decreases to a constant low value as drop size increases. The asymptotic value for large drops in Fig. 10 is presumably related to the filmwise condensation rate.

Fig. 10.

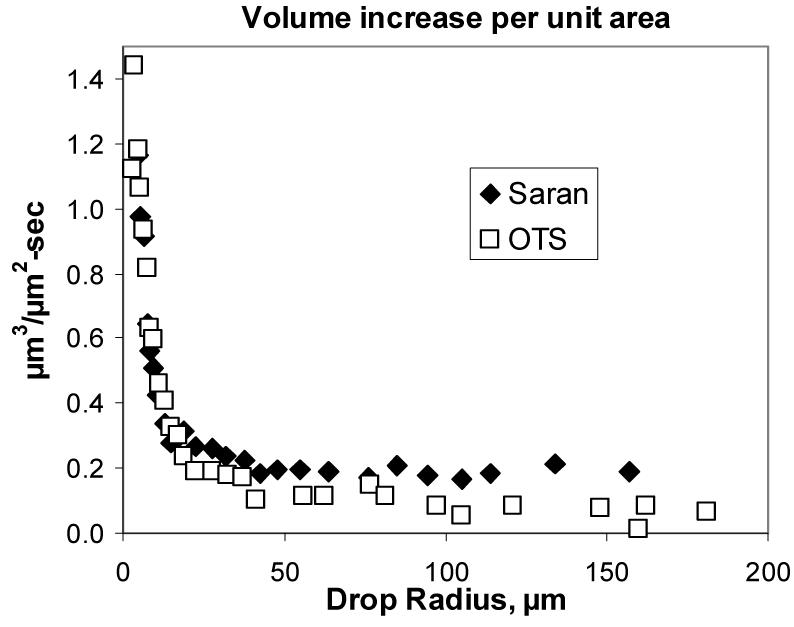
Calculated condensation rates per unit substrate area occupied by drops of the indicated size for Saran® and OTS-treated glass over water baths with initial temperatures of 97 °C.

The data of Fig. 10 suggests that the smallest drops contribute about 15 times more condensation per unit surface area than the largest drops, so they could substantially contribute to the growth rate if they occupy as much as 5% of the surface. Small drops are difficult to measure experimentally, but calculations can readily be made from the simulations. Extending the drop size distribution of Fig. 4 to small drop sizes, the simulation suggests that 13% of the surface is occupied by drops of 50 μm radius or smaller, and that about 7% of the surface is occupied by drops of 20 μm radius or smaller. While acknowledging the limitations of simulations, it appears that these small drops can strongly impact the total condensation rate. Understanding the nucleation process and how it is influenced by contact angle, drop coalescence, and other effects is therefore critical in efforts to predict and optimize condensation rates.

6. Conclusion

Between coalescence events, drops on Saran® and OTS-coated glass suspended over cooling water reservoirs grow by incorporating both adsorbed water from the substrate (via surface diffusion) and gas-phase water (by direct collisions with vapor molecules). Smaller drops grow principally by the diffusion of adsorbed water to the perimeter of the drop. Drops with radii greater than 25 μm for Saran® and 50 μm for OTS-coated glass grow principally by the accretion of vapor onto the surface of the drop.

After many generations of coalescence and nucleation, the drop size distribution is determined principally by coalescence events. Simulations incorporating an appropriate water flux and properly treating coalescence provided a good match to the experimental results, over a broad range of values for parameters such as initial nucleation density, renucleation density, fitting constants, location of renucleation, and heterogeneous vs. homogeneous nucleation. The basic features of the observed patterns of droplets on hot beverage cup lids and plastic wrap over hot foods are explained by our simple model. Simulation results do not depend strongly on the choice of parameters over a broad range. This robust behavior helps explain why so many natural and human-made systems display similar drop patterns, and why a variety of prior simulations have all successfully modeled the main features of drop growth.

Our results show that condensation rates per unit substrate area are much higher for areas occupied by small drops than for areas occupied by large drops. Thus the heat transferred per unit substrate area is expected to be especially large for the smallest drops, which explains the high heat transfer rates observed for dropwise condensation. This suggests that heat transfer rates can be increased by maximizing the surface coverage by very small drops. This might be accomplished by increasing the drop nucleation density, removing large drops to open up areas for nucleation of new drops, or both.

Appendix I. Details of Computer Simulations

Although we varied many of the computational parameters (as discussed in the text) a typical computer model started by positioning an initial set of drops randomly in the simulation area. The initial drop radius was fixed at 0.5 μm. This is approximately the minimum size for a stable water drop, and is also smaller than the smallest drops which could be imaged optically. Because very small drops grow rapidly, small changes in initial drop size had little effect on the final drop size distribution. Drops were created at random positions, rejecting any new drop that overlapped existing drops, until the desired number and density of drops was established. For randomly distributed 0.5 μm drops, the jamming limit of ∼55% coverage corresponds to 7 × 10⁷ drops/cm²; typical starting densities for our simulations ranged from 10⁴ to 10⁶ drops/cm².

New drops (also 0.5 μm) were nucleated during the simulation. Several different rules for nucleating new drops were tested. Drop nucleation was modeled by assuming either random nucleation in any open area, or by limiting nucleation to areas near drops that had recently coalesced. Typical simulations employed a substrate area of 1 × 1 cm² with periodic boundary conditions, with 25,000 initial drops. Simulations were evolved over several thousand growth cycles, where each cycle corresponds to about one second of real time. Parameters could be varied to match a specific experiment.

During each cycle, the collection of drops was tested for coalescence. The area under study was partitioned into a grid, each square possibly enclosing the centers of several drops. The largest drop in each square was identified, and the sizes of these largest drops were used to identify those nearby squares with potentially interacting drops. All the drops in these nearby squares were tested for possible coalescence events. Drops with overlapping edges were flagged and replaced by a new single drop with the same total volume centered at the center of mass of the coalescing drops. After each coalescence event, nearby squares were again checked for coalescence events triggered by the presence of the larger, repositioned drop.

Drop growth between coalescence events was modeled as the sum of a term describing the capture of water molecules directly from the gas phase and a term describing the capture of water molecules from the water film on the condenser surface. Both growth mechanisms are proportional to the flux of water from the vapor phase. The vapor flux, F(t), and vapor pressure, p_vap(t), above a hot liquid surface are represented by:

$$F\left(t\right)=\frac{P_{\mathit{vap}}\left(t\right)}{2n_w}{\left(\frac{1}{k_{b}T\left(t\right)m_w}\right)}^{\frac{1}{2}},$$ (A1)

and

$$p_{\mathit{vap}}\left(t\right)=p_{\text{boil}}\frac{T\left(t\right)}{T_{\text{boil}}}\mathit{exp}\left[\frac{-L_i}{R}\left(\frac{1}{T\left(t\right)}-\frac{1}{T_{\text{boil}}}\right)\right]$$ (A2)

where n_w is the number density of water molecules in the liquid phase, m_w is the mass of a water molecule, k_b is Boltzmann’s constant, T(t) is the temperature in Kelvin, P_boil and T_boil are boiling pressure and temperature of water, L_i is the latent heat of evaporation per mole of water, and R is the gas constant. The temperature of the water vapor source decreased with time and was determined from Newton’s law of cooling:

$$T\left(t\right)=A{e}^{-t∕\tau }+T_{RT}.$$ (A3)

with τ = 1145 s, T_RT = 20 °C, and A chosen so that A + TRT is the initial temperature, Eq .

The adsorption of water from the vapor phase is proportional to the vapor flux [from Eq. (A1)] and the surface area of the (truncated) spherical cap of the water drop. Similarly, the adsorption of water from the liquid film is proportional to the vapor flux and the perimeter of the water drop. This adsorption from both surface and perimeter increases the drop volume, V(t), as:

$$\frac{d}{dt}V\left(t\right)=F\left(t\right)[S\left(\theta \right)r{\left(t\right)}^2\alpha +2\pi r\left(t\right)\beta ]$$ (A4)

where r is the radius of the drop where it is in contact with the surface, S(θ)r(t)² is the surface area of the drop (which depends on the contact angle, θ), and 2πr(t) is the circumference of the drop. The constants α and β account for sticking probabilities, diffusion constants, and other limiting factors, such as evaporation. Writing V(t) as

$$V\left(t\right)=C\left(\theta \right)r{\left(t\right)}^3$$ (A5)

where C(θ) is similar to S(θ), only for volume instead of area, allows one to express Eq. (A4) in terms of r(t):

$$\frac{d}{dt}r\left(t\right)=F\left(t\right)\left[\frac{S\left(\theta \right)}{3C\left(\theta \right)}\alpha +\frac{2\pi }{3C\left(\theta \right)r\left(t\right)}\beta \right]$$ (A6)

Fitting Eq. (A6) to experimental measurements, yielded best fit values α = 5.15 × 10^-7 and β = 7.25 × 10^-10 cm. Although Eq. (A6) does not explicitly incorporate evaporation from the drop, the numerical adjustment of parameters α and β essentially refer to the net flux of water molecules, and thus account for the effect of evaporation.

Note that this model does not account for any interactions between drops other than coalescence. While we do observe relatively weak interactions at small drop separations, this effect can be neglected without impairing the ability of the model to describe our data.