Electrospray ionization mass spectrometry can provide estimates of protein surface areas in solution

Abstract

The extent of multiple charging of protein ions in electrospray ionization (ESI) mass spectra depends on the solvent-exposed surface area, but it may be also influenced by a variety of other extrinsic and intrinsic factors. Gas phase ion chemistry (charge transfer and charge partitioning reactions) appears to be the major extrinsic factor influencing the extent of protonation as detected by ESI MS. In this work we demonstrate that under carefully controlled conditions, which limit the occurrence of the charge transfer reactions in the gas phase, charge state distributions of protein ions can be used to assess the solvent-exposed surface area in solution. A set of proteins ranging from a 5 kDa insulin to 500 kDa ferritin show a clear correlation between the average charge in ESI mass spectra acquired under native conditions and their surface areas calculated based on the available crystal structures. An increase of the extent of charge transfer reactions in the ESI interface results in a noticeable decrease of the average charge of protein ions across the entire range of tested proteins, while the charge-surface correlation is maintained. On the other hand, the intrinsic factors (e.g., a limited number of basic residues) do not appear to play a significant role in determining the protein ion charge. Based on these results, it is now possible to obtain estimates of the surface areas of proteins and protein complexes, for which crystal structures are not available. We also demonstrate how the ESI MS measurements can be used to characterize protein-protein interaction in solution by providing quantitative information on the subunit interfaces formed in protein associations.

INTRODUCTION

Proteins carry out their diverse tasks in vivo by interacting with small ligands, each other and/or other biopolymers. Therefore, understanding the mechanisms of the plethora of processes occurring in living organisms at the molecular level often requires detailed characterization of both stable and transient macromolecular complexes that serve as critical nodes in sophisticated protein interaction networks. Currently, NMR and X-ray crystallography remain the only experimental techniques capable of providing a wealth of structural information on proteins and their associations at the atomic level. However, X-ray is always biased towards the stable protein complexes and is usually unable to provide information on protein complexes that form only transiently in solution. The drawbacks of NMR include molecular weight limitations, low tolerance to paramagnetic ligands, as well as a requirement to carry out measurements at high protein concentration, which may lead to non-specific protein association and/or aggregation. Electrospray mass spectrometry (ESI MS) has recently emerged as a powerful alternative tool to study protein interactions in solution.^1–3 Under appropriate conditions it is often possible to preserve intact protein complexes upon their transition from solution to the gas phase, where they can be manipulated and detected using a variety of mass spectrometric tools. This allows the information on the stoichiometry of macromolecular complexes to be obtained directly based on the mass measurement of the respective ions. ESI MS offers several important advantages, when compared to other biophysical tools often used to determine stoichiometry of non-covalent associations. First, the superior sensitivity of ESI MS allows many experiments to be carried out using only minute quantities of proteins, which in many cases enables the study of protein behavior at, or even below, endogenous levels and to avoid artifacts associated with protein aggregation in solution. Second, ESI MS greatly outperforms high-field NMR in its ability to handle larger proteins and their complexes; in fact, the practical upper mass limit of ESI MS is yet to be established, as the bar is being continuously raised. Finally, ESI MS is very successful in addressing a serious problem inherent to most other biophysical tools, namely the great difficulty associated with the analysis of protein structure and dynamics in heterogeneous systems, since the ionic signals from different species in multi-component systems, e.g. solutions containing mixtures of several proteins, as well as other biopolymers, do not generally overlap.

In addition to providing information on protein complex stoichiometry, a variety of MS-based strategies can be employed to probe structure and dynamic behavior of protein complexes.⁴ Arguably, the most popular among these approaches is amide hydrogen/deuterium exchange (HDX) coupled with MS detection. HDX MS has been particularly useful in studies aimed at identification of protein-protein interfaces based on the dramatic changes of their solvent accessibility upon complex formation.^{5, 6} Additionally, various methods that use covalent modifications to characterize higher order structure of biopolymers, i.e. cross-linking, selective chemical labeling and foot-printing, have become increasingly reliant on MS as a method of detection.⁷

Analysis of protein ion charge state distributions in ESI mass spectra is another method that is often used to probe macromolecular behavior in solution. The extent of multiple charging of monomeric protein ions in ESI MS reflects the integrity of their tertiary structure in solution,⁸ as the tightly folded conformers cannot accommodate as many charges as their less compact partially unfolded isomers. In addition to monitoring large-scale dynamic events within monomeric proteins,^8–10 analysis of protein ion charge state distributions in ESI MS can be used to study dynamic behavior of subunits of larger protein assemblies.^{11, 12}

The average number of charges accommodated by protein ions generated under native conditions in solution was shown by Fenselau to exhibit a strong dependence on the surface area of the native conformations in solution.¹³ De la Mora¹⁴ and, more recently, Heck² and Nesatyy¹⁵ analyzed compiled sets of ESI MS data for a variety of globular proteins under native conditions and used Dole’s Charged Residue Model (CRM) to rationalize the apparent correlation between the calculated gyration radii of proteins in solution and their average and highest charges in the gas phase, as determined from the ESI mass spectra. While these analyses clearly showed a general trend, the observed correlations were not perfect. This is not particularly surprising, since the experimental conditions used to acquire the individual data sets were very different. As a result, the outcomes of such measurements were affected by extrinsic factors to various degrees, causing random deviations from a putative protein ion charge-protein geometry correlation. In this work we use a set of proteins ranging from a small polypeptide insulin (5 kDa) to a large multi-unit protein ferritin (500 kDa) in order to test the validity of the protein ion charge-protein geometry or, more specifically, charge-surface area N vs. S correlation under conditions that minimize variation of the extrinsic factors. The experimentally determined empirical correlation (N = N_o + S_α, where N_o and α are constants) is in excellent agreement with the current view of ESI processes and CRM predictions. We also evaluated the influence of various extrinsic and intrinsic factors on the number of charges carried by protein ions in the gas phase.

The results of our work suggest that the experimentally determined number of charges accommodated by protein ions generated under native conditions can be used to provide quantitative estimates of their surface areas in solution. This method can be used to characterize macromolecular complexes in solution, which cannot be probed by classical biophysical techniques due to their transient nature, sample heterogeneity, etc. In this case, the estimation of the solvent-exposed surface area can be obtained by measuring the average charge of the complex and using the charge-surface correlation obtained for model proteins as a ‘calibration curve.’ This approach has been tested by estimating the solvent-exposed surface area of sickle cell hemoglobin octamer and comparing this value with the one derived from the crystallographic data.

EXPERIMENTAL

Mass Spectrometry

All mass spectra were acquired on a JMS-700 MStation (JEOL, Tokyo, Japan) magnetic sector (double focusing) mass spectrometer equipped with a standard ESI source. The nominal resolution was set at 1000 and the spectra were obtained by scanning the magnet at a rate of 5 sec/decade. Protein solutions were continuously infused into the ESI source at a flow rate of 3 µL/min. All ESI source parameters, i.e. desolvating plate temperature, electrostatic potentials on ion optics elements, etc. were kept constant throughout the measurements to insure constancy in protein ion desorption and transmission conditions. De-clustering potential was set to a lowest possible value to avoid/minimize charge stripping in the gas phase (the exceptions are expressly specified in the text).

Materials

Apo-form of human Ferritin (HuHf) was generously provided by Prof. N. Dennis Chasteen, University of New Hampshire. The recombinant form of human serum transferrin (hTf) was provided by Prof. Anne B. Mason, University of Vermont Medical School, and soluble transferrin receptor (TfR) was purchased from the Protein Expression Facility at California Institute of Technology, Pasadena, CA. Chymotrypsin inhibitor 2 (CI2) was a generous gift of Prof. Sophie E. Jackson, Cambridge University, Cambridge, U.K.. Ligand binding domain of retinoic acid receptor (RARγ) was provided by Prof. Michael I. Schimerlik, Oregon State University. All other proteins used in this work were purchased from Sigma-Aldrich Chemical Co., St. Louis, MO and used without further purification. Protein solutions for MS analysis were prepared by diluting stock solutions (100 µM in de-ionized water) to a final concentration of 5–10 µM in 10 mM ammonium acetate or 10 mM methylammonium acetate. If needed, the pH was adjusted to a desired level with either glacial acetic acid, concentrated ammonia or methylammonium as appropriate. All chemicals and solvents were of analytical grade or higher.

Solvent-accessible surface areas of the proteins were calculated with Insight II, Accelrys, San Diego, CA using crystal structures available from the Research Collaboratory for Structural Bioinformatics Protein Data Bank (http://www.rcsb.org/pdb). The probe radius was set at 1.4 Å for all calculations. Similar calculations can be carried out using a variety of packages, many of which are freely available, such as GETAREA¹⁶ at http://www.scsb.utmb.edu/cgi-bin/get_a_form.tcl.

RESULTS AND DISCUSSION

Charge-surface correlation under carefully controlled conditions

In order to evaluate the charge-surface correlation, a set of ESI mass spectra were acquired for proteins ranging from relatively small polypeptides to large multi-unit protein assemblies (Table 1). Crystal structures of all proteins from this set are available from the Protein Data Bank and can be used to calculate the solvent-accessible surface area. To reduce potential variation of the influence of extrinsic factors, e.g., gas phase ion chemistry on the observed charge state distributions, a set of standard conditions was used throughout all experiments. For example, elevated de-clustering potential in the ESI interface is known to induce the so-called ‘charge stripping’ that results in an apparent shift of protein ion charge state distributions to lower charges. As will be shown later, the extent of charge stripping depends very strongly on certain intrinsic characteristics of protein molecules, e.g., number of basic residues. Therefore, unless specifically stated otherwise, the de-clustering potential was kept at its lowest possible value throughout the entire set of measurements. We had also shown in our previous work that solvent composition exerts a significant influence on the observed charge state distributions of protein ions, an effect whose extent is largely determined by the presence of ion pairing agents in protein solutions.¹⁷ To minimize the spectral variability caused by these effects, all protein solutions used for data acquisition were prepared in 10 mM ammonium acetate, unless specifically stated otherwise.

Table 1.

Proteins used to obtain a charge-surface correlation shown in Figure 2

Protein	PDB id	Number of basic residues (R, K, H)	Number of acidic residues (D, E)	Average charge of protein ions	Surface area Å2 (crystal structure)
insulin (bovine)	1APH	1,1,2	0,4	4.4	3396
chymotrypsin inhibitor II	1CIQ	4,6,0	4,6	5.42	4052
ubiquitin (human)	1UBQ	4,7,1	5,6	5.9	4758
cytochrome C (equine)	1HRC	2,19,3	3,9	7.2	6232
cellular retinoic acid binding protein I (mice)	1CBI	9,9,2	8,14	8.13	7341
β-lactoglobulin A (bovine)	1BSY	3,15,2	11,16	8.65	8321
myoglobin (equine)	1WLA	2,19,11	8,13	8.7	8017
H-chain of ferritin (human)	2FHA	7,12,10	15,16	9.33	9816
α1 chymotrypsinogen (bovine)	1EX3	4,14,2	9,5	10.56	10317
ligand binding domain of retinoic acid receptor (human)	3LBD	16,13,10	15,20	11.17	11230
carbonic anhydrase I (human)	2CAB	7,18,11	14,13	10.54	10997
pepsin (porcine)	5PEP	2,1,1	28,13	10.74	13351
β-lactoglobulin dimer (bovine)	1BEB	6,30,4	22,32	12.9	14698
apo-transferrin, N-lobe (human)	1BTJ	12,27,9	25,17	13.1	14970
holo-transferrin, N-lobe (human)	1A8E	12,27,9	25,17	12.93	13973
ovalbumin (hen egg)	1OVA	15,20,7	14,33	13.89	15586
serum albumin (human)	1AO6	24,59,16	36,62	17.2	28103
hemoglobin (human)	1A3N	12,44,38	30,24	17.8	24548
transferrin (rabbit)	1JNF	26,57,18	43,46	19.8	27395
soluble transferrin receptor (human)	1CX8	48,88,24	74,72	27.2	46530
Transferrin-transferrin receptor complex (human)	1SUV1	100,202,62	166,154	40.5	91258
H-chain ferritin 24-mer (human)	2FHA	168,288,240	360,384	62.16	141541

¹cryo-EM structure of the assembly is refined using X-ray structures of individual subunits

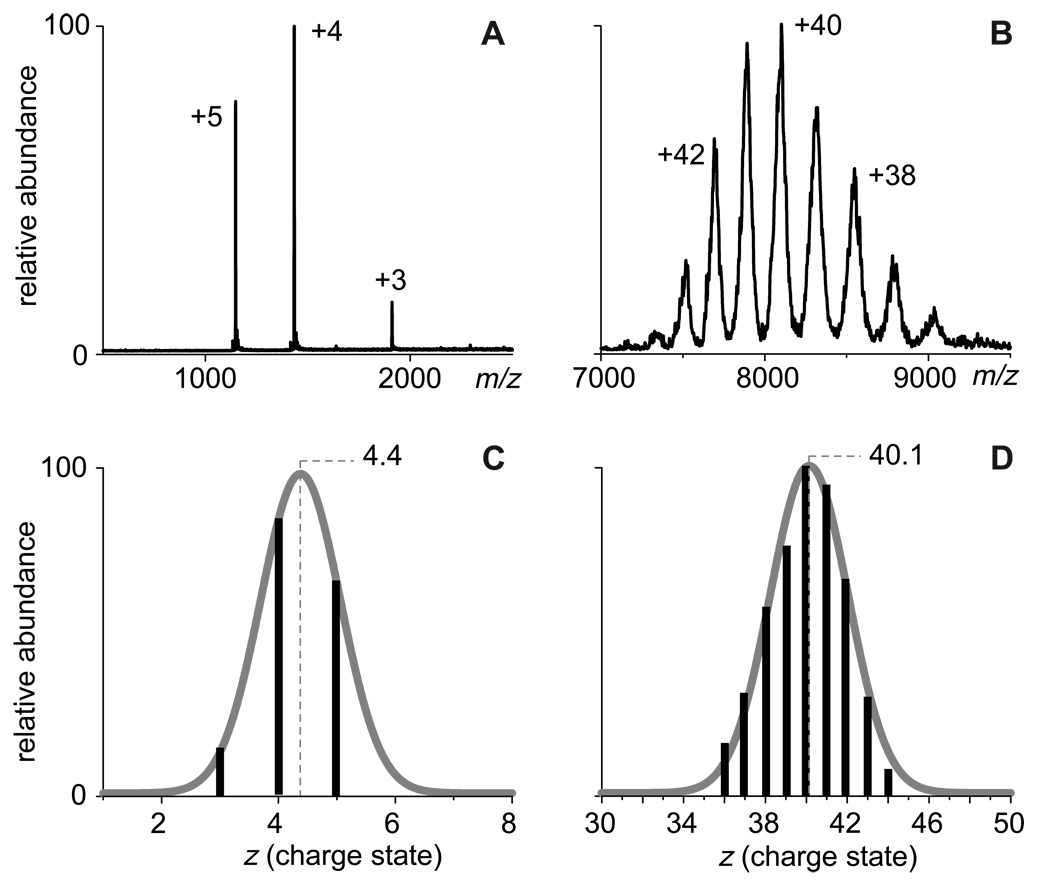
Typical ESI spectra acquired under these conditions are shown in Figure 1. The charge state distributions are narrow, indicating conformational homogeneity of the protein molecules in solution. Changing solution conditions to mildly denaturing, e.g., by lowering solution pH and/or adding alcohol, resulted in the emergence of protein ions peaks at lower m/z values (higher charge states) for all single-chain polypeptides (data not shown). These higher charge state ion peaks formed distinct groups (or clusters) for all single-chain polypeptides used in our study, except the two smallest ones (insulin and CI2), indicating that the ion peaks observed under native conditions indeed represent the native conformations. The average charges of the protein ions representing such native conformations were calculated using the procedure described elsewhere^{9, 10} and plotted as a function of the calculated surface area using a log-log scale (Figure 2). The graph clearly shows a very strong linear correlation with a slope 0.69±0.02, indicating that the empirical charge-surface correlation is a power function:

$$N=A·S^{\alpha }$$ (1)

where N is the average number of charges of protein ions representing native proteins and protein complexes, S is the protein surface area calculated based on the available crystal structures; α the slope of the curve representing the empirical charge-surface correlation in log-log coordinates; and A is a constant whose logarithm determines the offset of the linear graph (Figure 2).

Figure 1.

ESI mass spectra of insulin (A) and human serum transferrin-transferrin receptor complex (B) used to calculate the average number of charges accommodated by the protein ions in the gas phase (C and D, respectively)

Figure 2.

Correlation between the average charge state of protein ions generated by ESI under near-native conditions (10 mM ammonium acetate, pH adjusted to 7) and their surface areas in solution, whose calculation was based upon their crystal structures (Table 1). The data are plotted in the logarithmic scale (a graph plotted in the normal scale is shown in the insert). A gray-shaded dot represents a pepsin data point, not used in calculation of the least squares linear fit for the entire data set. An open circle represents the highest charge of pepsin if the extent of multiple charging were limited by the number of basic residues within the protein molecule.

The dependence of the protein ion charge in the gas phase on its compactness in solution is usually explained within the framework of the Charged Residue Model (CRM),^{14, 18} which was initially put forward by Dole.¹⁹. According to this model, generation of protein ions is caused by an efficient droplet atomization process, which is a consequence of the so-called Rayleigh instability. The electrostatic repulsion among the like charges on the droplet formed by ESI is initially offset by cohesive action of the surface tension. The potential energy of the former is inversely proportional to the radius of the droplet, while the energy of the latter is proportional to the square of the radius, assuming a spherical symmetry of the droplet. If solvent evaporation from the droplet proceeds without loss of charge, the electrostatic component of the potential energy will increase dramatically upon droplet shrinkage, while the stabilizing role of the surface tension will be diminished. Eventually, the droplet will become unstable with respect to high multipole oscillations, resulting in “liquid … thrown out in fine jets.”²⁰ The instability criterion is²⁰

$$\gamma =\frac{{(Ne)}^2}{8\pi {\epsilon }_o{d}_{\mathrm{o}}^3},$$ (2)

where γ is the solvent surface tension, ε_o is the permittivity of vacuum, Ne represents a net charge of the droplet and d_o its diameter in the spherical shape. Numerous measurements have confirmed that droplet fission does occur at or slightly below the Rayleigh limit.²¹

Droplets composed of conducting liquids (such as water and alcohols) decompose in a fine fission mode²² by emitting a jet, in which a significant proportion of the net charge is removed from the droplet (up to 25–33%), while the mass loss is negligible (on the order of 0.3% or even less).^{21, 23} Following such a significant loss of charge during the jet expulsion, the main droplet relaxes to a spherical form, as its net charge falls comfortably below the Rayleigh instability limit. In the meantime, the droplets generated during jet disintegration (the so-called progeny droplets) are of similar size and close to an instability criterion (2), which means they undergo fission soon after separation from the main droplet. In contrast to this, a second fission of the parent droplet would require substantial solvent evaporation in order to bring it back to the unstable conditions (2). The protein molecule is likely to remain in the parent droplet following the Coulombic explosion, if it was residing in its interior just prior to the fission event. At the same time, the protein molecules positioned close to the droplet surface are likely to be ejected with the progeny droplets. In any event, the fission process is likely to occur several times prior to generating a droplet whose size is barely adequate for encapsulating the protein molecule. If the protein structure disruption does not occur or is minimal during the ESI process, the geometry of the native conformation will actually be one of the major determinants of the physical size of the smallest droplet still capable of encapsulating the protein. This would set a limit for a total charge accumulated by the protein upon complete evaporation of any residual solvent from such a droplet.

De la Mora used similar arguments, as well as the assumption of a near-spherical shape of the protein molecule in its native conformation, to predict the following limit on the number of charges accumulated by protein ions:¹⁴

$$N=\frac{8\pi }{e}{\left(\gamma {\epsilon }_o{R}_i^3\right)}^{1/2}=\frac{4}{e}·{\left(4\pi {\gamma }^2{\epsilon }_o^2·S_i^3\right)}^{1/4},$$ (3)

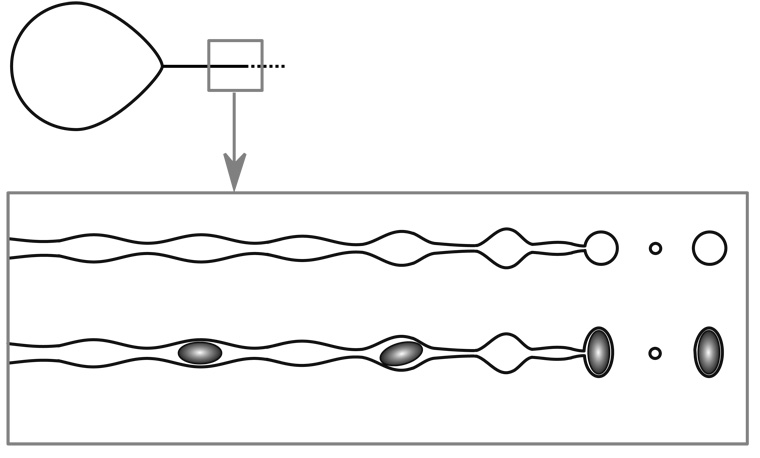
where e is the elementary charge, and R_i (S_i) is the radius (surface area) of the globular protein ion in a spherical approximation. Spherical approximation, however, does not provide adequate description of shape for the majority of proteins, even globular ones. In order to extend equation 3 to proteins whose shapes deviate significantly from the ideal sphere, we need to consider the electrohydrodynamic processes of the parent droplet disintegration and progeny droplet formation in greater detail. Disintegration of the parent droplet in the fine fission mode results in ejection of a jet in the direction of the external field gradient (Figure 3). The jet itself is unstable and eventually disintegrates giving rise to an ensemble of progeny droplets. A critical question here is how the charge on the jet is distributed among these droplets. There is an apparent disagreement in the literature as to what the scaling law is. De la Mora suggested that the jet charge “remains nearly tied to the liquid during the break-up process,” so that the charge density is nearly constant for a given spray:²⁴

$$q~V~R^3,$$ (4)

where V is the volume and R is the radius of a given progeny droplet immediately after jet disintegration. In this case, the charge is assumed to be tied-up to the bulk volume of the jet. The bulk of the solvent, however, is a conducting liquid, which would remain charge- and field-free in the quasi-static approximation, forcing the net charge to be distributed along the surface of the jet. Therefore, it appears that constancy of the charge volume-density (4) should be substituted with constancy of the charge surface (S) density:

$$q~S~R^2.$$ (5)

A more rigorous consideration of these processes by Hartman and co-workers led to a suggestion that the progeny droplet charge-size correlation is weaker still:

$$q~V^{1/2}~S^{3/4}~R^{3/2}.$$ (6)

This group also presented experimental evidence that the power function coefficients can actually be as low as 80% of those presented in equation (6), i.e. q~R^1.2.²⁵

Figure 3.

A schematic representation of a fission process for a droplet, whose charge is equal to or exceeds the Rayleigh limit. The straight line projecting from the pointed end of the droplet (top diagram) represents emission of a highly charged liquid in the form of a jet. The axisymmetric disintegration of this jet according to a simle one-dimensional model⁴⁰ is represented schematically in the boxed drawings. Capillary break-up in the absence of internal constraints produces two groups of homogeneous droplets (main and satellite). Presence of internal constraints in the stream (such as particles of a certain size) is likely to have a significant influence on the size and shape of the droplets.

While most progeny droplets assume near-spherical shapes following jet disintegration, some internal constrains, e.g. presence of non-spherical particles inside the jet, may lead to generation of non-spherical droplets as well (Figure 3). In order to estimate the charge transferred to such droplets, one would need to use the surface of the non-spherical particle as a limiting factor:

$$q~{\left(\frac{S}{a}\right)}^{3/4},$$ (7)

where a is a measure of the droplet surface deviation from that of the encapsulated particle. This correction factor is expected to be close to unity for particles with topologically simple (smooth) surfaces. However, the value of a is expected to increase as the particle surface topology becomes more complicated, e.g. due to the presence of cavities, grooves, etc.. We note that the scaling law (7) gives the same charge-surface area dependence as the estimation of the charge limit for spherical progeny droplets (3) after taking into account the correction factor a.

If the non-ideality parameter a does not exhibit significant variation within a set of proteins, one should expect to observe a linear charge-surface dependence in the log-log coordinates with a slope of 0.75. Our empirical observation of the charge-surface correlation (1) appears to be in remarkably good agreement with this conclusion. The slight deviation of the actual slope of the charge-surface plot (Figure 2, 0.69±0.02) from the theoretical value of ¾ is in line with the earlier measurements of charge scaling by Hartman and co-workers (vide supra).²⁵ A particularly striking observation is the apparent near-constancy of the parameter a throughout the range of the proteins tested as suggested by the excellent linear fit of the experimental data (Figure 2). We note that the only notable deviation from the empirical linear charge-surface dependence is seen in the case of human serum albumin, a protein whose surface is ‘burrowed’ with cavities that serve as binding pockets for various ligands.²⁶

Protein ion charge is a measure of surface area, not protein mass

While the observed protein ion charge-surface correlation (Figure 2) is consistent with the notion of the protein surface area being the major determinant of the average charge accommodated by the protein ions, it does not necessarily prove it. It is often argued that the seemingly harsh conditions of the ESI process are likely to affect the higher order structure of proteins. Indeed, field-induced formation of the liquid jet at the tip of the Taylor cone, its consequent break-up leading to generation of highly charged droplets and a series of Coulombic explosions events leading to the disintegration of these droplets and, eventually, to formation of multiply charged protein ions, as well as the presence of a strong external electrostatic field in the ESI interface, are often thought of as factors that may influence the protein conformation within the electrosprayed droplet prior to the protein ion formation. However, it is important to realize that a charged conducting droplet placed in an external electrostatic field will maintain uneven charge distribution on its surface to maintain field-free conditions in the bulk of the liquid.²⁷ With a sufficiently high concentration of charge carrier in the liquid, a quasi-equilibrium charge layer will be formed at the liquid-gas interface, and the bulk of the liquid will remain essentially charge- and field-free.²⁸ As a result, even a weakly conducting liquid would conform to a quasi-electrostatic model with the charge confined to the surface and the bulk of the liquid remaining quasi-neutral and field-free. Therefore, the solute molecules residing in the bulk of the liquid should remain “oblivious” to the harsh conditions on the droplet surface and the environment beyond it until the last of the solvent is gone. This assertion, however, is not universally accepted,²⁴ and it is possible to argue that the seemingly violent nature of the charged jet break-up and subsequent Coulombic explosions of the electrospray droplets may cause a major disruption of the protein structure. The overwhelming amount of experimental evidence suggests that such a disruption, if it indeed occurs, is unlikely to affect the integrity of multi-subunit protein assemblies, as indicated by the measurements of the stoichiometry of ESI-generated protein assemblies in the gas phase.^{1, 29} However, preservation of the protein complex integrity during the ion formation process does not automatically guarantee that the higher-order structure of such a complex be preserved. For example, it is possible to argue that the violent nature of the jet break-up (Figure 3) and subsequent formation of the fission-incompetent droplet encapsulating proteins and their complexes may cause re-packing of the assemblies, forcing them to assume minimal volume. Should such processes occur during ion formation, one would expect that the extent of multiple charging would reflect the protein (or protein complex) mass, rather than its surface.

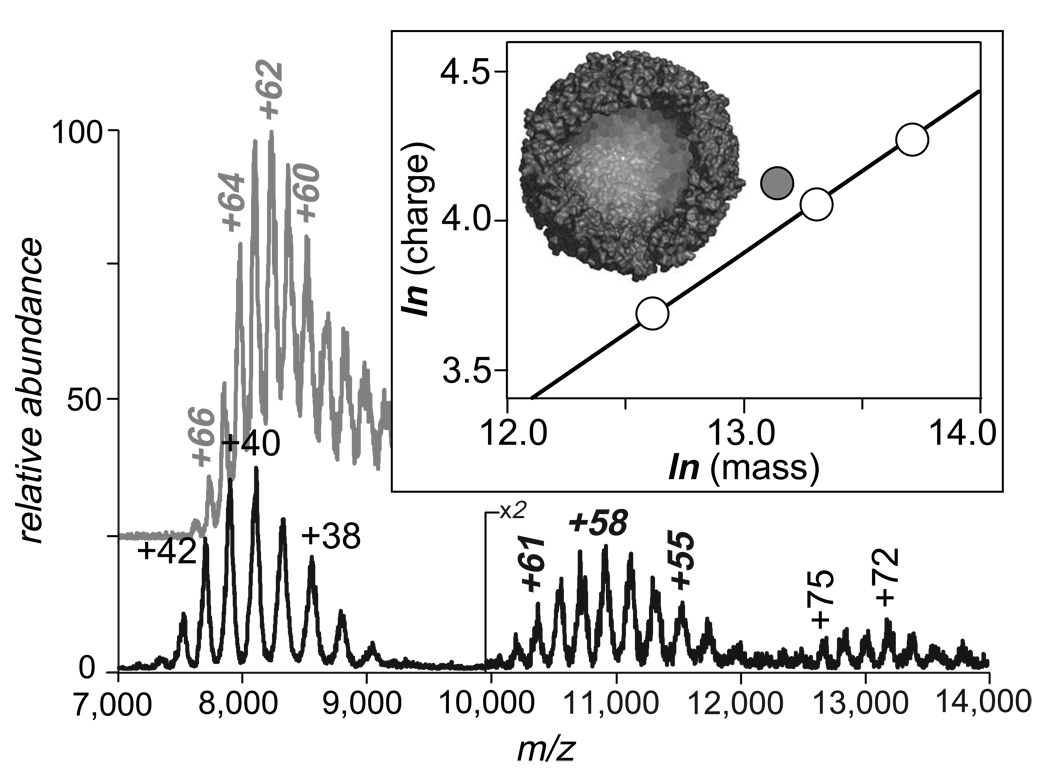
Since most proteins in their native states are already tightly packed, their surface areas are expected to increase monotonically with the molecular weight. An example of such a trend is presented by aggregation of transferrin-transferrin receptor complex Tf₂TfR (Figure 4, bottom trace). The molecular weight of the native complex Tf₂TfR is ca. 316 kDa, but the ESI mass spectrum of the complex solution also contains ionic signals corresponding to complex aggregates, (Tf₂TfR)₂ and (Tf₂TfR)₃. Masses of these aggregates exceed 600 kDa and 900 kDa, respectively. The mass increase within the (Tf₂TfR)_i set is paralleled by the increase in the average ionic charge, as well their m/z ratios, as is expected for tightly packed globular proteins.

Figure 4.

ESI mass spectra of ferritin (gray trace, top) and human serum transferrin-transferrin receptor complex (Fe₂hTf)₂TfR (black trace, bottom). The ionic species appearing in m/z range 7,500–9,000 correspond to the (Fe₂hTf)₂TfR complex itself, while other ionic species present in the spectrum correspond to the complex dimer (m/z 10,000–12,000) and trimer (m/z 12,500–14,000). The boxed insert shows the relationship between the average charges and their masses in logarithmic coordinates, where open circles correspond to the (Fe₂hTf)₂TfR and its aggregates; shaded circle corresponds to ferritin. Also shown is the dissected crystal structure of apo-ferritin.

There are very few proteins that are not tightly packed in their native conformations. Measurements of an average charge accumulated by such proteins during the electrospray process allow us to provide definitive proof that it is the surface area of the native protein, rather than its mass, that is the major determinant of the extent of charging. Of particular interest here is ferritin, an iron storage protein found in plants and animals.³⁰ The crystal structure of human heavy chain ferritin (HuHf) indicates that the functional protein consists of an assembly of 24 identical subunits, the so-called H-chain monomers.³⁰ Each H-type monomer has a molecular weight of ca. 21 kDa, giving a total mass of the apo-protein (iron-free) assembly of ca. 0.5 MDa. The assembly has a symmetrical spherical shape and forms a large cavity (see the insert in Figure 4), which is filled with mineralized iron in the holo-form of the protein. The presence of such a cavity inside the protein leads to a disproportionate increase in surface area, which is not usually seen in protein assemblages. An ESI mass spectrum of ferritin acquired under near-native conditions (gray trace in Figure 4) reveals a charge state distribution centered around +62 – +63, with the maximum number of charges accommodated by ferritin molecules being as high as +67. Both average and maximum charges of ferritin ions are noticeably higher than those of the tightly packed macromolecular assemblage (Tf₂TfR)₂ whose mass exceeds ferritin by over 100 kDa (the average charge of (Tf₂TfR)₂ is +58, and the maximum observed charge is +62). We also note that the m/z range of ferritin ions has a significant overlap with that of Tf₂TfR ions, even though their masses differ by as much as 40%. The extent of multiple charging of ferritin, however, does not appear to be anomalous when its loosely packed structure is taken into consideration. Indeed, the average charge of this assembly appears to fit the general trend, when plotted as a function of the surface area, rather then the protein mass (Figure 2).

Is the extent of multiple charging limited by the number of basic residues?

A very intriguing question that arises when the extent of multiple charging of proteins is considered, relates to the importance of the number of functional groups that can readily accommodate the charges. Kebarle and co-workers noted that the number of basic residues in most proteins is so high, that multiple protonation up to the Rayleigh limit can be easily afforded.³¹ However, there are few examples of highly acidic proteins whose basic residue content is so low, that it falls far short of the number of charges expected on the basis of the Rayleigh limit. One particularly intriguing protein from this class is pepsin, which has only four basic side chain groups (two arginine residues, one lysine and one histidine) in addition to a basic primary amine at the N-terminus. The presence of only five high-proton affinity sites within this protein led to a suggestion that only a limited number of charges can be accommodated and retained by positive pepsin ions.³¹ Prediction of the average number of charges of pepsin ions based on surface calculation for the natively folded protein and the empirical charge-surface correlation (Figure 2) provides the number, which is more than twice as high (expected average charge +11.2).

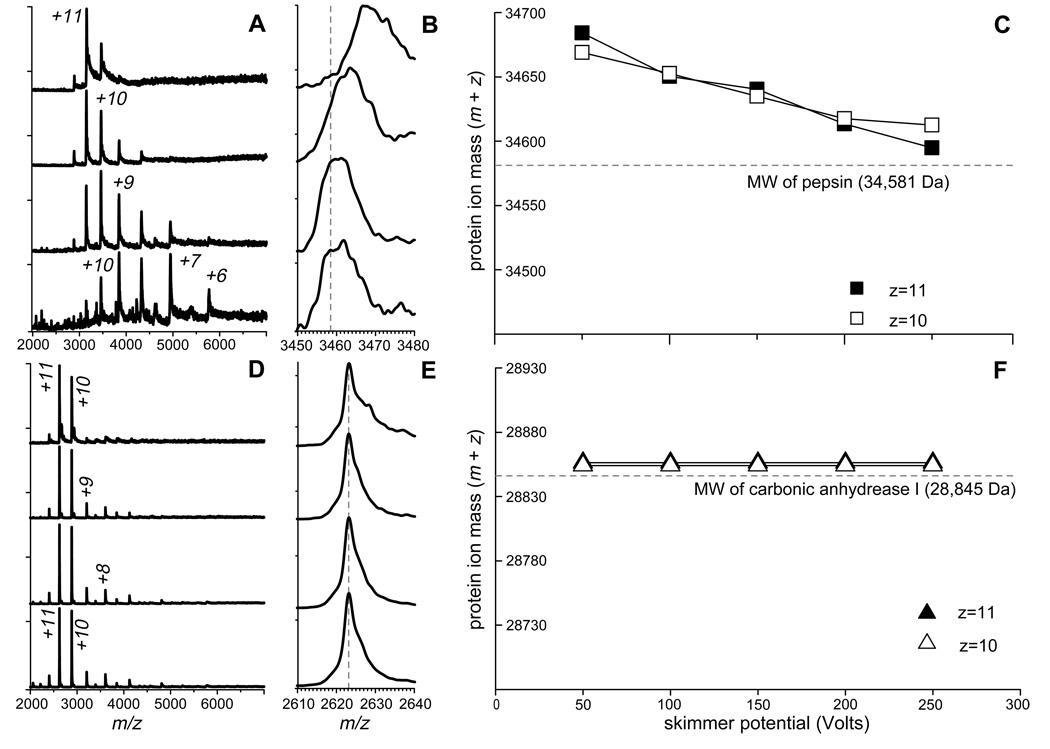
Pepsin is biologically active and remains folded under extreme acidic conditions,³² and it also appears to maintain its native conformation at pH as high as 5. Further increase in the pH may result in denaturation.³³ Interestingly, the ESI mass spectrum of pepsin acquired at pH 5.0 shows a well-defined charge state distribution centered at around +11 (Figure 5A, top trace). We note, however, that the average charge of pepsin ions generated by ESI is readily reduced once an attempt is made to enhance their desolvation in the ESI interface region. For example, increasing the de-clustering potential from its minimal value by 50 V increments clearly alters the charge state distribution, moving its centroid eventually to +8 (Figure 5A, top to bottom). Similar experiments carried out with carbonic anhydrase I (CA I), a protein of a size comparable to pepsin, but with much higher content of basic sites (seven arginine residues, eighteen lysine residues and eleven histidine residues), fail to produce a noticeable shift in the average number of charges carried out by the protein (Figure 5D).

Figure 5.

ESI MS of pepsin (A–C) and carbonic anhydrase I (D–F) acquired at pH 5 (pepsin) and 7 (CA I). Panels (A) and (D) show evolution of protein ion charge state distributions as a function of increasing de-clustering potential from top to bottom in 50 V increments. Panels (B) and (E) show evolution of protein ion peak shapes under the same conditions. Dotted lines represent masses of multiply protonated proteins, which are calculated based solely on their molecular weights and the requisite number of protons. Protein ion mass change as a function of de-clustering potential is shown in panels (C) and (F) for the most abundant ionic species.

Another dramatic difference between pepsin and CA I, which becomes apparent upon close examination of their ESI spectra, is a significant reduction of the protein ion mass upon increasing declustering potential in the case of pepsin (Figure 5B), a feature that is notably absent in the CA I spectra acquired under the same conditions (Figure 5E). Even under the harshest conditions in the ESI interface region, the measured average mass of pepsin ions exceeds the molecular weight of this protein (Figure 5C). At the same time, the “extra” mass carried by the CA I ions in the gas phase is minimal and corresponds to the mass of protons as charge carriers (Figure 5F). The observed correlation between the charge reduction and mass loss of pepsin ions in the gas phase is consistent with the notion of protein-cation (most likely NH₄⁺) adduct formation as a mechanism of multiple charging of pepsin above the limit imposed by the number of basic residues. The apparent absence of such adducts in the case of CA I is due to the presence of a large number of high proton affinity sites, which are likely to interact with ubiquitous cations (e.g., NH₄⁺) primarily through proton transfer, not through complex formation.³¹

It is quite remarkable that minimization of collision-induced charge partitioning in the ESI interface leads to observation of highly charged pepsin ions. The extent of multiple charging of pepsin ions is actually very close to the average charge predicted on the basis of the crystal structure of this protein, when only its surface area is taken into account. Even though a small deviation from the empirical charge-surface correlation does exist for pepsin (represented with a gray dot in Figure 2), its magnitude is significantly less compared to the prediction based on the number of basic sites (un-shaded gray circle in Figure 2). It is possible that some dissociation of the pepsin-cation adducts occurs in the gas phase even under mild conditions in the ESI interface, leading to small, but noticeable charge loss. Overall, these experiments provide convincing evidence that the number of sites with high proton affinity plays a secondary role in determining the extent of multiple charging, and that this role can be reduced even further by careful control of the ESI interface conditions (minimization of collision-induced charge stripping).

Influence of solvent composition on the extent of multiple charging of protein ions

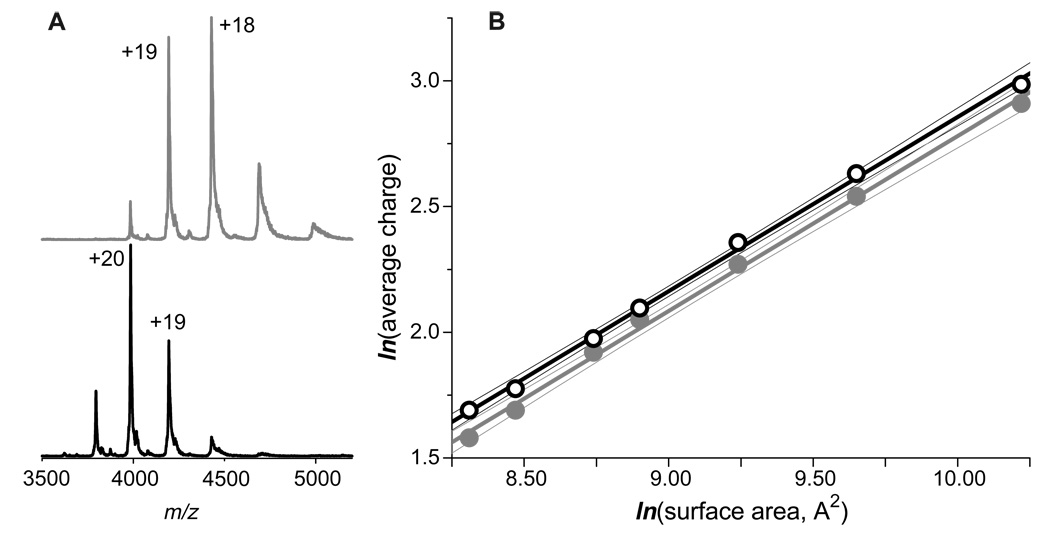
The appearance of charge state distributions of protein ions in ESI mass spectra is known to be influenced by solvent composition.^{17, 31, 34–36} We already mentioned in the previous section a possibility of protein-ubiquitous cation adduct formation in solution followed by their dissociation and charge partitioning in the gas phase. Another distinct possibility is a transfer of a neutral basic component of solution into the gas phase, where it can participate in proton-exchange reactions with protein ions. In each case the protein ion charge reduction is expected to be more efficient when mediated by stronger bases. All ESI MS data reported in the previous sections of this paper have been collected from 10 mM ammonium acetate solution. Proton affinity of the most basic component of this solvent, ammonia is only 853.6 kJ/mol, which is significantly below that of basic amino acid residues.³⁷ This makes ammonia a very inefficient competitor for charges with all protein ions considered in this work, with the exception of pepsin (vide supra). However, replacing ammonia with its more basic derivative, methylamine (proton affinity 899 kJ/mol³⁷) does result in a noticeable charge reduction of protein ions, as is evident from the ESI mass spectra of a recombinant human serum transferrin acquired from 10 mM ammonium acetate and 10 mM methyl ammonium acetate solutions (top and bottom traces in Figure 6A).

Figure 6.

Influence of solvent composition in the extent of multiple charging of protein ions. Panel (A) shows ESI mass spectra of a recombinant form of human serum transferrin acquired in 10 mM methyl ammonium acetate (top) and ammonium acetate (bottom) solutions, whose pH was adjusted to 7.0. Panel B shows the charge-surface correlation for a set of proteins whose ESI mass spectra were acquired in 10 mM methyl ammonium acetate solution acetate (gray dots). The data acquired for the same proteins in 10 mM ammonium acetate solution. A subset of the data presented in Figure 2 is shown here with open circles for comparison.

To explore the generality of this phenomenon, ESI MS spectra were acquired for a limited set of proteins from a 10 mM CH₃CO₂N(CH₃)H₃ solution whose pH was adjusted to 7.0 and the average charge states of the generated protein ions were plotted as a function of protein surface area in their native conformations (Figure 6B). Acquisition of high quality spectra for proteins larger than 100 kDa from this solvent was problematic and their average charge states are not reported here. It is interesting to note that despite the noticeable reduction of average charges for all tested proteins, the charge-surface correlation appears to be maintained. Indeed, the line representing the least squares fit for the CH₃CO₂N(CH₃)H₃ data has the same slope as the CH₃CO₂NH₄ data fit (gray and black lines in Figure 6B). This remarkable result suggests that the charge-surface correlation reported in the present work is a universal feature of ESI, rather than an isolated phenomenon specific to one particular type of solvent.

Using the empirical charge-surface correlation to estimate surface area of a non-globular protein assembly

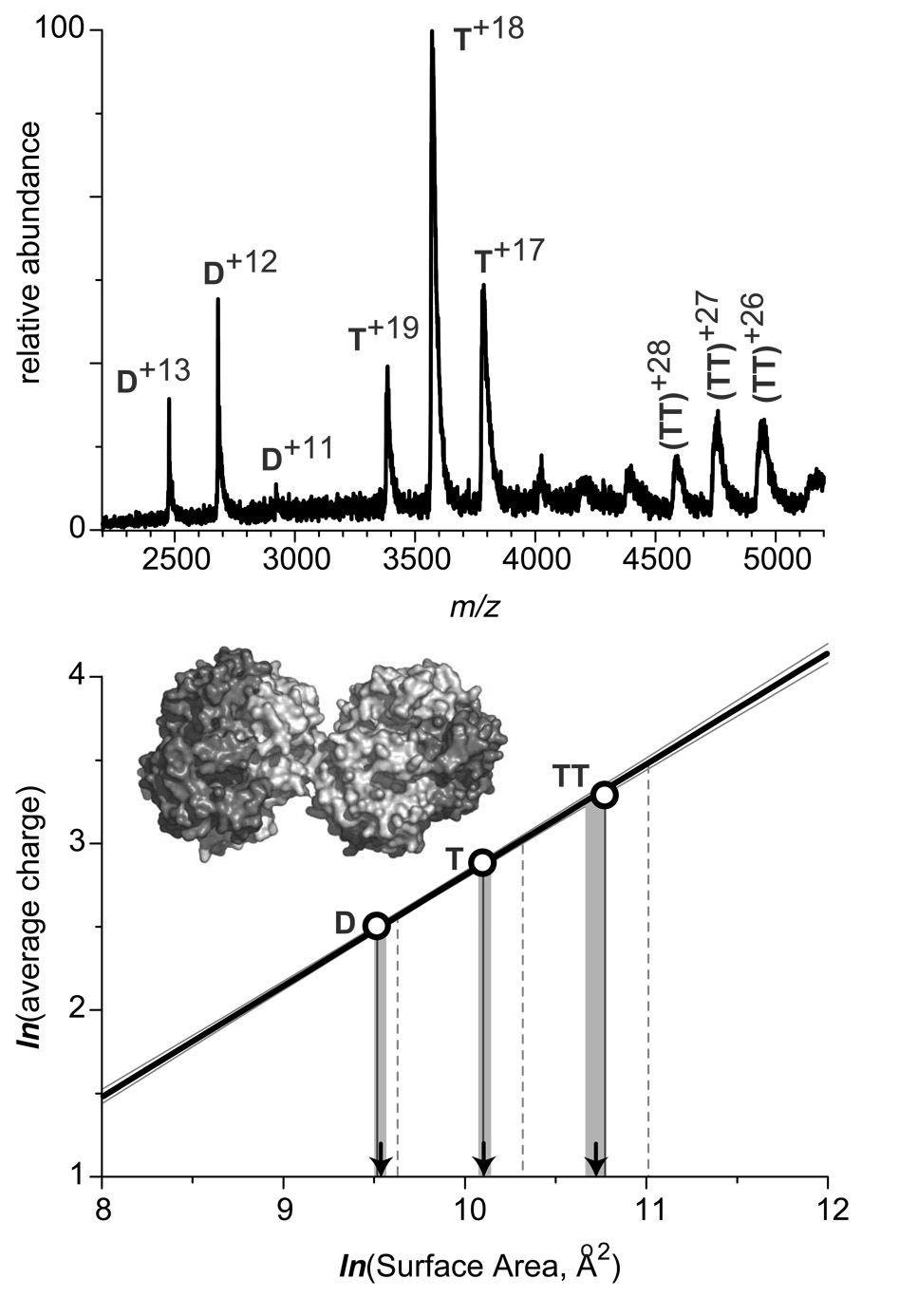
In order to evaluate the usefulness of the charge-surface correlation reported in this work as a means of characterizing protein assemblies in solution, we have attempted to estimate surface area of a non-globular protein assembly by measuring the average charge of protein ions in ESI MS and using the charge-surface correlation (Figure 2) as a “calibration curve.” A very clear example of a non-globular protein assembly is presented by the octameric form of sickle cell hemoglobin (HbS), which is often viewed as a precursor to HbS polymerization in red blood cells, a process leading to erythrocyte deformation.³⁸ The contact area between two tetramers in the octameric structure of HbS is very limited, giving the entire assembly an appearance of “touching spheres” (see the insert in Figure 7).

Figure 7.

ESI mass spectrum of human sickle cell hemoglobin (40 µM solution, calculation of molar concentration is based on the tetrameric structure) acquired at neutral pH in 10 mM ammonium acetate. The diagram at the bottom illustrates evaluation of surface areas of dimers (D), tetramers (T), and octamers (TT) based on the experimentally measured average number of charges accommodated by the respective protein ions and the previously determined charge-surface correlation. The calibration line in this diagram is the least squares fit for the experimental data presented in Figure 2 (none of the sickle cell hemoglobin species was used to construct the calibration curve). Vertical lines projected from the x-axis represent the numerical values of surfaces of the protein species based upon crystal structures of oligomers (solid) and simple summation of the surfaces of the constituent monomeric species (dashed). Arrows indicate the numerical value of surfaces estimated based on the ESI MS data, with shaded areas representing confidence intervals for such estimates.

In order to avoid excessive HbS oligomerization, an ESI mass spectrum of a diluted HbS sample was acquired under aerobic conditions (shown in the upper panel of Figure 7). The octamer ion signal (labeled TT) is prominent in the spectrum, as are the dimer (D) and tetramer (T) ionic components. Average charges have been calculated for each of these three species, and the surface areas of the corresponding assemblies were calculated using the previously found charge-surface correlation as a calibration curve (bottom panel on Figure 7). Surface areas of all three species estimated using this procedure are indicated with arrows on the graph (1.40·10⁴ Ų for D, 2.48·10⁴ Ų for T, and 4.56·10⁴ Ų for TT) and appear to match reasonably well the surfaces calculated based on the available crystal structure, which are indicated with solid vertical lines on the graph (1.36·10⁴ Å2 for D, 2.43·10⁴ Ų for T, and 4.76·10⁴ Ų for TT). The most significant deviation (4%) is observed for the octameric species, most likely due to its highly concave shape. This deviation, however, is insignificant when compared to the difference between the crystal structure-based surface of HbS octamer and the surface estimate produced by simple summation of the solvent-exposed surface areas of its monomeric constituents of 60,900 Ų (Figure 7B, vertical dashed lines), which corresponds to a 34% deviation from the surface calculated based on HbS crystal structure. Therefore, it appears that the charge-surface correlation can be used to provide reasonable estimates of solvent-shielded surface at protein-protein interfaces within macromolecular assemblies in solution.

The present example also illustrates an important advantage of protein surface estimation based on ESI MS measurements, namely its ability to carry out the analyses in heterogeneous systems. At least three different protein species are present in solution at equilibrium, yet evaluations of their solvent-exposed surfaces can be carried out simultaneously and do not require sophisticated signal deconvolution procedures to be employed in the case when scattering techniques are used for the same purpose.

CONCLUSIONS

The results of the present study provide very strong indication that protein surface area is the major determinant of the number of charges accommodated by the protein ions generated by ESI MS, even when the protein does not have an adequate number of basic residues. While some previous reports hinted that the charge-surface correlation is nearly linear,³⁹ such a conclusion was based upon a limited set of relatively small proteins. Careful measurements of the extent of multiple charging within an expanded set of proteins used in the present study, ranging from a 5 kDa insulin to 0.5 MDa ferritin, allows us to conclude that the charge-surface correlation is represented mathematically as a power function of 0.69±0.02. This notion is in excellent agreement with the current understanding of charge partitioning during the electrospray process and disintegration of jets emitted from conducting liquid droplets charged to the Rayleigh limit. It appears that the observed charge-surface correlation can be used to provide reasonable estimates of protein surface areas in solution. Although this method cannot presently rival the established techniques as far as measurement precision, it may be extremely useful for characterization of protein assemblies in solution that are not amenable to analysis using traditional biophysical tools due to their transient nature or heterogeneous character. Other important advantages offered by the ESI MS-based method include very modest sample consumption and relative ease of sample work-up and data analysis.

We have previously observed a noticeable increase in the average charge of protein ions in ESI mass spectra as a result of glycosylation,¹⁷ although it remains to be seen if the surfaces of extensively glycosylated proteins can be quantitated in the same straightforward fashion as carbohydrate-free proteins. We are also beginning to explore the utility of this technique as a tool for estimating solvent-exposed surface areas of other non-protic biopolymers, such as oligonucleotides, as well their non-covalent associations with proteins. We are keen on determining whether or not this straightforward analysis can be applied for quantitatively estimating the increases in solvent-accessible surface areas of proteins upon their unfolding in solution, a task that is currently out of reach of any other experimental technique.