Semiparametric estimation of covariance matrices for longitudinal data

Abstract

Estimation of longitudinal data covariance structure poses significant challenges because the data are usually collected at irregular time points. A viable semiparametric model for covariance matrices was proposed in Fan, Huang and Li (2007) that allows one to estimate the variance function nonparametrically and to estimate the correlation function parametrically via aggregating information from irregular and sparse data points within each subject. However, the asymptotic properties of their quasi-maximum likelihood estimator (QMLE) of parameters in the covariance model are largely unknown. In the current work, we address this problem in the context of more general models for the conditional mean function including parametric, nonparametric, or semi-parametric. We also consider the possibility of rough mean regression function and introduce the difference-based method to reduce biases in the context of varying-coefficient partially linear mean regression models. This provides a more robust estimator of the covariance function under a wider range of situations. Under some technical conditions, consistency and asymptotic normality are obtained for the QMLE of the parameters in the correlation function. Simulation studies and a real data example are used to illustrate the proposed approach.

1 Introduction

Longitudinal data (Diggle, Heagerty, Liang and Zeger, 2002) are characterized by repeated observations over time on the same set of individuals. Observations on the same subject tend to be correlated. As a result, one core issue for analyzing longitudinal data is the estimation of its covariance structure. Good estimation of the covariance structure improves the efficiency of model estimation and results in better predictions of individual trajectories over time. However, the challenge of covariance matrix estimation comes from the fact that measurements are often taken at sparse and subject-dependent irregular time points, as illustrated in the following typical example.

Progesterone, a reproductive hormone, is responsible for normal fertility and menstrual cycling. The longitudinal hormone study on progesterone (Sowers et al., 1998) collected urine samples from 34 healthy women in a menstrual cycle on alternative days. Zhang et al. (1998) analyzed the data using semi-parametric stochastic mixed models. A total of 492 observations were made on the 34 subjects in the study, with between 11 and 28 observations per subject. Menstrual cycle lengths of the subjects ranged from 23 to 56 days and averaged 29.6 days. Biologically it makes sense to assume that the change in progesterone level for a woman depends on the time during a menstrual cycle relative to her cycle length. So the menstrual cycle length of each woman was standardized (Sowers et al., 1998). A typical logarithmic transformation is applied on the progesterone level to make the data more homoscedastic. The progesterone data are unbalanced in that different subjects have different numbers of observations, and observation times are not regular and differ from one subject to another.

To address these challenges in covariance matrix estimation, Fan et al. (2007) modeled the variance function nonparametrically and correlation structure parametrically. They mainly focused on the improvement in the estimation of the mean regression function using a possibly misspecified covariance structure. In this work, we focus on semiparametric modeling of the covariance matrix itself with emphasis on the asymptotic properties of the QMLE of parameters in correlation function. We therefore study the problem under a general mean-regression model

$$y(t)=m(\mathit{x}(t))+\epsilon (t),t\in \mathcal{T},$$ (1)

where t indexes time in the longitudinal data and the conditional mean function m(x) = E(Y|X = x) can be parametric, nonparametric, or semi-parametric. The semi-parametric covariance structure is specified as

$$\text{Var}(\epsilon (t))={\sigma }^2(t),\text{corr}(\epsilon (s),\epsilon (t))=\rho (s,t,\mathit{\theta }),$$

where ρ(·, ·, θ) is a positive definite function for any θ ∈ θ ⊂ ℝ^d. The model is flexible, especially when the number of parameters in θ is large. On the other hand, the model is estimable even when individuals have only a few data points observed sparsely in time. The variance function can be estimated using the marginal information of the data, as long as the aggregated time points of all subjects are dense in time. The parameters θ can be estimated by aggregating information from all individuals whose responses are observed at two or more time points. The novelty of this family of models is that it takes time sparsity and irregularity of longitudinal data at its heart.

This semiparametric covariance structure is very flexible and basically covers any possibility by allowing more parameters in the correlation structure. For example, one may consider a convex combination of different parametric correlation structures such as ARMA or random effect models. However, generally correct specification of the correlation structure requires relatively few parameters. For the progesterone data, the response is taken as the change of progesterone level from an individual’s average level. Biologically we can imagine that, for two observations on the same subject, the closer their observation times the higher correlation in the response. Hence we use an ARMA(1, 1) correlation structure while analyzing the progesterone data in Section 6.

Our approach of flexible covariance structure estimation sheds light on solving a longstanding problem on improving the efficiency of parameter estimation using ideally the unknown true covariance structure. In a seminal paper, Liang and Zeger (1986) introduced generalized estimating equations (GEE), extending generalized linear models to longitudinal data, and proposed using a working correlation matrix to improve efficiency. However, misspecification of the working correlation matrix is possible. To improve efficiency under misspecification, Qu, Lindsay and Li (2000) represented the inverse of the working correlation matrix by a linear combination of basis matrices and proposed a method using quadratic inference functions. Their theoretical and simulated results showed better efficiency than GEE when misspecification occurs. In a nonparametric setting, Lin and Carroll (2000) extended GEE to kernel GEE and showed a rather unexpected result that higher efficiency is obtained by assuming independence, than by using the true correlation structure. In their later work, it was shown that the true covariance function can be used to improve the variance of a nonparametric estimator. Wang (2003) provided a deep understanding for this result, proposed an alternative kernel smoothing method, and established the asymptotic result that the new estimator achieves the minimum variance when the correlation is correctly specified. Wang, Carroll and Lin (2005) extended it to the semi-parametric, partially linear models. All these works require specifying a true correlation matrix, but do not provide a systematic estimation scheme. Our method provides a flexible approach to this important endeavor.

There are several approaches for estimating a covariance matrix. Most are nonpara-metric. Wu and Pourahmadi (2003) used non-parametric smoothing to regularize the estimation of large covariance matrix based on the method of two-step estimation studied by Fan and Zhang (2000). Huang, Liu and Liu (2007) used the modified Cholesky decomposition of the covariance matrix, proposed a more direct approach of smoothing, and claimed their estimation is more efficient than Wu and Pourahmadi (2003)’s. Bickel and Levina (2006) investigated the regularization of covariance matrix via the idea of banding and obtained many insightful results. See also Rothman et al. (2007). All these aforementioned estimation methods have the same limitation that observations are assumed to be made over a grid, i.e., balanced or nearly balanced longitudinal data. But this assumption is often not tenable, especially for longitudinal data that are commonly collected at irregular and possibly subject-specific time points. This feature of longitudinal data makes it challenging to study its covariance structure. Yao, Müller and Wang (2005a,b) took a different approach based on functional data analysis.

The remainder of the paper is organized as follows. In Section 2 we discuss estimation of the conditional mean function m(x). We focus on semi-parametric, varying-coefficient, partially linear models for which we propose a more robust estimation scheme. Section 3 presents the estimation method for the semi-parametric covariance structure. The asymptotic properties of the estimated variance function and correlation structure parameter are given in Section 4. Extensive simulation studies and an application to the progesterone data are given in Sections 5 and 6, respectively. Technical proofs appear in the Appendix.

2 Semi-parametric varying-coefficient partially linear model

Our data consist of a series of observations made on a random sample of n subjects from model (1). We denote a generic subject with J pairs of observation (x(t_j), y(t_j)) at times {t_j} from model (1) by = {J, (t_j, x(t_j), y(t_j)), j = 1, 2, ···, J} , with data from subject i denoted by _i = {J_i, (t_ij, x_i(t_ij), y_i(t_ij)), j = 1, 2, ···, J_i} . Thus the complete data set is represented as { ₁, ₂, ···, _n} .

Note that our semiparametric specification of the covariance structure has little requirement on m(x) in (1). It can be of any form as long as it is consistently estimated. In this section we focus on the semi-parametric, varying-coefficient, partially linear model considered in Fan et al. (2007),

$$m(\mathit{x}(t))=m({\mathit{x}}_1(t),{\mathit{x}}_2(t))={\mathit{x}}_1{(t)}^T\mathit{\alpha }(t)+{\mathit{x}}_2{(t)}^T\mathit{\beta },$$ (2)

where $\mathit{x}={({\mathit{x}}_1^T,{\mathit{x}}_2^T)}^T$, x₁ ∈ℝ^d₁, and x₂ ∈ℝ^d₂. It includes parametric and nonparametric models as special cases. Denote the true coefficients by α₀(·) and β₀. In this case, denote the covariates at the j-th observation time of subject i by x_1,i(t_ij) and x_2,i(t_ij).

To estimate the varying-coefficient partially linear model, Fan et al. (2007) assumed the existence of a second-order derivative of α₀(·). However this assumption is not always desirable. For example, it does not hold for continuous piecewise linear α₀(·). When α₀(·) is rough as in Example 5.3 in Section 5, estimation can be badly affected. In reality, α₀(·) can be rough as well. For example, it occurs when there is some structure break or technical innovation that cause the change-point in time.

Departing from Fan et al. (2007), we consider (2) under a much weaker smoothness assumption on α₀(·) as stated in Condition [L] and propose a more robust estimation scheme for m(·) than their profiling scheme.

[L] There are constants a₀ > 0 and κ > 0 such that || α₀(s) − α₀(t) || ≤ a₀|t − s|^κ when |t − s| is small for 0 ≤ s, t ≤ T.

2.1 Difference-based estimator of β

In this section we use a difference-based technique to estimate the parametric regression coefficient β under the Lipschitz condition [L] on α₀(·). A comparison study in Section 5 shows its remarkable improvement when α₀(·) is rough. This technique has been used to remove the nonparametric component in the partial linear model or nonparametric heteroscedastic model by various authors (Yatchew, 1997; Fan and Huang, 2001, 2005; Brown and Levine, 2007, to name a few), but all in the univariate nonparametric setup. In our setting, multiple nonparametric functions are needed to be removed and new ideas are required.

To apply the difference-based technique, we sort our data in the increasing order of the observation time t_ij and denote them as {(t_(j), x_1(j), x_2(j), y_(j)), j = 1, 2, ···, N}, where $N={\sum }_{i=1}^n{J}_i$. Under mild conditions, the spacing t_(i+j) − t_(i) can be shown to be of order O_p(1/N) = O_p(1/n) for each given j. Condition [L] implies that

$$\parallel {\mathit{\alpha }}_0(t_{(i+j)})-{\mathit{\alpha }}_0(t_{(i)})\parallel =O_p({(t_{(i+j)}-t_{(i)})}^{\kappa })=O_p(1/n^{\kappa }),\text{for}j=1,2,\cdots ,d_1.$$ (3)

For any i between 1 and N − d₁, choose weights w_i,j, j = 1, 2, ···, N, and define the following weighted variables:

$$y_{(i)}^{\ast }=\sum _{j=i}^{i+d_1}{w}_{i,j}{y}_{(j)},{\mathit{x}}_{2(i)}^{\ast }=\sum _{j=i}^{i+d_1}{w}_{i,j}{\mathit{x}}_{2(j)},{\epsilon }_{(i)}^{\ast }=\sum _{j=i}^{i+d_1}{w}_{i,j}{\epsilon }_{(j)}.$$

The weights w_i,j’s are selected such that

$$\sum _{j=i}^{i+d_1}{w}_{i,j}{\mathit{x}}_{1(j)}=\mathbf{0},\text{for}\text{all}i,1\le i\le N-d_1$$ (4)

to remove the nonparametric component x₁(t)^Tα(t). The weights are further normalized as in Hall, Kay and Titterington (1990) such that ${\sum }_{j=1}^N{w}_{i,j}^2=1$. Note that if x_1(i), x_1(i+1), ···, x_{1(i+ d1− 1)} are linearly independent (which holds with probability one under some mild conditions for continuously distributed x₁), the weights are uniquely determined up to a sign change. More explicitly,

$$(w_{i,i},w_{i,i+1},\cdots ,w_{i,i+d_1})=\pm \frac{({({({\mathit{x}}_{1(i)},{\mathit{x}}_{1(i+1)},\cdots ,{\mathit{x}}_{1(i+d_1-1)})}^{-1}{\mathit{x}}_{1(i+d_1)})}^T,-1)}{\parallel ({({({\mathit{x}}_{1(i)},{\mathit{x}}_{1(i+1)},\cdots ,{\mathit{x}}_{1(i+d_1-1)})}^{-1}{\mathit{x}}_{1(i+d_1)})}^T,-1)\parallel }.$$ (5)

Without loss of generality, we can take positive sign in (5) and denote the corresponding (N − d₁) × N weight matrix by W whose (i, j)-element is w_i,j. Denoting X̃₂ = (x₂₍₁₎, x₂₍₂₎, ···, x_2(N))^T, we have ${\mathit{X}}_2^{\ast }={({\mathit{x}}_{2(1)}^{\ast },{\mathit{x}}_{2(2)}^{\ast },\cdots ,{\mathit{x}}_{2(N-d_1)}^{\ast })}^T=\mathit{W}{\stackrel{\sim }{\mathit{X}}}_2$.

A combination of (2)–(4) leads to

$$y_{(i)}^{\ast }\approx {({\mathit{x}}_{2(i)}^{\ast })}^T\mathit{\beta }+{\epsilon }_{(i)}^{\ast },i=1,2,\cdots ,N-d_1,$$ (6)

where the approximation error is of order O_p(1/n^κ).

Model (6) is a standard multivariate linear regression problem. Applying the OLS technique on (6) with data $\left\{({\mathit{x}}_{2(i)}^{\ast },y_{(i)}^{\ast }),i=1,2,\cdots ,N-p\right\}$, we get the difference-based estimator (DBE) of β. Due to the fact that the approximation error in (6) is of order O_p(1/n^κ), standard result for the OLS implies that our DBE β̂ is consistent with order n^−κ∧0.5, where a ∧ b = min(a, b).

In general, one may use d₁ + k (k > 1) neighboring observations to remove the nonparametric terms. In such a case, the weights are not uniquely determined and it is complicated to find an optimal weighting scheme.

2.2 Kernel smoothing estimator of α(·)

Plug the consistent DBE β̂ into model (2) and define ỹ(t) = y(t) − x₂(t)^Tβ̂. Model (2) becomes

$$\stackrel{\sim }{y}(t)\approx {\mathit{x}}_1{(t)}^T\mathit{\alpha }(t)+\epsilon (t),$$ (7)

with approximation error of order O_p(n^−κ∧0.5). Model (7) is exactly a varying-coefficient model, and was studied by Hastie and Tibshirani (1993) for the case of i.i.d. observations and also by Fan and Zhang (2000) in the context of longitudinal data. Local smoothing technique can be used to estimate α(·). Due to the weak Lipschitz Condition [L] on true α₀(·), we use the local constant regression (Nadaraya-Watson estimator) to estimate α(·) based on data {(t_ij, x_1,i(t_ij), ỹ_i(t_ij)), j = 1, 2, ···, J_i; i = 1, 2, ···, n}.

Note that, for any t in a neighborhood of t₀, due to Condition [L] we have

$${\alpha }_{0l}(t)\approx {\alpha }_{0l}(t_0)+O(\mid t-t_0{\mid }^{\kappa }),\text{for}l=1,2,\cdots ,q,$$

where α_0l(·) is the l-th component of α₀(·). Local constant regression estimates α(t₀) by minimizing

$$\sum _{i=1}^n\sum _{j=1}^{J_i}{({\stackrel{\sim }{y}}_i(t_{ij})-{\mathit{a}}^T{\mathit{x}}_{1,i}(t_{ij}))}^2{K}_b(t_{ij}-t_0)$$ (8)

with respect to a = (a₁, a₂, ···, a_q)^T. Denote ỹ = (ỹ₁(t₁₁), ỹ₁(t₁₂), ···, ỹ_n(t_nJn))^T and K_t0= diag(K_b(t₁₁ − t₀), K_b(t₁₂ − t₀), ···, K_b(t_nJn − t₀)). The local constant regression estimator of α(t₀) is

$$\widehat{\mathit{\alpha }}(t_0)\equiv \widehat{\mathit{\alpha }}(t_0,\widehat{\mathit{\beta }})=\widehat{\mathit{a}}={({\mathit{X}}_1^T{\mathit{K}}_{t_0}{\mathit{X}}_1)}^{-1}{\mathit{X}}_1^T{\mathit{K}}_{t_0}\stackrel{\sim }{\mathit{y}},$$

where X₁ = (x_1,1(t₁₁), x_1,1(t₁₂), ···, x_1,n(t_nJn))^T. Typical asymptotic nonparametric convergence rate applies to the local constant regression estimator α̂(·) and the rate is of order $O_p(b^{\kappa }+1/\sqrt{nb})=O_p(n^{-\kappa /(2\kappa +1)})$ when b = O(n^−1/(2κ+1)).

3 Estimation of semi-parametric covariance

We assume that m(·) can be consistently estimated by some method depending on its particular form. This consistency assumption is formulated as Condition (iii) in the Appendix. We next present our estimation scheme of the semi-parametric covariance structure.

3.1 Estimation of the variance function

Denote the estimated conditional mean function by m̂(·). Plug it into (1) and define the estimated realizations of the random errors as follows

$$r_{ij}\equiv r_{ij}(\widehat{m}(·))=y_i(t_{ij})-\widehat{m}({\mathit{x}}_i(t_{ij})),$$ (9)

that consistently estimate the realized random errors ε_i(t_ij) due to the consistency assumption on m̂(·).

Based on r_ij, we use the kernel smoothing to estimate the variance function σ²(t) = Eε²(t), via

$${\widehat{\sigma }}^2(t)=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{r}_{ij}^2{K}_h(t-t_{ij})}{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{K}_h(t-t_{ij})},$$ (10)

where h is a smoothing parameter and K_h(·) = K(·/h)/h is a rescaling of the kernel K(·). The estimator of σ²(t) was studied by Fan and Yao (1998) using local linear regression.

3.2 Estimation of the correlation structure parameter

For each subject i, denote corr(ε_i) by C(θ; i) whose (j, k)-element is ρ(t_ij, t_ik, θ), r_i = (r_i1, r_i2, ···, r_iJi)^T, and V̂_i = diag{σ̂(t_i1), σ̂(t_i2), ···, σ̂(t_iJi)} .

We estimate the correlation structure parameter θ by quasi-maximum likelihood method,

$$\widehat{\mathit{\theta }}=\underset{\mathit{\theta }\in \mathrm{\Theta }}{\text{argmax}}\sum _{i=1}^n\left\{-\frac{1}{2}log\mid \mathit{C}(\mathit{\theta };i)\mid -\frac{1}{2}{\mathit{r}}_i^T{\widehat{\mathit{V}}}_i^{-1}\mathit{C}{(\mathit{\theta };i)}^{-1}{\widehat{\mathit{V}}}_i^{-1}{\mathit{r}}_i\right\}.$$

Denote by ζ(t) ≡ ε(t)/σ(t). For a generic subject with J observations, the “standardized” random error vector ζ= (ζ(t₁), ζ(t₂), ···, ζ(t_J ))^T is assumed to follow an elliptically contoured distribution, having a multivariate density function proportional to |C(θ₀)|^−1/2 h₀(ζ^TC(θ₀)⁻¹ζ), where C(θ₀) is the correlation matrix with its (i, j)-element ρ(t_i, t_j, θ₀) for 1 ≤ i, j ≤ J and h₀(·) is an arbitrary univariate density function defined on [0, ∞).

In the next section, we show that the QMLE θ̂ is consistent and also enjoys asymptotic normality when the correlation structure ρ(·, ·, θ) is correctly specified.

When the gaps between some observation times are too close (below a threshold) for some individuals, the matrix C(θ; i) can be ill-conditioned. In this case, we can either delete some of their observations or remove those cases, thus reducing the influence of those individuals. Under Condition (ii), such cases are rare as individuals have no more than (log n) observations.

4 Sampling properties

In this section, we study large-sample properties of the estimators presented in Section 3 for the semi-parametric covariance structure in our model (1).

To derive asymptotic properties, we assume that the data is a random sample collected from the population process {y(t), x(t)} as described by model (1) with true conditional mean function m₀(·), variance function ${\sigma }_0^2(·)$, and correlation structure parameter θ₀ over a bounded time domain, t ∈[0, T] for some T > 0. To ease our presentation, we further assume that observation numbers J_i, i = 1, 2, ···, n, are independent and identically distributed and Condition (ii) is satisfied. For each subject i, given the number of observations J_i, observation times t_ij, j = 1, 2, ···, J_i, are independently and identically distributed with density function f(t). Large-sample properties of our estimators are stated in Theorems 1-3. Technical conditions and proofs are relegated to the Appendix.

4.1 Estimator of the covariance structure

Denote by ${\stackrel{.}{\sigma }}_0^2(·)$ and ${\ddot{\sigma }}_0^2(·)$ the first and second derivatives of the variance function ${\sigma }_0^2(·)$, respectively.

Theorem 1

Under Conditions (i-v), if $h\propto n^{-\frac{1}{5}}$, then, as n → ∞,

$$\sqrt{nh}\{{\widehat{\sigma }}^2(t)-{\sigma }_0^2(t)-b(t)\}\stackrel{ℒ}{\to }N(0,v(t)),$$ (11)

where the bias and variance are given by $b(t)=h^2{\mu }_2[{\ddot{\sigma }}_0^2(t)+2{\stackrel{.}{\sigma }}_0^2(t)f^{\prime }(t)/f(t)]/2$ and υ(t) = Var(ε²(t))ν₀/(f(t)E(J₁)), respectively, with μ₂ = u²K(u)du and ν₀ = K²(u)du.

When the correlation structure ρ(·, ·, θ) is correctly specified, our next two theorems establish the consistency and asymptotic normality of the QMLE θ̂.

Theorem 2 (Consistency)

For model (1) with the elliptical density assumption on the random error trajectory, under Conditions (i)-(x) listed in Appendix, and with h specified in Theorem 1, the QMLE θ̂ is consistent, i.e.,

$$\widehat{\mathit{\theta }}\to {\mathit{\theta }}_0,in\mathit{probability},asn\to \infty .$$ (12)

Denote the d× d Fisher information-like matrix by I(θ₀) whose (i, j)-element is given by

$$E_{\mathbb{X}}\left\{\frac{1}{2}tr[{\mathit{C}}^{-1}({\mathit{\theta }}_0){\mathit{C}}_i({\mathit{\theta }}_0){\mathit{C}}^{-1}({\mathit{\theta }}_0){\mathit{C}}_j({\mathit{\theta }}_0)]\right\},$$

where C(θ₀) is the correlation matrix of a generic subject , ${\mathit{C}}_i(\mathit{\theta })=\frac{\partial \mathit{C}(\mathit{\theta })}{\partial {\theta }_i},{\mathit{C}}^i(\mathit{\theta })=\frac{\partial {\mathit{C}}^{-1}(\mathit{\theta })}{\partial {\theta }_i}=-{\mathit{C}}^{-1}(\mathit{\theta }){\mathit{C}}_i(\mathit{\theta }){\mathit{C}}^{-1}(\mathit{\theta })$ and the expectation is due to the randomness of the observation times and taken with respect to the true underlining population distribution of . The subscript in E is dropped whenever there is no confusion. Similarly, derivatives are defined for C(θ, m) and Σ(θ) denotes a d × d matrix whose (i, j)-element is given by

$$E_{\mathbb{X}}\left\{\frac{1}{4}(-tr[{\mathit{C}}^{-1}(\mathit{\theta }){\mathit{C}}_i(\mathit{\theta })]tr[{\mathit{C}}^{-1}(\mathit{\theta }){\mathit{C}}_j(\mathit{\theta })]+{\mathit{\zeta }}^T{\mathit{C}}^i(\mathit{\theta })\mathit{\zeta }{\mathit{\zeta }}^T{\mathit{C}}^j(\mathit{\theta }))\mathit{\zeta }\right\}.$$

Theorem 3 (Asymptotic normality)

Under conditions of Theorem 2, we have

$$\sqrt{n}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)\stackrel{ℒ}{\to }N(0,\mathit{I}{({\mathit{\theta }}_0)}^{-1}\mathbf{\sum }({\mathit{\theta }}_0)\mathit{I}{({\mathit{\theta }}_0)}^{-1}).$$ (13)

Remark 1

In Theorem 3, the asymptotic variance-covariance matrix of θ̂ has the sandwich form Δ = I(θ₀)⁻¹Σ(θ₀)I(θ₀)⁻¹, that can be estimated by Δ̂ = Î⁻¹Σ̂Î⁻¹. More explicitly, the (i, j)-element of Î and Σ̂ are given by

$$\frac{1}{2n}\sum _{m=1}^{n}tr\left[{\mathit{C}}^{-1}(\widehat{\mathit{\theta }};m){\mathit{C}}_i(\widehat{\mathit{\theta }};m){\mathit{C}}^{-1}(\widehat{\mathit{\theta }};m){\mathit{C}}_j(\widehat{\mathit{\theta }};m)\right]$$

and

$$\frac{1}{4n}\sum _{m=1}^n\left\{-tr[{\mathit{C}}^{-1}(\widehat{\mathit{\theta }};m){\mathit{C}}_i(\widehat{\mathit{\theta }};m)]tr[{\mathit{C}}^{-1}(\widehat{\mathit{\theta }};m)C_j(\widehat{\mathit{\theta }};m)]+{\widehat{\mathit{\zeta }}}_m^T{\mathit{C}}^i(\widehat{\mathit{\theta }};m){\widehat{\mathit{\zeta }}}_m{\widehat{\mathit{\zeta }}}_m^T{C}^j(\widehat{\mathit{\theta }};m){\widehat{\mathit{\zeta }}}_m\right\},$$

where ζ̂_m is the estimated “standardized” random errors for the m-th subject as defined in the Appendix.

4.2 Verification of spectrum condition on correlation matrices

Note that the structural condition (viii) in the Appendix is very common when studying covariance matrices. In this section, we consider several parametric correlation structures: AR(1), ARMA(1,1), and more generally CARMA(p, q) (Continuous-time ARMA of orders p and q, q < p), for which we show that Condition (viii) holds.

For AR(1) and ARMA(1,1), the parametric correlation structure ρ(s, t, θ) can be parameterized as ρ(s, t, ϕ) = exp(− |s − t|/ϕ) and ρ(s, t, (γ, ϕ)^T) = γ exp(− |s − t|/ϕ), respectively, with ϕ ≥ 0 and 0 ≤ γ ≤ 1. According to the autocovariance formula (A.2) of Phadke and Wu (1974), the correlation structure of CARMA(p, q) is a convex combination of p AR(1) correlation structures, i.e., $\rho (s,t,\mathit{\theta })={\sum }_{i=1}^p{\gamma }_{i}exp(-\mid s-t\mid /{\varphi }_i)$ with ϕ_i ≥ 0, 0 ≤ γ_i ≤ 1, and ${\sum }_{i=1}^p{\gamma }_i=1$.

Proposition 1

Let A be a K × K matrix with (i, j)-element (A)_ij = exp(− a|s_i − s_j|) where s₁ < s₂ < ···< s_K and a > 0.

1. Then the (i, j)-element of A⁻¹ is given by: (A⁻¹)₁₁ = (1 + coth(a(s₂ − s₁)))/2; (A⁻¹)_ii = (coth(a(s_i − s_i−1)) + coth(a(s_i+1 − s_i)))/2 for i = 2, 3, ···, K − 1; (A⁻¹)_KK = (1 + coth(a(s_K − s_K−₁)))/2; (A⁻¹)_ij = − (csch(a|s_i − s_j|))/2 for |i − j| = 1; (A⁻¹)_ij = 0 when |i − j| > 1, where coth(·) and csch(·) are the hyperbolic cotangent and cosecant functions.

2. If $\underset{i=2,3,\cdots ,K}{min}(s_i-s_{i-1})=s_0>0$, the eigenvalues of A⁻¹ are bounded between δ₀(s₀, a) = tanh(as₀/2) and δ₁(s₀, a) = 2 coth(as₀), where tanh(·) is the hyperbolic tangent function. Moreover, both δ₀ and δ₁ do not depend on K.

Proposition 2

Consider a generic subject , when $\underset{1\le j\ne k\le J}{min}\mid t_j-t_k\mid \ge t_0>0$, Condition (viii) is satisfied for either of the following three cases with some ϕ₀ > 0:

1. The AR(1) correlation structure: ρ(s, t, ϕ) = exp(− |s − t|/ϕ) with ϕ ∈[0, ϕ₀].

2. The ARMA(1, 1) correlation structure: ρ(s, t, (γ, ϕ)^T) = γ exp(− |s − t|/ϕ) when s ≠ t and 1 otherwise for (γ, ϕ) ∈[0, 1] × [0, ϕ₀].

3. The CARMA(p, q) correlation structure: $\rho (s,t,{({\gamma }_1,{\gamma }_2,\cdots ,{\gamma }_p,{\varphi }_1,{\varphi }_2,\cdots ,{\varphi }_p)}^T)={\sum }_{i=1}^p{\gamma }_{i}exp(-\mid s-t\mid /{\varphi }_i)$ with q < p, (γ_i, ϕ_i) 2 [0, 1] × [0, ϕ₀] for i = 1, 2, ··· , p, and ${\sum }_{i=1}^p{\gamma }_i=1$.

Remark 2

In practice, one may face the problem of identifying the order (p, q) for the CARMA correlation structure. This can be achieved using an AIC/BIC-related procedure because the estimation of the parametric correlation structure is based on maximum likelihood once we have estimated the regression function m(x) and the variance function σ²(t).

5 Monte Carlo Study

In this section, we study the finite-sample performance of the semi-parametric covariance matrix estimator presented in Section 3. While focusing on the varying-coefficient partially linear model in Example 5.2, we use Example 5.1 to demonstrate the efficiency improvement by incorporating the estimated covariance structure for the case of parametric models. A comparison study is provided in Example 5.3 to illustrate the robustness of our new proposed difference-based estimation scheme.

For all simulation examples, we set = [0, 13]. Each subject has a set of “scheduled” observation times {0, 1, ···, 12} and each scheduled time has a probability of 20% being skipped except the time 0. For each non-skipped scheduled time, the corresponding actual observation time is obtained by adding a standard uniform random variable on [0, 1]. The true variance function is chosen to be σ²(t) = 0.5 exp(t/12). Either a true AR(1) (Example 5.1) or a true ARMA(1,1) (Examples 5.2 and 5.3) correlation structure is assumed. That is, corr(ε(s), ε(t)) = γρ^|s−t| when s ≠ t and 1 otherwise. In AR(1), γ= 1. For a particular subject, given the number of observations J and the observation times t₁, t₂, ···, t_J , the “standardized” random error vector (ζ(t₁), ζ(t₂), ···, ζ(t_J ))^T have marginal Normal (N) or Double Exponential (DE) distribution with mean zero, variance one, and correlation matrix C(γ, ρ; t₁, t₂, ···, t_J ) whose (i, j)-element is γρ^|t_i−t_j| when i ≠ j and 1 otherwise.

If not specified, our simulation result is based on 1000 independent repetitions and each training sample is of size 200. The Epanechnikov kernel is used whenever a kernel is needed. For an estimator of a functional component, say σ²(·), we report its Root Average Squared Errors (RASE), which is defined as $\text{RASE}({\widehat{\sigma }}^2)=\sqrt{{\sum }_{k=1}^K{({\widehat{\sigma }}^2(t_k)-{\sigma }^2(t_k))}^2/K}$, where {t_k : k = 1, 2, ···, K} form a uniform grid. The number of grid points K is set to be 200 in our simulations. After tuning, these necessary smoothing parameters are fixed and used for each independent repetition.

In Tables 1-5, the first and the second column blocks designate the marginal distribution type of the “standardized” random error and the correlation structure parameter, respectively.

Table 1.

Finite-sample performance for estimating β, σ²(·) and ρ.

Noise	ρ	β̂1	β̂2	β̂3	RASE(σ̂2)	ρ̂	ASE
N	0.30	1.9993 (0.0236)	1.5002 (0.0266)	2.9991 (0.0237)	0.0493 (0.0456)	0.2997 (0.0219)	0.0263
	0.60	1.9995 (0.0237)	1.5002 (0.0264)	2.9993 (0.0235)	0.0565 (0.0509)	0.5988 (0.0172)	0.0165
	0.90	1.9996 (0.0238)	1.4998 (0.0259)	3.0000 (0.0231)	0.0702 (0.0605)	0.8981 (0.0077)	0.0041
DE	0.30	1.9992 (0.0244)	1.5001 (0.0260)	2.9999 (0.0235)	0.0692 (0.0622)	0.3000 (0.0227)	0.0241
	0.60	1.9993 (0.0246)	1.5002 (0.0257)	2.9997 (0.0235)	0.0732 (0.0656)	0.5992 (0.0173)	0.0172
	0.90	1.9995 (0.0246)	1.5003 (0.0258)	2.9994 (0.0241)	0.0797 (0.0704)	0.8981 (0.0075)	0.0050

Table 5.

Finite-sample performance of prediction

Noise	(γ, ρ)	prediction 1	prediction 2	prediction 3	prediction 4	prediction 5	# of predictions
N	(0.85, 0.30)	1784.06	1799.02 (10.28)	1799.77 (10.48)	1884.51	1899.89 (10.22)	2124
	(0.85, 0.60)	1327.10	1352.88 (9.65)	1353.64 (9.82)	1766.82	1794.50 (10.32)	2095
	(0.85, 0.90)	754.34	788.16 (11.33)	788.27 (11.32)	1891.00	1917.81 (19.54)	2068

Example 5.1[Parametric model]

In this example, the covariate is three-dimensional, i.e., x = (x₁, x₂, x₃)^T ∈ℝ ³, with standard normal marginal distribution and correlation corr(x_i, x_j) = 0.5^|i−j|. The true regression parameter vector is set to be β₀ = (2, 1.5, 3)^T. An AR(1) correlation structure is used with three different parameter values, ρ = 0.3, 0.6, 0.9. After tuning, the best smoothing bandwidth h = 2.53 is used for estimating σ²(t).

Table 1 reports the mean and standard deviation (in parenthesis) of the OLS estimator of β in the third column block. The fourth and fifth correspond to the kernel estimator of σ²(·) and the QMLE of ρ, respectively. The last column gives the asymptotic standard errors (ASE) of QMLE ρ∘ using the formula (13) in Theorem 3 with estimated matrix I(θ₀) and Σ(θ₀) based on 1000 simulations.

The result indicates that our semiparametric covariance matrix estimation scheme works effectively. The RASE of σ̂²(·) and the QMLE ρ̂ are close to zero and the corresponding true ρ, respectively, for each case. This is consistent with the theoretical results. The standard deviation of QMLE ρ̂ is close to the corresponding ASE except for the high correlation case with ρ = 0.9. This can be explained by noting the proof of our asymptotic normality result. While proving Theorem 3, we need the upper bound of the eigenvalue of the inverse correlation matrix to control the effect of the estimation error in the previous estimation steps. For the AR(1) model this upper bound is guaranteed by Proposition 1. However ρ = 0.9 implies that, in Proposition 1, ϕ = − / log(0.9) = 9.49, which is relatively large. The problem disappears when the sample size is large. Similar phenomenon is observed as well for ARMA(1,1) correlation structure in Example 5.2.

For the parametric model m(x) = x^Tβ, we can incorporate the estimated covariance structure to estimate β using weighted least squares regression, whose performance is reported in Table 2. Comparing OLS and WLS estimators, we see that the standard deviation of the estimator of β is significantly reduced by incorporating the estimated covariance structure, especially in the case of high correlation ρ = 0.9.

Table 2.

Finite-sample performance of WLS estimator of β using estimated covariance structure.

Noise	ρ	β̂1	β̂2	β̂3
N	0.30	1.9994 (0.0190)	1.4996 (0.0217)	2.9993 (0.0199)
	0.60	1.9995 (0.0143)	1.4996 (0.0164)	2.9995 (0.0151)
	0.90	1.9998 (0.0069)	1.4998 (0.0079)	2.9998 (0.0073)
DE	0.30	1.9992 (0.0192)	1.5005 (0.0220)	3.0004 (0.0189)
	0.60	1.9994 (0.0144)	1.5004 (0.0167)	3.0004 (0.0143)
	0.90	1.9997 (0.0069)	1.5002 (0.0080)	3.0002 (0.0069)

Example 5.2[Semi-parametric varying-coefficient partially linear model]

In this example, data are generated from model (2), with ARMA(1,1) correlation structure on ε(t). In this case, x is four-dimensional with x₁ = (x₁, x₂)^T ∈ℝ ² and x₂ = (x₃, x₄)^T ∈ℝ ². We set the first component of x₁ to be constant one to include the intercept term, i.e., x₁(t) ≡ 1. For any given time t, x₂(t) and x₃(t) are jointly generated such that they have standard normal marginal distribution and correlation 0.5, and x₄(t) is Bernoulli-distributed with success probability 0.5, independent of x₂(t) and x₃(t). The regression coefficients are specified as follows,

$${\alpha }_1(t)=\sqrt{t/12},{\alpha }_2(t)=sin(2\pi t/12),\mathit{and}\mathit{\beta }={(1,2)}^T.$$

After tuning, we select the best smoothing bandwidths b = 1.25 and h = 2.53 for estimating α(·) and σ²(·), respectively.

Performance of estimating β, α(·) and σ²(·)

As x₁ ∈ℝ², DBE uses three neighboring (sorted) observations with weights given by (5) with positive sign. Mean and standard deviation (in parenthesis) of our DBE of β₁ and β₂ over 1000 repetitions are reported in the third column of Table 3 for three pairs of ARMA(1,1) correlation structure parameter θ^T = (γ, ρ) = (0.85, 0.30), (0.85, 0.60), (0.85, 0.90). Table 3 also displays the mean and standard deviation (in parenthesis) of the RASEs of α̂(·) and σ̂²(·) in the fourth and the fifth column blocks, respectively. From Table 3, we can see that the DBE of β, the local constant regression estimator of α(·), and the local kernel smoothing estimator of σ²(·) are very precise in the finite-sample case.

Table 3.

Finite-sample performance of estimating β, α(·), and σ²(·)

Noise	(γ, ρ)	β̂1	β̂2	RASE(α̂1)	RASE(α̂2)	RASE(σ̂2)
N	(0.85, 0.30)	1.0003 (0.0322)	1.9993 (0.0582)	0.0695 (0.0186)	0.0814 (0.0157)	0.0618 (0.0227)
	(0.85, 0.60)	1.0006 (0.0334)	2.0030 (0.0565)	0.0712 (0.0218)	0.0817 (0.0155)	0.0673 (0.0245)
	(0.85, 0.90)	1.0003 (0.0347)	1.9985 (0.0571)	0.0718 (0.0280)	0.0827 (0.0157)	0.0786 (0.0335)
DE	(0.85, 0.30)	0.9994 (0.0339)	1.9993 (0.0584)	0.0667 (0.0179)	0.0821 (0.0152)	0.0884 (0.0330)
	(0.85, 0.60)	0.9995 (0.0337)	1.9987 (0.0576)	0.0694 (0.0205)	0.0822 (0.0153)	0.0919 (0.0356)
	(0.85, 0.90)	0.9998 (0.0331)	2.0001 (0.0581)	0.0718 (0.0289)	0.0826 (0.0155)	0.0950 (0.0393)

Performance of QMLE of θ

Our QMLE θ̂ is based on the estimation of other components in our model. The result in Table 3 indicates that the estimators β̂, α̂(·) and σ̂²(·) perform very well. Hence we expect similarly good performance for the QMLE θ̂. Its simulation results are shown in Table 4. In Table 4, column three reports the mean of γ̂ and ρ̂, with their standard deviations in parentheses and their correlation in square bracket, and the last column gives asymptotic standard errors and correlation of γ̂ and ρ̂ using the formula (13) in Theorem 3 with estimated matrix I(θ) and Σ(θ) based on 1000 simulations.

Table 4.

Finite-sample performance of QMLE of θ

Noise	(γ, ρ)	(γ̂, ρ̂)	asymptotic covariance
N	(0.85, 0.30)	0.8458 (0.0677) 0.2995 (0.0439) [−0.7749]	(0.0636), (0.0407) [−0.7547]
	(0.85, 0.60)	0.8428 (0.0327) 0.6000 (0.0301) [−0.6432]	(0.0303), (0.0272) [−0.7281]
	(0.85, 0.90)	0.8427 (0.0153) 0.8990 (0.0106) [0.0351]	(0.0112), (0.0083) [−0.5898]
DE	(0.85, 0.30)	0.8479 (0.0772) 0.2996 (0.0462) [−0.7734]	(0.0741), (0.0442) [−0.7492]
	(0.85, 0.60)	0.8441 (0.0353) 0.5983 (0.0315) [−0.6638]	(0.0344), (0.0304) [−0.6545]
	(0.85, 0.90)	0.8421 (0.0155) 0.8984 (0.0113) [−0.0011]	(0.0129), (0.0094) [−0.3307]

From Table 4, we can see that the estimated parameters in the correlation structure are very close to the corresponding true ones for each case. This agrees with our consistency result. Next we check the accuracy of the estimated standard errors. For the cases with true correlation structure parameters θ^T = (γ, ρ) = (0.85, 0.3) or (0.85, 0.6), the standard deviation and correlation of our QMLE θ̂ is very close to the asymptotic standard errors and correlation (in the last column) using our asymptotic normality formulas. Similarly as in the previous example, we observe that the sample correlations deviate a lot from their corresponding simulated correlations using formula (13) for the two cases of higher correlation (γ, ρ) = (0.85, 0.9) and the same explanation applies here.

Prediction

As mentioned in the introduction, estimating the covariance structure can improve the prediction accuracy for a particular trajectory. In this example, we study the improvement of prediction after estimating the covariance structure. For each case, we generate an independent prediction data set of size 400 exactly in the same way as the training data set for estimation is generated. For each observation of these 400 subjects in the prediction data set, an independent Bernoulli random variable with success probability 0.5 is generated; if it is zero, the response of this observation is treated as \missing” and needs to be predicted; if it is one, this observation is fully observed and used to predict the \missing” ones. Prediction is made using the prediction formula given in Section 5.3 of Fan et al. (2007).

Table 5 reports the mean and standard deviation (in parenthesis) over 1000 repetitions of the sum of squared prediction errors (SSPE) for five different types of prediction in the case of normal “standardized” random errors. Similar result can be carried out for the case with double exponential “standardized” random errors. Prediction 1 corresponds to the oracle, i.e., using true β, α(·), σ²(·) and θ; prediction 2 uses estimated β̂, α̂(·), σ̂²(·) and true θ; prediction 3 use all estimated parameters, i.e., β̂, α̂(·), σ̂²(·) and θ̂; predictions 4 and 5 correspond to predictions that ignore the covariance structure, based on true β and α(·) and estimated β̂ and α̂(·), respectively. The numbers in parentheses are their corresponding standard deviations. The last column of Table 5 gives the number of points where the prediction is made for each case, namely, the number of \missing” observations in the independent prediction data set.

Notice first, in Table 5, that the difference between SSPE(prediction 5) and SSPE(prediction 1) is much larger than that between SSPE(prediction 3) and SSPE(prediction 1). This implies that, compared to prediction ignoring the covariance structure, incorporating the estimated covariance structure reduces prediction error significantly. Furthermore we see that the difference between SSPE(prediction 3) and SSPE(prediction 1) is much larger than that between SSPE(prediction 3) and SSPE(prediction 2). This indicates that using the true correlation structure parameter θ and the estimated θ̂ does not make much difference after including the estimated covariance structure and demonstrates the accuracy of θ̂ for prediction.

Example 5.3[Comparison with the method in Fan et al. (2007)]

For estimating the varying-coefficient partially linear model, the major difference between our method and Fan et al. (2007)’s is that we estimate β using the difference-based technique, plug it into model (2), and estimate α(·) via the local constant regression whereas they estimate β and α(·) simultaneously using the local linear regression and profile-likelihood techniques. Next we use another simulation to study the impact of rough α(·) on these two different estimation schemes. This occurs when there is some structure break or technological innovation that cause the change-point in time.

In this comparison study we set α₁(t) = 2 and α₂(t) = 4/(1 + exp(− 40(t − 7))) − 2. Notice that α₂(·) is a scaled sigmoid function and is close to a jump function as shown by the dotted line in panel (D) of Figure 1. For each t, the regressor x₁(t) takes constant 8, and x₂(t) and x₃(t) are jointly simulated from a bivariate normal distribution, namely, $\left[\begin{array}{c}{x}_2(t)\\ x_3(t)\end{array}\right]\sim N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left(\begin{array}{cc}{a}_1& a_2\\ a_3& a_4\end{array}\right)\right)$, where a₁ = 64, a₂ = a₃ = 0.95 × sign(7 − t) × 8, a₃ a₄ and a₄ = 1. All other components in our model are simulated the same way as in the previous example. Sample size is n = 100; the true ARMA(1,1) correlation structure parameters are γ = 0.85 and ρ = 0.6. After tuning, Fan et al. (2007)’s profiling method chooses the best smoothing bandwidth pair b = 0.8, h = 3.80 and our new proposed estimation scheme selects b = 0.4, h = 0.75 for estimation α(·) and σ²(·). A box-plot of the estimated correlation structure parameters over these 100 samples for each method is shown in panel (A) of Figure 1.

Figure 1.

For Example 5.3, panel (A) gives the box-plot of our estimator (γ₁ and ρ₁) and Fan et al. (2007)’s estimator (γ₂ and ρ₂) of the correlation structure parameter; panels (B-D) plot the true (dotted line), our new estimate (solid line), and Fan et al. (2007)’s estimate (dashed line) of α₁(·), σ²(·), and α₂(·), respectively, for one typical sample.

From the box-plot in Figure 1, we see that Fan et al. (2007)’s estimator is far off the true correlation structure parameters while our method still performs very well. The underlining reason is that, in Fan et al. (2007)’s method, smoothing the rough α(·) causes a big bias in the profile-likelihood estimator of β due to the strong correlation between x₂(·) and x₃(t). To see this, the profile-likelihood estimators of β for different smoothing band-widths are depicted in Figure 2, showing that the profile-likelihood method does not provide a consistent estimator of β₁ at all. However our DBEs of β are β̂₁ = 0.9163(0.1651) and β̂₂ = 2.0037(0.0828), which are very close to their corresponding true values. This means that our difference-based method still performs very well. Hence our DBE of β is more robust to the smoothness assumption of α(·). For a random sample, we plot the estimated α₁(·), α₂(·), and σ²(·) using two different methods in panels (B-D) of Figure 1. The RASE for estimating α₁(·) and α₂(·) is reported in Table 6. We can see that our new estimation scheme improves significantly the estimation of the rough component α₂(·). However, there is no improvement on the estimation of α₁(·). Note that here we use the same bandwidth to estimate α₁(·) and α₂(·). The performance of our method can be improved by allowing different bandwidths for different components of α(·), as studied in Fan and Zhang (1999).

Figure 2.

The solid curves (average estimate) with error bars (one sample standard deviation) in the left and right panels plot the profile-likelihood estimators of the regression coefficient β₁ and β₂ respectively for different smoothing bandwidth h. The dashed curves denote their corresponding true coefficients.

Table 6.

RASE for estimating α₁(·) and α₂(·) using our method(FW) and Fan et al. (2007)’s method(FHL)

Noise	FW	FHL
α1(·)	0.0381 (0.0164)	0.0281 (0.0090)
α2(·)	0.1946 (0.0277)	0.4525 (0.0403)

This comparison study alarms us to using the profiling technique for the case of rough varying regression coefficient α(·) in the varying-coefficient partially linear model. However, while handling real data, we never know the a priori smoothness of α(·). In our new estimation scheme, one can do a visual check or even apply some advanced technique to diagnose the smoothness of α(·) after getting the DBE β̂.

6 Application to the Progesterone data

In this section, we apply the proposed methods to the longitudinal progesterone data. For the i-th subject, denote x_i and z_i to be age and body mass index (both are standardized to have mean zero and standard deviation one); we consider as the response the difference between the j-th log-transformed progesterone level measured at standardized day t_ij and the individual’s average log-transformed progesterone level. We consider the following semi-parametric model

$$y_{ij}={\beta }_1{x}_i+{\beta }_2{z}_i+f(t_{ij})+\epsilon .$$ (14)

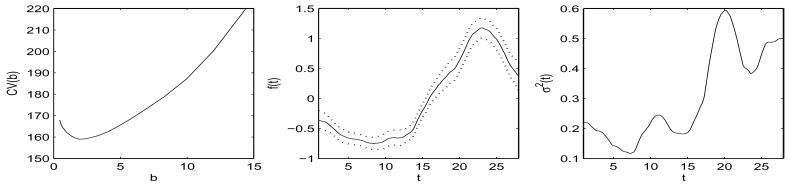
Note that f(t) is the sole varying-coefficient term. After sorting, our DBE is based on two neighboring observations with weights ( $1/\sqrt{2},-1/\sqrt{2}$) as there is only one varying-coefficient term f(t_ij). DBE of (14) gives estimates β̂₁ = 0.0306 and β̂₂ = 0.0195. The leave-one-subject-out cross-validation procedure suggested by Rice and Silverman (1991) is used to select the bandwidth for estimating f(·) using local constant regression. The left panel of Figure 3 depicts the cross-validation score function defined as the sum of residual squares and suggests the optimal bandwidth 1.9349. The corresponding estimate f̂(·) is plotted in the center panel of Figure 3 with a pointwise 95% confidence interval. The plug-in bandwidth selector (Ruppert, Sheather and Wand, 1995) is implemented to choose the smoothing bandwidth for the one-dimensional kernel regression of the variance function σ²(·) and selects the bandwidth 2.5864. The resulting estimate of the variance function is shown in the right panel of Figure 3.

Figure 3.

The left panel plots the leave-one-subject-out cross-validation score against the bandwidth. The center panel depicts the estimated varying-coefficient function f(·) with a pointwise 95% confidence interval (dotted line). The right panel gives the estimated variance function σ²(·).

We consider an ARMA(1,1) correlation structure corr(ε(s), ε(t)) = γρ^{|s −t|} if s ≠ t and 1 otherwise. The QMLEs of γ and ρ are 0.6900(0.3662) and 0.6452(0.1319), respectively. The numbers in parentheses are the corresponding standard errors, obtained using (13) based on estimated γ, ρ and ε(t_ij). This indicates a strong correlation structure.

We next consider testing the hypothesis H₀ : γ = 1 vs H₁ : γ < 1, i.e., whether the correlation structure is AR(1). The p-value for this hypothesis test exceeds .10 and as a result H₀ cannot be rejected.

As the null hypothesis is not rejected, an AR(1) correlation structure corr(ε(s), ε(t)) = ρ^{js − t|} is applied on this data. The QMLE ρ̂ is 0.5049 with standard error given by 0.0831.

Via incorporating the estimate covariance structure in DBE, weighted least squares regression gives new estimates of β: β̂₁ = − 0.0059 and β̂₂ = − 0.0074. The corresponding new plots of Figure 3 are very similar and thus not reproduced.

It is straightforward to understand how the estimated regression function and the estimated variance function affect the pointwise prediction as shown in Fan et al. (2007). However it is not easy to quantify the sensitivity of pointwise prediction with respect to the estimated correlation structure parameter. We study this sensitivity using two randomly selected subjects. In order to provide a visual quantification of this sensitivity, the pointwise prediction and 95% predictive interval using the estimated AR(1) correlation structure parameter ρ̂ with a perturbation of one standard error are shown in the left column panels of Figure 4 for one subject and the right column panels for the other one, where the same prediction formula of Fan et al. (2007) is used. In this prediction, the same estimated β̂, α̂(·), and σ̂²(·) are used. From these figures, we can not see much change in the prediction for different correlation structure parameters and this suggests that the pointwise prediction is not sensitive to the correlation structure parameter.

Figure 4.

The observed values (circle), the corresponding pointwise predictions (dotted line), and 95% predictive intervals (solid line) are plotted for two randomly selected subjects, one in the left three panels and the other in the right three panels. For each column, the top, middle, and bottom panels correspond to the prediction using ρ̂, ρ̂ − se(ρ̂), and ρ̂+ se(ρ̂), respectively.

Appendix

The following technical conditions are imposed.

1. On the domain [0, T], the density function f(·) is Lipschitz continuous and bounded away from zero. The kernel function K(·) is a symmetric density function with a compact support.

2. The moment generating function of J_i is finite in some neighborhood of the origin.

3. The estimator m̂(·) of the mean function is consistent with polynomial convergence rate, i.e., ∃ τ > 1/4 such that m₀(x) − m̂(x) = O_p(n^−τ) uniformly in x.

4. It holds that sup |m̂(x) − m̂_−i(x)| = O_p(n^−ς) uniformly in x for some ς > 2/5, where m_−i(·) is the leave-one-subject-out estimation of the conditional mean function by excluding the i-th subject.

5. ${\sigma }_0^2(·)$ has a continuous second derivative and is bounded away from zero in its domain. Eε(t)⁴ < ∞.

6. The true parameter θ₀ of the correlation structure lies in the interior of a compact set Θ.

7. For any θ, $\frac{\partial }{\partial {\theta }_i}\rho (t,s,\mathit{\theta })$ and $\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}\rho (t,s,\mathit{\theta })$ are bounded bivariate functions of t and s.

8. For any θ ∈ Θ, it holds with probability one that the eigenvalues of the correlation matrix C(θ) of a generic subject are between ϱ₀ and ϱ₁, where 0 < ϱ₀ < ϱ₁ < ∞.

9. Assume E log(g₀(ε; C(θ₀))/f (ε; C(θ))) exists, where the expectation is taken with respect to the true elliptical density g₀(ε; C(θ₀)) of the ε, i.e., ε ~g₀(ε; C(θ₀)) ∝|C(θ₀)|^−1/2 h₀(ε^TC(θ₀)⁻¹ε), and f(ε; C(θ)) is corresponds to the density used in QMLE by treating ε normally distributed.

10. Correlation structure is identifiable, i.e., ρ(s, t, θ₀) ≠ ρ(s, t, θ) for any θ ≠ θ₀ when s ≠ t.

Remark 3

Technical condition (iii) seems strong. However, once the form of the conditional mean function is available, it can be relaxed. For parametrical model m(x(t)) = x(t)^Tβ, Condition (iii) can be replaced by $\underset{t\in [0,T]}{sup}E\parallel \mathit{x}(t)\parallel <\infty$ and the estimator of β is consistent with a polynomial rate O_p(n^−τ) for any τ > 1/4; for the varying-coefficient model m(x(t)) = x(t)^Tα(t), it can be replaced by $\underset{t\in [0,T]}{sup}E\parallel \mathit{x}(t)\parallel <\infty$ and the estimator of α(t) is consistent with a polynomial rate O_p(n^−τ) for any τ > 1/4 uniformly in t; for nonparametric model m(x) = m(x) without any constraint, it is enough to assume that m(·) can be consistently estimated at a polynomial rate O_p(n^−τ) for τ > 1/4 uniformly in the domain of m(·). These are reasonable assumptions for the corresponding models of the conditional mean function. Similar argument applies to Condition (iv).

Proof of Theorem 1

Note that Condition (ii) implies ${max}_{i=1}^n{J}_i=O_p(logn)$ and it is unlikely for each individual to have two observations in the same neighborhood [t− h, t+h]. So in the following, the ε_i(t_ij)s can be treated as independent.

Define e_ij = m̂(x_i(t_ij)) − m(x_i(t_ij)). Noting that $r_{ij}^2={\epsilon }_i^2(t_{ij})-2{\epsilon }_i(t_{ij})e_{ij}+e_{ij}^2$, we can accordingly decompose σ̂²(t) as

$$\begin{array}{l}{\widehat{\sigma }}^2(t)=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{\epsilon }_i^2(t_{ij})K_h(t_{ij}-t)}{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{K}_h(t_{ij}-t)}-2\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{\epsilon }_i(t_{ij})e_{ij}{K}_h(t_{ij}-t)}{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{K}_h(t_{ij}-t)}\\ +\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{e}_{ij}^2{K}_h(t_{ij}-t)}{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{K}_h(t_{ij}-t)}\\ =A_1+A_2+A_3.\end{array}$$

Using Condition (iii), we get $\sqrt{nh}{A}_3=O_p(\sqrt{nh}{n}^{-2\tau })=o_p(1)$ When τ > 1/5 and h ∝ n^−1/5. Note $\text{Var}(A_2)\le n^{-2\tau }\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{\sigma }^2(t_{ij})K_h^2(t_{ij}-t)}{{({\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{K}_h(t_{ij}-t))}^2}\le n^{-2\tau }(sup{\sigma }^2(t))/(nh)$ and

$$\begin{array}{l}\mid E(A_2)\mid =\mid E\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{\epsilon }_i(t_{ij})(\widehat{m}({\mathit{x}}_i(t_{ij}))-{\widehat{m}}_{-i}({\mathit{x}}_i(t_{ij})))K_h(t_{ij}-t)}{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{K}_h(t_{ij}-t)}\mid \\ \le E\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{J_i}\mid {\epsilon }_i(t_{ij})\mid \mid K_h(t_{ij}-t)\mid }{\mid {\sum }_{i=1}^n{\sum }_{j=1}^{J_i}{K}_h(t_{ij}-t)\mid }sup\mid \widehat{m}(\mathit{x})-{\widehat{m}}_{-i}(\mathit{x})\mid ,\end{array}$$

where m̂_−i(·) is the leave-one-subject-out estimator of m(·) by excluding the i-th subject. By Condition (iv) and the mean-variance decomposition, we get

$$\sqrt{nh}{A}_2=O_p(\sqrt{nh}\left[n^{-\tau }/\sqrt{nh}+O_p(n^{-\varsigma })\right])=o_p(1).$$

It remains to show that the main term is asymptotically normal. Applying the standard techniques to derive asymptotic bias and variance for a kernel regression estimator of type A₁, it follows from $E{\epsilon }_i{(t)}^2={\sigma }_0^2(t)$ that

$$\sqrt{nh}[A_1-{\sigma }_0^2(t)-b(t)]\stackrel{ℒ}{\to }N(0,v(t)).$$

Using Slutsky’s Theorem, we have

$$\sqrt{nh}[{\widehat{\sigma }}^2(t)-{\sigma }_0^2(t)-b(t)]\stackrel{ℒ}{\to }N(0,v(t)).$$

This completes the proof of Theorem 1.

We need the following observations and results to prove Theorem 2. Notice that ζ(t) = ε(t)/σ(t). Then Eζ(t) = 0 and Var ζ(t) = 1, cov(ζ_i(t_ij), ζ_i(t_ik)) = ρ(t_ij, t_ik, θ). After plugging the estimators m̂(·) and σ̂²(·), we obtain the corresponding estimators of the \standardized” random errors ζ_i(t_ij)’s and denote them by ζ̂_i(t_ij)’s. Then they can be decomposed as follows.

$$\begin{array}{l}{\widehat{\zeta }}_i(t_{ij})=\frac{y_{ij}-\widehat{m}({\mathit{x}}_i(t_{ij}))}{\widehat{\sigma }(t_{ij})}=\frac{m({\mathit{x}}_i(t_{ij}))-\widehat{m}({\mathit{x}}_i(t_{ij}))}{\widehat{\sigma }(t_{ij})}+\frac{{\sigma }_0(t_{ij}){\zeta }_i(t_{ij})}{\widehat{\sigma }(t_{ij})}\\ ={\zeta }_i(t_{ij})+\frac{m({\mathit{x}}_i(t_{ij}))-\widehat{m}({\mathit{x}}_i(t_{ij}))}{\widehat{\sigma }(t_{ij})}+\frac{[{\sigma }_0(t_{ij})-\widehat{\sigma }(t_{ij})]{\zeta }_i(t_{ij})}{\widehat{\sigma }(t_{ij})}.\end{array}$$ (15)

For each subject i, by vectorizing the residuals, we denoteζ_i = (ζ_i(t_i1), ζ_i(t_i2), ···, ζ_i(t_iJi))^T and its corresponding estimator ζ̂_i = (ζ̂_i(t_i1), ζ̂_i(t_i2), ···, ζ̂_i(t_iJi))^T. Note that while proving Theorem 1, we can also use the technique related to Fan and Huang (2005) to show that ${\widehat{\sigma }}^2(t)-{\sigma }_0^2(t)$ converges to zero uniformly in t. Based on Conditions (iii) and the result of Theorem 1, we have ζ_i − ζ̂_i converges in probability to zero at a polynomial rate both elementwise and in the 2-norm due to Condition (v) and the fact that max_i J_i = O_p(log n). The QMLE θ̂ is defined via

$$\widehat{\mathit{\theta }}=\underset{\mathit{\theta }}{\text{argmax}}\sum _{m=1}^n\left\{-\frac{1}{2}log\mid \mathit{C}(\mathit{\theta };m)\mid -\frac{1}{2}{({\widehat{\mathit{\zeta }}}_m)}^T\mathit{C}{(\mathit{\theta };m)}^{-1}{\widehat{\mathit{\zeta }}}_m\right\}=\underset{\mathit{\theta }}{\text{argmax}}{l}_n(\mathit{\theta }).$$ (16)

To save space, when there is no confusion, we use the generic notation C or C(θ)to denote the correlation matrix function C(θ; m). For 1 ≤ i, j ≤ d, denote ${\mathit{C}}_i=\frac{\partial \mathit{C}}{\partial {\theta }_i},{\mathit{C}}^i=\frac{\partial {\mathit{C}}^{-1}}{\partial {\theta }_i}=-{\mathit{C}}^{-1}{\mathit{C}}_i{\mathit{C}}^{-1},{\mathit{C}}_{ij}=\frac{{\partial }^2\mathit{C}}{\partial {\theta }_i\partial {\theta }_j},\text{and}{\mathit{C}}^{ij}={\frac{{\partial }^2{\mathit{C}}^{-1}}{\partial {\theta }_i\partial \theta }}_j={\mathit{C}}^{-1}({\mathit{C}}_i{\mathit{C}}^{-1}{\mathit{C}}_j+{\mathit{C}}_j{\mathit{C}}^{-1}{\mathit{C}}_i-{\mathit{C}}_{ij}){\mathit{C}}^{-1}$.

Lemma 1

For any given J_i and T_i, if C(θ; i) ≠ C(θ₀; i) for any θ ≠ θ₀, then there is a unique minimizer of log |C(θ ; i)| + tr[C(θ ; i)⁻¹C(θ ₀; i)] and the unique minimizer is θ₀.

Proof

Given J_i and T_i, to prove Lemma 1, tentatively we assume that ζ_i is normally distributed with mean 0 and covariance C(θ₀; i). Noticing that log x ≤ x − 1, we have

$$E_{{\mathit{\theta }}_0}log\frac{f({\mathit{\zeta }}_i;\mathit{C}(\mathit{\theta };i))}{f({\mathit{\zeta }}_i;\mathit{C}({\mathit{\theta }}_0;i))}\le E_{{\mathit{\theta }}_0}\left\{\frac{f({\mathit{\zeta }}_i;\mathit{C}(\mathit{\theta };i))}{f({\mathit{\zeta }}_i;\mathit{C}({\mathit{\theta }}_0;i))}-1\right\}=0,$$

where equality holds only when f(ζ_i; C(θ ; i))/f (ζ_i; C(θ₀; i)) = 1 almost surely, i.e., C(θ; i) = C(θ₀; i) due to normality assumption.

Noticing that the left hand side of the above equation is equal to

$$-\frac{1}{2}(log\mid C(\mathit{\theta };i)\mid +tr[\mathit{C}{(\mathit{\theta };i)}^{-1}\mathit{C}({\mathit{\theta }}_0;i)])+\frac{1}{2}(log\mid \mathit{C}({\mathit{\theta }}_0;i)\mid +tr[\mathit{C}{({\mathit{\theta }}_0;i)}^{-1}\mathit{C}({\mathit{\theta }}_0;i)]),$$

we have

$$log\mid \mathit{C}({\mathit{\theta }}_0;i)\mid +tr[\mathit{C}{({\mathit{\theta }}_0;i)}^{-1}\mathit{C}({\mathit{\theta }}_0;i)]\le log\mid \mathit{C}(\mathit{\theta };i)\mid +tr[\mathit{C}{(\mathit{\theta };i)}^{-1}\mathit{C}({\mathit{\theta }}_0;i)]$$

with equality holds only when C(θ; i) = C(θ₀; i). So Lemma 1 is proved.

Proof of Theorem 2

The log-likelihood function can be decomposed as follows:

$$\begin{array}{l}\frac{1}{n}{l}_n(\mathit{\theta })=-\frac{1}{2n}\sum _{m=1}^n\left\{log\mid \mathit{C}(\mathit{\theta };m)\mid +{({\widehat{\mathit{\zeta }}}_m)}^T\mathit{C}{(\mathit{\theta };m)}^{-1}{\widehat{\mathit{\zeta }}}_m\right\}\\ =-\frac{1}{2n}\sum _{m=1}^n\left\{log\mid \mathit{C}(\mathit{\theta };m)\mid +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}{\widehat{\mathit{\zeta }}}_m{\widehat{\mathit{\zeta }}}_m^T]\right\}\\ =-\frac{1}{2n}\sum _{m=1}^n\left\{log\mid \mathit{C}(\mathit{\theta };m)\mid +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}({\mathit{\zeta }}_m+({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)){({\mathit{\zeta }}_m+({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m))}^T]\right\}\\ =-\frac{1}{2n}\sum _{m=1}^n\{log\mid \mathit{C}(\mathit{\theta };m)\mid +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}{\mathit{\zeta }}_m{\mathit{\zeta }}_m^T]\\ +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m){({\mathit{\zeta }}_m+{\widehat{\mathit{\zeta }}}_m)}^T]\}.\end{array}$$

Condition (viii) implies that, for any θ ∈ Θ,

$$\mid {({\mathit{\zeta }}_m+{\widehat{\mathit{\zeta }}}_m)}^T\mathit{C}{(\mathit{\theta };m)}^{-1}({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)\mid \le (1/{\varrho }_0)\parallel ({\mathit{\zeta }}_m+{\widehat{\mathit{\zeta }}}_m)\parallel ·\parallel {\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)\parallel .$$

_P

Condition (v), ${max}_{m=1}^n{J}_m=O(logn)$, and the fact that ${\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m\stackrel{P}{\to }\mathbf{0}$ at a polynomial rate imply that E || (ζ_m + ζ̂_m) || · || ζ̂_m − ζ_m) || → 0. As a result, the Law of Large Numbers implies that

$$\begin{array}{l}\mid \frac{1}{n}{l}_n(\mathit{\theta })-(-\frac{1}{2n}\sum _{m=1}^n\{log\mid \mathit{C}(\mathit{\theta };m)\mid +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}{\mathit{\zeta }}_m{({\mathit{\zeta }}_m)}^T]\})\mid \\ \le \frac{1}{2n}\sum _{m=1}^n\mid {({\mathit{\zeta }}_m+{\widehat{\mathit{\zeta }}}_m)}^T\mathit{C}{(\mathit{\theta };m)}^{-1}({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)\mid \\ \le \frac{1}{2n{\varrho }_0}\sum _{m=1}^n\parallel ({\mathit{\zeta }}_m+{\widehat{\mathit{\zeta }}}_m)\parallel ·\parallel {\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)\parallel \stackrel{P}{\to }0\end{array}$$

uniformly for θ ∈ Θ. Hence we have

$$\widehat{\mathit{\theta }}-{\widehat{\mathit{\theta }}}^{(1)}\stackrel{P}{\to }\mathbf{0},$$

where ${\widehat{\mathit{\theta }}}^{(1)}=\underset{\mathit{\theta }\in \mathrm{\Theta }}{\text{argmax}}\left(-\frac{1}{2}{\displaystyle \sum _{m=1}^n}\{log\mid \mathit{C}(\mathit{\theta };m)\mid +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}{\mathit{\zeta }}_m{\mathit{\zeta }}_m^T]\}\right)$.

Condition (viii) implies that, for each m, the absolute value of

$$log\mid \mathit{C}(\mathit{\theta };m)\mid +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}{\mathit{\zeta }}_m{\mathit{\zeta }}_m^T]$$

is bounded by

$$J_{i}max(\mid log{\varrho }_0\mid ,\mid log{\varrho }_1\mid )+(1/{\varrho }_0)tr({\mathit{\zeta }}_m{\mathit{\zeta }}_m^T)$$

whose expectation exists, is finite, and does not depend on θ. Hence, Condition (ix) and the Law of Large Numbers imply that, for each θ,

$$\begin{array}{l}-\frac{1}{2n}\sum _{m=1}^n\{log\mid \mathit{C}(\mathit{\theta };m)\mid +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}{\mathit{\zeta }}_m{\mathit{\zeta }}_m^T]\}\\ \stackrel{P}{\to }{E}_{g_0}logf(\mathit{\zeta };\mathit{C}(\mathit{\theta }))\\ \equiv -E_{g_0}log\frac{g_0(\mathit{\zeta };\mathit{C}({\mathit{\theta }}_0))}{f(\mathit{\zeta };\mathit{C}(\mathit{\theta }))}+E_{g_0}log{g}_0(\mathit{\zeta };\mathit{C}({\mathit{\theta }}_0))\end{array}$$ (17)

(c.f. White, 1982), where g₀(·; ·) specifies the true spherical density and f(·; ·) denotes the multivariate normal density of ζ with mean 0 and covariance matrix C(θ). Note that the continuity enforced by Condition (vii) on our correlation structure ρ(·, ·, θ) implies that E_g0 log f (ζ; C(θ)) is continuous with respect to θ. Then for any ε > 0, there is a neighborhood (θ₁) of θ₁ such that

$$\underset{\mathit{\theta }\in \mathcal{N}({\mathit{\theta }}_1)}{sup}\mid -\frac{1}{2n}\sum _{m=1}^n\{log\mid \mathit{C}(\mathit{\theta };m)\mid +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}{\mathit{\zeta }}_m{\mathit{\zeta }}_m^T]\}-E_{g_0}logf(\mathit{\zeta };\mathit{C}(\mathit{\theta }))\mid <\epsilon$$

in probability for large n. It follows that Θ may be covered by such neighborhoods and, since Θ is compact as enforced by Condition (vi), by a finite collection of such neighborhoods. As a result, the convergence of (17) is uniform with respect to θ since the small number ε is arbitrary. Thus θ̂⁽¹⁾ converges in probability to the minimizer of the Kullback-Leibler Information Criterion

$$I(g_0:f,\mathit{\theta })\equiv E_{g_0}log(g_0(\mathit{\zeta };\mathit{C}({\mathit{\theta }}_0))/f(\mathit{\zeta };\mathit{C}(\mathit{\theta }))).$$

For each subject m, conditional on its number J_m of observations and observation times T_m,

$$\begin{array}{l}{E}_{g_0}(log(g_0({\mathit{\zeta }}_m;\mathit{C}({\mathit{\theta }}_0;m))/f({\mathit{\zeta }}_m;\mathit{C}(\mathit{\theta };m)))\mid J_m,{\mathit{T}}_m)\\ =\frac{1}{2}(log\mid \mathit{C}(\mathit{\theta };m)\mid +tr[\mathit{C}{(\mathit{\theta };m)}^{-1}\mathit{C}({\mathit{\theta }}_0;m)])+\mathit{constant}\end{array}$$ (18)

has global minimizer θ ₀ due to Lemma 1 and Condition (x).

Notice that

$$I(g_0:f,\mathit{\theta })=E[E_{g_0}(log(g_0({\mathit{\zeta }}_m;\mathit{C}({\mathit{\theta }}_0;m))/f({\mathit{\zeta }}_m;\mathit{C}(\mathit{\theta };m)))\mid J_m,{\mathit{T}}_m)].$$

Hence θ ₀ minimizes I(g₀ : f, θ) globally, which implies that ${\widehat{\mathit{\theta }}}^{(1)}\stackrel{P}{\to }{\mathit{\theta }}_0$ due to (17). Theorem 1 is proved by noting that we have shown $\widehat{\mathit{\theta }}-{\widehat{\mathit{\theta }}}^{(1)}\stackrel{P}{\to }\mathbf{0}$.

Proof of Theorem 3

By routine calculation as in the proof of Theorem 2, we have

$$\begin{array}{l}\frac{1}{n}\frac{\partial l_n(\mathit{\theta })}{\partial {\theta }_i}=-\frac{1}{2n}\sum _{m=1}^n\left\{2{\mathit{\zeta }}_m^T{\mathit{C}}^i(\mathit{\theta };m)({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)+{({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)}^T{\mathit{C}}^i(\mathit{\theta };m)({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)\right\}\\ -\frac{1}{2n}\sum _{m=1}^n\{tr[{\mathit{C}}^{-1}(\mathit{\theta };m){\mathit{C}}_i(\mathit{\theta };m)]+tr[{\mathit{C}}^i(\mathit{\theta };m){\mathit{\zeta }}_m{\mathit{\zeta }}_m^T]\}.\end{array}$$ (19)

Note that Cⁱ(θ, m) = C⁻¹(θ, m) C_i(θ, m)C⁻¹(θ, m) and ζ_m has mean zero and finite variance. The uniform convergence of m(·) and σ²(·) in the decomposition (15) implies that the first term on the right hand side of (19) converges to zero in probability. As a result, we have

$$\frac{1}{n}\frac{\partial l_n(\mathit{\theta })}{\partial {\theta }_i}{\mid }_{\mathit{\theta }={\mathit{\theta }}_0}-\left[-\frac{1}{2n}\sum _{m=1}^n\{tr[{\mathit{C}}^{-1}(\mathit{\theta };m){\mathit{C}}_i(\mathit{\theta };m)]+tr[{\mathit{C}}^i(\mathit{\theta };m){\mathit{\zeta }}_m{\mathit{\zeta }}_m^T]\}{\mid }_{\mathit{\theta }={\mathit{\theta }}_0}\right]\stackrel{P}{\to }0.$$ (20)

Hence

$$\begin{array}{l}\frac{1}{n}\frac{\partial l_n(\mathit{\theta })}{\partial {\theta }_i}{\mid }_{\mathit{\theta }={\mathit{\theta }}_0}\stackrel{P}{\to }-\frac{1}{2}E\{tr[{\mathit{C}}^{-1}({\mathit{\theta }}_0;m){\mathit{C}}_i({\mathit{\theta }}_0;m)]+tr[{\mathit{C}}^i({\mathit{\theta }}_0;m)E_{{\mathit{\theta }}_0}({\mathit{\zeta }}_m{\mathit{\zeta }}_m^T)]\}\\ \equiv 0.\end{array}$$

Similarly, we can show that

$$\frac{1}{n}\frac{{\partial }^2{l}_n(\mathit{\theta })}{\partial {\theta }_i\partial {\theta }_j}{\mid }_{\mathit{\theta }={\mathit{\theta }}_0}\stackrel{P}{\to }-\frac{1}{2}E\{tr[{\mathit{C}}^{-1}({\mathit{\theta }}_0;m){\mathit{C}}_i({\mathit{\theta }}_0;m){\mathit{C}}^{-1}({\mathit{\theta }}_0;m){\mathit{C}}_j({\mathit{\theta }}_0;m)]\},$$

and $\frac{1}{n}\frac{{\partial }^3{l}_n(\mathit{\theta })}{\partial {\theta }_i\partial {\theta }_j\partial {\theta }_k}{\mid }_{\mathit{\theta }={\mathit{\theta }}_0}$ converges in probability to

$$\begin{array}{l}-\frac{1}{2}E\{tr[{\mathit{C}}_{ij}{\mathit{C}}^{-1}{\mathit{C}}_k{\mathit{C}}^{-1}+{\mathit{C}}_{jk}{\mathit{C}}^{-1}{\mathit{C}}_i{\mathit{C}}^{-1}+{\mathit{C}}_j{\mathit{C}}^{-1}{\mathit{C}}_{ik}{\mathit{C}}^{-1}\\ -2{\mathit{C}}_i{\mathit{C}}^{-1}{\mathit{C}}_j{\mathit{C}}^{-1}{\mathit{C}}_k{\mathit{C}}^{-1}-2{\mathit{C}}_j{\mathit{C}}^{-1}{\mathit{C}}_i{\mathit{C}}^{-1}{\mathit{C}}_k{\mathit{C}}^{-1}]{\mid }_{\mathit{\theta }={\mathit{\theta }}_0}\}.\end{array}$$

The existence and boundedness of the above expectations can easily be proved by using Conditions (ii), (vii), and (viii).

Notice that $\mathit{I}({\mathit{\theta }}_0)=\underset{n\to 0}{lim}(-\frac{1}{n}\frac{{\partial }^2{l}_n(\mathit{\theta })}{\partial \mathit{\theta }\partial {\mathit{\theta }}^T}{\mid }_{\mathit{\theta }={\mathit{\theta }}_0})$ is a d by d matrix whose (i, j)-element is the limit of $-\frac{1}{n}\frac{{\partial }^2{l}_n(\mathit{\theta })}{\partial {\theta }_i\partial {\theta }_j}{\mid }_{\mathit{\theta }={\mathit{\theta }}_0}$ as n → ∞. Taylor expand $\frac{\partial }{\partial \mathit{\theta }}{l}_n(\widehat{\mathit{\theta }})\text{a}{\mathit{\theta }}_0$, i.e.,

$$\mathbf{0}=\frac{1}{n}\frac{\partial }{\partial \mathit{\theta }}{l}_n(\widehat{\mathit{\theta }})=\frac{1}{n}\frac{\partial }{\partial \mathit{\theta }}{l}_n({\mathit{\theta }}_0)+\frac{1}{n}\frac{{\partial }^2{l}_n({\mathit{\theta }}_0)}{\partial \mathit{\theta }\partial {\mathit{\theta }}^T}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)+{\mathit{R}}_n({\mathit{\theta }}^{\ast }),$$ (21)

where θ* is between θ₀ and θ and R_n(θ) = M(θ)((θ̂ − θ₀), where M(θ) is a d-by-d matrix whose m-th row is given by

$$\frac{1}{2}{(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)}^T[\frac{1}{n}\frac{{\partial }^2}{\partial \mathit{\theta }\partial {\mathit{\theta }}^T}(\frac{\partial }{\partial {\theta }_m}{l}_n(\mathit{\theta }))].$$

So we have

$$\sqrt{n}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)=-{(\frac{1}{n}\frac{{\partial }^2{l}_n({\mathit{\theta }}_0)}{\partial \mathit{\theta }\partial {\mathit{\theta }}^T}+\mathit{M}({\mathit{\theta }}^{\ast }))}^{-1}(\frac{\sqrt{n}}{n}\frac{\partial }{\partial \mathit{\theta }}{l}_n({\mathit{\theta }}_0)).$$

Since θ̂ is consistent, every element of the matrix M(θ*) converges to zero in probability.

Notice that, from above, we have $\frac{1}{n}\frac{\partial l_n(\mathit{\theta })}{\partial \mathit{\theta }}{\mid }_{\mathit{\theta }={\mathit{\theta }}_0}\to \mathbf{0}$ and $-\frac{1}{n}\frac{{\partial }^2{l}_n(\mathit{\theta })}{\partial \mathit{\theta }\partial {\mathit{\theta }}^T}{\mid }_{\mathit{\theta }={\mathit{\theta }}_0}\to \mathit{I}({\mathit{\theta }}_0)$ as n → ∞. To get the desired asymptotic normality result we need to show that $-\frac{1}{2n}{\sum }_{m=1}^n\left\{2{\mathit{\zeta }}_m^T{\mathit{C}}^i(\mathit{\theta };m)({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)+{({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)}^T{\mathit{C}}^i(\mathit{\theta };m)({\widehat{\mathit{\zeta }}}_m-{\mathit{\zeta }}_m)\right\}=o_p(n^{-1/2})$. The second term can be easily shown to be of order o_p(n^−1/2) due to Conditions (iii), (vii), (viii) and the result of Theorem 1. Denote C̃ⁱ(θ; m) to be a $({max}_{j=1}^n{J}_j)-\text{by}-({max}_{j=1}^n{J}_j)$ matrix whose top-left J_m-by-J_m submatrix is Cⁱ(θ; m) and other elements are all filled by zeros. Similarly, $\stackrel{\sim }{{\widehat{\mathit{\zeta }}}_m}$ and ζ̃_m are vectors of length ( ${max}_{i=1}^n{J}_i$) with first J_m elements given by ζ̂_m and ζ_m, respectively, and other elements are filled by zeros. Then the first term is equal to $-\frac{1}{n}{\sum }_{m=1}^n{\stackrel{\sim }{\mathit{\zeta }}}_m^T{\stackrel{\sim }{\mathit{C}}}^i(\mathit{\theta };m)(\stackrel{\sim }{{\widehat{\mathit{\zeta }}}_m}-{\stackrel{\sim }{\mathit{\zeta }}}_m)$, which can be shown to be of order o_p(n^−1/2) by using techniques similar to the proof of Lemma 2 in Lam and Fan (2008). Applying the Central Limit Theorem, we have that

$$\sqrt{n}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)\stackrel{ℒ}{\to }N(0,\mathit{I}{({\mathit{\theta }}_0)}^{-1}\mathbf{\sum }({\mathit{\theta }}_0)\mathit{I}{({\mathit{\theta }}_0)}^{-1}).$$

Proof of Proposition 1

Part [a] of Proposition 1 can be verified using basic algebra and is skipped here. Next we prove part [b]. With the assumption that min_{i=2,3,·,·,·,K}(s_i − s_i−1) = s₀ > 0 and based on part [a], we can easily show that A⁻¹ is diagonal dominated. The basic properties of hyperbolic function implies that

$$\underset{i=1,2,\cdots ,K}{min}({({\mathit{A}}^{-1})}_{ii}-\sum _{j\ne i}{({\mathit{A}}^{-1})}_{ij})\ge {\delta }_0(t_0,a).$$

Let b = (b₁, b₂, ···, b_K)^T be an arbitrary vector in the K-dimensional space. We have

$$\begin{array}{l}{\mathit{b}}^T{\mathit{A}}^{-1}\mathit{b}=\sum _{i=1}^K\sum _{j=1}^K{({\mathit{A}}^{-1})}_{ij}{b}_i{b}_j\\ \ge \sum _{i=1}^K{({\mathit{A}}^{-1})}_{ii}{b}_i^2+\sum _{1\le i\ne j\le K}{({\mathit{A}}^{-1})}_{ij}(b_i^2+b_j^2)/2\\ =\sum _{i=1}{({\mathit{A}}^{-1})}_{ii}{b}_i^2+\sum _{i=1}^K{b}_i^2(\sum _{j\ne i}{({\mathit{A}}^{-1})}_{ij}+\sum _{j\ne i}{({\mathit{A}}^{-1})}_{ji})/2.\end{array}$$

Noticing that A⁻¹ is symmetric, we have

$${\mathit{b}}^T{\mathit{A}}^{-1}\mathit{b}\ge \sum _{i=1}^K[{({\mathit{A}}^{-1})}_{ii}-\sum _{j\ne i}{({\mathit{A}}^{-1})}_{ij}]b_i^2\ge \sum _{i=1}^K{\delta }_0{b}_i^2={\delta }_0\parallel \mathit{b}\mid {\mid }^2.$$

This immediately implies that the smallest eigenvalue of A⁻¹ is not smaller than δ₀ which does not depend on the number J of observations. Similarly we can show that the largest eigenvalue of A⁻¹ is at most $2{max}_{i=1}^J{({\mathit{A}}^{-1})}_{ii}\le {\delta }_1(t_0,a)$.

Proof of Proposition 2

The i-th subject has observations at times t = t_i1, t_i2, ···, t_iJi, which are assumed to be in increasing order. According to Proposition 1, the eigenvalues of the correlation matrix of the i-th subject are between

$$\frac{1}{{\delta }_1(t_0,1/{\varphi }_0)}=\underset{a\ge 1/{\varphi }_0}{inf}\frac{1}{{\delta }_1(t_0,a)}$$

and

$$\frac{1}{{\delta }_0(t_0,1/{\varphi }_0)}=\underset{a\ge 1/{\varphi }_0}{inf}\frac{1}{{\delta }_0(t_0,a)}.$$

So part A is proved.

Part [B] can be easily proved by noticing that the correlation matrix for ARMA(1, 1) model is exactly (1 − γ)I + γD, where D is the corresponding correlation matrix of AR(1) with the same parameter ϕ and I is the identity matrix.

To prove Part [C], note that the correlation matrix for CARMA(p, q) model can be expressed as ${\sum }_{i=1}^p{\gamma }_i{\mathit{D}}_i$, where Di is the corresponding correlation matrix of AR(1) with parameter ϕ_i. Part [C] follows straightforwardly by applying Weyl’s inequality.