The Association of Dropout and Outcome in Trials of Antipsychotic Medication and Its Implications for Dealing With Missing Data

Abstract

Objective: The extent to which noncompletion of a clinical trial relates to outcomes has implications for choosing the most appropriate method for contending with missing data due to dropout. We examined whether dropout relates to outcome in clinical trials of antipsychotic medication. Methods: Data from 5 large clinical trials of schizophrenia (n = 3483) were examined separately. Patients were aggregated into groups based on their final study visit. Group mean Positive and Negative Syndrome Scale (PANSS) total scores for each visit were computed and graphed. Change from baseline to end point for each group was computed and examined using ANCOVA. Cox regression modeling was used to examine baseline PANSS total and change as predictors of time to dropout. Results: In all 5 trials there was a statistically significantly relationship between time in trial and improvement. The longer the patients remained in the trial the more that they improved, with trial completers showing the most improvement at each time point. Higher baseline PANSS scores and symptom deterioration indicated by increased PANSS preceding the final study visit prior to dropout corresponded significantly with a greater likelihood of dropout. Conclusions: Dropout in clinical trials of antipsychotic medications corresponds with efficacy outcomes, the dynamics of symptom change and baseline symptom severity. Therefore, methods for statistical analysis should examine both efficacy and dropout and cannot assume that missing data due to dropout are completely at random.

Introduction

High dropout rates characterize clinical trials of antipsychotic medication. It is not uncommon for them to exceed 50%.^1,2 Accordingly, questions have been raised about the most appropriate method for analyzing efficacy data in clinical trials of antipsychotic medication in general.³ Specifically, research questions the validity of the commonly used last observation carried forward (LOCF) method^4,5 and of mixed effects models⁶ and other methods used in these trials.⁵

Dropout leads to missing data that vary as to the extent to which it affects modeling and analysis. The literature distinguishes between 3 mechanisms of missing data.⁷ First, “missing completely at random” (MCAR) that refers to a situation where missingness does not depend on either observed or unobserved data. A possible example is data lost because some patient records were destroyed in a flood. MCAR can readily be handled in the analysis. Nevertheless, MCAR leads to loss of power due to diminished sample size. Second, “missing at random” (MAR) that occurs if the missing data depend on variables that are observed during the trial but not on unobserved data. An example of MAR could be increased dropout in the placebo arm of a study or high dropout rates in a particular study center. In such cases, dropout is explained by the observed data and can be accounted for in the data analysis. Third, “missing not at random” (MNAR) that occurs if the missingness depends on unobserved data. An example could be a patient who was doing well and then was lost to follow-up because he/she had relapsed after the last observed visit and was admitted to a different hospital. In this case, the observed data could not predict the missing data. The unobserved data contained information not foreseen by the observed data.⁸ MNAR cannot be corrected without explicitly specifying a model for the missing data mechanism, which by definition cannot be observed or tested.

MCAR and MAR are termed “ignorable nonresponse” because the first requires no special attention when analyzing the data and the second can be controlled for in the analysis. MNAR is termed “nonignorable nonresponse” because it cannot be ignored. MAR and MNAR are also sometimes referred to as “informative” as the data that are missing is informative as it relates to study variables.

Missing data in clinical trials of antipsychotic medication because of dropout are problematic because they are rarely MCAR and it is generally difficult to determine if they are MAR or MNAR. Supporting the view that missing data due to dropout in these trials are informative, and thus not MCAR, Ali and Siddiqui⁵ have presented data on 181 patients from a clinical trial of antipsychotic medication that demonstrates that patients who dropped out tended to be doing worse at the time of dropout as measured by change on the Positive and Negative Syndrome Scale (PANSS), than those who went on to complete the study. These data demonstrate that in that study dropout was informative as it related to study variables.

A standard approach used in clinical trials is LOCF that uses the last completed observation while on treatment to estimate a hypothetical last study visit value. This is problematic because it assumes that the data are MCAR and that symptoms would remain absolutely unchanged from the last visit before dropout to the end of the study thereby underestimating variability in the data and may inflate the Type I error rate to an unacceptable extent under reasonable assumptions about causes for dropout.⁹ Some recent trials^6,10,11 have applied a mixed effects model⁸ that is thought to provide more accurate estimates of treatment than LOCF.⁸ These estimates are based on data available at each given time point. Mixed effects models and imputation methods work if data are MCAR or MAR; however, if the data are MNAR then inferences based on these methods will not be valid. Key to choosing an appropriate method for analyzing data in clinical trials is the extent to which dropout and outcomes are related. Accordingly, the current study examines whether dropout is related to outcome in clinical trials of antipsychotic medication.

METHOD

Participants and Procedure

Data on 3275 patients were extracted from 5 large clinical trials^12–16 of antipsychotic medication. The trials are described in table 1. The data for these trials were available to the authors and selected because all used the PANSS¹⁸. The trials varied as to duration, population treated, and the treatment given. All treatment groups in the studies were included. Studies had been approved by the relevant Institutional Review Boards and participants gave informed written consent after being given a complete description of the study.

Table 1.

Description of Trials Included in Current Analysis

	Int-212 (n = 1358)	Int-314 (n = 513)	Int-3513 (n = 553)	USA-12115 (n = 458)	Int-5717 (n = 582)
Duration	8 weeks	8 weeks	At least 2 years. In current analysis, data up to 1 year included.	12 weeks	1 year
Population	Chronic inpatients, International	Chronic inpatients, USA	First episode, International	Acute, USA	Symptomatically stable, International
Design	RCT, double blind, 6 parallel groups (5 fixed doses risperidone and 1 haloperidol)	RCT, double blind, 6 parallel groups (4 fixed doses risperidone, 1 haloperidol and placebo)	RCT, double blind, 2 parallel groups (risperidone and haloperidol)	RCT, double blind, 2 parallel groups (injections of long-acting risperidone and placebo)	Open label single arm long-acting risperidone injectable
Female	34.3%	16.6%	28.6%	22.6%	31.3%
Age, females	40.5 SD 12.0	42.8 SD 11.0	26.6 SD 7.6	41.0 SD 8.9	46.6 SD 14.8
Age, males	36.8 SD 10.9	36.2 SD 9.8	24.9 SD 6.5	36.7 SD 9.5	39.6 SD 13.1
Diagnosis, schizophrenia	All	All	65.4%a	All	All
PANSS, baselineb	89.7 SD 17.8	92.6 SD 18.9	82.4 SD 20.2	82.0 SD 13.8	67.1 SD 18.9
PANSS, mean change to end point	−16.3 SD 22.7	−8.0 SD 24.3	−20.8 SD 23.5	−4.2 SD 18.0	−6.6 SD 16.6

Note: PANSS, Positive and Negative Syndrome Scale; RCT, randomized controlled trial.

^a6.7% schizoaffective, 27.9% schizophreniform.

^bBaseline and change results are for all treatment groups in the studies.

Data Analysis

At the first step of the analysis, patients were grouped based on the final scheduled study visit that they attended. Mean PANSS total score for each visit was computed for each group and these data were graphed for each study. Second, to further examine trends revealed in the graphs, an ANCOVA of change to end point for each trial controlling for baseline PANSS with visits completed as a factor was conducted. Third, we compared baseline PANSS scores of those who completed and did not complete each study using an independent sample's t test. Fourth, logistic regression was used to estimate the odds of dropping out based on baseline PANSS score and to distinguish between those who did and did not dropout. Fifth, Cox regression modeling, a widely used form of regression modeling, was used to predict time to dropout. This model included as predictors change on the PANSS (segmented time dependent) and baseline PANSS (nontime dependent). Two models were conducted for each trial: one examined change from baseline to final visit and the other examined change from previous visit to final visit.

Results

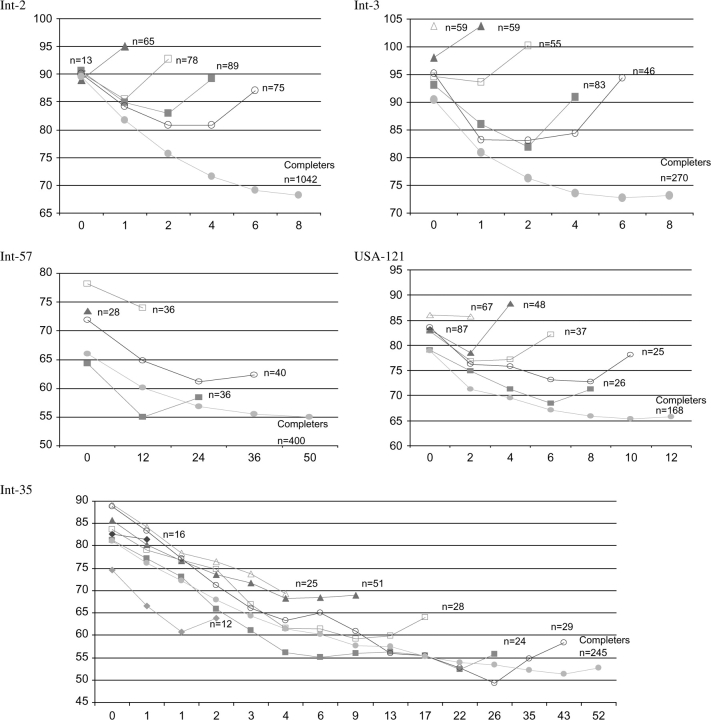
Figure 1 presents the mean PANSS values at each time point for each group by number of weeks (visits) until ending the study. Each line represents a group of patients who dropped out after a different visit. The longest line represents those patients who completed the trial. These graphs clearly illustrate that those who dropped out before the scheduled end of the trials showed less improvement or even deteriorated relative to the number of weeks (visits) that they remained in the trial. Furthermore, trial completers (ie, the longest line) showed the most improvement at each time point. For example, in Int-2 (figure 1, top left graph) the groups started off with similar baseline PANSS values. The group who dropped out after the first week of treatment (ie, second visit, line with solid triangles, n = 65) increased on PANSS values as did those who dropped out after the second week (ie, third visit, line with empty squares, n = 78) and fourth week (ie, fourth visit, line with solid squares, n = 89). Those who dropped out after week 6 (ie, fifth visit, line with empty circles, n = 75) showed a decline in symptom severity and then increased toward their baseline PANSS levels and then dropped out. The group that completed the study (ie, line with solid circles, n = 1042) showed constant improvement throughout. Although each graph differed these same general trends occurred across the trials of worse symptom severity at the last visit for those groups who did not complete the trial. ANCOVA of change to end point for each trial by visits completed showed a monotonic trend of the more visits until dropout, the more change thus corroborating the results in figure 1.

Fig. 1.

Mean Positive and Negative Syndrome Scale Total Score by Study Week Grouped by Final Visit Attended for 5 Clinical Trials.

The graphs also suggested that baseline values were related to dropout. In Int-57, there was an almost monotonic relationship between baseline scores and trial completion with the completers having the second lowest baseline score. Table 2 shows that in Int-3, Int-57, and USA-121, the baseline PANSS values were significantly lower among the completers group as compared with those who did not complete the studies. The last column of table 2 presents beta (ie, estimated coefficient), OR, and CI. Beta shows the increase in the logarithm of OR for a 1-unit increase in the PANSS. The table presents the ORs for a 10-point increase in the PANSS. Using beta, the OR increase can be calculated in the following way¹⁹: for example, if we wanted to compare in USA-121 the likelihood of dropout of a patient with a baseline PANSS of 60 to one with a PANSS of 100 we would use β = .0237 and multiply it by 40, the difference between the patients, then compute the exponential of .0237 × 40 which is 2.58. Thus, a patient with a PANSS score of 40 higher would be 2.58 times more likely to dropout.

Table 2.

Comparison of Positive and Negative Syndrome Scale (PANSS) Total Baseline of Completers vs Noncompleters (t Tests and Logistic Regression Models)

	Means and SD		t Test	Logistic Regression, OR (95% CI) for Difference of 10 Points on the PANSS
	Completer	Noncompleter
Int-2a	90.06 SD 17.46	89.47 SD 17.9	P = .61	β = .0002, OR = 1.002 (0.995–1.009), P = .667
Int-3b	90.47 SD 18.94	95.06 SD 18.58	P = .006	β = .0129, OR = 1.14 (1.013–1.262), P = .006
Int-57c	66.84 SD 18.88	71.49 SD 20.31	P = .014	β = .0119, OR = 1.126 (1.101–1.24), P = .014
USA-121d	78.93 SD 13.90	83.45 SD 14.08	P = .001	β = .0237, OR = 1.267 (1.252–1.282), P = .001
Int-35e	81.09 SD 20.34	83.63 SD 20.15	P = .15	β = .0059, OR = 1.06 (1.052–1.07), P = .15

^a23.2% (n = 316/1358) dropped out prior to week 8.

^b47.4% (n = 243/513) dropped out prior to week 8.

^c24.7% (n = 144/582) dropped out prior to week 12.

^d58.2% (n = 267/458) dropped out prior to week 12.

^e62.9% (n = 349/553) dropped out prior to 2 years.

The 2 Cox regression models for each study presented in table 3 showed that in all trials baseline PANNS total scores, change from baseline (columns 1 and 3), and change since previous visit (columns 2 and 4) significantly predicted time to dropout. Using beta, the hazard ratio increase can be calculated in the following way¹⁹: for example, if we wanted to compare in Int-2 the likelihood of dropout of a patient who deteriorated since their last visit by increasing from baseline by 30 PANSS points as compared with a patient who improved by showing a decline of 30 points we would use β = .0372 and multiply it by 60, the difference between these 2 patients, then compute the exponential of .0372 × 60 which is 2.23. Higher baseline scores and more deterioration (ie, positive change or increase on PANSS) corresponded with an increased likelihood of dropout.

Table 3.

Results of 2 Cox Regression Models per Study Predicting Time to Dropout Based on Positive and Negative Syndrome Scale Values (RR for 10 Points With 95% CI)

	Time to Dropout Based on Baseline and Difference Between Last Visit Value and Baseline		Time to Dropout Based on Baseline and Last Change From Previous Visit
	PANNS Baseline	Last Change From Baseline	PANNS Baseline	Last Change From Previous Visit
Int-2	β = .0139, RR = 1.149 (1.143; 1.155)	β = .0129, RR = 1.138 (1.136; 1.140)	β = .0129, RR = 1.138 (1.132; 1.144)	β = .0372, RR = 1.450633 (1.447; 1.455)
Int-3	β = .0237, RR = 1.267 (1.260; 1.274)	β = .0119, RR = 1.126 (1.124; 1.128)	β = .0198, RR = 1.219 (1.212; 1.226)	β = .0286, RR = 1.331 (1.325; 1.337)
Int-57a	β = .0178, RR = 1.195 (1.185; 1.205)	β = .0099, RR = 1.104 (1.100; 1.108)	β = .0149, RR = 1.161 (1.151; 1.171) (P = .001)	β = .0129, RR = 1.138 (1.129; 1.147) (P = .01)
USA-121b	β = .0178, RR = 1.195 (1.185; 1.205)	β = .0129, RR = 1.138 (1.135; 1.141)	β = .0188, RR = 1.207 (1.198; 1.216)	β = .0227, RR = 1.255 (1.250; 1.260)
Int-35c	β = .0256, RR = 1.292 (1.287; 1.297)	β = .006, RR = 1.062 (1.061; 1.062)	β = .0256, RR = 1.292 (1.286; 1.298)	β = 0247, RR = 1.280 (1.276; 1.284)

Note: All P values < .0001.

^a24.7% (n = 144/582) dropped out prior to week 12.

^b58.2% (n = 267/458) dropped out prior to week 12.

^c62.9% (n = 349/553) dropped out prior to 2 years.

Discussion

The current results based on 5 large clinical trials suggest that dropout in clinical trials of antipsychotic medication is informative because the data that are missing relate to study variables. Specifically, we found that patients who drop out prematurely tend to show a trend of progressive deterioration, indicated by change on their PANSS scores as well as higher baseline scores. Trial completers showed a trend of progressive amelioration throughout the trial.

Because dropout is related to symptom severity, the missing data mechanism is clearly not MCAR. The pattern of deterioration before dropout may suggest that MAR or MNAR is present. MNAR cannot be ruled out. The results suggest that in these trials dropout needs appropriate consideration. There is no consensus as to the most appropriate method. Complete case analysis would not be appropriate unless the study's aim was to examine how the drug works for those who remain on the drug. This is because it would tend to exaggerate the extent of improvement and, given a dropout rate difference between study arms, would also underestimate efficacy differences between study arms. Because missingness is informative, analyses based on the observed data likelihood (eg, random effects model and multiple imputation-based analyses) may not be appropriate if the data are MNAR^5,6. Seen this way methods based on comparing slopes such as conditional linear models,²⁰ pattern mixture models²¹ and unweighted least squares are more appropriate.⁵ We note that in our data the trajectories for the patients who dropped out appear to be nonlinear, which argues against doing endpoint analyses.

In real life, dropout is probably often related to symptomatology and it is also an important outcome. In these situations, MNAR cannot be ruled out. Therefore, methods that can handle MNAR are needed. One such method that is not dependent on the mechanism of missing data is the composite approach that does not impute data but simultaneously tests the combined outcome of completing the trial and improvement.^22,23 In addition to expanding the armamentarium of analytic methods, it may also be possible for investigators to continue interviewing patients even after dropout from random assignment. This could alleviate some of the problems of missing data and allow one to see the final trajectories of those patients who leave random assignment before the end of the study.

In conclusion, because dropout corresponds with symptom severity attention to missing data due to dropout in analyzing efficacy data in trials of antipsychotic medication is warranted.