Broadband Slab Selection with B₁⁺ Mitigation at 7T via Parallel Spectral-Spatial Excitation

Abstract

Chemical shift imaging benefits from SNR and chemical shift dispersion increases at stronger main field such as 7 Tesla, but the associated shorter RF wavelengths encountered require B₁⁺ mitigation over both the spatial FOV and a specified spectral bandwidth. The bandwidth constraint presents a challenge for previously proposed spatially tailored B₁⁺ mitigation methods, which are based on a type of echovolumnar trajectory referred to as “spokes” or “fast-k_z”. While such pulses, in conjunction with parallel excitation methodology, can efficiently mitigate large B₁⁺ inhomogeneities and achieve relatively short pulse durations with slice-selective excitations, they exhibit a narrow-band off-resonance response and may not be suitable for applications that require B₁⁺ mitigation over a large spectral bandwidth. This work outlines a design method for a general parallel spectral-spatial excitation that achieves a target-error minimization simultaneously over a bandwidth of frequencies and a specified spatial-domain. The technique is demonstrated for slab-selective excitation with in-plane B₁⁺ mitigation over a 600 Hz bandwidth. The pulse design method is validated in a water phantom at 7T using an 8-channel transmit array system. The results show significant increases in the pulse’s spectral bandwidth with no additional pulse duration penalty and only a minor tradeoff in spatial B₁⁺ mitigation compared to the standard spoke-based parallel RF design.

Introduction

Parallel excitation offers the means to accelerate RF waveforms for complicated 2D and 3D spatially tailored excitations, resulting in shorter excitation duration when compared to the single-channel case (1–4). A number of successful demonstrations of this concept on a multi-channel transmit system have been reported such as in (5–8). Accelerations of 4–6 fold have been achieved via an 8-channel transmit system (6), potentially enabling several important applications, including flexibly shaped excitation volumes, and mitigation of RF field inhomogeneity at high field for slice or slab-selective pulses.

Nonetheless, previous work on parallel excitation methods have been limited to the design of excitation profiles at a single frequency, resulting in RF pulses with a narrow bandwidth characteristic. The off-resonance behavior stems from the lengthy echoplanar, spiral or echovolumnar excitation k-space trajectories, which incur off-resonance effects analogous to the image encoding case. This narrow-band property was apparent in (9), where it was shown that B₀ inhomogeneity in standard in-vivo imaging condition at 3T can have a detrimental effect on the excitation profile if a field map information was not incorporated into the RF design.

The narrow-band nature of the spatially tailored excitation pulses particularly complicates their use in high field chemical shift imaging. Chemical shift imaging (CSI) benefits from high main magnetic field strength (such as 7T) through higher SNR, increased chemical shift dispersion, and weaker spin coupling. However, the detrimental effects of B₁⁺ inhomogeneities at high-field pose significant problems, and in order to realize the benefits of high-field to CSI, broadband RF excitations that mitigate B₁⁺ inhomogeneity and achieve uniform flip angle over both the spatial field of view and a specified spectral bandwidth are necessary. This additional bandwidth constraint over conventional imaging presents a substantial challenge for current parallel RF design methods which, to date, have not explicitly incorporated this constraint into the design problem.

We describe a method for a general parallel spectral-spatial excitation based on extending the spatial domain formulation of the parallel RF design proposed by Grissom et al (4), with an explicit incorporation of the spectral bandwidth into the minimization problem. Additionally, we incorporate a Magnitude Least Squares (MLS) optimization (10,11) for improved mitigation properties over conventional least-squares minimization. In demonstrating the capability of this new technique, a uniform wideband slab-selective excitation was designed using a type of echovolumnar trajectory referred to as “spokes” or “fast-k_z^” (6,12) to mitigate the extensive B₁⁺ inhomogeneity present in a head-sized water phantom at 7T over a 600 Hz spectral bandwidth. The performance of the resulting 1.76-ms duration, 5-cm thick slab-selective excitation RF pulse was validated using an 8-channel transmit array system on a 7T human MRI scanner.

Theory

In this work we based our parallel excitation formulation on the spatial-domain approach by Grissom et al (4) with the extension of MLS optimization presented in (11). In brief, the multi-dimensional excitation calculated for R coils in the low-flip-angle approximation (13) is written as

$$m(x)=i\gamma \sum _{r=1}^R{S}_r(x)\int B_{1,r}(t)e^{ix·k(t)}dt$$ [1]

where, S_r and B_1,r are the spatial transmit sensitivity profiles and the RF voltage waveforms for coils indexed by r, x is the spatial variable, m(x) is the target transverse magnetization after excitation, and k(t) is the excitation k-space trajectory, defined as $k(t)=-\gamma \underset{t}{\overset{T}{\int }}G(\tau )d\tau$, where γ is the gyromagnetic ratio, and G is the gradient, and T is the duration of the gradient waveform. After discretization in space and time, this expression can be written as a matrix equation, m = Ab, where the A-matrix incorporates the B₁⁺ coil profiles modulated by the Fourier kernel due to the k-space traversal, m is the target profile in space, and b contains the RF waveforms. With this formulation, the RF pulses can be designed by solving the following MLS optimization:

$$b={arg}_{b}min\{{\Vert \mid Ab\mid -m\Vert }_w^2+\beta \parallel b\mid {\mid }_2^2\}.$$ [2]

Here, m is specified as a non-negative real vector, the optimization is performed over the region of interest (ROI) implied by a weighting, w, and $\beta \parallel b\mid {\mid }_2^2$ denotes the Tikhonov regularization term that is used to control the integrated RF power. The MLS optimization, as represented by |Ab| in Eq. [2], is used instead of the standard Least Square (LS) optimization to limit the optimization to the excitation magnitude profile, allowing for phase-profile variation. This has been found to achieve substantial gains in excitation magnitude performance over conventional LS optimization with little penalty in image phase. For applications such as spectroscopic imaging where the reconstructed data are often phased for the purpose of display or quantification, the information about the spatial as well as the spectral phase offset due to the excitation is known and can be incorporated into the spectral processing as a priori information. Therefore the phase variation introduced by the MLS algorithm should not cause deterioration to the achievable spectral quality.

The spectral-spatial excitation design is a direct extension of the above formulation. To design for spatial excitation profile (m) at a set of N different frequencies, we extend the set of equations and concatenate the m vector and the A matrix corresponding to the N design frequencies (1, 2, ….., N) to form:

$$\left[\begin{array}{c}{\overline{m}}_{\mathit{Freq}1}\\ {\overline{m}}_{\mathit{Freq}2}\\ ⋮\\ {\overline{m}}_{\mathit{Freq}N}\end{array}\right]=\left[\begin{array}{c}{[A}_{\mathit{Freq}1}]\\ {[A}_{\mathit{Freq}2}]\\ ⋮\\ {[A}_{\mathit{Freq}N}]\end{array}\right]\times \overline{b}$$ [3]

The concatenated equation can then be solved, as before, via MLS optimization.

The MLS optimization is crucial to the proposed spectral-spatial formulation. Generally the excitation profile at different frequencies will have different spatial phase and the design is generally ill-conditioned as an LS optimization with a fixed, uniform target phase.

For accurate spatial excitation in the presence of B₀ inhomogeneity, B₀ inhomogeneity correction (B₀ tracking) is also incorporated into the RF design by modifying the individual A_Freq matrix in Eq. [3] to include a measured field map using a procedure similar to (4,9)

Method

System Hardware

Experiments were performed on a 7T whole-body scanner (Siemens Healthcare Erlangen, Germany), equipped with a prototype 8-channel transmit RF system, with a body gradient system capable of maximum gradient amplitude of 40 mT/m and slew rate of 200 T/m/s. The RF hardware components relevant to this study include a 16-channel stripline transmit-receive (Tx/Rx) degenerate birdcage coil array and a 16-channel Butler matrix (14) (Fig 1a). The Butler matrix was used to drive the 8 bright birdcage transmit modes from the 16 channel coil, and serves to make the best use of the RF excitation system, which is limited to 8 RF transmit channels and power amplifiers. The 16-channel RF coil array was built on a 28-cm diameter acrylic tube and driven through a transmit-receive switch at each coil. Signal was received in a birdcage mode of the 16 receive channels of the array. All experiments were performed using a 17-cm diameter spherical phantom of doped water, containing 1.25 g/l of Nickel Sulfate and 5 g/l of Sodium Chloride.

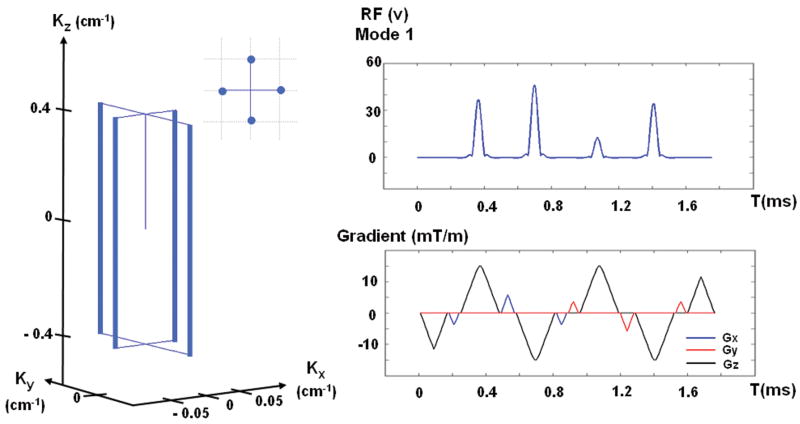
Figure 1.

k-space trajectory for the 4-spokes excitation is shown on the left. On the right are the RF waveform for one of the eight transmission modes (mode 1), and the gradient waveforms that were used for the excitation.

RF Design

To demonstrate the capability of the proposed spectral-spatial design method, the technique was used with a 4-spoke trajectory (shown in figure 1) to obtain parallel RF pulses that uniformly excite a 5-cm thick slab over a target bandwidth of 600 Hz, which corresponds to 2 ppm at 7T. The sinc sub-pulses in the RF waveform have time-bandwidth-product of 4, and the gradient trajectory is designed for a maximum gradient amplitude and slew rate limited to 40 mT/m and 150 T/m/s, resulting in pulse duration of 1.76 ms. Flat magnitude target excitation profiles were specified at 3 spatial locations in z (0, ±1.75 cm), to account for the z-variation in the coil transmit profiles. A set of N=5 frequency points, at [−300 −150 0 150 300] Hz, were used to create the 600 Hz excitation bandwidth for B₁⁺ mitigation. The resulting k-space trajectory, gradient waveforms, and RF waveform for mode 1 are shown in Figure 1.

B₁⁺ and B₁⁻ mapping

In this work, an efficient B₁⁺ mapping technique described in (15) was used to estimate the B₁⁺ maps of the eight transmit modes of the RF array. From this mapping technique, an estimate for the spin-density weighted birdcage receive profile, ρ̀(x,y) R̀X (x,y), was also obtained, and this receive profile estimate was used in dividing the reconstructed image in subsequent parallel excitation experiments to obtain excitation profiles. The magnitude estimates of the density-weighted birdcage reception profile and the transmit birdcage profile are shown in figure 2a, along with the magnitude image of a low-flip angle birdcage transmit-receive profile. The magnitude and phase estimates of the transmit profile of the eight transmit mode are shown in figure 2b.

Figure 2.

a) Sixteen-channel transmit/receive stripline coil array for 7T, and the butler matrix hardware that was used for the experiments in this work. The insert on the right panel of a) shows the estimated transmit (TX) and receive (RX) profiles and the transmit-received image (TX-RX) of the birdcage mode of the array for a water-filled spherical phantom. b) The upper panel shows the estimated magnitude profile (intensity scale normalized to a maximum value of 1), and the lower panel shows the phase profile (in degrees) of the eight butler transmission modes used.

Due to a small but non-negligible B₁ profile variation in the z-direction over the target field-of-excitation (FOX), a set of in-plane B₁ maps were obtained at a set of positions along z. The B₁⁺ profiles for all of the 8 transmit modes were obtained at z = 0, ±1.75 cm, and were used in the RF design. The birdcage receive profiles were obtained at z = 0, ±1, ±2 cm, and were used in the parallel excitation experiments to divide out the reconstructed images to obtain excitation profiles.

B₀ Mapping

B₀ maps were estimated using two gradient-echo acquisitions at TE1/TE2=5/6 ms. This estimation was performed at 3 slice locations (z = 0, ±1.75 cm), and the resulting maps were incorporated into the pulse design (4,9) to improve the robustness of the desired excitation, thereby implementing B₀ tracking in the presence of unavoidable B₀ inhomogeneity.

Comparisons and Experiments

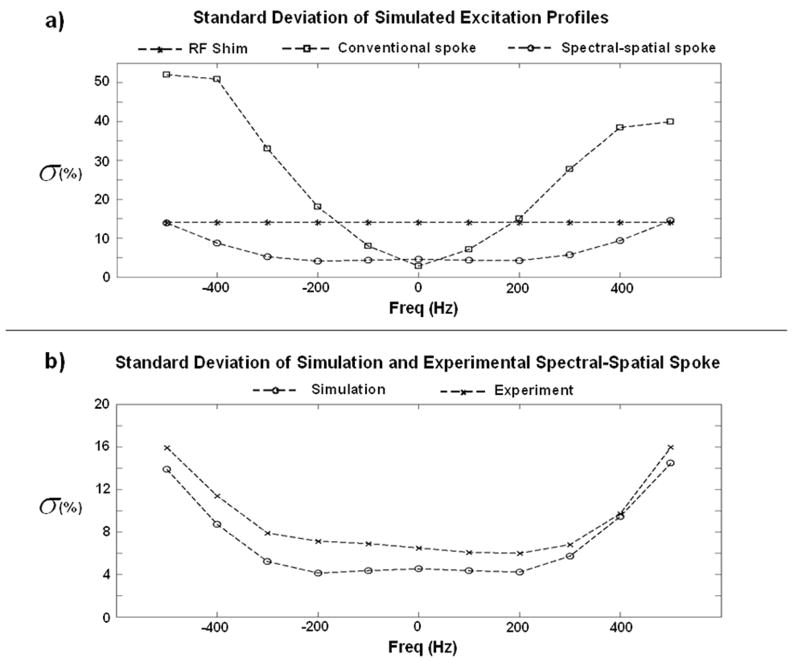
To illustrate the benefit of the spectral-spatial design, its excitation performance over a 1000 Hz bandwidth was compared with RF shimming and a standard 4-spoke MLS parallel excitation (11). The excitation profiles at a set of offset frequencies ranging from −500 to +500 Hz in steps of 100 Hz were simulated for all three designs. The uniformity of the excitations was quantified and compared using standard deviation ( σ ) of the pixels in the FOX. For a fair comparison, the same Tikhonov regularization parameter value ( β ) was used for all three designs, where it was empirically determined that the β value of 0.001 provides a good tradeoff between excitation error and RF power for all three designs.

For the RF shimming design, a multidimensional Powell optimization method (16) was used instead of the MLS optimization algorithm presented in (11). Empirically, it has been observed that the MLS optimization algorithm in (11) tends to produce solutions that contain smooth and slowly varying excitation phase. However, apart from the uniform birdcage mode, the phase profile of all the other excitation modes of the coil exhibit rapid spatial phase variation (figure 2b), and as a result the MLS optimization solution to RF shimming mainly employed the uniform birdcage mode, and contain very small contributions from the other modes. In trying to obtain the best-case performance of RF shimming that will be used to compare with the other two design techniques, multidimensional Powell optimization method (16) was employed for the RF shimming design. The solution to this optimization method for RF shimming results in a more uniform magnitude excitation profile although it contains a much more rapidly varying phase.

For experimental validation, RF pulses for the spectral-spatial design were transmitted at a set of offset frequencies ranging from −500 to +500 Hz in steps of 100 Hz. The uniformity of the resulting excitation profiles was then compared to the ones obtained from simulation.

All the excitations were imaged with a 3D gradient-recalled echo sequence with receive matrix size of 128×128×32 voxels, FOV = 256 mm × 256 mm × 160 mm, spatial resolution = 2 mm × 2 mm × 5 mm, and TR, TE, BW = 100 ms, 6 ms, 260 Hz/pixel. The excitation profiles were then inferred by dividing the reconstructed image by the estimated spin-density weighted birdcage receive profile, ρ̀ (x,y) R̀X (x,y). The RF excitation pulse amplitudes were adjusted so that all the experimental excitations were for the target flip angle of 5°.

Results

Figure 2a) shows the measured B₁⁺ excitation and B₁⁻ reception profile of the “uniform” mode of the array as excited by the Butler matrix. In this mode the pattern is equivalent to that of a uniform birdcage coil. Figure 2b) shows the B₁⁺ profiles obtained with the eight transmit channels, showing the standard spatial modes of the birdcage coil.

Figure 3 shows the in-plane excitation profiles at the center frequency (0 Hz) for RF shimming, a conventional water-only spoke design, and spectral-spatial spoke excitations. These three methods yielded excitation deviations from the ideal uniform target (as measured by the standard deviation) of 14%, 2.84%, and 4.54 % respectively, while in contrast the standard birdcage mode resulted in a standard deviation of 23.5%. Even though RF shimming provided an improvement over the standard birdcage excitation, significant spatially-varying flip-angle inhomogeneity remained. Particularly noticeable is the low excitation region near the center of the FOX leading to a max/min excitation magnitude ratio of 36, compared to 3.29 in the standard birdcage, and 1.28 and 1.38 in the conventional and spectral-spatial spoke excitations. On the other hand, the conventional 4-spoke excitation mitigated essentially all of the B₁⁺ inhomogeneity (for this on-resonance excitation), while the spectral-spatial version of the 4-spoke excitation resulted in slightly less on-resonance uniformity than the narrow-band design, but significantly better mitigation than RF shimming alone.

Figure 3.

In-plane excitation profiles at center frequency for RF shimming, conventional spoke, and spectral-spatial spoke excitations respectively.

Figure 4a) shows the standard deviation ( σ ) plots comparing the performance of the three excitation designs over a ±500 Hz frequency range. While RF shimming has the advantage of being essentially unaffected by off-resonant effects (dictated by the short duration (0.5ms) sinc-like pulse used), its σ value is high. The performance, as measured by the σ value, for the conventional 4-spoke excitation is excellent at the center frequency but deteriorates rapidly with off-resonance, for example, outside the ±200 Hz off-resonance range, the σ value obtained from this design becomes larger than one obtained from the RF Shimming design. On the other hand, the spectral-spatial pulse trades off a small amount of on-resonance homogeneity for a better uniformity over a much wider bandwidth. For this design, the σ value remains below 6% over the entire ±300 Hz design bandwidth.

Figure 4.

Standard deviation plots comparing a) the simulated performance of the three types of excitation designs, and b) the simulated and experimental performance of the spectral-spatial spoke excitation design over a ±500 Hz frequency range.

Figure 4b) shows the standard deviation ( σ ) plots comparing simulation and experimental performances of the spectral-spatial spoke excitation over a ±500 Hz frequency range. In general, the experimental performance matches well with the predicted performance from simulation; with σ value from both cases following a similar trend across frequency, and with the experimentally determined σ at all frequencies being only slightly larger than one obtained from simulation.

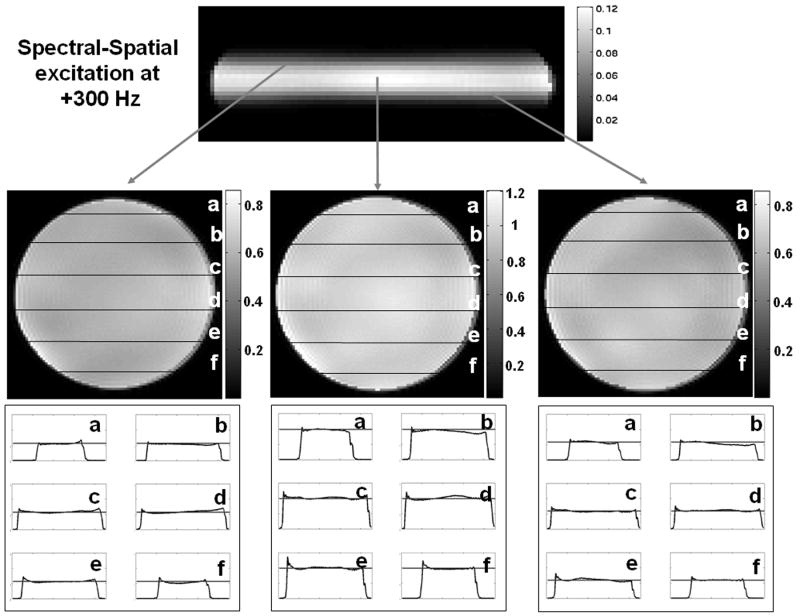
Figure 5 summarizes the excitation performance of the spectral-spatial pulse at +300 Hz off-resonance frequency. This is representative of the excitation performance achieved along the pass-band. The figure shows the through-slice and in-plane profiles at 3 different positions in z, along an image of the excited slab. Excellent slice selection and good in-plane uniformity can be observed. A minor horizontal shift in the in-plane profiles (along the readout direction) as a result of an off-resonance artifact during readout can also be seen.

Figure 5.

Excitation performance achieved by the spectral-spatial pulse at 300 Hz off-resonance with the through-slice profile (top), the in-plane profiles at 3 different though plane positions along the excited slab (center), and the corresponding 1-D profiles at several cuts through the in-plane profiles (bottom). Excellent slice selection and good in-plane profiles can be observed.

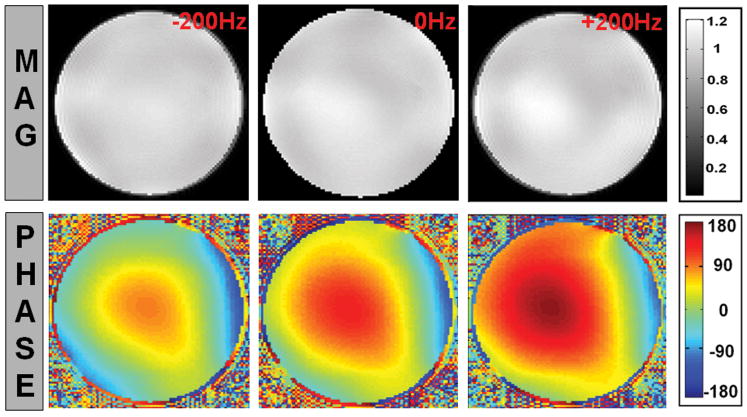
Figure 6 shows the magnitude and phase profiles for the center slice of the excited slab at 0, ±200 Hz. The magnitude profile is uniform at all frequencies, while, as a result of MLS optimization, the phase profile varies both spatially and spectrally. The phase profile variation is smoothly varying and resulted in negligible intra-voxel dephasing.

Figure 6.

From left to right: the magnitude and phase profiles for the center slice of the excited slab at −200, 0, and +200 Hz respectively. The magnitude profile exhibits good uniformity at all three frequencies while, as expected from the MLS optimization, the phase profile varies smoothly both spatially and spectrally.

Discussion and Conclusions

In this work we generalized the spatial domain method for spectral-spatial parallel RF design and utilized this approach for the design of wideband uniform slab selection excitation pulses that mitigates large B₁⁺ variation over a 600 Hz bandwidth. A significant improvement in the spectral performance was achieved over the conventional parallel RF design, at the cost of only a minor reduction in excitation uniformity at the center frequency. Given that this improvement was demonstrated in a water phantom with B₁⁺ variation comparable to that of the largest variation observed in a recent six-subject in vivo study at 7T which utilizes the same Tx-Rx coil array setup (15) (signal peak-to-through ratio of ~ 3:1 in the birdcage mode), we expect the design to play an important role in improving in vivo chemical shift imaging at high field as well as other applications needing broad-band excitations, such as water-fat imaging.

Figure 4a illustrates the narrow bandwidth characteristic of the spoke-based excitation when designed via conventional parallel RF technique. The bandwidth is particularly narrow for an excitation with a pulse duration of 1.76 ms. This narrowband characteristic is a direct result of the nature of the spoke excitation, whereby the final excitation profile can be thought of as a summation of the individual spoke’s excitation profiles (with accounts of the effect of the gradient lobe in between the spokes). With the conventional design technique, the individual spoke’s excitation profiles are chosen such that they combine to create a profile that is as uniform as possible at the center frequency. This is done without consideration of the performance at off-resonance frequency positions. The wideband design on the other hand, chooses individual spoke’s excitation profiles which combine well over a range of frequencies, and in doing so, trade off some in-plane spatial uniformity at the center frequency for a much wider excitation bandwidth.

In prior work described in (11), by using MLS optimization and allowing for spatial phase variation in the excitation profile, spoke-based slice-selective excitation performance was shown to improve significantly both in term of excitation uniformity and power requirements compared to parallel RF pulses designed with conventional LS. For the design of the spectral-spatial pulse, in addition to allowing for spatial phase variation, permitting spectral phase variation is crucial to achieve the desired magnitude performance target. In figure 6, most of the spectral phase variation is from a bulk phase shift resulting from differences in spin frequency. Relaxing the target design phase both spectrally and spatially enables the incorporation of a natural spectral phase variation, avoiding designs that are ill-conditioned, and would result in very poor magnitude excitation.

With B₀ tracking, the 600 Hz excitation bandwidth (~2 ppm. at 7T) achieved by the spectral-spatial spoke excitation would be sufficient in providing uniform excitation to many important metabolites in proton chemical shift imaging (CSI), for instance covering the range from 2 ppm to 4 ppm, with B₀ tracking to minimize adverse effects of spatially-varying main field inhomogeneity (17). In designing this excitation, no modification was made to the spoke gradient trajectory; therefore excitation duration of the spectral-spatial pulse was the same as the one for conventional spoke excitation.

Due to the non-convex nature of MLS optimization, global optimality of the solution cannot be guaranteed. In this work, the method presented in (11) was used to solve the posed problem. Other methods exist, including the relaxed semi-definite programming method (18). Future work includes an exploration of alternate means to allow for further improvements in the solution.

In the k-space trajectory design, we observed that the placements as well as the order in which the spokes are traversed affect the bandwidth of the excitation. In this work, we experimented with several possible k-space trajectories for the 4 spokes design. Two types of trajectories were examined: 1) a trajectory with a DC spoke and three surrounding spokes equally distributed on a circle centered at DC, and 2) a trajectory with four spokes equally distributed on a circle, but without a DC spoke. Various orders of the spokes’ traversal and various angular rotations of the spoke placements on the circle were examined for both types of trajectories. Based on our experimental setup, the spokes trajectory without DC sampling allowed a wider bandwidth. This type of trajectory along with the optimal traversal combination (as shown in figure 1) was used to obtain the results presented in this work. Future work will explore the theoretical underpinnings on the placement and order of spokes and their effect to the excitation bandwidth.

The proposed spectral-spatial excitation design formulation has been utilized for the design of spoke-based wideband slab selection with B₁⁺ mitigation. To provide a preliminary analysis of the benefit of this design methodology in increasing the bandwidth for other types of excitations, simulation of 2D spiral as well as spoke-based uniform thin-slice excitation were performed using the obtained B₁ maps. For the spiral design, a 4x accelerated spiral trajectory was used with a 5×5 cm square target excitation at the center of FOV. The excitations were designed for a 3.52 ms long RF pulse, with design FOV and resolution of 18 cm and 4 mm respectively. Based on the simulation the excitation bandwidth resulting from the standard MLS design is ~100 Hz, whereas with the proposed spectral-spatial design, a bandwidth of ~500 Hz could be achieved with a minor reduction in the excitation performance at the center frequency. For the spoke-based uniform thin-slice excitation, a slice prescription of 0.5 cm was used. Employing the same k-space trajectory and time-bandwidth-product as in the previous slab selection design, the pulse duration of the excitation is 4.38 ms. With this design, the excitation bandwidth of the standard MLS design is very narrow at around 30 Hz, whereas the spectral-spatial design achieved a bandwidth of ~120 Hz, again accompanied by a minor reduction in spatial homogeneity of the excitation at the center frequency. This increase in bandwidth is not significant enough to make the pulse suitable for CSI application. However, it would improve the robustness of excitation by allowing the excitation to be much more immune to error in the B₀ map estimation that is used in the designing the RF pulses.

For other types of spectral-spatial excitation specifications where finer spectral control is required, e.g. narrow band or multi-band frequency selective excitation, longer gradient trajectory would be needed to capture higher frequency components required in such designs. One possible approach for this problem is to concatenate a set of several separate spoke excitations. This is analogous to the single-channel spectral-spatial excitation described in (19) which is based on the concatenation of sinc pulses. Future work includes design methods to determine optimal gradient trajectory for different types of parallel spectral-spatial excitations.