Improved Slice Selection for R2* Mapping during Cryoablation with Eddy Current Compensation

Abstract

Purpose

To improve the slice profile and image quality of R2* mapping in the iceball during cryoablation with ultra short echo time (UTE) imaging by compensating for eddy currents induced by the selective gradient when half pulse RF excitation is employed to achieve UTEs.

Materials and methods

A method to measure both B0 and linear eddy currents simultaneously is first presented. This is done with a least square fitting process on calibration data collected on a phantom. Eddy currents during excitation are compensated by redesigning the RF pulse and the selective gradient accordingly, while that resultant from readout gradient are compensated for during image reconstruction. In vivo data were obtained continuously during the cryoablation experiments to calculate the R2* values in the iceball and to correlate them with the freezing process.

Results

Image quality degradation due to eddy currents is significantly reduced with the proposed approaches. R2* maps of iceball throughout the cryoablation experiments have been achieved with improved quality.

Conclusion

The proposed approaches are effective for compensating eddy currents during half pulse RF excitation as well as readout. TEs as short as 100 µs have been obtained, allowing R2* maps to be obtained from frozen tissues with improved quality.

INTRODUCTION

MR imaging with ultra-short echo times (UTEs) is gaining interests for visualizing short T2 spins in applications such as brain and tendon imaging (1,2,3). In addition, it has also been shown to be useful for monitoring the iceball evolution and potentially mapping tissue temperature within the frozen region during cryoablation since frozen tissues demonstrate short T2* (4). MR-guided cryoablation is a promising minimally invasive therapy for localized prostate tumors. For effective cryoablation, thermal probes are usually implanted to ensure sufficiently low temperature is reached throughout the tumor (<−40 °C) while damage to vital organs is avoided. However, the placement of the probes is invasive and time consuming and only provides information at discrete locations. Therefore temperature mapping within the frozen tissue would be preferable. Previous studies with ultra short TE imaging have shown in vitro that normalized signal intensity in the frozen tissue decay monotonically with decrease in temperature and therefore can be indicative of temperature (5). Tissue R2* is another promising MR parameter to quantify and relate to temperature as it appears to be relatively linear over the temperature range of interest (5).

To achieve UTEs while having slice selectivity, self-refocused half-pulse RF excitation is often employed along with center-out radial or spiral readout (6,7), where the minimum TE available is only limited by the hardware switching time from excitation to reception. However, the half pulse excitation scheme requires collecting k-space data twice with opposite selective gradients and then combining them to get signal from the desired slice, which makes it sensitive to system imperfections such as eddy currents. Quantitative applications such as R2* mapping of the frozen tissues during cryoablation in particular may suffer from the slice profile distortion resultant from eddy currents induced by the selective gradient. Among all eddy current components, the spatially invariant term (B0 eddy currents) and the linearly spatially dependent term (linear eddy currents) are often of major concern (8). While B0 eddy currents result in an unwanted constant phase offset between the two acquisitions, linear eddy currents cause mismatch between RF energy deposition and the corresponding k-space trajectory. Both terms need to be compensated to achieve a desired slice profile.

Several strategies have been proposed to compensate for eddy currents for half-pulse excitation (9, 10). Schroeder et al. (9) suggests pre-compensating the selective gradient for linear eddy current correction using an empirical system impulse response. One-dimensional slice profiles are additionally acquired with opposite selective gradient polarities to characterize B0 eddy currents. However, the system impulse response is usually unknown and difficult to obtain. Alternatively, Wansapura et al. (10) avoided the need to derive the system response function explicitly by calculating the pre-compensated gradient from the ideal gradient and the corresponding gradient measured. For B0 eddy current compensation, an extra scan with spatial saturation pulses is performed to obtain the phase offset between the two excitations with positive and negative selective gradients.

Non-Cartesian acquisition strategies such as those with radial readout are sensitivity to eddy currents induced by the readout gradients. These eddy currents cause distortion and miscentering of k-space trajectories, which may also introduce noticeable image distortion. Correcting for eddy currents is therefore important in order to obtain high quality images. Although Peters et al. has shown that improved image quality can be achieved by compensating for k-space trajectory miscentering due to hardware timing error and eddy currents alone (11), measuring the actual k-space trajectories allows the compensation of both effects (12).

Duyn et al. (13) has proposed a simple method to measure the actual k-space trajectories by relating them to the phases of signals acquired from an off-isocenter slice and then use these during image reconstruction to correct for the k-space deviation, especially in spiral and radial acquisitions. The k-space trajectories measured this way include effects from both linear and B0 eddy current terms, and ideally measurements need to be performed for all k-space trajectories. In (14), Gurney et al. extended this approach to characterize B0 eddy current components by acquiring signals from two opposite slices with respect to the isocenter. Based on these methods, this work first presents a generalized least square fitting approach to extract both B0 and linear eddy currents simultaneously with data collected with different gradient amplitude at several slice positions. Eddy current compensation schemes are then proposed to achieve better slice selectivity and to improve the image reconstruction. The improvement in image quality is demonstrated in images acquired with a multiple-echo projection reconstruction (PR) sequence (15). Our phantom study and in vivo experiments show significant improvement in slice profile after the compensation, and improved temperature dependent R2* maps have been obtained in the frozen tissue throughout our canine prostate cryoablation experiments.

MATERIALS AND METHODS

Pulse Sequence for Ultra Short TE Imaging and R2* Mapping

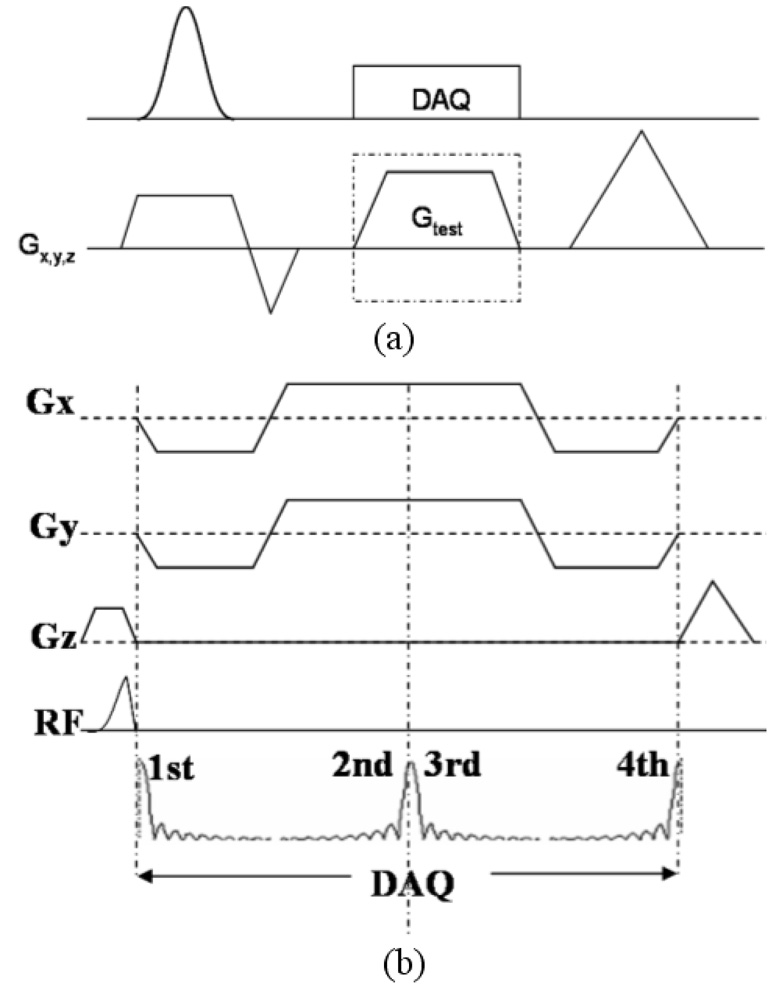
The pulse sequence used for imaging is shown in Figure 1a. Half pulse RF excitation is employed to achieve ultra-short TEs. Starting immediately after the RF pulse, four echoes are acquired in each TR with a multiple-echo PR readout gradient. Eddy current compensation is applied as described in the “eddy current compensation for half pulse excitation” section. For R2* mapping, the readout gradients were shifted with respect to the RF pulse to obtain a series of TE intervals. To demonstrate the capability of the UTE sequence for imaging short T2 species, and to compare the slice profiles of the half pulse RF excitation, Data were also obtained with a full pulse RF excitation using this sequence by switching the RF pulses. No eddy current compensation is used during full pulse RF excitation.

Figure 1.

(a) Pulse sequence for eddy current characterization. The test gradient can either be the selective gradient or the readout gradient. (b) Half-pulse RF excitation sequence with a four-radial-line readout. The gradient (arrow) applied at the end of the ideal trapezoidal gradient is used to compensate for linear eddy currents induced by the trapezoidal gradient.

Eddy Current Characterization Model

Eddy currents induced the gradients can be represented using Taylor series (8). Among all the eddy current terms, B0 eddy currents are spatially invariant while linear eddy currents are vary linearly with location; both eddy current terms scale with the gradient amplitude. Ignoring cross-term and/or high order (2^nd order and higher) eddy currents, the magnetic field B(r⃗,G⃗,t) in the presence a gradient G⃗ at location r⃗ can be written as:

$$B(\overrightarrow{r},\overrightarrow{G},t)=\overrightarrow{G}(t)·\overrightarrow{r}+{\overrightarrow{e}}_l(\overrightarrow{G}(t))·\overrightarrow{r}+B_{B0}(\overrightarrow{G}(t))+B_{\mathit{\text{other}}}(\overrightarrow{r},t)$$ (1)

Where e_l and B_B0 are the linear and the B0 eddy current terms induced by G⃗ (t), respectively; B_other is the magnetic field resultant from all other sources. The MR signal is:

$$S(t)={\displaystyle \underset{V}{\int }m(\overrightarrow{r},t)e^{-i\gamma {\displaystyle \int B(\overrightarrow{r},\overrightarrow{G},\tau })d\tau }d\overrightarrow{r}}$$ (2)

For a thin slice in ×direction at x0 with slice thickness Δx, when only gradient along × axis is applied and phase variation through the slice is ignored, the received signal becomes:

$$\begin{array}{cc}S(t)& =\mathrm{\Delta }x{\displaystyle \int m(x_0,y,z,t)e^{-i\gamma {\displaystyle \int ((G(\tau )+e_l(G(\tau )))x_0+B_{B0}(G(\tau ))+B_{\mathit{\text{other}}}(x_0,y,z,\tau ))d\tau }}dydz}\hfill \\ & =e^{-i\gamma {\displaystyle \int ((G(\tau ){+}_{el}(G(\tau )))x_0+B_{B0}(G(\tau )))d\tau }}\mathrm{\Delta }x{\displaystyle \int m(x_0,y,z,t)e^{-i\gamma {\displaystyle \int B_{\mathit{\text{other}}}(x_0,y,z,\tau )d\tau }}dydz}\hfill \\ & =M(x_0,t)e^{-i(\gamma {\displaystyle \int ((G(\tau )+e_l(G(\tau )))x_0+B_{B0}(\tau ))d\tau +\varphi (x_0,t))}}\hfill \end{array}$$ (3)

Where:

$$\{\begin{array}{l}M(x_0,t)=|\mathrm{\Delta }x{\displaystyle \int m(x_0,y,z,t)e^{-i\gamma {\displaystyle \int B_{\mathit{\text{other}}}(x_0,y,z,\tau )d\tau }}dydz|}\\ \varphi (x_0,t)=\text{arg(}\mathrm{\Delta }x{\displaystyle \int m(x_0,y,z,t)e^{-i\gamma {\displaystyle \int B_{\mathit{\text{other}}}(x_0,y,z,\tau )d\tau }}dydz)}\end{array}$$ (4)

Assume the amplitude of the applied gradient is g, the phase of the signal can now be rearranged as follows:

$$\phi (x_0,g,t)=(\widehat{k}(t)x_0+{\widehat{\varphi }}_{B0}(t))g+\varphi (x_0,t)$$ (5)

With $\widehat{k}(t)=\frac{\gamma }{g}{\displaystyle {\int }_0^t(G(\tau )+e_l(G(\tau )))d\tau }$ and ${\widehat{\varphi }}_{B0}(t)=\frac{\gamma }{g}{\displaystyle {\int }_0^t{B}_{B0}}(G(\tau ))d\tau .\widehat{k}(t)$ can be considered as the effective k-space trajectory generated by the applied gradient waveform and linear eddy currents induced by it; while ϕ^_B0(t) is the phase modulation due to B0 eddy currents. Both are normalized by the gradient amplitude.

As can be seen from Eq. 5, linear least square fitting can first be performed on φ (x₀,g,t) with respect to g to extract k^(t)x₀ + ϕ^_B0 (t), then with respect to x₀ on k^(t) x₀ + ϕ^_B0 (t) to separate ϕ^_B0 (t) and k^(t). Figure 1b illustrates the pulse sequence used for eddy current characterization. Full pulse RF excitation is used in this case. The test gradient can either be the selective gradient or the readout gradient. On each given axis, eddy current correction data are collected from m off-isocenter slices and with the gradient G(t) under investigation sweeping n different amplitudes at each slice location (m, n >= 2). These slices are then compared to the off-isocenter distance so the phase variation through the slice can be neglected.

Eddy Current Compensation for Half Pulse Excitation

To compensate for eddy currents induced by the selective gradient, B0 eddy currents and linear eddy currents are first measured using the approach described above. The long time constant components of both eddy currents may extend to the data acquisition period. For this reason, the slowly decaying “tail” of the measured gradient exceeding the length of the applied ideal trapezoidal gradient was inverted and appended to the end of the latter to serve as the new selective gradient. The corresponding B0 eddy currents and linear eddy currents of the new gradient are again measured. In case the gradient employed to cancel the long time constant eddy currents from the ideal selective gradient introduces additional eddy currents, this process can be repeated several times to improve the compensation.

The RF pulse is designed according to the measured gradients using VERSE (16). B0 eddy current effects during the excitation are compensated by dynamically varying the RF phase. Long time constant components of B0 eddy currents extending to data acquisition was compensated by correcting the phase of the acquired signal on a per data point basis before adding the two acquisitions. Explicitly, for data acquired with positive selective gradient, each data point is multiplied by exp(-iϕ^_B0(t)); whereas for data acquired with positive selective gradient, each data point is multiplied by exp(iϕ^ _B0(t)), with ϕ^ _B0(t) being the phase resultant from the residual B0 eddy currents induced by the selective gradient when the k-space point is sampled. This can also be done during data acquisition by dynamically varying the receiver phase. Alternatively, B0 eddy current effects can also be corrected by removing the constant phase offset between data acquired with opposite selective gradients polarities, or by changing the phase of the receiver during data collection. For this purpose, 1D slice profiles of the two excitations were obtained by the Fourier transform of the data acquired with readout gradient on the slice selection direction. The phase difference at the center of the slice profiles is then the phase offset due to B0 eddy currents

Eddy Current Correction for Readout Gradient

Eddy currents resulting from the readout gradient can also be problematic in the radial acquisition scheme adopted here and need to be corrected. For this purpose, the corresponding k^ (t) and ϕ^_B0(t) on logical x- and y-axis are first measured. As the cross and higher order eddy current terms were ignored, the calibration data acquired on the two readout gradient axes could be used to compensate for eddy currents on a per-sample basis regardless of the orientation of the radial lines. The B0 eddy current phase (ϕ _B0 (n,t)) of the nth radial line at time point t is calculated according to the following matrix:

$$\varphi {}_{B0}(n,t)=[{\widehat{\varphi }}_{B0x}(t){\widehat{\varphi }}_{B0y}(t)]\left[\begin{array}{l}{G}_x(n)\\ G_y(n)\end{array}\right]$$ (6)

with G_x(n) and G_y(n) being the corresponding peak projection gradient amplitudes. Similarly, the corresponding k-space trajectories can be calculated. During reconstruction, the phase offset due to B0 eddy currents is first removed from the k-space data on a per sample basis. The compensated data are then re-sampled to Cartesian grids based on the calculated k-space trajectories (16).

Experiment Setup

Phantom studies and in vivo experiments were performed on a 0.5T GE Signa SP scanner (GE Healthcare, Milwaukee, WI), with a maximum gradient amplitude of 1.2 G/cm and a maximum slew rate 1.2 G/cm/ms. Given the performance of our gradient systems, the length of the half pulse RF pulse was designed to be 1.6 ms with Gaussian slice profile. Unless otherwise specified, imaging experiments were carried out with the four echo sequence with acquisition parameters TR/flip angle/FOV/slice thickness /receiver BW = 14 ms /30°/ 32cm /7mm / 31.25 kHz, and in plane resolution of 1.25 mm by 1.25 mm. Echo times were TE1/TE2/TE3/TE4 = 0.1 ms/2.55 ms /2.55 ms /5.0 ms.

Eddy Current Characterization

For characterizing the selective gradients and readout gradients, eight off-isocenter slices were sampled each with eleven gradients amplitudes on each axis for each gradient waveform under investigation. The characterization of the eddy current with the proposed fitting approach readout gradient was also tested on data collected from four acquisitions, where two off-isocenter slices were sampled with two gradients amplitudes each. Calibration data were acquired with a quadrature head coil on a uniform spherical phantom filled with doped water. The experiment was performed once to characterize the eddy currents induced by the ideal trapezoidal selective gradient for designing the eddy current compensated RF pulse and the new selective gradient. To observe the performance of the linear eddy current compensation for the long time constant components, the new gradient was also measured. The characterization of the readout gradient was performed once for each gradient waveform, which changed with different field of views in the imaging experiments. Unless otherwise mentioned, eddy current correction was applied to all imaging experiments.

Eddy current compensation for Half Pulse Excitation

Three phantom experiments were performed to demonstrate the improved slice selectivity using the proposed techniques. In one experiment, FID signals were collected from the spherical phantom that has long T2 (~ 1s) with and without eddy current compensation. In the second experiment, two dimensional slice profiles were also obtained on the same phantom by placing of the one readout gradient on the slice selection axis with the spherical phantom. Data were then acquired without eddy current correction, with linear eddy current correction and with both eddy current corrections. To extract the constant phase offset between the data acquired with positive and negative selective gradients, one dimensional slice profiles were collected. In the third experiment, an object consists of a phantom with several short T2 components, a cylinder and a ball phantom (Figure 4b) was imaged to demonstrate both the slice selectivity and the capability to image short T2s of the ultra short TE sequence. The short T2 components have T2s on the order of 1–2 ms. A slice close to the edge of the ball (dotted vertical line in Figure 4a) was scanned. For comparison, four images were collected in experiment 2 and 3: with regular full RF pulse excitation, with non-compensated half RF pulse excitation, with linear eddy compensated RF excitation and with both linear and B0 eddy current compensated RF excitation.

Figure 4.

Phantom experiments show significant improvement in slice selectivity with eddy current correction. (a) Free induction decay signals of a slice from a uniform ball phantom (long T2) with (blue solid line) both linear and B0 eddy current correction and without (red dashed line) eddy current correction. (b) The phantom schematic shows that the cylindrical phantom is not in the desired scan plane. Image acquired with a full pulse RF excitation acquisition for reference (c) has good slice selectivity with no artifact from the cylinder. However, the short T2 compartments have low signals and are difficult to discriminate. With half pulse RF excitation and no eddy current correction, the short T2 compartments are readily depicted in image (d), which also exhibits an artifact from the cylindrical phantom due to imperfect slice profile. With the linear eddy current correction, the artifact is reduced but still visible in (e). With both linear and B0 eddy current correction, the out of slice artifact is eliminated in (f). The arrows in (d) and (e) indicate the undesired out-of-slice signal from the cylindrical phantom.

Eddy current compensation for Readout Gradient

To demonstrate the effectiveness of the proposed approach for correcting eddy currents induced by the readout gradient, studies were performed on the spherical phantom and the knee of a volunteer. Images were acquired with a field-of-view of 24cm, the slice thickness was 5 mm and in plane resolution was 0.94 mm by 0.94 mm. Other acquisition parameters include TR/TE1/Flip angle = 14.7 ms/0.1 ms/15°. Phantom images were reconstructed from the fourth echo data, while knee images were reconstructed using all echoes.

In Vivo Cryoablation Experiments

In-vivo canine experiments were approved by our institutional animal care and use committee. A total of nine canines were used in our experiments. Two MRI compatible gas-driven cryoablation probes (Galil Medical, Yokneam, Israel) were inserted through the anterior abdominal wall into the prostate with MR guidance (Fig. 2a). The cryoablation system uses argon gas for cooling (−187 °C) and helium for heating (67 °C). For direct measurement of the temperature, two fiberoptic temperature sensors were placed medially in the prostate, each 7–8 mm away from the cryoprobes. During the experiments, one side of the prostate experienced two freeze/thaw cycles while the other side was frozen once. Images were taken in coronal plane during freezing and thawing, an endorectal coil and a surface coil were used simultaneously for reception. Data were acquired with the TEs of the first echoes being 0.1 ms, 0.4 ms, 0.7 ms and 1.0 ms at each temporal point during the procedure for R2* calculation. The total acquisition time for each R2* map was ~35 seconds, where 300 radial lines were sampled at each TE. Images reconstructed from these relatively short TE intervals were designed to quantify short T2*. For better calculation of R2* for tissues with longer T2*, especially those surrounding the iceball, images reconstructed from the 3^rd echo were also used with a total of eight different TEs for the fitting. Signal intensity was corrected to minimize the noise bias before the fitting (17). R2* maps were obtained by exponentially fitting the signals acquired at different TEs on a pixel-by-pixel basis (18). To exam the quality of the fit for short T2 components, the average correlation coefficients of the fit in a 3 by 3 region near one thermal probe were calculated.

Figure 2.

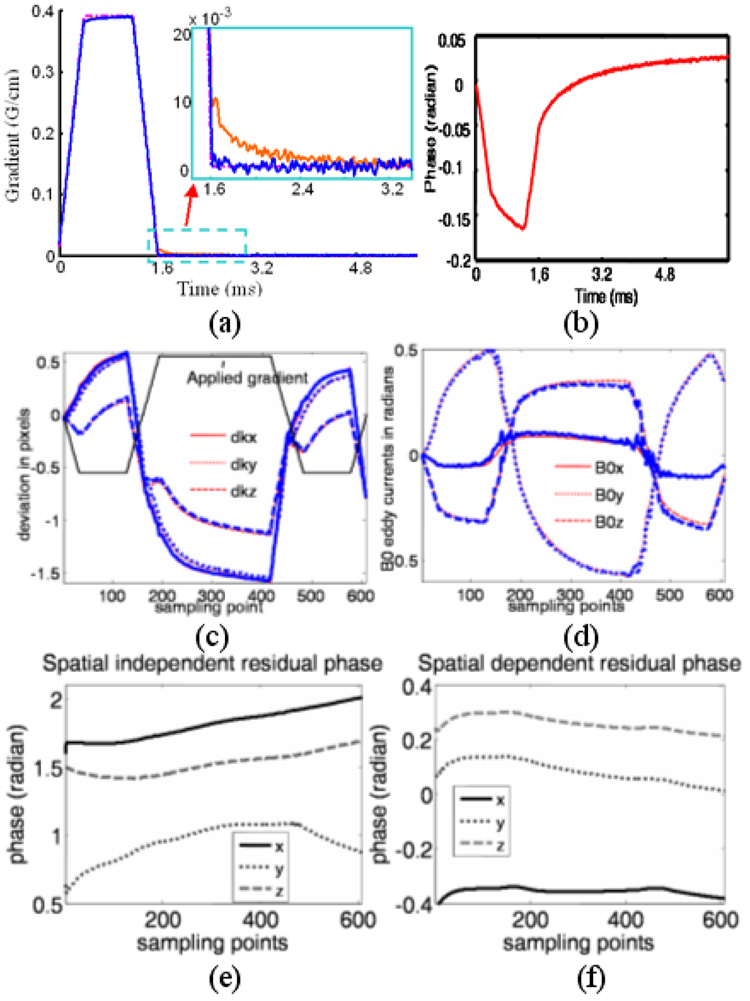
a) Ideal (dash-dotted), measured selected gradients before (red) and after (blue) correction. Inset) an enlarged portion, showing the long time constant linear eddy current component in red. b) Measured phase due to B0 eddy currents before correction. The measured k-space deviations due to linear eddy currents from the applied gradient (arrow, not proportionally scaled) are shown in (c). The phase accumulated by B0 eddy currents is shown in (d). The thin, red lines show the eddy current terms calculated from data acquired with eleven gradients amplitudes and eight slice locations, while the thick, blue lines show the eddy current terms calculated using only four acquisitions. The residual phase that is independent of gradient amplitude, but linearly depends on position is shown in (e), and the phase that is independent of gradient amplitude and position is shown in (f). Both show little correlation with the readout gradient.

RESULTS

Eddy Current Characterization

Figure 2a and 2b show an example of the measured gradient and phase accumulated by B0 eddy currents induced by the selective gradients. Both terms show relatively long time constant components (~ 1–2 ms). The measured linear and B0 eddy currents resulting from a typical readout gradient waveform on all three axes are shown in Figure 2c and 2d, respectively. The thin, red lines show the eddy current terms calculated from data acquired with eleven gradients amplitudes and eight slice locations, while the thick, blue lines show the eddy current terms calculated using only four acquisitions. The waveforms of both eddy current terms show a close correlation with either the applied selective gradients or the readout gradient. On the contrary, as shown in Figure 2e and 2f, residual phases from the fitting process for the characterization of the readout gradient separated into spatially dependent and independent channels show little correlation to the applied readout gradient.

Eddy Current Compensation for Half Pulse Excitation

As shown in Figure 2a, the long time constant linear eddy currents that extend to the data acquisition period are greatly attenuated after the proposed compensation, though oscillation that may come from the noise of the measurement is still seen. Figure 3 shows the 2D slice profiles obtained using different eddy current compensation strategies. In addition to linear eddy current correction, B0 eddy currents were compensated during reconstruction in Figure 3c and the measured phase offset between excitations with positive and negative selective gradient was ~0.67 radian in this case. B0 eddy currents were compensated by varying the phase of the RF pulse in Figure 3d. Both schemes gave significantly improved slice profiles. The effectiveness of the proposed method for improving the slice profile is also demonstrated in Figure 4. The FID in Figure 4a obtained from the spherical phantom that has long T2 is severely distorted due to eddy currents without any compensation (red), while an exponential decay as expected (almost linear in the time interval shown due to the long T2 of the phantom) is obtained after the proposed compensation (blue). The uncorrected the FID shows a larger signal at the beginning due to the contribution of out-of-slice signal. Images in Figure 4c–f were acquired at the same slice position on the phantom shown in Figure 4b. Figure 4c was acquired with a regular full RF pulse. Images in Figure 4d–f were acquired with half pulse excitation. Significantly higher signal can be appreciated in short T2 components with the half pulse excitation, and the tube with the shortest T2 (the one that the lowest signal intensity in Figure 4e) has a SNR of 2 and 17 in Figure 4c and 4f respectively. Without eddy current compensation, Figure 4d shows high out-of-slice signal contamination from the cylinder (arrow). The out-of-slice signal is greatly reduced but still noticeable in Figure 4e (arrow) with linear eddy current correction. With both B0 and linear eddy current correction, a much better slice profile is achieved in Figure 4f, and the out-of-slice signal from the cylinder phantom is hardly visible.

Figure 3.

Images of the slice profiles acquired by placing one readout gradient on the slice selection axis. Without eddy current correction (a), there is signal from outside the slice that is decreased with linear eddy current correction (b) and eliminated with both eddy current corrections (c,d). In (c), B0 eddy currents are compensated during reconstruction while in (d) they are compensated during excitation. Both methods give significantly improved slice profiles.

Eddy Current Correction for Readout Gradient

The accrual of eddy current is seen in Figure 2c and 2d, which indicates different distortion effects for images reconstructed from different echoes. As demonstrated in Figure 5a–c, the images of the spherical phantom were reconstructed from the fourth echo data. Without eddy current correction, significant distortion is seen in Figure 5a as evidenced by the high signal intensity at the edge of the image and the low signal intensity in the middle. With linear eddy current correction, the bight rim in Figure 5a disappears and signal is more evenly distributed in Figure 5b. Further B0 eddy current correction results in a sharper and more uniform image (Figure 5c). The effectiveness of the correction is again demonstrated in the knee images, which are reconstructed using all four echoes without eddy current correction (Figure 5a), with linear eddy current correction (Figure 5b) and with both correction (Figure 5c). Improvement in image sharpness can be appreciated (arrows). Fat is inherently suppressed in these images due to the phase difference of fat signal at different echo times.

Figure 5.

Images demonstrating improved image quality with the eddy current correction during reconstruction using the eddy current correction data shown in Figure 2c and 2b. Without correction, images (a,d) show significant distortion evidenced by the bright rim in (a) and the blurring in (d) as shown be the arrow. These are improved with linear eddy current correction (b,e) and are eliminated with both linear and B0 eddy current correction (c,f).

In Vivo Cryoablation Experiments

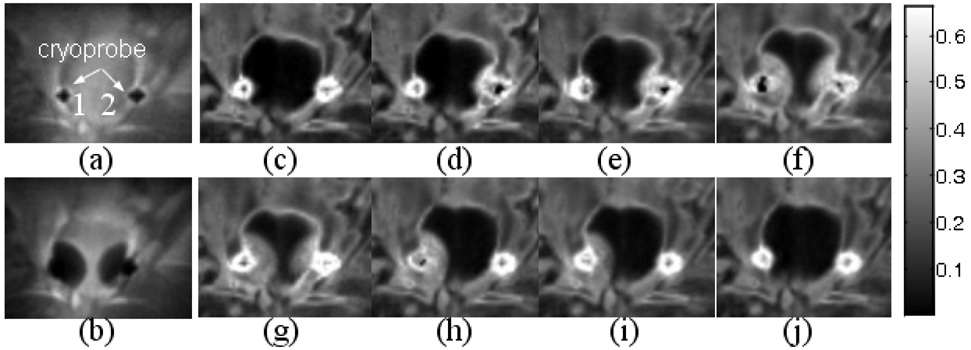
The benefit of compensating eddy currents during the half-pulse excitation in our in vivo cryoablation experiments is shown in Figure 6. Both magnitude images and R2* maps from two consecutive scans (with the same scan parameters and similar temperatures) demonstrate reduced streaking artifacts (arrows) and improved SNR with the compensation, with more dramatic improvement seen in the R2* maps. All images in Figure 7 were obtained with eddy current correction. The magnitude images (Figure 7a, b) were reconstructed from the first echo of the signal acquired at the beginning and in the middle of cryoablation experiment. Figure 7c–j show several images from a time series of R2* maps during the experiment. An average correction coefficient value of approximately 0.9 for R2* mapping was obtained in the frozen region at temperatures as low as −30°C owing to the ultra-short TEs. The evolution of the iceball is depicted in all R2* images. Figure 7c and 7g are the corresponding R2* maps for Figure 7a and 7b, respectively. Figure 7c and 7d were acquired when probe 1 had relatively high temperature, while probe 2 was slowly freezing. Figure 7e–i were acquired when probe 2 was thawing and probe 1 was turned on. Figure 7j was acquired at the end of the experiment with temperature near both probes back to normal. From figure 7c–j, the temperature readings near cryoprobe 1 were 36.6 °C, 33.5 °C, 20.6 °C, −1.0 °C, 0.1 °C, −8.4 °C, −0.8 °C, 11.0 °C and were 36.4 °C, 3.0 °C, 2.0 °C, −23.9 °C, −1.8 °C, 30.9 °C, 30.4 °C, 31.4 °C near cryoprobe 2. No R2* elevation is seen at normal body temperature.

Figure 6.

Coronal magnitude images and R2* maps from two consecutive scans during a canine prostate cryoablation experiment demonstrate improved quality with linear and B0 eddy current correction for the half-pulse excitation. The time delay between these two scans is negligible. Two iceballs are shown, each created by a cryoprobe inserted on side of the prostate. (a) and (b) are magnitude image and R2* map acquired without correction. (c) and (d) are magnitude image and R2* map acquired with correction. The increase in signal to noise ratio and decrease in the streak artifact can be clearly appreciated in especially the R2* maps (arrows). The color bar on the right of the images shows the scale of R2* values in milliseconds. The SNR measured in a ROI indicated by the rectangle in b) and d) was 5 and 9 respectively.

Figure 7.

Images acquired at several points during cryoablation. Magnitude images taken before at the height of freezing (a,b) demonstrate the cryoprobe position and the maximum size of the iceballs. The time series of R2* maps (c–j) show an iceball that is well depicted and the positions of the probes well defined in all images. The increase in R2* intensity with decrease in temperature is clearly seen. The color bar on the right of the images shows the scale of R2* values in ms. From figure 7c–j, the temperature readings near cryoprobe 1 were 36.6 °C, 33.5 °C, 20.6 °C, −1.0 °C, 0.1 °C, −8.4 °C, −0.8 °C, 11.0 °C and were 36.4 °C, 3.0 °C, 2.0 °C, −23.9 °C, −1.8 °C, 30.9 °C, 30.4 °C, 31.4 °C.

DISCUSSION

Improved excitation profile and image quality has been clearly demonstrated in our phantom and in-vivo studies by compensating for B0 and linear eddy currents separately. These methods are easy to implement. To collect eddy current correction data, theoretically only four acquisitions are needed on each axis. As shown in Figure 2c and 2d, the linear and B0 eddy current terms measured this way are fairly consistent with those calculated from data acquired with eleven gradients amplitudes and eight slice locations. The result can be further improved with the use of high performance scanners where calibration data can be obtained with higher SNR. Collecting data from more slices and gradient amplitude steps improve the robustness of the fitting process and give less noisy measurement. Acquiring eddy current correction data can be done within a few seconds since signal averaging that is often employed to improve the SNR of the measurements using methods presented in (12,13) is no longer necessary. Since eddy current characteristics on the commercial scanners are usually relatively stable with time, the compensation data only needs to be updated periodically. The residual phases from the fitting process for the eddy current characterization show little correlation to the applied gradient as shown in Figure 2e and 2f. Therefore the assumption that higher order eddy current terms can be ignored here is reasonable. Possible sources contributing to residual phase linearly dependent on location may include long time constant linear eddy currents from the gradient preceding the test gradient and imperfect linear shimming. Residual phase independent of position may include long time constant B0 eddy current from the preceding gradient, or off-resonance effects.

The eddy current compensation mechanism for half pulse excitation works well when the imaging plane is orthogonal to one of the three physical axes, where eddy current compensated RF pulses and gradients can be pre-designed for imaging in either axial, saggittal or coronal plane. As both B0 and linear eddy currents scale with the gradient amplitude played on the three physical axes, the compensation can be easily adapted to excite a desired slice thickness on the scanner. Imaging an oblique slice may present a challenge for the proposed approach since redesigning of the RF pulse for oblique angle according to combination of the linear eddy currents on all three physical axes is required for each oblique angle. Correct timing between the RF pulse, RF phase modulation for B0 eddy current correction and the selective gradient is also crucial for obtaining good slice profile and is currently adjusted empirically. This can potentially be improved by adopting the delay measurement method presented in (19).

Our phantom studies have demonstrated that B0 eddy current effects can also be corrected by removing the constant phase offset between the two acquisitions with opposite selective gradients polarities. The phase offset was extracted from the onedimensional slice profiles. Since the one-dimensional profiles can be obtained in as short as two repetitions, either approach can be used for B0 eddy current compensation.

To compensate for eddy current induced by readout gradient, the separation of B0 and linear eddy current terms using the proposed methods allows the use of linear operations to calculate trajectories at arbitrary angles from measurements made on the orthogonal axes when the trajectories only differ in position or rotation angle, therefore removes the need to collect eddy current correction data for each trajectory. In case B0 eddy currents can be ignored, the trajectories measured on the physical axes using the method in (13) is then equivalent to k^ (t ) measured here and therefore can be linearly combined to calculate trajectories at other angles. Significant improvement in image quality has been demonstrated in (15, 19) with this approach. The measurement of linear eddy current effect with this method was also indicated in (14). However, the effectiveness of these approaches highly depends on the B0 eddy current characteristic of the scanners used. This is shown in the phantom images acquired on the scanner used in this work, where the measured B0 eddy currents are about one order higher than that observed on other high performance scanners. Figure 8 shows images reconstructed with different correction strategies from the fourth echo of the same data acquired on the spherical phantom. Again without eddy current correction, the image in Figure 8a is significantly distorted. Improvement in image quality is seen in image reconstructed using k-space trajectories measured with method in ref (13) (Figure 8b) and image reconstructed using k-space trajectories measured with method in ref (13) to account for linear eddy currents and B0 eddy currents measured with method in ref (14) to account for B0 eddy currents (Figure 8c). However, image distortions are still seen in both images. The distortion-free image was obtained in Figure 8d with the approach in this work. Though the corrections shown here are for 2D radial readout, they can be easily adapted to other readout trajectories such as 3D projection reconstruction and spiral acquisition.

Figure 8.

Phantom images reconstructed with different correction strategies. (a) Reconstructed without correction. (b) Reconstructed using k-space trajectories measured with method in ref (13). (c) Reconstructed using k-space trajectories measured with method in ref (13) to account for linear eddy currents and B0 eddy currents measured with method in ref (14) to account for B0 eddy currents. (d) Reconstructed using the proposed approach.

With effective compensation for both B0 and linear eddy current for half-pulse excitation and a multiple-echo readout, signal intensity images and R2* maps with improved quality have been obtained throughout the whole freezing process. However, subject motion during the in vivo experiments complicates the registration of the measured temperatures to the pixels in the collected 2D images, consequently relating the measured temperatures to the R2* values accurately to generate the calibration curve has been difficult. In addition, the motion observed in our images during cryoablation may also be an issue for accurately map R2*. Future work will optimize the experiment setup or pulse sequence to better visualize the thermal probes in the images for better localization of the temperature readouts and for motion compensation through image registration.

Our experiments were performed on a low filed strength scanner (0.5 T) with relatively low gradient performance. Therefore, relatively long RF pulse (1.6 ms) was used for excitation along with a readout bandwidth of 31.25 kHz. The readout time for each radial line was ~2 ms. Signal loss during the excitation and signal decay during readout for the short T2 components is therefore not negligible. T2 decay during the readout causes image blurring and consequently affects the achievable image resolution. Several methods have been proposed to improve the SNR efficiency of short T2 imaging (20). Use of high field strength scanners that are friendly to intervention will significantly improved quality of the R2* mapping by providing higher SNR, higher temporal and spatial resolution, where shorter RF duration and readout duration can be used.

In conclusion, an effective approach to compensate for both B0 and linear eddy currents for half-RF pulse excitation is presented based on the measured actual B0 and linear eddy currents. The significant improvement in the excitation slice profile allows better characterization of short T2* tissues as shown in the cryoablation experiments. The proposed techniques should be useful in imaging tissues with short T2s in general, especially when quantification is desired. The eddy current measurement approach has also been applied to dramatically improve the image reconstruction by compensating for eddy currents induced by the readout gradient.