Dynamic Loading of Deformable Porous Media Can Induce Active Solute Transport

Abstract

Active solute transport mediated by molecular motors across porous membranes is a well-recognized mechanism for transport across the cell membrane. In contrast, active transport mediated by mechanical loading of porous media is a non-intuitive mechanism that has only been predicted recently from theory, but not yet observed experimentally. This study uses agarose hydrogel and dextran molecules as a model experimental system to explore this mechanism. Results show that dynamic loading can enhance the uptake of dextran by a factor greater than 15 over passive diffusion, for certain combinations of gel concentration and dextran molecular weight. Upon cessation of loading, the concentration reverts back to that achieved under passive diffusion. Thus, active solute transport in porous media can indeed be mediated by cyclical mechanical loading.

Introduction

The concepts of active and passive mechanisms are well understood for solute transport across a porous-permeable membrane. Passive solute transport occurs by diffusion down the concentration gradient, whereas active solute transport requires chemical energy-consuming transmembrane pumps, as found in cell membranes. Active mechanisms can transport solutes against their concentration gradient. Yet, it is intriguing that active solute transport mechanisms mediated by mechanical loading of porous media have not been reported in previous experimental studies. While mechanical loading has been shown to accelerate solute uptake or desorption in biological tissues via diffusion-convection mechanisms (Bonassar et al., 2001; Evans and Quinn, 2006; O'Hara et al., 1990; Urban et al., 1982), an active mechanical pumping mechanism that can raise solute concentration within a hydrated tissue or gel above its passive diffusion limit has not been observed previously.

There is no theoretical principle preventing such a mechanism. The foundational framework for studying solute transport can be traced to the classical field of irreversible thermodynamics (Groot and Mazur, 1962) which elaborated on the earlier work of Fick (Fick, 1855) by relating solute and solvent transport to any number of driving forces via linear phenomenological equations constrained by Onsager’s reciprocal relations (Onsager, 1931). Starting in the 1950’s, the field of rational mechanics offered a mixture theory framework whose rigorous mathematical foundations facilitated the analysis of transport in deformable porous media (Bedford and Drumheller, 1983; Bowen, 1976; Truesdell and Toupin, 1960), and has subsequently been applied to biomechanical analyses of soft tissues (Gu et al., 1998; Huyghe and Janssen, 1997; Kenyon, 1976; Lai et al., 1991; Mow et al., 1980).

In a theoretical and computational study we showed that this framework can predict enhanced solute uptake in a cylindrical disk of porous deformable tissue or gel in response to sustained dynamic loading in unconfined compression between rigid impermeable platens (Mauck et al., 2003), establishing the theoretical premise for the current experimental study. An essential feature of this framework, which had not been incorporated in previous models, was the introduction of a frictional drag term between the solute and solid matrix, complementing the well-recognized frictional drag between solute and solvent. This term provided an additional driving force on the solute, exerted by the solid matrix, and led to an explicit distinction between the diffusivity of the solute in the porous tissue and in free solution.

Predictions showed that under steady-state sinusoidal loading, the solute concentration in the disk could exceed that achieved under passive diffusion by multiple factors. This enhancement depends on dimensionless numbers that relate the characteristic diffusive velocities of solvent and solute in the porous tissue, the hindrance imparted by the porous solid matrix to solute diffusivity, the loading frequency, the amplitude of relative deformation, and lesser factors such as the porous matrix compressibility (Poisson’s ratio) and porosity. When translating these dimensionless numbers to dimensional values relevant to solute transport in gels, the theory essentially predicts that mechanical pumping of solutes at physiological loading frequencies (~1 Hz) and compressive strain amplitudes (~10%) is enhanced with higher solute molecular weights and higher gel concentrations. Importantly, this enhancement would not occur if the frictional drag term between the solute and solid matrix were neglected.

To verify these predictions experimentally, we adopted a model system of dextran molecules into agarose hydrogels, frequently used in prior studies (Leddy et al., 2004; Pluen et al., 1999). Agarose is an inert, stable, thermo-reversible hydrogel, readily prepared at various concentrations where it exhibits a wide range of mechanical and transport properties. Dextran, a linearly configured polysaccharide, is readily conjugated to fluorophores in a wide range of molecular weights. Based on prior studies (Leddy et al., 2004; Pluen et al., 1999), there is no indication that dextran binds to agarose, though this potential interaction is explored in the current study, by analyzing solute concentration after cessation of loading, to preclude confounding interpretations.

Materials and Methods

Materials

Type VII 2-hydroxyethyl agarose (Sigma, St. Louis, MO) was prepared at nominal concentrations of 5.75, 6.9, and 9.2% w/v. The following protocol was adopted in an effort to minimize batch-to-batch variability of agarose gels. Agarose powder was placed in a glass bottle followed by the addition of 25 mL of phosphate buffered saline (PBS). The bottle was then heated in a beaker of boiling water on a hotplate for 30 minutes. For the final minute, the liquid agarose was gently mixed with a magnetic stir bar. The agarose was then cast as a slab between glass slides (100 × 80 × 2.3 mm) and allowed to cool at room temperature for 45 minutes before being transferred to a PBS bath. Disks were then punched at random positions in the gel to the desired dimensions (Ø4 × 2.3 mm). In all experiments, agarose gels were tested immediately after casting. Tracer solutions of 10kDa, 70kDa and 500kDa fluorescein conjugated dextran (Invitrogen, Carlsbad, CA) were prepared in PBS at respective concentrations of 0.5, 0.5 and 0.2 mg/mL.

Volume Fraction of Agarose Gels

For three separate castings of agarose at each gel concentration, Ø5 × 2.3mm disks (n=6 per casting) were punched at random positions in the slab to determine the porosity of each agarose gel used in this study. The volume fraction of water, φ ^w, was determined through the approximate equation φ ^w = 1 −W^dry/W^wet where it is assumed that the gel density (~1.04 g/mL) is approximately the same as the density of water. Each sample’s wet weight (W^wet ) was initially determined and the dry weight (W^dry ) was measured after 48 h of freeze-drying (Labconco Freezone vacuum chamber). The volume fraction of water yielded φ ^w = 0.934±0.006, 0.918±0.004, and 0.902±0.005 for respective nominal concentrations of 5.75, 6.9 and 9.2% agarose.

Loading Device

Dynamic unconfined compression was applied with a custom-made loading device. An acrylic loading platen mounted to a vertical translating stage was actuated by a rotating micrometer head. The micrometer was rotated by a timing belt pulley system driven by a micro-controlled stepper motor. During testing, the platen displacement was controlled continuously under a feedback loop, using an optical encoder, to ensure accurate application of the desired deformation profile.

Testing Protocol

For each experimental loading time point a fresh agarose gel was cast and disks (n=7) were placed in an acrylic dish containing the dextran solution. To prevent excessive lateral motion under loading, the disks were each placed within a Ø5 mm recess well of a 0.5 mm thick layer of 3% w/v type I-B agarose cast at the bottom of the acrylic dish. Disks were subjected to unconfined compression with a dynamic compressive strain (±5% amplitude) superposed over a static strain offset (15%) at a frequency of 1 Hz for up to 40 hours. Unconfined compression of gel disks between impermeable platens permits solute and solvent transport across their lateral cylindrical surface only.

Concurrently, a second control group of disks (n=5) from the same casting was immersed in a petri dish filled with dextran solution, under unloaded conditions. For these disks, solute and solvent could transport across the top axial surface as well as the lateral cylindrical surface.

Experiments were conducted for five durations ranging from 5 to 40 hours. Testing with 6.9% agarose gels was performed while varying the dextran molecular weight (10kDa, 70kDa, and 500kDa) and testing in the 70kDa dextran solution was performed while varying the agarose gel concentration (5.75, 6.9, 9.2%).

An additional study was conducted where 9.2% agarose disks were loaded for 40 hours in 70kDa dextran solution alongside a group of unloaded control disks. At the end of this period, loaded disks were transferred to a dextran filled petri dish and maintained unloaded. At four time points during this recovery period, disks from both groups (n=4 per group) were removed and assayed for their interstitial solute content.

All experiments were conducted in a light-protected environment with the device and petri dishes mounted and gently agitated on an orbital shaker (Bellco, Vineland, NJ) to promote stirring.

At the completion of each test, samples of bathing solution were collected and stored for subsequent analysis while agarose disks were removed and immediately processed. To measure the solute concentration in the disks, samples were blotted, sectioned into quadrants, and allowed to desorb for 48 hours in Eppendorf tubes, containing a 120 µL volume (V_d ) of PBS. Samples were weighed to determine the volume of each disk (V_ag ) using the previously characterized agarose gel density (ρ = 1.04 g/mL).

The fluorescent intensity of 35 µL of each agarose desorption solution and a 1:5 diluted sample of the corresponding bath solution were measured in a 96 well plate with a fluorescent plate reader at an excitation and emission wavelength of 485 nm and 535 nm, respectively (SpectraFluor Plus, Tecan, Research Triangle Park, NC). Measurements were interpolated with a standard specific solute curve covering the intensity working range to obtain the concentration of dextran in the desorption tube (c_d) and external bathing solution (c^*). The solute concentration in the gel was calculated on a total solvent volume basis, accounting for the solute remaining in the desorbed sample. The result was normalized to the concentration of the bathing solution, yielding the normalized concentration

$$ĉ=\frac{c_d}{c^{*}}\frac{V_d}{{\phi }^w{V}_{ag}}+\kappa$$

where κ is the equilibrium partition coefficient for the corresponding solute molecular weight and gel concentration. For passive diffusion experiments, at equilibrium, let ĉ = κ and rearrange this formula to yield an expression for κ. For all other conditions, this formula assumes prior knowledge of κ.

Statistical Analyses

A two-way analysis of variance (α = 0.05) was performed to examine the factors of loading and time in the experiment analyzing solute uptake with and without dynamic loading, and the experiment analyzing solute recovery following loading cessation. Statistical significance was accepted for p < 0.05; post hoc testing of the means was performed with Bonferroni correction (SAS 9.1, Cary, NC). A one-tailed test using a T-statistic was performed to determine whether the ratio of internal to external solute concentration under dynamic loading, ĉ_DL, is greater than unity at 40 h.

Platen Lift-Off Characterization

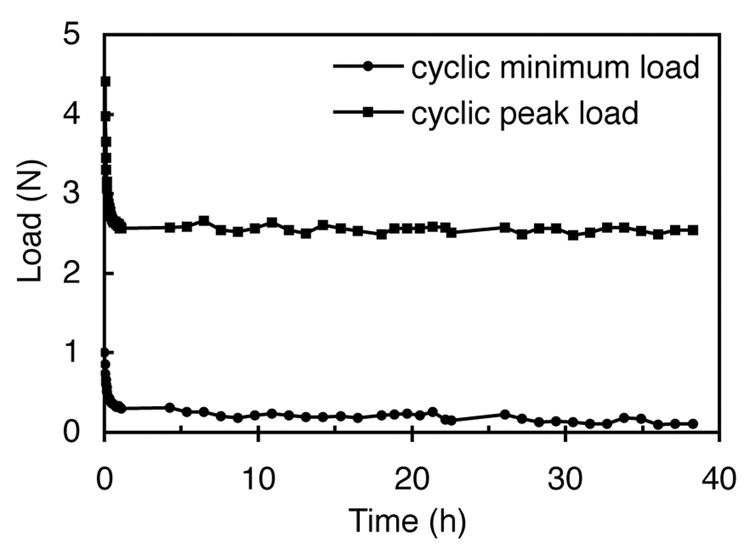
Due to their viscoelastic response, hydrogels subjected to dynamic loading may recover slower than the prescribed motion of the loading platen, causing the platen to separate or lift off the gel during its upstroke. Since lift-off would effectively reduce the strain amplitude applied to the disks in this study, and provide an additional pathway for passive diffusion across the top surface, its incidence in the dynamic loading of agarose was examined in preliminary tests. Five disks (Ø5×2.3 mm) of 6.9% agarose were simultaneously subjected to the experimental dynamic loading regimen as described above while the normal reaction force was monitored with a load cell (±44.5 N range, Sensotec, Columbus, OH) for a duration of 40 hours. Results showed that while the minimum reaction force relaxed with time, it did not drop to zero at any point, indicating that the loading platen was in full contact with the agarose samples during the entire 40 h loading routine (Fig. 1).

Fig. 1.

Envelope of dynamic load response for five 6.9% agarose disks simultaneously subjected to cyclical deformation with ±5% strain amplitude superposed over 15% static compressive strain.

Results

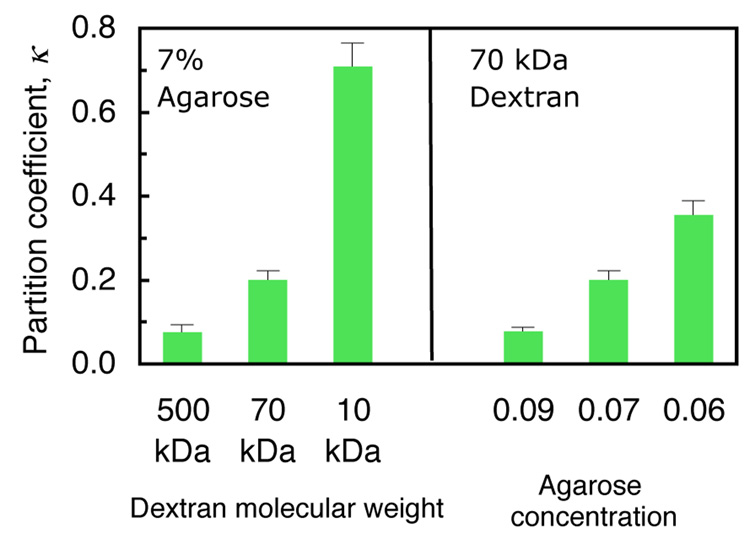
Under passive diffusion, the steady-state dextran concentration in unloaded agarose is typically lower than that of the external bath, due to the exclusion of solutes from smaller pores in the gel resulting from steric effects. Therefore, solute uptake results are typically reported as a partition coefficient, κ , which is the ratio ĉ_PD of internal to external concentration at steady state under passive diffusion (Laurent and Killander, 1963; Lazzara and Deen, 2004). In 7% w/v agarose, κ ranges from 0.71±0.05 to 0.076±0.019 with dextran molecular weights increasing from 10 to 500 kDa (Fig. 2). Similarly, for 70 kDa dextran, κ decreases from 0.36±0.03 to 0.079±0.010 as the gel concentration increases from 6% to 9% w/v.

Fig. 2.

Equilibrium partition coefficient κ of dextran in agarose under passive diffusion (mean ± standard deviation).

The concept of equilibrium solute partitioning is best understood by recognizing that the pore sizes in the gel are distributed over a spectrum; some pores are too small for solutes of a given molecular weight, while other pores are sufficiently large to accommodate them. κ represents the volume fraction of solvent in the gel which fills the pores accessible to the solute. This partitioning effect does not place a ceiling on the solute concentration in the gel, as long as these larger pores can accommodate more solutes; thus, doubling the external bath concentration similarly doubles the solute concentration in the gel.

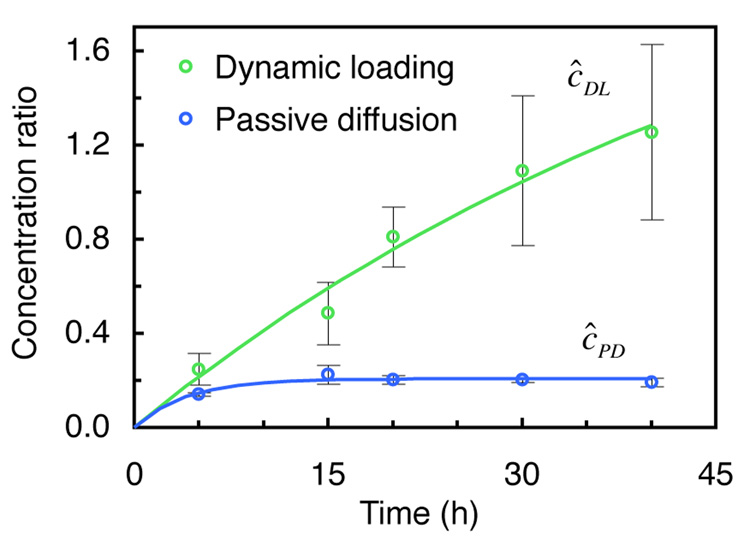
In contrast to passive diffusion, when applying dynamic loading to agarose gels (±5% strain amplitude at 1 Hz, superimposed on 15% static strain), the ratio ĉ _DL of internal to external concentration rises markedly. Dynamically loaded 7% agarose disks with 70kDa dextran exhibit a nearly exponential rise in concentration over time (Fig. 3), reaching a value of ĉ_DL = 1.25 ±0.37 after 40 hours, significantly higher than the corresponding passive diffusion equilibrium value, ĉ_PD =κ = 0.19± 0.02 (p<0.001). This outcome represents an enhancement over passive diffusion by a factor greater than six ( ĉ_DL/ĉ_PD = 6.6) and over the external bathing concentration (ĉ_DL > 1, p=0.06). The finding that ĉ_DL can approach or exceed unity implies that dextran molecules occupy those agarose pores large enough to accommodate them at much higher concentrations than in the bath.

Fig. 3.

Ratio of internal to external concentration versus time of 70kDa dextran in 7% agarose under dynamic loading, ĉ_DL , and unloaded, passive diffusion conditions, ĉ_PD (mean ± standard deviation). At equilibrium, ĉ_PD =κ.

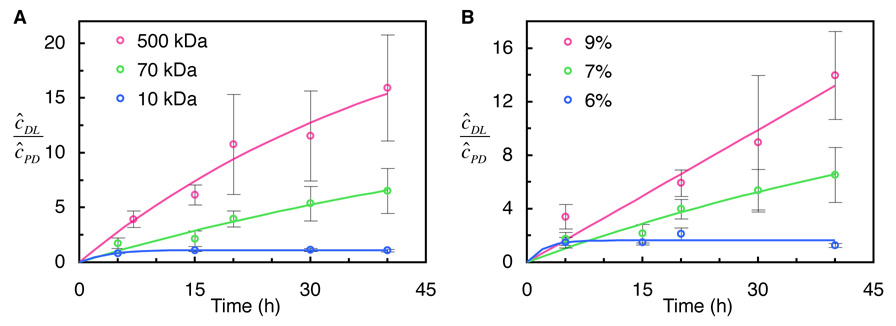
Increasing the dextran molecular weight at a given gel concentration produces greater enhancement in uptake relative to passive diffusion (Fig. 4A). Dynamic loading with 500kDa dextran solution in 7% agarose gel exhibits an enhancement by a factor of 16 over passive diffusion, whereas loading with 10kDa dextran shows an enhancement by a factor of 1.15 only. A similar outcome is observed when increasing the gel concentration for a given dextran molecular weight (Fig. 4B). Here, after 40 hours of loading, the more concentrated 9% gel shows an enhancement by a factor of 14 for 70 kDa dextran, while the 6% gel shows an enhancement by a factor no greater than 2.1.

Fig. 4.

Enhancement of solute uptake with dynamic loading, as a function of dextran molecular weight and agarose gel concentration. The ratio of internal solute concentrations under dynamic loading and passive diffusion (ĉ_DL/ĉ_PD ) at each time point is given for (A) 7% agarose and three dextran molecular weights; and (B) 70 kDa dextran and three agarose concentrations (mean ± standard deviation).

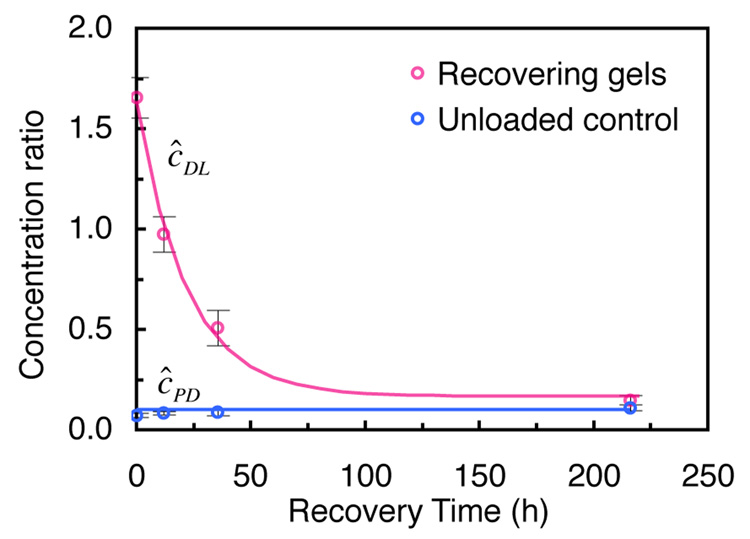
To validate these results, an additional experiment is reported where dynamic loading was halted after 40 h and the gel was allowed to recover unloaded for an additional 216 h. For this case, which used 70 kDa in 9% agarose gel, the relative solute concentration at the end of the loading period reaches ĉ_DL = 1.66 ± 0.11 (ĉ_DL > 1, p<0.005). After cessation of loading, it decays exponentially back down to the free swelling equilibrium value, ĉ_PD =κ = 0.15 ±0.02 (Fig. 5).

Fig. 5.

70 kDa dextran concentration recovery response in 9% agarose gels following 40 h of dynamic loading, and corresponding response in never-loaded agarose control specimens (mean ± standard deviation).

Discussion

The experimental results of this study reveal a non-intuitive fundamental physicochemical phenomenon, whose existence was suggested from theory only recently (Mauck et al., 2003). As shown here, dynamic loading can pump solutes into deformable porous media, yielding steady concentrations beyond the physical limit under passive diffusion. This pumping mechanism can be highly effective for certain combinations of gel and solute properties; dynamically loaded 7% agarose gels are shown to produce an enhancement over passive diffusion by a factor ĉ_DL/ĉ_PD greater than 15 for 500kDa dextran. In some cases, through this enhancement mechanism, the solute concentrations in the gels were also observed to exceed the external bathing solution concentration (ĉ_DL > 1), effectively overcoming the partitioning effect and reinforcing our understanding that this observed mechanism represents active solute transport, not some putative enlargement of the agarose pores by viscoelastic or viscoplastic deformation over repeated loading cycles.

Except for the lowest dextran molecular weight (Fig. 4A) and lowest gel concentration (Fig. 4B), the solute uptake in response to dynamic loading did not reach steady state by 40 h of loading in this study. Therefore the values of ĉ_DL for these cases do not represent the true steady-state response, which may potentially show even greater enhancement than seen here. The observed trends for 70 kDa and 500 kDa dextran in 7% agarose suggest that steady state may be reached within two to four additional days of loading. A practical reason for limiting dynamic loading to 40 h is that the viscoelastic nature of the gel produces a slow stress-relaxation that may eventually lead to separation of the loading platen (lift-off) from the disk with longer loading durations (Fig. 1), potentially confounding the findings.

A critical verification of the role of dynamic loading was demonstrated by the recovery experiment (Fig. 5). The demonstration that solute concentration in the gel returns to its free-swelling value after loading cessation further proves that this phenomenon is in fact due to active transport by mechanical pumping, and not to a solute binding mechanism or a physical alteration of the agarose. Upon cessation of dynamic loading, the accumulated solute concentration in the gel desorbs by passive transport, back to its passive diffusion equilibrium value.

From an energy balance perspective, the general theoretical basis for this active transport mechanism is that dynamic loading supplies mechanical free energy to the gel, part of which is stored in the form of potential energy and the rest is dissipated through frictional interactions (including solute diffusion, solvent permeation, and intrinsic viscoelasticity of the solid matrix). The stored potential energy includes the strain energy in the solid matrix, the pressure in the solvent, and the chemical potential in the solute. The latter component manifests itself as a higher steady-state solute concentration in dynamic loading than would be achieved under passive diffusion.

The detailed mechanism driving solute uptake with dynamic loading may be deduced from a closer examination of our earlier theoretical analysis (Mauck et al., 2003). Basically, the active transport process is driven by a cumulative pumping mechanism localized at the periphery of the loaded disk. Three important factors need to be taken into account, which are represented by dimensionless numbers in the theoretical analysis.

The most critical factor rests on the recognition that the solid matrix can exchange momentum with the solute. This mechanism, which can be expressed as an internal body force proportional to a frictional drag coefficient, is classically recognized in the observation that the diffusivity of the solute in the porous gel is usually smaller than in free solution (given the same solvent). Thus, the ability of the porous solid to drag the solute as it deforms is given by the dimensionless hindrance ratio R_d = D/φ^wD₀ (D = solute diffusivity in the gel, D₀ = solute diffusivity in free solution, φ ^w = gel porosity). A value of R_d = 1 implies that there is no hindrance, while decreasing values of R_d imply increasingly greater hindrance.

Upon the downstroke of a loading cycle, the pores at the periphery of the gel disk reduce in volume as a result of solvent exudation (Armstrong et al., 1984); since the solute efflux is hindered (R_d < 1), the relatively greater loss of solvent volume produces a small spike in solute concentration near the periphery. Upon the upstroke of the loading cycle, this spike is advected inward by the recoiling solid matrix. On the downstroke of the subsequent loading cycle this spike is advected outward again, though this time, as it approaches the periphery, it gets strengthened by the repeating pore contraction mechanism. This cycle repeats itself, and as the spike keeps being reinforced near the periphery, the solute penetrates deeper and deeper into the disk, along the radial direction. This mechanism reaches steady state when the concentration inside the disk has elevated sufficiently to balance the inward active pumping process with outward passive diffusion.

The second important factor derives from the recognition that the solvent and solute may have different characteristic diffusive velocities in the gel (Kosto and Deen, 2005; Urban et al., 1982). For a porous medium with a linear isotropic elastic solid matrix, the ratio of these velocities is given by the dimensionless number R_g = H_Ak/D (H_A = aggregate modulus of the gel solid matrix (Mow et al., 1980), k = hydraulic permeability of the solvent in the gel). In the pumping mechanism described above, the ability of the gel to retain solute upon the downstroke of the loading cycle is considerably enhanced when the solute transports through the gel much slower than the solvent (R_g ≫ 1). Thus, increasing values of R_g produce increasingly bigger solute concentration spikes at the periphery.

Finally, this active transport mechanism is also contingent upon the condition that the solute concentration spike produced in one loading cycle has not substantially dissipated by passive diffusion before the subsequent loading cycle. This is achieved when the convective velocity imparted by the solid matrix is greater than the characteristic solute diffusive velocity in the gel, a ratio represented by the solute Peclet number, Pe = ε₀f πr₀²/D (ε ₀ = amplitude of cyclical compressive strain, f = loading frequency, r₀ = disk radius).

In addition to these three important factors, it is also necessary to recognize that the interstitial pores of the gel must be able to change in volume upon loading, or else the peripheral solute concentration spike would not occur. For a porous medium with a linear isotropic elastic solid matrix, this is equivalent to requiring that the equilibrium Poisson’s ratio ν be less than 0.5 (Armstrong et al., 1984).

The theoretical analysis (Mauck et al., 2003) suggests that all these conditions ( R_g ≳1, R_d < 1, Pe ≳1, ν < 0.5 ) should be met in order to produce enhanced solute uptake with dynamic loading. Furthermore, the enhancement factor ĉ_DL/ĉ_PD increases with increasing R_g and Pe, and decreasing R_d and ν. In the experiments described in this study, for a given gel concentration, higher molecular weight solutes typically encounter greater hindrance in the gel relative to free solution, thus exhibiting a lower R_d; they also exhibit a lower solute diffusivity D in the gel, thus a higher R_g. Therefore, the higher enhancement factor observed with higher molecular weights (Fig. 4A) is consistent with the theory.

Similarly, for a given solute molecular weight, increasing the gel concentration produces greater solute hindrance, thus reducing R_d. However the effect of gel concentration on R_g is not easily predicted, as it is dependent on competing mechanisms; indeed, while increasing the gel concentration typically increases the gel equilibrium modulus H_A and decreases the solute diffusivity D in the gel, it also decreases the gel hydraulic permeability k. From the results of Fig. 4B, which show increased uptake enhancement with increasing gel concentration, we can conclude that the concomitant decrease in R_d was either sufficient to overcome a possible adverse decrease, or else assisted by an increase, in R_g.

The theoretical framework that motivated this experimental study also predicts that solute uptake will vary with the magnitude and frequency of the applied compressive strain, exhibiting lower uptake for smaller strains and loading frequencies. Variations in these parameters were not considered in the current study but may be addressed in future investigations.

This study demonstrates that mechanical loading can induce active solute transport in gels, pumping solutes against their concentration gradient. In principle this finding is applicable to any porous hydrated deformable material, and it may have considerable biological implications, particularly for solute transport in the extracellular matrix of mechanically loaded tissues, such as articular cartilage, skeletal and cardiac muscle, skin, lung, etc. As molecular transport plays a key role in maintaining cellular metabolic activity, active mechanisms to enhance diffusion pathways may prove beneficial to tissue growth and development.

In the field of tissue engineering, dynamic mechanical stimulation is currently used as a means of enhancing biosynthetic activity. Cell-seeded constructs for cartilage and tendon tissue have all shown greater matrix elaboration when subjected to such stimulation (Mauck et al., 2000; Shearn et al., 2007). While the beneficial effects of dynamic loading have been well characterized for a variety of tissue types, their underlying mechanisms are still unclear. The results from this study suggest that large nutrients and macromolecules can potentially transport actively in these dynamically loaded tissues. Similarly, the results of this study may be used to investigate new methods of drug delivery, where drug transport may be enhanced by dynamic loading.

In summary, this experimental study uncovers a fundamental mechanism of solute transport in porous deformable media. It shows that active solute transport can be achieved with mechanical loading, consistent with the predictions of a recently developed theoretical framework. Implications of this finding are not limited to solute transport in mechanically loaded biological tissues, but may also serve as the basis for experimental and industrial processes that require solute pumping.