Abstract
The objective of this study was to provide a detailed experimental assessment of the two-dimensional cartilage strain distribution on the cross-section of immature and mature bovine humeral heads subjected to contact loading at a relatively rapid physiological loading rate. Six immature and six mature humeral head specimens were loaded against glass and strains were measured at the end of a 5 s loading ramp on the textured articular cross-section using digital image correlation analysis. The primary findings indicate that elevated tensile and compressive strains occur near the articular surface, around the center of the contact region. Few qualitative or quantitative differences were observed between mature and immature joints. Under an average contact stress of ~1.7 MPa, the peak compressive strains averaged −0.131 ± 0.048, which was significantly less than the relative change in cartilage thickness, −0.104 ± 0.032 (p < 0.05). The peak tensile strains were significantly smaller in magnitude, at 0.0325 ± 0.013. These experimental findings differ from a previous finite element analysis of articular contact, which predicted peak strains at the cartilage-bone interface even when accounting for the porous-hydrated nature of the tissue, its depth-dependent inhomogeneity, and the disparity between its tensile and compressive properties. These experimental results yield new insights into the local mechanical environment of the tissue and cells, and suggest that further refinements are needed in the modeling of contacting articular layers.
INTRODUCTION
Despite a wealth of studies on the biomechanics of articular cartilage, it is interesting that detailed measurements of the strain distribution in articular layers under physiological loading conditions have yet to be reported. Here, physiological loading conditions refer to relatively rapid loading rates (but not impact loading) and contact stress magnitudes achieved during normal activities of daily living. Load magnitudes (Cooney and Chao, 1977; Paul, 1976; Poppen and Walker, 1978; Rydell, 1973) and articular contact tractions (Ahmed and Burke, 1983; Ahmed et al., 1983; Brown and Shaw, 1983; Brown and Shaw, 1984; Clark et al., 2002; Huberti and Hayes, 1984; Huberti and Hayes, 1988; Matthews et al., 1977) have been reported for a number of activities of daily living. However, there are only a few reports of measurements of relative cartilage deformation under physiological conditions, using radiographic techniques (Armstrong et al., 1979), ultrasound (Macirowski et al., 1994) and magnetic resonance imaging, (Eckstein et al., 2000; Eckstein et al., 1999), typically reporting relative deformations ranging from 6% to 20%. In contrast, the relative change in thickness of cartilage under prolonged static loading is on the order of 57% (Herberhold et al., 1999; Herberhold et al., 1998). However, this type of loading is not physiological and large changes in thickness under static conditions are not representative of in vivo cartilage deformation.
Cartilage deformation, as measured by change in thickness, has been characterized under various loading conditions using radiographic methods (Armstrong et al., 1979; Wayne et al., 1998), ultrasound (Macirowski et al., 1994; Suh et al., 2001), cryofixation followed by scanning electron microscopy (Kaab et al., 1998), chemical fixation followed by light microscopy (Clark et al., 2003), and magnetic resonance imaging (Eckstein et al., 2000; Herberhold et al., 1999; Herberhold et al., 1998).
Local strain measurements in articular cartilage explants have been reported under equilibrium static loading conditions using optical methods, by tracking distances between cells or cell nuclei (Guilak et al., 1995; Schinagl et al., 1997; Schinagl et al., 1996) or with digital image correlation (DIC) (Bae et al., 2003; Canal et al., 2003; Erne et al., 2005; Wang et al., 2003; Wang et al., 2002). These studies have yielded valuable insights into the equilibrium properties of the tissue, but the equilibrium response is not representative of physiologic loading conditions, and the explant geometry used in these studies was not representative of the articular geometry. More recently, strain fields in cartilage explants have been reported using magnetic resonance tagging (Neu et al., 2005) under steady-state dynamic loading. This approach holds great promise for delivering 3D dynamic strain measurements in situ but has only been applied to small explants to date.
The objective of this study is to complement these valuable literature findings by providing a detailed experimental assessment of the 2D cartilage strain distribution on the cross-section of immature and mature bovine humeral heads subjected to contact loading at a physiological loading rate. Mature and immature joints are compared to explore whether significant differences may arise due to the well-recognized evolution in material properties (Kempson, 1991; Williamson et al., 2003) and composition (Front et al., 1989; Garg and Swann, 1981; Wachtel et al., 1995) with age. The strain measurement method employed in this study, which uses digital image correlation, builds upon our earlier application in the study of cartilage explants under static loading (Wang et al., 2002). The characterization of localized strains from experiments can aid in the understanding of the biomechanics of articular cartilage under physiological loading conditions, the structure-function relationships of this tissue, and the interpretation of degenerative and acute failure patterns observed in osteoarthritis and traumatic injuries. It also sets the stage for refining constitutive models of articular cartilage.
MATERIALS AND METHODS
Specimen Preparation
Humeral heads were dissected from six-month-old calf joints (N=6) and mature 2-year-old shoulder joints (N=4). All samples were observed to be normal by visual inspection. The humeral heads were sectioned by band saw to create samples with smooth cross-sectional areas of the articular layer and underlying bone. The resulting sample groups were labeled ‘immature’ (n = 6) and ‘mature’ (n = 6, with two joints providing two samples each). The cartilage layers were kept moist with phosphate buffered saline (PBS) during all specimen preparation. A Badger Model 200 airbrush (Badger Air-Brush Co., Franklin Park, IL) was used to spray the cross sectional surface with Verhoeff’s stain to produce an optically textured surface (Narmoneva et al., 1999) (Figure 1). Specimens were mounted into the loading apparatus along a line of action perpendicular to the articular surface and parallel to the cross-sectional surface. The textured cross-section of the sample was placed flush against the glass face of a specimen chamber to ensure that motion of the specimen relative to the camera was parallel to the image plane, and to minimize out-of-plane deformation. The specimen chamber was filled with PBS at room temperature (Figure 2).
Figure 1.
Immature bovine humeral head osteochondral sample, mounted in the loading apparatus. The cross-section has been sprayed with Verhoeff’s stain to produce an optically textured surface. This representative image shows the joint in its loaded configuration at t=5s (* contact width).
Figure 2.
Schematic diagram of the loading apparatus. The load is applied with a voice-coil actuator and the deformation is measured with a LVDT. The osteochondral sample is loaded against a glass slide. A side view of the chamber shows that the sectioned specimen is mounted with its cross-section nearly flush with the transparent chamber wall, to produces images as shown in Figure 1.
Loading Protocol
Images of the joint cross-section were acquired before and during deformation using a video camera (Sony SSC-C50, Japan, 640 × 480 pixel resolution) mounted on a stereoscope (Olympus model SZ40, Olympus America, Melville, NY, 20–25 µm/pixel). The articular surface of the osteochondral sample was loaded against the flat glass bottom of the chamber (Figure 1) using a voice-coil force actuator (Model LA17-28-000A; BEI Kimco Magnetics Division, San Marcos, CA, 71N peak force, 28 N stall force). An earlier study (Park et al., 2004) of the response of bovine cartilage to dynamic sinusoidal loading under physiological stress magnitudes (~5 MPa) reported that the cartilage thickness decreases on average by 9% to 16% for loading frequencies from 40 Hz down to 0.1 Hz (loading cycles of 0.025 s to 10 s); from preliminary studies, it was determined that bovine articular layers loaded against glass would undergo comparable deformations for a load of 36 N. Thus, using a feedback load-control loop, a load of 36 N was applied over a 5 second ramp (comparable to a sawtooth loading cycle at 0.1 Hz) and sustained for a total loading time of 30 seconds. The observed stress-relaxation response did not achieve equilibrium over this testing duration. Images of the cross-section were acquired at intervals of 500 ms over the entire testing duration. The load was measured using a load cell (Model 8523, Burster, Sterling Heights, MI, ±200 N). All data control and acquisition was implemented with a personal computer (Intel Pentium4 CPU) and data acquisition card (Model PCI-MIO-16XE-10, National Instruments, Austin, TX), running through a Labview software interface (National Instruments, Austin, TX).
Data Analysis
Strain analysis was performed using 2D digital image correlation software (Vic 2D, West Columbia, SC) whose accuracy was validated against the results of our earlier study (Wang et al., 2002) (data not shown). The analysis was performed by comparing an image of the unloaded specimen to subsequent images of the specimen in a loaded state. All analyses utilized search window sizes of 39×39 pixels surrounding data analysis points which were incrementally chosen at every fourth pixel horizontally and vertically throughout the region of interest, being the articular layer. Localized in-plane deformation was calculated by the software, smoothed over 9 point segments to create a continuous field and differentiated spatially to yield the Lagrangian strain tensor. Lateral (Exx) and axial (Eyy) normal strains, and shear (Exy) strains, were subsequently plotted, where y represents the loading direction and x is at the intersection of the contact plane and the plane of the cross-section.
To calculate principal normal strains (E1 and E2) in the plane of the cross-section, it was assumed that the strain tensor has the general form
This implies that the out-of-plane shear strains can be neglected even if the normal strain out of the plane of the cross-section is not necessarily negligible. A preliminary finite element analysis was used to validate this approximation.
Each specimen yielded 2D strain maps over the entire articular layer, and an averaging algorithm was formulated to combine results from all specimens, for each of the relevant strain components. The strain map for each specimen was sampled uniformly over a 2D rectangular grid scaled vertically to the thickness of the unloaded specimen, and horizontally to the loaded contact width (Figure 1); the grid was centered horizontally at the half-width of the contact. The contact width was determined from the images at the end of the loading ramp (at 5 s). The sampled grid values were averaged over all specimens to yield average and standard deviation strain maps; if a particular grid point contained data from fewer than half the specimens, it was not included in the final map.
The average contact stress was calculated from the applied load and the contact width, by assuming that the contact region was semi-circular; consequently, the contact half-width is reported below as the contact radius.
Statistical comparisons between the immature and mature groups were performed using a Tukey HSD Post-Hoc analysis, with a level of α = 0.05 considered significant (Statistica Software, StatSoft, OK).
Polarized Light Microscopy
Polarized light microscopy was used to identify the superficial, middle and deep zones in the immature and mature bovine humeral head. A total of eight unfixed cartilage slices were imaged (two slices each from two immature and two mature joints), and 80 µm thick samples were observed through an inverted microscope (Olympus IX70; Olympus America, Melville, NY, USA) equipped with differential interference contrast optics (Olympus America, Melville, NY, USA). Samples were observed with the superficial zone oriented at 45° to cross polarizers. Intensity profiles of the acquired grayscale images (Figure 3) were analyzed (ImageJ, Bethesda, MD) to reveal locations of light extinction or fiber reorientation at the middle zone boundary points, from superficial to middle and from middle to deep. The boundaries between these zones were identified from inflexion points in the grayscale profile; their fractional location through the thickness was averaged over immature and mature samples.
Figure 3.
Polarized light microscopy was used to identify the superficial, middle and deep zones of immature and mature bovine humeral head cartilage. This representative image of an 80 µm thick slice from a mature sample exhibits the highest light intensity where collagen fibers are at 0° (superficial zone) and 90° (deep zone) to the articular surface; the lowest intensity is representative of fiber orientations deviating from these principal directions (middle zone).
The temporal evolution in the axial normal strain Eyy under the prescribed ramp-and-hold loading profile is depicted for a representative immature specimen in Figure 4a, b, and c, showing that the strain magnitude increased with time after the applied load had reached its peak value at 5 s. Repeatability measurements, illustrated in this representative specimen (Figure 4a, b, and c versus d, e, and f), demonstrated that reloading the tissue sample (after a 5 min recovery) and evaluating the strain distribution anew produced satisfactorily consistent results. A quantitative analysis of repeatability was performed on the six immature specimens. The root mean square of the difference in principal normal strain measurements between the first and second test, at t=5 s, was 0.0066 for peak E1, 0.0072 for peak E2, and 0.0008 and 0.0022 respectively for the mean values of E1 and E2 across the entire articular layer.
Figure 4.
Plots of axial normal strain (Eyy) for a representative immature specimen as a function of time, at (a) 5 s (end of loading ramp), (b) 10 s, and (c) 30 s. Corresponding time points for a repeated test on the same specimen are also shown, (d, e, f).
All subsequent results represent measurements at the end of the loading ramp (t=5 s). The articular layer thickness of the immature specimens was significantly larger than that of the mature specimens (p < 0.001; immature: 2.20 ± 0.29 mm , mature : 1.06 ± 0.16 mm); the opposite was observed for the articular surface radius of curvature (p<0.0005; immature: 22.5 ± 1.7 mm, mature: 54.5 ± 9.5 mm). There was no significant difference in contact radius (p=0.28; immature: 3.60 ± 0.38 mm , mature : 3.93 ± 0.65 mm) and therefore no significant difference in contact stress (immature: 1.84 ± 0.36 MPa , mature : 1.56 ± 0.57 MPa).
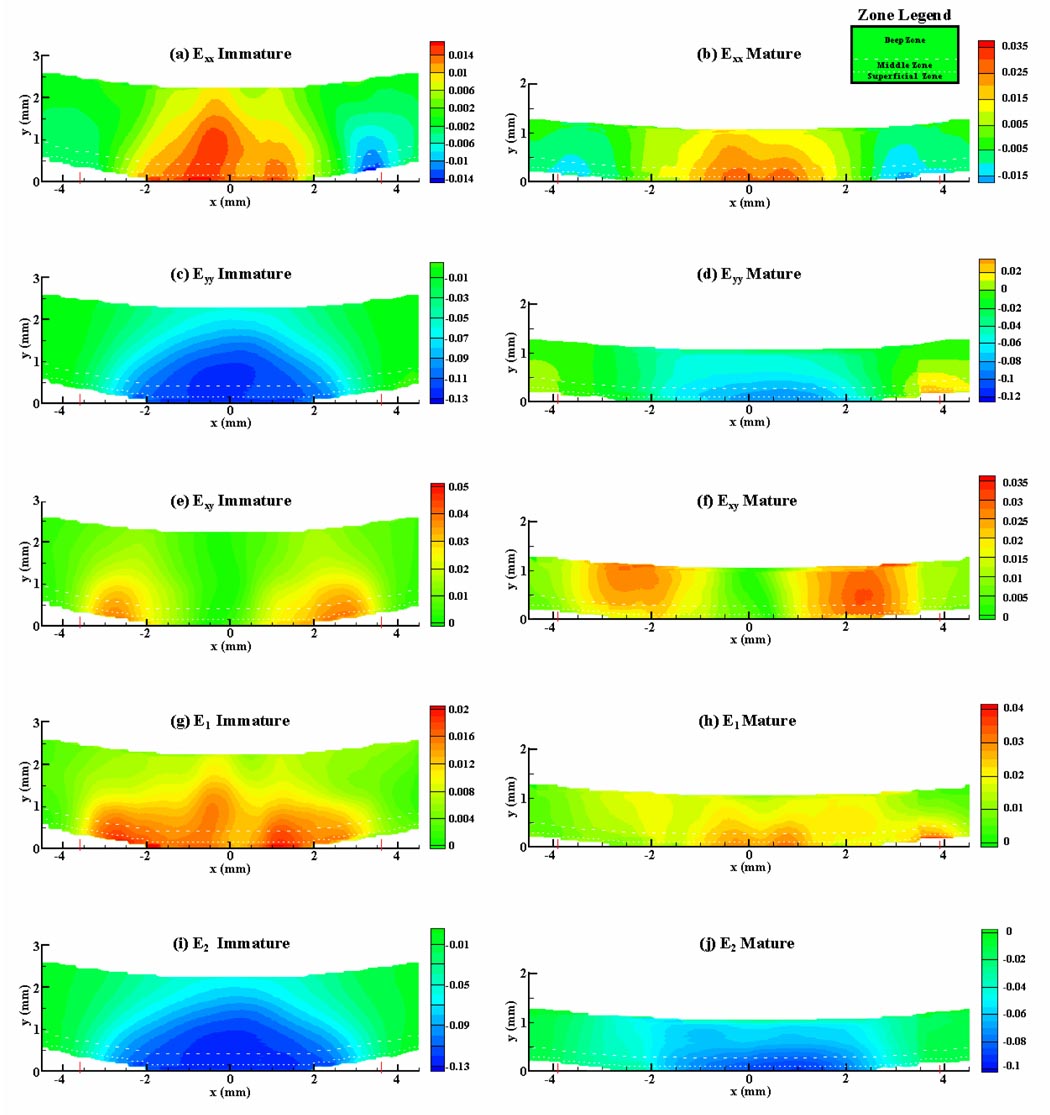
Contour plots of lateral normal strain (Exx) showed similar patterns for immature (Figure 5a) and mature (Figure 5b) joints: Exx was tensile over the central contact region, highest at the articular surface and decreased with increasing depth from the surface and distance from the center of contact, and compressive at the edges of contact. Contour plots of the axial strain (Eyy) also showed similar patterns for immature (Figure 5c) and mature (Figure 5d) joints: Eyy was compressive over the entire cross-section, highest at the articular surface, particularly at the center of the contact region, and decreased with increasing depth from the surface. Shear strain (Exy) was concentrated at the edge of contact and was highest in intensity at the articular surface in the immature samples (Figure 5e), and at varying depths in the mature samples (Figure 5f).
Figure 5.
Strain contour plots over the cross-section of osteochondral samples, at t=5 s, averaged over all immature (a, c, e, g, i), and all mature (b, d, f, h, j) specimens; x-axis represents distance from center of contact and y-axis represents distance from articular surface. Dashed lines indicate zonal delineations, based on polarized light microscopy results (Figure 3).
The contour plot of the maximum principal normal strain E1 shows that it was tensile over the entire cross-section and highest near the articular surface, at the center of contact (Figure 5g, h). Similarly, the minimum principal normal strain E2 was compressive over the entire cross-section, with greatest magnitude near the articular surface at the center of contact (Figure 5i, j). The maximum shear strain (not shown), which can be deduced from (E1–E2)/2, exhibited a similar pattern.
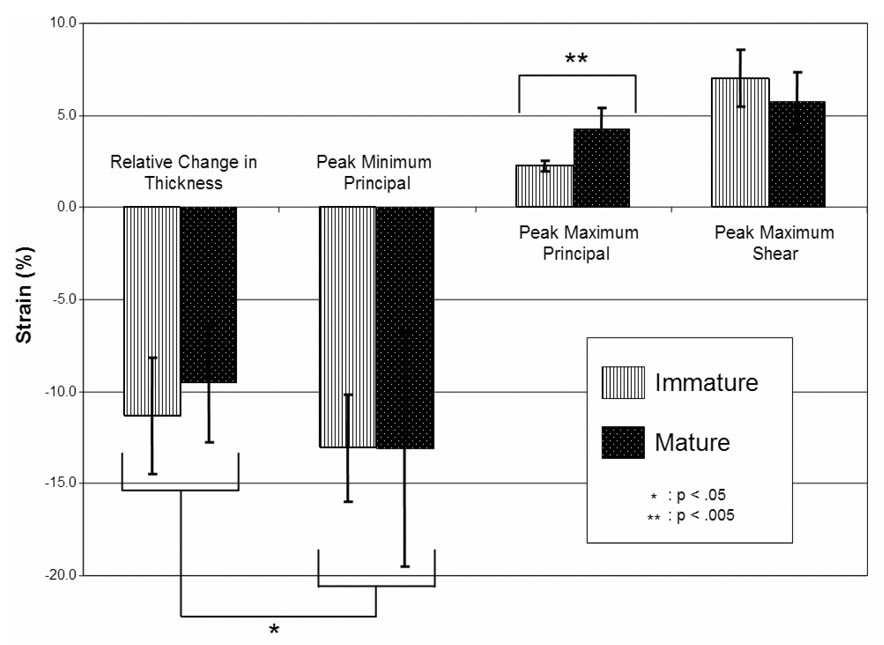
The average of the peak value of E2 over all specimens, immature and mature, was −0.131 ± 0.048, which was significantly less than the relative change in cartilage thickness, −0.104 ± 0.032 (p < 0.05) (Figure 6), reflecting the inhomogeneity of the strain distribution through the thickness of the articular layer. There were no significant differences between immature and mature joints for the average peak value of E2 (p=0.99) and the relative change in thickness (p=0.36). The average peak value of E1 in immature samples was 0.0225 ± 0.031, which was significantly smaller from that of the mature sample group of 0.0426±0.012 (p < 0.005).
Figure 6.
Averages and standard deviations of mean, peak and engineering strain values over all immature and mature sample groups, at t=5 s.
Polarized light microscopy results indicate that the superficial and middle zones respectively occupy 4.6±1.0% and 12.1±2.3% of the articular layer thickness in immature joints, and 6.5±1.4% and 17.0±1.5% in mature joints. These average zonal delineations are indicated with dashed lines in Figure 5.
In this study, strain distributions throughout full thickness cross-sections of the articular layer of the bovine humeral head were characterized under physiological loading rates (average contact stresses of ~1.5–2.0 MPa applied over 5s) which, for humans, would represent moderate activities of daily living (Ahmed and Burke, 1983; Brown and Shaw, 1983). Both mature and immature joints were analyzed to investigate how age related differences in material properties and composition affect strain profiles; however, few qualitative and quantitative differences were observed in the strains. The primary findings indicate that elevated tensile and compressive strains occur near the articular surface of the humeral head (Figure 5). In particular, the peak values of the principal normal strains occur around the center of the contact region (Figure 5g–j). The qualitative difference in the distribution of the shear strain Exy over the cross-section of immature and mature joints may be attributed to differences in the variation of cartilage material properties through the thickness of the articular layer: The concentration of shear strain near the articular surface in immature joints (Figure 5e) suggests that the deep zone has a much higher shear modulus relative to the superficial zone than in mature joints (Figure 5f).
The strain fields are significantly inhomogeneous through the depth, as attested by the contour plots, as well as the statistically significant difference between the relative change in cartilage thickness and the peak compressive strain values (Figure 6). Based on these results, the peak compressive strain is approximately 30% greater than the relative change in thickness.
It is well known that the equilibrium compressive modulus of articular cartilage is smallest near the articular surface, and increases toward the deep zone (Guilak et al., 1995; Schinagl et al., 1997; Wang et al., 2002). Therefore it is tempting to conclude that the inhomogeneous strain distribution observed in the current study derives directly from this property. However, there are additional subtleties that need to be considered in order to obtain a more comprehensive picture of this problem. First, cartilage is also known to exhibit a higher equilibrium tensile modulus at the articular surface than in the deep zone (Akizuki et al., 1986). Second, unlike the case of equilibrium loading, rapid loading causes significant interstitial fluid pressurization (Mow et al., 1980) which is enhanced by the disparity between tensile and compressive equilibrium moduli (Soltz and Ateshian, 2000), and this disparity is greatest at the articular surface (Park et al., 2003). These competing mechanisms (lower equilibrium compressive stiffness but higher dynamic interstitial fluid pressurization at the articular surface) could produce a different outcome for the strain distribution, since the dynamic compressive modulus of cartilage may not necessarily be smallest at the articular surface. Indeed, the temporal evolution of the strain (Figure 4) confirms that it increases in magnitude and spreads toward the deep zone as the interstitial fluid pressure subsides, implying that the short-term strain response is not necessarily representative of the long-term equilibrium response (not measured in this study) because of fluid pressurization.
In a previous biphasic finite element articular contact study which incorporated experimentally-measured depth-dependent tensile and compressive properties of human patellofemoral articular cartilage, it was predicted that the peak principal normal strains appeared at the cartilage-bone interface (Krishnan et al., 2003), contrary to the experimental findings of the current study. Other analytical studies have incorporated inhomogeneous properties when modeling cartilage (Julkunen et al., 2007; Li et al., 2000; Mow et al., 1980; Mow and Mansour, 1977; Wang et al., 2001), but these have not addressed articular contact. Clearly, the experimental results of this study provide an opportunity to refine existing models of the articular layer, and may motivate the formulation of new constitutive relations for articular cartilage that can capture the observed response.
It is also important to assess the advantages and limitations of 2D strain measurements on a joint cross-section. Evidently, 2D strain contour plots over an entire cross-section provide more useful information than measurements of the relative change in cartilage thickness alone. The local distribution of the strain is uncovered, which can be valuable for understanding the local mechanical environment of the tissue and its embedded chondrocytes, and for refining constitutive models of cartilage. However, cutting through the tissue may introduce measurement artifacts that need to be assessed. One clear limitation is that the tissue properties may be compromised precisely on the plane of the cross-section where strain measurements are being performed. The true extent of this limitation is difficult to assess, since there is currently no practical method of measuring accurate 3D strain fields in intact articular layers for comparison purposes. This limitation is inherent to all studies of cartilage mechanics where the tissue is excised or partially cut to measure its properties or strain distribution (Schinagl et al., 1997; Wang et al., 2002), and future studies may have to investigate this issue more closely.
A more readily measurable experimental limitation is the assumption that the testing configuration constrained the articular layer from deforming out of the plane of the cross-section (Figure 2). If this were true, then Ezz=0 and no interstitial fluid could escape from the presumably well-sealed sectioned cartilage surface. Since it is well known that cartilage deformation is isochoric in the short-term loading response (Armstrong et al., 1984; Ateshian et al., 2007; Jurvelin et al., 1997), due to the near-incompressibility of the solid matrix and interstitial fluid (Bachrach et al., 1998), and the low permeability which prevents rapid fluid exudation, we would thus expect that Exx+Eyy+Ezz = 0 (under small strains), or equivalently here, Exx= −Eyy. Since the experimental results do not confirm this relation, we can conclude that fluid exudation did occur on the cartilage cross-section (implying that Exx+Eyy+Ezz ≠ 0), and thus the cross-section did not form an effective seal with the chamber wall.
This observation has two important ramifications. First, it implies that the strain measurements reported here do not replicate exactly what would happen in an intact articular layer under contact loading. Second, it implies that in future finite element analyses that attempt to replicate these experimental results, it would be more appropriate to model the cross-section as free-draining rather than impermeable. Indeed, the logical progression is to perform a finite element analysis that reproduces the boundary conditions of the current experimental setup, use it to refine constitutive models of articular cartilage until good agreement is achieved with the current experimental strain results, then apply this refined model to analyze the contact mechanics of intact articular layers to get a more accurate estimate of the strain and stress fields in normal contact.
Another limitation of this study is that it examined contact between an articular layer and a flat glass slide. This configuration is more realistic than earlier strain measurements on plugs of cartilage (Neu et al., 2005; Schinagl et al., 1996; Wang et al., 2002), yet it is not entirely representative of cartilage-on-cartilage contact, which would generally be expected to yield more congruent contact. However, the methodological insights and strain results gained from this study serve as a useful guide toward future studies of cartilage-on-cartilage contact (Canal et al., 2007). In particular, this study shows that strain measurements on the entire cross-section of an articular layer can be performed with good repeatability, as the root-mean-square difference observed between repeated measurements was ~0.007 (0.7% strain) or less.
In contrast to earlier studies that have investigated the equilibrium response of cartilage under loading, the current study focuses on the early-time response of the tissue to loading. Thus the strain distributions reported here are expected to be more representative of physiological loading conditions. Elevated tensile and compressive strains in the superficial zone are consistent with findings of fibrillation and fissures as reported from impact studies (Atkinson et al., 2001; Atkinson and Haut, 2001; Bentley, 1985), from the natural progression of wear in osteoarthritis (Hollander et al., 1995) or as a result of induced osteoarthritis (Panula et al., 1998; Setton et al., 1994; Stoop et al., 2001). The presence of these elevated strain patterns at the articular surface in these experimental results is an important parallel with the location of initial degradation of the extra-cellular matrix of cartilage.
This study uniquely contributes to the characterization of the non-uniform 2D-strain distributions across a fully contacting articular layer. Future studies will expand this technique to characterize the strain distribution between two articulating layers at physiological load magnitudes (Canal et al., 2007). In addition, a more extensive characterization of the local material properties, as well as refinements in cartilage constitutive modeling, will facilitate the prediction of the stress distribution across the cartilage layer, and therefore advance our understanding of local stress and strain distributions in articular layers under physiological loading conditions.
ACKNOWLEDGMENTS
This study was funded by the National Institute of Arthritis, Musculoskeletal and Skin Diseases of the U.S. National Institutes of Health (AR46532). This material is also based upon work supported under a National Science Foundation Graduate Research Fellowship. We would like to thank Ms. Christine Schwaller and Ms. Elizabeth Chorney for their assistance in this study.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Ahmed AM, Burke DL. In-vitro measurement of static pressure distribution in synovial joints--Part I: Tibial surface of the knee. J Biomech Eng. 1983;105:216–225. doi: 10.1115/1.3138409. [DOI] [PubMed] [Google Scholar]
- Ahmed AM, Burke DL, Yu A. In-vitro measurement of static pressure distribution in synovial joints--Part II: Retropatellar surface. J Biomech Eng. 1983;105:226–236. doi: 10.1115/1.3138410. [DOI] [PubMed] [Google Scholar]
- Akizuki S, Mow VC, Muller F, Pita JC, Howell DS, Manicourt DH. Tensile properties of human knee joint cartilage: I. Influence of ionic conditions, weight bearing, and fibrillation on the tensile modulus. J Orthop Res. 1986;4:379–392. doi: 10.1002/jor.1100040401. [DOI] [PubMed] [Google Scholar]
- Armstrong CG, Bahrani AS, Gardner DL. In vitro measurement of articular cartilage deformations in the intact human hip joint under load. J Bone Joint Surg Am. 1979;61:744–755. [PubMed] [Google Scholar]
- Armstrong CG, Lai WM, Mow VC. An analysis of the unconfined compression of articular cartilage. J Biomech Eng. 1984;106:165–173. doi: 10.1115/1.3138475. [DOI] [PubMed] [Google Scholar]
- Ateshian GA, Ellis BJ, Weiss JA. Equivalence between short-time biphasic and incompressible elastic material responses. J Biomech Eng. 2007;129:405–412. doi: 10.1115/1.2720918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson PJ, Ewers BJ, Haut RC. Blunt injuries to the patellofemoral joint resulting from transarticular loading are influenced by impactor energy and mass. J Biomech Eng. 2001;123:293–295. doi: 10.1115/1.1378576. [DOI] [PubMed] [Google Scholar]
- Atkinson PJ, Haut RC. Impact responses of the flexed human knee using a deformable impact interface. J Biomech Eng. 2001;123:205–211. doi: 10.1115/1.1372320. [DOI] [PubMed] [Google Scholar]
- Bachrach NM, Mow VC, Guilak F. Incompressibility of the solid matrix of articular cartilage under high hydrostatic pressures. J Biomech. 1998;31:445–451. doi: 10.1016/s0021-9290(98)00035-9. [DOI] [PubMed] [Google Scholar]
- Bae WC, Lewis CW, Sah RL. Intra-tissue strain distribution in normal human articular cartilage during clinical indentation testing. 49th Annual Meeting of the Orthopaedic Research Society; 2003. p. 254. [Google Scholar]
- Bentley G. Articular cartilage changes in chondromalacia patellae. J Bone Joint Surg Br. 1985;67:769–774. doi: 10.1302/0301-620X.67B5.4055879. [DOI] [PubMed] [Google Scholar]
- Brown TD, Shaw DT. In vitro contact stress distributions in the natural human hip. J Biomech. 1983;16:373–384. doi: 10.1016/0021-9290(83)90071-4. [DOI] [PubMed] [Google Scholar]
- Brown TD, Shaw DT. In vitro contact stress distribution on the femoral condyles. J Orthop Res. 1984;2:190–199. doi: 10.1002/jor.1100020210. [DOI] [PubMed] [Google Scholar]
- Canal CE, Gardner TR, Ateshian GA. Optical strain measurements on the mid-sagittal cross-section of the human patellofemoral joint under physiological loading. 53rd Annual Meeting of the Orthopaedic Research Society; 2007. p. 0618. [Google Scholar]
- Canal CE, Meade NK, Wang CCB, Hung CT, Ateshian GA. Optical measurement of in situ strain fields within osteochondral tissue under indentation. Summer Bioengineering Conference; Key Biscayne, FL. 2003. p. 363. [Google Scholar]
- Clark AL, Barclay LD, Matyas JR, Herzog W. In situ chondrocyte deformation with physiological compression of the feline patellofemoral joint. J Biomech. 2003;36:553–568. doi: 10.1016/s0021-9290(02)00424-4. [DOI] [PubMed] [Google Scholar]
- Clark AL, Herzog W, Leonard TR. Contact area and pressure distribution in the feline patellofemoral joint under physiologically meaningful loading conditions. J Biomech. 2002;35:53–60. doi: 10.1016/s0021-9290(01)00165-8. [DOI] [PubMed] [Google Scholar]
- Cooney WP, III, Chao EY. Biomechanical analysis of static forces in the thumb during hand function. J Bone Joint Surg Am. 1977;59:27–36. [PubMed] [Google Scholar]
- Eckstein F, Lemberger B, Stammberger T, Englmeier KH, Reiser M. Patellar cartilage deformation in vivo after static versus dynamic loading. J Biomech. 2000;33:819–825. doi: 10.1016/s0021-9290(00)00034-8. [DOI] [PubMed] [Google Scholar]
- Eckstein F, Tieschky M, Faber S, Englmeier KH, Reiser M. Functional analysis of articular cartilage deformation, recovery, and fluid flow following dynamic exercise in vivo. Anat Embryol (Berl) 1999;200:419–424. doi: 10.1007/s004290050291. [DOI] [PubMed] [Google Scholar]
- Erne OK, Reid JB, Ehmke LW, Sommers MB, Madey SM, Bottlang M. Depth-dependent strain of patellofemoral articular cartilage in unconfined compression. J Biomech. 2005;38:667–672. doi: 10.1016/j.jbiomech.2004.04.005. [DOI] [PubMed] [Google Scholar]
- Front P, Aprile F, Mitrovic DR, Swann DA. Age-related changes in the synthesis of matrix macromolecules by bovine articular cartilage. Connect Tissue Res. 1989;19:121–133. doi: 10.3109/03008208909043893. [DOI] [PubMed] [Google Scholar]
- Garg HG, Swann DA. Age-related changes in the chemical composition of bovine articular cartilage. The structure of high-density proteoglycans. Biochem J. 1981;193:459–468. doi: 10.1042/bj1930459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guilak F, Ratcliffe A, Mow VC. Chondrocyte deformation and local tissue strain in articular cartilage: a confocal microscopy study. J Orthop Res. 1995;13:410–421. doi: 10.1002/jor.1100130315. [DOI] [PubMed] [Google Scholar]
- Herberhold C, Faber S, Stammberger T, Steinlechner M, Putz R, Englmeier KH, Reiser M, Eckstein F. In situ measurement of articular cartilage deformation in intact femoropatellar joints under static loading. J Biomech. 1999;32:1287–1295. doi: 10.1016/s0021-9290(99)00130-x. [DOI] [PubMed] [Google Scholar]
- Herberhold C, Stammberger T, Faber S, Putz R, Englmeier KH, Reiser M, Eckstein F. An MR-based technique for quantifying the deformation of articular cartilage during mechanical loading in an intact cadaver joint. Magn Reson Med. 1998;39:843–850. doi: 10.1002/mrm.1910390522. [DOI] [PubMed] [Google Scholar]
- Hollander AP, Pidoux I, Reiner A, Rorabeck C, Bourne R, Poole AR. Damage to type II collagen in aging and osteoarthritis starts at the articular surface, originates around chondrocytes, and extends into the cartilage with progressive degeneration. J Clin Invest. 1995;96:2859–2869. doi: 10.1172/JCI118357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huberti HH, Hayes WC. Patellofemoral contact pressures. The influence of q-angle and tendofemoral contact. J Bone Joint Surg Am. 1984;66:715–724. [PubMed] [Google Scholar]
- Huberti HH, Hayes WC. Contact pressures in chondromalacia patellae and the effects of capsular reconstructive procedures. J Orthop Res. 1988;6:499–508. doi: 10.1002/jor.1100060405. [DOI] [PubMed] [Google Scholar]
- Julkunen P, Kiviranta P, Wilson W, Jurvelin JS, Korhonen RK. Characterization of articular cartilage by combining microscopic analysis with a fibril-reinforced finite-element model. J Biomech. 2007;40:1862–1870. doi: 10.1016/j.jbiomech.2006.07.026. [DOI] [PubMed] [Google Scholar]
- Jurvelin JS, Buschmann MD, Hunziker EB. Optical and mechanical determination of Poisson's ratio of adult bovine humeral articular cartilage. J Biomech. 1997;30:235–241. doi: 10.1016/s0021-9290(96)00133-9. [DOI] [PubMed] [Google Scholar]
- Kaab MJ, Ito K, Clark JM, Notzli HP. Deformation of articular cartilage collagen structure under static and cyclic loading. J Orthop Res. 1998;16:743–751. doi: 10.1002/jor.1100160617. [DOI] [PubMed] [Google Scholar]
- Kempson GE. Age-related changes in the tensile properties of human articular cartilage: a comparative study between the femoral head of the hip joint and the talus of the ankle joint. Biochim Biophys Acta. 1991;1075:223–230. doi: 10.1016/0304-4165(91)90270-q. [DOI] [PubMed] [Google Scholar]
- Krishnan R, Park S, Eckstein F, Ateshian GA. Inhomogeneous cartilage properties enhance superficial interstitial fluid support and frictional properties, but do not provide a homogeneous state of stress. J Biomech Eng. 2003;125:569–577. doi: 10.1115/1.1610018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li LP, Buschmann MD, Shirazi-Adl A. A fibril reinforced nonhomogeneous poroelastic model for articular cartilage: inhomogeneous response in unconfined compression. J Biomech. 2000;33:1533–1541. doi: 10.1016/s0021-9290(00)00153-6. [DOI] [PubMed] [Google Scholar]
- Macirowski T, Tepic S, Mann RW. Cartilage stresses in the human hip joint. J Biomech Eng. 1994;116:10–18. doi: 10.1115/1.2895693. [DOI] [PubMed] [Google Scholar]
- Matthews LS, Sonstegard DA, Henke JA. Load bearing characteristics of the patello-femoral joint. Acta Orthop Scand. 1977;48:511–516. doi: 10.3109/17453677708989740. [DOI] [PubMed] [Google Scholar]
- Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- Mow VC, Mansour JM. The nonlinear interaction between cartilage deformation and interstitial fluid flow. J Biomech. 1977;10:31–39. doi: 10.1016/0021-9290(77)90027-6. [DOI] [PubMed] [Google Scholar]
- Narmoneva DA, Wang JY, Setton LA. Nonuniform swelling-induced residual strains in articular cartilage. J Biomech. 1999;32:401–408. doi: 10.1016/s0021-9290(98)00184-5. [DOI] [PubMed] [Google Scholar]
- Neu CP, Hull ML, Walton JH, Buonocore MH. MRI-based technique for determining nonuniform deformations throughout the volume of articular cartilage explants. Magn Reson Med. 2005;53:321–328. doi: 10.1002/mrm.20343. [DOI] [PubMed] [Google Scholar]
- Panula HE, Hyttinen MM, Arokoski JP, Langsjo TK, Pelttari A, Kiviranta I, Helminen HJ. Articular cartilage superficial zone collagen birefringence reduced and cartilage thickness increased before surface fibrillation in experimental osteoarthritis. Ann Rheum Dis. 1998;57:237–245. doi: 10.1136/ard.57.4.237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S, Hung CT, Ateshian GA. Mechanical response of bovine articular cartilage under dynamic unconfined compression loading at physiological stress levels. Osteoarthritis Cartilage. 2004;12:65–73. doi: 10.1016/j.joca.2003.08.005. [DOI] [PubMed] [Google Scholar]
- Park S, Krishnan R, Nicoll SB, Ateshian GA. Cartilage interstitial fluid load support in unconfined compression. J Biomech. 2003;36:1785–1796. doi: 10.1016/s0021-9290(03)00231-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul JP. Force actions transmitted by joints in the human body. Proc R Soc Lond B Biol Sci. 1976;192:163–172. doi: 10.1098/rspb.1976.0004. [DOI] [PubMed] [Google Scholar]
- Poppen NK, Walker PS. Forces at the glenohumeral joint in abduction. Clin Orthop Relat Res. 1978:165–170. [PubMed] [Google Scholar]
- Rydell N. Biomechanics of the hip-joint. Clin Orthop Relat Res. 1973:6–15. doi: 10.1097/00003086-197305000-00003. [DOI] [PubMed] [Google Scholar]
- Schinagl RM, Gurskis D, Chen AC, Sah RL. Depth-dependent confined compression modulus of full-thickness bovine articular cartilage. J Orthop Res. 1997;15:499–506. doi: 10.1002/jor.1100150404. [DOI] [PubMed] [Google Scholar]
- Schinagl RM, Ting MK, Price JH, Sah RL. Video microscopy to quantitate the inhomogeneous equilibrium strain within articular cartilage during confined compression. Ann Biomed Eng. 1996;24:500–512. doi: 10.1007/BF02648112. [DOI] [PubMed] [Google Scholar]
- Setton LA, Mow VC, Muller FJ, Pita JC, Howell DS. Mechanical properties of canine articular cartilage are significantly altered following transection of the anterior cruciate ligament. J Orthop Res. 1994;12:451–463. doi: 10.1002/jor.1100120402. [DOI] [PubMed] [Google Scholar]
- Soltz MA, Ateshian GA. A Conewise Linear Elasticity mixture model for the analysis of tension-compression nonlinearity in articular cartilage. J Biomech Eng. 2000;122:576–586. doi: 10.1115/1.1324669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoop R, Buma P, van der Kraan PM, Hollander AP, Billinghurst RC, Meijers TH, Poole AR, van den Berg WB. Type II collagen degradation in articular cartilage fibrillation after anterior cruciate ligament transection in rats. Osteoarthritis Cartilage. 2001;9:308–315. doi: 10.1053/joca.2000.0390. [DOI] [PubMed] [Google Scholar]
- Suh JK, Youn I, Fu FH. An in situ calibration of an ultrasound transducer: a potential application for an ultrasonic indentation test of articular cartilage. J Biomech. 2001;34:1347–1353. doi: 10.1016/s0021-9290(01)00088-4. [DOI] [PubMed] [Google Scholar]
- Wachtel E, Maroudas A, Schneiderman R. Age-related changes in collagen packing of human articular cartilage. Biochim Biophys Acta. 1995;1243:239–243. doi: 10.1016/0304-4165(94)00134-j. [DOI] [PubMed] [Google Scholar]
- Wang CC, Chahine NO, Hung CT, Ateshian GA. Optical determination of anisotropic material properties of bovine articular cartilage in compression. J Biomech. 2003;36:339–353. doi: 10.1016/s0021-9290(02)00417-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang CC, Deng JM, Ateshian GA, Hung CT. An automated approach for direct measurement of two-dimensional strain distributions within articular cartilage under unconfined compression. J Biomech Eng. 2002;124:557–567. doi: 10.1115/1.1503795. [DOI] [PubMed] [Google Scholar]
- Wang CC, Hung CT, Mow VC. An analysis of the effects of depth-dependent aggregate modulus on articular cartilage stress-relaxation behavior in compression. J Biomech. 2001;34:75–84. doi: 10.1016/s0021-9290(00)00137-8. [DOI] [PubMed] [Google Scholar]
- Wayne JS, Brodrick CW, Mukherjee N. Measurement of articular cartilage thickness in the articulated knee. Ann Biomed Eng. 1998;26:96–102. doi: 10.1114/1.76. [DOI] [PubMed] [Google Scholar]
- Williamson AK, Chen AC, Masuda K, Thonar EJ, Sah RL. Tensile mechanical properties of bovine articular cartilage: variations with growth and relationships to collagen network components. J Orthop Res. 2003;21:872–880. doi: 10.1016/S0736-0266(03)00030-5. [DOI] [PubMed] [Google Scholar]