Hydrogen Atom Transfer Reactions of a Ruthenium Imidazole Complex: Hydrogen Tunneling and the Applicability of the Marcus Cross Relation

Abstract

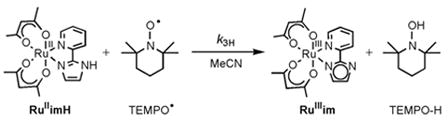
The reaction of Ru^II(acac)₂(py-imH) (Ru^IIimH) with TEMPO^• (2,2,6,6-tetramethyl-piperidine-1-oxyl radical) in MeCN quantitatively gives Ru^III(acac)₂(py-im) (Ru^IIIim) and the hydroxylamine TEMPO-H by transfer of H^• (H⁺ + e⁻) (acac = 2,4-pentanedionato, py-imH = 2-(2′-pyridyl)imidazole). Kinetic measurements of this reaction by UV-vis stopped-flow techniques indicate a bimolecular rate constant k_3H = 1400 ± 100 M⁻¹ s⁻¹ at 298 K. The reaction proceeds via a concerted hydrogen atom transfer (HAT) mechanism, as shown by ruling out the stepwise pathways of initial proton or electron transfer due to their very unfavorable thermochemistry (ΔG°). Deuterium transfer from Ru^II(acac)₂(py-imD) (Ru^IIimD) to TEMPO^• is surprisingly much slower at k_3D = 60 ± 7 M⁻¹ s⁻¹, with k_3H/k_3D = 23 ± 3 at 298 K. Temperature dependent measurements of this deuterium kinetic isotope effect (KIE) show a large difference between the apparent activation energies, E_a3D − E_a3H = 1.9 ± 0.8 kcal mol⁻¹. The large k_3H/k_3D and ΔE_a values appear to be greater than the semi-classical limits and thus suggest a tunneling mechanism. The self-exchange HAT reaction between Ru^IIimH and Ru^IIIim, measured by ¹H NMR line broadening, occurs with k_4H = (3.2 ± 0.3) × 10⁵ M⁻¹ s⁻¹ at 298 K and k_4H/k_4D = 1.5 ± 0.2. Despite the small KIE, tunneling is suggested by the ratio of Arrhenius pre-exponential factors, log(A_4H/A_4D) = −0.5 ± 0.3. These data provide a test of the applicability of the Marcus cross relation for H and D transfers, over a range of temperatures, for a reaction that involves substantial tunneling. The cross relation calculates rate constants for Ru^IIimH(D) + TEMPO^• that are greater than those observed: k_3H,calc/k_3H = 31 ± 4 and k_3D,calc/k_3D = 140 ± 20 at 298 K. In these rate constants and in the activation parameters, there is a better agreement with the Marcus cross relation for H than for D transfer, despite the greater prevalence of tunneling for H. The cross relation does not explicitly include tunneling, so close agreement should not be expected. In light of these results, the strengths and weaknesses of applying the cross relation to HAT reactions are discussed.

Introduction

Hydrogen atom transfer (HAT) – the transfer of a H^• (H⁺ + e⁻) from one reagent to another in a single kinetic step – is important in many chemical and biological processes.^1–6 Examples include reactions of alkoxyl,⁷ nitroxyl⁸ and other radicals, peroxidation of poly-unsaturated fatty acids by lipoxygenases,⁹ hydrocarbon oxidation by oxo-metal complexes,¹⁰ and terephthalic acid manufacture from p-xylene.¹¹ The involvement of transition metal ions in many of these processes has broadened the traditional view of HAT, which is now viewed as one subset of proton-coupled electron transfer (PCET) processes.^12–14

Rate constants of organic HAT reactions have traditionally been analyzed using the Evans-Polanyi correlation with enthalpic driving force and bond dissociation enthalpies.¹⁵ Our studies of transition metal reactions have shown that analyses of HAT processes should use free energies¹⁶ and that the Marcus cross relation (eq 1) gives reasonably accurate predictions in

$$k_{\text{XY}}=\sqrt{k_{\text{XX}}{k}_{\text{YY}}{K}_{\text{XY}}{f}_{\text{XY}}}$$ (1)

many cases^17,18 (even though it was originally developed for electron transfer¹⁹). The cross rate constant (k_XY) is calculated from the self-exchange rate constants (k_XX and k_YY, eq 2), equilibrium constant (K_XY), and a factor f_XY.^19,20 The cross relation holds well for a number of reactions of

$${\text{X}}^{•}+\text{HX}\stackrel{k_{\text{XX}}}{\to }\text{XH}+{\text{X}}^{•}$$ (2)

iron–tris(α-diimine) complexes, including the unusual inverse temperature dependence for the HAT reaction of [Fe^II(H₂bip)₃]²⁺ with TEMPO^• (H₂bip = 2,2′-bi-1,4,5,6-tetrahydropyrimidine).¹⁸ The cross relation has also been found to give good predictions – within one to two orders of magnitude – for some purely organic reactions¹⁷ and for reactions of ruthenium and vanadium-oxo compounds.²¹ However, larger deviations from the predictions of eq 1 have been found for osmium-anilido compounds²² and other systems.^17,23,24 Modern theoretical treatments of HAT and PCET are much more sophisticated, including non-adiabatic effects, hydrogen tunneling, and involvement of vibrational excited states.²⁵ They do not simply reduce to the cross relation. Bridging the gap between experimental systems and theoretical treatments is not simple because many of the parameters in the theories are not experimentally accessible.²⁶

This report describes what is perhaps the first comprehensive dataset for an HAT reaction: measurements of cross and self-exchange rate constants and equilibrium constants for both H and D as a function of temperature. To obtain such a dataset, we chose ruthenium complexes because of their substitution inertness and the accessibility of the Ru^II and Ru^III oxidation states. Complexes with a 2-(2′-pyridyl)imidazole (py-imH) ligand and two acac (2,4-pentanedionato) ligands have been prepared, and have the advantages of a single ionizable proton and accessible redox potentials.²⁷ Ru^II(acac)₂(py-imH) (Ru^IIimH) undergoes clean hydrogen atom transfer to excess TEMPO^• (transferring one proton and one electron) to give Ru^III(acac)₂(py-im) (Ru^IIIim) and TEMPO-H (eq 3),²⁷ making this reaction appropriate for HAT

(3)

studies and Marcus analysis. The deuterium transfer from Ru^II(acac)₂(py-imD) (Ru^IIimD) to TEMPO^• is much slower, with a large deuterium kinetic isotope effect (KIE), k_3H/k_3D = 23 ± 3 at 298 K. As discussed below, this and other results indicate that hydrogen tunneling is occurring. Tunneling is also implicated in the HAT self-exchange between Ru^IIimH and Ru^IIIim. Tunneling has come to be viewed as a seminal feature of hydrogen transfer reactions, from catalysis to laboratory reactions to enzymatic processes.¹ HAT from a fatty-acid substrate to the Fe^IIIOH active site in lipoxygenase enzymes, for instance, exhibits large k_H/k_D values of up to ~80.⁹ In light of the data reported here for ruthenium HAT reactions and the involvement of tunneling, the applicability of the Marcus cross relation is discussed.

Results

I. Equilibrium Constant Measurements

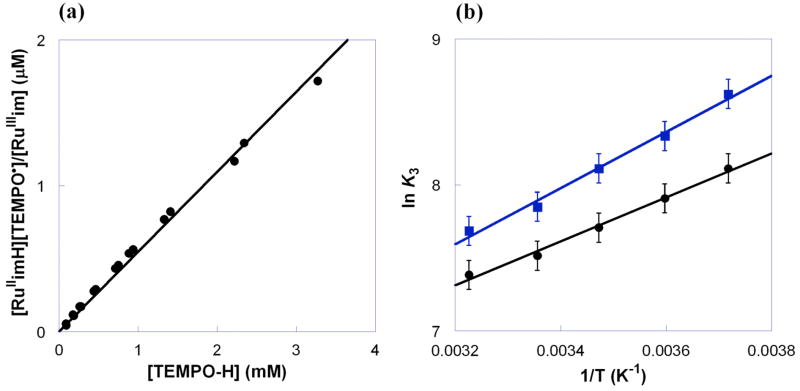
The reaction of Ru^IIimH with 1 equiv of TEMPO^• in CD₃CN at room temperature under N₂ rapidly yields Ru^IIIim and TEMPO-H (eq 3), as observed by ¹H NMR and UV-vis spectroscopies.²⁷ The equilibrium constant K_3H was determined by titrating a MeCN solution of Ru^IIIim (0.48 mM) with TEMPO-H (0.096–3.3 mM) in the reverse, uphill direction. Using the known ε values,²⁷ the optical spectra give the equilibrium concentrations of Ru^IIimH and Ru^IIIim. A plot of [Ru^IIimH][TEMPO^•]/[Ru^IIIim] vs. [TEMPO-H] (Figure 1a) is linear with a slope of 1/K_3H, yielding K_3H = (1.8 ± 0.2) × 10³ at 298 K and ΔG°_3H = −4.4 ± 0.1 kcal mol⁻¹. This is in excellent agreement with the ΔG°_3H of −4.5 ± 0.9 kcal mol⁻¹ derived from the difference in bond dissociation free energies (ΔBDFE) of Ru^IIimH and TEMPO-H, as determined from electrochemical and pK_a measurements.²⁷ The equilibrium constant for deuterium atom transfer in eq 3 was determined analogously to be K_3D = (2.5 ± 0.3) × 10³ (ΔG°_3D = −4.6 ± 0.1 kcal mol⁻¹), indicating an inverse equilibrium isotope effect of K_3H/K_3D = 0.72 ± 0.12 at 298 K. An inverse isotope effect is expected because reaction 3 converts a lower-frequency N–H bond into a higher-frequency O–H bond. Using measurements of ν_NH and ν_ND in Ru^IIimH(D) (KBr pellets) and ν_OH and ν_OD in TEMPO-H(D) (MeCN solution), K_H/K_D = 0.78 is calculated from a simple one-dimensional oscillator model.^28,29 van’t Hoff analysis of K_3H and K_3D values from 269–310 K gives ΔH°_3H = −3.0 ± 0.3 kcal mol⁻¹ and ΔS°_3H = 4.9 ± 1.1 cal mol⁻¹ K⁻¹, and ΔH°_3D = −3.8 ± 0.4 kcal mol⁻¹ and ΔS°_3D = 2.8 ± 1.5 cal mol⁻¹ K⁻¹ (Figure 1b).³⁰

Figure 1.

(a) Plot of [Ru^IIimH][TEMPO^•]/[Ru^IIIim] vs. [TEMPO-H], with the slope 1/K_3H = (5.5 ± 0.6) × 10⁻⁴ at 298 K and (b) van’t Hoff plot for Ru^IIimH(D) + TEMPO^• ⇌Ru^IIIim + TEMPO-H(D) (K_3H = ●, K_3D = ■) in MeCN.

II. Kinetic Measurements

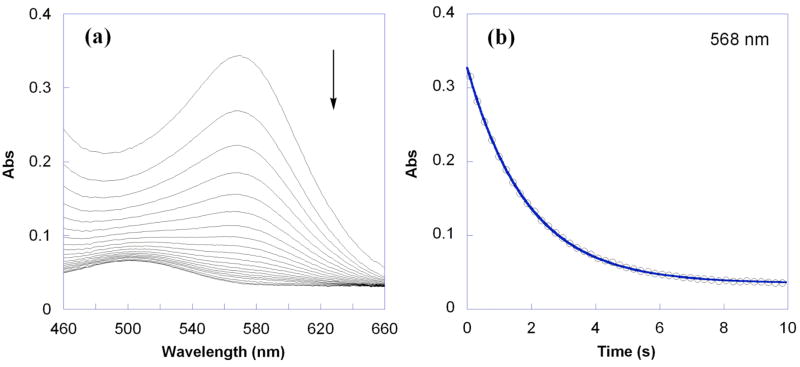
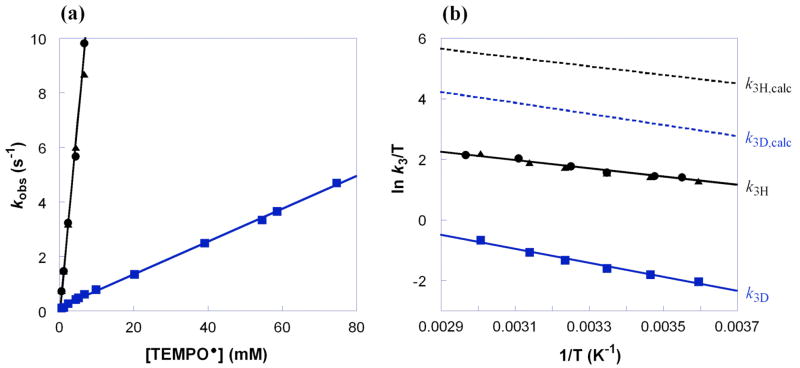
The kinetics for the HAT reaction of Ru^IIimH (0.047–0.053 mM) with TEMPO^• (0.53–6.7 mM) in MeCN at 298 K have been determined under pseudo-first order conditions (>10 equiv of TEMPO^• using stopped-flow optical measurements in the visible region). Ru^IIimH (λ_max = 568 nm, ε = 7000 M⁻¹ cm⁻¹) converts to Ru^IIIim (λ_max = 486 nm, ε = 1600 M⁻¹ cm⁻¹) in 90 ± 10% yield (Figure 2a); the absorbances of TEMPO^• and TEMPO-H are negligible in the observed spectral region at these concentrations. Global analysis of the spectra (460–660 nm) using SPECFIT software³¹ showed a good fit to a simple first order A → B model (Figure 2b), indicating that the rate is first order in [Ru^IIimH]. Plotting the derived pseudo-first order k_obs vs. the concentration of TEMPO^• yields a straight line (Figure 3a), showing that the rate is also first order in [TEMPO^•], and yields the bimolecular rate constant, k_3H = 1400 ± 100 M⁻¹ s⁻¹.

Figure 2.

(a) Overlay of UV-vis spectra for the reaction of Ru^IIimH (0.053 mM) with TEMPO^• (0.53 mM) in MeCN at 298 K over 10 s. (b) Absorbance at 568 nm showing the raw data (○) and first order A → B fit using SPECFIT (—).

Figure 3.

(a) Pseudo first order plot of k_obs vs. [TEMPO^•] at 298 K and (b) Eyring plot for the reactions of Ru^IIimH(D) with TEMPO^• in MeCN [k_3H = ● (no CH₃OH), ▲ (25 mM CH₃OH); k_3D = ■ (25 mM CD₃OD)]. The Eyring plot also shows the calculated k_3H,calc and k_3D,calc values in dashed lines (---) using the Marcus cross relation (see below).

The addition of CD₃OD to a solution of Ru^IIimH in CD₃CN rapidly exchanges the imidazole NH to form Ru^II(acac)₂(py-imD) (Ru^IIimD), so that the δ 11.3 NH resonance does not appear in the ¹H NMR spectrum. Ru^IIimD was therefore prepared in situ in the presence of >400 equiv CD₃OD (99.8% D from Cambridge Isotope Laboratories) in MeCN. The kinetics for Ru^IIimD (0.047–0.053 mM) plus excess TEMPO^• (0.53–75 mM) in MeCN (with 25 mM CD₃OD) at 298 K were measured as above to give k_3D = 60 ± 7 M⁻¹ s⁻¹ (Figure 3a). Thus, there is a large deuterium KIE of k_3H/k_3D = 23 ± 3 at 298 K. Measurements of k_3H and k_3D from 282–337 K (Figure 3b) give the Eyring and Arrhenius parameters shown in Table 1. The presence of 25 mM CH₃OH does not affect the rate constants or activation parameters for Ru^IIimH and TEMPO^• (Figure 3a), ruling out the presence of methanol as the cause of the much slower k_3D.

Table 1.

Rate Constants, Eyring and Arrhenius Parameters for H- and D-Atom Transfer Reactions.^a

Reaction	k (M−1 s−1)	ΔH‡b	ΔS‡c	Eab	log A
RuIIimH + TEMPO•	(1.4 ± 0.1) × 103	2.7 ± 0.5	−35 ± 4	3.3 ± 0.5	5.6 ± 0.3
RuIIimD + TEMPO•	60 ± 7	4.6 ± 0.6	−35 ± 5	5.2 ± 0.6	5.6 ± 0.4
RuIIimH + TEMPO• (calc)d	(4.3 ± 0.6) × 104	2.9 ± 0.4	−28 ± 2	3.5 ± 0.4	7.0 ± 0.2
RuIIimD + TEMPO• (calc)d	(8.4 ± 1.1) × 103	3.6 ± 0.5	−28 ± 3	4.2 ± 0.5	7.0 ± 0.3
RuIIimH + RuIIIim	(3.2 ± 0.3) × 105	4.7 ± 0.2	−17.4 ± 0.4	5.3 ± 0.2	9.4 ± 0.2
RuIIimD + RuIIIim	(2.1 ± 0.2) × 105	5.7 ± 0.3	−15.3 ± 0.5	6.3 ± 0.2	9.9 ± 0.2
TEMPO• + TEMPO-He	4.7 ± 1.0	3.8 ± 0.4	−43 ± 2	4.4 ± 0.4	3.8 ± 0.2
TEMPO• + TEMPO-De	0.20 ± 0.04	5.1 ± 0.4	−44 ± 2	5.7 ± 0.4	3.5 ± 0.2

^aIn MeCN at 298 K.

^bkcal mol⁻¹.

^ccal mol K⁻¹.

^dCalculated from the Marcus cross relation.

^eRefs. ¹⁸ and ³².

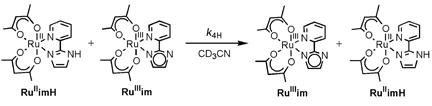
III. Self-Exchange Reactions of Ru^IIimH(D) plus Ru^IIIim

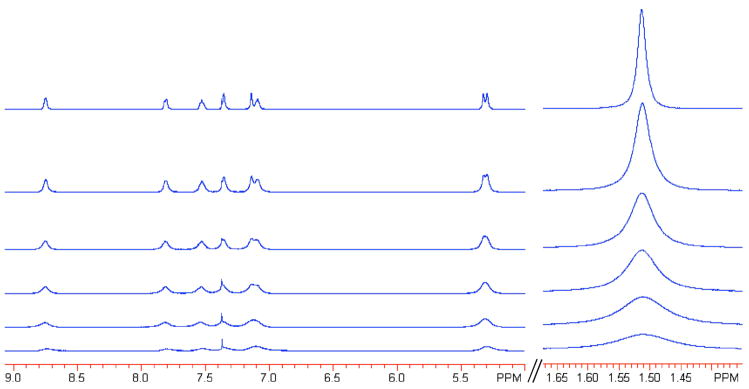
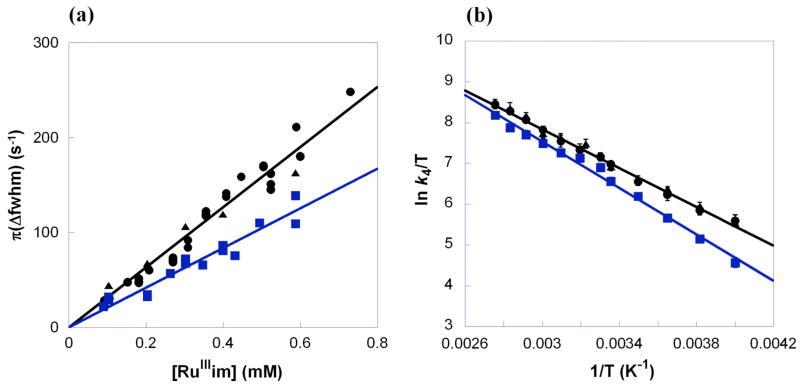
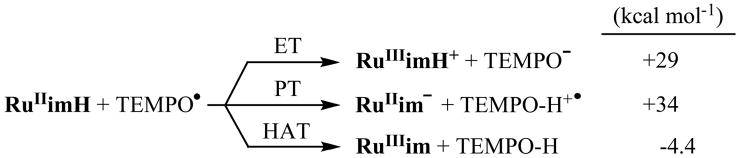
The diamagnetic ¹H NMR resonances of Ru^IIimH (2.0 mM) in CD₃CN broaden upon addition of small amounts of Ru^IIIim (0.092–0.73 mM), indicating exchange (self-exchange) between the two complexes (Figure 4, eq 4). The peaks broaden but do not shift, indicating that the NMR dynamics are in the slow-exchange limit.³³ The line width (fwhm) of the δ1.51 methyl resonance of Ru^IIimH in CD₃CN was determined by Lorentzian line fitting using NUTS software.^34,35 A plot of π(Δfwhm) vs. [Ru^IIIim] yields a straight line (Figure 5a), with a slope equal to the self-exchange rate constant,

Figure 4.

Partial ¹H NMR spectra of Ru^IIimH (2.0 mM, top spectrum) in CD₃CN at 298 K, showing line broadening with increasing concentrations of Ru^IIIim (0.092–0.73 mM).

Figure 5.

(a) Plot of π(Δfwhm) vs. [Ru^IIIim] at 298 K and (b) Eyring plot for the self-exchange reactions of Ru^IIimH(D) with Ru^IIIim in CD₃CN [k_4H = ● (no CH₃OH), ▲ (250 mM CH₃OH); k_4D = ■ (250 mM CD₃OD)].

(4)

k_4H = (3.2 ± 0.3) × 10⁵ M⁻¹ s⁻¹ at 298 K. The linewidths of the two overlapping CH-acac singlets (δ5.29, 5.32) and the pyridine doublet at δ8.75 were fitted (less precisely) using gNMR,³⁶ and analysis of their broadening gave the same rate constant as above within error. The broadening is uniform and proportional to the concentration of Ru^IIIim, which indicates that it is due to the self-exchange reaction. The deuterium self-exchange rate constant, Ru^IIimD + Ru^IIIim in CD₃CN with 250 mM CD₃OD was measured analogously to be k_4D = (2.1 ± 0.2) × 10⁵ M⁻¹ s⁻¹ (Figure 5a), so k_4H/k_4D = 1.5 ± 0.2 at 298 K. Activation parameters for the H and D self-exchange, determined from rate constants from 250–363 K (Figure 5b), are given in Table 1 and discussed below. As for reaction 3, the presence of 250 mM CH₃OH did not affect the protio rate constant or activation parameters within error (Figures 5a and 5b).

The mechanism of net H-atom self exchange could be concerted HAT or transfer of the electron and proton in two separate steps, as discussed below. As part of this mechanistic analysis, we have investigated the effect of solvent and of added base. The line broadening observed in a solution of Ru^IIimH (2.0 mM) and Ru^IIIim (0.040 mM) in CD₃CN is unaffected by the addition of Et₃N (0.020–0.10 mM). Since the rate of HAT self-exchange is unaffected by base, catalysis by trace acid²² is not occurring. The self-exchange rate constant k_4H was also measured in THF-d₈ and found to be an order of magnitude faster than in CD₃CN, (3.4 ± 1.0) × 10⁶ M⁻¹ s⁻¹ at 298 K. In these experiments, the initial resonances of Ru^IIimH were quite broad (for the methyl signal at δ1.48, fwhm = 16 Hz), indicating the presence of a trace amount of Ru^IIIimH⁺ and/or Ru^IIIim. Adding a small amount of Cp₂Co (0.011 mM) sharpened the signal to 5 Hz, by reduction of any Ru^III species. This solution gave the same measured self-exchange rate constant k_4H within error as the solution without Cp₂Co pretreatment, similarly indicating that catalysis by trace oxidized impurities is not occurring.

Discussion

The Ru^IIimH/Ru^IIIim system provides a unique opportunity to examine cross and self-exchange hydrogen and deuterium atom transfer reactions as a function of temperature. We first discuss the cross reaction of Ru^IIimH + TEMPO^• and its mechanism, then the self-exchange reaction and its pathway. The results are then used to discuss the applicability of the Marcus cross relation for HAT reactions, particularly for reactions involving significant tunneling.

I. HAT Reaction of Ru^IIimH(D) plus TEMPO^•

A. Mechanism

The reaction of Ru^IIimH + TEMPO^• → Ru^IIIim + TEMPO-H in MeCN (eq 3) could proceed through three possible pathways.^4a It could proceed via (i) initial electron transfer (ET) forming [Ru^III(acac)₂(py-imH)]⁺ (Ru^IIIimH⁺) and TEMPO⁻ intermediates, (ii) initial proton transfer (PT) forming [Ru^II(acac)₂(py-im)]⁻ (Ru^IIim⁻) and TEMPO-H^+•, or (iii) concerted HAT in a single kinetic step. The free energy changes for these three initial steps (Chart 1) can be calculated using the known thermochemistry of the ruthenium complexes²⁷ and TEMPO^•/TEMPO-H in MeCN.³⁷ These ground state energies, which are the minimum values of the free energies of activation ΔG^‡, rule out the initial ET and initial PT pathways because they are much larger than the measured barrier, ΔG^‡_3H = +13 kcal mol⁻¹ at 298 K. Thus reaction 3 must proceed by HAT, with ΔG°_3H =−4.4 kcal mol⁻¹. Similar arguments apply to the deuterium reaction. The unfavorable energetics of the ET and PT pathways are predominately due to high energy of the intermediates TEMPO-H^+• (very acidic, pK_a ≈ −3) and TEMPO⁻ (very reducing, E° ≈ −1.9 V vs. Cp₂Fe^+/0).³⁷ This kind of thermochemical analysis has been used to establish HAT mechanisms for a variety of reactions.^{4–6,12a,13,17–21,38}

Chart 1.

Ground state free energy changes for possible initial steps in reaction 3.

B. Tunneling

In the one dimensional semi-classical transition state limit, the ΔG^‡_D − ΔG^‡_H for a reaction is at most the difference in zero-point energies. The large observed k_3H/k_3D = 23 ± 3 at 298 K for reaction 3 is significantly greater than this semi-classical limit, k_H/k_D = 6.9 (calculated from ν_NH/ν_ND = 3068/2267 cm⁻¹ of Ru^IIimH(D)).^39,40 Taking into account other vibrational modes, the observed k_3H/k_3D is still twice as large as Bell’s estimate of the maximum semi-classical k_H/k_D ≈ 11 for reaction of an O–H bond at 298 K.³⁹ Bell also proposed that tunneling is indicated when E_aD − E_aH (= ΔH^‡_D − ΔH^‡_H) is larger than the difference in zero-point energies (1.1 kcal mol⁻¹ for Ru^IIimH vs. Ru^IIimD) and/or when the ratio of the protio and deutero pre-exponential factors deviate from unity: |log (A_H/A_D)| > 0.15 (A_H/A_D < 0.7 or A_H/A_D > 1.4).³⁹ For reaction 3, the E_a3D − E_a3H of 1.9 ± 0.8 kcal mol⁻¹ appears to be greater than the semi-classical limit, while log(A_3H/A_3D) = 0.0 ± 0.5 is within the limit. The k_3H/k_3D and E_a3D − E_a3H together indicate that hydrogen tunneling plays a significant role in this reaction.

Insight about the nature of the tunneling can be derived from the activation parameters using a model that considered four temperature regimes, as suggested by Klinman.⁴¹ In the high-temperature limit (region I), the reaction proceeds classically, without tunneling, and E_aD − E_aH and A_H/A_D are within the semi-classical limits. At somewhat lower temperatures (region II), hydrogen tunneling becomes significant (smaller E_aH and A_H) but D predominantly transfers over the barrier, so E_aD − E_aH is large and A_H ≪ A_D [log(A_H/A_D) < 0]. At the low-temperature limit (region IV), both hydrogen and deuterium tunnel extensively so that E_aD − E_aH is small and A_H ≫ A_D [log(A_H/A_D) > 0]. Since A_H is less than A_D in the limited tunneling region (II) but greater than A_D in the extensive tunneling regime (IV), there must be a crossover region (III) in which E_aD − E_aH is still larger than the semiclassical value, but A_H ≈ A_D [log(A_H/A_D) ≈ 0]. For reaction 3, the E_a3D − E_a3H = 1.9 ± 0.8 kcal mol⁻¹ and log(A_3H/A_3D) = 0.0 ± 0.5 values indicate a reaction that falls in region III, where there is extensive tunneling for the H-atom transfer and limited tunneling in the D-transfer reaction. The low A_3H and A_3D values (both 10^5.6 M⁻¹ s⁻¹) are also consistent with tunneling, since they are much lower than the typical bimolecular A values (10^8.5 to 10^11.5 M⁻¹ s⁻¹).^14d

Tunneling has been implicated in a number of metal-mediated HAT reactions and in a few cases the temperature dependence of the isotope effect has been measured. The closest analogy to reaction 3 are Meyer’s reactions of cis-[Ru^IV(bpy)₂(py)O]²⁺ with H₂O₂,⁴² hydroquinone,⁴³ and cis-[Ru^II(bpy)₂(py)(OH₂)]^{2+ 44} in H₂O vs. D₂O, which have quite similar KIEs and activation parameters (k_H/k_D = 16.1–28.7 at 298 K; ΔH^‡_D − ΔH^‡_H = 1.5–3.0 kcal mol⁻¹; |ΔS^‡_H − ΔS^‡_D| ≤ 2 cal mol⁻¹ K⁻¹ implying A_H ≈ A_D) [bpy = 2,2′-bipyridine, py = pyridine]. In contrast, quite different parameters are found for the intramolecular HAT reactions in the decay of Theopold’s cobalt μ-peroxo dimer [(Tp″Co)₂(μ-O₂)]⁴⁵ and Tolman’s μ-oxo copper dimers [(LCu)₂(μ-O)₂](ClO₄)₂⁴⁶ [Tp″ = hydridotris(3-isopropyl-5-methylpyrazolyl)borate; L = N,N′,N″-R₃triazacyclononane, R = CH₂Ph, ⁱPr]. Both of these reactions have large KIEs and large differences in barriers [(E_aD − E_aH)/kcal mol⁻¹ = 2.8 (Co), 2.5 and 1.9 (Cu)], and A_H < A_D [A_H/A_D = 0.13 (Co), 0.20 and 0.49 (Cu)], indicating more extensive tunneling for H than for D (region II of the Klinman model).⁴¹ Lipoxygenase enzymes show the unusual combination of temperature independent isotope effects (E_aD − E_aH close to zero) for reactions with significant activation energies (E_aH, E_aD ≫ 0), which suggests extensive tunneling by both H and D gated by protein motion.⁹ There are also many metal-mediated HAT reactions that show modest KIEs.^12a There is thus a substantial diversity in the tunneling behavior of HAT reactions, and no simple pattern based on structure or driving force is yet evident.

II. Self-Exchange Reaction: Ru^IIimH(D) + Ru^IIIim

A. Rate and Mechanism

The success of the Marcus cross relation (eq 1) for many HAT reactions has focused attention on degenerate self-exchange HAT reactions (eq 2).^{8g,17,47–51} In the adiabatic Marcus picture, the self-exchange reactions carry the intrinsic kinetic information.

For the reaction of Ru^IIimH and Ru^IIIim, the observed NMR line broadening could be due to a true HAT self-exchange reaction or could be the result of a stepwise ET-PT or PT-ET reaction, analogous to the discussion above. For such a self-exchange reaction, we have earlier shown that the stepwise ET-PT and PT-ET pathways have the same ΔG^‡ and rate constant, based on the principle of microscopic reversibility.⁴⁷ For the ET-PT pathway, the rate constant for the initial ET step (eq 5) can be estimated using the Marcus cross relation. This estimate requires the driving force for reaction 5, which is known from the relevant redox potentials,²⁷ and the ET

$$\mathbf{R}{\mathbf{u}}^{\mathbf{II}}\mathbf{imH}+\mathbf{R}{\mathbf{u}}^{\mathbf{III}}\mathbf{im}\stackrel{k_{\text{ET}}}{\to }\mathbf{R}{\mathbf{u}}^{\mathbf{III}}\mathbf{im}{\mathbf{H}}^{+}+\mathbf{R}{\mathbf{u}}^{\mathbf{II}}\mathbf{i}{\mathbf{m}}^{-}$$ (5)

self-exchange rate constant, which is well bracketed by known values for related compounds.⁵² Application of the cross relation predicts the rate constant: 5 × 10² M⁻¹ s⁻¹ < k_ET < 4 × 10⁵ M⁻¹ s⁻¹.⁵³ The measured Ru^IIimH + Ru^IIIim self-exchange k_4H = (3.2 ± 0.3) × 10⁵ M⁻¹ s⁻¹ lies toward the upper limit of the estimated ET rate constant. This means that it is unlikely but not impossible that the self-exchange reaction proceeds by initial ET. Similarly, the H/D isotope effect on the self-exchange rate constant, k_4H/k_4D = 1.5 ± 0.2 at 298 K, appears to be too large for rate-limiting outer-sphere ET but is not conclusive.

To distinguish between concerted and stepwise mechanisms, the self-exchange rate constant of Ru^IIimH plus Ru^IIIim was measured in the less polar solvent THF-d₈, and was found to be an order of magnitude faster than in CD₃CN. This is opposite to the expected effect if initial ET or PT were occurring: those paths would generate charged intermediates from the neutral reactants and therefore be less favorable in THF-d₈ than in CD₃CN.⁵⁴ An HAT path, however, would be expected to be faster in the poorer hydrogen bond accepting solvent THF.⁵⁴ Experiments described above also ruled out pathways catalyzed by trace acid (Ru^IIIimH⁺) or base (Ru^IIim⁻).⁵⁵ Thus the evidence, taken all together, indicates a concerted HAT mechanism for self-exchange.

The Ru^IIimH + Ru^IIIim self-exchange rate constant k_4H = (3.2 ± 0.3) × 10⁵ M⁻¹ s⁻¹ is close to those for a number of related reactions. HAT self-exchange and pseudo-self-exchange reactions interconverting polypyridyl-ruthenium oxo, hydroxo, and aquo complexes have rate constants from 7.6 × 10⁴ to 7.5 × 10⁵ M⁻¹ s⁻¹, the last for a reaction downhill by −2.5 kcal mol⁻¹ (Table 2; all self-exchange rate constants are corrected for statistical factors so as to be comparable).^21a,44,56 Iron biimidazoline and bipyrimidine systems have k_s.e. values a little slower (by 330 and 180 times) than k_4H, both in MeCN at 298 K.^47,48

Table 2.

Self-Exchange and Pseudo Self-Exchange HAT Rate Constants and Deuterium Kinetic Isotope Effects for Transition Metal Coordination Complexes.^a

Reaction	ΔG° b	kH (M−1 s−1) per H•	kH/kD	Reference
RuIIimH+ RuIIIimc	0	(3.2 ± 0.3) ×105	1.5 ± 0.2	this work
[FeII(H2bim)3]2+ + [FeIII(H2bim)2(Hbim)]2+c	0	(9.7 ± 0.1) ×102	2.4 ± 0.3d	47
[FeII(H2bip)3]2+ + [FeIII(H2bip)2(Hbip)]2+c	0	(1.8± 0.3) ×103	1.6± 0.5	48
[RuIII(bpy)2(py)(OH)]2+ + [RuIV(bpy)2(py)O]2+e	0	(7.6 ± 0.4) ×104	1.2 ± 0.1	21a
[RuII(bpy)2(py)(OH2)] 2+ + [RuIV(bpy)2(py)O]2+e	−2.5	(1.09± 0.02) × 105	16.1 ± 0.2	44
[RuII(tpy)(bpy)(OH2)]2+ + [RuIV(tpy)(bpy)O]2+e,f	−2.5	(7.45 ± 0.55) × 105	11.4 ± 1.3	56
[RuII(bpy)2(py)(OH2)]2+ + [RuIII(tpy)(bpy)(OH)]2+e	−1.3	(2.1 ± 0.1) ×105	5.8 ± 0.4	44
TpCl2OsIII(NH2Ph) + TpCl2OsIV(NHPh)c,g	0	(1.5 ± 1.0) ×10−3	ND	22
[VIV(4,4′-Me2bpy)2(O)(OH)]+ + [VV(4,4′-tBu2bpy)2(O)2]+c	~0	(6.5 ± 0.5) ×10−3	ND	21b

^aAt 298 K.

^bkcal mol⁻¹.

^cIn MeCN.

^dAt 324 K.

^eIn H₂O/D₂O; tpy = 2,2′:6′,2″-terpyridine.

^fOther analogous Ru(H₂O)/Ru(O) reactions, not shown in Table 2, have k_H = 2.1 × 10⁵ to 1.5 × 10⁶ M⁻¹ s⁻¹ per H^• and k_H/k_D = 9.8–12.3 at 298 K.⁵⁶

^gTp = hydrotris(pyrazolyl)borate.

Much slower HAT self-exchanges – by many orders of magnitude – have been observed between osmium aniline/anilide complexes,²² cobalt-biimidazoline complexes⁴⁸ and vanadium oxo/hydroxo complexes (Table 2).^21b The sluggishness of these reactions have been ascribed to large reorganization energies and/or to difficulty in assembly of the HAT precursor complexes, X–H···X. The cobalt reactions, for instance, are most likely slow because they interconvert high-spin Co^II and low-spin Co^III so that there is a large change in the Co–N bond lengths. The same issue could account for the iron-biimidazoline self-exchange (k_4H) being a bit slower than the Ru^IIimH + Ru^IIIim reaction reported here: the average difference in Fe–N bond lengths for [Fe^II(H₂bim)₃]²⁺ vs. [Fe^III(H₂bim)₂(Hbim)]²⁺ is 0.086(5) Å,⁴⁷ while the analogous difference in Ru–O and Ru–N bond lengths is only 0.026(8) Å.²⁷ On the other hand, the very slow self-exchange in the osmium aniline reaction was suggested to be due to a precursor complex that is disfavored both by sterics and by very weak OsNH···NOs hydrogen bonding.²² Differences in precursor complex formation could also play a role in comparing reactions of the neutral Ru^IIimH and Ru^IIIim species vs. the iron complexes. The electrostatic work required to bring two dicationic iron complexes together in MeCN (ionic strength = 0.1) can be estimated to be 1.4 kcal mol⁻¹,⁴⁷ which would lead to about an order of magnitude slower rate constant.

B. Kinetic Isotope Effects and Tunneling

The ruthenium HAT self-exchange reaction 4 has a small k_4H/k_4D = 1.5 ± 0.2 at 298 K, which is similar to those found in the iron biimidazoline and bipyrimidine systems (Table 2).^47,48 In the reactions of ruthenium polypyridyl oxo, hydroxo, and aquo complexes, the pseudo self-exchange reactions have substantial k_H/k_D values, 5.8–16.1,^44,56 while the KIE for “true” self-exchange is apparently much smaller (Table 2).^21a As noted above, activation parameters are a more direct probe of tunneling than KIE values. Ru^IIimH(D) + Ru^IIIim self-exchange shows substantial E_a4D − E_a4H = 1.0 ± 0.4 kcal mol⁻¹ (= ΔH^‡_4D − ΔH^‡_4H) and negative log(A_4H/A_4D) = −0.5 ± 0.3 values, which are perhaps surprising for a reaction with such a small k_4H/k_4D. The log(A_4H/A_4D) meets one of Bell’s tunneling criteria, log(A_H/A_D) < −0.15,³⁹ suggesting that hydrogen tunneling plays a role. A_4H being a factor of ~3 smaller than A_4D suggests that H tunnels more significantly than D (region II of the Klinman model).⁴¹ The ruthenium-oxo reactions with large KIEs also likely involve tunneling, as may the [Fe^II(H₂bip)₃]²⁺ + [Fe^III(H₂bip)₂(Hbip)]²⁺ reaction based on its log(A_H/A_D) = 0.9 ± 1.2.⁴⁸ Tunneling in the iron-biimidazoline and ruthenium-oxo self-exchange reactions has been analyzed in detail by Iordanova, Hammes-Schiffer et al. using their multistate continuum model, as is discussed below.^57,58

III. Applying the Marcus Cross Relation to Ru^IIimH(D) + TEMPO^•

The Marcus cross relation has been found to give fairly accurate predictions of HAT rate constants – within one to two orders of magnitude – for a number of systems.^17,18,21 It provides a framework for understanding HAT beyond the traditional Bell-Evans-Polanyi (BEP) correlation of rates with driving force. Unlike the BEP correlation, the cross relation is not limited to comparing similar reactions. However, the generality and limitations of using Marcus approach for HAT are not well understood. The measurements in this study provide a key test of the cross relation, for hydrogen and deuterium atom transfers as a function of temperature, in a system where tunneling is significant.

The calculated Marcus cross rate constant for Ru^IIimH(D) + TEMPO^• (k_3,calc, eq 6) is derived from the self-exchange rate constants k₄ and TEMPO-H(D)/TEMPO^• (k₇, eq 7),^18,32 the equilibrium constant (K₃), and f.^19,20 Reaction 7 has a large k_7H/k_7D = 24 ± 7 at 298 K and

$$k_{3,\text{calc}}=\sqrt{k_4{k}_7{K}_{3}f}$$ (6)

(7)

involves significant hydrogen tunneling (as described elsewhere³²). The calculated protio and deutero cross rate constants at 298 K are k_3H,calc = (4.3 ± 0.6) × 10⁴ M⁻¹ s⁻¹ and k_3D,calc = (8.4 ± 1.1) × 10³ M⁻¹ s⁻¹ (Table 1). Thus, the calculated rate constants for H and D are larger than the observed values by 31 ± 4 and 140 ± 20 times (= k_3,calc/k₃). These deviations of 1.5 and 2.1 orders of magnitude in applying the Marcus cross relation to HAT reaction 3 are greater than the deviations found for the two iron tris(α-diimine) systems plus TEMPO^•/TEMPO-H (k_calc/k_obs = 2.9 and 13).¹⁷

Activation parameters have been calculated by Eyring analysis (Figure 3b) of the calculated cross rate constants for H and D from 278–318 K using the measured self-exchange rates and equilibrium constants at different temperatures (Table 1).⁵⁹ For hydrogen transfer, the calculated ΔH^‡_3H,calc of 2.9 ± 0.4 kcal mol⁻¹ is in excellent agreement with the observed ΔH^‡_3H = 2.7 ± 0.5 kcal mol⁻¹. Thus, the factor of 31 deviation between k_3H and k_3H,calc is mainly due to the difference in the activation entropies, ΔS^‡_3H − ΔS^‡_3H,calc = −7 ± 4 cal mol⁻¹ K⁻¹. For deuterium, deviations appear to occur in both ΔH^‡_D and ΔS^‡_D terms: ΔH^‡_3D − ΔH^‡_3D,calc = 1.0 ± 0.8 kcal mol⁻¹ and ΔS^‡_3D − ΔS^‡_3D,calc = −7 ± 6 cal mol⁻¹ K⁻¹. Thus, for both the KIE and the activation parameters, the Marcus cross relation gives a better agreement for hydrogen than for deuterium. Interestingly, no effect of isotopic substitution is predicted or observed for the entropies/pre-exponential factors: ΔS^‡_3H = ΔS^‡_3D and log(A_3H/A_3D) ≅ 0 in both the observed and calculated values.

The Marcus calculated k_3H,calc/k_3D,calc = 5.1 ± 1.0 at 298 K and E_a3D,calc − E_a3H,calc = 0.7 ± 0.6 kcal mol⁻¹ are within the semi-classical limits,³⁹ and are smaller than the large observed k_3H/k_3D = 23 ± 3 and E_a3D − E_a3H = 1.9 ± 0.8 kcal mol⁻¹ values.

The Marcus cross relation was not derived for hydrogen atom transfer, although Marcus discussed it in this context in the 1960s.⁶⁰ From one perspective, the cross relation (eqs 1 and 6) can be viewed as little more than an interpolation, one step more sophisticated than a linear free energy relationship (LFER). It averages the kinetic information from the self-exchange rate constants and adjusts them by the overall free energy of reaction. However, the cross relation is more than an extended LFER because all of the parameters can be independently measured and have independent physical meaning. While LFERs are typically limited to a series of quite similar reactions, the cross relation has connected HAT reactions of O–H, N–H and C–H bonds, and connected purely organic and transition metal containing HAT reactions. In reaction 3, for instance, the cross reaction and one of the self-exchange reactions involve ruthenium imidazole/imidazolate complexes while the other self-exchange reaction involves only a nitroxyl and a hydroxylamine.

Recent years have seen much effort in theoretical treatments of reactions such as equation 3, which in this context would be called proton-coupled electron transfer reactions.²⁵ The most widely discussed approach, Hammes-Schiffer’s multistate continuum theory, includes a large number of effects, including the electronic coupling, the Frank-Condon overlaps between reactant and product vibrational wavefunctions in ground and excited states, different reorganization energies for each vibrational transition, and the dependence of most of these parameters on the proton donor-acceptor distance.^12g None of these are included in the cross relation. In the simple form used here, the cross relation does not explicitly include hydrogen tunneling, the possible non-adiabatic character of the reactions, the involvement of vibrational excited states, or the energetics of forming the precursor complexes. In this light, it is remarkable that the cross relation holds for HAT reactions as well as it does.

The cross relation often holds because of its inherent averaging. This has been discussed for electron transfer reactions that are significantly non-adiabatic or have different energetics for precursor complex formation (w_r).¹⁹ When reactions are non-adiabatic, there is a small probability of crossing from the reactant surface to the product (κ ≪ 1). Even when κ is not explicitly included, the cross relation will hold if κ for the cross reaction is close to the geometric mean of the κ’s for the self-exchange reactions. Tunneling presents a similar situation. Taking the simplistic perspective of tunneling as a correction to the transition state theory rate constant, the cross relation should hold when the tunneling contribution to the cross reaction XH + Y is close to the geometric mean of the tunneling contributions to the self-exchange reactions. There is, to our knowledge, no reason why there should be such a relationship among the tunneling contributions. Close adherence to the cross relation should not be expected for reactions in which there is a substantial contribution of tunneling.

In the chemistry described here, hydrogen tunneling is significant for the cross reaction Ru^IIimH(D) + TEMPO^• (eq 3) and for both of the self-exchange reactions (eqs 4 and 7). For all of these reactions, tunneling makes a larger contribution to the rate constant for H than for D. Given that the cross relation does not explicitly include tunneling, one would therefore expect a larger deviation for H-atom transfer than for D-transfer. For reaction 3, however, the agreement with the cross relation is better for H than for D. This suggests that tunneling may not be the primary reason for the 31- and 140-fold deviations observed. Because tunneling corrections are rarely much more than an order of magnitude for reactions near ambient temperatures, the interpolation inherent in the cross relation probably does not introduce errors larger than that order. These deviations observed for reaction 3 could be due to steric, non-adiabatic, and/or hydrogen bonding effects as well as tunneling.

A few words in defense of the cross relation for HAT are warranted. While it is not a sophisticated or by any means a complete treatment, in our view it captures the two most important features of an HAT reaction: the driving force ΔG° and the reorganization energy.⁴ Of all the HAT reactions we have examined, the largest deviation from the cross relation is a factor of about 300. While this is poor agreement for a LFER, it is still better than can typically be done with ab initio calculations, particularly for solution reactions with movement of charges, formation of hydrogen bonds, non-adiabatic effects, and significant hydrogen tunneling. In general, to understand the details of a reaction, such as the temperature dependence of the kinetic isotope effect or the influence of protein motions on HAT processes within an active site, the cross relation is not an adequate model. However, if the questions are why a reaction does or does not proceed, or why one reaction is orders of magnitude faster than another, in our view the cross relation proves a very valuable and very accessible approach to the answers.

Conclusions

The reaction of Ru^IIimH(D) + TEMPO^• (eq 3) and the self-exchange reaction Ru^IIimH(D) + Ru^IIIim (eq 4) both occur via a concerted HAT mechanism, rather than a stepwise H⁺/e⁻ pathway. Reaction 3 involves substantial tunneling as indicated by the large k_3H/k_3D = 23 ± 3 at 298 K and E_a3D − E_a3H = 1.9 ± 0.8 kcal mol⁻¹. Tunneling is also important in each of the self-exchange reactions, as indicated by the experimental activation parameters. This is the first system where H and D transfer rates have been measured for both cross and self-exchange reactions over a range of temperatures, allowing a detailed probe of the applicability of the Marcus cross relation. The rate constants for reaction 3 calculated using the cross relation are larger by 31 ± 4 and 140 ± 20 times at 298 K for hydrogen and deuterium, respectively. The cross relation does not predict the large observed k_3H/k_3D. Application of the cross relation over a range of temperatures gives a calculated ΔH^‡_3H,calc = 2.9 ± 0.4 kcal mol⁻¹ for H transfer that is in excellent agreement with the observed ΔH^‡_3H = 2.7 ± 0.5 kcal mol⁻¹; the primary deviation is in the activation entropy (ΔS^‡_3H − ΔS^‡_3H,calc = −7 ± 4 cal mol⁻¹ K⁻¹). For deuterium, there appear to be discrepancies in both the ΔH^‡_D and ΔS^‡_D.

The simple application of the cross relation does not explicitly account for hydrogen tunneling and therefore close agreement should not be expected. The cross relation includes only the driving force and the intrinsic barriers, the latter estimated from the self-exchange rates. The cross relation does have, however, some implicit averaging and even though tunneling is not included, it should hold if the effective tunneling correction for the cross relation is the mean of the corrections for the self-exchange reactions. In the case of Ru^IIimH(D) + TEMPO^• (eq 3), the agreement is better for H transfer than for D despite the greater tunneling for H, suggesting that tunneling is not the primary origin of the discrepancy from the cross relation prediction. While this study better defines the limitations of applying the cross relation to HAT reactions, it also illustrates the value of this approach. The cross relation succeeds as well as it does because if its inherent averaging and because it captures the effects of driving force and intrinsic barrier that are the two largest influences on the rate constant.

Experimental

Physical Techniques and Instrumentation

¹H NMR (500 MHz) spectra were recorded on a Bruker Avance spectrometer, referenced to a residual solvent peak. UV-vis spectra were acquired with a Hewlett-Packard 8453 diode array spectrophotometer in anhydrous MeCN, and are reported as λ_max/nm (ε/M⁻¹ cm⁻¹). UV-vis stopped-flow measurements were obtained on an OLIS RSM-1000 stopped-flow spectrophotometer. IR spectra were obtained as KBr pellets or as CD₃CN solution in a NaCl solution cell using a Bruker Vector 33 or Perkin-Elmer 1720 FT-IR spectrometer. All reactions were performed in the absence of air using glove box/vacuum line techniques.

Materials

All reagent grade solvents were purchased from Fisher Scientific, EMD Chemicals, or Honeywell Burdick & Jackson (anhydrous MeCN). MeCN was sparged with Ar and piped from a steel keg directly into a glove box. Deuterated solvents were obtained from Cambridge Isotope Laboratories. CD₃CN was dried over CaH₂, vacuum transferred to P₂O₅, then over to CaH₂, and then to an empty glass vessel. THF-d₈ was dried over Na/Ph₂CO. TEMPO^• (λ_max = 460 nm, ε = 10.3 M⁻¹ cm⁻¹)¹⁸ and Cp₂Co were purchased from Aldrich, and were sublimed onto a cold-finger before use. Ru^IIimH (λ_max = 568 nm, ε = 7000 M⁻¹ cm⁻¹),²⁷ Ru^IIIim (λ_max = 486 nm, ε = 1600 M⁻¹ cm⁻¹),²⁷ and TEMPO-H^18,61 were prepared according to literature procedures. TEMPO-D was prepared in 70% yield analogously to TEMPO-H, using (CD₃)₂CO/D₂O (99.9% D in D₂O) as the solvent. TEMPO-D deuteration was 98 ± 1%, as determined by NMR integration of the residual OH resonance (δ 5.34 in CD₃CN).

The errors on K₃, k₃, k₄, ΔH°₃, ΔS°₃ and the activation parameters are reported as 2σ, derived from the least-squares linear fits (using KaleidaGraph⁶²) to plots vs. [TEMPO-H(D)] or to the van’t Hoff, Eyring, or Arrhenius equations.

Ru^IIIim + TEMPO-H(D) ⇄ Ru^IIimH(D) + TEMPO^• Equilibrium Constant Measurements

Stock solutions of Ru^IIIim (0.48 mM) and TEMPO-H (240 mM) in MeCN were prepared inside a glove box. An aliquot of Ru^IIIim (2.5 mL) was transferred to a UV-vis cuvette, which was allowed to thermally equilibrate at 269–310 K. The solution was titrated with TEMPO-H (0.2–7 equiv, 10 μL = 0.2 equiv). UV-vis spectra were recorded for the initial Ru^IIIim, and after each addition of TEMPO-H when the solution has reached equilibrium. The UV-vis data were analyzed using the absorbance at 568 nm, yielding [Ru^IIimH]/[Ru^IIIim] = (A − A_RuIII)/(A_RuII − A), where A_RuII and A_RuIII are the absorbances for pure Ru^IIimH and Ru^IIIim at 568 nm (ε = 7000 M⁻¹ cm⁻¹ for Ru^IIimH, 670 M⁻¹ cm⁻¹ for Ru^IIIim).²⁷ By mass balance, [Ru^IIimH] = [TEMPO^•] = {((A − A_RuIII)/(A_RuII − A_RuIII)) × [Ru]_total}, and [TEMPO-H] = [TEMPO-H]_total – [TEMPO^•] = [TEMPO-H]_total − {((A − A_RuIII)/(A_RuII − A_RuIII)) × [Ru]_total}. Plotting [Ru^IIimH][TEMPO^•]/[Ru^IIIim] vs. [TEMPO-H] yielded a straight line, whose slope is the equilibrium constant for the uphill reaction: Ru^IIIim + TEMPO-H ⇄ Ru^IIimH + TEMPO^• (1/K_3H = (5.5 ± 0.6) × 10⁻⁴ at 298 K; Figure 1a). The deutero K_3D was determined analogously using TEMPO-D in MeCN.

Kinetic Measurements of Ru^IIimH(D) with TEMPO^•

Solutions of Ru^IIimH (0.093–0.11 mM) and TEMPO^• (1.1–13 mM) in MeCN were prepared and loaded into gas-tight syringes inside a N₂ glovebox. The stopped-flow apparatus was flushed with anhydrous MeCN, and a background spectrum was acquired. The syringes were immediately loaded onto the stopped-flow apparatus to minimize air exposure. The stopped-flow drive syringes were flushed with the reagents, then filled and allowed to thermally equilibrate. The contents of the two syringes were rapidly mixed at equal volume resulting in half of the original concentrations (0.047–0.053 mM Ru^IIimH and 0.53–6.7 mM TEMPO^•). A minimum of six kinetic runs were performed for each set of concentrations from 282–337 K. Kinetic data were fit to a first order A → B model over the entire spectral region (460–660 nm, Figure 2) using SPECFIT global analysis software.³¹ The derived k_obs for each TEMPO^• concentration was plotted vs. [TEMPO^•], and the slope of the straight line is the bimolecular rate constant k_3H (Figure 3a). The presence of CH₃OH (25 mM) in the reactions of Ru^IIimH (0.047–0.053 mM) and TEMPO^• (0.53–6.7 mM) from 278–333 K did not affect the same rate constant within error. The deuterium reaction was studied analogously (278–333 K) using syringes loaded with Ru^IIimD (0.093–0.11 mM), with 49 mM CD₃OD (99.8% D) as deuteration agent, and TEMPO• (1.1–150 mM).

Ru^IIimH(D)/Ru^IIIim Self-Exchange Measurements

Stock solutions of Ru^IIimH (2.0 mM, 4.5 mg in 5.0 mL) and Ru^IIIim (9.2 mM, 4.1 mg in 1.0 mL) in CD₃CN were prepared inside a N₂ glove box. Each of seven J-Young NMR tubes was loaded with Ru^IIimH solutions (0.5 mL), and 5–30 μL of Ru^IIIim solutions were added to six tubes to give Ru^IIIim concentrations of 0.092–0.73 mM, with one tube containing a solution of only Ru^IIimH. ¹H NMR spectra were obtained at 250–363 K for each tube. The CH₃-acac resonance (δ 1.51; initial fwhm = 2–4 Hz) of Ru^IIimH was Lorentzian line fitted using NUTS software³⁴ to determine the line width (fwhm) in each sample. Plotting π(Δfwhm) vs. [Ru^IIIim] yielded a straight line, where Δfwhm = [fwhm(Ru^IIimH/Ru^IIIim) − fwhm(Ru^IIimH)], and the slope is the self-exchange rate constant k_4H (Figure 5a). Experiments with Ru^IIimH (2.0 mM) with Ru^IIIim (0.10–0.59 mM) in the presence of CH₃OH (250 mM) in CD₃CN gave the same rate constant within error from 250–363 K. The deutero rate constant, k_4D was measured similarly using Ru^IIimD (2.0 mM) and Ru^IIIim (0.089–0.59 mM) in the presence of CD₃OD (250 mM) in CD₃CN at 250–363 K. The same procedure, line fitting the δ1.48 CH₃-acac resonance, was used to measure k_4H in THF-d₈ at 298 K for the reaction of Ru^IIimH (2.0 mM) [with and without pre-treatment with 0.011 mM Cp₂Co] and Ru^IIIim (0.011–0.16 mM).