Abstract
The reaction of RuII(acac)2(py-imH) (RuIIimH) with TEMPO• (2,2,6,6-tetramethyl-piperidine-1-oxyl radical) in MeCN quantitatively gives RuIII(acac)2(py-im) (RuIIIim) and the hydroxylamine TEMPO-H by transfer of H• (H+ + e−) (acac = 2,4-pentanedionato, py-imH = 2-(2′-pyridyl)imidazole). Kinetic measurements of this reaction by UV-vis stopped-flow techniques indicate a bimolecular rate constant k3H = 1400 ± 100 M−1 s−1 at 298 K. The reaction proceeds via a concerted hydrogen atom transfer (HAT) mechanism, as shown by ruling out the stepwise pathways of initial proton or electron transfer due to their very unfavorable thermochemistry (ΔG°). Deuterium transfer from RuII(acac)2(py-imD) (RuIIimD) to TEMPO• is surprisingly much slower at k3D = 60 ± 7 M−1 s−1, with k3H/k3D = 23 ± 3 at 298 K. Temperature dependent measurements of this deuterium kinetic isotope effect (KIE) show a large difference between the apparent activation energies, Ea3D − Ea3H = 1.9 ± 0.8 kcal mol−1. The large k3H/k3D and ΔEa values appear to be greater than the semi-classical limits and thus suggest a tunneling mechanism. The self-exchange HAT reaction between RuIIimH and RuIIIim, measured by 1H NMR line broadening, occurs with k4H = (3.2 ± 0.3) × 105 M−1 s−1 at 298 K and k4H/k4D = 1.5 ± 0.2. Despite the small KIE, tunneling is suggested by the ratio of Arrhenius pre-exponential factors, log(A4H/A4D) = −0.5 ± 0.3. These data provide a test of the applicability of the Marcus cross relation for H and D transfers, over a range of temperatures, for a reaction that involves substantial tunneling. The cross relation calculates rate constants for RuIIimH(D) + TEMPO• that are greater than those observed: k3H,calc/k3H = 31 ± 4 and k3D,calc/k3D = 140 ± 20 at 298 K. In these rate constants and in the activation parameters, there is a better agreement with the Marcus cross relation for H than for D transfer, despite the greater prevalence of tunneling for H. The cross relation does not explicitly include tunneling, so close agreement should not be expected. In light of these results, the strengths and weaknesses of applying the cross relation to HAT reactions are discussed.
Introduction
Hydrogen atom transfer (HAT) – the transfer of a H• (H+ + e−) from one reagent to another in a single kinetic step – is important in many chemical and biological processes.1–6 Examples include reactions of alkoxyl,7 nitroxyl8 and other radicals, peroxidation of poly-unsaturated fatty acids by lipoxygenases,9 hydrocarbon oxidation by oxo-metal complexes,10 and terephthalic acid manufacture from p-xylene.11 The involvement of transition metal ions in many of these processes has broadened the traditional view of HAT, which is now viewed as one subset of proton-coupled electron transfer (PCET) processes.12–14
Rate constants of organic HAT reactions have traditionally been analyzed using the Evans-Polanyi correlation with enthalpic driving force and bond dissociation enthalpies.15 Our studies of transition metal reactions have shown that analyses of HAT processes should use free energies16 and that the Marcus cross relation (eq 1) gives reasonably accurate predictions in
| (1) |
many cases17,18 (even though it was originally developed for electron transfer19). The cross rate constant (kXY) is calculated from the self-exchange rate constants (kXX and kYY, eq 2), equilibrium constant (KXY), and a factor fXY.19,20 The cross relation holds well for a number of reactions of
| (2) |
iron–tris(α-diimine) complexes, including the unusual inverse temperature dependence for the HAT reaction of [FeII(H2bip)3]2+ with TEMPO• (H2bip = 2,2′-bi-1,4,5,6-tetrahydropyrimidine).18 The cross relation has also been found to give good predictions – within one to two orders of magnitude – for some purely organic reactions17 and for reactions of ruthenium and vanadium-oxo compounds.21 However, larger deviations from the predictions of eq 1 have been found for osmium-anilido compounds22 and other systems.17,23,24 Modern theoretical treatments of HAT and PCET are much more sophisticated, including non-adiabatic effects, hydrogen tunneling, and involvement of vibrational excited states.25 They do not simply reduce to the cross relation. Bridging the gap between experimental systems and theoretical treatments is not simple because many of the parameters in the theories are not experimentally accessible.26
This report describes what is perhaps the first comprehensive dataset for an HAT reaction: measurements of cross and self-exchange rate constants and equilibrium constants for both H and D as a function of temperature. To obtain such a dataset, we chose ruthenium complexes because of their substitution inertness and the accessibility of the RuII and RuIII oxidation states. Complexes with a 2-(2′-pyridyl)imidazole (py-imH) ligand and two acac (2,4-pentanedionato) ligands have been prepared, and have the advantages of a single ionizable proton and accessible redox potentials.27 RuII(acac)2(py-imH) (RuIIimH) undergoes clean hydrogen atom transfer to excess TEMPO• (transferring one proton and one electron) to give RuIII(acac)2(py-im) (RuIIIim) and TEMPO-H (eq 3),27 making this reaction appropriate for HAT
 |
(3) |
studies and Marcus analysis. The deuterium transfer from RuII(acac)2(py-imD) (RuIIimD) to TEMPO• is much slower, with a large deuterium kinetic isotope effect (KIE), k3H/k3D = 23 ± 3 at 298 K. As discussed below, this and other results indicate that hydrogen tunneling is occurring. Tunneling is also implicated in the HAT self-exchange between RuIIimH and RuIIIim. Tunneling has come to be viewed as a seminal feature of hydrogen transfer reactions, from catalysis to laboratory reactions to enzymatic processes.1 HAT from a fatty-acid substrate to the FeIIIOH active site in lipoxygenase enzymes, for instance, exhibits large kH/kD values of up to ~80.9 In light of the data reported here for ruthenium HAT reactions and the involvement of tunneling, the applicability of the Marcus cross relation is discussed.
Results
I. Equilibrium Constant Measurements
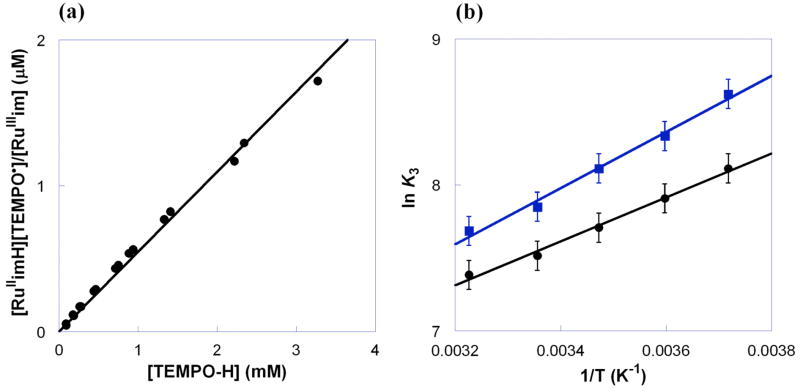
The reaction of RuIIimH with 1 equiv of TEMPO• in CD3CN at room temperature under N2 rapidly yields RuIIIim and TEMPO-H (eq 3), as observed by 1H NMR and UV-vis spectroscopies.27 The equilibrium constant K3H was determined by titrating a MeCN solution of RuIIIim (0.48 mM) with TEMPO-H (0.096–3.3 mM) in the reverse, uphill direction. Using the known ε values,27 the optical spectra give the equilibrium concentrations of RuIIimH and RuIIIim. A plot of [RuIIimH][TEMPO•]/[RuIIIim] vs. [TEMPO-H] (Figure 1a) is linear with a slope of 1/K3H, yielding K3H = (1.8 ± 0.2) × 103 at 298 K and ΔG°3H = −4.4 ± 0.1 kcal mol−1. This is in excellent agreement with the ΔG°3H of −4.5 ± 0.9 kcal mol−1 derived from the difference in bond dissociation free energies (ΔBDFE) of RuIIimH and TEMPO-H, as determined from electrochemical and pKa measurements.27 The equilibrium constant for deuterium atom transfer in eq 3 was determined analogously to be K3D = (2.5 ± 0.3) × 103 (ΔG°3D = −4.6 ± 0.1 kcal mol−1), indicating an inverse equilibrium isotope effect of K3H/K3D = 0.72 ± 0.12 at 298 K. An inverse isotope effect is expected because reaction 3 converts a lower-frequency N–H bond into a higher-frequency O–H bond. Using measurements of νNH and νND in RuIIimH(D) (KBr pellets) and νOH and νOD in TEMPO-H(D) (MeCN solution), KH/KD = 0.78 is calculated from a simple one-dimensional oscillator model.28,29 van’t Hoff analysis of K3H and K3D values from 269–310 K gives ΔH°3H = −3.0 ± 0.3 kcal mol−1 and ΔS°3H = 4.9 ± 1.1 cal mol−1 K−1, and ΔH°3D = −3.8 ± 0.4 kcal mol−1 and ΔS°3D = 2.8 ± 1.5 cal mol−1 K−1 (Figure 1b).30
Figure 1.
(a) Plot of [RuIIimH][TEMPO•]/[RuIIIim] vs. [TEMPO-H], with the slope 1/K3H = (5.5 ± 0.6) × 10−4 at 298 K and (b) van’t Hoff plot for RuIIimH(D) + TEMPO• ⇌RuIIIim + TEMPO-H(D) (K3H = ●, K3D = ■) in MeCN.
II. Kinetic Measurements
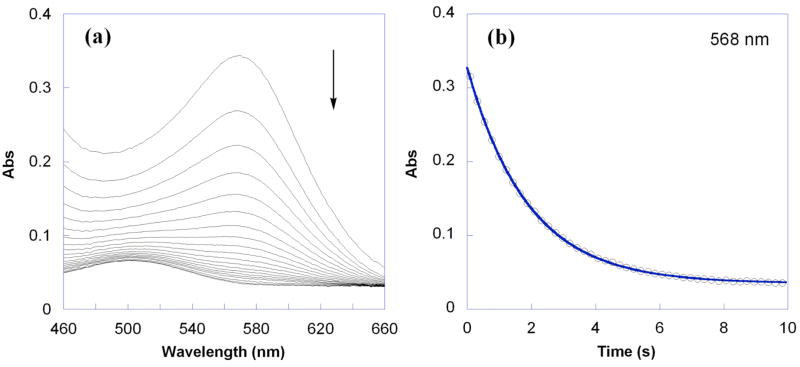
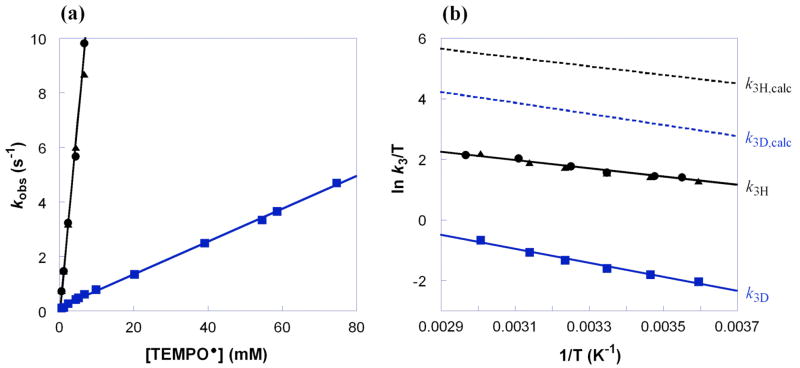
The kinetics for the HAT reaction of RuIIimH (0.047–0.053 mM) with TEMPO• (0.53–6.7 mM) in MeCN at 298 K have been determined under pseudo-first order conditions (>10 equiv of TEMPO• using stopped-flow optical measurements in the visible region). RuIIimH (λmax = 568 nm, ε = 7000 M−1 cm−1) converts to RuIIIim (λmax = 486 nm, ε = 1600 M−1 cm−1) in 90 ± 10% yield (Figure 2a); the absorbances of TEMPO• and TEMPO-H are negligible in the observed spectral region at these concentrations. Global analysis of the spectra (460–660 nm) using SPECFIT software31 showed a good fit to a simple first order A → B model (Figure 2b), indicating that the rate is first order in [RuIIimH]. Plotting the derived pseudo-first order kobs vs. the concentration of TEMPO• yields a straight line (Figure 3a), showing that the rate is also first order in [TEMPO•], and yields the bimolecular rate constant, k3H = 1400 ± 100 M−1 s−1.
Figure 2.
(a) Overlay of UV-vis spectra for the reaction of RuIIimH (0.053 mM) with TEMPO• (0.53 mM) in MeCN at 298 K over 10 s. (b) Absorbance at 568 nm showing the raw data (○) and first order A → B fit using SPECFIT (—).
Figure 3.
(a) Pseudo first order plot of kobs vs. [TEMPO•] at 298 K and (b) Eyring plot for the reactions of RuIIimH(D) with TEMPO• in MeCN [k3H = ● (no CH3OH), ▲ (25 mM CH3OH); k3D = ■ (25 mM CD3OD)]. The Eyring plot also shows the calculated k3H,calc and k3D,calc values in dashed lines (---) using the Marcus cross relation (see below).
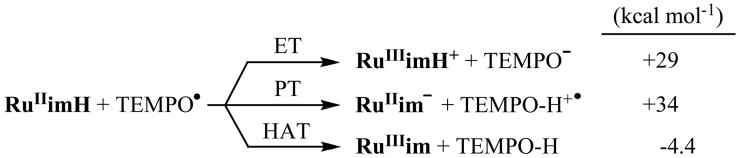
The addition of CD3OD to a solution of RuIIimH in CD3CN rapidly exchanges the imidazole NH to form RuII(acac)2(py-imD) (RuIIimD), so that the δ 11.3 NH resonance does not appear in the 1H NMR spectrum. RuIIimD was therefore prepared in situ in the presence of >400 equiv CD3OD (99.8% D from Cambridge Isotope Laboratories) in MeCN. The kinetics for RuIIimD (0.047–0.053 mM) plus excess TEMPO• (0.53–75 mM) in MeCN (with 25 mM CD3OD) at 298 K were measured as above to give k3D = 60 ± 7 M−1 s−1 (Figure 3a). Thus, there is a large deuterium KIE of k3H/k3D = 23 ± 3 at 298 K. Measurements of k3H and k3D from 282–337 K (Figure 3b) give the Eyring and Arrhenius parameters shown in Table 1. The presence of 25 mM CH3OH does not affect the rate constants or activation parameters for RuIIimH and TEMPO• (Figure 3a), ruling out the presence of methanol as the cause of the much slower k3D.
Table 1.
Rate Constants, Eyring and Arrhenius Parameters for H- and D-Atom Transfer Reactions.a
| Reaction | k (M−1 s−1) | ΔH‡b | ΔS‡c | Eab | log A |
|---|---|---|---|---|---|
| RuIIimH + TEMPO• | (1.4 ± 0.1) × 103 | 2.7 ± 0.5 | −35 ± 4 | 3.3 ± 0.5 | 5.6 ± 0.3 |
| RuIIimD + TEMPO• | 60 ± 7 | 4.6 ± 0.6 | −35 ± 5 | 5.2 ± 0.6 | 5.6 ± 0.4 |
| RuIIimH + TEMPO• (calc)d | (4.3 ± 0.6) × 104 | 2.9 ± 0.4 | −28 ± 2 | 3.5 ± 0.4 | 7.0 ± 0.2 |
| RuIIimD + TEMPO• (calc)d | (8.4 ± 1.1) × 103 | 3.6 ± 0.5 | −28 ± 3 | 4.2 ± 0.5 | 7.0 ± 0.3 |
| RuIIimH + RuIIIim | (3.2 ± 0.3) × 105 | 4.7 ± 0.2 | −17.4 ± 0.4 | 5.3 ± 0.2 | 9.4 ± 0.2 |
| RuIIimD + RuIIIim | (2.1 ± 0.2) × 105 | 5.7 ± 0.3 | −15.3 ± 0.5 | 6.3 ± 0.2 | 9.9 ± 0.2 |
| TEMPO• + TEMPO-He | 4.7 ± 1.0 | 3.8 ± 0.4 | −43 ± 2 | 4.4 ± 0.4 | 3.8 ± 0.2 |
| TEMPO• + TEMPO-De | 0.20 ± 0.04 | 5.1 ± 0.4 | −44 ± 2 | 5.7 ± 0.4 | 3.5 ± 0.2 |
III. Self-Exchange Reactions of RuIIimH(D) plus RuIIIim
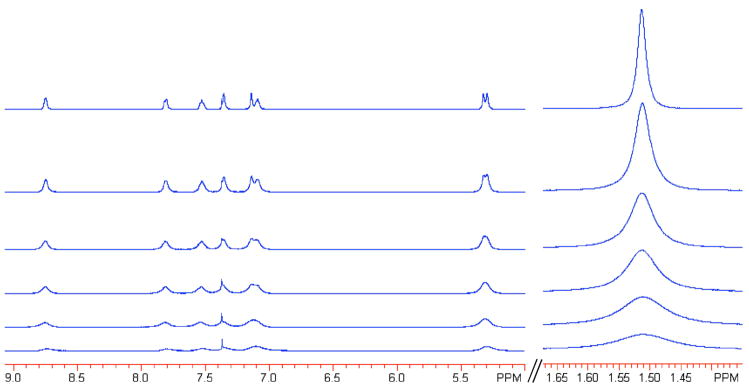
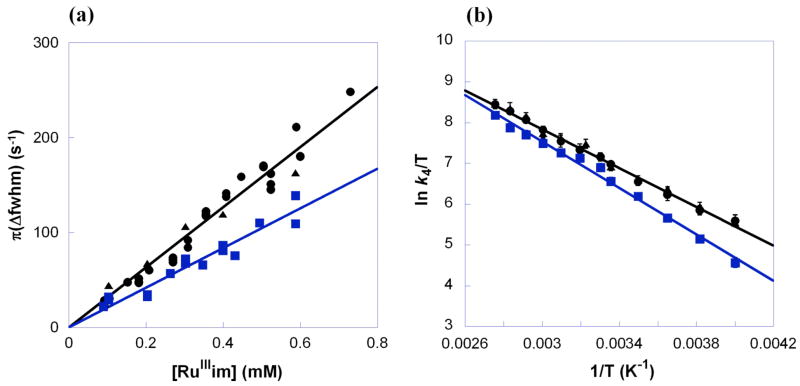
The diamagnetic 1H NMR resonances of RuIIimH (2.0 mM) in CD3CN broaden upon addition of small amounts of RuIIIim (0.092–0.73 mM), indicating exchange (self-exchange) between the two complexes (Figure 4, eq 4). The peaks broaden but do not shift, indicating that the NMR dynamics are in the slow-exchange limit.33 The line width (fwhm) of the δ1.51 methyl resonance of RuIIimH in CD3CN was determined by Lorentzian line fitting using NUTS software.34,35 A plot of π(Δfwhm) vs. [RuIIIim] yields a straight line (Figure 5a), with a slope equal to the self-exchange rate constant,
Figure 4.
Partial 1H NMR spectra of RuIIimH (2.0 mM, top spectrum) in CD3CN at 298 K, showing line broadening with increasing concentrations of RuIIIim (0.092–0.73 mM).
Figure 5.
(a) Plot of π(Δfwhm) vs. [RuIIIim] at 298 K and (b) Eyring plot for the self-exchange reactions of RuIIimH(D) with RuIIIim in CD3CN [k4H = ● (no CH3OH), ▲ (250 mM CH3OH); k4D = ■ (250 mM CD3OD)].
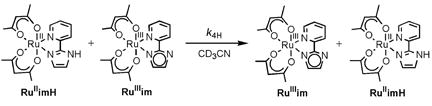 |
(4) |
k4H = (3.2 ± 0.3) × 105 M−1 s−1 at 298 K. The linewidths of the two overlapping CH-acac singlets (δ5.29, 5.32) and the pyridine doublet at δ8.75 were fitted (less precisely) using gNMR,36 and analysis of their broadening gave the same rate constant as above within error. The broadening is uniform and proportional to the concentration of RuIIIim, which indicates that it is due to the self-exchange reaction. The deuterium self-exchange rate constant, RuIIimD + RuIIIim in CD3CN with 250 mM CD3OD was measured analogously to be k4D = (2.1 ± 0.2) × 105 M−1 s−1 (Figure 5a), so k4H/k4D = 1.5 ± 0.2 at 298 K. Activation parameters for the H and D self-exchange, determined from rate constants from 250–363 K (Figure 5b), are given in Table 1 and discussed below. As for reaction 3, the presence of 250 mM CH3OH did not affect the protio rate constant or activation parameters within error (Figures 5a and 5b).
The mechanism of net H-atom self exchange could be concerted HAT or transfer of the electron and proton in two separate steps, as discussed below. As part of this mechanistic analysis, we have investigated the effect of solvent and of added base. The line broadening observed in a solution of RuIIimH (2.0 mM) and RuIIIim (0.040 mM) in CD3CN is unaffected by the addition of Et3N (0.020–0.10 mM). Since the rate of HAT self-exchange is unaffected by base, catalysis by trace acid22 is not occurring. The self-exchange rate constant k4H was also measured in THF-d8 and found to be an order of magnitude faster than in CD3CN, (3.4 ± 1.0) × 106 M−1 s−1 at 298 K. In these experiments, the initial resonances of RuIIimH were quite broad (for the methyl signal at δ1.48, fwhm = 16 Hz), indicating the presence of a trace amount of RuIIIimH+ and/or RuIIIim. Adding a small amount of Cp2Co (0.011 mM) sharpened the signal to 5 Hz, by reduction of any RuIII species. This solution gave the same measured self-exchange rate constant k4H within error as the solution without Cp2Co pretreatment, similarly indicating that catalysis by trace oxidized impurities is not occurring.
Discussion
The RuIIimH/RuIIIim system provides a unique opportunity to examine cross and self-exchange hydrogen and deuterium atom transfer reactions as a function of temperature. We first discuss the cross reaction of RuIIimH + TEMPO• and its mechanism, then the self-exchange reaction and its pathway. The results are then used to discuss the applicability of the Marcus cross relation for HAT reactions, particularly for reactions involving significant tunneling.
I. HAT Reaction of RuIIimH(D) plus TEMPO•
A. Mechanism
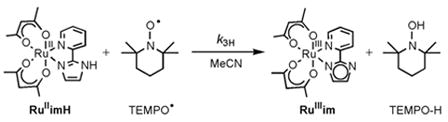
The reaction of RuIIimH + TEMPO• → RuIIIim + TEMPO-H in MeCN (eq 3) could proceed through three possible pathways.4a It could proceed via (i) initial electron transfer (ET) forming [RuIII(acac)2(py-imH)]+ (RuIIIimH+) and TEMPO− intermediates, (ii) initial proton transfer (PT) forming [RuII(acac)2(py-im)]− (RuIIim−) and TEMPO-H+•, or (iii) concerted HAT in a single kinetic step. The free energy changes for these three initial steps (Chart 1) can be calculated using the known thermochemistry of the ruthenium complexes27 and TEMPO•/TEMPO-H in MeCN.37 These ground state energies, which are the minimum values of the free energies of activation ΔG‡, rule out the initial ET and initial PT pathways because they are much larger than the measured barrier, ΔG‡3H = +13 kcal mol−1 at 298 K. Thus reaction 3 must proceed by HAT, with ΔG°3H =−4.4 kcal mol−1. Similar arguments apply to the deuterium reaction. The unfavorable energetics of the ET and PT pathways are predominately due to high energy of the intermediates TEMPO-H+• (very acidic, pKa ≈ −3) and TEMPO− (very reducing, E° ≈ −1.9 V vs. Cp2Fe+/0).37 This kind of thermochemical analysis has been used to establish HAT mechanisms for a variety of reactions.4–6,12a,13,17–21,38
Chart 1.
Ground state free energy changes for possible initial steps in reaction 3.
B. Tunneling
In the one dimensional semi-classical transition state limit, the ΔG‡D − ΔG‡H for a reaction is at most the difference in zero-point energies. The large observed k3H/k3D = 23 ± 3 at 298 K for reaction 3 is significantly greater than this semi-classical limit, kH/kD = 6.9 (calculated from νNH/νND = 3068/2267 cm−1 of RuIIimH(D)).39,40 Taking into account other vibrational modes, the observed k3H/k3D is still twice as large as Bell’s estimate of the maximum semi-classical kH/kD ≈ 11 for reaction of an O–H bond at 298 K.39 Bell also proposed that tunneling is indicated when EaD − EaH (= ΔH‡D − ΔH‡H) is larger than the difference in zero-point energies (1.1 kcal mol−1 for RuIIimH vs. RuIIimD) and/or when the ratio of the protio and deutero pre-exponential factors deviate from unity: |log (AH/AD)| > 0.15 (AH/AD < 0.7 or AH/AD > 1.4).39 For reaction 3, the Ea3D − Ea3H of 1.9 ± 0.8 kcal mol−1 appears to be greater than the semi-classical limit, while log(A3H/A3D) = 0.0 ± 0.5 is within the limit. The k3H/k3D and Ea3D − Ea3H together indicate that hydrogen tunneling plays a significant role in this reaction.
Insight about the nature of the tunneling can be derived from the activation parameters using a model that considered four temperature regimes, as suggested by Klinman.41 In the high-temperature limit (region I), the reaction proceeds classically, without tunneling, and EaD − EaH and AH/AD are within the semi-classical limits. At somewhat lower temperatures (region II), hydrogen tunneling becomes significant (smaller EaH and AH) but D predominantly transfers over the barrier, so EaD − EaH is large and AH ≪ AD [log(AH/AD) < 0]. At the low-temperature limit (region IV), both hydrogen and deuterium tunnel extensively so that EaD − EaH is small and AH ≫ AD [log(AH/AD) > 0]. Since AH is less than AD in the limited tunneling region (II) but greater than AD in the extensive tunneling regime (IV), there must be a crossover region (III) in which EaD − EaH is still larger than the semiclassical value, but AH ≈ AD [log(AH/AD) ≈ 0]. For reaction 3, the Ea3D − Ea3H = 1.9 ± 0.8 kcal mol−1 and log(A3H/A3D) = 0.0 ± 0.5 values indicate a reaction that falls in region III, where there is extensive tunneling for the H-atom transfer and limited tunneling in the D-transfer reaction. The low A3H and A3D values (both 105.6 M−1 s−1) are also consistent with tunneling, since they are much lower than the typical bimolecular A values (108.5 to 1011.5 M−1 s−1).14d
Tunneling has been implicated in a number of metal-mediated HAT reactions and in a few cases the temperature dependence of the isotope effect has been measured. The closest analogy to reaction 3 are Meyer’s reactions of cis-[RuIV(bpy)2(py)O]2+ with H2O2,42 hydroquinone,43 and cis-[RuII(bpy)2(py)(OH2)]2+ 44 in H2O vs. D2O, which have quite similar KIEs and activation parameters (kH/kD = 16.1–28.7 at 298 K; ΔH‡D − ΔH‡H = 1.5–3.0 kcal mol−1; |ΔS‡H − ΔS‡D| ≤ 2 cal mol−1 K−1 implying AH ≈ AD) [bpy = 2,2′-bipyridine, py = pyridine]. In contrast, quite different parameters are found for the intramolecular HAT reactions in the decay of Theopold’s cobalt μ-peroxo dimer [(Tp″Co)2(μ-O2)]45 and Tolman’s μ-oxo copper dimers [(LCu)2(μ-O)2](ClO4)246 [Tp″ = hydridotris(3-isopropyl-5-methylpyrazolyl)borate; L = N,N′,N″-R3triazacyclononane, R = CH2Ph, iPr]. Both of these reactions have large KIEs and large differences in barriers [(EaD − EaH)/kcal mol−1 = 2.8 (Co), 2.5 and 1.9 (Cu)], and AH < AD [AH/AD = 0.13 (Co), 0.20 and 0.49 (Cu)], indicating more extensive tunneling for H than for D (region II of the Klinman model).41 Lipoxygenase enzymes show the unusual combination of temperature independent isotope effects (EaD − EaH close to zero) for reactions with significant activation energies (EaH, EaD ≫ 0), which suggests extensive tunneling by both H and D gated by protein motion.9 There are also many metal-mediated HAT reactions that show modest KIEs.12a There is thus a substantial diversity in the tunneling behavior of HAT reactions, and no simple pattern based on structure or driving force is yet evident.
II. Self-Exchange Reaction: RuIIimH(D) + RuIIIim
A. Rate and Mechanism
The success of the Marcus cross relation (eq 1) for many HAT reactions has focused attention on degenerate self-exchange HAT reactions (eq 2).8g,17,47–51 In the adiabatic Marcus picture, the self-exchange reactions carry the intrinsic kinetic information.
For the reaction of RuIIimH and RuIIIim, the observed NMR line broadening could be due to a true HAT self-exchange reaction or could be the result of a stepwise ET-PT or PT-ET reaction, analogous to the discussion above. For such a self-exchange reaction, we have earlier shown that the stepwise ET-PT and PT-ET pathways have the same ΔG‡ and rate constant, based on the principle of microscopic reversibility.47 For the ET-PT pathway, the rate constant for the initial ET step (eq 5) can be estimated using the Marcus cross relation. This estimate requires the driving force for reaction 5, which is known from the relevant redox potentials,27 and the ET
| (5) |
self-exchange rate constant, which is well bracketed by known values for related compounds.52 Application of the cross relation predicts the rate constant: 5 × 102 M−1 s−1 < kET < 4 × 105 M−1 s−1.53 The measured RuIIimH + RuIIIim self-exchange k4H = (3.2 ± 0.3) × 105 M−1 s−1 lies toward the upper limit of the estimated ET rate constant. This means that it is unlikely but not impossible that the self-exchange reaction proceeds by initial ET. Similarly, the H/D isotope effect on the self-exchange rate constant, k4H/k4D = 1.5 ± 0.2 at 298 K, appears to be too large for rate-limiting outer-sphere ET but is not conclusive.
To distinguish between concerted and stepwise mechanisms, the self-exchange rate constant of RuIIimH plus RuIIIim was measured in the less polar solvent THF-d8, and was found to be an order of magnitude faster than in CD3CN. This is opposite to the expected effect if initial ET or PT were occurring: those paths would generate charged intermediates from the neutral reactants and therefore be less favorable in THF-d8 than in CD3CN.54 An HAT path, however, would be expected to be faster in the poorer hydrogen bond accepting solvent THF.54 Experiments described above also ruled out pathways catalyzed by trace acid (RuIIIimH+) or base (RuIIim−).55 Thus the evidence, taken all together, indicates a concerted HAT mechanism for self-exchange.
The RuIIimH + RuIIIim self-exchange rate constant k4H = (3.2 ± 0.3) × 105 M−1 s−1 is close to those for a number of related reactions. HAT self-exchange and pseudo-self-exchange reactions interconverting polypyridyl-ruthenium oxo, hydroxo, and aquo complexes have rate constants from 7.6 × 104 to 7.5 × 105 M−1 s−1, the last for a reaction downhill by −2.5 kcal mol−1 (Table 2; all self-exchange rate constants are corrected for statistical factors so as to be comparable).21a,44,56 Iron biimidazoline and bipyrimidine systems have ks.e. values a little slower (by 330 and 180 times) than k4H, both in MeCN at 298 K.47,48
Table 2.
Self-Exchange and Pseudo Self-Exchange HAT Rate Constants and Deuterium Kinetic Isotope Effects for Transition Metal Coordination Complexes.a
| Reaction | ΔG° b | kH (M−1 s−1) per H• | kH/kD | Reference |
|---|---|---|---|---|
| RuIIimH+ RuIIIimc | 0 | (3.2 ± 0.3) ×105 | 1.5 ± 0.2 | this work |
| [FeII(H2bim)3]2+ + [FeIII(H2bim)2(Hbim)]2+c | 0 | (9.7 ± 0.1) ×102 | 2.4 ± 0.3d | 47 |
| [FeII(H2bip)3]2+ + [FeIII(H2bip)2(Hbip)]2+c | 0 | (1.8± 0.3) ×103 | 1.6± 0.5 | 48 |
| [RuIII(bpy)2(py)(OH)]2+ + [RuIV(bpy)2(py)O]2+e | 0 | (7.6 ± 0.4) ×104 | 1.2 ± 0.1 | 21a |
| [RuII(bpy)2(py)(OH2)] 2+ + [RuIV(bpy)2(py)O]2+e | −2.5 | (1.09± 0.02) × 105 | 16.1 ± 0.2 | 44 |
| [RuII(tpy)(bpy)(OH2)]2+ + [RuIV(tpy)(bpy)O]2+e,f | −2.5 | (7.45 ± 0.55) × 105 | 11.4 ± 1.3 | 56 |
| [RuII(bpy)2(py)(OH2)]2+ + [RuIII(tpy)(bpy)(OH)]2+e | −1.3 | (2.1 ± 0.1) ×105 | 5.8 ± 0.4 | 44 |
| TpCl2OsIII(NH2Ph) + TpCl2OsIV(NHPh)c,g | 0 | (1.5 ± 1.0) ×10−3 | ND | 22 |
| [VIV(4,4′-Me2bpy)2(O)(OH)]+ + [VV(4,4′-tBu2bpy)2(O)2]+c | ~0 | (6.5 ± 0.5) ×10−3 | ND | 21b |
Much slower HAT self-exchanges – by many orders of magnitude – have been observed between osmium aniline/anilide complexes,22 cobalt-biimidazoline complexes48 and vanadium oxo/hydroxo complexes (Table 2).21b The sluggishness of these reactions have been ascribed to large reorganization energies and/or to difficulty in assembly of the HAT precursor complexes, X–H···X. The cobalt reactions, for instance, are most likely slow because they interconvert high-spin CoII and low-spin CoIII so that there is a large change in the Co–N bond lengths. The same issue could account for the iron-biimidazoline self-exchange (k4H) being a bit slower than the RuIIimH + RuIIIim reaction reported here: the average difference in Fe–N bond lengths for [FeII(H2bim)3]2+ vs. [FeIII(H2bim)2(Hbim)]2+ is 0.086(5) Å,47 while the analogous difference in Ru–O and Ru–N bond lengths is only 0.026(8) Å.27 On the other hand, the very slow self-exchange in the osmium aniline reaction was suggested to be due to a precursor complex that is disfavored both by sterics and by very weak OsNH···NOs hydrogen bonding.22 Differences in precursor complex formation could also play a role in comparing reactions of the neutral RuIIimH and RuIIIim species vs. the iron complexes. The electrostatic work required to bring two dicationic iron complexes together in MeCN (ionic strength = 0.1) can be estimated to be 1.4 kcal mol−1,47 which would lead to about an order of magnitude slower rate constant.
B. Kinetic Isotope Effects and Tunneling
The ruthenium HAT self-exchange reaction 4 has a small k4H/k4D = 1.5 ± 0.2 at 298 K, which is similar to those found in the iron biimidazoline and bipyrimidine systems (Table 2).47,48 In the reactions of ruthenium polypyridyl oxo, hydroxo, and aquo complexes, the pseudo self-exchange reactions have substantial kH/kD values, 5.8–16.1,44,56 while the KIE for “true” self-exchange is apparently much smaller (Table 2).21a As noted above, activation parameters are a more direct probe of tunneling than KIE values. RuIIimH(D) + RuIIIim self-exchange shows substantial Ea4D − Ea4H = 1.0 ± 0.4 kcal mol−1 (= ΔH‡4D − ΔH‡4H) and negative log(A4H/A4D) = −0.5 ± 0.3 values, which are perhaps surprising for a reaction with such a small k4H/k4D. The log(A4H/A4D) meets one of Bell’s tunneling criteria, log(AH/AD) < −0.15,39 suggesting that hydrogen tunneling plays a role. A4H being a factor of ~3 smaller than A4D suggests that H tunnels more significantly than D (region II of the Klinman model).41 The ruthenium-oxo reactions with large KIEs also likely involve tunneling, as may the [FeII(H2bip)3]2+ + [FeIII(H2bip)2(Hbip)]2+ reaction based on its log(AH/AD) = 0.9 ± 1.2.48 Tunneling in the iron-biimidazoline and ruthenium-oxo self-exchange reactions has been analyzed in detail by Iordanova, Hammes-Schiffer et al. using their multistate continuum model, as is discussed below.57,58
III. Applying the Marcus Cross Relation to RuIIimH(D) + TEMPO•
The Marcus cross relation has been found to give fairly accurate predictions of HAT rate constants – within one to two orders of magnitude – for a number of systems.17,18,21 It provides a framework for understanding HAT beyond the traditional Bell-Evans-Polanyi (BEP) correlation of rates with driving force. Unlike the BEP correlation, the cross relation is not limited to comparing similar reactions. However, the generality and limitations of using Marcus approach for HAT are not well understood. The measurements in this study provide a key test of the cross relation, for hydrogen and deuterium atom transfers as a function of temperature, in a system where tunneling is significant.
The calculated Marcus cross rate constant for RuIIimH(D) + TEMPO• (k3,calc, eq 6) is derived from the self-exchange rate constants k4 and TEMPO-H(D)/TEMPO• (k7, eq 7),18,32 the equilibrium constant (K3), and f.19,20 Reaction 7 has a large k7H/k7D = 24 ± 7 at 298 K and
| (6) |
 |
(7) |
involves significant hydrogen tunneling (as described elsewhere32). The calculated protio and deutero cross rate constants at 298 K are k3H,calc = (4.3 ± 0.6) × 104 M−1 s−1 and k3D,calc = (8.4 ± 1.1) × 103 M−1 s−1 (Table 1). Thus, the calculated rate constants for H and D are larger than the observed values by 31 ± 4 and 140 ± 20 times (= k3,calc/k3). These deviations of 1.5 and 2.1 orders of magnitude in applying the Marcus cross relation to HAT reaction 3 are greater than the deviations found for the two iron tris(α-diimine) systems plus TEMPO•/TEMPO-H (kcalc/kobs = 2.9 and 13).17
Activation parameters have been calculated by Eyring analysis (Figure 3b) of the calculated cross rate constants for H and D from 278–318 K using the measured self-exchange rates and equilibrium constants at different temperatures (Table 1).59 For hydrogen transfer, the calculated ΔH‡3H,calc of 2.9 ± 0.4 kcal mol−1 is in excellent agreement with the observed ΔH‡3H = 2.7 ± 0.5 kcal mol−1. Thus, the factor of 31 deviation between k3H and k3H,calc is mainly due to the difference in the activation entropies, ΔS‡3H − ΔS‡3H,calc = −7 ± 4 cal mol−1 K−1. For deuterium, deviations appear to occur in both ΔH‡D and ΔS‡D terms: ΔH‡3D − ΔH‡3D,calc = 1.0 ± 0.8 kcal mol−1 and ΔS‡3D − ΔS‡3D,calc = −7 ± 6 cal mol−1 K−1. Thus, for both the KIE and the activation parameters, the Marcus cross relation gives a better agreement for hydrogen than for deuterium. Interestingly, no effect of isotopic substitution is predicted or observed for the entropies/pre-exponential factors: ΔS‡3H = ΔS‡3D and log(A3H/A3D) ≅ 0 in both the observed and calculated values.
The Marcus calculated k3H,calc/k3D,calc = 5.1 ± 1.0 at 298 K and Ea3D,calc − Ea3H,calc = 0.7 ± 0.6 kcal mol−1 are within the semi-classical limits,39 and are smaller than the large observed k3H/k3D = 23 ± 3 and Ea3D − Ea3H = 1.9 ± 0.8 kcal mol−1 values.
The Marcus cross relation was not derived for hydrogen atom transfer, although Marcus discussed it in this context in the 1960s.60 From one perspective, the cross relation (eqs 1 and 6) can be viewed as little more than an interpolation, one step more sophisticated than a linear free energy relationship (LFER). It averages the kinetic information from the self-exchange rate constants and adjusts them by the overall free energy of reaction. However, the cross relation is more than an extended LFER because all of the parameters can be independently measured and have independent physical meaning. While LFERs are typically limited to a series of quite similar reactions, the cross relation has connected HAT reactions of O–H, N–H and C–H bonds, and connected purely organic and transition metal containing HAT reactions. In reaction 3, for instance, the cross reaction and one of the self-exchange reactions involve ruthenium imidazole/imidazolate complexes while the other self-exchange reaction involves only a nitroxyl and a hydroxylamine.
Recent years have seen much effort in theoretical treatments of reactions such as equation 3, which in this context would be called proton-coupled electron transfer reactions.25 The most widely discussed approach, Hammes-Schiffer’s multistate continuum theory, includes a large number of effects, including the electronic coupling, the Frank-Condon overlaps between reactant and product vibrational wavefunctions in ground and excited states, different reorganization energies for each vibrational transition, and the dependence of most of these parameters on the proton donor-acceptor distance.12g None of these are included in the cross relation. In the simple form used here, the cross relation does not explicitly include hydrogen tunneling, the possible non-adiabatic character of the reactions, the involvement of vibrational excited states, or the energetics of forming the precursor complexes. In this light, it is remarkable that the cross relation holds for HAT reactions as well as it does.
The cross relation often holds because of its inherent averaging. This has been discussed for electron transfer reactions that are significantly non-adiabatic or have different energetics for precursor complex formation (wr).19 When reactions are non-adiabatic, there is a small probability of crossing from the reactant surface to the product (κ ≪ 1). Even when κ is not explicitly included, the cross relation will hold if κ for the cross reaction is close to the geometric mean of the κ’s for the self-exchange reactions. Tunneling presents a similar situation. Taking the simplistic perspective of tunneling as a correction to the transition state theory rate constant, the cross relation should hold when the tunneling contribution to the cross reaction XH + Y is close to the geometric mean of the tunneling contributions to the self-exchange reactions. There is, to our knowledge, no reason why there should be such a relationship among the tunneling contributions. Close adherence to the cross relation should not be expected for reactions in which there is a substantial contribution of tunneling.
In the chemistry described here, hydrogen tunneling is significant for the cross reaction RuIIimH(D) + TEMPO• (eq 3) and for both of the self-exchange reactions (eqs 4 and 7). For all of these reactions, tunneling makes a larger contribution to the rate constant for H than for D. Given that the cross relation does not explicitly include tunneling, one would therefore expect a larger deviation for H-atom transfer than for D-transfer. For reaction 3, however, the agreement with the cross relation is better for H than for D. This suggests that tunneling may not be the primary reason for the 31- and 140-fold deviations observed. Because tunneling corrections are rarely much more than an order of magnitude for reactions near ambient temperatures, the interpolation inherent in the cross relation probably does not introduce errors larger than that order. These deviations observed for reaction 3 could be due to steric, non-adiabatic, and/or hydrogen bonding effects as well as tunneling.
A few words in defense of the cross relation for HAT are warranted. While it is not a sophisticated or by any means a complete treatment, in our view it captures the two most important features of an HAT reaction: the driving force ΔG° and the reorganization energy.4 Of all the HAT reactions we have examined, the largest deviation from the cross relation is a factor of about 300. While this is poor agreement for a LFER, it is still better than can typically be done with ab initio calculations, particularly for solution reactions with movement of charges, formation of hydrogen bonds, non-adiabatic effects, and significant hydrogen tunneling. In general, to understand the details of a reaction, such as the temperature dependence of the kinetic isotope effect or the influence of protein motions on HAT processes within an active site, the cross relation is not an adequate model. However, if the questions are why a reaction does or does not proceed, or why one reaction is orders of magnitude faster than another, in our view the cross relation proves a very valuable and very accessible approach to the answers.
Conclusions
The reaction of RuIIimH(D) + TEMPO• (eq 3) and the self-exchange reaction RuIIimH(D) + RuIIIim (eq 4) both occur via a concerted HAT mechanism, rather than a stepwise H+/e− pathway. Reaction 3 involves substantial tunneling as indicated by the large k3H/k3D = 23 ± 3 at 298 K and Ea3D − Ea3H = 1.9 ± 0.8 kcal mol−1. Tunneling is also important in each of the self-exchange reactions, as indicated by the experimental activation parameters. This is the first system where H and D transfer rates have been measured for both cross and self-exchange reactions over a range of temperatures, allowing a detailed probe of the applicability of the Marcus cross relation. The rate constants for reaction 3 calculated using the cross relation are larger by 31 ± 4 and 140 ± 20 times at 298 K for hydrogen and deuterium, respectively. The cross relation does not predict the large observed k3H/k3D. Application of the cross relation over a range of temperatures gives a calculated ΔH‡3H,calc = 2.9 ± 0.4 kcal mol−1 for H transfer that is in excellent agreement with the observed ΔH‡3H = 2.7 ± 0.5 kcal mol−1; the primary deviation is in the activation entropy (ΔS‡3H − ΔS‡3H,calc = −7 ± 4 cal mol−1 K−1). For deuterium, there appear to be discrepancies in both the ΔH‡D and ΔS‡D.
The simple application of the cross relation does not explicitly account for hydrogen tunneling and therefore close agreement should not be expected. The cross relation includes only the driving force and the intrinsic barriers, the latter estimated from the self-exchange rates. The cross relation does have, however, some implicit averaging and even though tunneling is not included, it should hold if the effective tunneling correction for the cross relation is the mean of the corrections for the self-exchange reactions. In the case of RuIIimH(D) + TEMPO• (eq 3), the agreement is better for H transfer than for D despite the greater tunneling for H, suggesting that tunneling is not the primary origin of the discrepancy from the cross relation prediction. While this study better defines the limitations of applying the cross relation to HAT reactions, it also illustrates the value of this approach. The cross relation succeeds as well as it does because if its inherent averaging and because it captures the effects of driving force and intrinsic barrier that are the two largest influences on the rate constant.
Experimental
Physical Techniques and Instrumentation
1H NMR (500 MHz) spectra were recorded on a Bruker Avance spectrometer, referenced to a residual solvent peak. UV-vis spectra were acquired with a Hewlett-Packard 8453 diode array spectrophotometer in anhydrous MeCN, and are reported as λmax/nm (ε/M−1 cm−1). UV-vis stopped-flow measurements were obtained on an OLIS RSM-1000 stopped-flow spectrophotometer. IR spectra were obtained as KBr pellets or as CD3CN solution in a NaCl solution cell using a Bruker Vector 33 or Perkin-Elmer 1720 FT-IR spectrometer. All reactions were performed in the absence of air using glove box/vacuum line techniques.
Materials
All reagent grade solvents were purchased from Fisher Scientific, EMD Chemicals, or Honeywell Burdick & Jackson (anhydrous MeCN). MeCN was sparged with Ar and piped from a steel keg directly into a glove box. Deuterated solvents were obtained from Cambridge Isotope Laboratories. CD3CN was dried over CaH2, vacuum transferred to P2O5, then over to CaH2, and then to an empty glass vessel. THF-d8 was dried over Na/Ph2CO. TEMPO• (λmax = 460 nm, ε = 10.3 M−1 cm−1)18 and Cp2Co were purchased from Aldrich, and were sublimed onto a cold-finger before use. RuIIimH (λmax = 568 nm, ε = 7000 M−1 cm−1),27 RuIIIim (λmax = 486 nm, ε = 1600 M−1 cm−1),27 and TEMPO-H18,61 were prepared according to literature procedures. TEMPO-D was prepared in 70% yield analogously to TEMPO-H, using (CD3)2CO/D2O (99.9% D in D2O) as the solvent. TEMPO-D deuteration was 98 ± 1%, as determined by NMR integration of the residual OH resonance (δ 5.34 in CD3CN).
The errors on K3, k3, k4, ΔH°3, ΔS°3 and the activation parameters are reported as 2σ, derived from the least-squares linear fits (using KaleidaGraph62) to plots vs. [TEMPO-H(D)] or to the van’t Hoff, Eyring, or Arrhenius equations.
RuIIIim + TEMPO-H(D) ⇄ RuIIimH(D) + TEMPO• Equilibrium Constant Measurements
Stock solutions of RuIIIim (0.48 mM) and TEMPO-H (240 mM) in MeCN were prepared inside a glove box. An aliquot of RuIIIim (2.5 mL) was transferred to a UV-vis cuvette, which was allowed to thermally equilibrate at 269–310 K. The solution was titrated with TEMPO-H (0.2–7 equiv, 10 μL = 0.2 equiv). UV-vis spectra were recorded for the initial RuIIIim, and after each addition of TEMPO-H when the solution has reached equilibrium. The UV-vis data were analyzed using the absorbance at 568 nm, yielding [RuIIimH]/[RuIIIim] = (A − ARuIII)/(ARuII − A), where ARuII and ARuIII are the absorbances for pure RuIIimH and RuIIIim at 568 nm (ε = 7000 M−1 cm−1 for RuIIimH, 670 M−1 cm−1 for RuIIIim).27 By mass balance, [RuIIimH] = [TEMPO•] = {((A − ARuIII)/(ARuII − ARuIII)) × [Ru]total}, and [TEMPO-H] = [TEMPO-H]total – [TEMPO•] = [TEMPO-H]total − {((A − ARuIII)/(ARuII − ARuIII)) × [Ru]total}. Plotting [RuIIimH][TEMPO•]/[RuIIIim] vs. [TEMPO-H] yielded a straight line, whose slope is the equilibrium constant for the uphill reaction: RuIIIim + TEMPO-H ⇄ RuIIimH + TEMPO• (1/K3H = (5.5 ± 0.6) × 10−4 at 298 K; Figure 1a). The deutero K3D was determined analogously using TEMPO-D in MeCN.
Kinetic Measurements of RuIIimH(D) with TEMPO•
Solutions of RuIIimH (0.093–0.11 mM) and TEMPO• (1.1–13 mM) in MeCN were prepared and loaded into gas-tight syringes inside a N2 glovebox. The stopped-flow apparatus was flushed with anhydrous MeCN, and a background spectrum was acquired. The syringes were immediately loaded onto the stopped-flow apparatus to minimize air exposure. The stopped-flow drive syringes were flushed with the reagents, then filled and allowed to thermally equilibrate. The contents of the two syringes were rapidly mixed at equal volume resulting in half of the original concentrations (0.047–0.053 mM RuIIimH and 0.53–6.7 mM TEMPO•). A minimum of six kinetic runs were performed for each set of concentrations from 282–337 K. Kinetic data were fit to a first order A → B model over the entire spectral region (460–660 nm, Figure 2) using SPECFIT global analysis software.31 The derived kobs for each TEMPO• concentration was plotted vs. [TEMPO•], and the slope of the straight line is the bimolecular rate constant k3H (Figure 3a). The presence of CH3OH (25 mM) in the reactions of RuIIimH (0.047–0.053 mM) and TEMPO• (0.53–6.7 mM) from 278–333 K did not affect the same rate constant within error. The deuterium reaction was studied analogously (278–333 K) using syringes loaded with RuIIimD (0.093–0.11 mM), with 49 mM CD3OD (99.8% D) as deuteration agent, and TEMPO• (1.1–150 mM).
RuIIimH(D)/RuIIIim Self-Exchange Measurements
Stock solutions of RuIIimH (2.0 mM, 4.5 mg in 5.0 mL) and RuIIIim (9.2 mM, 4.1 mg in 1.0 mL) in CD3CN were prepared inside a N2 glove box. Each of seven J-Young NMR tubes was loaded with RuIIimH solutions (0.5 mL), and 5–30 μL of RuIIIim solutions were added to six tubes to give RuIIIim concentrations of 0.092–0.73 mM, with one tube containing a solution of only RuIIimH. 1H NMR spectra were obtained at 250–363 K for each tube. The CH3-acac resonance (δ 1.51; initial fwhm = 2–4 Hz) of RuIIimH was Lorentzian line fitted using NUTS software34 to determine the line width (fwhm) in each sample. Plotting π(Δfwhm) vs. [RuIIIim] yielded a straight line, where Δfwhm = [fwhm(RuIIimH/RuIIIim) − fwhm(RuIIimH)], and the slope is the self-exchange rate constant k4H (Figure 5a). Experiments with RuIIimH (2.0 mM) with RuIIIim (0.10–0.59 mM) in the presence of CH3OH (250 mM) in CD3CN gave the same rate constant within error from 250–363 K. The deutero rate constant, k4D was measured similarly using RuIIimD (2.0 mM) and RuIIIim (0.089–0.59 mM) in the presence of CD3OD (250 mM) in CD3CN at 250–363 K. The same procedure, line fitting the δ1.48 CH3-acac resonance, was used to measure k4H in THF-d8 at 298 K for the reaction of RuIIimH (2.0 mM) [with and without pre-treatment with 0.011 mM Cp2Co] and RuIIIim (0.011–0.16 mM).
Acknowledgments
We acknowledge US National Institutes of Health (GM50422) and University of Washington for financial support. We also thank Christopher Waidmann, Virginia Manner, Jeffrey Warren, and Todd Markle for useful discussions.
References
- 1.Hynes JT, Klinman JP, Limbach H-H, Schowen RL, editors. Hydrogen-Transfer Reactions. Wiley-VCH; Weinheim: 2007. [Google Scholar]
- 2.(a) Olah GA, Molnár Á. Hydrocarbon Chemistry. 2. Wiley; Hoboken, NJ: 2003. [Google Scholar]; (b) Sheldon RA, Kochi JK. Metal-Catalyzed Oxidations of Organic Compounds. Academic Press; New York: 1981. [Google Scholar]; (c) Kochi JK. Free Radicals. Wiley; New York: 1973. [Google Scholar]; (d) Halliwell B, Gutteridge JMC. Free Radicals in Biology and Medicine. Oxford University Press; Oxford: 1999. [Google Scholar]; (e) Fossey J, Lefort D, Sorba J. Free Radicals in Organic Chemistry. Wiley; New York: 1995. [Google Scholar]; (f) Lazár M, Rychlý J, Klimo V, Pelikán P, Valko L. Free Radicals in Chemistry and Biology. CRC Press; Boca Raton, Fl: 1989. [Google Scholar]
- 3.For recent references, see Gansäuer A, Fan CA, Piestert F. J Am Chem Soc. 2008;130:6916. doi: 10.1021/ja801232t.Nieto I, Ding F, Bontchev RP, Wang H, Smith JM. J Am Chem Soc. 2008;130:2716. doi: 10.1021/ja0776834.Maiti D, Lee D-H, Gaoutchenova K, Würtele C, Holthausen MC, Narducci Sarjeant AA, Sundermeyer J, Schindler S, Karlin KD. Angew Chem Int Ed. 2008;47:82. doi: 10.1002/anie.200704389.Lam WWY, Man WL, Leung CF, Wong CY, Lau TC. J Am Chem Soc. 2007;129:13646. doi: 10.1021/ja074282f.Zdilla MJ, Dexheimer JL, Abu-Omar MM. J Am Chem Soc. 2007;129:11505. doi: 10.1021/ja073027s.Choi J, Tang L, Norton JR. J Am Chem Soc. 2007;129:234. doi: 10.1021/ja066325i.Vasbinder MJ, Bakac A. Inorg Chem. 2007;46:2921. doi: 10.1021/ic070015z.Zhang J, Grills DC, Huang KW, Fujita E, Bullock RM. J Am Chem Soc. 2005;127:15684. doi: 10.1021/ja0555724.
- 4.(a) Mayer JM. Annu Rev Phys Chem. 2004;55:363. doi: 10.1146/annurev.physchem.55.091602.094446. [DOI] [PubMed] [Google Scholar]; (b) Mayer JM, Rhile IJ. Biochim Biophys Acta. 2004;1655:51. doi: 10.1016/j.bbabio.2003.07.002. [DOI] [PubMed] [Google Scholar]; (c) Mayer JM, Rhile IJ, Larsen FB, Mader EA, Markle TF, DiPasquale AG. Photosynth Res. 2006;87:3. doi: 10.1007/s11120-005-8164-3. [DOI] [PubMed] [Google Scholar]; (d) Mayer JM, Mader EA, Roth JP, Bryant JR, Matsuo T, Dehestani A, Bales BC, Watson EJ, Osako T, Valliant-Saunders K, Lam W-H, Hrovat DA, Borden WT, Davidson ER. J Mol Catal A: Chem. 2006;251:24. [Google Scholar]; (e) Isborn C, Hrovat DA, Borden WT, Mayer JM, Carpenter BK. J Am Chem Soc. 2005;127:5794. doi: 10.1021/ja050024b. [DOI] [PubMed] [Google Scholar]
- 5.Warren JJ, Mayer JM. J Am Chem Soc. 2008;130:2774–2776. doi: 10.1021/ja711057t. [DOI] [PubMed] [Google Scholar]
- 6.Manner VW, DiPasquale AG, Mayer JM. J Am Chem Soc. 2008;130:7210–7211. doi: 10.1021/ja801672w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.(a) Hernández-García L, Quintero L, Sánchez M, Sartillo-Piscil F. J Org Chem. 2007;72:8196. doi: 10.1021/jo0709551. [DOI] [PubMed] [Google Scholar]; (b) Hartung J. Eur J Org Chem. 2001:619. [Google Scholar]; (c) Lucarini M, Pedrielli P, Pedulli GF, Valgimigli L, Gigmes D, Tordo P. J Am Chem Soc. 1999;121:11546. [Google Scholar]
- 8.(a) Sheldon RA, Arends IWCE. J Mol Catal A: Chem. 2006;251:200. [Google Scholar]; (b) Sheldon RA, Arends IWCE. Adv Synth Catal. 2004;346:1051. [Google Scholar]; (c) Sheldon RA, Arends IWCE, Brink GJT, Dijksman A. Acc Chem Res. 2002;35:774. doi: 10.1021/ar010075n. [DOI] [PubMed] [Google Scholar]; (d) Ishii Y, Sakaguchi S, Iwahama T. Adv Synth Catal. 2001;343:393. [Google Scholar]; (e) Koshino N, Saha B, Espenson JH. J Org Chem. 2003;68:9364. doi: 10.1021/jo0348017. [DOI] [PubMed] [Google Scholar]; (f) Koshino N, Cai Y, Espenson JH. J Phys Chem A. 2003;107:4262. [Google Scholar]; (g) Cai Y, Koshino N, Saha B, Espenson JH. J Org Chem. 2005;70:238. doi: 10.1021/jo048418t. [DOI] [PubMed] [Google Scholar]; (h) Amorati R, Lucarini M, Mugnaini V, Pedulli GF. J Org Chem. 2003;68:1747. doi: 10.1021/jo0342931. [DOI] [PubMed] [Google Scholar]; (i) Barreca AM, Sjögren B, Fabbrini M, Galli C, Gentili P. Biocatal Biotransform. 2004;22:105. [Google Scholar]
- 9.(a) Knapp MJ, Meyer M, Klinman JP. 4:1241–1284. In ref. 1. [Google Scholar]; (b) Knapp MJ, Rickert K, Klinman JP. J Am Chem Soc. 2002;124:3865. doi: 10.1021/ja012205t. [DOI] [PubMed] [Google Scholar]; (c) Lewis ER, Johansen E, Holman TR. J Am Chem Soc. 1999;121:1395. [Google Scholar]
- 10.(a) Mayer JM. Acc Chem Res. 1998;31:441. [Google Scholar]; (b) Gardner KA, Mayer JM. Science. 1995;269:1849. doi: 10.1126/science.7569922. [DOI] [PubMed] [Google Scholar]
- 11.Partenheimer W. Catal Today. 1995;23:69. [Google Scholar]
- 12.(a) Huynh MHV, Meyer TJ. Chem Rev. 2007;107:5004. doi: 10.1021/cr0500030. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Fecenko CJ, Thorp HH, Meyer TJ. J Am Chem Soc. 2007;129:15098. doi: 10.1021/ja072558d. [DOI] [PubMed] [Google Scholar]; (c) Meyer TJ, Huynh MHV. Inorg Chem. 2003;42 [Google Scholar]; (d) Hodgkiss JM, Rosenthal J, Nocera DG. 2:503–562. In ref. 1. [Google Scholar]; (e) Stubbe J, Nocera DG, Yee CS, Chang MCY. Chem Rev. 2003;103:2167. doi: 10.1021/cr020421u. [DOI] [PubMed] [Google Scholar]; (f) Cukier RI, Nocera DG. Annu Rev Phys Chem. 1998;49:337. doi: 10.1146/annurev.physchem.49.1.337. [DOI] [PubMed] [Google Scholar]; (g) Hammes-Schiffer S. 2:479–502. In ref. 1. [Google Scholar]; (h) Irebo T, Reece SY, Sjödin M, Nocera DG, Hammarström L. J Am Chem Soc. 2007;129:15462. doi: 10.1021/ja073012u. [DOI] [PubMed] [Google Scholar]; (i) Lomoth R, Magnuson A, Sjödin M, Huang P, Styring S, Hammarström L. Photosynth Res. 2006;87:25. doi: 10.1007/s11120-005-9005-0. [DOI] [PubMed] [Google Scholar]; (j) Costentin C, Robert M, Savéant JM. J Am Chem Soc. 2007;129:9953. doi: 10.1021/ja071150d. [DOI] [PubMed] [Google Scholar]
- 13.(a) Markle TF, Rhile IJ, DiPasquale AG, Mayer JM. Proc Nat Acad Sci USA. 2008;105:8185–8190. doi: 10.1073/pnas.0708967105. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Markle TF, Mayer JM. Angew Chem Int Ed. 2008;47:738. doi: 10.1002/anie.200702486. [DOI] [PubMed] [Google Scholar]; (c) Rhile IJ, Markle TF, Nagao H, DiPasquale AG, Lam OP, Lockwood MA, Rotter K, Mayer JM. J Am Chem Soc. 2006;128:6075. doi: 10.1021/ja054167+. [DOI] [PMC free article] [PubMed] [Google Scholar]; (d) Rhile IJ, Mayer JM. J Am Chem Soc. 2004;126:12718. doi: 10.1021/ja031583q. [DOI] [PubMed] [Google Scholar]; (e) Lingwood M, Hammond JR, Hrovat DA, Mayer JM, Borden WT. J Chem Theory Comput. 2006;2:740. doi: 10.1021/ct050282z. [DOI] [PMC free article] [PubMed] [Google Scholar]; (f) Mayer JM, Hrovat DA, Thomas JL, Borden WT. J Am Chem Soc. 2002;124:11142. doi: 10.1021/ja012732c. [DOI] [PubMed] [Google Scholar]
- 14.(a) Tishchenko O, Truhlar DG, Ceulemans A, Nguyen MT. J Am Chem Soc. 2008;130:7000. doi: 10.1021/ja7102907. [DOI] [PubMed] [Google Scholar]; (b) Neta P, Grodkowski J. J Phys Chem Ref Data. 2005;34:109. [Google Scholar]; (c) Nielsen MF, Ingold KU. J Am Chem Soc. 2006;128:1172. doi: 10.1021/ja0548081. [DOI] [PubMed] [Google Scholar]; (d) Foti M, Ingold KU, Lusztyk J. J Am Chem Soc. 1994;116:9440. [Google Scholar]; (e) Skone JH, Soudackov AV, Hammes-Schiffer S. J Am Chem Soc. 2006;128:16655. doi: 10.1021/ja0656548. [DOI] [PubMed] [Google Scholar]
- 15.(a) Ingold KU. In: Free Radicals. Kochi JK, editor. Chapter 2. Wiley; New York: 1973. p. 69ff. [Google Scholar]; Russell GA. In: Free Radicals. Kochi JK, editor. Chapter 7. Wiley; New York: 1973. pp. 283–293. [Google Scholar]; (b) Tedder JM. Angew Chem, Int Ed Engl. 1982;21:401. [Google Scholar]
- 16.Mader EA, Davidson ER, Mayer JM. J Am Chem Soc. 2007;129:5153. doi: 10.1021/ja0686918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Roth JP, Yoder JC, Won TJ, Mayer JM. Science. 2001;294:2524. doi: 10.1126/science.1066130. [DOI] [PubMed] [Google Scholar]
- 18.Mader EA, Larsen AS, Mayer JM. J Am Chem Soc. 2004;126:8066. doi: 10.1021/ja049246k. [DOI] [PubMed] [Google Scholar]
- 19.(a) Marcus RA, Sutin N. Biochim Biophys Acta. 1985;811:265. [Google Scholar]; (b) Sutin N. Prog Inorg Chem. 1983;30:441. [Google Scholar]
- 20.fXY = exp[(ln(KXY))2/(4ln(kXXkYY/Z2))], where the collision frequency, Z ≈ 1011 M−1 s−1.19
- 21.(a) Bryant JR, Mayer JM. J Am Chem Soc. 2003;125:10351–10361. doi: 10.1021/ja035276w. [DOI] [PubMed] [Google Scholar]; (b) Waidmann CR, Zhou X, Kaminsky W, Hrovat DA, Borden WT, Mayer JM. manuscript in preparation. [Google Scholar]
- 22.Soper JD, Mayer JM. J Am Chem Soc. 2003;125:12217. doi: 10.1021/ja036328k. [DOI] [PubMed] [Google Scholar]
- 23.Manner, V. W.; Lindsay, A.; Mayer, J. M., work in progress.
- 24.Goldsmith CR, Jonas RT, Stack TDP. J Am Chem Soc. 2002;124:83–96. doi: 10.1021/ja016451g. [DOI] [PubMed] [Google Scholar]
- 25.(a) Refs. 1, 12, and 14a. (b) Hammes-Schiffer S, Hatcher E, Ishikita H, Skone JH, Soudackov AV. Coord Chem Rev. 2008;252:384–394. doi: 10.1016/j.ccr.2007.07.019.Marcus RA. Phil Trans R Soc Lond B Biol Sci. 2006;361:1445–1455. doi: 10.1098/rstb.2006.1873.Cukier RI. J Phys Chem B. 2002;106:1746–1757.Kotelnikov AI, Medvedev ES, Medvedev DM, Stuchebrukhov AA. J Phys Chem B. 2001;105:5789–5796.
- 26.cf., (a) Ref. 12b. (b) Hodgkiss JM, Damrauer NH, Presse S, Rosenthal J, Nocera DG. J Phys Chem B. 2006;110:18853–18858. doi: 10.1021/jp056703q.
- 27.Wu A, Masland J, Swartz RD, Kaminsky W, Mayer JM. Inorg Chem. 2007;46:11190. doi: 10.1021/ic7015726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bell RP. The Proton in Chemistry. 2. Cornell University Press; Ithaca, NY: 1973. pp. 226–296. [Google Scholar]
- 29.KH/KD = exp[hc((νNH −νND) − (νOH − νOD))/2kBT] = 0.78, where T = 298 K, νNH = 3068 cm−1 and νND = 2267 cm−1 for RuIIimH(D) in KBr pellets, and νOH = 3495 cm−1 and νOD = 2592 cm−1 for TEMPO-H(D) in CD3CN.
- 30.Mader EA, Manner VW, Wu A, Mayer JM. manuscript in preparation. [Google Scholar]
- 31.SPECFIT/32, versions v3.0.26 and v3.0.36. Spectrum Software Associates; Marlborough, MA: 2000. [Google Scholar]
- 32.Wu A, Datta A, Mader EA, Hrovat DA, Borden WT, Mayer JM. to be submitted. [Google Scholar]
- 33.Sandström J. Dynamic NMR Spectroscopy. Academic Press; London: 1982. [Google Scholar]
- 34.NUTS − NMR Utility Transform Software, 1D version. Acorn NMR Inc.; Livermore, CA: 2003. [Google Scholar]
- 35.The singlet at δ 1.51 corresponds to two accidentally degenerate methyl groups. This peak remained degenerate and unobscured throughout the entire measured temperature range (250–363 K), and was suitable for line broadening analysis by NUTS software. The other two methyl singlets (δ 2.00, 2.05) were obscured by the residual solvent pentet at δ 1.94 (CD2HCN), and were not suitable for line fitting. The two overlapping CH-acac singlets (δ 5.29, 5.32) and other non-singlet aromatic resonances were unable to be line fitted by NUTS, but instead using gNMR software.
- 36.gNMR software, v4.1.0. Ivory Soft; Rancho Palos Verdes, CA: 1999. [Google Scholar]
- 37.(a) ΔG°(ET) = −23.1[E(TEMPO•) − E(RuIIimH)] = +29 kcal mol−1; ΔG°(PT) = −1.37[pKa(TEMPO-H•+) − pKa(RuIIimH)] = +34 kcal mol−1; ΔG°(HAT) = −4.4 kcal mol−1 from K3H = 1.8 × 103. (b) E(RuIIimH) = −0.64 V vs. Cp2Fe+/0, pKa(RuIIimH) = 22.1: ref. 27. (c) E(TEMPO•) ≈ −1.91 V vs. Cp2Fe+/0: Mori Y, Sakaguchi Y, Hayashi H. J Phys Chem A. 2000;104:4896.(d) pKa(TEMPO-H•+) = pKa(TEMPO-H) + 23.1[E(TEMPO•) − E(TEMPO-H)]/1.37 ≈ −3. (e) E(TEMPO-H) ≈ 0.71 V vs. Cp2Fe+/0: Semmelhack MF, Chou CS, Cortes DA. J Am Chem Soc. 1983;105:4492.(f) pKa(TEMPO-H) ≈ 41 in MeCN is estimated from pKa(TEMPO-H) = 31.0 in DMSO: Bordwell FG, Liu WZ. J Am Chem Soc. 1996;118:10819.(g) pKa conversion from DMSO to MeCN: Chantooni MK, Jr, Kolthoff IM. J Phys Chem. 1976;80:1306.
- 38.(a) Njus D, Kelley PM. FEBS Lett. 1991;284:147–151. doi: 10.1016/0014-5793(91)80672-p. [DOI] [PubMed] [Google Scholar]; (b) Vuina D, Pilepic V, Ljubas D, Sankovic K, Sajenko I, Uršic S. Tet Lett. 2007;48:3633–3637. [Google Scholar]
- 39.Bell RP. The Tunnel Effect in Chemistry. Chapman and Hall; London: 1980. pp. 77–105. [Google Scholar]
- 40.Semi-classical kH/kD = exp[hc(νNH − νND)/2kBT] = 6.9, where T = 298 K.
- 41.(a) Klinman JP. Phil Trans R Soc B. 2006;361:1323. doi: 10.1098/rstb.2006.1870. [DOI] [PMC free article] [PubMed] [Google Scholar]; (b) Kohen A, Klinman JP. Acc Chem Res. 1998;31:397. [Google Scholar]; (c) Jonsson T, Glickman MH, Sun S, Klinman JP. J Am Chem Soc. 1996;118:10319. [Google Scholar]
- 42.(a) Gilbert JA, Gersten SW, Meyer TJ. J Am Chem Soc. 1982;104:6872. [Google Scholar]; (b) Gilbert J, Roecker L, Meyer TJ. Inorg Chem. 1987;26:1126. [Google Scholar]
- 43.Binstead RA, McGuire ME, Dovletoglou A, Seok WK, Roecker LE, Meyer TJ. J Am Chem Soc. 1992;114:173. [Google Scholar]
- 44.Binstead RA, Meyer TJ. J Am Chem Soc. 1987;109:3287. [Google Scholar]
- 45.Reinaud OM, Theopold KH. J Am Chem Soc. 1994;116:6979. [Google Scholar]
- 46.Mahapatra S, Halfen JA, Tolman WB. J Am Chem Soc. 1996;118:11575. [(LCu)2(μ-O)2](ClO4)2 with L = 1,4,7-tribenzyl-7-benzyl-1,4,7-triazacyclononane or 1,4,7-triisopropyl-7-benzyl-1,4,7-triazacyclononane. [Google Scholar]
- 47.Roth JP, Lovell S, Mayer JM. J Am Chem Soc. 2000;122:5486. [Google Scholar]
- 48.Yoder JC, Roth JP, Gussenhoven EM, Larsen AS, Mayer JM. J Am Chem Soc. 2003;125:2629. doi: 10.1021/ja0273905. [DOI] [PubMed] [Google Scholar]
- 49.Kiss G, Zhang K, Mukerjee SL, Hoff CD. J Am Chem Soc. 1990;112:5657. The CpCr(CO)3H + CpCr(CO)3• self-exchange rate constant k ~ 102 M−1 s−1 is estimated from k = 910 M−1 s−1 at 298 K for CpCr(PPh3)(CO)2H + (C5Me5)Cr(CO)3• in toluene (ΔH° = −2.5 kcal mol−1). [Google Scholar]
- 50.Protasiewicz JD, Theopold KH. J Am Chem Soc. 1993;115:5559. [Google Scholar]
- 51.Song J, Bullock RM, Creutz C. J Am Chem Soc. 1991;113:9862. [Google Scholar]
- 52.The self-exchange rate constant for RuIIimH + RuIIIimH+ is estimated to be between 4 × 106 and 1 × 108 M−1 s−1 in MeCN based on the following k(self-exchange) values: (a) 1.4 × 108 M−1 s−1 for [Ru(acac)2(4,4′-Me2bpy)]0/+, 4.5 × 106 M−1 s−1 for [Ru(hfac)2(4,4′-Me2bpy)]0/+, 5.0 × 106 M−1 s−1 for [Ru(hfac)3]−/0, 8.3 × 106 M−1 s−1 for [Ru(bpy)3]2+/3+, and 1 × 108 M−1 s−1 for [Ru(L)3]2+/3+ (L = 3,4,7,8-Me4phen, 3,5,6,8-Me4phen, or 4,7-Me2bpy) [hfac = 1,1,1,5,5,5-hexafluoro-2,4-pentanedionato, phen = 1,10-phenanthroline]. (b) Wherland S. Coord Chem Rev. 1993;123:169.Chan MS, Wahl AC. J Phys Chem. 1982;86:126.
- 53.(a) The range of rate constants from footnote 52, using k = Ze−ΔG*/RT and a collision frequency Z of 1011 M−1 s−1 gives ΔG* = 5.0 ± 1.0 kcal mol−1.19 From the (adiabatic) Marcus equation, ΔG* = wr + (λ/4)(1 + ΔG°′/λ)2, the intrinsic barrier λET = 4ΔG* = 20 ± 4 kcal mol−1 (the work term wr = 0).19 Reaction 5 has ΔE1/2 = −0.36 V27 or ΔG° = +8.3 kcal mol−1. After correcting for the electrostatic effects,53b ΔG°′ = 7.3 kcal mol−1. Inserting this value and the λET above into the Marcus equation above gives ΔG* = 9.3 ± 2.0 kcal mol−1 which (using Z = 1011 M−1 s−1) gives 5 × 102 < kET < 4 × 105 M−1 s−1. Eberson L. Electron Transfer Reactions in Organic Chemistry. Springer-Verlag; Berlin: 1987. pp. 27–28.
- 54.Litwinienko G, Ingold KU. Acc Chem Res. 2007;40:222. doi: 10.1021/ar0682029. [DOI] [PubMed] [Google Scholar]
- 55.Cf., Refs. 22, 54, and Soper JD, Rhile IJ, DiPasquale AG, Mayer JM. Polyhedron. 2004;23:323.
- 56.Farrer BT, Thorp HH. Inorg Chem. 1999;38:2497. [Google Scholar]
- 57.Iordanova N, Hammes-Schiffer S. J Am Chem Soc. 2002;124:4848. doi: 10.1021/ja017633d. [DOI] [PubMed] [Google Scholar]
- 58.Iordanova N, Decornez H, Hammes-Schiffer S. J Am Chem Soc. 2001;123:3723. doi: 10.1021/ja0100524. [DOI] [PubMed] [Google Scholar]
- 59.The Eyring parameters, ΔH‡3,calc and ΔS‡3,calc were determined from k3,calc values, which were calculated from the k4, k8, and K3 terms at different temperatures derived from their respective Eyring or van’t Hoff equation.
- 60.Marcus RA. J Phys Chem. 1968;72:891–899.See also: Albery WJ. Faraday Disc Chem Soc. 1982;74:245–256. and ref. 25c.
- 61.Ozinskas AJ, Bobst AM. Helv Chim Acta. 1980;63:1407. [Google Scholar]
- 62.KaleidaGraph, version 3.5; Synergy Software: 2000.