MATHEMATICAL MODEL THAT PREDICTS THE FORCE-INTENSITY AND FORCE-FREQUENCY RELATIONSHIPS AFTER SPINAL CORD INJURIES

Abstract

We have previously developed and tested a muscle model that predicts the effect of stimulation frequency on muscle force responses. The aim of this study was to enhance our isometric mathematical model to predict muscle forces in response to stimulation trains with a wide range of frequencies and intensities for the quadriceps femoris muscles of individuals with spinal cord injuries. Isometric forces were obtained experimentally from 10 individuals with spinal cord injuries (time after injury, 1.5-8 years) and then compared to forces predicted by the model. Our model predicted accurately the force-time integrals (FTI) and peak forces (PF) for stimulation trains of a wide range of frequencies (12.5-80 HZ) and intensities (150-600-μs pulse duration), and two different stimulation patterns (constant-frequency trains and doublet-frequency trains). The accurate predictions of our model indicate that our model, which now incorporates the effects of stimulation frequency, intensity, and pattern on muscle forces, can be used to design optimal customized stimulation strategies for spinal cord-injured patients.

Functional electrical stimulation (FES) is the application of electrical stimulation to generate functional movements such as standing, walking, and grasping in individuals with upper motor neuron lesions.^2,25 However, in spite of the potential advantage of FES for improving the functional mobility of paralyzed individuals, it has not gained widespread application. Two of the limitations in current FES systems include rapid muscle fatigue and imprecise control of movements.^25,27,31 During volitional activation, the central nervous system (CNS) modulates both the firing frequency and the number of activated motor units to control force output precisely for functional tasks and delay the onset of muscle fatigue.²¹ However, current FES systems typically only vary the stimulation intensity to control muscle force and maintain a constant stimulation frequency. In addition, current FES systems only use one stimulation pattern, namely, constant-frequency trains (CFTs) (see Fig. 1 for an example). Previous studies, however, showed that stimulation trains that contained two closely spaced pulses (doublet) throughout the train, doublet-frequency trains (DFTs), produced greater isometric forces from fatigued human skeletal muscles and greater power during dynamic contractions than the traditionally used CFTs.^3-5,22,23 Modulating the stimulation frequency, pattern, and intensity during FES may help obtain more precise control of skeletal muscle force output and delay the onset of fatigue.

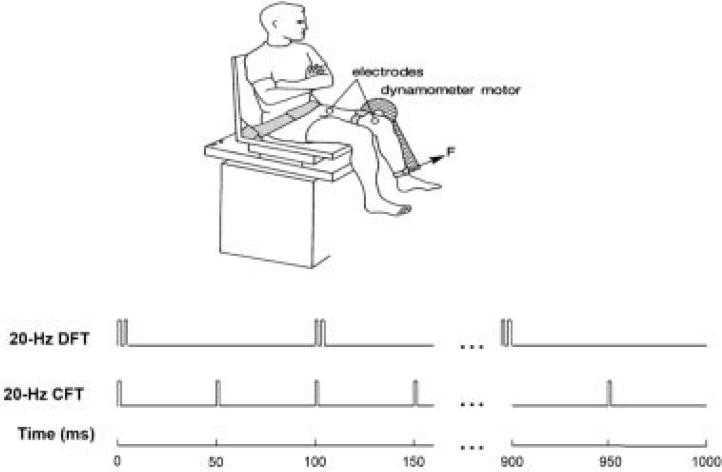
FIGURE 1.

Schematic representation of experimental arrangement for data collection and examples of stimulation trains used in the study. The top stimulation train is a 20-HZ doublet-frequency train (DFT) that contains pairs of doublets (two pulses separated by 5 ms) separated by 95-ms interdoublet intervals. The bottom stimulation train is a 20-HZ constant-frequency train (CFT) that contains pulses separated by 50-ms intervals.

To generate task-specific muscle forces during FES, it is important to determine the stimulation scheme that produces the targeted muscle force responses. The stimulation strategy that maximizes skeletal muscle performance, however, varies from person to person²² and, even for the same individual, varies with the physiological conditions of the muscle, such as the level of fatigue or muscle length.²⁶ Thus, numerous tests would be needed to identify the best stimulation strategy for each individual and each task. Mathematical models that predict force responses to stimulation trains of different frequencies, intensities, and patterns can decrease the number of experimental sessions required to determine the best stimulation strategy for each subject. In addition, mathematical models can help to design subject-specific and task-specific stimulation trains as part of closed-loop feedback controllers in FES systems.^15,31

Using data collected from soleus muscles of individuals with spinal cord injuries (SCIs), Frey Law and Shields¹⁸ evaluated the mathematical model that we developed using healthy subjects' muscles activated with 6-pulse stimulation trains.¹³ Their results showed that our model predicted the paralyzed muscle forces for all stimulation frequencies and pulse patterns reasonably well.¹⁸ Another recent study,⁸ which compared seven different muscle models, showed that our model¹⁴ and Bobet-Stein's⁷ model provided the best fits for ankle dorsiflexor forces over a range of joint angles in able-bodied individuals. Recently, we tested a newer version of our isometric model on quadriceps femoris muscles of SCI individuals and showed good predictions for stimulation trains containing up to 50 pulses.¹⁶ Thus, our previous model can predict the effect of stimulation frequency and pattern very well,¹⁶ but the effect of stimulation intensity on muscle force has not yet been incorporated into the model.

In the current study the effects of stimulation intensity, frequency, and pattern on muscle forces were incorporated into our isometric mathematical model. The purpose of this study was to test the model's ability to predict force responses of the quadriceps femoris muscles of individuals with SCI to stimulation trains with a wide range of frequencies, stimulation patterns, and physiologically relevant stimulation intensities.

MATERIALS AND METHODS

Isometric Force Model

Our previously developed mathematical model predicted isometric forces from human quadriceps femoris muscle in response to stimulation trains of different frequencies and patterns with the stimulation intensity kept constant throughout a testing session.^12,14,16 The various physiological processes involved in the generation of skeletal muscle force were classified as two basic steps, muscle activation and force generation, modeled by two first-order ordinary differential equations.¹⁶

Muscle Activation Dynamics

Physiologically, the binding of Ca²⁺ to troponin is necessary to free the binding sites on actin for myosin. Similarly, the first step of our model captures the release and uptake of Ca²⁺ from the sarcoplasmic reticulum and the binding of Ca²⁺ to troponin. The rate-limiting steps leading to the formation of the Ca²⁺-troponin complex are modeled by equation 1,

$$\frac{d{C}_N}{dt}=\frac{1}{{\tau }_c}\sum _{i=1}^n{R}_i\exp \left(-\frac{t-t_i}{{\tau }_c}\right)-\frac{C_N}{{\tau }_c}$$ (1)

with

$$R_i=1+(R_0-1)\exp [-(t_i-t_{i-1})∕{\tau }_c]$$

where C_N quantitatively describes the rate-limiting step before the myofilaments mechanically slide across each other and generate force, R_i accounts for the nonlinear summation of C_N in response to two closely spaced pulses,¹² and τ_C is the time constant controlling the transient shape of C_N.

Force Generation

The force output of a muscle depends on the number and rate of formation of strongly bound actin-myosin cross bridges. In addition, visco-elastic components such as the connective tissue and tendon affect the muscle force. Similarly, in our model the instantaneous force (F) was driven by the strongly bound force-producing cross-bridges and mediated by a Michaelis-Menten term, C_N/K_m + C_N. The rate of change of instantaneous force F was modeled by equation 2, which was derived from a linear spring, damper, and motor in series, representing the elastic, connective, and contractile component during muscle contraction, respectively.³⁵

$$\frac{dF}{dt}=A\frac{C_N}{K_m+C_N}-\frac{F}{{\tau }_1+{\tau }_2\frac{C_N}{K_m+C_N}}$$ (2)

In this equation parameter K_m represents the sensitivity of the force development to C_N and parameter A represents a scaling factor for force. The second term in equation 2 accounts for the force decay due to two time constants, τ₁ and τ₂. Parameter τ₁ models the force decay due to the visco-elastic components of the muscle following stimulation when C_N is small, whereas parameter τ₂ models the force decay due to these visco-elastic muscle components during stimulation.

Intensity Modulation

Two methods can be used to modulate stimulation intensity during electrical stimulation—varying the stimulation pulse duration or the stimulation pulse amplitude. We decided to vary the stimulation intensity by changing the stimulation pulse duration because it is easier to quantify and control than the stimulation pulse amplitude, provides a more consistent response across subjects, requires a smaller charge per stimulus pulse, and allows for greater selectivity of recruitment than amplitude modulation.^10,20,33 In the present study the pulse amplitude was kept constant throughout the testing sessions while the pulse duration was varied to modulate the stimulation intensity. Preliminary studies on able-bodied subjects showed that most of the effects of stimulation intensity on force could be accounted for by modulating parameter A as a function of stimulation intensity (i.e., pulse duration).¹¹ Thus, among all the parameters, we assumed that only parameter A is affected by stimulation intensity and that the intensity modulation is given by:

$$A=a\prime [1-\exp (-(pd-p{d}_0)∕p{d}_t)]$$ (3)

where a′ is a scaling factor; pd is the stimulation pulse duration; pd₀ is the offset for stimulation pulse duration characterizing how sensitive the muscle is to the stimulation intensity; and pd_t is the time constant controlling the steepness of the A-pd relationship.

Subjects

Ten subjects (six male, four female) with complete lower-extremity paralysis due to spinal cord injuries (American Spinal Injury Association, classification A or B) and with mean age of 14 years (range, 8-17 years) participated in this study. The mean time after injury was 4.8 years (range, 1.5-8 years).

At the beginning of each testing session the subject and parents were informed about the nature of the study, the testing procedures, how the force dynamometer, stimulator, and computer worked together for the testing, and the potential risks involved. Subjects were also told that participation was voluntary and that they could withdraw from the study at any time. Then, the subject (if not a minor) or parents signed an informed consent form approved by both the University of Delaware and the Temple University Human Subject Review Boards. Children 8 years of age and older signed an approved assent form.

Experimental Arrangement

Subjects were seated on a computerized force dynamometer (KinCom; Chat-tecx Corp., Chattanooga, Tennessee) with their hips flexed to ~75° and the tested knees flexed to 65° (Fig. 1). The force transducer pad was positioned against the anterior aspect of the leg to be tested about 5 cm proximal to the lateral malleolus. The axis of the dynamometer was aligned with the anatomical axis of the knee. The thigh, waist, and upper trunk were stabilized with straps. A Grass S8800 stimulator (Grass Instruments, West Warwick, Rhode Island) with a Grass Model SIU8T stimulus isolation unit was used to deliver the stimulation pulses. A custom-written LabView program was used to control the stimulator (National Instruments, Austin, Texas). A custom-made switch was connected in series with the stimulator to enable the control of stimulus pulse duration via the computer. Force data were collected directly from the force dynamometer, transferred to a personal computer via an analog-to-digital board at a sampling rate of 200 Hz, and analyzed using custom-written software (LabView; National Instruments).

After positioning the leg to be tested, two appropriately sized surface electrodes (Pals Platinum by Axelgaard Manufacturing Co., Fall Brook, California; 7.5 × 10 cm) were placed over the quadriceps femoris muscle. One electrode was placed over the proximal thigh and the other was placed distally, ~2 cm above the patella, over the vastus medialis. The electrode placement was checked using 770-ms, 14-Hz trains to ensure consistent and effective recruitment of the muscle. If inconsistent activation of the muscle was observed (i.e., lack of a clear response to each pulse within the train) the electrodes were repositioned and the placement was rechecked.

Next, the maximal twitch force of the subject's quadriceps muscle was recorded by stimulating the muscle with a series of single 600-μs pulses delivered at a rate of 1 pulse every 10 s. The pulse amplitude was gradually increased until the maximum twitch force was reached. The maximal twitch force ranged from 23 to 87N. The stimulation amplitude was then adjusted using 1-s, 100-Hz stimulation trains with pulse duration of 600 μs to produce a force equal to the subject's maximal twitch force. Because 100 Hz was the highest frequency and 600 μs was the longest pulse duration (i.e., the highest stimulation intensity) used during the testing session, subsequent testing trains produced lower forces. Previous work by others^19,32 showed that the quadriceps femoris muscles of subjects with SCI have elevated twitch-to-tetanus ratios (0.25) compared to able-bodied subjects (0.13). Thus, we estimate that in response to the higher frequencies tested, ~25% of the force-generating ability of the muscles would be recruited. Once set, the stimulation amplitude was kept constant throughout the remainder of the testing session.

Experimental Testing

In this study, CFTs and DFTs with stimulation frequencies ranging from 12.5 to 80 Hz and stimulation pulse durations ranging from 150 to 600 μs were investigated (see Table 1 for the specific trains tested). The 12.5-Hz train with a 150-μs pulse duration was not tested because of the very low forces produced by this train. After the stimulation amplitude was set, a series of trains (40 trains) were delivered to the muscle at the rate of one train every 10 s to avoid fatigue (Table 1). The 50-Hz CFTs and 20-Hz DFTs at 150, 200, 300, and 500 μs were used to determine the model's parameter values for each subject (see the next section). The remaining trains were used to test the model's predictive ability for stimulation frequencies and intensities different from those used to calculate the model's parameter values for each subject. All 40 trains were either 1 s in duration or contained 50 pulses, whichever yielded the shorter train duration. Each testing train was delivered twice: first, trains were delivered in a random order, and then delivered again in reversed order.

Table 1.

Identification of stimulation trains used during testing.

	CFTs					DFTs
	12.5 HZ	20 HZ	33 HZ	50 HZ	80 HZ	12.5 HZ	20 HZ	33 HZ	50 HZ
CFT, constant-frequency train; DFT, doublet-frequency train.
o: the stimulation trains used to determine model parameter values.
x: the stimulation trains used to test the model's predictive ability.
Blank cells refer to trains that were not delivered.
150 μs		x	x	o	x		o	x	x
200 μs				o			o
250 μs	x	x	x	x	x	x	x	x	x
300 μs				o			o
350 μs	x	x	x	x	x	x	x	x	x
500 μs				o			o
600 μs	x	x	x	x	x	x	x	x	x

Model Simulation

The modeling was carried out using a C++ program. The values for each free parameter in equations 1-3 were calculated for each subject using the force responses to the 50-Hz CFTs and 20-Hz DFTs collected at stimulation intensities of 150, 200, 300, and 500 μs using the following procedures. Once the parameter values were calculated, the model was used to predict the force responses to the remaining 32 trains tested. Because the simplest FES model is desired,¹ we minimized the number of free parameters without affecting the model's predictive ability. Pilot testing of the model showed that parameter R₀ could be fixed at 5 and parameter τ_C could be fixed at 11 ms for the quadriceps femoris muscles of individuals with SCI. Thus, the values of only seven free parameters, A as a function of (a′, pd₀, pd_t), K_m, τ₁, and τ₂, needed to be calculated (Table 2). The following steps were involved to obtain predicted forces using the model.

Table 2.

Model parameter values determined for each subject.

	τ1 (ms)	τ2 (ms)	Km	a' (N/ms)	pdo (μs)	pdt (μs)
For each subject, parameter Ro was fixed at 5 and τc was fixed at 11 ms.
Subject 1	53.645	1	0.159	0.421	118.357	89.827
Subject 2	22.154	38.559	0.028	0.653	106.078	35.131
Subject 3	51.684	1	0.109	1.034	76.986	355.973
Subject 4	60.601	1	0.137	0.492	131.405	194.138
Subject 5	28.163	1	0.189	1.359	96.285	184.054
Subject 6	54.41	30.549	0.14	0.879	91.753	89.569
Subject 7	76.472	1	0.546	0.200	60.963	64.378
Subject 8	39.516	62.981	0.177	0.416	67.877	88.884
Subject 9	19.62	12.462	0.092	0.620	47.752	162.760
Subject 10	34.622	35.668	0.227	0.847	71.601	119.699
Average	44.099	18.522	0.180	0.692	86.906	138.441

Step 1: Calculation of parameter values for 300-μs pulse duration. Forces in response to 50-Hz CFT and 20-Hz DFT trains with pulse duration of 300 μs were collected. First, parameter τ₁ was calculated by fitting the forces immediately following the tetanic stimulation while the muscle relaxed for forces between 50% to 25% of the peak force. This method has previously been described in detail.¹⁵ Then, the values of A, K_m and μ₂ were obtained by minimizing the objective function:

$$G(A,K_m,{\tau }_2)=\sum _p{(F^{pred}(t_{p;}A,K_m,{\tau }_2)-F^{meas}\left(t_p\right))}^2$$ (4)

where F^pred were the forces predicted by the model (eqs. 1 and 2) and F^meas were the measured forces.^15,16

Steps 2 and 3: Identification of the A-pd relationship. All the aforementioned parameters, except parameter A, were fixed at the values obtained at the stimulation intensity of 300-μs pulse duration as described above (step 1). Next, the measured force responses to the 50-Hz CFTs and 20-Hz DFTs collected at the stimulation intensities of 150-, 200-, and 500-μs pulse durations were used to determine the values of parameter A by minimizing the objective function:

$$G\left(A\right)=\sum _p{(F^{pred}\left(t_{p;}A\right)-F^{meas}\left(t_p\right))}^2$$ (5)

where F^pred were the forces predicted by the model (eqs. 1 and 2) and F^meas were the measured forces. Next, using the A-values at these three pulse durations and the A-value calculated at the pulse duration of 300 μs in step 1, the A-pd relationship (eq. 3) was determined.

Step 4: Prediction of force responses to all stimulation trains. Finally, with all the parameter values calculated, the forces in response to two stimulation patterns (CFT and DFT) over a range of stimulation frequencies (12.5-80 Hz) and intensities (150-600 μs) were predicted and then compared to measured forces (see Figs. 2, 3).

FIGURE 2.

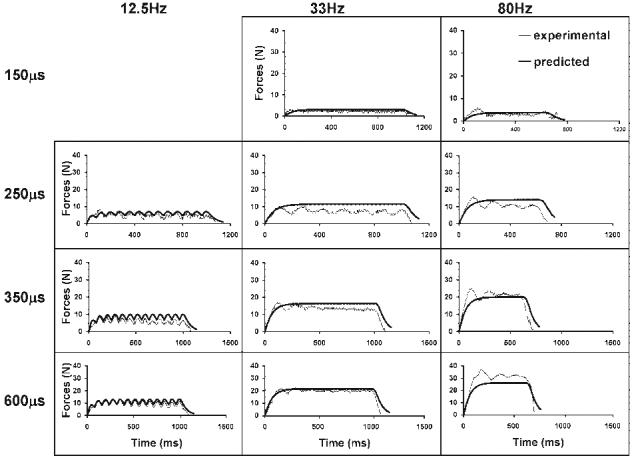
Force responses to constant-frequency trains (CFTs) of 12.5, 33, and 80 HZ at four intensities (150, 250, 350, and 600 μs) are shown for a typical subject.

FIGURE 3.

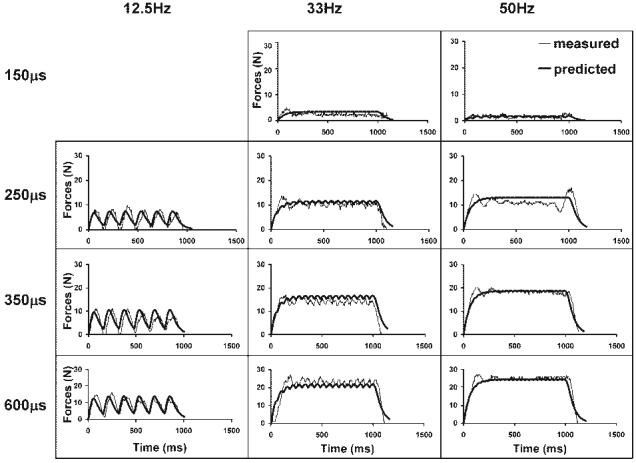
Force responses to doublet-frequency trains (DFTs) of 12.5, 33, and 50 HZ at four intensities (150, 250, 350, and 600 μs) are shown for a typical subject. Data were taken from the same subject shown in Figure 2.

Data Analysis

For each subject the two occurrences of each testing train were averaged and used as the measured force and then compared to the predicted force. Three statistical analyses were done to evaluate the predictions of the model.

First, to evaluate how well the model predicted the shape of the force response, R² values (predicted R²) were calculated for each testing train between the predicted force and the averaged measured force. In addition, for each testing intensity the physiological R² values were also calculated by comparing the first and second occurrence of each testing train. The R² values for each testing train were then averaged across trains and then across subjects to determine the averaged physiological R² for each intensity. The physiological R² value between the first and second occurrence of each testing train showed an average value of 0.49, 0.58, 0.73, and 0.65 at a stimulation intensity of 150, 250, 350, and 600 μs, respectively. Then, for each intensity the percentage of testing trains with predicted R² values above the calculated physiological R² value was calculated.

Second, the peak force (PK) and force-time integral (FTI) were computed for both predicted and measured forces. Intraclass correlation coefficients (ICCs) between the predicted and measured data were calculated for FTIs and PKs. The predicted PKs and FTIs were plotted against the measured PKs and FTIs, respectively. Trendlines with intercepts of zero were used to evaluate agreement between the measured and predicted values. A slope of 1 and ICC value of 1 would represent a perfect prediction of the model.

Third, the force-frequency relationship was plotted for each testing intensity using measured and predicted FTIs and PKs data (averaged across subjects) plotted against the stimulation frequencies. To obtain a measure of physiological variability for both PKs and FTIs, the absolute percentage differences in PKs and FTIs between the two occurrences of each testing train were calculated using the formula:

$$\%physiolgicalvariability=\mid \frac{measured1-measured2}{average(measure1,measure2)}\mid \times 100$$ (6)

and then averaged across all testing trains and subjects for each intensity (Table 3). For each testing train, the model error was calculated using the formula:

$$\%modelerror=\mid \frac{predicted-measured}{measured}\mid \times 100$$ (7)

Table 3.

Physiological variability at each testing intensity.^*

Intensity tested	FTI	PK
FTI, force-time integral; PK, peak force.
150 μs	24%	17%
250 μs	31%	24%
350 μs	20%	16%
600 μs	33%	24%

^*At each pulse duration, % variability was calculated for each train, then averaged across trains and subjects (see text for details).

If the percentage difference in FTI or PK between the measured and predicted forces (%model error) was larger than the % physiological variability, a paired t-test was used to determine whether there was a significant difference between the predicted and the measured forces for that testing train.

RESULTS

Complete data were collected from 10 subjects. Model parameter values that were used to obtain predicted forces are shown in Table 2. Inspection of measured and predicted force-time responses showed that the model was able to predict well the shape of the force-time responses (see Figs. 2 and 3 for examples from a representative subject). The model predicted well the shape of the force responses with the averaged predicted R² values of 0.61, 0.71, 0.73, and 0.77 between the predicted and measured forces for stimulation intensity of 150, 250, 350, and 600 μs, respectively. About 77%, 79%, 61%, and 80% of the model's predictions produced R² values above the physiological R² values for the tested stimulation intensity 150, 250, 350, and 600 μs, respectively.

In addition, the model predicted well the FTI and PK. The trendline comparing the predicted to the measured FTI produced a slope of 0.99 and ICC values of 0.96 (Fig. 4). Similarly, the trendline comparing predicted to measured PK produced a slope of 0.88 and ICC value of 0.94 (Fig. 4). For both the CFTs and DFTs, the model predicted well the PK-frequency and FTI-frequency relationships for each of the four stimulation intensities tested (Figs. 5, 6). For FTI, significant differences on a paired t-test observed only for the 12.5-Hz DFT at 250-μs pulse duration (%model error = 33%, P < 0.05) and the 12.5-Hz CFT at 350-μs pulse duration (%model error = 59%, P < 0.05) (Fig. 5). For PK, significant differences were seen on the paired t-tests only for the 20-Hz CFT (%model error = 18%, P < 0.05) and the 20-Hz DFT (%model error = 22%, P < 0.05) at 150-μs pulse duration and the 20-Hz DFT with (%model error = 16%, P < 0.05) at 350-μs pulse duration (Fig. 6). Both the measured and predicted results showed that the 50-Hz trains produced the maximum FTI for all pulse durations tested and that the FTI declined at higher frequencies for CFTs (note that 50 Hz was the highest frequency tested for DFTs). Similarly, for PK the measured and predicted forces showed the maximum values at the same frequency, which was always the highest frequency tested. These data are consistent with previous reports.¹⁶

FIGURE 4.

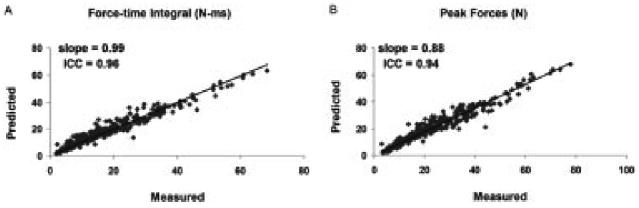
Plots of measured versus predicted force-time integrals (A) and peak forces (B) for all stimulation trains for 10 subjects. Trendlines were plotted using an intercept of zero and the slopes were reported.

FIGURE 5.

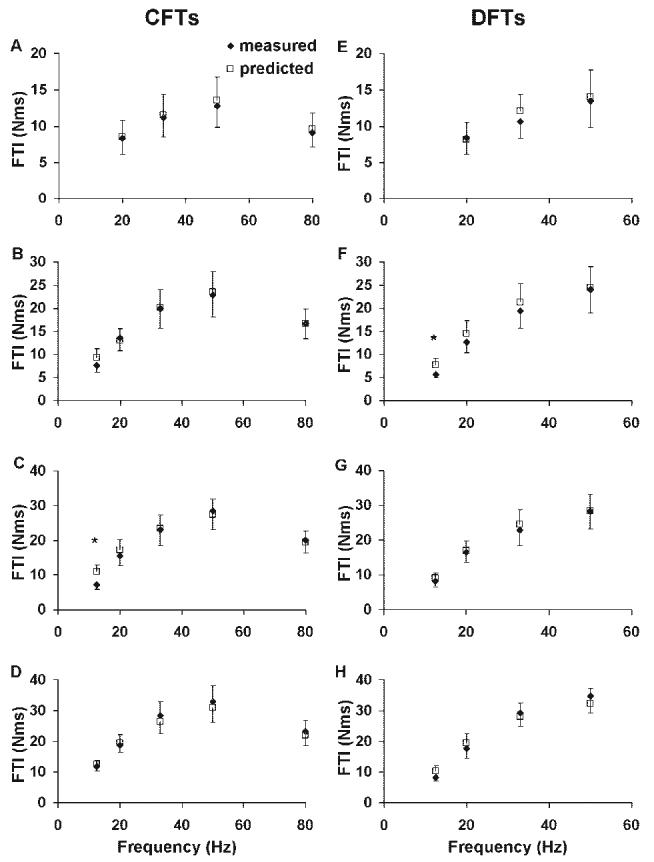
Comparisons between the measured (filled diamonds) and predicted (open squares) force-time integrals (FTIs) for CFTs (A-D) and DFTs (E-H) at each frequency tested. Data were collected at four different stimulation levels from the 10 subjects. Stimulus duration (intensity) was 150 μs, 250 μs, 350 μs, and 600 μs from the top panel down.

FIGURE 6.

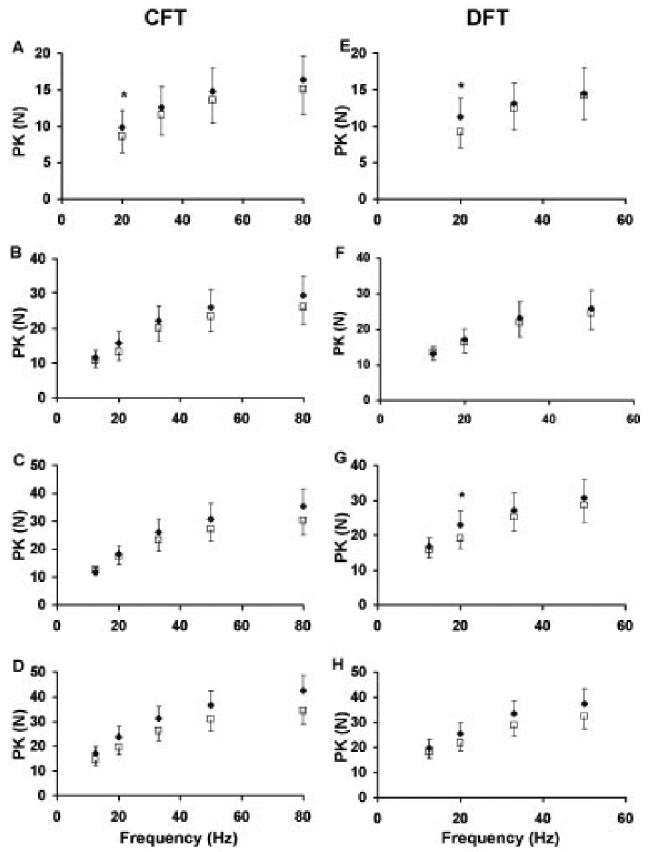
Comparisons between the measured (filled diamonds) and predicted (open squares) peak forces (PKs) for CFTs (A-D) and DFTs (E-H) at each frequency tested. Data were collected at four different stimulation levels from the 10 subjects. Stimulus duration (intensity) was 150 μs, 250 μs, 350 μs, and 600 μs from the top panel down.

DISCUSSION

Previously, we developed a model¹⁶ that successfully predicted the effects of stimulation frequency and pattern on force output of paralyzed skeletal muscle for patients with SCIs. In the current study the addition of an intensity component to our model, with only three additional parameters, enabled us to predict the effect of stimulation frequency, intensity (i.e., pulse duration), and pattern on muscle forces of SCI individuals. For each subject, after the values of the seven free model parameters (A, a′, pd₀, pd_t, K_m, τ₁, and τ₂) were determined using measured forces in response to eight stimulation trains (50-Hz CFTs and 20-Hz DFTs at stimulation intensities of 150-, 200-, 300-, and 500-μs pulse durations), the model successfully predicted PKs and FTIs for trains of two different patterns (CFTs and DFTs) over a wide range of stimulation frequencies (10-80 Hz) and intensities (150-, 250-, 350-, and 600-μs pulse durations). It is notable that our model successfully predicted forces at intensities different from the ones that were used to determine the parameter values (see Table 1).

Accurate predictive mathematical models can help to enhance FES systems. An ideal FES system needs both a feedforward model, which designs subject-specific and task-specific stimulation patterns, and a feedback controller, which corrects errors by informing the feedforward model when changes in stimulation patterns are needed.^1,6 When used in conjunction with a closed-loop controller, mathematical models can allow FES stimulators to deliver customized patient-specific stimulation patterns and perform FES tasks while continuously adapting stimulation parameters to the actual needs of the patient.³¹ The use of closed-loop control systems using customized stimulation patterns can reduce the energy expenditure and improve the speed at which functional tasks are performed during FES.³¹ Mathematical models have been developed to predict FES-induced standing movements,²⁴ to derive and optimize open-loop and closed-loop controllers,³⁰ and to provide insights into the internal dynamics of FES-induced muscle contractions.¹⁷

To our knowledge, only three previous modeling efforts^9,29,34 have taken into account the effects of both frequency and intensity on muscle force output. A detailed musculoskeletal model of the human knee to describe shank motion was developed by Riener et al.²⁹ and tested using measured data from quadriceps femoris muscles of paraplegic patients. The model was designed to take into account physiological conditions such as fatigue and the variation in the stimulation intensity at one stimulation frequency (20 Hz).²⁹ The authors reported good matching between measured and simulated data. Two major shortcomings are noted regarding this model.²⁹ First, the model is unable to predict the effects of varying stimulation frequency on force output. Second, the model is complex: it requires many parameters to describe the musculoskeletal system and would take longer to determine the parameter values for each subject. Watanabe et al.³⁴ developed a model with both stimulation frequency and intensity as inputs. Their model was tested with force-frequency data obtained from the tibialis anterior and the triceps surae muscles of rabbits and the flexor carpi radialis and flexor carpi ulnaris muscles of one neurologically intact patient at one testing intensity. The results showed that the model fitted well the normalized isometric force-frequency relationship for all the muscles tested. However, the effect of varying recruitment order on force output (i.e., the effect of varying stimulation intensity on force output) was not evaluated.³⁴ Chizeck et al.⁹ tested a muscle model on human subjects with lower-extremity paralysis due to SCI. Their model was able to predict the torque for stimulation trains up to 500 ms in duration; however, no predictive ability in stimulation pattern was demonstrated because the same stimulation patterns were used to determine model parameter values and to test the model.⁹ Once the stimulation pattern changed, the model parameter values needed to be recalculated, rendering their model incapable of identifying the optimal pattern for generating the targeted force.⁹

In 2005 we reported the ability of our isometric force model to predict the effects of stimulation frequency and pattern on quadriceps muscle forces of SCI individuals.¹⁶ The current version of our model has the advantage of also being able to predict the effects of stimulation intensity on paralyzed muscle forces. During previous testing of our model in SCI, τ_C was calculated by multiplying the subject's half-relaxation time by 0.22,¹⁶ resulting in an averaged τ_C value of 11 ms for both nonfatigued and fatigued muscles. In the present study, parameter τ_C was fixed at 11 ms because preliminary testing also showed that the model predicted well even with τ_C fixed at 11 ms. The scaling factor A from our previous model¹⁶ was modified with equation 3, which consists of three parameters—a, pd₀, and pd_t—to take into account the effect of stimulation intensity on muscle force output. Thus, the current model consists of seven free parameters, τ₁, τ₂, K_m, and A as a function of (a, pd₀, pd_t) (Table 2) that need to be determined for each subject. Our present model, which is able to predict the effects of stimulation intensity and frequency on muscle force, showed similar predictive ability to our previous testing on SCI individuals¹⁶ with ICCs (measuring agreement between measured and predicted muscle forces) in our present study (≥0.94) comparable to the ICCs obtained in our previous study on SCI (>0.90).¹⁸

In conclusion, a simple modification to our previously developed model¹⁶ (eq. 3) enabled successful prediction of effects of stimulation intensity on muscle force for two different pulse patterns (CFTs and DFTs) over a wide range of frequencies (12.5-80 Hz) in SCI subjects. With this ability to predict forces in response to a wide range of physiologically relevant stimulation trains of different frequencies, intensities, and patterns, the model provides a multidimensional prediction of skeletal-muscle force responses. Our model can identify subject-specific optimal stimulation schemes and accurately predict muscle forces for feedforward control, making it ideal for use in FES systems. This study is another step toward our long-term goal of incorporating an intensity component into our recently developed nonisometric model²⁸ to enable it to predict the effects of stimulation frequency, pattern, and intensity on muscle performance during FES for different muscle types in patient populations. We plan to incorporate this enhanced model into an FES control system to provide a more precise control of muscle output using both frequency and intensity modulation during FES tasks.

Abbreviations

CFT

constant-frequency trains

CNS

central nervous system

DFT

doublet-frequency train

FES

functional electrical stimulation

FTI

force-time integral

ICC

intra-class correlation coefficient

PK

peak force

SCI

spinal cord injury