Optimization of gene expression by natural selection

Abstract

It is generally assumed that stabilizing selection promoting a phenotypic optimum acts to shape variation in quantitative traits across individuals and species. Although gene expression represents an intensively studied molecular phenotype, the extent to which stabilizing selection limits divergence in gene expression remains contentious. In this study, we present a theoretical framework for the study of stabilizing and directional selection using data from between-species divergence of continuous traits. This framework, based upon Brownian motion, is analytically tractable and can be used in maximum-likelihood or Bayesian parameter estimation. We apply this model to gene-expression levels in 7 species of Drosophila, and find that gene-expression divergence is substantially curtailed by stabilizing selection. However, we estimate the selective effect, s, of gene-expression change to be very small, approximately equal to Ns for a change of one standard deviation, where N is the effective population size. These findings highlight the power of natural selection to shape phenotype, even when the fitness effects of mutations are in the nearly neutral range.

Abundant evidence indicates that natural selection is remarkably powerful in shaping nucleotide sequences (1, 2). Many tests of natural selection rely on a comparison between nonsynonymous sites, in which mutations affect protein sequence, and synonymous sites, in which mutations do not. Synonymous sites serve as a proxy for neutral sites, enabling the effects of selection to be distinguished from background mutational and demographic patterns. Although changes in gene expression are hypothesized to play a major role in adaptation (3, 4), changes in expression cannot be so easily partitioned into neutral and selected categories. Thus, methods derived to analyze selection in coding sequences cannot be readily applied to gene-expression data. In part because of this ambiguity, general forces acting on gene-expression divergence have remained unclear. At this point, there exists considerable debate over the relative importance of selection and random drift in shaping gene-expression levels (5–8).

The benefits of optimal gene regulation seem in many ways obvious. In the simple case of metabolic enzymes, under-expression may slow metabolic flux, while over-expression may expose the cell to additional toxic misfolded proteins (9). At the morphological level, gene regulation can be tightly coupled to phenotype (10, 11). Genetic mutations whose effects cascade into morphological differences are expected to have especially large fitness impacts, and as such will be heavily influenced by natural selection. A straightforward example of selection on gene-expression level can be seen in ribosomal proteins, which contrary to the neutral prediction are found to be highly expressed across a variety of organisms (12).

In this article, we present a model of gene-expression divergence that explicitly distinguishes between the forces of random genetic drift and natural selection. This work is based upon prior models of phenotypic trait evolution (13, 14). Our population genetic model is fundamentally similar to the Brownian motion model used to describe the random movements of physical particles (15). In both cases, the system is impacted by numerous tiny perturbations, in Brownian motion caused by collision but in the evolutionary context caused by mutations that are fixed in an evolving population. Owing to the central limit theorem, the resulting state of the system can be accurately described as a normally distributed random variable. In the simplest case, the probability of fixation of a random mutation is assumed to be independent of the current state of the system, and thus movement is not favored in one direction over the other. This scenario corresponds to selective neutrality. However, a slightly more complex model, described by the Ornstein-Uhlenbeck (OU) process, assumes that perturbations are more likely to shift the system toward some optimal value than away from it (16). This model does well to capture the essence of natural selection; mutations that produce a phenotype closer to some optimum are favored over those that produce a phenotype farther away.

Here, we analyze gene-expression levels across 7 species of Drosophila using the framework provided by the OU model. In the analysis, we compare expression divergence between species with estimates of time since their divergence based on sequence data. The pattern at which divergence in gene-expression levels accumulates over time does much to reveal the underlying forces of selection and drift. Using only species-level data, we find that stabilizing selection plays a major role in limiting divergence of gene-expression level. We also quantify the degree of selection and drift for specific genes, which illuminates the relationship between changes in gene sequence and changes in gene expression. Finally, we reconstruct the fitness landscape of gene-expression level, and find that although natural selection is pervasive in shaping gene expression, the individual fitness effects of changes in gene expression are rather weak.

Modeling Expression Divergence

Analogy to Brownian Motion.

Here we apply models of Brownian motion to describe the variance in gene-expression level between orthologous genes as a function of the time separating these orthologs (13, 14). Brownian motion, also known the Wiener process, represents one of simplest continuous-time, continuous-state stochastic processes. In a Brownian motion, the degree of stochastic change away from the current state is independent of both state and time. The increment that a Brownian motion makes over a time interval of length 1 is normally distributed with mean 0 and variance σ². The “volatility” parameter σ completely describes the Brownian motion and determines the rate at which a trait's value diffuses away from its current state. In an evolutionary context, σ describes that rate of “phenotypic drift” experienced by a gene. Our use of the term drift differs from the classic usage, wherein drift refers to a systematic trend in the evolution of a Brownian motion. Genes in which expression has a larger mutational target size (17) are expected to show larger values of σ. The probability density function of a Brownian motion is:

where x₀ is equal to the state of the process at time 0. Thus, Brownian motion predicts that the extent of variance in gene-expression increases in proportion to time. This scenario corresponds to selective neutrality, as the model assumes that change in expression is independent of current expression level.

Selection favoring an optimal level of gene expression can be incorporated using a simple extension to the Brownian motion model (13, 14, 18). This addition results in an OU or mean-reverting process (16). If Brownian motion is thought of as a particle that is subject to random perturbations from its surroundings, then an OU process can be thought of as adding an elastic spring to this particle, attaching it at some fixed point. As random perturbations push the particle farther away from this fixed point, the strength of elastic return increases proportionally. Thus, in addition to the stochastic force of drift, an OU process includes the deterministic force of selection pulling the trait toward some optimal value. The instantaneous motion of an OU process is described by:

where μ represents the optimal trait value, λ is proportional to the strength of selection, and σ is proportional to the strength of drift. Solving this yields the density function of an OU process:

Here we see that variance does not increase in proportion to time, and instead saturates at a stable equilibrium:

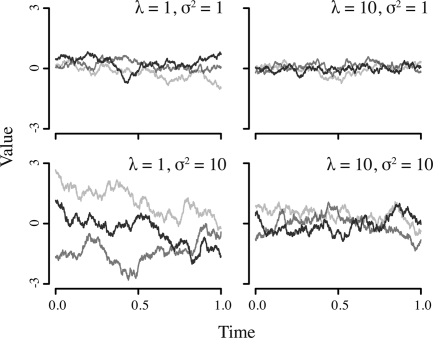
The temporal character of the OU model for various values of λ and σ is shown in Fig. 1.

Fig. 1.

Realizations of the OU process. Three individual realizations are shown for each of four different parameter values. The drift parameter σ determines the degree of mutational pressure randomly impacting the trait value, while λ determines the pull of selection toward some optimal trait value (in this case 0). In each realization, the starting value was sampled from the equilibrium distribution.

Inferring Fitness Landscapes.

We convert the OU parameters λand σ into population-genetic estimates of the strength of selection through comparison of the ratio of the instantaneous rates of positive change and negative change in the OU model to the ratio of fixation rates of selectively advantageous and disadvantageous mutations. We find that the ratio of instantaneous rates of change for the OU model is:

Following Kimura (19), we find the ratio of fixation rates between mutants of +Ns and −Ns effect to be:

Here, the equation is simplified by multiplying numerator and denominator by e^2Ns. Thus, the rate difference between positive and negative change in the OU model can be used to derive an Ns value by setting these two equations equal to each other and solving for Ns:

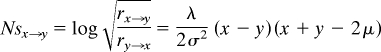If we measure relative to the optimum (i.e., fitness at optimum = 1), then this expression reduces to Ns(z) = 1 − z²λ/2σ² = 1 − z²/4v, where z represents the distance to the optimum in terms of standard deviations, and v represents expected equilibrium variance. Thus, the curvature of the fitness landscape is inversely proportional to the level of equilibrium variance observed. As such, we will refer to equilibrium variance as measuring the degree of selective constraint that the expression level of a gene experiences. It is this measure of selective constraint rather than the λ parameter that should be used in comparing selection across genes or across species, as the observed value of λ depends upon both selective constraint and mutational input.

Results

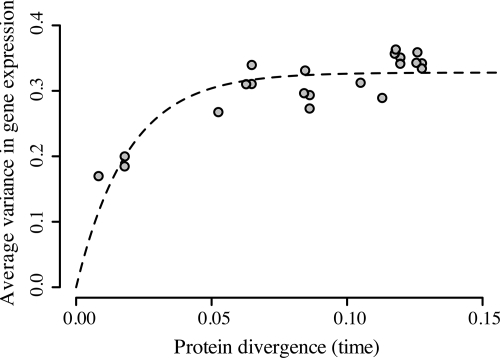
One key finding is that the accumulation of variance in gene-expression level between 7 species of Drosophila is not proportional to the amount of time separating each species (Fig. 2). This result immediately suggests that continuous neutral evolution of gene expression is unlikely. Instead, we find that expression divergence between orthologous genes saturates rapidly in evolutionary time. This general pattern was previously hypothesized to exist by Whitehead and Crawford (20). Species pairs of Drosophila do not show a significant increase in expression divergence beyond that present between D. melanogaster and D. ananasse. Saturation of gene-expression divergence is expected if expression levels are under stabilizing selection.

Fig. 2.

Average pairwise variance in expression level for Drosophila species. Each point represents the average variance between a species pair. This variance initially increases with time, but eventually saturates. In the absence of stabilizing selection, pairwise variance is expected to saturate at 1. Nonlinear regression fit of pairwise variance vs. time for the OU model is represented as a dashed line (λ = 26.14; σ = 4.14).

We describe this effect using the OU model of quantitative trait divergence. We find that the two-parameter OU model describes the observed saturation of gene-expression divergence remarkably well, accounting for 75.7% of the mean squared error in pairwise expression variance (see Fig. 2). Nonlinear regression estimates the selection parameter λ at 26.14 (95% confidence interval [CI]: 17.78–34.49) and the drift parameter σ at 4.14 (95% CI: 3.52–4.76). This value of σ suggests that, in the absence of selection, drift will perturb gene expression one standard deviation in the time it takes to accumulate 0.058 aa substitutions per site, or in Drosophila, roughly 41.7 million years (see Methods). Conversely, this value of λ suggests that selection will bring gene-expression level halfway toward its optimum value in the time it takes to accumulate 0.027 aa substitutions per site, or 19.0 million years. This result provides the timescale at which the phylogenetic signal of gene-expression variance decays with evolutionary distance.

Divergence in gene expression is limited physically by biochemical constraints on maximum transcription, and there must eventually be saturation effects because of these constraints. However, because the distribution of gene-expression values within each species is normalized, the predominate limitation will be statistical. Complete saturation of gene-expression divergence would cause orthologs to show independent values of gene expression: that is, expression in species A would be random relative to expression in species B. In this case, the variance in gene expression between pairs of independent genes is expected to equal 1. Hence, without selection, pairwise expression variance is expected to saturate at 1. However, we infer saturation of gene-expression divergence at σ²/2λ = 0.328 (95% CI: 0.309–0.337), consistent with stabilizing selection acting to limit expression divergence.

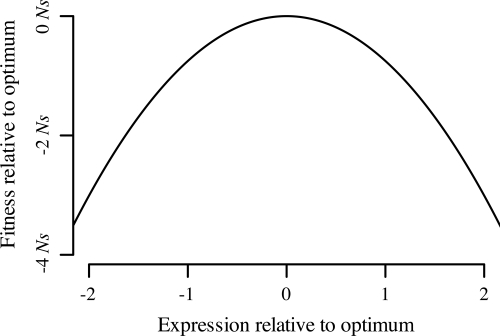
Additional insight into the underlying evolutionary process can be gained by using the OU model to estimate the fitness landscape for gene expression (Fig. 3). We estimate that an evolutionary change that causes gene expression to move from a point one standard deviation distant from optimal expression to a point matching the optimum exactly will have a selective effect of λ/2σ² = +0.763 Ns (see Fig. 3). To confirm these findings, we simulated evolution on this landscape under a strong-selection/weak-mutation model (19). We find that the equilibrium distribution of simulated trait values is normally distributed with a variance matching that predicted by the OU model [supporting information (SI) Fig. S1].

Fig. 3.

Fitness landscape of gene-expression level estimated from OU parameters. Expression level is measured in terms of standard deviations relative to other genes in the genome. Fitness is equal to −(λ/2σ²)(μ−z)², where z represents the current trait value. The quadratic shape of the fitness landscape is assumed by the OU model; the data provides the magnitude of curvature.

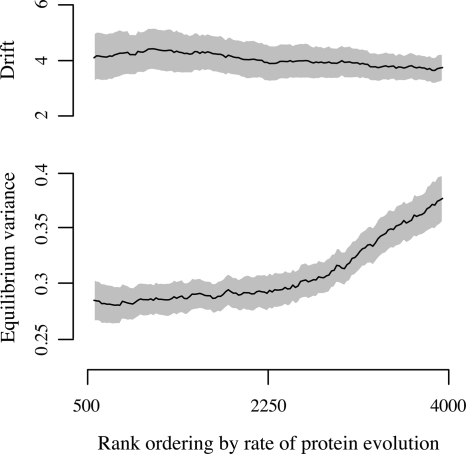
In agreement with previous research (21), we find that a gene's rate of protein-sequence evolution correlates with its level of gene-expression variance across the Drosophila phylogeny (ρ = 0.112, P < 10⁻¹⁵, Spearman rank correlation). However, using the OU model, expression variance can be decomposed into drift and selection. We find that the rate of protein-sequence evolution impacts a gene's level of selective constraint, but not its rate of phenotypic drift (Fig. 4). These results make intuitive sense, and support the OU process as a model for the evolution of gene expression.

Fig. 4.

Effect of protein-sequence evolution on patterns of gene-expression divergence. Nonlinear regression was used to estimate the drift parameter σ and equilibrium variance σ²/2λ in sliding windows across gene rank ordered according to their rate of protein-sequence evolution. Each window consists of 1,125 genes, or 25% of the total set of genes in which reliable alignments could be made. Mean estimates are shown as solid lines and 95% CIs shown as gray boundaries. Fast-evolving genes show similar rates of drift, but significantly greater levels of equilibrium variance, compared to slow-evolving genes.

Using gene-specific maximum-likelihood estimates, we find substantial differences in σ and λ across genes (complete data set available as Table S1). Selective constraint, measured as the equilibrium variance σ²/2λ, also varies significantly across genes (Fig. S2). However, even on a single-gene basis, very few genes show evidence for neutral evolution of gene expression (see Fig. S2). Only 68 genes out of 6,085 (1.1%) have an equilibrium variance greater than 1. However, because of small sample size (n = 7), the power of gene-specific inference is weak. On an individual basis, 2,459 genes out of 6,085 (40.4%) can reject equilibrium variance equal to 1 at the 5% level. For each gene, the gain in likelihood going from the neutral model (σ estimated; λ set to σ²/2) to the selective model (σ and λ estimated) was assessed, where 2 log (L_sel/L_neu) is assumed to be χ² distributed with one degree of freedom.

Discussion

Stabilizing Selection on Gene-Expression Level.

Differences in levels of gene expression between extant species have accumulated over time through the processes of random genetic drift and natural selection. We use a model of genetic drift and natural selection based upon the OU process to assess differences in gene-expression level between 7 species of Drosophila. Drift and selection act together to shape expression pattern in Drosophila (see Fig. 2). Each gene has an expression optimum, which selection seeks to preserve. Changes that move the population toward this optimum level are selected for, while changes that move the population away from this optimum are selected against. Interestingly, the magnitude of the selection we infer is quite small, on the order of Ns for a difference in expression deviating from the optimum by one standard deviation (see Fig. 3). This is within the range that many evolutionary biologists would regard as “nearly neutral” (22). Nevertheless, these small effects significantly limit the divergence of gene-expression levels. These findings highlight the “overwhelming odds against the less fit” (23) and the power of natural selection to shape phenotypic variation.

The extent of stabilizing selection on gene-expression divergence has been a contentious topic. Khaitovich et al. (5), using a similar approach to the present study, find that pairwise divergence in expression level increases in proportion to time across primates. The discrepancy between these results and our own may come from multiple sources. Khaitovich et al. examine chimpanzee, orangutan, and macaque expression levels using probes designed for human genes. In this case, sequence differences among species will mimic expression divergence (7), and so apparent expression divergence will continue to increase with time, even when the underlying expression divergence has saturated. Additionally, Khaitovich et al. define expression divergence as squared mean difference between species-specific expression levels. This statistic (unlike our measure of average variance, mean of one half of squared differences) is biased by an amount proportional to sampling variance. Phylogenetically distant comparisons had a smaller sample size than close comparisons and so were biased toward large estimates of expression divergence (7). Another study of primate-expression divergence using species-specific probes found that, in the majority of cases, a constant level gene expression across the phylogeny could not be rejected (24). Although this result is consistent with stabilizing selection, a low rate of neutral divergence will have the same effect. Other studies using various methodologies have suggested that stabilizing selection acts upon expression divergence (25–28). However, identifying stabilizing selection in these studies has relied on information in addition to species-specific expression levels. The OU model provides a simple framework for investigating stabilizing selection that requires only expression data from orthologous genes. The OU model allows the degree of stabilizing selection to be compared not only between genes but also between organisms.

Mutational Input and Genetic Drift.

Random genetic drift eventually results in the conversion of standing genetic variation into fixed differences. We find that empirical estimates of the rate of phenotypic drift in expression level are remarkably consistent with expected rates of random genetic drift, given levels of standing variation and effective population size. Phenotypic drift results in σ² = 17.14 units of variance in the time it takes to accumulate 1.0 aa substitutions per site. This is equivalent to 8.68 × 10⁻¹⁰ units of expression variance per generation (see Methods). Lande (13) gives the expected variance per generation because of random genetic drift as h²π²/N, where h² is the heritability of the trait, π² is the level of variance across individuals within a population, and N is the effective population size. Assuming h² = 0.5, π² = 0.0726 (based upon empirical comparisons between two strains of D. simulans), and N = 9.05 × 10⁶ [determined from synonymous genetic diversity in D. simulans (29) and inferred Drosophila mutation rate (30)], we arrive at an expectation of 4.02 × 10⁻⁹ units of variance per generation. The reasonably close correspondence between the empirical estimate and the theoretical prediction suggests that the OU model does well to describe the underlying evolutionary process.

However, mutation-accumulation experiments have suggested much larger values of mutational variance in gene-expression level, or ≈2.4 × 10⁻⁵ units of variance per generation (31). In this study, a relatively small number of individual mutations resulted in widespread changes in gene-expression level. This discrepancy can be reconciled by assuming that mutations of large effect would be purged by natural selection before reaching appreciable frequency and, hence, do not end up contributing to standing genetic variation. This phenomenon is another aspect of selective constraint. Our calculated rate of phenotypic drift of ≈10⁻⁹ represents the population-level turnover of standing variation into fixed differences, and not the input of variation because of new mutations.

Model Assumptions.

Our analysis has made several simplifying assumptions, including constant gene-expression optima, symmetrical mutation rates, and strong-selection/weak-mutation dynamics. If the optimum itself is subject to stochastic variation, then our analysis will underestimate the true strength of stabilizing selection. This is because movement of the optimum and subsequent tracking by natural selection will appear similar to weak selection poorly tracking a constant optimum. However, strong selection tracking a shifting optimum will result in decreased levels of standing variation compared to levels expected under a constant optimum. We find levels of within-population variation that are highly compatible with the observed rate of drift, suggesting that shifting optima have not had a major influence on our results.

We find that asymmetrical mutation should not significantly impact our results. We simulated evolution on the fitness landscape shown in Fig. 3 under a strong-selection/weak-mutation model, where the rate of mutation to lower expression was twice the rate of mutation to higher expression. We found that asymmetrical mutation had no discernable effect on equilibrium variance (Fig. S3), suggesting our estimates are robust to the presence of mutational asymmetry. Additionally, the results of Lande (13) suggest that our model is robust to the assumption of strong-selection/weak-mutation dynamics.

Throughout our analysis, we have assumed that species-specific normalization (see Methods) had little effect on our estimates of OU parameters. To assess the impact of this assumption, we performed simulations wherein expression levels of 10,000 genes were evolved according to the OU model and subsequently normalized in a species-specific fashion (Fig. S4). We find that normalization results in overestimation of the degree of selective constraint, suggesting that our conclusion of nearly neutral evolution is conservative.

Conclusions

It is well known that purifying selection constrains the rate of sequence change. Often, the reduction in evolutionary rate estimated using d_N/d_S is taken as a measurement of the degree of selective constraint. We find that selection, rather than simply decreasing the overall rate of expression divergence, instead curtails expression divergence in a nonlinear fashion. Thus, measurement of selective constraint on the evolution of continuous traits requires comparison of multiple orthologous trait values to be successful, but fortunately does not require a neutral proxy in the way of sequence evolution.

The OU framework presented here may be substantially extended to model further intricacies of gene-expression evolution. For example, large-scale fluctuations in λ and σ could be investigated by allowing branch-specific parameter values. We would expect fluctuations of effective population size to significantly impact inferred levels of selection. Additionally, it is possible to identify lineage-specific adaptation for a particular gene by allowing for multiple trait optima across a phylogeny (i.e., μ of D. melanogaster may differ from μ of other Drosophila). Standard methods, such as likelihood-ratio tests, could then be used to assess significance. It would be highly interesting to see whether lineages undergoing adaptive-sequence evolution also show evidence of adaptive gene-expression evolution. We believe that the OU model presented here will prove useful to the future study of gene-expression evolution, and to the study of phenotypic evolution in general.

Methods

One-to-One Orthologous Genes in 7 Drosophila Species.

Orthologous relationships from 7 Drosophila species (D. ananasse, D. melanogaster, D. mojavensis, D. pseudoobscura, D. simulans, D. virilis, and D. yakuba) were obtained from the AAAWiki (http://rana.lbl.gov/drosophila/wiki/index.php/; accessed March 2008) (32). Ortholog predictions were based upon fuzzy reciprocal BLAST clustering, and regions of poor alignment were screened via sliding window filter (32). To avoid complications caused by gene duplication and gene loss, only those genes that maintain a 1:1 orthologous relationship among all 7 species were analyzed. This methodology identified 7,415 orthologous genes.

Protein Sequence Change.

Alignments of orthologous coding sequences were also obtained from the AAAWiki (32). To control for alignment errors, we eliminated all alignments in which gaps accounted for >25% of total alignment length. The remaining 5,380 alignments were translated into amino acids and concatenated across proteins. These concatenated sequences were used to estimate evolutionary distance via the methods implemented in the amino acid-based likelihood (AAML) package of Phylogenetic Analysis by Maximum Likelihood (PAML) v3.13d (33). These methods give per-branch estimates of evolutionary distance that account for saturation effects because of multiple-hit sites. We take these estimates of evolutionary distance as proxies for evolutionary time. Evolutionary distances are shown in Fig. S5. Ref. 30 dates Drosophila species divergence by calibration based upon Hawaiian Drosophila. This yields a rough conversion of 707.7 million years for the accumulation of 1.0 aa substitutions per site, or alternatively 1.978 × 10¹⁰ generations, assuming 20 generations per year. Additionally, we used PAML to make gene-specific estimates of the rate of amino acid substitution. Gene-specific substitution rate is taken as the total rate of substitution across the phylogeny.

Gene-Expression Data.

Present-day gene-expression levels for all 7 Drosophila species were based upon data from Zhang et al. (34). Raw hybridization data were obtained from the Gene Expression Omnibus under accession GSE6640 (http://www.ncbi.nlm.nih.gov/geo/; accessed March 2008). For each array, we took the log₂ intensities of its probes and normalized these intensities to have mean 0 and variance 1. After normalization, we took the mean of all probes corresponding to a specific protein-coding mRNA as the expression level of that gene. We then took the mean of these gene-specific expression levels across 4 male and 4 female replicates. This resulted in a single expression level for each gene in each species. We limited the data set to include only those genes with unambiguous 1:1 orthologous relationships. Of the orthologous groups, 6,085 of 7,415 had expression data. We then renormalized the data so that each species shows mean 0 and variance 1. This methodology only stretches and shifts expression values, it does not alter the shape of the distribution. Regardless, we find that expression levels are approximately normally distributed (Fig. S6). Additionally, we compared the expression level of each of the 8 replicates of each species, finding very little differences. The square of the standard error across replicates was 0.012, suggesting that error variance did not significantly affect our results. Comparing 4 replicates of D. simulans strain 14021-0251.011 to 4 replicates of D. simulans strain 14021-0251.198 showed an average variance of 0.085, about half that of the average variance between D. melanogaster and D. simulans. As discussed in ref. 35, it is possible that species-specific probe effects may have added a small, but significant, proportion of the expression variance observed between orthologous genes.

Maximum-Likelihood Estimation of OU Parameters.

Gene-specific estimates of the OU parameters μ, λ, and σ were made through numerical optimization of the likelihood function. We take D. melanogaster expression as the starting point for the OU process, but obtain similar results using other species' values. The starting expression level x_mel is assumed to be drawn from the equilibrium distribution of the OU process:

Orthologous expression values in the other 6 species are distributed according to the multivariate normal distribution:

with vector of means:

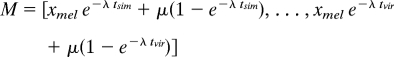and covariance matrix:

where t_sim represents the total divergence time separating D. melanogaster and D. simulans, t_vir represents the total divergence time separating D. melanogaster and D. virilis, and s_sim/vir represents the divergence time shared by D. simulans and D. virilis in their evolution away from D. melanogaster. Formulas for other species pairs follow the same pattern. Parameters μ, λ, and σ are estimated as those that maximize the likelihood function:

A step-by-step tutorial of this maximum-likelihood estimation technique can be found in the SI Appendix.