A zipper network model of the failure mechanics of extracellular matrices

Abstract

Mechanical failure of soft tissues is characteristic of life-threatening diseases, including capillary stress failure, pulmonary emphysema, and vessel wall aneurysms. Failure occurs when mechanical forces are sufficiently high to rupture the enzymatically weakened extracellular matrix (ECM). Elastin, an important structural ECM protein, is known to stretch beyond 200% strain before failing. However, ECM constructs and native vessel walls composed primarily of elastin and proteoglycans (PGs) have been found to fail at much lower strains. In this study, we hypothesized that PGs significantly contribute to tissue failure. To test this, we developed a zipper network model (ZNM), in which springs representing elastin are organized into long wavy fibers in a zipper-like formation and placed within a network of springs mimicking PGs. Elastin and PG springs possessed distinct mechanical and failure properties. Simulations using the ZNM showed that the failure of PGs alone reduces the global failure strain of the ECM well below that of elastin, and hence, digestion of elastin does not influence the failure strain. Network analysis suggested that whereas PGs drive the failure process and define the failure strain, elastin determines the peak and failure stresses. Predictions of the ZNM were experimentally confirmed by measuring the failure properties of engineered elastin-rich ECM constructs before and after digestion with trypsin, which cleaves the core protein of PGs without affecting elastin. This study reveals a role for PGs in the failure properties of engineered and native ECM with implications for the design of engineered tissues.

Tissue failure is characteristic of several life-threatening diseases, including capillary stress failure in the lung (1), pulmonary emphysema (2), vessel wall aneurysms (3, 4), and prosthetic heart valve failure (5). Whereas emergency surgery can be life saving for aneurysm patients (6), there is no cure for emphysema (7). These diseases are caused by various changes in the extracellular matrix (ECM) that lead to a weakening of ECM. A better understanding of the structure of the ECM, and how its components contribute to functional behavior (8), is necessary to provide insight into the development and progression of these diseases and will also be important if future tissue-engineered constructs are to be implanted in the body.

Elastin, collagen, and proteoglycans (PGs) are the principle components that form the complex structural network of the ECM that is necessary for tissues to function properly (9). Elastin and collagen are fibrous proteins capable of carrying loads and resisting tension (10, 11). PGs make up the gel in which elastin and collagen fibers are embedded and are necessary for the stability of the ECM (12). Varying the structure and composition of the ECM has major effects on its mechanical (9, 13–15) and failure properties (3, 16–21).

Independently, 2 groups have obtained similar surprising results related to failure of tissues composed primarily of elastin and PGs: Black et al. (17), using tissue-engineered ECM constructs, and Goodall et al. (22), studying the inferior mesenteric vein of patients with abdominal aortic aneurysm. Both groups found that elastin degradation led to a significant decrease in the maximum stress during a failure test (peak stress). Surprisingly, independent of digestion, the strains at which these tissues failed (failure strain) were in the range of 60–120%, much lower than the known failure strain of elastin, which is at least 200% (9). If elastin fibers percolate, i.e., reach uninterrupted from one end of the tissue to the other (23), one would expect the failure strain of the composite to be near that of elastin. Furthermore, in both cases, elastin degradation had no effect on the failure strain. These findings suggest that something other than elastin must contribute to failure.

We hypothesized that PGs contribute significantly to tissue failure. Specifically, if elastin does not form a percolating network, the failure of PG bridges between the elastin fibers should reduce the global failure strain of the ECM below that of elastin. To test this hypothesis, we developed a spring network model, the zipper network model (ZNM). The predictions of ZNM were then compared with measurements made on engineered ECM constructs containing mostly elastin and PGs before and after digestion with trypsin, a protease known to cleave the core protein of PGs (24) with little effect on elastin (5).

Results

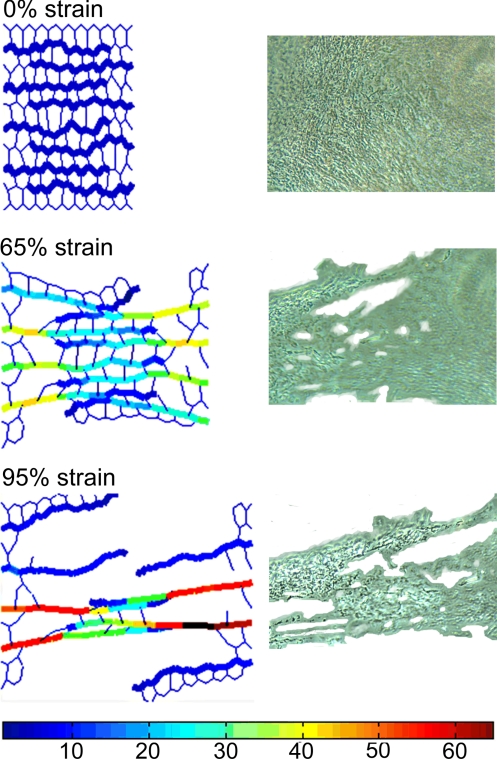
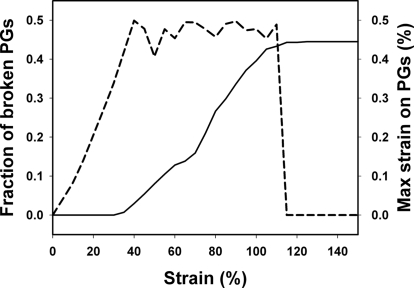
Sample images of the ZNM being stretched during a failure test are shown in Fig. 1Left. In the undeformed network, the elastin fibers, composed of a contiguous set of elastin springs, are wavy and arranged in a zipper-like formation. During stretch, these fibers gradually become straight while carrying most of the forces in the network (see animation in supporting information (SI) Movie S1). The individual elastin and PG springs fail when they experience 200% and 0.5% local strain, respectively. The maximum strain on PGs increases first nearly linearly with global strain (Fig. 2). Above 35% global strain, the maximum strain on PGs fluctuates near 0.5% as more and more PGs reach failure, whereas the fraction of failed PGs gradually increases to 45%. It is thus the failure of the PG bridges that eventually leads to a complete network failure at ≈100% global strain.

Fig. 1.

Failure of the ZNM and an engineered ECM construct. (Left) Images of the ZNM being stretched to various strains. The elastin fibers are drawn as thick lines and the PGs as thin lines. Note that the elastin does not percolate across the network. The color scale shows the relative forces on each spring. (Right) Phase-contrast images of a region of a tissue sample undergoing failure taken at strains comparable with those in the network model on the left.

Fig. 2.

The fraction of broken PG springs (solid line) and the maximum strain on the PGs (dashed line) as a function of global strain during a failure test of the ZNM. Curves represent the average of 7 simulations.

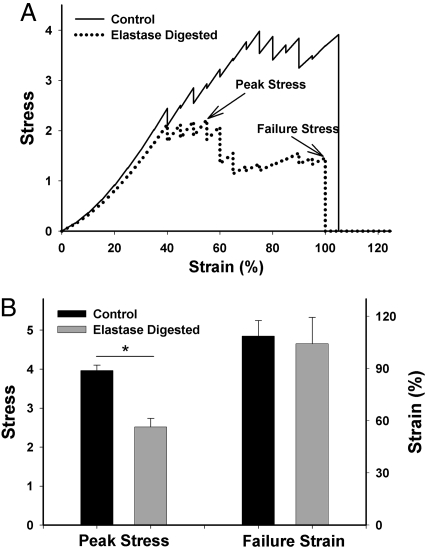
To mimic elastin digestion, half of the elastin fibers were cut into 2 fragments. This resulted in an elimination of 3.1% of the elastin springs from the network. Fig. 3A compares the stress–strain curves for a control and an elastin-digested failure simulation. The tests were repeated for 7 realizations of the random network. The peak stress significantly decreased by ≈40% (P < 0.001), whereas the failure strain of the network was 109 ± 9% and did not change with digestion (Fig. 3B).

Fig. 3.

Failure curves and the corresponding peak stresses and failure strains of the ZNM. (A) Sample stress–strain curves for model simulations with and without simulated elastase digestion. Peak stress and stress at failure, or failure stress, are indicated by arrows. (B) Failure data comparing control (n = 7) and elastase (n = 7) digestion simulations. Digestion leads to a significant drop in peak stress but no change in failure strain. Stress is in arbitrary units. *, P < 0. 001.

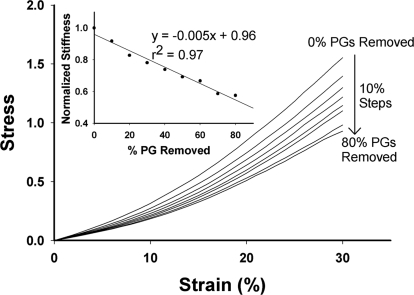
The effects of graded digestion of PGs on the stress–strain curves of the network are illustrated in Fig. 4. With progressive elimination of PGs, the curves shift down and to the right. The stiffness, defined as the local slope at 20% strain, decreased linearly with the amount of PGs eliminated (Fig. 4 Inset). Table 1 summarizes the failure data for several digestion groups. The model predicts that the removal of 60% of PGs decreases the peak stress and the failure strain by only 29% and 15%, respectively (P < 0.05).

Fig. 4.

Stress–strain curves of the model undergoing graded removal of PGs. (Inset) Stiffness of the model evaluated at 20% strain for the various PG digestion simulations. Stress and stiffness are in arbitrary units.

Table 1.

Failure data for control networks and networks with PGs removed

Simulation	Peak stress	Failure strain, %
Control	3.96 ± 0.14	108.6 ± 9.0
PGs digested, 30%	3.36 ± 0.19*	93.6 ± 5.6*
PGs digested, 40%	3.08 ± 0.14*†	94.3 ± 7.3*
PGs digested, 50%	2.97 ± 0.20*†	93.6 ± 6.9*
PGs digested, 60%	2.80 ± 0.35*†	92.6 ± 6.4*

For all simulations, the number of random networks used was 7.

*, significant difference from control (P < 0.05);

†, significant difference form 30% PGs digested (P < 0.05).

The ≈30% decrease in peak stress at 60% PG removal is a result of leaving dangling pieces of elastin that can no longer contribute to the stress. This is similar to the case when the elastin fibers are cut. Table 2 shows the total elastic energy of the springs as well as the percentage energy carried by elastin when the network reaches the peak stress. Note that for all simulations, the majority of the energy is carried by the elastin fibers. As PGs are removed, the absolute energy carried by elastin decreases, and this is the main cause of the decrease in total network energy and peak stress. Furthermore, although the elastin digestion results in a much larger decrease in total energy than PG digestion, the energy carried by the elastin is still near 90%.

Table 2.

Mean total elastic energy of the springs in the network for various simulations and the percentage of contribution of elastin to the total energy

Simulation	Total energy	Percentage carried by elastin
Control	95.8	93.3
PGs removed, 30%	67.5	93.3
PGs removed, 60%	56.0	94.8
Elastin digestion	38.6	89.7

The total energy (in arbitrary units) does not include bond bending (more details in Table S1).

Sensitivity analysis demonstrates that both the peak stress and the failure strain of the network linearly increase with the failure strain of the PG springs (see Fig. S1) while all other model parameters were held constant. These failure parameters also linearly depend on the spring constant k of the PG springs (see Fig. S2).

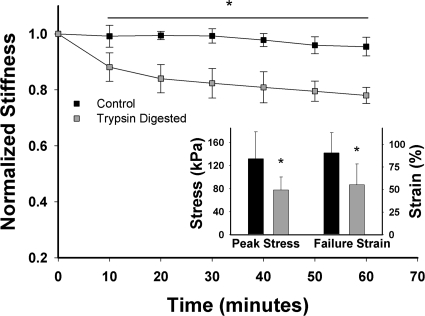
Microscopic images of a region of an engineered ECM sheet during failure test are compared with the failure of the model in Fig. 1. The quantitative predictions of the model (Fig. 4) are compared with experimentally measured stiffness and failure parameters in Fig. 5. Compared with controls, the stiffness decreased significantly during trypsin digestion of the constructs. After 30 min, the control samples did not change, whereas the stiffness in trypsin-digested samples dropped significantly to ≈75–80% of baseline. The trypsin digestion led to 31% and 29% drop in peak stress and failure strain (Fig. 5 Inset; P < 0.05). Biochemical analysis showed that the trypsin digestion eliminated 65% of chondroitin sulfate and 45% of heparan sulfate from the samples.

Fig. 5.

The mean and SD of stiffness measured at 20% strain as a function of time for control (n = 11) and trypsin-digested (n = 13) engineered ECM constructs. Values are normalized to the baseline at time 0. (Inset) Peak stress and failure strain for the control and trypsin digested groups. *, P < 0.05.

Discussion

We have developed a network model, the ZNM, to account for the structural roles PGs play in the mechanical and failure properties of elastin-rich ECM. The main findings are as follows. (i) The ZNM reproduces the essential stress–strain and failure properties of the ECM, such that the network fails at ≈100% strain while keeping elastin at its known failure strain of 200%. (ii) The ZNM also accounts for the previously reported effects of elastin digestion on the failure properties of engineered ECM sheets (17) and native vessels (22). (iii) The predictions of the ZNM were tested by using mechanical and biochemical assays after PG digestion. Of particular importance is the fact that, whereas in the above studies, elastin digestion did not alter the failure strain, PG digestion in this study did reduce the failure strain both in the experiment and the simulations. (iv) Finally, an important result of the network analysis is that elastin carries the load and determines the peak stress, whereas PGs reduce the failure strain of the network. Although many models have been proposed to mimic ECM mechanics (25–28), and the importance of PGs and their interaction with fibers have been recognized (29–31), these models have not been used to account for the macroscopic failure of the ECM. The overall success of the ZNM can be attributed to 2 features: its inclusion of separate failure properties for elastin and PGs and the unique organization of the elastin fibers into a particular formation in which fibers overlap one another in a zipper formation but do not percolate across the tissue.

The mechanism of failure of the ZNM is a gradual straightening of the elastin fibers, followed by pulling them out of the matrix by successively breaking the PG bridges, a previously uncharacterized network phenomenon. In an attempt to relate the ZNM to the composition and structure of the ECM, we estimated the average number of elastin fibers per unit area (≈10 fibers per μm²) from electron microscopic images (32). We also measured the total glycosaminoglycan (GAG) content of 3 ECM constructs (≈1 μg/cm²) using elastase digestion (33), followed by dimethylmethylene blue assay (34). Although various PGs have very different numbers of GAG chains (35), for simplicity, we assume that on average, there are 10 GAGs on each PG. Taking 45 kDa as the average mass of GAGs, the number of PGs per unit area is ≈1,300 PGs per μm². This calculation is, however, based on dry weight without taking hydration into account. Elastin is not sensitive to hydration (36), whereas PGs in solution inflate, and we estimated that hydration can increase their volume at least by a factor of 10 (37). Therefore, an elastin fiber would be surrounded by ≈10–100 hydrated PGs, which is the same order of magnitude used in the ZNM.

Although there are no simple ways to selectively eliminate all of the various PGs from the ECM without altering the levels of other proteins, we chose trypsin digestion because trypsin is known to digest the protein core of PGs (24). Trypsin cleaves after arginine and lysine residues (38), also found in elastin. To ensure that elastin was not degraded by trypsin, we measured the amount of elastin in the ECM samples with an ELISA after trypsin digestion at increasing concentrations up to 33 times that used in the mechanical tests. We found no effect of trypsin on elastin levels, suggesting that the mechanical changes in Fig. 5 were not the result of elastin digestion but were instead due to elimination of PGs.

To compare the modeling results of PG digestion (Table 1) to experimental data (Fig. 5), we determined the relative amounts of the various GAGs in these ECM sheets using ³⁵SO₄ radiolabeling and cationic nylon filtration (39) and found that ≈85% of the GAGs in these ECM sheets is chondroitin sulfate. Thus, the total amount of GAGs eliminated during trypsin digestion was 61%, and hence the experimental data should be compared with the simulation results in Table 1 at 60% PG removal. Note that during simulated digestion, the 60% is removed randomly, whereas during stretch (Fig. 2), 45% of PGs break in a correlated manner as a result of avalanching (see Methods).

The elastin-related model parameters were chosen based on literature (9) and our previous study (19). The failure properties of the PG springs were optimized to match published failure data after elastin digestion (17). These model parameters were then used to a priori predict the effects of trypsin digestion. The drop in peak stress (Table 1) is in excellent agreement with experiments (Fig. 5). However, the failure strain and its drop after trypsin digestion are lower in the model. The likely reason is that the failure strain in our previous study (17) was higher than in this study because of the variability between different batches of the cell culture-based ECM sheets. Nevertheless, the peak stress and failure strain of the model are linearly related to the failure strain (see Fig. S1) and the spring constant of the PG springs (Fig. S2). Hence, it is possible to find parameter combinations such that the model simultaneously matches all of the measured properties reported here.

The PG failure threshold used in this study may seem unrealistically low. Redaelli et al. (40) suggest a much higher failure strain for PGs in tendons. However, there are several mechanisms that can contribute to an increased network failure strain. For example, one can find another ratio of the spring constants for elastin and PGs such that the PG failure threshold can be much higher. Because these parameters are interdependent, it is difficult to predict the precise physiological values for each because of the lack of relevant experimental data.

The model does make several assumptions and simplifications. Elastin fibers in the ZNM are organized, much more so than in real tissue. Because of this organization, the model produces realistic failure mechanics only when stretched in the direction of the fibers. The elastin fibers do not percolate, and there is no vertical cross-section composed only of PGs. Hence, failure occurs by pulling the elastin fibers out of the PG matrix. However, if the ZNM was stretched in the direction perpendicular to the fibers, its failure strain would be equal to that of the PG's, because there are horizontal cross-sections composed purely of PGs. It is therefore expected that if the fibers had random orientation, the failure strain of the PGs would have to be between their current value of 0.5% and the failure of the whole network, ≈100%, which would provide more realistic estimates of PG failure.

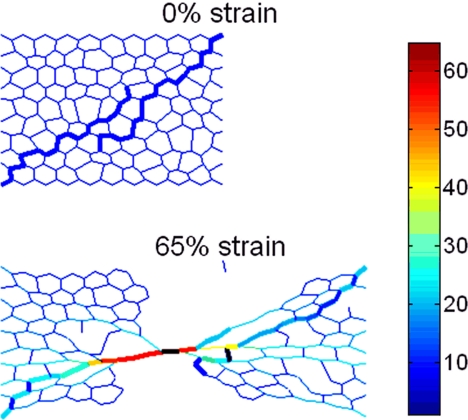
Fiber alignment was further investigated through additional simulations that include 2 elastin fibers initially not aligned with the direction of strain. These fibers overlay one another such that the PG network does not percolate (Fig. 6A). As the network is stretched, the PGs begin to break, and the elastin fibers show increasing alignment with the direction of strain (Fig. 6B). This network has a failure strain of ≈70% (see animation in Movie S2). The decrease from the 100% failure strain of the ZNM is due to several factors. First, because PGs are initially more aligned with the direction of strain, they will also experience a larger local strain for any given global strain. This again could indicate that the actual failure strain of PGs is higher than the one chosen for the ZNM. Second, this simulation possesses a much smaller elastin-to-PG ratio and, hence, more springs in the network with a very low failure strain. Finally, although the fibers in this simulation were longer than those in the original ZNM, they are directly connected by fewer PGs. Hence, fewer PGs share the same load, and hence, there is an increased strain on individual PGs. Thus, an important limitation of the ZNM is the lack of random orientation of fibers, which leads to an underestimation of the failure strain of PGs. The ZNM was constructed as a 2D model because the thickness-to-width ratio of the ECM sheets that we used was <0.005. It is difficult to construct a network with random orientation of fibers in 2D, a limitation that can be overcome in 3D models. Thus, apart from the limitation of fiber orientation, the ZNM is a realistic model of the failure process, and the model's results suggest a previously uncharacterized role for PGs: Because it is the PGs that fail in the end, they control the strain at which the macroscopic tissue fails.

Fig. 6.

Images of a network that contains 2 elastin fibers at network strains of 0% and 65% strains. Note that at 0% strain, the fibers are not aligned with the direction of strain.

The model also suggests that elastin plays an important role structurally and in the mechanics of elastin-rich constructs or native tissue. Elastin fibers carry the bulk of the load when tension is applied, and thus elastin determines the maximum stress that the tissue can carry before failure. This conclusion is also based on the fact that removing only 3.1% of the elastin springs produced the greatest decrease in peak energy of all of the model simulations (Table 2).

Besides the role identified for PGs in tissue failure, our results have implications for tissue engineering. In designing tissue-engineered materials, it is important to match the mechanical properties of the native tissue if the replacement tissue is to function properly in the body. However, the replacement tissue should also be able to withstand the naturally occurring stresses and strains even during diseases with proteolytic activity. Our results now provide an understanding of what components and organizational features of the ECM determine these properties and hence may offer a rational basis for future design of engineered materials with target functional properties.

Methods

Network Model.

The model consists of 286 linear springs accounting for the stiffness of elastin and PGs combined into a hexagonal lattice, with pin joints connecting the springs. The network also contains torsional springs, which resist angular rotation of the springs around the pin joints. The total elastic energy, E, of the network is given by E=1/2 Σ (kΔl²+bΔθ²), where Δl is the change in length of the spring from its stress-free initial length, k is the spring constant, b is the angular spring or bond bending constant, and Δθ is the change in angle between 2 springs from the stress-free initial angle. The summation runs through all linear and bond-bending springs. Bond bending resists the springs from aligning with the direction of strain and is related to the compressibility of the PGs and possibly the bending stiffness of elastin fibers.

During the simulations, the left boundary was fixed; the right boundary was moved in small steps to mimic stretching, whereas the top and bottom boundaries together with internal nodes were free to move. The network configuration was found by minimizing E by using simulated annealing (41). Specifically, each node was moved in the direction of its equilibrium by a small amount. If the change in total energy (ΔE) was negative, the new configuration was accepted, otherwise it was accepted based on the probability P = exp(−ΔE/T), where T is a control parameter. This procedure was then repeated until ΔE/E remained lower than a threshold for 10 iterations. Stress was calculated at each strain by numerical differentiation of E (42).

ZNM.

In the ZNM, elastin and PG springs have k values of 6 and 2 and strain failure thresholds of 200% and 0.5%, respectively. The bond-bending constant is b = 0.1. Because the ratios of spring constants determine the behavior of the ZNM, these constants have arbitrary units. The springs are arranged such that there are long fibers of elastin springs that are embedded in a network of PG springs (Fig. 1). Note that the elastin fibers do not percolate across the tissue; instead, they reach ≈3/4 of the way across and overlap from opposite sides creating a “zipper-like” formation. This topology, selected after preliminary testing with various configurations, was the simplest that allowed the largest number of fibers in the network without reaching percolation. Variability was introduced by setting k of all springs first in the range of 1 ± 0.9. The network was then solved, providing variability in the hexagonal “cell” size of ≈30%. The resulting node locations were saved and loaded into place for the ZNM. The new spring lengths were then set as the initial conditions of the network, and k was reassigned as above. This procedure allows for an initial heterogeneity of the model mimicking intersample variability in the experiments.

Testing the ZNM.

The ZNM was stretched in steps of 5% strain until failure. At each strain, the model was solved, and springs were removed if they had been stretched beyond their strain threshold. Initial testing provided model parameters that produced failure parameters of the network similar to data from actual experiments (17). Next, the ZNM was used to test a phenomenon referred to as avalanching. This occurs when the breaking of one spring leads to a condition that causes other springs to break without the network being further stretched. We found that without avalanching, increasing strain step sizes led to increasing values of peak stress and failure strain. During avalanching, however, the model was insensitive to step size. Because the peak stress and failure strain should not depend on how the stress–strain curve is recorded, the more realistic avalanching was kept throughout. To examine finite size effects, the size of the ZNM was doubled, and the failure properties were calculated. The wider model showed a slight increase in maximum stress but no change in failure strain. The effects of enzymatic degradation were obtained through simulations. It is believed that elastase cleaves the elastin at certain amino acids and does not completely dissolve the protein (43). This leaves behind shorter strands of elastin still embedded in the PGs. Thus, elastin digestion was mimicked by removing a single spring from an elastin fiber. The digestion of PGs was simulated in 2 ways. First, because of their negative charges, GAGs draw water into the tissue (44), and they help to fill volume, thus keeping ECM proteins from easily aligning with the direction of strain (42). This is precisely the role of bond bending. Thus, simulations with and without bond bending were compared. Second, PGs should also play a role in transferring shear stress during stretch. To test this, increasing percentages of the PG springs were removed from the network. Eliminating the PG springs had a stronger effect on the failure properties than eliminating bond bending, and hence, only the former was used in subsequent simulations.

Tissue Culture.

The ECM constructs containing elastin and proteoglycans were obtained as described by Stone et al. (45). Briefly, the constructs were acquired from neonatal rat aortic smooth muscle cells (NNRSMC) isolated from Sprague–Dawley rats, 1–3 days of age. The NNRSMCs were then grown in culture containing 3.1 mg/ml sodium bicarbonate, 1% sodium pyruvate, 1% penicillin and streptomycin (DV3.7), and 20% FBS. The samples were maintained for 6 weeks, and the media was changed twice a week. The cells were killed by using 5% sodium azide in Puck's solution and the constructs stored at 4 °C. A gelatin solution was then added to the cultures that allowed the constructs to be removed safely.

Mechanical Testing.

Tissue mechanics were tested by using a method similar to that described by Black et al. (17). Tissue strips, with dimensions 15 × 5 mm, were attached to metal plates by using cyanoacrylate glue. The plates were then attached to steel wires connected to a force transducer (model 403A; Aurora Scientific) and a dual force transducer and lever arm (model 300B; Aurora Scientific). The larger-scale transducer was required for failure test data, whereas the more sensitive transducer was used to obtain stress–strain curves for lower strains. The 22-ml sample bath was filled with PBS, and the entire apparatus was placed on a heat stand until the gel melted away at 50 °C. The PBS was then removed, and the bath was refilled with PBS and maintained at 37 °C.

Samples were preconditioned by stretching up to 25% strain 3 times, followed by 5 min of equilibration. Baseline stress–strain curves were taken, and 66 μg (2.6 nmol) of porcine pancreatic trypsin (type IX; Sigma) was added to the baths of the digestion groups. The trypsin was treated with succinyl alanyl prolyl valyl chloromethyl ketone to inactivate any elastase contaminant. This trypsin preparation exhibited undiminished activity against the synthetic trypsin substrate, tosyl arginine methyl ester (26). Stress–strain curves from each sample were then collected every 5 min for up to 30 min. Separate control and trypsin-treated groups were prepared in a similar fashion and were stretched to failure after 30 min of digestion.

To obtain stress–strain data, samples were stretched uniaxially by using a triangular wave, up to 25% strain at a rate of 0.75% strain per second. Strain is defined as the displacement divided by the initial length of the sample, and stress is defined as the force over the cross-sectional area of the sample at zero strain. Stiffness was obtained by calculating the slope of the stress–strain curve at 20% strain.

Imaging.

Thickness of the samples was determined by using a laser scanning confocal microscope (FV-1000; Olympus). Because elastin autofluoresces, no specific labeling was necessary. The emission spectrum was mapped by using a 488-nm argon laser excitation, and images were collected from emission between 500 and 600 nm. Multiple stacked images with varying Z-position were collected, and the thickness of the samples was determined as the half-width of the mean intensity profile in the Z-direction. Thickness data were taken on samples, with and without trypsin digestion, at strains between 0 and 40%, at 10 locations in 1 sample per group. At 20% strain, the thickness of the control and trypsin-digested sample was 21 ± 3 μm and 10 ± 2 μm, respectively. These values were used in the calculation of stress.

Proteoglycan ELISA.

NNRASMC cultures were subject to trypsin and GAGase treatment, and the matrices were fixed by using a 2-step fixation process with 95% methanol and 3.7% formaldehyde. For heparan sulfate detection, control and Heparinase III-treated cells were incubated with a 1 μg/ml solution of heparan sulfate stub antibody (clone F69-3G10) and a 0.16 μg/ml solution of peroxidase-conjugated goat anti-mouse IgG. For chondroitin sulfate (CS) detection, control and chondroitinase ABC-treated cells were incubated with a 0.5 μg/ml solution of anti-proteoglycan Di-4S (clone 2B6; Seikagaku Biobusiness Corporation) and 0.4 μg/ml solution of peroxidase-conjugated goat anti-mouse IgG. The reactions were developed by using the TMB Microwell Peroxidase Substrate System (KPL) and stopped with the addition of 0.5 M sulfuric acid. The absorbance was read at 450 nm and at 570 nm (background correction). Relative levels of HS and CS were determined by the magnitude of the signal observed with the relative enzyme lyase treatment minus that observed without lyase.

Statistical Analysis.

All data are presented as the mean ± standard deviation. Different groups were tested with 1- and 2-way ANOVA, and a significant difference was defined as P < 0.05.