Signaling gradients in cascades of two-state reaction-diffusion systems

Abstract

Biological networks frequently use cascades, generally defined as chain-like arrangements of similar modules. Spatially lumped cascades can serve as noise filters, time-delay, or thresholding elements. The operation and functional capabilities of spatially distributed cascades are much less understood. Motivated by studies of pattern formation in the early Drosophila embryo, we analyze cascades of 2-state reaction-diffusion systems. At each stage within such as a cascade, a diffusible particle is reversibly bound by immobile traps and can be annihilated in both mobile and immobile states. When trapped, these particles drive the next stage by converting mobile particles of a different type from a passive to active form. The cascade initiated by injection of mobile particles into the first stage. We derive analytical expressions for the steady-state concentration profiles of mobile and immobile particles and analyze how the output of a cascade is controlled by properties of the constituent stages.

Biological networks frequently use cascades, generally defined as chain-like arrangements of similar modules. Among the numerous examples of cascades are proteolytic cascades in blood clotting, phoshorylation cascades in intracellular signal transduction systems, and gene expression cascades that control cell differentiation. Biophysical studies of lumped cascades have shown that they can serve as noise filters, time-delay, or thresholding elements, but the operation and functional capabilities of spatially distributed cascades are much less understood (1–6). One class of problems where this understanding is necessary arises in studies of embryonic pattern formation.

In a common mode of developmental patterning, a layer of cells is presented with a concentration field of a molecule that acts, not necessarily directly, as a dose-dependent regulator of gene expression. Thus, one spatially distributed signal, called a morphogen gradient, can generate a precise spatial arrangement of cell fates (7, 8). A patterning gradient can lead to the production of another molecule which can act as an intermediate link between the original signal and its transcriptional targets. For instance, in the developing Drosophila wing, a short-ranged gradient of a diffusible ligand Hedgehog, induces the production of a long-ranged diffusible ligand Dpp, which controls the expression of multiple genes responsible for wing patterning (9).

Similar cascades exist in other developmental contexts, but their quantitative understanding, required for interpreting the wild-type patterns and defects in mutant genetic backgrounds, is yet to be developed (10). In particular it is not clear how the output of the cascade is shaped by its individual stages. Here, we answer this question for cascades of 2-state reaction-diffusion systems. Each of the individual stages within such a cascade is a system where a diffusible particle is reversibly bound by immobile traps and can be annihilated in both mobile and immobile states. The output of a stage, given by the distribution of immobile particles, provides an input to the next stage.

Our interest in such models is motivated by experimental studies of patterning of the early Drosophila embryo, which is initiated by four different morphogen gradients (11, 12). Two of these gradients, responsible for the dorsoventral and terminal patterning, are established by cascades of reaction-diffusion modules (11). The dorsoventral gradient depends on a cascade of extracellular proteolysis reactions, similar to the ones characterized in the blood clotting system (13, 14). The transcriptional response to this gradient has been extensively studied, but the gradient itself is yet to be quantified (15, 16). On the other hand, the terminal gradient has been recently quantified, and, as we argue below, it can be viewed as a cascade of 2-state systems (17).

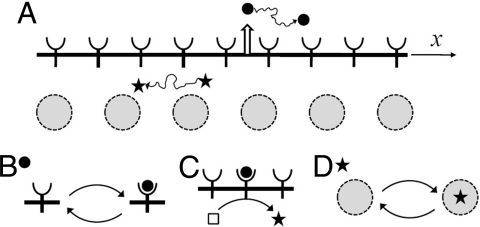
The terminal gradient depends on a highly conserved MAPK pathway (18), which is activated by Torso, a receptor that is uniformly distributed along the surface of the embryo (Figs. 1A and 2A) (19, 20). Torso, in turn, is activated by Trunk, its diffusible extracellular ligand produced at the embryonic poles. Binding to Torso interrupts diffusion of Trunk and generates a ligand–receptor complex that can either dissociate or be internalized by the cell (21). The complex does not diffuse at appreciable rates along the plasma membrane of the early embryo and can be considered immobile (22). This set of processes is thus a 2-state system, where diffusible Trunk is reversibly bound by immobile Torso receptors (Fig. 1 A and B).

Fig. 1.

Summary of the processes in a 2-stage cascade of two-state systems. (A) A diffusible ligand (solid circle) is reversibly bound by cell surface receptors. A diffusible intracellular molecule (star) shuttles in and out of the nuclei. (B) Transitions between mobile and immobile states for a particle in the extracellular stage of the cascade. (C) Immobile particles in the first stage initiate the production of mobile particles in the second stage. In this case, a ligand-receptor complex is an enzyme acting on a pool of inactive intarcellular molecules (present in excess; denoted by an empty square). (D) A mobile intracellular molecule is reversibly trapped by immobile traps. In this case, the traps are nuclei distributed in a shared cytoplasm of the early embryo.

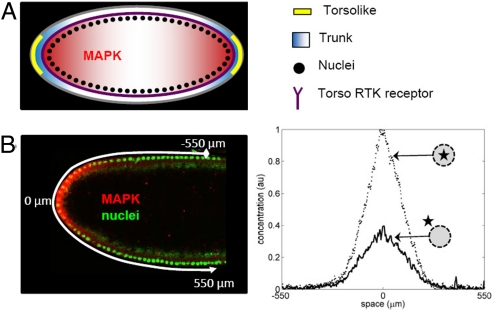
Fig. 2.

Terminal patterning system in the early Drosophila embryo. (A) Torso receptors (purple) are uniformly distributed along the plasma membrane of the embryo. Inactive ligand (Trunk) is distributed uniformly in the extracellular matrix; it is converted into an active and diffusible form (blue) by Torsolike (yellow), a protein localized at the poles of the embryo. The Torso-Trunk complex signals through the MAPK signalin cascade, which leads to MAPK phosphorylation and nuclear import. (B) Quantified pattern of MAPK phosphorylation. (Left) Fluorescent image of the anterior of the embryo; nuclei are stained in green, and phosphorylated MAPK is stained in red. (Right) Gradients of nuclear and cytoplasmic phosphorylated MAPK.

The cytoplasmic tail of the Torso–Trunk complex acts as a tyrosine kinase (21, 23, 24), setting in motion a sequence of events that lead to MAPK phosphorylation (Fig. 1C). The pattern of phosphorylated MAPK, with 2 peaks at the poles of the embryo, can be visualized using an antibody that recognizes the phosphorylated form of MAPK (25) (Fig. 2B Left). Phosphorylated MAPK diffuses inside the early emrbyo, where multiple nuclei are uniformly distributed in the shared cytoplasm (26). Phosphorylated MAPK shuttles in and out of the nuclei, which interrupts its cytoplasmic diffusion, and can be dephosphorylated in both of these compartments (27–29). These processes define another two-state system, in which nuclei trap phosphorylated MAPK (Fig. 1D).

This model, suggested in our recent studies of the terminal gradient, motivates the mathematical analysis presented here. The article is organized as follows. In the next section, we derive the propagator for a particle in a 2-state system. We then use this propagator to analyze the concentration fields in 2 state systems. Next, we analyze the output of a 2-stage cascade with either localized or distributed inputs. Finally, we discuss the applicability of the model to the terminal patterning system.

Results

Propagator for a 2-State System.

Consider a particle that can be in the mobile (m) and immobile (im) states. The mobile (diffusible) particle reversibly binds to one of the immobile traps. Diffusion is 1D and occurs along the x-coordinate. The diffusion constant is denoted by D. The particle binding and release are first-order processes characterized by the rate constants α and β, respectively. The particle can be annihilated in both mobile and immobile states. The annihilation step is also a first-order process, characterized by the rate constants k_m and k_im in the mobile and immobile states, respectively.

The particle is injected at the origin, x = 0, in the mobile state at time t = 0. The 2-component propagator, G_v (x, t), is the probability density of finding the particle at point x and state v at time t, v = m, im. The components of G_v (x, t) satisfy:

The initial conditions are:

After the Fourier-Laplace transformations defined in the conventional way,

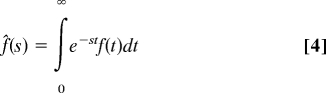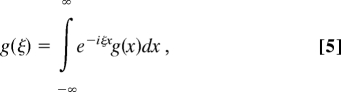the evolution equations for the components of the propagator take the following form:

From this, we find:

Below, we use these transforms to find the gradients (concentration profiles).

Gradients in 2-State Systems.

Consider time-dependent concentration profiles, C_v (x, t), v = m, im, when particles are injected into the mobile state with the injection rate j(x, t). The injection begins at t = 0. Concentrations C_v (x, t) satisfy:

with C_v (x, 0) = 0. Solutions to these equations can be written as convolutions of the propagators and the injection rate:

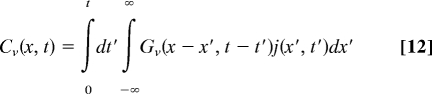The Fourier–Laplace transforms of these solutions are

where ĵ (ξ, s) is the Fourier-Laplace transform of j (x, t).

When particles are injected at the origin with time-independent rate Q, we have j (x, t) = Qδ(x) H(t), where H(t) is the Heaviside step function. In this case ĵ(ξ, s) = Q/s and Eq. 13 takes the form

As t → ∞, the concentration profiles approach their steady states (ss), C_v,ss (x), given by

The Fourier tranform of C_v,ss (x) is

Using Eqs. 8 and 9, we obtain

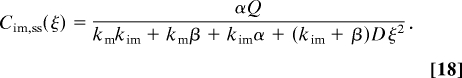Inverting these transforms, we find the gradients of the mobile and immobile particles:

where λ is the characteristic length scale of the gradient, and N_v,ss are the total numbers of particles in the steady-state concentration profiles

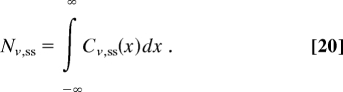N_v,ss and λ can be expressed in terms of the parameters of the problem:

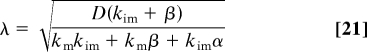Gradients in a 2-Stage Cascade.

Consider now a 2-stage cascade of 2-state systems (Fig. 1). Mobile particles are injected into the first stage by a point source at the origin. Injection starts at t = 0 and generates particles with a constant rate Q. These particles are reversibly trapped by the boundary separating the 2 stages of the cascade. Trapped particles initiate the generation of mobile particles in the second system, with the generation rate, j₂ (x, t), given by

where g is the rate constant of the generation process, and C_v⁽ⁱ⁾ (x,t) are the concentrations of mobile and immobile particles, v = m, im, in the i th stage of the cascade. The concentration C_v⁽ⁱ⁾ (x, t) satisfies

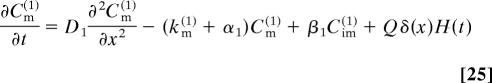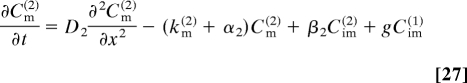and the initial conditions are C_v⁽ⁱ⁾ (x, 0) = 0. Here, D_i, α_i, β_i, and k_v⁽ⁱ⁾ are the diffusion constant and rate constants of the corresponding processes in the i-th stage.

Using the result in Eq. 14, we can write the Fourier-Laplace transforms of the gradients in the first stage as

where Ĝ_v⁽ⁱ⁾ (ξ, s) is the Fourier-Laplace transform of the propagator G_v⁽ⁱ⁾ (x, t) in the i th stage. Then the Fourier-Laplace transform of j₂ (x, t) in Eq. 24 is

Using Eq. 13 to find the transforms of the concentrations in the second stage, we obtain

As t → ∞, the gradients in both stages approach their steady states, C_v,ss⁽ⁱ⁾ (x):

The Fourier transform of C_v,ss⁽ⁱ⁾ (x) is

For the first stage, we have

where λ₁ is the characteristic length associasted with this stage:

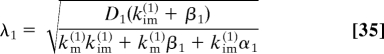and N_v⁽¹⁾ are the total numbers of mobile and immobile particles in the steady-state concentration profiles in the first stage:

Inverting the transform in Eq. 34, we find

The Fourier transforms of the steady-state gradients in the second stage are given by

Using Eqs. 8 and 9, we obtain

where λ₂ is the characteristic length of the second stage:

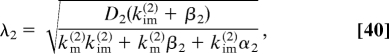and N_v⁽²⁾ are the total numbers of mobile and immobile particles in the steady-state gradient in the second stage

where Q₁ is the intensity of the δ source located at the origin

Inverting the transform in Eq. 39, we find the steady-state gradients:

where p₂ (x) can be interpreted as the probability density of finding a particle at point x

This function determines the shape of the steady-state gradients in the second stage.

The length L₂, which characterizes the decay of p₂ (x) from its maximum value at x = 0, p₂ (0) = 1/[2(λ₁ + λ₂)], is given by

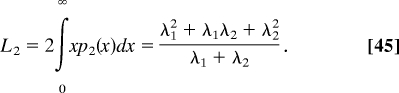As might be expected, this length is greater than λ₁ and smaller than the sum (λ₁ + λ₂).

Cascades with Distributed Sources.

Our approach allows us to analyze not only delta-sources of the particles but distributed sources as well. As an example, consider a Gaussian source, j_G (x, t), with width σ,

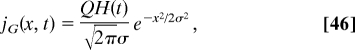which injects mobile particles in the first stage of the cascade. In this case, C_v,ss⁽¹⁾ (x) in Eq. 37 is replaced by

where the probability density p₁ (x|λ, σ) is given by

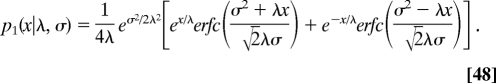The characteristic length λ₁ given in Eq. 35 is replaced by

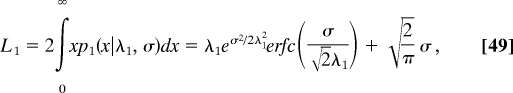which reduces to λ₁ as σ → 0.

The concentration profiles in the second stage are given by Eqs. 43 and 44, in which p₂ (x) is replaced by p₂ (x|λ₁, λ₂, σ):

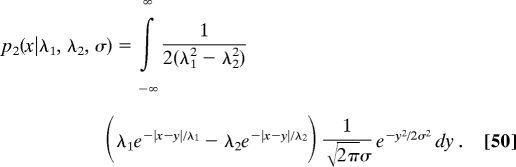Carrying out the integration, one can obtain

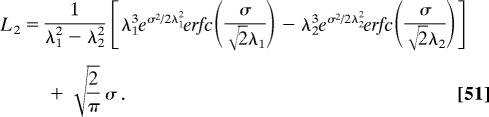Respectively, the characteristic length L₂ given in Eq. 45 is replaced by

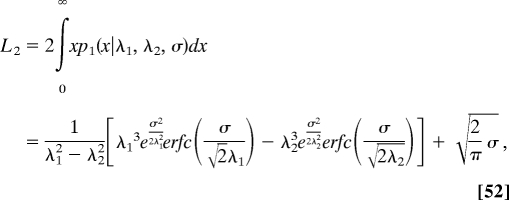which reduces L₂ in Eq. 45 as σ → 0.

Discussion

We have developed a linear theory for signaling gradients in cascades of 2-state systems. Our main results are the expressions for the steady-state concentration profiles and characteristic length scales of mobile and immobile particles, as well as the general approach used to derive these expressions. Our approach can be straighforwardly extended to cascades with more than 2 stages and to models where particles move by mechanisms other than diffusion and in more than 1 dimension (30, 31). We conclude with discussion of the potential applications of our results to the terminal patterning system in the Drosophila embryo (12, 19, 20).

Taken together, the extracellular diffusion of Trunk, its trapping by Torso receptors, and receptor-mediated internalization can be viewed as a 2-state reaction–diffusion system. Similarly, the intracellular diffusion of phosphorylated MAPK, its dephosphorylation, and trapping by nuclei define the second 2-state system. We assume that the rate of MAPK phosphorylation at a particular point along the embryo is proportional to the number of occupied receptors at this point. This approximation, which lumps a number of processes between the activated Torso and MAPK phosphorylation into a single step, is supported by the fact that the expression boundaries of the genes controlled by MAPK signaling can be shifted by manipulations of the Trunk (ligand) levels (32). This approximation is also supported, indirectly, by experiments with cultured cells stimulated by soluble growth factors (27, 33). A number of such studies demonstrated that MAPK phosphorylation is correlated with ligand concentration and receptor occupancy.

Full activation of MAPK requires 2 phosphorylations (18), but because it is currently possible to detect only MAPK in its twice-phosphorylated state, our model contains only a single form of phosphorylated MAPK. We model dynamics of MAPK activation using a simple phosphorylation/dephosphorylation cycle. In such a model, the reversible activation and deactivation of a substrate (unphosphorylated MAPK) is mediated by 2 separate enzymes (kinase and phosphatase). To a first approximation, both reactions are modeled using the Michaelis-Menten (MM) kinetics.

We assume that the unphosphorylated MAPK is in excess (17). Within the framework of the MM kinetics, this implies that phosphorylation exhibits zeroth-order with respect to unphosphorylated MAPK and first order with respect to the activating enzyme. Based on the discussion above, this rate is proportional to the local level of the occupied Torso receptors. We also assume that dephosphorylation operates in a first-order regime, with the rate constant proportional to the concentration of the phosphatase. Because the precise identity and subcellular (nuclear vs. cytoplasmic) localization of the MAPK phosphatase in the terminal system are currently unknown (34, 35), in our model, dephosphorylation can occur both in the nucleus and in the cytoplasm.

Thus, MAPK phosphorylation in the terminal system appears to be controlled by a 2-stage cascade of 2-state linear reaction-diffusion systems, each of which can be characterized by its own length scale (λ₁ and λ₂). Our recent experiments revealed that MAPK phosphorylation gradients at a given nuclear density are at steady state (17). Thus, they can be analyzed using the results derived above. By quantifying MAPK phosphorylation in mutants with different levels of Torso, we concluded that the pattern of Torso occupancy is highly localized to the poles of the embryo, and the length scale of the pattern of phosphorylated MAPK is determined by processes inside the embryo (17). Within the framework of the our model (see Eq. 45), this implies that λ₁<<λ₂, hence, the resulting expressions would not depend on the length scale of the first stage and will be a function of λ₂ alone.

Our experiments detect the total level of phosphorylated MAPK, which can be viewed as the sum of the nuclear and cytoplasmic levels of MAPK given by C_tot,ss⁽²⁾ (x) ≡ C_m,ss⁽²⁾ (x) + C_im,ss⁽²⁾ (x). Under the assumptions discussed above, C_tot,ss⁽²⁾ (x) is given by the following expression (with λ₂ is given by Eq. 40):

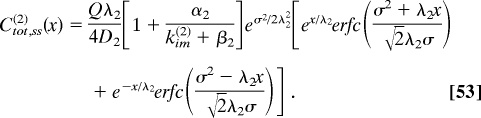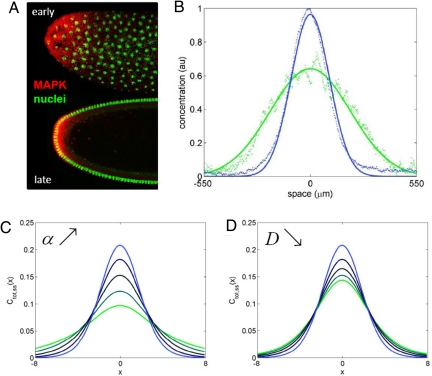
This expression can be used to analyze how MAPK phosphorylation changes with nuclear density. We found that, with every nuclear division, the level of MAPK phosphorylation increases near the poles (at x = 0, in the model) and decreases in the rest of the embryo (17) (Fig. 3A).Analysis of this effect requires a theory for predictng how the parameters appearing in Eq. 53 depend on nuclear density. This theory can be based on the analysis of the dynamics of nuclear divisions and recent live-imaging studies of protein mobility in the syncytium (26, 36–38). We expect that the diffusivity and trapping rate will be decreasing and increasing functions of the nuclear density, respectively. Each of these effects can amplify the signal close to the poles and attenuate it in the rest of the system (Fig. 3B and C). Thus, a 2-stage cascade of 2-state systems provides an adequate qualitative description for the dynamics of MAPK phosphorylation in the early Drosophila embryo.

Fig. 3.

Dynamics of MAPK phosphorylation profiles in the terminal system. (A) Fluorescent images of nuclei (green) and phosphorylated MAPK (red) at 2 different nuclear densities. (B) Quantified gradients of total (nuclear and cytoplasmic) phosphorylated MAPK. The green/blue curves show the patterns of MAPK phosphorylation at nuclear cycles 10 and 14, respectively. Increase in the nuclear density amplifies the total level of MAPK phosphorylation near the poles of the embryo and attenuates it in the rest of the system. (C) Increase in the nuclear trapping rate sharpens the profile of C_tot,ss⁽²⁾ (x), computed with Eqs. 53 and 40: α = 0.05, 0.1 0.2, 0.4, 0.8 (green to blue curves, respectively). Other parameters: k_{im zbe 2, km} = 0, β = 1, σ = 1.5, and D = 0.5. (D) Decrease in the diffusivity sharpens C_tot,ss⁽²⁾ (x). D = 2.5, 2, 1.5, 1, and 0.5 (green to blue curves, respectively), α = 0.8, other parameters as in C.

Several assumptions of our model, such as the linearity of the connection between the 2 stages, can be tested experimentally, using the recently developed approach for the quantitative comparison of MAPK phosphorylation across multiple genetic backgrounds (17).