Imaging Informational Conflict: A Functional Magnetic Resonance Imaging Study of Numerical Stroop

Abstract

We employed a parametric version of the comparison Stroop paradigm to investigate the processing of numerical magnitude and physical size under task-relevant and -irrelevant conditions to investigate two theoretical issues: (1) What is the neural fate of task-irrelevant information? (2) What is the neural basis of the resolution of the conflict between task-relevant and -irrelevant information? We show in 18 healthy adults that numerical magnitudes of numbers call for higher processing requirements than physical sizes. The enhanced activation elicited by numerical magnitudes is not modulated by task relevance, indicating autonomous processing. Moreover, the normal behavioral distance effect when the numerical dimension is task relevant and reversed distance effect when it is not show that autonomous processing fully encodes numerical magnitudes. Conflict trials elicited greater activation in bilateral inferior frontal gyri, right middle frontal gyri, and right superior frontal gyri. We postulate two sources to the conflict, namely, at cognitive and response levels.

INTRODUCTION

Task-irrelevant information can interfere with performance. This was classically demonstrated by Stroop (1935), using a task where naming the ink color of a word is more error prone and slower when the word is a conflicting color word, for example, where the word GREEN is printed in red. This is now known as the “Stroop effect.” Nevertheless, the majority of responses in Stroop task performance are correct, indicating appropriate resolution of the conflict between task-relevant and task-irrelevant information (Derbyshire, Vogt, & Jones, 1998; Carter, Mintun, & Cohen, 1995; George et al., 1994; Bench et al., 1993; Pardo, Pardo, Janer, & Raichle, 1990).

Functional neuroimaging experiments of Stroop interference effects potentially provide insight into two important general theoretical questions: (1) What is the neural fate of task-irrelevant information? More specifically, are there qualitative or quantitative differences in the activation patterns that can be assumed to imply different cognitive processing, or is the processing of the stimulus dimensions autonomous so that task does not modulate neural activity? (2) What is the neural basis of the resolution of the conflict between task-relevant and -irrelevant information?

We suggest that the classical color-word task is not well suited to answering these questions because the competing dimensions are unbalanced. Although words interfere with color naming, color has little effect on word naming: There is rarely a significant slowing when naming the word “GREEN” printed in red, even when color information has been manipulated to precede the word by 400 msec (Glaser & Glaser, 1982). Furthermore, it is impossible to order color names on a continuum, so even if one is able to parametrically vary the hue of a color, it is impossible to have a parametric modulation on the color name dimension.

The number Stroop task provides a more appropriate alternative, as described originally by Besner and Coltheart (1979), and uses the dimensions numerical magnitude and physical size. In a typical experiment, both numerical magnitudes and physical sizes of the numbers displayed vary; subjects have to select the larger number in either the numerical or the physical dimension. Trials may be congruent, where the numerically larger number is physically larger (e.g., 3​ 5); incongruent, where the numerically larger number is physically smaller (e.g., 3​ 5); and, in some experiments, neutral where the numbers are displayed in the same size (e.g., 3 5) for the numerical comparison task and where the same numbers are displayed in different sizes (e.g., 3​ 3) for the physical comparison task. The Stroop effect manifests as interference (an increase in reaction time and/or error rate in incongruent trials compared with neutral trials) and/or facilitation (a decrease in reaction time and/or error rate in congruent trials compared with neutral trials) (e.g., Girelli, Lucangeli, & Butterworth, 2000; Tzelgov, Meyer, & Henik, 1992; Foltz, Poltrock, & Potts, 1984; Henik & Tzelgov, 1982; Besner & Coltheart, 1979). Facilitation is always substantially smaller than interference (for a review, see MacLeod, 1991).

A further advantage of the number Stroop task is that it provides a metric for processing “refinement”: the numerical distance effect (Moyer & Landauer, 1967). This effect, like other symbolic and nonsymbolic distance effects, means that it is harder to discriminate similar stimuli than dissimilar stimuli. In the case of numbers, similarity is on the semantic dimension of numerical magnitude. Comparison times are inversely related to the numerical distance between two numbers, so that, for example, 3 4 takes longer to compare than 3 5 (Moyer & Landauer, 1967), and, generally, comparisons times are well captured by the Welford function (Zorzi & Butterworth, 1999, and see below). The distance effect holds for written number words (Foltz et al., 1984) and dot patterns (Buckley & Gillman, 1974). Thus, the presence of a distance effect shows that processing has gone beyond a mere large-small categorization and that the numbers have been processed to a semantic level that discriminates between the magnitudes of each number (Tzelgov et al., 1992).

The effect can be observed in numerical Stroop tasks (Pinel, Piazza, Le Bihan, & Dehaene, 2004; Fias, Lammertyn, Reynvoet, Dupont, & Orban, 2003; Pinel, Dehaene, Rivière, & Le Bihan, 2001; Foltz et al., 1984; Hinrichs, Yurko & Hu, 1981; Duncan & MacFarland, 1980), but when physical size is manipulated as the task-relevant dimension and numerical magnitude as the task-irrelevant dimension, the numerical distance effect can vanish (Rubinsten, Henik, Berger, & Shahar-Shalev, 2002) or even reverse (Girelli et al., 2000; Henik & Tzelgov, 1982). See below for an account of the reversed distance effect.

In this study, we further examined the autonomous aspect of numerical information processing. Autonomy, by definition, is a property of automatic processes, that is, processes that are fast, effortless, and unconscious (e.g., Logan, 1980; Shiffrin & Schneider, 1977; Posner & Snyder, 1975). Here we use the concept autonomous to refer to a process that takes place even when it is irrelevant to the task at hand, so that it begins and runs to completion without intention (Zbrodoff & Logan, 1986). The number Stroop paradigm is particularly well suited to investigate the depth of processing because it uses the distance effect and the reversed distance effect as metrics.

A reversed distance effect in the task-irrelevant dimension (e.g., Girelli et al., 2000; Henik & Tzelgov, 1982) does not necessarily suggest that information is processed differently in the task-irrelevant channel. Following Girelli et al. (2000), if both dimensions are processed autonomously, conflict will arise only when competing outcomes are simultaneously active. It takes less time to generate a candidate response when the distance is greater. Thus, this candidate response in the task-irrelevant dimension will be generated more quickly to interfere with the generation of the task-relevant response. For example, selecting the numerically larger item will be slower for 3​ 5 than 3​ 5 because it will be quicker to resolve the size difference in the first case. Indeed, the reversed distance effect, like the normal distance effect, can be construed as evidence that the processing of numerical information has continued autonomously to its normal completion.

There is already considerable evidence as to where semantic processing of numbers is expressed in the brain. Pinel et al. (2001) has described two distinct stages of numerical processing, namely, identification and semantic processing. The ventral occipitotemporal areas are activated bilaterally by the visual shapes of Arabic numerals (Dehaene & Cohen, 1995) during the identification process. Word identification is thought to be strictly left lateralized and to rely on the left “visual word form area,” a region of the left fusiform gyrus that is involved in the recognition of visual words (Shallice, 1988). However, Pinel and colleagues (Pinel et al., 2001; Pinel et al., 1999) have provided evidence that the right fusiform gyrus is implicated in the identification of Arabic numerals.

Several studies implicate the parietal lobes in supporting a notation-independent semantic representation of quantities (see Dehaene & Cohen, 1995, for a review). More specifically, the intraparietal sulcus and the precuneus have been implicated in the comparison process of numbers, and the activity of these regions is modulated by the numerical distance effect—smaller numerical distances associated with high activation levels (Pinel et al., 2001). Pinel et al. (2004) extended these findings to other nonsymbolic continua, such as physical size and luminance. By using a number Stroop paradigm, they reported that during the numerical comparison task, the numerical distance effect was associated with enhanced bilateral activity of the horizontal segment of the intraparietal sulci and the left precentral gyrus. In contrast, during physical size comparisons with number stimuli, correlates of the physical distance effect were found predominantly in the right hemisphere, in particular the right prefrontal and occipital cortices and much of the right intraparietal sulcus. Intersections of the correlates between numerical magnitude and physical size distance effects were observed in bilateral regions of the anterior intraparietal sulcus. The authors concluded that during comparative judgements, these continuous quantities are engaged in common parietal representations.

It is important to note that the studies by Pinel and colleagues (Pinel et al., 2004; Pinel et al., 2001) rest on the basic assumption that for any given task, the first stage is to translate the input into the appropriate representation, and in the case of comparison, the stimuli are converted to analogue representations of quantity (Dehaene, 1992). Although Pinel et al.’s (2004) findings support common parietal representations in processing numerical magnitude and physical size, it was also observed that comparative judgements of numerical magnitudes yielded larger activation in several parietal regions (bilateral inferior parietal foci and the left intraparietal sulcus) than those of physical sizes. No explanation was provided by the authors for such a difference.

Problems with Previous Studies of Numerical Stroop

In previous number Stroop studies, the attended and unattended dimensions are not properly balanced. For example, nine numbers have been used to create two levels of numerical distance, distant and close pairs (in addition to distance 0 for neutral pairs), whereas three physical sizes were often employed to create large, small, and neutral stimuli; hence, only one level of physical distance (in addition to distance 0 for neutral pairs) was used. This meant that the two competing dimensions were not appropriately matched, limiting the inferences about the amount of information available in the task-relevant and -irrelevant channels (e.g., Girelli et al., 2000; Henik & Tzelgov, 1982). Rubinsten et al. (2002) used three levels of numerical distance and two levels of physical distance, and, more recently, Pinel et al. (2004) varied both numerical distance and physical distance, but the stimuli were grouped in the analyses, so that the factor distance consisted of only two levels (distant and close pairs). With such a design, Pinel et al. failed to observe any distance effect in either numerical magnitude or physical size when they were task irrelevant.

In the present experiment, we parametrically varied both numerical distance and physical distance and tested for distance effects under both task-relevant and -irrelevant conditions. Here, we viewed distance effects as indicators for refined information processing; this contrasts with the coarse large-small dichotomous classification implicated by the Stroop effect.

Neural Basis of Conflict Resolution

Specific brain regions have been implicated in processing and resolution of informational conflict from task-irrelevant features. In particular, enhanced activation in the anterior cingulate cortex (ACC) has been reported in color-word Stroop tasks where subjects have to name the color of a conflicting color word, for example, the word GREEN printed in red, compared to a nonconflicting stimulus (e.g., Derbyshire et al., 1998; Carter et al., 1995; George et al., 1994; Bench et al., 1993; Pardo et al., 1990). Similarly, greater ACC activation has also been observed during incompatible compared to compatible trials, in flanker tasks (e.g., Durston et al., 2003; Bunge, Dudukovic, Thomason, Vaidya, & Gabrieli, 2002; van Veen, Cohen, Botvinick, Stenger, & Carter; 2001; Casey et al., 2000; Hazeltine, Poldrack, & Gabrieli, 2000; Botvinick, Nystrom, Fissell, Carter, & Cohen, 1999). These findings have been interpreted as suggesting a role in conflict resolution.

However, more recent research has indicated that the precise function of the ACC rests in the detection of conflict, rather than in the resolution of conflict per se. The model proposed by Botvinick, Braver, Barch, Carter, and Cohen (2001) assumes that conflict monitoring (e.g., detection) influences cognitive control. In particular, during a period of high conflict, more attention is directed to the relevant task, and if another conflict follows close in time, less interference is expected due to the already heightened state of the system. In other words, the model predicts that not only behavior, but also ACC activation would be affected by (1) variations in trial type frequency and (2) the preceding trial’s trial type.

Evidence to support Botvinick et al.’s (2001) model has come from various types of interference tasks. In a color-word Stroop task, Carter et al. (2000) reported that ACC activation during incongruent trials was higher when such trials were infrequent than when they were frequent, paralleling the behavioral finding that incongruent trials induced more conflict when such trials were rare. Similarly, in a flanker task, greater ACC activation was observed in incompatible trials that followed compatible trials than those that followed incompatible trials (Botvinick et al., 1999), a finding replicated and extended by Durston et al. (2003). Furthermore, in a go/no-go task, the increase in ACC activation to a no-go trial is a function of increasing number of preceding go trials (Durston et al., 2002). All these findings are consistent with the involvement of the ACC in conflict detection and support Botvinick et al.’s (2001) proposal that high ACC activation triggers an increased attention on the relevant task, leading to less interference in cases where conflicts are frequent or consecutive.

Another well-established finding is that ACC activity has been associated with error commission (e.g., Critchley, Tang, Glaser, Butterworth, & Dolan, 2005; Braver, Barch, Gray, Molfese, & Snyder, 2001; Menon, Adleman, White, Glover, & Reiss, 2001; Falkenstein, Hoormann, Christ, & Hohnsbein, 2000; Kiehl, Kiddle, & Hopfinger, 2000; Carter et al., 1998; Gehring, Goss, Coles, Meyer, & Donchin, 1993; for a review, see Botvinick, Cohen, & Carter, 2004). Behavioral and electromyographic observations indicate that errors in speeded response tasks are frequently associated with response conflict (Yeung, Botvinick, & Cohen, 2004). The reason that errors are committed even when there is a conflict detection system is that even as an error response is being executed, ongoing processing of the stimulus often leads to a belated activation of the correct response, giving rise to a transient period during with both correct and incorrect responses are activated. Thus, ACC activation during errors reflects the detection of a postresponse conflict.

Conflict can occur at numerous levels of information processing, ranging from perceptual representation to response selection. Several studies have reported that the ACC is engaged most strongly during conflicts at the level of response selection (Milham, Banich, & Barad, 2003; Nelson, Reuter-Lorenz, Sylvester, Jonides, & Smith, 2003; Weissman, Giesbrecht, Song, Mangun, & Woldorff, 2003; Bunge et al., 2002; Milham et al., 2001; van Veen et al., 2001). On the other hand, there was a lack of substantial ACC activation when comparing between conflict and nonconflict trials in a color-word matching Stroop task (Zysset, Müller, Lohmann, & von Cramon, 2001). Instead, Zysset et al. (2001) observed enhanced activation in regions along the left inferior frontal sulcus (IFS) during conflict trials compared to nonconflict trials (neutral and congruent trials) and concluded that “regions along the IFS appear to be involved in solving interference effect and task management.”

Research employing other paradigms supports this. Go/no-go and stop-signal tasks require subjects to perform speeded responses on “go” trials and to inhibit their response on “no-go” or “stop” trials. Such response inhibition has been reported to activate regions along the right inferior frontal gyrus in neuroimaging studies (e.g., Bunge et al., 2002; Durston et al., 2002; Menon et al., 2001; Garavan, Ross, & Stein, 1999; Rubia et al., 1999; Konishi, Nakajima, Uchida, Sekihara, & Miyashita, 1998, 1999). In some studies, enhanced activation was observed bilaterally (e.g., Menon et al., 2001).

The idea that ACC activation is associated with conflict detection suggests an effect on attentional allocation (for a review, see Botvinick et al., 2004). On the other hand, there is evidence to suggest that regions in the inferior frontal cortex are responsible for inhibiting prepotent responses (e.g., Bunge et al., 2002; Durston et al., 2002; Menon et al., 2001; Garavan et al., 1999; Rubia et al., 1999; Konishi et al., 1998, 1999) and are perhaps involved in conflict resolution (Zysset et al., 2001). More recently, van Veen and Carter (2005) reported distinct neural substrates for cognitive (semantic) interference and response conflict in a modified color-word Stroop task. Bilateral middle frontal gyri, right superior frontal gyrus, and the ACC were activated in response to cognitive interference. Response conflict activated the bilateral middle/inferior frontal gyri and a more anterior region in the ACC. Conjunction analysis revealed no overlap in activation between the two contrasts.

The present study investigates the neural fate of task-irrelevant information using a modified version of the number Stroop paradigm with two comparable dimensions, namely, numerical magnitude and physical size. The parametric design allows us to vary and measure systematically the amount of interference exerted by the task-irrelevant channels during conflict trials in each of the comparison tasks, and hence characterize the information-processing fate of task. A reversed numerical distance effect in physical comparisons would indicate that exact numerical values had been computed despite task irrelevance (Girelli et al., 2000; Henik & Tzelgov, 1982). Furthermore, the current design allows us to test, for the first time, for a reversed physical distance effect in numerical comparisons (i.e., task-irrelevant condition). The reversed effects are indicators for autonomous information processing.

In terms of brain activation, parietal activation levels were predicted to be inversely related to numerical distance in line with previous findings (Pinel et al., 2004; Pinel et al., 2001). The key issue in the experiment was whether task relevance modulates parietal activity. If the fate of task-irrelevant information in this task was autonomous processing, then an absence of a modulation would be suggestive. The second key issue was to identify the neural basis of the resolution of the conflict between task-relevant and irrelevant information. Again, balanced dimensions in a parametric design could reveal activations specific to conflict and to errors arising from conflict. We expected that conflict and errors would modulate activity in frontal rather than parietal regions where numbers and size are primarily represented.

METHODS

Tasks

The two tasks were numerical magnitude and physical size comparisons. Subjects had to select the larger number numerically or physically according to the task requirement. Subjects responded by pressing the left or right button to indicate the side of the larger relevant attribute. Reaction times and responses were recorded. A program written in Cogent (which runs on a MATLAB Version 6.1 platform; The MathWorks, Natick, MA) was used.

Stimuli

The stimuli, presented on a screen situated outside the scanner, were reflected onto a mirror (of size 20 × 9 cm²) placed inside the scanner. In each trial, two digits appeared simultaneously in white on a black background. Each presentation lasted 1000 msec with an interstimulus interval of 3000 msec.

The stimuli were Arabic digits (1 to 9) in Arial font. Each digit might appear in one of the nine different sizes (subtending from approximately 3.8° to 9.7° with a mean ratio of 1.1 between adjacent sizes). Four numerical distances (ND = 1, 2, 3, and 4) and four physical distances (PD = 1, 2, 3, and 4 units) were used. The pairs used were as follows:2 3, 34, 6 7, 78 (for ND of 1); 13,24,68,79 (for ND of 2); 14,2 5, 58,69 (for ND of 3); 1 5, 2 6, 4 8, 5 9 (for ND of 4). The equivalent physical sizes were used to systematically vary PD.

There were three experimental conditions: congruent, when the numerically larger digit was physically larger (e.g., 2​ 6); incongruent, when the numerically larger digit was physically smaller (e.g., 2​ 6) or vice versa; and neutral, when the two digits were of the same physical size in the numerical comparison task (e.g., 2 6) or when the same digit appeared in different sizes in the physical comparison task (e.g., 2​ 2).

The total number of trials in each task was 217 (i.e., 64 congruent + 64 neutral + 64 incongruent + 25 blank = 217 trials). Stimuli were presented in a pseudorandom order to avoid carryover effects.

Subjects

There were 18 right-handed subjects (11 men and 7 women), aged 21 to 38 years (M = 25.0 years, SD = 4.01 years). They performed two tasks (numerical and physical comparison tasks); half of them participated in the numerical task first, and the other half in the physical task first. All subjects had normal or corrected-tonormal eyesight.

Scanning Procedures and Imaging Data Processing

Whole-brain functional magnetic resonance imaging (fMRI) data was acquired on a 1. 5-T Magnetom VISION system (Siemens Sonata, Erlangen, Germany). Functional images were obtained with a gradient-echo-planar sequence using blood oxygenation level-dependent (BOLD) contrast, each comprising a full-brain volume of 28 contiguous axial slices, 3.5-mm thickness). Volumes were acquired continuously with a repetition time (TR) of 2.52 sec. A total of 275 scans were acquired for each participant in two sessions (approximately 10 min each), with the first six volumes subsequently discarded to allow for T1 equilibration effects. During fMRI scanning, pupil diameter was recorded online by an infrared eye tracker. The data were analyzed using SPM2 (Wellcome Department of Imaging Neuroscience; www.fil.ion.ucl.ac.uk/spm) implemented in MATLAB 6.1.0.450 Release 12.1. Individual scans were realigned, slice time corrected, normalized to the MNI template with voxels of 2 × 2 × 2 mm³ and spatially smoothed by an 8-mm full width half-maximum (FWHM) Gaussian kernel using standard SPM methods.

Event-related activity for each voxel, for each condition and each subject was modeled using a canonical hemodynamic response function plus temporal and dispersion derivatives. Statistical parametric maps of the t statistic (SPM{t}) were generated for each subject and the contrast images were further smoothed by an 8-mm FWHM Gaussian kernel.

At the second-level random-effects analysis, a 2 × 4 analysis of variance (ANOVA) model was applied; the factors were task (numerical comparison task and physical comparison task) and trial type (congruent, neutral, incongruent, and error trials). Congruent and incongruent trials were modeled parametrically with respect to task-relevant and task-irrelevant distance, and neutral trials were modeled parametrically with respect to task-relevant distance. This allowed us to construct t contrasts to test specifically for distance-modulated activities. Our model was optimized to detect linear increase/decrease in activities related to numerical and/or physical distance. In the present study, congruent and neutral trials were classified as nonconflict trials, whereas incongruent trials were conflict trials. To compare between conflict and nonconflict trials, and error and correct trials in each task, t contrasts were constructed. Threshold significance was set at .001 uncorrected for multiple comparisons.

RESULTS

Behavioral Data

Errors were incorrect responses made in the comparison tasks, that is, trials where subjects pressed the wrong key. Reaction time outliers were identified by the standard SPSS procedure (values that lay more than 1.5 times the interquartile range above the third quartile or 1.5 times the interquartile range below the first quartile) and removed. ANOVAs were used to analyze mean error rates and mean reaction times, and whenever Mauchly’s test of sphericity assumption was violated, the Greenhouse-Geisser epsilon was used to correct the degrees of freedom. A 2 × 3 repeated measures ANOVA was conducted on mean error rates. The factors were task (numerical comparison task and physical comparison task) and congruent (congruent, neutral, and incongruent). The ANOVA revealed a significant main effect of congruity, F(1,22) = 38.10, p = .001; a nonsignificant main effect of task, F(1,17) = 3.34, ns; and a nonsignificant Task × Congruity interaction, F(1,21) < 1, ns. Tests of within-subjects contrasts revealed a significant difference in error rates between incongruent and neutral trials, F(1,17) = 52.00,p < .001, and a nonsignificant difference between neutral and congruent trials, F(1,17) < 1, ns. The mean error rates were 11.55%, 4.43%, and 3.95%, respectively.

A 2 × 3 repeated measures ANOVA was conducted on mean reaction times. The factors were task (numerical and physical comparison tasks) and congruent (congruent, neutral, and incongruent). The ANOVA revealed a significant main effect of task, F(1,17) = 16.55, p = .001, a significant main effect of congruity, F(2,34) = 156.62, p < .001, and a significant Task × Congruity interaction, F(2,34) = 8.07, p = .001. The mean reaction times for numerical and physical comparison tasks were 617 and 570 msec, respectively.

Considering only the numerical comparison task, the main effect of congruity was significant, F(2,34) = 112.52, p < .001. Tests of within-subjects contrasts revealed a significant difference between congruentand neutral trials, F(1,17) = 47.84, p < .001, and between the latter and incongruent trials, F(1,17) = 81.60, p < .001. The mean reaction times were 585, 614, and 652 msec, respectively. Similarly for the physical comparison task, the main effect of congruity was significant, F(2,34) = 41.62, p < .001. Tests of within-subjects contrasts revealed a significant difference between congruent and neutral trials, F(1,17) = 5.16, p < .050, and between the latter and incongruent trials, F(1,17) = 56.16,p < .001. The mean reaction times were 553, 564, and 593 msec, respectively.

Further analyses were conducted on mean reaction times to test for distance effects in both the task-relevant and -irrelevant dimensions for each task focusing on incongruent trials, because only here was there informational conflict. For the numerical comparison task, a 2 × 4 repeated measures ANOVA was conducted on mean reaction times of the incongruent trials. The factors were task relevance (task-relevant and -irrelevant) and distance (1, 2, 3, and 4). The ANOVA revealed a significant Attention × Task Relevance interaction, F(3,51) = 13.02, p < .001. There was no significant main effect (all nonsignificant). Further analyses were conducted at each level of task relevance.

At the task-relevant level, the factor distance (in this case, the numerical distance) showed a significant main effect, F(3,51) = 8.61,p < .001. Tests of within-subjects contrasts revealed a significant negative linear trend for this factor, F(1,17) = 19.20, p < .001 (see Figure 1). No other trend was significant. At the task-irrelevant level, the factor distance (in this case, the physical distance) showed a significant main effect, F(3,51) = 4.78, p = .005. Tests of within-subjects contrasts revealed a significant positive linear trend for this factor, F(1,17) = 7.51, p < .050 (see Figure 1). No other trend was significant.

Figure 1.

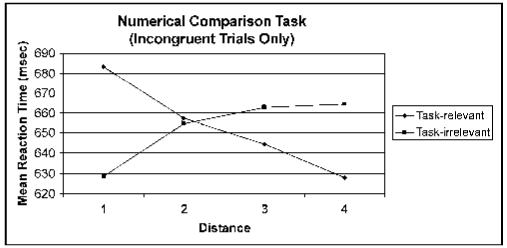
Distance effects in task-relevant and -irrelevant dimensions of the numerical magnitude comparison task.

When considering the physical comparison task, we conducted a 2 × 4 repeated measures ANOVA on mean reaction times of the incongruent trials. The factors were task relevance (task-relevant and -irrelevant) and distance (1, 2, 3, and 4). The ANOVA revealed a significant main effect of task, F(1,17) = 19.11, p < .001, a significant main effect of distance, F(3,51) = 16.26, p < .001, and a significant Attention × Task Relevance interaction, F(3,51) = 55.58, p < .001. Further analyses were conducted at each level of task relevance.

At the task-relevant level, the factor distance (in this case, the physical distance) showed a significant main effect, F(2,33) = 53.49,p <.001. Tests of within-subjects contrasts revealed a significant negative linear trend, F(1,17) = 96.44, p < .001, and a significant quadratic trend, F(1,17) = 8.98, p < .010, for this factor (see Figure 2). At the task-irrelevant level, the factor distance (in this case, the numerical distance) showed a significant main effect, F(3,51) = 7.59, p < .001. Tests of within-subjects contrasts revealed a significant positive linear trend, F(1,17) = 30.95,p < .001 (see Figure 2). No other trend was significant.

Figure 2.

Distance effects in task-relevant and -irrelevant dimensions of the physical size task.

In summary, during conflict trials, the task-relevant dimension showed a classic distance effect (indicated by a negative linear trend), whereas the task-irrelevant dimension showed a reversed distance effect (indicated by a positive trend), regardless of task.

Functional Imaging Data

Functional imaging data analysis at the first level allowed for neural responses associated with congruent, neutral, incongruent, and error trials to be modeled independently. Second-level t contrasts were constructed to test for brain regions associated with the parametric modulation of numerical distance and physical distance during neutral conditions. An F contrast was then constructed to compare processing of the two dimensions. Analysis on the conflict trials allowed us to test for a Task × Distance interaction. To identify regions involved in conflict and error trials, t contrasts were used. Conjunction analyses by inclusive masking were also performed to identify common regions for conflict and error processing across numerical and physical comparison tasks. Brain activations are summarized in Tables 1-3. Voxels reported are in Talairach coordinate space.

Table 1.

An F Contrast Revealed Regions that Showed Enhanced Activation when Processing Numerical Distance Compared with Physical Distance

Voxels	z Score	Talairach Coordinates			Brain Area
		x	y	z
F contrast (numerical distance > physical distance)
758	4.72	46	7	24	Right frontal lobe; inferior frontal gyrus; white matter
169	3.86	—36	17	—3	Left frontal lobe; inferior frontal gyrus; gray matter; BA 47
55	3.69	46	—77	17	Right occipital lobe; middle occipital gyrus; white matter
501	3.68	40	-39	42	Right parietal lobe; inferior parietal lobule; gray matter; BA 40
	3.53	22	—64	42	Right parietal lobe; precuneus; white matter
	3.45	32	—56	45	Right parietal lobe; inferior parietal lobule; white matter
95	3.45	50	-53	—9	Right temporal lobe; subgyral; white matter
	3.39	46	—61	—9	Right occipital lobe; subgyral; white matter
24	3.22	-22	—66	46	Left parietal lobe; superior parietal lobule; gray matter; BA 7
23 (SVC)	3.67	38	—41	41	Right inferior parietal lobule

No significant voxel was found in the opposition direction. Regions that showed enhanced activation under task-relevant conditions compared with task-irrelevant conditions with respect to increasing distance in numerical and physical distance were revealed by t contrasts. BA = Brodmann’s area; SVC = small volume correction.

Table 3.

Regions Revealed by t Contrasts Showed Enhanced Activation during Error Trials Compared with Correct Trials in Numerical and Physical Comparison Tasks

Voxels	z Score	Talairach Coordinates			Brain Area
		x	y	z
Numerical task error trials > numerical task correct trials—t contrast
2107	6.88	3	-42	11	Right superior temporal gyrus
	5.52	51	-26	-7	Right temporal subgyral
1200	5.32	-32	17	-11	Left inferior frontal gyrus; BA 47
	3.99	-32	10	-29	Left superior frontal gyrus
619	4.93	-51	-46	13	Left superior frontal gyrus
3058	4.66	42	27	-6	Right inferior frontal gyrus
	4.56	55	20	12	Right inferior frontal gyrus; BA 45
	4.56	34	16	-29	Right superior temporal gyrus
341	4.47	6	-15	3	Right thalamus; medial dorsal nucleus
	4.08	-4	-15	3	Left thalamus; medial dorsal nucleus
127	4.13	-18	-77	-25	Left postertior lobe; uvula
392	4.03	0	26	15	Interhemispheric
72	3.70	4	-22	-19	Right brainstem; pons
166	3.65	-50	-2	31	Left precentral gyrus; BA 6
22	3.46	36	-5	-18	Right temporal subgyral
53	3.34	-46	13	20	Left frontal subgyral
27	3.25	-26	32	24	Left frontal subgyral
21	3.17	-59	-31	31	Left inferior parietal lobule
Physical task error trials >physical task correct trials—t contrast
1807	5.83	53	-42	13	Right superior temporal gyrus
	5.08	50	-27	-5	Right middle temporal gyrus
1837	5.00	53	23	1	Right inferior frontal gyrus
	4.43	32	19	-9	Right inferior frontal gyrus; BA 47
909	4.89	-34	17	-11	Left inferior frontal gyrus; BA 47
335	4.15	-16	-73	-25	Left posterior lobe; uvula
149	4.04	4	-35	-35	Right brainstem; medulla
Conjunction by masking across tasks (error trials > correct trials), corrected for family wise error at .050
715	6.88	53	-42	11	Right superior temporal gyrus
72	5.52	51	-26	-7	Right superior temporal subgyral
181	5.32	-32	17	-11	Left inferior frontal gyrus; BA 47
37	4.93	-51	-46	13	Left superior temporal gyrus
32	4.66	42	27	-6	Right inferior frontal gyrus

A conjunction (by inclusive masking) across the two tasks revealed regions that were commonly activated during error trials.

In neutral trials, distance only varied parametrically in the task-relevant dimension, that is, only numerical distance was manipulated in the numerical task, and only physical distance in the physical task. No parietal region parametrically modulated by numerical distance or physical distance during these trials were revealed by t contrasts. However, the F contrast (see Table 1) comparing the processing of numerical distance and physical distance during neutral trials revealed several parietal regions that showed enhanced activation in processing numerical relative to physical distance including the right inferior parietal lobule [40 —39 42], right precuneus [22 —64 42], right inferior parietal lobule [32 —56 45], and left superior parietal lobule [—22 —66 46], as well as the bilateral inferior frontal gyri and right temporal and occipital regions (see Table 1 and Figure 3). Small volume correction searches (5-mm radius) were performed with reference to Pinel et al. (2004) and revealed that the right inferior parietal lobule [38 —41 43] also showed enhanced activation processing numerical distance compared to physical distance. No enhanced activation was observed processing physical distance relative to numerical distance. Conjunction by inclusive masking across the two tasks revealed no commonly activated voxel.

Figure 3.

Parietal regions showing enhanced activation when processing numerical distance relative to physical size (clockwise from top left: regions in the right inferior parietal lobule (40 —39 42] and 32 —56 45]), right precuneus 22 —64 42], and left superior parietal lobule —22 —66 46]).

However, the parietal regions that showed enhanced activation processing numerical relative to physical distance were not affected by task requirement during conflict trials. The F contrast constructed to test for a Task (numerical task and physical task) × Dimension (numerical distance and physical distance) revealed no significant difference in parietal activation.

To test for differences in brain activity between conflict and nonconflict trials, t contrasts were constructed (see Table 2). In the numerical task, enhanced activation in conflict trials compared to nonconflict trials was observed in right inferior frontal [44 9 31] and middle frontal [36 52 —14] gyri, left fusiform gyrus [—44 —49 —13], right occipital lobe [34 —76 —1], and various other regions. In the physical task, enhanced activation in conflict trials was observed only in the left inferior frontal gyrus [—40 30 8]. Conjunction by inclusive masking across the two tasks revealed no commonly activated voxel. To test for differences in brain activity between error and correct trials, t contrasts were constructed (see Table 3). Conjunction by inclusive masking (corrected for familywise error at 0.05) was performed across task and revealed enhanced activation in error trials compared to correct trials in bilateral inferior frontal gyri:left [—32 17 —11] and right [42 27 —6], and several regions along the bilateral superior temporal gyri (see Table 3).

Table 2.

Regions Revealed by t Contrasts Showed Enhanced Activation during Conflict Trials Compared with Nonconflict Trials in Numerical and Physical Comparison Tasks

Voxels	z Score	Talairach Coordinates			Brain Area
		x	y	z
Numerical task conflict trials > numerical task nonconflict trials—t contrast
224	4.32	32	-48	48	Right superior parietal lobule; BA 7
112	4.08	-10	12	51	Left superior frontal gyrus; BA 6
613	4.08	14	-5	11	Right thalamus; ventral anterior nucleus
	3.93	18	6	9	Right sublobar; lentiform nucleus; putamen
	3.60	8	6	0	Right sublobar; caudate; caudate head
42	3.73	16	16	49	Right superior frontal gyrus
34	3.66	-22	-17	5	Left sublobar; extranuclear
16	3.43	36	52	-14	Right middle frontal gyrus
56	3.42	34	-76	-1	Right occipital lobe; subgyral
14	3.28	-44	-49	-13	Left fusiform gyrus
28	3.25	44	9	31	Right inferior frontal gyrus
Physical task conflict trials >physical task nonconflict trials—t contrast
12	3.20	-40	30	8	Left inferior frontal gyrus

DISCUSSION

In the present experiment we examined processing of numerical magnitude and physical size using bidimensional stimuli. By varying the two dimensions, we were able to create conflicting situations as well as systematically vary the amount of interference for each of task-relevant dimensions. We made efforts to match the two dimensions by difficulty. In terms of error commission, the two tasks did not differ in either rate or pattern. However, with respect to reaction times, the physical comparison task was significantly faster than the numerical comparison task. Such a difference could be explained by the different nature of these tasks—physical size comparisons require processing at the perceptual level, whereas numerical magnitude comparisons require higher cognitive processing. On this basis, it is not surprising that processing time was shorter for the former. It is important to note that the two tasks showed the same reaction time patterns with respect to congruity—significant interference and facilitation in both numerical and physical tasks; in other words, the classical Stroop effect. Although not perfectly matched in terms of reaction time, the Stroop effect was observed in both tasks, indicating that two directions influenced one another and, hence, the present paradigm is a moresuitable choice for studying informational conflict than the traditional color-word task in which direction of influence is unidirectional—from word to color.

The Stroop effect we observed is consistent with the number Stroop literature (Girelli et al., 2000; Tzelgov et al., 1992; Foltz et al., 1984; Henik & Tzelgov, 1982; Besner & Coltheart, 1979). Thus, subjects were unable to ignore the irrelevant information regardless of task. Facilitation was reflected by reaction times but not error rates, consistent with the general finding in the Stroop literature that facilitation is virtually always substantially smaller than interference (see review, MacLeod, 1991).

Distance effects (indicated by negative linear trends) were observed in task-relevant channels, that is, numerical distance effect in the numerical task and physical distance effect in the physical task. Reversed distance effects were observed in both tasks, that is, a reversed numerical distance effect in the physical task (consistent with Girelli et al., 2000; Henik & Tzelgov, 1982) and the novel finding of a reversed physical distance effect in the numerical task. Because distance effect was used as an indicator of refined information processing, the observed reversed distance effects under task-irrelevant conditions suggest that numerical distance and physical distance are processed in an autonomous fashion, similar to task-relevant processing.

As proposed in the Introduction, the reversed distance effect can be explained in terms of amount of interference. Information that would normally require little effort to process under task-relevant conditions (e.g., the salient difference between two numbers with a large physical distance) is harder to ignore under task-irrelevant conditions (e.g., in numerical comparison). In contrast, information that requires more effort to process under task-relevant conditions (e.g., numerical comparison of two numerically close numbers) would exert little interference when such information is to be ignored under task-irrelevant conditions (in physical comparison).

Our brain imaging data revealed that when the task-irrelevant dimensions were kept constant (i.e., in neutral trials), the parietal lobes (regions in the right inferior parietal lobule, right precuneus, and left superior parietal lobule) showed enhanced activation when processing numerical distance compared to physical distance. This extends the findings of Pinel et al. (2004) who observed enhanced activation in parietal lobes (regions in bilateral inferior parietal foci and left intraparietal sulcus) during numerical comparisons compared to physical comparisons, implying a processing difference between numerical and physical dimensions.

Although there was no evidence to suggest that processing numerical magnitude and physical size activated different parietal regions, the enhanced activation when processing numerical distance relative to physical distance indicates a quantitative difference in the processing of these two dimensions. This is consistent with (although does not demonstrate) the distinction made by Zorzi and Butterworth (1999) between numerical magnitudes that are conceptualized as “discrete numerosities” and physical sizes that are represented in an analogue (or continuous) fashion, and with the suggestion that comparative judgements on discrete numerosity representations evoked by numbers call for higher processing requirements compared with those on analogue representations evoked by physical sizes. We postulate that the processing streams of these two types of representation converge at a cognitive level (where conflict occurs when the streams of information are incompatible).

In line with our a priori prediction, the parietal regions (in right inferior parietal lobule, right precuneus, and left superior parietal lobule) that showed enhanced activation processing numerical relative to physical distance were not affected by task requirement in conflict situations. In other words, these parietal regions were equally active whether or not required by the task to process numerical magnitudes. The lack of difference in parietal activation level across numerical and physical comparison tasks provides a strong evidence for autonomous processing of numerical magnitude.

Interestingly, we found no evidence to suggest that parietal activation was parametrically modulated by either numerical or physical distance. This appears inconsistent with numerical-distance-modulated parietal regions identified by Pinel and colleagues (Pinel et al., 2004; Pinel et al., 2001). However, a closer look their findings suggests that the numerical-distance-modulated parietal activation might not be as robust as the authors claimed. In the Pinel et al. (2001) study, numerical distances were not modeled parametrically. The reported distance-modulated parietal activation was in fact a main effect of distance (across three levels) rather than a significant linear decrease in activation with increasing numerical distance. When masking the main effect of distance for close > medium and medium > far, the only surviving significant region was in the precuneus. Moreover, the reported numerical distance-modulated parietal regions in the bilateral intraparietal sulci and the right precuneus were from a single-subject analysis. Of the four subjects tested, only two showed these effects; one failed to show any strong correlation between brain activation and numerical distance. The inconsistent findings cast doubts on whether parietal activation is truly modulated by numerical distance.

The current paradigm is arguably more complex than that used by Pinel et al. (2001), and this could mean that any numerical-distance-modulated parietal activation was less likely to emerge. Pinel et al. (2001) used a comparison task to a fixed reference, in which subjects had to judge whether a visually presented number was smaller or larger than the reference (65). Such a task is probably easier than the current paradigm that involves comparing bidimensional stimuli. Because Pinel et al.’s stimuli only varied in one dimension (numerical magnitude), there was neither irrelevant information nor conflict to influence subjects’ judgements, and the subjects were likely to perform the task without much difficulty.

When confronted with a conflict, subjects had to inhibit the task-irrelevant information in order to perform the task correctly. The enhanced activation in the right inferior frontal gyrus in conflict trials compared to nonconflict trials during numerical comparisons is consistent with findings in go/no-go and stop-signal tasks (e.g., Bunge et al., 2002; Menon et al., 2001; Garavan et al., 1999; Rubia et al., 1999; Konishi et al., 1998, 1999). In Durston et al.’s (2002) go/no-go task, activity associated with successful response inhibition extended to the right middle frontal gyrus. In the current experiment, enhanced activation in this area was also observed in conflict trials during numerical comparisons. The current findings provide support for the suggestion that regions in the inferior frontal cortex are responsible for inhibiting prepotent responses and perhaps even conflict resolution.

The left fusiform gyrus showed enhanced activation in conflict trials relative to nonconflict trials during numerical comparisons. Such activation does not only reflect the recognition of the visual shapes of the numbers, but also suggests that the computation over the perceptual properties of the numbers interacted with the semantic processing of the numbers during numerical comparisons. This suggestion is further supported by the enhanced activation in the right occipital lobe—an area involved in visual processing—in conflict trials during numerical comparisons.

During physical comparisons, enhanced activation in the left inferior frontal gyrus was observed in conflict trials relative to nonconflict trials, but there was no evidence to suggest that differential activity in the visual cortex, supporting the idea that the source of interference comes from higher cognitive processing of the numbers.

There was also evidence to suggest that conflict may also occur at the response level. In van Veen and Carter’s (2005) study, bilateral middle frontal gyri and right superior frontal gyrus were activated in response to cognitive interference, whereas response conflict activated the bilateral middle/inferior frontal gyri. The activations observed in this study—bilateral inferior frontal gyri, right middle and right superior frontal gyri—imply that there were two sources to the conflict, namely, at cognitive and response levels.

No evidence was found to support an involvement of the ACC in conflict resolution. Small volume correction searches (5-mm radius) were performed with reference to ACC coordinates identified by Menon et al. (2001), van Veen et al. (2001), Bush et al. (1999), and Barch et al. (1997), but no significant voxel was found. This appears inconsistent with van Veen and Carter’s (2005) finding that different parts of the ACC were involved in cognitive interference and response conflict. However, in a related article using the present paradigm (Critchley et al., 2005), we constructed a model optimized for the detection of ACC activation and reported such an activation during conflict trials. Critchley et al. (2005) reported a region in the ACC [6 22 38] very close to that reported by van Veen and Carter during semantic conflict [7 18 42]. This provides strong evidence for a semantic level conflict. Nonetheless, we have stated earlier that there was another possible source of conflict, namely, at the response level, which has been reflected by the activation in bilateral inferior frontal gyri.

Moreover, we found no evidence to support the involvement of the ACC in error commission. We performed small volume correction searches (5-mm radius) with reference to ACC coordinates identified by Menon et al. (2001), who reported its associated activity with error processing and found no significant effects. We have proposed an alternative explanation that the ACC acts as an interface between cognitive and bio-behavioral systems based on evidence that its activation strongly predicted trial-by-trial variability in autonomic response magnitude (reflected by changes in pupil size) that peaked during error trials (Critchley et al., 2005). In summary, we set out to investigate whether numerical magnitude and physical size are processed in an autonomous fashion. By parametrically varying the amount of interference exerted by the task-irrelevant dimension on the task-relevant one in either task, a reversed distance effect—the indicator of refined information processing—was observed in each of the dimensions when these were task irrelevant. Such a novel finding strongly supports autonomous, refined information processing in both dimensions. The reversed distance effect appears to be a robust indicator of information processing and may prove to be a more sensitive measure than the Stroop effect itself in Stroop variants where an interference effect is not easily elicited. Parietal regions have been described as comprising a notation-independent representation of their semantic content as quantities (Dehaene & Cohen, 1995). We found no evidence to suggest that parietal regions were modulated by numerical distance. However, we provided strong evidence for the autonomous processing of numerical magnitude. Finally, we conclude that prefrontal regions, especially bilateral inferior frontal and right middle frontal gyri, are associated with conflict resolution when these sources of conflict could come from both cognitive and response levels.