Dependence of Amide Vibrations on Hydrogen Bonding

Abstract

The effect of hydrogen bonding on the amide group vibrational spectra has traditionally been rationalized by invoking a resonance model where hydrogen bonding impacts the amide functional group by stabilizing its [^-O-C=NH⁺] structure over the [O=C-NH] structure. However, Triggs and Valentini’s UV-Raman study of solvation and hydrogen bonding effects on ε-caprolactum, N,N-dimethylacetamide (DMA) and N-methylacetamide (NMA) (J .Phys. Chem., 1992; 96, 6922-31) cast doubt on the validity of this model by demonstrating that contrary to the resonance model prediction, carbonyl hydrogen bonding does not impact the AmII’ frequency of DMA. In this study we utilize density functional theory (DFT) calculations to examine the impact of hydrogen bonding on the C=O and N-H functional groups of NMA, which is typically used as a simple model of the peptide bond. Our calculations indicate that, as expected, the hydrogen bonding frequency dependence of the AmI vibration predominantly derives from the C=O group, whereas the hydrogen bonding frequency dependence of the AmII vibration primarily derives from N-H hydrogen bonding. In contrast, the hydrogen bonding dependence of the conformation sensitive AmIII band derives equally from both C=O and N-H groups, and, thus, is equally responsive to hydrogen bonding at the C=O or N-H site. Our work shows that a clear understanding of the normal mode composition of the amide vibrations is crucial for an accurate interpretation of the hydrogen bonding dependence of amide vibrational frequencies.

INRODUCTION

Hydrogen bonding is known to play a significant role in the formation and stabilization of protein secondary structure.¹ Inter-peptide hydrogen bonding stabilizes secondary structures such as the α-helix and β-sheet conformations,¹ while, peptide-water hydrogen bonding competes against peptide bond-peptide bond hydrogen bonding. Peptide-water hydrogen bonding stabilizes extended conformations such as the PPII conformation.^2-4

Considering the central role hydrogen bonding plays in protein folding, finding potential markers for tracking the peptide bond hydrogen bonding state is of great importance.^5-8 The frequency of the AmI vibration (mainly C=Os), AmII and the AmIII vibration (C-N_s and N-H_b) as well as the N-H stretch vibration are known to depend upon the hydrogen bonding state of the peptide bond.^5-12 Previous theoretical calculations of NMA and NMA-water complexes suggested that the AmI band frequency is predominantly sensitive to hydrogen bonding at the C=O group, while the AmII vibration is equally responsive to the state of hydrogen bonding at the C=O and NH sites.^13-15 Experimental studies of aqueous NMA and alanine-based polypeptide, AP indicate that a temperature increase downshifts the AmII (-0.11 cm^-1/°C) and AmIII band frequencies (-0.09 cm^-1/°C),¹⁰ while, the AmI band shows a small upshift^6,10 as the peptide-water hydrogen bonds weaken. Similarly, in D₂O the AmI’ band (75% C=O_s) upshifts, while the AmII’ band (55% N-D_b)¹⁶ downshifts (-0.11 cm^-1/°C).¹⁰ The AmII’ band (predominately C-N_s), which appears as a Fermi doublet in N-methylacetamde (NMA) and ala peptides shows a smaller downshift (-0.07 cm^-1/°C).¹⁰ These temperature dependent shifts in amide band frequencies are due to weakened hydrogen bonding of the peptide bond to water at higher temperatures.^6,7,10,17

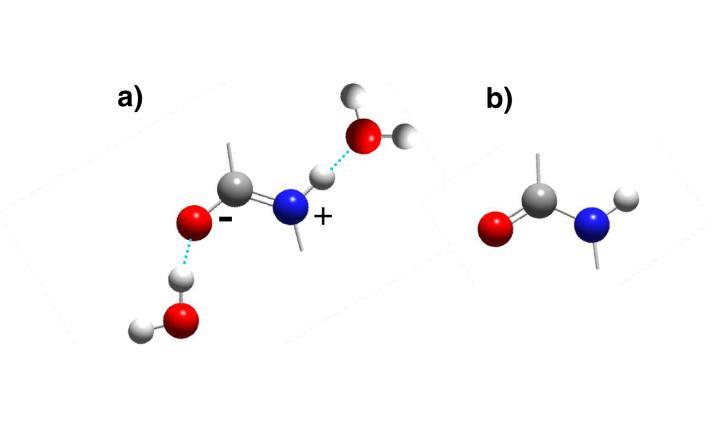
The amide band frequency dependence on hydrogen bonding has been rationalized by arguing that hydrogen bonding at the carbonyl stabilizes the charged resonance structure of the amide bond (Fig 1),^17,18 which results in an increase in the C-N double bond character as the C=O bond order decreases; the C-N bond length decreases while, the C=O bond lengthens.¹⁸ Thus, the AmII’ band frequency would be expected to increase while the AmI band frequency decreases.¹⁹

Figure 1.

The (a) charged and (b) uncharged amide bond resonance structures. Hydrogen bonding is thought to stabilize the charged resonance structure.

The UV-Raman results of Triggs and Valentine,²⁰ however, appear to contradict this “resonance model” interpretation of hydrogen bonding’s impact on the amide bond. In their UV-Raman study utilizing pre-resonance enhancement, Triggs and Valentini systematically examined the impact of solvation and hydrogen bonding using ε-caprolactum, N,N-dimethylacetamide (DMA) and N-methylacetamide (NMA).²⁰ The authors found that the AmI (predominantly C=O_s) frequency is sensitive to hydrogen bonding. However, the AmII’ like vibrations (predominantly C-N_s) of DMA (a tertiary amide) and ε-caprolactum (a cis amide) do not show any significant frequency dependence on hydrogen bonding. The authors suggested that the lack of noticeable hydrogen bond dependence of the d-NMA AmII’ frequency could be due to the absence of N-H_b component.²⁰ Based on their Raman results the authors concluded that “the absence of an upshift in the C-N stretch vibration (AmII’), while the C=O_s vibration (AmI) downshifts is not consistent with the resonance model”.²⁰

Here, we re-examine the impact of hydrogen bonding on the model peptide bond, NMA using density functional theory (DFT)²¹ calculations at B3LYP/6-311+G(d,p)²² level of theory as provided in the Gaussian’03 calculation package.²³ Furthermore, we utilize Natural Bond Orbital Analysis (NBO) to examine hydrogen bond induced charge redistribution in the amide bond. Our results indicate that the NMA hydrogen bond induced shifts of the AmII frequency derives from its large NH_b component (∼50%) and that the AmII vibration is exclusively sensitive to the state of NH hydrogen bonding, while the AmI vibration (>75% C=O_s) is predominantly sensitive to C=O hydrogen bonding. We find that the AmIII₃ vibration has similar contributions from N-H b and C=O s components, and it is equally sensitive to hydrogen bonding of the N-H and C=O groups.

Results and Discussion

We evaluate the impact of hydrogen bonding on the AmI, AmII, and AmIII band frequencies by optimizing the geometries of NMA and NMA-water complexes in vacuo and then calculating their vibrational frequencies, normal mode compositions and charge distributions (Fig. 2). The water molecule is hydrogen bonded to NMA to either the C=O or the N-H site.

Figure 2.

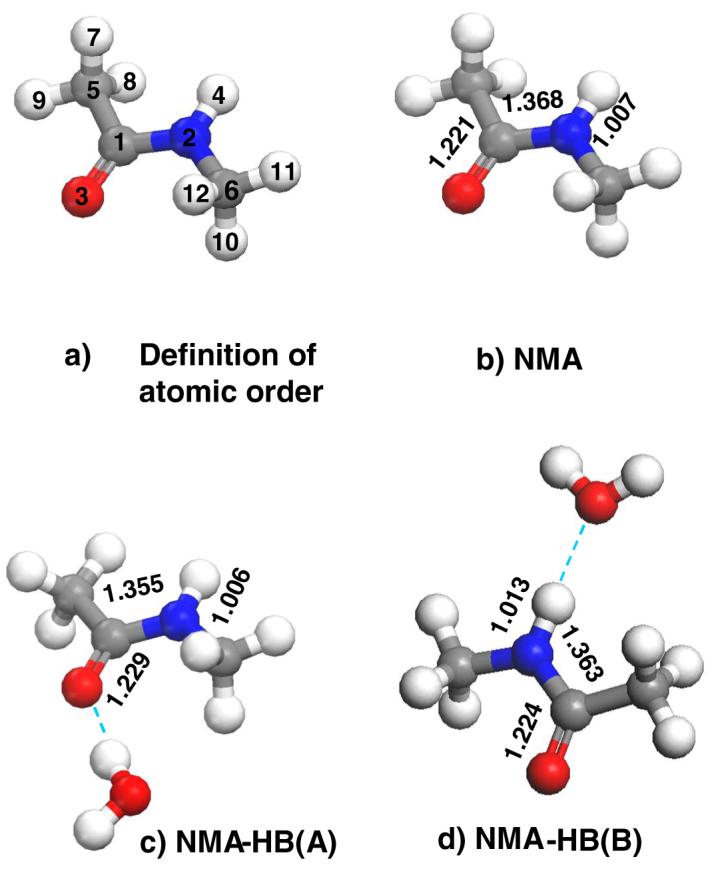
Calculated structures of NMA and NMA-Water complexes demonstrate hydrogen bonding induced changes in amide bond geometry.

We evaluated the validity of the resonance model to correctly predict the impact of amide hydrogen bonding on the frequency of the amide vibrations. The resonance model does not take in account any electronic interactions (such as charge redistribution, dipole-dipole interactions, etc) between the peptide bond and water. The model explains hydrogen bonding frequency shifts only through C-N and C=O bond length alterations caused by the water hydrogen bond.

In order to isolate the impact of electronic interactions from hydrogen bondinduced geometry changes we calculated the vibrational spectrum and charge distribution of NMA at geometries close to that of the water-hydrogen bonded complexes, but in the absence of the water molecule. We refer to these NMA species as “perturbed NMA”. Perturbed NMA was calculated by removing the water molecule from the optimized structure of corresponding NMA-water complex and then re-optimizing the NMA structure while fixing the C-N, N-H and C=O bond lengths and torsion angles ω (C-C-N-C) and Θ (O-C-N-H). Consequently, the perturbed NMA molecule has the geometry of hydrogen bonded NMA but without any electronic interactions with water molecule.

Hydrogen bonding at the NMA C=O site increases the C=O bond length by 0.008 Å, while the C-N and N-H bond lengths decrease by 0.013 and 0.001 Å, respectively (Fig. 2). Similarly, hydrogen bonding at the N-H elongates the N-H and C=O bond lengths by 0.006 Å and 0.003 Å, respectively, while the C-N bond length decreases by 0.005 Å.

Furthermore, our analysis of the charge distribution in NMA and in the NMA-water complexes indicates that hydrogen bonding at the C=O results in a significant increase in electron density at the carbonyl oxygen, while the rest of the peptide bond shows a decreased electron density. In contrast, hydrogen bonding at the N-H decreases electron density on the amide hydrogen atom, while, the rest of the molecule acquires an increased electron density (Table 2). The calculated bond length and electron density changes are consistent with the resonance model^17,18 and indicate that the hydrogen bonding at the C=O site should downshift the AmI and upshift the AmII/AmII’ like vibrations more profoundly than does hydrogen bonding to N-H.

Table 2.

Calculated charge distribution of isolated, water hydrogen bonded and perturbed NMA molecule

Atom	eqgas	fqHB(A)	gqprt(A)	hqHB(B)	iqprt(B)
C1	0.670	0.684	0.665	0.669	0.669
N2	-0.636	-0.622	-0.632	-0.653	-0.634
O3	-0.642	-0.681	-0.643	-0.658	-0.645
H4	0.383	0.390	0.387	0.419	0.384
C5	-0.659	-0.656	-0.659	-0.661	-0.658
C6	-0.377	-0.377	-0.368	-0.374	-0.376
H7	0.229	0.231	0.229	0.223	0.229
H8	0.194	0.231	0.229	0.204	0.193
H9	0.229	0.197	0.194	0.223	0.229
H10	0.188	0.195	0.192	0.184	0.188
H11	0.188	0.207	0.199	0.184	0.188
H12	0.232	0.218	0.226	0.228	0.232
j ΣqNMA	0.000	0.017	0.000	-0.011	0.000
O13	N/A	-0.958		-0.938
H14	N/A	0.489	N/A	0.475	N/A
H15	N/A	0.453		0.475
Water  k ΣqWater	N/A	-0.017	N/A	0.011	N/A

^eq^gas — natural atomic charges of NMA molecule with gas-phase geometry

^fq^HB(A) — natural atomic charges of NMA H-bonded at the carbonyl

^gq^prtA -natural atomic charges of NMA with HB(A) perturbed geometry

^hq^HB(B) — natural atomic charges of NMA H-bonded at the N-H

ⁱq^prtB - natural atomic charges of NMA with HB(B) perturbed geometry

^jΣ^qNMA — sum of natural atomic charges of corresponding NMA species

^kΣ^qWater — sum of natural atomic charges of water molecule

As shown in Table 1, the calculated AmI frequencies of NMA-water complexes change, as expected, with changes in the C=O bond length. Water hydrogen bonding to the C=O site downshifts the AmI band by 23 cm^-1. In contrast, the AmI vibration of perturbed NMA shows a 33 cm^-1 downshift. The smaller frequency downshift of the NMA-water complex as compared to perturbed NMA is likely due to an increased electronic density on the C=O oxygen caused by the hydrogen bonded water (Table 2) and by coupling between the C=O_s and the water bending mode.²⁴

Table 1.

Calculated AmII and AmI frequencies and normal mode compositions for NMA and NMA-H₂O complexes

	Am II/ cm-1	PED (>5%)	Am I/ cm-1	PED (>5%)†
NMA	1529	N-H ib (41) C-N s (23) CH3 ad’ (11) CH3 rock’ (8) N-C s (5)	1709	C=O s (81) C-N s (6) C- C (4)
NMA-HB(A)	1525	N-H ib (41) C-N s (28) CH3 ad’ (6) CH3 rock (6) N-C s (5) C=O ib (5)	1686	C=O s (74) C-N s (7) NCC def (7) C-C s (3)
NMA-perturb (A)‡	1525	N-H ib (41) C-N s (28) CH3 rock (6) N- C s (5) CH3 ad’ (5) C=O ib (5)	1676	C=O s (74) C-N s (8) NCC def (7)
NMA-HB(B)§	1558	N-H ib (54) C-N s (23) CH3 rock N-C s (4)	1699	C=O s (74) NCC def (7) C-N s (7) C-C s (3)
NMA-perturb (B)	1542	N-H ib (46) C-N s (25) CH3 ad (7) CH3 rock’ (7) N-C s (5)	1695	C=O s (75) NCC def (7) C-N s (6) C-C s (3) N-H ib (3)

^†ib- in plane bending; s- stretching; ab’- asymmetrical deformation’; rock- rocking; def-deformation.

^‡NMA-perturb (A)-perturbed NMA structure representing geometry of C=O hydrogen bonded NMA-water complex without the water molecule.

^§NMA-perturb (B)-perturbed NMA structure representing geometry of NH hydrogen bonded NMA-water complex without the water molecule.

Hydrogen bonding to the N-H site downshifts the AmI vibration of the NMA-water complex by only 10 cm^-1. Removal of the water hydrogen bonded to the NH site in the perturbed NMA results in an additional 4 cm^-1 AmI frequency downshift. This 4 cm^-1 additional frequency shift derives from perturbation of the electronic density of peptide bond due to the removal of the hydrogen bonded water at the NH site. Our charge distribution analysis indicates that the water molecule donates some electronic density to the nitrogen and oxygen (Table 2). Thus, these results indicate that the impact of C=O hydrogen bonding on the AmI vibration is considerably larger than is N-H hydrogen bonding, which is fully consistent with the resonance model.

In contrast to the AmI band, the calculated AmII band frequency of NMA shows a hydrogen bonding dependence opposite to that predicted by the resonance model. The calculated water-NMA bond length changes predict that hydrogen bonding to the C=O should upshift the AmII vibration since the C-N bond contracts upon hydrogen bonding. Our calculation, however, shows that hydrogen bonding at C=O downshifts the AmII frequency by 4 cm^-1, while hydrogen bonding at the N-H upshifts the AmII frequency by 29 cm^-1 (Table 1). For the NMA-water complex hydrogen bonding to C=O gives the same AmII frequency downshift (4 cm^-1) as occurs for perturbed NMA molecule. This indicates that the 4 cm^-1 AmII frequency downshift is the direct result of the C-N and C=O bond length changes induced by the water hydrogen bonded to C=O.

Comparison of AmII frequencies of the N-H hydrogen bonded NMA-water complex and perturbed NMA indicates that ∼45% (13 cm^-1) of AmII frequency hydrogen bonding upshift (Δν = 29 cm^-1) derives from geometry changes (Table 1). The remaining ∼55% (16 cm^-1) derives from changes in the electron distribution due to the presence of the hydrogen bonded water at the N-H site. The water hydrogen bonded to the N-H site donates electronic density (Table 2) which results in an increase in the oxygen and nitrogen negative charge, while the positive charge on the amide hydrogen increases. This results in the AmII frequency upshift. Electron density redistribution caused by interaction with the water hydrogen bonded to the C=O does not affect the AmII frequency.

Our results allow us to conclude that the AmII frequency shift predominantly derives from N-H hydrogen bonding which alters both the geometry and electronic density distribution. The surprisingly small impact of the C=O hydrogen bonding on the AmII frequency is due to the relatively small contribution (∼25 %) of C-Ns to the AmII mode composition (Table 1). Both isolated NMA and NMA with water hydrogen bonded to the C=O show an AmII vibration which contains 41% N-H_b, which gives rise to large hydrogen bond induced upshift.¹⁰

The small experimentally measured hydrogen bond dependence of the AmII’ frequency of d-NMA¹⁰ likely derives from its remaining small N-D_b component.²⁰ Our calculation shows that upon the ND isotopic substitution the N-D_b contribution in the resulting AmII’ vibration is less than 5% (Table 3). Furthermore, the impact of C=O hydrogen bonding is minimal because the C-N_s contribution to the AmII’ normal mode composition is also small (<10%). As expected the AmI’ ( ≥ 75% C=O_s) frequency is predominantly sensitive to hydrogen bonding at the C=O (Table 3).

Table 3.

Calculated frequencies and normal mode composition of d-NMA and d-NMA-D₂O complexes

	Am II’/ cm-1	PED (>5%)	Am I/(cm-1)	PED (>5%)
d-NMA	1487	CH3 ab’ (59) CH3 rock’ (9) CH3 sb (8) C-N s (8) N-D ib (3)	1704	C=O s (82) C-N s (7) C-C s (4)
Fermi band	839+606*	C-Ns + C=O inp b
d-NMA-HB(A)	1485	CH3 ab’ (51) CH3 ab (19) CH3 rock (12) C-N s (6)	1681	C=O s (75) C-N s (9) NCC def (7) C-C s (3)
Fermi band	851+614*	C-N s + C=O inp b
d-NMA-HB(B)	1489	CH3 ab (55) C-N s (10) CH3 rock’ (9) CH3 ab (7) ND ib (4)	1694	C=O s (75) C-N s (9) NCC def (7) C-C s (3)
Fermi band	846+616*	C-N s + C=O inp b

^*combinational band which is in Fermi resonance with the CH₃ asymmetric bending fundamental

In tertiary amides such as DMA or proline, the peptide bond lacks the amide N-H hydrogen. Hence the AmII’ frequency of tertiary amides does not show any significant hydrogen bond dependence¹⁰.

These results, thus, allow us to reconcile the observations of the Triggs and Valentini²⁰ with the resonance model. As discussed above for the NMA, hydrogen bond dependence of the AmII/AmII’ frequency derives from its N-H_b/N-D_b component, while the AmI frequency shifts predominantly derive from C=O hydrogen bonding. Although C=O hydrogen bonding does have an impact on the C-N bond length, the relative contribution of C-N_s motion to the AmII’ band is small. Thus, the impact of C=O hydrogen bonding on the AmII’ frequency is small. Triggs and Valentini’s²⁰ results therefore do not indicate a general breakdown of the resonance model, but highlight that a clear understanding of normal mode composition of the amide vibration is crucial for accurate interpretation of the hydrogen bonding dependence of amide vibrations.

We note that our calculations indicate a larger dependence of NMA’s AmII frequency on hydrogen bonding at the N-H site than did Torii et al’s¹³ computational study. Torri et al¹³ suggest the AmII frequency is equally responsive to hydrogen bonding at the carbonyl and N-H site. The larger dependence of the AmII frequency on N-H hydrogen bond in our work correlates with our larger computed N-H_b component. Torri et al¹³ suggest N-H_b constitutes only ∼30% to the AmII normal mode composition, while our calculations indicate N-H_b contribution can be as large as 50%. These differences likely arise due to the fact that Torri et al¹³ utilized HF-level calculations, while we utilized DFT level of theory which was shown to produce more reliable results than HF in calculations of ground state properties, potential energies and especially vibrational frequencies.^25,26 To some extent DFT is comparable in accuracy to high-level post-HF methods such as MP2, CASSCF and CIS.^25-29

In contrast to the AmI and AmII vibrations, the normal mode composition of the conformation sensitive AmIII vibration contains nearly equal contribution from C-N stretching (29%) and N-H bending (22%), and hence is equally responsive to hydrogen bonding at either site (Table 4). Thus, hydrogen bonding to the carbonyl site and to the NH site upshift the AmIII frequency almost equally (22 cm^-1 and 23 cm^-1, respectively). However, comparison with perturbed NMA reveals that in case of NH hydrogen bonding the frequency shift results from both changes in geometry (11 cm^-1) and electronic interactions due to the hydrogen bonded water molecule (12 cm^-1) while the frequency shift induced by C=O hydrogen bonding results mostly from changes in the NMA bond lengths.

Table 4.

Calculated AmIII₃ frequencies and normal mode compositions for NMA and NMA-H₂O complexes

	Am III3/ cm-1	PED (>5%)
NMA	1241	C-N s (29) N-H ib (22) C=O ib (14) C-C s (11) N-C s (5)
NMA-HB(A)	1263	N-H ib (27) C-N s (26) C=O ib (13) C-C s (10)
NMA-perturb (A)l	1260	N-H ib (28) C-N s (25) C=O ib (13) C-C s (10)
NMA-HB(B)	1264	C-N s (33) N-H ib (18) C=O ib (14) C-C s (10) N-C s (6)
NMA-perturb (B)m	1252	C-N s (30) N-H ib (22) C=O ib (14) C-C s (11) N-C s (5)

^lNMA-perturb (A)-perturbed NMA structure representing geometry of C=O hydrogen bonded NMA-water complex without the water molecule.

^mNMA-perturb (B)-perturbed NMA structure representing geometry of NH hydrogen bonded NMA-water complex without the water molecule.

Conclusion

We utilized DFT calculations of NMA and NMA-water complexes to examine the impact of C=O and NH hydrogen bonding on the amide bond geometry and on the AmI, AmII and AmIII vibrations. Our calculations indicate that, as expected, the hydrogen bond dependence of the AmI vibration predominantly derives from hydrogen bonding to the C=O group, whereas the hydrogen bond dependence of the AmII vibration primarily derives from its large N-H_b component which is exclusively sensitive to the state of N-H hydrogen bonding. In contrast, the hydrogen bonding dependence of the conformationally sensitive AmIII band derives equally from both C=O and N-H groups and thus is equally responsive to hydrogen bonding at either the carbonyl or N-H site. Our results indicate that due to the different sensitivity to hydrogen bonding states the frequency shifts of the AmI and AmII bands potentially can be utilized to determine the state of hydrogen bonding at the C=O and the N-H site of an individual peptide bonds.