Stability of nonrelativistic quantum mechanical matter coupled to the (ultraviolet cutoff) radiation field

Abstract

We announce a proof of H-stability for the quantized radiation field, with ultraviolet cutoff, coupled to arbitrarily many non-relativistic quantized electrons and static nuclei. Our result holds for arbitrary atomic numbers and fine structure constant. We also announce bounds for the energy of many electrons and nuclei in a classical vector potential and for the eigenvalue sum of a one-electron Pauli Hamiltonian with magnetic field.

In this note, we describe a variety of mathematical results concerning the quantum theory of systems of static nuclei and nonrelativistic electrons with spin coupled to a classical, static magnetic field and/or to the ultraviolet cutoff quantized radiation field. Our results and their proofs are based, in part, on earlier work in refs. 1 through 7. Details will appear in refs. 8–10.

A typical system we propose to study consists of an arbitrary number, N, of nonrelativistic electrons with electric charge −e, bare mass m > 0, spin ½ and a bare gyromagnetic factor g = 2, an arbitrary number, M, of nuclei of atomic number ≤Z, for some arbitrary, but fixed integer Z < ∞, and an arbitrary number of photons which describe the transverse degrees of freedom of the quantized electromagnetic field. The dynamics of the system, generated by a self-adjoint Hamilton operator H, conserves the number of nuclei and electrons, but the number of photons is arbitrary and changes in time.

Our concern is to show that, in the ground state of the system corresponding to the infimum of the spectrum of H, the energy per charged particle (electron or nucleus) is bounded uniformly in N and M, for fixed Z < ∞. This property of nonrelativistic, quantum-mechanical matter is called H-stability. In ref. 11 the reader may find many important results and background material on stability of matter, as well as applications thereof.

When the coupling of nuclei to the transverse degrees of freedom of the electromagnetic field is turned off H-stability of the systems described above is a mathematical consequence of the H-stability of systems in which nuclei are treated as static. In this note we consider static nuclei, in accordance with the fact that their masses are much larger than the mass of an electron, but we emphasize that, because of their magnetic moments, this is not an entirely innocent approximation for most realistic nuclei; see the discussion in refs. 7 and 8. Furthermore, interactions between electrons and photons with energies large compared with a typical energy of an electron in an atom of atomic number ≤Z are turned off with the help of an ultraviolet cutoff.

The Hilbert space of pure state vectors of a system of N electrons and an arbitrary number of photons is given by

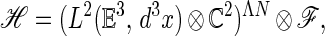1

where L²(𝔼³, d³x) ⊗ ℂ² is the Hilbert space for one electron of spin ½ in physical space 𝔼³, Λ denotes an antisymmetric tensor product, and ℱ is the photon Fock space—i.e., the symmetric tensor algebra—over the one-photon Hilbert space L²(ℝ³, d³k) ⊗ ℂ². The factors ℂ² account for the spin states of electrons and the helicities of photons, respectively. Electrons are fermions—i.e., they satisfy the Pauli principle, giving rise to antisymmetric tensor products—while photons are bosons corresponding to symmetric tensor products.

The Hamiltonian of the system, in the presence of M static nuclei, is given by

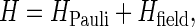2

where

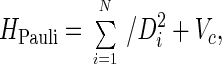3

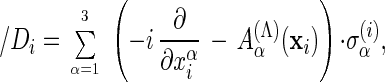4

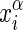is the αth component of the position, x_i ∈ 𝔼³, of the ith electron; A_α^(Λ)(x) is the αth component of the quantized electromagnetic vector potential, A^(Λ)(x), with an ultraviolet cutoff Λ, at the point x ∈ 𝔼³ (see below); σ_α⁽ⁱ⁾ stands for the matrix

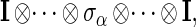5

on spin space (ℂ²)^⊗N, where σ_α, α = 1, 2, 3 are the three Pauli matrices, and the 2×2 matrix σ_α in Eq. 5 appears in the ith factor of the tensor product; V_C denotes the Coulomb potential—i.e.,

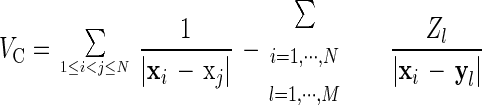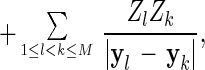6

where y_l ∈ 𝔼³ denotes the position of the lth static nucleus and Z_l ≤ Z its atomic number, l = 1, ⋯ , M; finally,

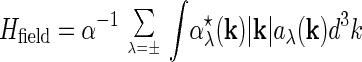7

is the Hamiltonian of the transverse degrees of freedom of the quantized electromagnetic field. The constant α = e²/ℏc (ℏ is Planck’s constant and c is the velocity of light) is the dimensionless fine-structure constant, with α ≈ (null)/1;137 in nature. We have chosen units for energy where 2mc²α² = 1, i.e., the ground state energy of a hydrogen atom is −4. Furthermore, we impose the Coulomb gauge on our choice of electromagnetic potentials; in particular, V_C is purely electrostatic and ∇·A^(Λ)(x) = 0. The ultraviolet cutoff vector potential A^(Λ)(x) is given by

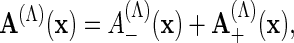where

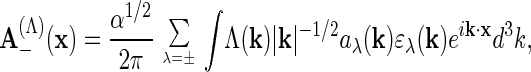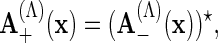8

k denotes a wave vector, and the direction of propagation, k/|k|, and the two polarization vectors ɛ_λ(k), λ = ±, form an orthonormal basis of ℝ³ ⊗ ℂ, for each k ∈ ℝ³; moreover, the cutoff function Λ(k) satisfies 0 ≤ Λ(k) ≤ 1, and

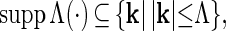9

where Λ is a finite constant. The operators a_λ(k)^★ and a_λ(k) are creation and annihilation operators on ℱ satisfying the canonical commutation relations

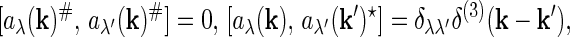10

where a^# = a or a^★.

We are now prepared to describe our main results concerning H-stability of the systems described above.

Theorem 1. (i) For an arbitrary number, N, of electrons, an arbitrary number, M, of static nuclei of atomic numbers ≤Z, for arbitrary values of Z < ∞ and of the fine-structure constant α, and for an arbitrary ultraviolet cutoff Λ (see expression 9), there exists a finite constant E(α, Z) (depending only on α and Z) such that

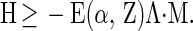11

(ii) For arbitrary N, M, and Z, as above, for an ultraviolet cutoff α⁻¹Λ ≤ Z²α^−3/4, and for sufficiently small values of αZ and α^5/2Z³, there exists a finite constant ɛ(Z) ≤ const. Z^3/2 independent of α, N, and M such that

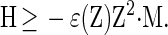12

Remarks: (i) The linear dependence on M (and independence of N) in bounds 11 and 12 implies H-stability of the systems considered here. The linear dependence on Λ of our bound 11 is related to the fact that the Hamiltonian H is the unrenormalized Hamiltonian of quantum electrodynamics with nonrelativistic matter (see the discussion in ref. 8 and, especially, in ref. 7).

(ii) In our units, a typical energy of an inner electron bound in an atom of atomic number Z is −Z². Thus the ultraviolet cutoff energy α⁻¹Λ ∼ Z²α^−3/4 for photons is much larger than a typical energy of such an electron, because, in nature, α ≈ (null)/1;137. A nucleus of atomic number Z can bind of the order of Z electrons (12). The ground state energy of the resulting bound state (an atom or ion) is therefore bounded from below by −const. Z³, in our units. We therefore conjecture that our estimates on ɛ(Z) in inequality 12 can be improved to ɛ(Z) ≤ const. Z (see also Theorem 2 below).

(iii) A proof of Theorem 1 can be found in ref. 8. It combines arguments in ref. 7 with a new result on H-stability of nonrelativistic quantum-mechanical matter in an arbitrary static, external magnetic field established in ref. 9, which is stated below.

Let A(x) be an arbitrary, classical electromagnetic vector potential with square-integrable second derivatives in x and with ∇·A(x) = 0 (Coulomb gauge). Let B(x) = curl A(x) denote the corresponding magnetic field. We set

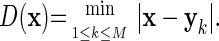13

Let ψ ∈ (L²(𝔼³, d³x) ⊗ ℂ²)^ΛN. We consider the energy functional

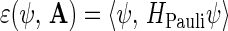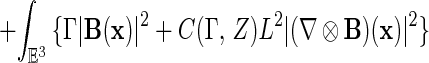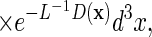14

where H_Pauli is the N-electron Hamiltonian defined in eqs. 3 and 4, but with A^(Λ) replaced by the classical vector potential A, and Γ, C(Γ, Z), and L are constants yet to be chosen.

The proof of Theorem 1 is based on a lower bound for the energy functional ℰ which we describe next.

Theorem 2. Given Γ > 0 and Z < ∞, and for a suitable choice of the constant C(Γ, Z) < ∞ in Eq. 14, there are finite, positive constants c(Γ, Z) and C′(Γ, Z) depending only on Γ and Z such that, for arbitrary L ≤ c(Γ, Z),

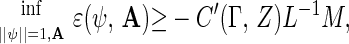15

where M is the number of nuclei. If Γ ≥ Z² there are finite, positive constants c and C such that, for the choices c(Γ, Z) = cZ⁻¹ [i.e., c(Γ, Z) is proportional to the Bohr radius of an electron bound to a nucleus of atomic number Z] and C(Γ, Z) = CZ², one has that

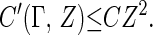16

Remarks: (i) The proof of Theorem 2 is outlined in ref. 8 and carried out in full detail in ref. 9. In ref. 9, bounds on the constants c(Γ, Z), C(Γ, Z), and C′(Γ, Z) are given in the three regimes Γ ≥ Z², Z² ≥ Γ ≥ 1, and Γ ≤ 1. In using Theorem 2 to prove Theorem 1, one sets Γ = const. α⁻². Since, in nature, α ≈ (null)/1;137 and Z < 100, the regime Γ ≥ Z² is the most important one for physics.

(ii) If Γ ≥ Z² the bounds in Theorem 2 imply that

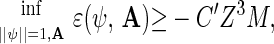17

for some finite constant C′ independent of the number N of electrons. In our units of energy, the ground state energy of an atom or ion consisting of a nucleus of atomic number Z and an arbitrary number of electrons is ≥−const. Z^7/3 (see refs. 12 and 13). The fact that, in part ii of Theorem 1, we only have that H ≥ −const. Z^7/2 M is a consequence of the ultraviolet divergence of the zero-point energy of the quantized electromagnetic field (see ref. 8).

(iii) The strategy developed in ref. 9 (see also ref. 6) to prove Theorem 2 is to reduce the stability bound 15 to local stability of matter in small cubes of physical space 𝔼³ whose sizes are chosen to depend on the configuration of nuclei and on the local behavior of the magnetic field B. These cubes form a Caldéron–Zygmund decomposition of 𝔼³.

To show that Theorem 2 implies Theorem 1, we write the Hamiltonian H introduced in Eqs. 2-7 as the sum of two terms,

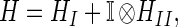where

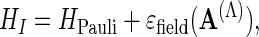with

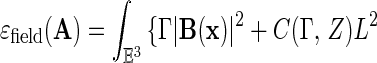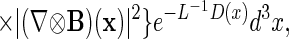and

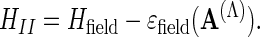It is clear that Theorem 2 proves an appropriate lower bound on H_I [because, in the “Schrödinger representation” of Fock space ℱ, A^(Λ) can be treated as a classical vector potential (8)], while a lower bound on H_II follows from surprisingly simple Fock space estimates (7, 8).

In refs. 7 and 10 the following result related to Theorem 2 is proven: Let

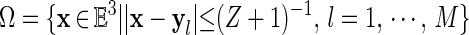and define the classical field energy in the region Ω by

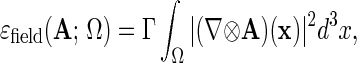with Γ = (8πα²)⁻¹.

Theorem 3. There is a constant ɛ > 0 such that if Γ⁻¹(Z + 1) < ɛ, then

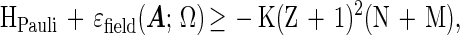for some finite constant K (depending only on Γ).

Theorem 3 can be used to prove a variant of part ii of Theorem 1 (see ref. 7) in the (physically relevant) range α ≤ (null)/1;132, Z ≤ 6, and α⁻¹Λ ≤ α^−5/4(Z + 1).

The proof of Theorem 3 is based on methods developed in ref. 5. Estimates extending the key estimates underlying the results in refs. 5 and 7 are proven in ref. 10. They have the following flavor: As in Eq. 4, define

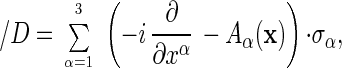where A(x) = (A₁(x), A₂(x), A₃(x)) is an arbitrary vector potential, and let B = curl A be the magnetic field corresponding to A. Let v(x) be a positive (bounded, measurable) function on 𝔼³. We consider the one-electron Pauli Hamiltonian

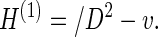18

Let {e_i}_{i=0,1,2,···} be the negative eigenvalues of H⁽¹⁾ (ordered such that e₀ ≤ e₁ ≤ e₂ ≤ ···). We define a basic, B-dependent length scale r(x) as the solution of the equation

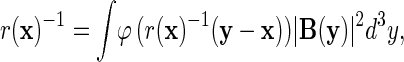19

with ϕ(x) = (1 + ½|x|²)⁻². For a homogeneous magnetic field B, r(x) is proportional to |B|^−1/2, which is the cyclotron radius of an electron, in our units. We also define b(x) = r(x)⁻² as the strength of an effective magnetic field.

Our main result on H⁽¹⁾, proven in ref. 10, is the following theorem.

Theorem 4. There are finite, positive constants C, C′, C" such that, for an arbitrary vector potential A(x),

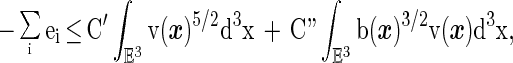20

and

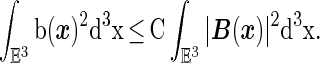21

As a corollary one obtains a result of ref. 5: There is a finite, positive constant K such that

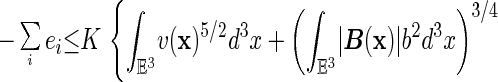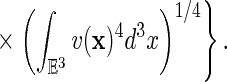22

The relevance of inequalities 20, 21, or 22 for proofs of stability of matter in magnetic fields is explained in ref. 10, respectively ref. 5. See also ref. 14.