Numerical study of water diffusion in biological tissues using an improved finite difference method

Abstract

An improved finite difference (FD) method has been developed in order to calculate the behaviour of the nuclear magnetic resonance signal variations caused by water diffusion in biological tissues more accurately and efficiently. The algorithm converts the conventional image-based finite difference method into a convenient matrix-based approach and includes a revised periodic boundary condition which eliminates the edge effects caused by artificial boundaries in conventional FD methods. Simulated results for some modelled tissues are consistent with analytical solutions for commonly used diffusion-weighted pulse sequences, whereas the improved FD method shows improved efficiency and accuracy. A tightly coupled parallel computing approach was also developed to implement the FD methods to enable large-scale simulations of realistic biological tissues. The potential applications of the improved FD method for understanding diffusion in tissues are also discussed.

1. Introduction

Diffusion-weighted MRI (DWI) provides a means to obtain structural information on tissues over scales that are much smaller than voxel sizes. For example, there has been extensive research that has shown that the apparent diffusion coefficient (ADC) of tissue water changes with tumour cellularity and necrotic fraction (Chenevert et al 1997, Sugahara et al 1999, Lyng et al 2000, Gauvain et al 2001). Thus, ADC may potentially be used as a biomarker to characterize and monitor a tumour’s response to treatment. Various mechanisms have been proposed to explain changes in ADCs (Latour et al 1994, Anderson et al 2000), and some analytical models have been previously presented to study restricted water self-diffusion (Szafer et al 1995, Callaghan 1995, Soderman and Jonsson 1995, Stanisz et al 1997). However, earlier attempts to relate MR signals in DWI with morphologic changes have been either qualitative or based on simple non-realistic geometries, such as cylinders and spheres.

For better understanding of the factors that affect water diffusion in biological tissues with more complex morphologies, numerical models have been proposed, such as Monte Carlo (MC) (Szafer et al 1995) and image-based finite difference (FD) methods (Hwang et al 2003). The MC method tracks individual spins that undergo Brownian motion over a large number of time steps. On the other hand, the FD method discretizes the tissue sample into a spatial grid and updates the magnetization at each point in every time step. The MC method is time consuming for complex tissues because it must track a large number of spins which encounter boundaries in the simulation in order to retrieve structural information. In contrast, the FD method determines the spin migration probabilities at the start of the simulation, which must therefore already contain tissue structural information. Thus, FD is usually computationally more efficient. However, due to the failure of conventional boundary conditions (BC) for the Bloch—Torrey equation, an edge effect artefact arises with the FD method, which is caused by the introduction of artificial boundaries into the computational domain (Hwang et al 2003, Chin et al 2002). This effect must either be reduced by additional computation over an extended domain or it becomes a source of significant errors. This shortcoming limits the practical usage of FD methods.

This paper presents a matrix-based FD method (MFD) that converts the conventional FD approach into a matrix-based algebra. This improvement not only simplifies the FD formula and increases the computational efficiency, but it is also easier to implement using parallel computing. In addition, a revised periodic boundary condition has been developed which eliminates the edge effect for any diffusion-weighted pulse sequences. This improvement increases the computing efficiency and accuracy. Finally, to further enable large-scale FD computing for complex tissues, an efficient tightly coupled parallel computing approach has also been devised in order to implement the MFD with the revised periodic boundary condition. For comparison, different parallel computing strategies are discussed. Results from some modelled tissues are presented and these are consistent with analytical solutions. The further potential of the method for studying water diffusion in realistic biological tissues is also discussed.

2. Theory

2.1. Conventional finite difference method

The FD method solves partial differential equations (PDE) on a spatial grid over a series of time steps. In our work, the main PDE is the Bloch—Torrey equation. For simplicity, only 1D formulae are considered below, but 2D and 3D cases can be easily derived in a similar way.

Using an explicit forward-time centred-space (FTCS) discretization scheme (Fletcher 1988) in a 1D three-point finite difference stencil (see figure 1), the transverse magnetization can be expressed as

$$m_j^{n+1}=\exp (-\Delta t∕T_{2,j})\exp (-\mathrm{i}\gamma g^n{x}_j\Delta t)\cdot m_j^{\prime n+1}$$ (1)

and

$$m_j^{\prime n+1}=\left(1-2\frac{D_x\Delta t}{\Delta x^2}\right)m_j^n+\frac{D_x\Delta t}{\Delta x^2}{m}_{j+1}^n+\frac{D_x\Delta t}{\Delta x^2}{m}_{j-1}^n,$$ (2)

where m = M_x + iM_y, i is the imaginary unit, γ is the gyromagnetic ratio for hydrogen, the superscript n indicates the temporal indices, the subscript j indicates the spatial index, D_x indicates the diffusion coefficients along the x direction and T_2,j is the transverse relaxation time at point (j). Equation (1) describes the transverse relaxation and the phase accumulation during the application of diffusion-sensitizing gradients and equation (2) describes the diffusion process itself. Since equation (1) is relatively easy to handle, the focus of this work is on equation (2), which deals only with the diffusion of magnetization.

Figure 1.

A 1D three-point finite difference stencil.

Note that equation (2) assumes that diffusion coefficients are homogeneous. However, the diffusion coefficients are not homogeneous for biological tissues and jump probabilities (Hwang et al 2003) must be used to describe the movement of water molecules between grid points. The jump probability is defined as the probability that a spin starts at one grid point and migrates to another point after a time interval Δt. The explicit form of each jump probability can be found in Hwang et al (2003). Thus, equation (2) may then be expressed in terms of the jump probabilities as

$$m_j^{\prime n+1}=(1-s_{j\to j-1}-s_{j\to j+1})m_j^n+s_{j-1\to j}{m}_{j-1}^n+s_{j+1\to j}{m}_{j+1}^n,$$ (3)

where s_j→j—1 is the jump probability from point (j) to (j — 1).

2.2. Matrix-based finite difference method

Equation (3) focuses on the individual grid points, but it can be rewritten in a more convenient way. If we label grid points with 1, 2, 3, …, N (N is the total number of grid points, shown in figure 3) and suppose there are impermeable barriers at boundaries (this is how conventional FD deals with the boundaries, which causes edge effects), the FD equations with explicit FTCS are given by

$$\begin{array}{cc}\hfill & m_1^{\prime n+1}=m_1^n-s_{1\to 2}{m}_1^n+s_{2\to 1}{m}_2^n\hfill \\ \hfill & m_2^{\prime n+1}=m_2^n-(s_{2\to 1}+s_{2\to 3})m_2^n+s_{1\to 2}{m}_1^n+s_{3\to 2}{m}_3^n\hfill \\ \hfill & m_3^{\prime n+1}=m_3^n-(s_{3\to 2}+s_{3\to 4})m_3^n+s_{2\to 3}{m}_2^n+s_{4\to 3}{m}_4^n\hfill \\ \hfill & ⋮\hfill \\ \hfill & m_N^{\prime n+1}=m_N^n-s_{N\to N-1}{m}_N^n+s_{N-1\to N}{m}_{N-1}^n.\hfill \end{array}$$

Alternatively, the matrix form of equation (2) may be written as

$${\mathbf{M}}^{\prime n+1}={\mathbf{M}}^n+{\mathbf{AM}}^n,$$ (4)

where Mⁿ denotes a vector containing magnetizations and the transition matrix A, which contains the biological tissue structural information, is given by

$$\left(\begin{array}{ccccc}\hfill -s_{1\to 2}\hfill & \hfill s_{2\to 1}\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill s_{1\to 2}\hfill & \hfill -s_{2\to 1}-s_{2\to 3}\hfill & \hfill s_{3\to 2}\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill s_{2\to 3}\hfill & \hfill -s_{3\to 2}-s_{3\to 4}\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill -s_{N\to N-1}\hfill \end{array}\right).$$ (5)

Note that equation (5) gives the maximum possible number of non-zero elements. If any two grid points do not exchange water molecules in a time step, the corresponding matrix element should be zero.

Figure 3.

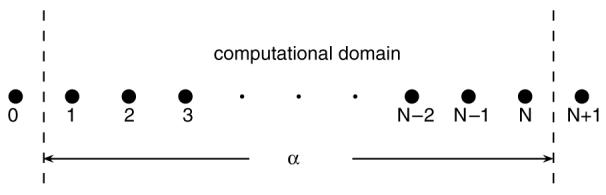
Diagram scheme of the 1D revised periodic boundary condition. The region between two dashed lines is the computational domain. The whole structure is periodic so that points 0 and N, and points 1 and N + 1 have identical structures and spin densities, respectively.

Finally, the discretized Bloch—Torrey equation for transverse magnetization using the MFD with explicit FTCS scheme can be written as

$${\mathbf{M}}^{n+1}={\Phi }^n\otimes (\mathbf{I}+\mathbf{A}){\mathbf{M}}^n,$$ (6)

where I is an identity matrix with the same size of A, ⊗ denotes the element-by-element vector multiplication and Φⁿ is a vector describing the phase accumulation and the transverse relaxation in every time step,

$$\begin{array}{c}\hfill {\Phi }^n=\left[\exp \right(-\mathrm{i}\gamma g^n{x}_1\Delta t-\Delta t∕T_{2,1}),\exp (-\mathrm{i}\gamma g^n{x}_2\Delta t-\Delta t∕T_{2,2}),\dots ,\hfill \\ \hfill \exp (-\mathrm{i}\gamma g^n{x}_N\Delta t-\Delta t∕T_{2,N})].\hfill \end{array}$$ (7)

Equation (6) converts the conventional FD formulism into matrix algebra which not only simplifies the notation, making it easier to implement into a simulation, but also increases the computing efficiency because most of the scientific languages such as MATLAB and C/C++ have optimized packages/subroutines for computing with large matrices. Moreover, different discretization schemes can be easily implemented using MFD. For example, MFD with the implicit FTCS is expressed as

$${\mathbf{M}}^{n+1}={\Phi }^n\otimes {(\mathbf{I}-\mathbf{A})}^{-1}{\mathbf{M}}^n,$$ (8)

and with the Crank—Nicolson scheme (Fletcher 1988) it is

$${\mathbf{M}}^{n+1}={\Phi }^n\otimes {\left(\mathbf{I}-\frac{\mathbf{A}}{2}\right)}^{-1}\left(\mathbf{I}+\frac{\mathbf{A}}{2}\right){\mathbf{M}}^n.$$ (9)

Another benefit from MFD is that the boundary conditions can be included in the matrix A. Since most of the simulations deal with invariable structures, such as image-based FD simulations, the matrix A can be determined at the start of simulation and that increases the computing efficiency significantly. Note that A has the dimensions of N × N which is usually extremely large and a sparse matrix should be used to avoid any possible memory allocation problems in the simulation.

2.3. Edge effects and revised periodic boundary conditions for the Bloch—Torrey equation

Most applications of FD methods rely on three basic boundary conditions, Dirichlet, Neumann and periodic. The first one assumes that the function values at the boundaries are predictable; the second one assumes the fluxes across the boundaries are predictable; and the third assumes the fluxes entering and leaving are equal. However, the applied magnetic gradients in the Bloch—Torrey equation break down the applicability of all these conventional boundary conditions because the magnetic gradients make the local magnetization increments dependent on location, so that after some time of undergoing Brownian motion, neither the magnetizations at the boundaries nor the magnetization fluxes across the boundaries are predictable and the magnetizations in the computational domain obviously do not conserve. If an assumption of impermeable boundaries is used, the apparent diffusion close to those artificial boundaries is highly restricted. Therefore, the simulated signals are enhanced significantly by error. This is the so-called edge effect, noted by Hwang et al (2003). To avoid the edge effect, they obtained results only from the unaffected central one-third grid points for a specific diffusion time (37 ms). However, when the diffusion time increases the influence of the boundaries propagates further into the centre of the computational domain, and then the central one-third region no longer produces reliable data. In this case, fewer grid points can be chosen or, equivalently, an even larger computational domain is necessary. This is either computationally expensive or a source of significant errors. Figure 2 shows how the edge effect increases with increasing diffusion time when using the conventional FD method.

Figure 2.

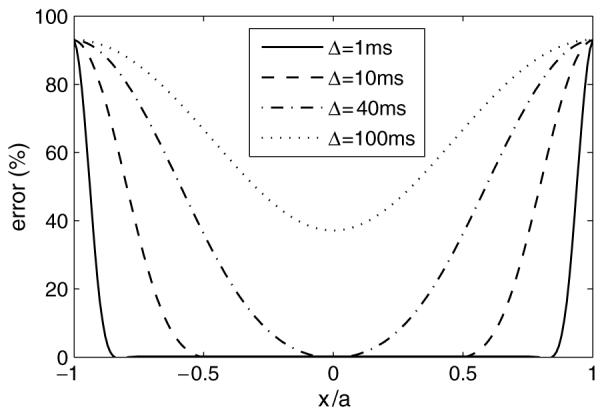
Error distributions of simulated magnetization as a function of spatial coordinates x and diffusion times using the conventional FD method. The error is expressed as the ratio |ADC_simulated — ADC_ideal|/ADC_ideal × 100% and the simulated parameters are the same in section 3.1.

A possible solution to reduce the edge effect is the hybrid discretization scheme algorithm (HDSA) (Xu et al 2006). However, HDSA still induces errors at the boundaries and, moreover, it becomes less stable when high b values (>100 ms μm⁻²) are used. A revised periodic boundary condition (RPBC) for the Bloch—Torrey equation has been developed in this paper to eliminate the edge effect completely.

Figure 3 shows the schematic diagram of the RPBC. The length of the computational domain is α which is the length of a unit cell. The conventional periodic boundary condition, m₀ = m_N and m_N+1 = m₁, is obviously not correct for our problem. However, using the relation of two corresponding points in a periodic structure (see the appendix), we obtain

$$m_0^n=\exp \left[\mathrm{i}\alpha \gamma \sum _{k=1}^n{g}^k\Delta t\right]\cdot m_N^n\text{and}{m}_{N+1}^n=\exp \left[-\mathrm{i}\alpha \gamma \sum _{k=1}^n{g}^k\Delta t\right]\cdot m_1^n.$$

Hence, the updating rules for the edge points 1 and N become

$$m_1^{\prime n+1}=m_1^n-(s_{1\to 2}+s_{1\to N})m_1^n+s_{2\to 1}{m}_2^n+s_{N\to 1}\exp \left(\mathrm{i}\alpha \gamma \sum _{k=1}^n{g}^k\Delta t\right)m_N^n$$ (10)

and

$$m_N^{\prime n+1}=m_N^n-(s_{N\to N-1}+s_{N\to 1})m_N^n+s_{N-1\to N}{m}_{N-1}^n+s_{1\to N}\exp \left(-\mathrm{i}\alpha \gamma \sum _{k=1}^n{g}^k\Delta t\right)m_1^n,$$ (11)

where s_1→N and s_N→1 are defined as the jump probabilities between points 1 and N as if they were adjacent. Equations (10) and (11) are the RPBC for the 1D Bloch—Torrey equation. Since the only assumption here is the periodic structure, this RPBC can be used for any gradient waveforms.

The transition matrix A with the RPBC becomes

$$\left(\begin{array}{ccccc}\hfill -s_{1\to 2}-s_{1\to N}\hfill & \hfill s_{2\to 1}\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill s_{N\to 1}\exp \left(\mathrm{i}\alpha \gamma \sum _{k=1}^n{g}^k\Delta t\right)\hfill \\ \hfill s_{1\to 2}\hfill & \hfill -s_{2\to 1}-s_{2\to 3}\hfill & \hfill s_{3\to 2}\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill s_{2\to 3}\hfill & \hfill -s_{3\to 2}-s_{3\to 4}\hfill & \hfill \dots \hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill 0\hfill \\ \hfill s_{1\to N}\exp (-\mathrm{i}\alpha \gamma \sum _{k=1}^n{g}^k\Delta t)\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \dots \hfill & \hfill -s_{N\to N-1}-s_{N\to 1}\hfill \end{array}\right).$$ (12)

With the substitution of equation (12), the RPBC is easy to implement into equation (6) (explicit FTCS), (8) (implicit FTCS) and equation (9) (Crank—Nicolson) for solving the Bloch—Torrey equation.

2.4. Tightly coupled parallel computing model

The intrinsic diffusion coefficients inside cells may be different from those outside the cells and it has already been shown that membrane permeability plays an important (maybe dominant) role in water diffusion in biological tissues (Beaulieu and Allen 1994; Szafer et al 1995). Therefore, the computational model should have a space resolution at least of the cellular level. In order to probe what intracellular structures affect diffusion, the resolution must be even greater and cells cannot be considered uniform or isotropic. Considering the small cellular dimensions of brain tissue (e.g. 2 μm for grey matter) and relatively large spatial resolution of DWI (>100 μm, typically), the computing problem has very large scale; >10⁶ nodes even for one voxel of an MRI image. Hence, a high performance computing technique is necessary to extend numerical methods suitable to larger-scale samples. We have implemented a parallel processing approach to address this problem.

The most time-consuming part in solving equation (6) is the matrix—vector multiplication which therefore should be parallelized. A frequently used parallel strategy is the master—slave model (Tu et al 2006) which can deal with numerous independent computing jobs. Each processor computes one job at a time and all processors work independently. However, this model might not be suitable for our problem due to the large size of our computing sample. An alternate parallelization strategy for our problem is (Quinn 2004)

$$\left(\begin{array}{c}\hfill 1\hfill \\ \hfill \_\hfill \\ \hfill 2\hfill \\ \hfill \_\hfill \\ \hfill ⋮\hfill \\ \hfill \_\hfill \\ \hfill n_p\hfill \end{array}\right)\times \left(\begin{array}{c}\hfill 1\hfill \\ \hfill \_\hfill \\ \hfill 2\hfill \\ \hfill \_\hfill \\ \hfill ⋮\hfill \\ \hfill \_\hfill \\ \hfill n_p\hfill \end{array}\right).$$ (13)

1, 2, …, denote the indices of strips calculated by corresponding processors and n_p is the total number of processors. This method splits the large matrices and vectors into smaller strips and a processor computes a strip so that the effective dimension of the problem is decreased. However, this method requests all processors to broadcast all their results to the other processors in every time step which is usually a bottleneck for the computing. To decrease the communication among processors and increase the computing efficiency, a tightly coupled parallel computing model was developed for our problem.

In this model, the whole sample tissue is first partitioned into a number of small sub-blocks (cubes in figure 4) according to the number of processors so that each sub-block is simulated by a single processor. Obviously, the processors are organized into a 3D Cartesian virtual topology which is the same as the topology of sub-blocks. Every processor simulates one sub-block using the MFD described above as if it was a single processor problem. However, the sample partition induces new artificial boundaries between the sub-blocks which usually cause larger errors. To avoid this influence, all of the processors should work synchronously and communicate with adjacent processors to swap boundary information in every time step. The effect of the new-formed artificial boundaries can be completely eliminated. For the boundaries of the whole computational domain, RPBC should be used to eliminate the edge effect. Hence, our tightly coupled parallel computing model does not induce any more errors in the simulation. Note that the communication burden of the tightly coupled model is of the order of Σ_m,n N_mN_n,(m,n = x, y, z), which is usually much less than the amount of equation (13) (N_xN_yN_z) and that is the reason why this model shows an increased efficiency.

Figure 4.

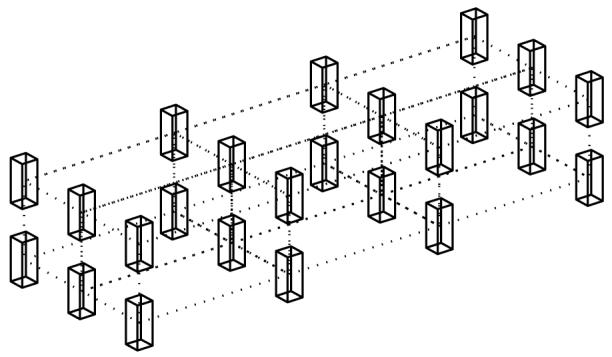
Topology of the tightly coupled parallel computing model. Cubes represent the sub-blocks processed by different processors. The virtual topology of processors should be the same and dotted lines represent the communications between adjacent processors.

All parallel computing simulations in this work were performed on the Vanderbilt University Advanced Computing Center for Research & Education (ACCRE) cluster. The programs were written in C with MPI (message passing interface) running on 2.0 GHz Opteron processors and a 32-bit Linux operation system with a Gigabit Ethernet network.

3. Simulations

3.1. Isotropic diffusion

To test the feasibility of our method, diffusion in a 1D sample of isotropic diffusion was simulated first. Four types of diffusion-weighted pulse sequences were used: the pulse gradient spin echo (PGSE) with short gradient approximation (PGSE-short) (Callaghan 1995), PGSE with finite duration of gradients (PGSE-finite) (Callaghan 1997), oscillating gradient spin echo (OGSE) with sine-modulated gradient waveforms (OGSE-sin) and OGSE with cosine-modulated waveforms (OGSE-cos) (Parsons et al 2003, Does et al 2003). The parameters used were diffusion coefficient D = 1 μm² ms⁻¹, b = 1 ms μm⁻², Δx = 0.2 μm, Δt = 10^-3 ms and total number of grid points N = 201 for all sequences; time between the onsets of two gradients Δ = TE/2 for both PGSE sequences; duration of gradient δ = 10⁻³ ms for PGSE-short, δ = Δ/2 for PGSE-finite and both OGSE sequences; frequency of the applied oscillating gradient f = 4/δ, i.e. 320 Hz—16 kHz for TE = 1–50 ms.

Figure 5 shows a comparison of the conventional FD and improved FD with RPBC methods for 1D isotropic diffusion with four types of pulse sequences. The conventional FD gives larger errors when TE increases, which shows the significant influence of the edge effect. In contrast, the errors of the improved FD with RPBC are all smaller than 1% for all pulse sequences and diffusion times, which confirms that the edge effect has been removed by the use of RPBC. One interesting feature is that both OGSE sequences give much smaller errors than the PGSE for the conventional FD method, which shows that the barrier-induced effect has been reduced. This may be explained in terms of the relatively smaller effective diffusion time obtained by the OGSE (Does et al 2003).

Figure 5.

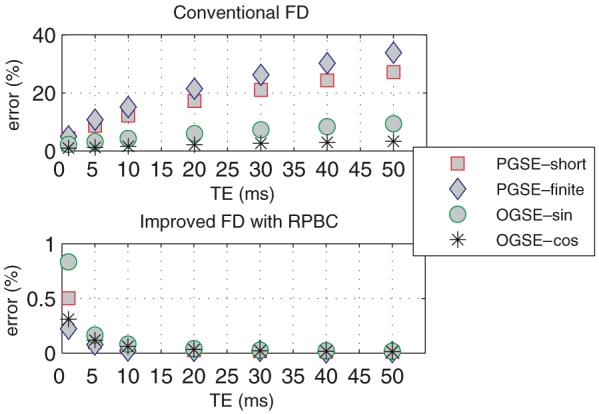
Comparison of conventional FD and improved FD with RPBC for a 1D isotropic diffusion sample with four types of pulse sequences: PGSE-short, PGSE-finite, OGSE-sin and OGSE-cos (for definitions see the first paragraph of section 3.1). Note that results with the conventional FD method are calculated from the whole computational domain and show large errors caused by the edge effect. In contrast, all results with RPBC have errors smaller than 1%, which shows the elimination of the edge effect. The definition of the error is the same as in figure 2.

When the FD method with explicit FTCS scheme is used as the simulation algorithm, the CFL condition (Fletcher 1988) should be satisfied to ensure the stability of the simulation, i.e., jump probability should be smaller than or equal to 1/2, 1/4, 1/6 for 1D, 2D and 3D, respectively. In addition, it has been found that the amplitudes of the applied magnetic gradients affect the results: larger amplitude gradients yield large errors. Figure 6 shows this effect. All simulation parameters are the same as above except b = 0.01–10 ms μm⁻² and a dimensionless factor β is defined as

$$\beta =Q\times \Delta x∕\pi$$ (14)

where

$$\begin{array}{cc}\hfill Q=\max \left\{f\left(t\right)\right\},\hfill & \hfill f\left(t\right)={\int }_0^{t}g\left(t^{\prime }\right)\mathrm{d}{t}^{\prime }.\hfill \end{array}$$ (15)

Figure 6.

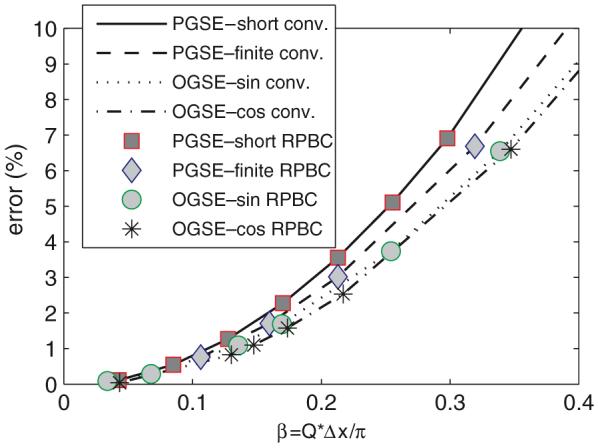
Simulation errors change with respect to a dimensionless factor β = Q × Δx/π. The results of the conventional FD method were taken from the central region unaffected by the edge effect.

Figure 6 shows that both conventional FD and the improved FD method with RPBC have increasing simulation errors with the amplitude of gradient increasing. Furthermore, both FD methods show the same behaviour with respect to β (noting that the results of the conventional FD method were only taken from the central region unaffected by the edge effect), which implies that this might be an intrinsic property when the FD algorithm is used to solve the Bloch—Torrey equation. In practice, β < 01 is needed to obtain a simulation error smaller than 1%.

3.2. Hexagonal array of permeable cylinders

Some neural tissues, such as white matter, are often modelled as a bunch of parallel cylinders for studying water diffusion. Exact expressions for the ADC have been published for a single cylinder with impermeable walls (Soderman and Jonsson 1995) and with wall relaxation (Callaghan 1995). An analytical expression for the thermal conductivity has been obtained for hexagonal arrays of perfectly conducting cylinders (Perrins et al 1979). Thermal conductivity and diffusion are analogous transport properties, so an analytical expression for the transverse ADC of hexagonal arrays of cylinders with perfect diffusivities at the cylinder boundaries may be obtained as (Hwang et al 2003)

$$\mathrm{ADC}(\Delta \to \infty )=D_e\left[1-2f{\left(\xi +f-\frac{0.075422f^6\xi }{{\xi }^2-1.060283f^{12}}-\frac{0.000076f^{12}}{\xi }\right)}^{-1}\right],$$ (16)

where

$$\begin{array}{cc}\hfill \xi =(1+\kappa )∕(1-\kappa ),\hfill & \hfill \kappa =D_i∕D_e\hfill \end{array}$$ (17)

and D_i, D_e are diffusion coefficients inside the cylinders (intra-cellular space) and outside the cylinders (extra-cellular space), respectively, and f is the volume fraction of the cylinders.

Figure 7 shows the cross-section of a hexagonal array of cylinders simulating white matter axons. Cylinders (grey in figure 7) are axons and the surrounding matrix (white) is extra-cellular space. To compare with the analytical results, the myelin was assumed to be non-space occupying and with infinite permeability, and the diffusion time is very long (TE = 50 ms). The conventional FD method should simulate a much larger image to avoid the edge effect, whereas the improved FD with RPBC only needs to simulate the smallest unit cell of the structure.

Figure 7.

Cross-section of a hexagonal array of cylinders: cylinders are grey and the surrounding matrix is white. To avoid the edge effect, the conventional FD method simulates the whole image and takes signals from the central barely affected domain for long diffusion times; whereas the improved FD method with RPBC only needs to simulate a unit cell (in the black box).

Simulated and analytical results for structures with different cylinder volume fractions are compared in figure 8. The sizes of the cylinders were kept constant so that the change of interspacing of cylinders yields the various volume fractions. A PGSE-short pulse sequence was used in the simulations and all parameters were the same as in section 3.1, except that D_i = 1.12 μm² ms⁻¹, D_e = 1.65 μm² ms⁻¹, Δx = Δy = 0.5 μm, TE = 50 ms and number of points N_x = N_y = 96 for the whole image.

Figure 8.

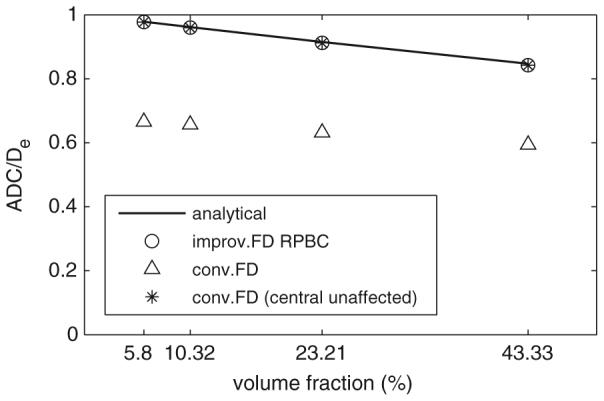
Comparison of simulated and analytical results for the hexagonal array of cylinders. For conventional FD, the results were taken from both whole domain and central unaffected domain for comparison.

Figure 8 shows again the large errors caused by the edge effect (26–32%). Taking results only from the central unaffected computational domain (Hwang et al 2003) did remove the edge effect for the conventional FD method. However, it is much less efficient that 88% (2D) or 96% (3D) of the computational domain (and thus the computing time) was actually wasted. In contrast, the improved FD with RPBC gave relatively accurate results but was much more efficient (less than 5% of the computing time of the conventional FD method in the simulations of figure 8).

3.3. Cubic cells on a cubic grid

It has been reported that ADC in brain tissue drops significantly soon after the onset of a stroke (Moseley et al 1990, Warach et al 1992). It has also been shown that ADC changes with intra-cellular volume fraction (Anderson et al 2000). Hence, the relationship between ADC and intra-cellular volume fraction is of considerable interest. Two analytical expressions for the ADC for cubic cells on a cubic grid have been developed using two types of models: parallel—series (PS) and series—parallel (SP) (Szafer et al 1995). For a cubic cell with size L and permeability P on a cubic grid, the ADC expressions are

$${\mathrm{ADC}}^{\mathrm{PS}}(\Delta \to \infty )=\frac{f^{2∕3}}{\frac{f^{1∕3}}{D_c}+\frac{1-f^{1∕3}}{D_e}}+(1-f^{2∕3})D_e$$ (18)

$${\mathrm{ADC}}^{\mathrm{SP}}(\Delta \to \infty )={\left[\frac{f^{1∕3}}{f^{2∕3}{D}_c+(1-f^{2∕3})D_e}+\frac{(1-f^{1∕3})}{D_e}\right]}^{-1}$$ (19)

where D_c is the effective ADC for a cell,

$$D_c={\left[\frac{2}{\mathit{PL}}+\frac{1}{D_i}\right]}^{-1}.$$ (20)

Simulated results for such an array using the improved FD method with RPBC are shown in figure 9. The parameters used the measured values for red blood cells: D_i = 0.63 μm² ms⁻¹, D_e = 2 μm² ms⁻¹ and P = 0.024 μm ms⁻¹ (Anderson et al 2000) and the others are the same in the above sections.

Figure 9.

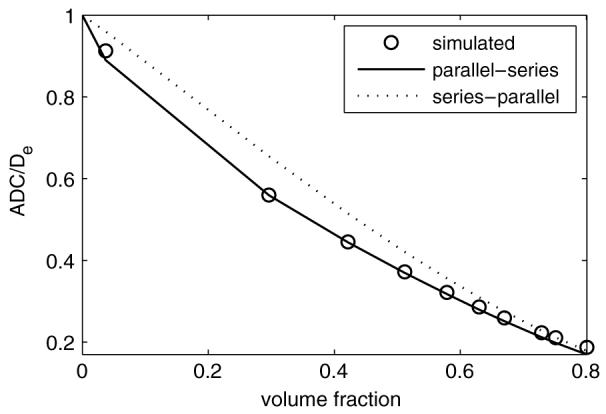
ADC changes with respect to the intra-cellular volume fraction for a diffusion system of cubic cells on a cubic grid. Simulated results show good agreement with the PS model which is consistent with the experimental data on packed red blood cells.

The simulated results match the PS model quite well, better than the SP model. This might imply that the PS model is more accurate for packed red blood cells, which is consistent with previous experiments (Anderson et al 2000). The simulations using the conventional FD method were not performed here because it requires thousands of times more computing time, whereas the improved FD with RPBC method took only seconds to run.

3.4. Large-scale sample of pure water

Although the improved FD with RPBC algorithm significantly reduces the effective dimensions of a tissue sample and, hence, increases the computing efficiency, heterogeneous tissue samples are usually very complicated and have large dimensions, especially for a simulation with sub-cellular resolution. High performance computing may be used to address such a large-scale computing problem. To test the computing performance of our tightly coupled parallel computing model, a large sample of pure water with a 101 × 101 × 101 grid was simulated using different number of processors using a PGSE-short pulse sequence. The parameters used were D = 2.5 μm² ms⁻¹, b = 1 ms μm⁻², temporal interval Δt = 0.001 ms, spatial interval Δx = 0.5 μm, TE = 100 ms and the size of computational domain along one direction = 2a, a = 50 μm.

Figure 10 shows that the total computing time decreases as more processors are used. The total computing time for 56 processors is only 2.5% of the time for a single processor. The advantage of using parallel computing is obvious. Note that the total computing time reaches its minimum when 56 processors were used in the simulation while the computing time increases when more (64 shown in figure 10) processors are used. The reason is that when more processors are used in the simulation, the communication and synchronization time spent among the processors increases. When the portion of the communication time is too large, the computing time begins to increase again and the efficiency of parallel computing decreases. This shows that, for a certain problem, the parallel computing technique cannot decrease the total computing time indefinitely as more processors are used. There is a minimum computing time for a specific problem with specific computing facilities.

Figure 10.

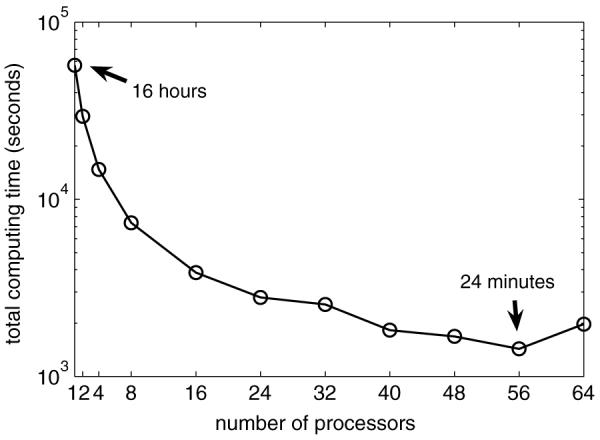
Total computing time changing with respect to the number of processors. Total computing time includes the processor execution time, communication and synchronization time.

To better understand the parallel computing performance of our model, a speedup chart is plotted in figure 11. Speedup is defined as S = t₁/t_n, t₁ is the computing time for a sequential program (one processor) and t_n is the total computing time for n processors. Our result reaches the ideal (theoretical maximum) speedup for up to 16 processors and the performance still increases when less than 56 processors are used, which verifies the computing performance of the tightly coupled parallel computing model. The speedup drops down as more time is spent on communication and synchronization, which means the parallel computing performance decreases.

Figure 11.

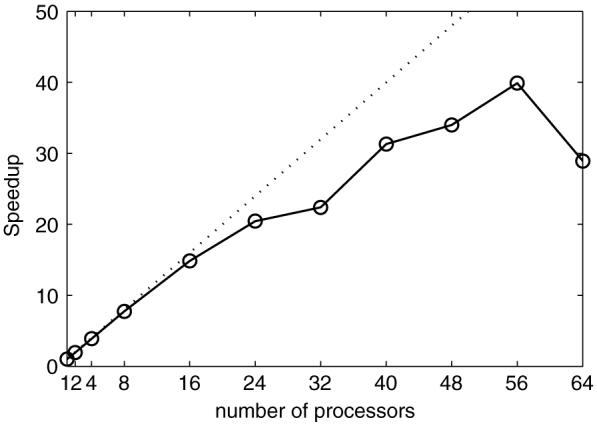
Speedup chart of the tightly coupled parallel computing model.

4. Discussion

For the conventional FD method, the transition matrix A remains invariant for a certain tissue sample which significantly increases the computing efficiency. In contrast, for the improved FD with RPBC method, A depends on the applied gradients, which are usually time dependent. Hence, extra computing time should be used to update A in every time step if a general diffusion-sensitizing gradient waveform is used for the RPBC method. This may decrease computing efficiency. Fortunately, only the matrix elements which describe the diffusion across the boundaries vary and they usually take only a small portion of the total matrix elements. Therefore, the extra time spent on updating A in the RPBC method increases only a small portion of the total computing time. Furthermore, the RPBC method significantly reduces the effective dimension of the tissue sample by removing the edge effects. Hence, the improved FD with RPBC method shows a better computing efficiency than the conventional FD method. In practice, the explicit FTCS discretization scheme is suggested for the improved FD with RPBC method to avoid the time-consuming calculations of matrix inversion in implicit FTCS or Crank—Nicolson schemes.

The tightly coupled parallel computing approach significantly reduces the communication overhead in the simulation and increases the parallel computing performance. In addition, since all simulations in this paper were performed with a Gigabit Ethernet network, an even better parallel computing performance may be obtained by using a Myrinet network (which has lower latency and higher bandwidth).

Not only model structures but also histological images can be used in the approach presented in this paper, which would enable the investigation of diffusion behaviour in large-scale realistic tissues. This has the potential to provide a means to better understand how the changes of tissue morphology influence ADC measurements. Another possible application of this approach is the inverse problem, i.e. deducing the structure or parameter changes caused by disease or injury from the changes observed in the diffusion measurements.

5. Conclusion

We have developed an improved finite difference method which not only eliminates the edge effect induced by the conventional FD approach but also enables the efficient large-scale simulation of diffusion in biological tissues with the implementation of a tight-coupled parallel computing model. This method is applicable to studies of water diffusion in MRI to aid the interpretation of diffusion-weighted imaging measures and their dependence of the morphology of biological tissues such as tumours.

Appendix

On the assumption that the structure is periodic with the computational domain as the unit cell, a simple relationship can be derived between any two corresponding points in different unit cells with any gradient waveforms. For simplicity, only the 1D case is discussed below. 2D and 3D cases can be derived in a similar way.

Suppose x_a and x_b are two points related as

$$x_a=x_b+n\alpha$$ (A.1)

where n is any integer and α is the length of the unit cell. The water diffusion propagator of the whole periodic structure can be defined as P(x|x’, Δ), which means the probability of a water molecule starts from position x and migrates to x’ after a diffusion time Δ. The explicit form of the propagator is usually unknown except for a few simple geometries (Callaghan 1995). However, the periodic structure yields

$$P(x\mid x^{\prime },\Delta )=P(x+n\alpha \mid x^{\prime }+n\alpha ,\Delta ),$$ (A.2)

transverse relaxation time

$$T_2\left(x\right)=T_2(x+n\alpha ),$$ (A.3)

and the spin density

$$\rho \left(x\right)=\rho (x+n\alpha ).$$ (A.4)

Since any general gradient waveform can be considered as a series of short gradients (Callaghan 1997, Sukstanskii and Yablonskiy 2002), the magnetizations at x_a and x_b can be calculated by

$$\begin{array}{cc}\hfill m(x_a,t)=\int & \mathrm{d}{x}_1\int \mathrm{d}{x}_2\cdots \int \mathrm{d}{x}_N\rho \left(x_1\right)\exp (-\mathrm{i}{q}_1{x}_1)\exp (-\Delta t∕T_2\left(x_1\right))P(x_1\mid x_2,\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_2{x}_2)\exp (-\Delta t∕T_2\left(x_2\right))P(x_2\mid x_3,\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_{N-1}{x}_{N-1})\exp (-\Delta t∕T_2\left(x_{N-1}\right))P(x_{N-1}\mid x_N,\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_N{x}_N)\exp (-\Delta t∕T_2\left(x_N\right))P(x_N\mid x_a,\Delta t)\hfill \end{array}$$ (A.5)

and

$$\begin{array}{cc}\hfill m(x_b,t)=\int & \mathrm{d}{x}_1\int \mathrm{d}{x}_2\cdots \int \mathrm{d}{x}_{N\rho }\left(x_1\right)\exp (-\mathrm{i}{q}_1{x}_1)\exp (-\Delta t∕T_2\left(x_1\right))P(x_1\mid x_2,\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_2{x}_2)\exp (-\Delta t∕T_2\left(x_2\right))P(x_2\mid x_3,\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_{N-1}{x}_{N-1})\exp (-\Delta t∕T_2\left(x_{N-1}\right))P(x_{N-1}\mid x_N,\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_N{x}_N)\exp (-\Delta t∕T_2\left(x_N\right))P(x_N\mid x_b,\Delta t)\hfill \end{array}$$ (A.6)

where q_n = γ g_n Δt, n = 1, …, N, g_n is the gradient at time t_n, Δt is the time step and t = N Δt, N is the total number of time steps. Considering the periodic structure, a substitution of x_N = x’_N + nα and (A.1) can be made and (A.5) becomes

$$\begin{array}{cc}\hfill m(x_a,t)=\exp & (-\mathrm{i}n\alpha q_N)\int \mathrm{d}{x}_1\int \mathrm{d}{x}_2\cdots \int \mathrm{d}{x}_N^{\prime }\rho \left(x_1\right)\exp (-\mathrm{i}{q}_1{x}_1)\hfill \\ \hfill & \times \exp (-\Delta t∕T_2\left(x_1\right))P(x_1\mid x_2,\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_2{x}_2)\exp (-\Delta t∕T_2\left(x_2\right))P(x_2\mid x_3,\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_{N-1}{x}_{N-1})\exp (-\Delta t∕T_2\left(x_{N-1}\right))P(x_{N-1}\mid x_N^{\prime }+n\alpha ,\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_N{x}_N^{\prime })\exp (-\Delta t∕T_2\left(x_N^{\prime }\right))P(x_N^{\prime }\mid x_b,\Delta t)\cdot \hfill \end{array}$$ (A.7)

After a series of substitutions x_i = x’_i + nα (i = N — 1, N — 2,…, 1), (A.7) becomes

$$\begin{array}{cc}\hfill m(x_a,t)=\exp & \left(-\mathrm{i}n\alpha \sum _{k=1}^{N}qk\right)\int \mathrm{d}{x}_1^{\prime }\int \mathrm{d}{x}_2^{\prime }\cdots \int \mathrm{d}{x}_N^{\prime }\rho \left(x_1^{\prime }\right)\hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_1{x}_1^{\prime })\exp (-\Delta t∕T_2\left(x_1^{\prime }\right))P(x_1^{\prime }\mid x_2^{\prime },\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_2{x}_2^{\prime })\exp (-\Delta t∕T_2\left(x_2^{\prime }\right))P(x_2^{\prime }\mid x_3^{\prime },\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_{N-1}{x}_{N-1}^{\prime })\exp (-\Delta t∕T_2\left(x_{N-1}^{\prime }\right))P(x_{N-1}^{\prime }\mid x_N^{\prime },\Delta t)\cdots \hfill \\ \hfill & \times \exp (-\mathrm{i}{q}_N{x}_N^{\prime })\exp (-\Delta t∕T_2\left(x_N^{\prime }\right))P(x_N^{\prime }\mid x_b^{\prime },\Delta t)\hfill \\ \hfill =& \exp \left(=\mathrm{i}n\alpha \sum _{k=1}^N{q}_k\right)m(x_b,t).\hfill \end{array}$$ (A.8)

In general, one can obtain

$$m(x_a,t)=\exp \left[-\mathrm{i}n\alpha \gamma {\int }_0^{t}g\left(t^{\prime }\right)\mathrm{d}{t}^{\prime }\right]\cdot m(x_b,t).$$ (A.9)

Recalling that x_a = x_b + nα, equation (A.9) shows that the magnetizations at two corresponding points in different unit cells are simply related to a phase factor which depends only on the integral of the applied gradients and the distance between these two points. Note that it is assumed that the whole structure is periodic but the structure inside each unit cell (the computational domain) is usually heterogeneous.