High-Field Dynamic Nuclear Polarization for Solid and Solution Biological NMR

Abstract

Dynamic nuclear polarization (DNP) results in a substantial nuclear polarization enhancement through a transfer of the magnetization from electrons to nuclei. Recent years have seen considerable progress in the development of DNP experiments directed towards enhancing sensitivity in biological nuclear magnetic resonance (NMR). This review covers the applications, hardware, polarizing agents, and theoretical descriptions that were developed at the Francis Bitter Magnet Laboratory at Massachusetts Institute of Technology for high-field DNP experiments. In frozen dielectrics, the enhanced nuclear polarization developed in the vicinity of the polarizing agent can be efficiently dispersed to the bulk of the sample via ¹H spin diffusion. This strategy has been proven effective in polarizing biologically interesting systems, such as nanocrystalline peptides and membrane proteins, without leading to paramagnetic broadening of the NMR signals. Gyrotrons have been used as a source of high-power (5–10 W) microwaves up to 460 GHz as required for the DNP experiments. Other hardware has also been developed allowing in situ microwave irradiation integrated with cryogenic magic-angle-spinning solid-state NMR. Advances in the quantum mechanical treatment are successful in describing the mechanism by which new biradical polarizing agents yield larger enhancements at higher magnetic fields. Finally, pulsed methods and solution experiments should play a prominent role in the future of DNP.

1 Introduction

As Abragam and Goldman [1] pointed out in their seminal review of dynamic nuclear polarization (DNP), three of the major breakthroughs in materials science in the 20th century involved access to low-temperature [2], high-pressure regimes [3] and the production of highly polarized nuclei. The latter was first targeted for a wide variety of physical and chemical applications. Among the known methods for enhancing nuclear polarization, microwave (mw)-driven DNP, which involves transfer of magnetization from electron to nuclear spins, has proven to be one of the most effective and versatile in its ability to polarize a wide range of systems. This is a consequence of the strong coupling of the electron spin to the surrounding nuclei. The corresponding increase in polarization is a natural complement to the rapidly developing field of solid-state and solution nuclear magnetic resonance (NMR) as a structural tool in biology. The inherent lack of sensitivity in NMR is a major limiting factor in its extension to larger and more interesting biological systems. Thus, DNP experiments that achieve even a fraction of the theoretical maximum sensitivity enhancement of 660 could revolutionize many aspects of NMR spectroscopy.

In 1953 Overhauser [4] originally proposed that it was possible to transfer polarization to nuclei from electrons in metals by saturating the electron transition. The idea that saturating one transition could increase the polarization in another was counterintuitive and not widely accepted until experimental verification by Carver and Slichter [5]. These studies served as the foundation for modern DNP and were soon expanded to solid dielectrics by Abragam and Proctor [6], who first characterized the solid effect (SE). In the 1980s Wind, Yannoni, Schaefer and their colleagues [7–9] performed DNP in conjunction with magic-angle-spinning (MAS) solid-state NMR (SSNMR). However, extending DNP to higher fields proved challenging due to a lack of high-power mw sources above 94 GHz. One approach to circumvent this problem, pioneered by Dorn et al. [10], is to polarize samples at lower magnetic fields and then transfer the sample to a higher field where the NMR spectrum is recorded. However, such methods employing field cycling have their technical limitations. Applying in situ high-power mw irradiation at the detection field strength without the need for field cycling has been the focus of our experiments at Massachusetts Institute of Technology. This approach has proven an effective means for gaining enhanced polarization in SSNMR aimed at biological solids. For other implementations of DNP, we direct the reader to other articles in this volume and to the recent review by Maly et al. [11].

Developments in instrumentation for high-power mw sources and cryogenic MAS, and theoretical and chemical advancements involving the cross effect (CE) and biradicals have allowed the expansion of DNP to higher magnetic fields as needed for modern biological SSNMR. This review describes applications demonstrating the ability to acquire contemporary multidimensional SSNMR spectra on various biological systems as well as the instrumental, theoretical, and chemical developments that led to the first DNP/SSNMR experiments performed at high magnetic fields (5 and 9 T). However, the continuous-wave (CW) methods discussed below exhibit an inverse field dependence $({\omega }_0^{-1}\text{to}{\omega }_0^{-2})$. Thus, extension of DNP to even higher magnetic fields will likely entail the development of pulsed experiments to increase the efficiency of the polarization transfer process. Accordingly, we review a number of time domain methods that have been explored at fields up to 5 T.

This review is organized as follows. In Sect. 2 we discuss applications of CW DNP techniques to biological systems that provide a rationale for the development of DNP experiments. Section 3 describes the instrumentation required for the experiments including gyrotron oscillators which are the source of the subterahertz radiation used to irradiate the electron paramagnetic resonance (EPR) spectrum and the low-temperature NMR probes used in the experiments. In Sect. 4 we discuss the CE and the biradical polarizing agents that have thus far proven most effective in producing large enhancements (ε ~ 290) in solids at 90 K. Finally, in Sect. 4 we discuss two areas for future development – temperature-jump DNP experiments for solution spectroscopy and time domain experiments. Both of these areas should undergo considerable development in the future.

2 Solid-State Applications to Biological Samples

2.1 Frozen Glass-Forming Solvents

DNP on frozen glycerol-water solutions doped with biradicals has been proven widely applicable as a means of providing signal enhancements on the order of 10²–10³ in a range of biological systems such as virus capsids and lipids [12], amyloidogenic peptides [13], and large membrane proteins [14, 15]. An aqueous solvent mixture consisting of deuterated glycerol, D₂O, water, and a soluble biradical polarizing agent [16, 17] provides a glass-forming matrix that distributes the polarizing agents uniformly and at the same time acts as a cryoprotectant. Experiments on non-glass-forming solvent matrices, which form crystals upon freezing, were found to yield significantly smaller DNP enhancements. This appears to be caused by an aggregation of the polarizing agents along the edge of the crystalline domains, concomitant with a degradation of the spectral resolution due to poor long-range homogeneity.

The DNP experiments described in this review rely on an efficient polarization transfer from electrons to nearby protons, relayed by nuclear spin diffusion among the proton network leading to an efficient and uniform signal enhancement of the bulk nuclei of interest [18]. Partially deuterated solvents yield larger enhancements because the biradicals can polarize the smaller proton reservoir more completely, and there is a minimal broadening of the nuclear resonances because the radicals are not in direct contact with the bulk nuclei. The experiment is typically performed at cryogenic temperatures (≤90 K) to lengthen the nuclear spin-lattice proton relaxation time (T_ln) allowing efficient pumping from the electron spin reservoir and appropriate ¹H spin diffusion. This approach yields enhancements that are a function of temperature and magnetic field, and ε = 400 is achieved at 20 K and 5 T [19]. In addition, enhancements of 10–25 are observed in some samples at room temperature [7, 20].

The low temperatures also affect the Boltzmann equilibrium, resulting in a Boltzmann population that is about three times higher at 90 K than at 270 K, thus giving a further increase in sensitivity. Even lower temperatures (ca. 20 K) accessible using helium as a spinning gas result in more polarization but also a longer T_ln. We note that the important parameter for improving signal-to-noise ratio in SSNMR is not only the magnitude of polarization, but rather the signal intensity recorded per square root unit time, which is dependent on the T_ln and thus the recycle delay. Bloembergen et al. [21] first showed that the presence of paramagnetic ions in a solution shortens the T_ln, an observation which has been more recently exploited in SSNMR experiments to reduce the low-temperature proton T_ln from 15 to 0.7 s, thus increasing the data collection rate by a factor of nearly 20 [22]. Thus, polarizing radicals serve not only as centers for DNP but also as relaxation agents because the magnetization between experiments is replenished from electron-nuclear polarization transfer and proton spin diffusion. Typical recycle delays in our experiments are 5–10 s.

We note that we refer to the enhancement, ε, as the ratio of the NMR signal intensities with and without microwaves. Other experimental parameters, such as the temperature, are identical between the two measurements (unless indicated otherwise). However, in the discussion of solution DNP experiments below we use the enhancement ε^† that includes a contribution from the Boltzmann temperature factor.

Multidimensional experiments increase the resolution of NMR spectra [24] but require repeated acquisitions, and thus a high level of experimental stability and reproducibility. Although the initial experiments discussed in Sect. 1 showed a marked signal enhancement, they were not suitable for recording multidimensional spectra mainly because of the difficulties of spinning with helium for extended periods. Rosay et al. [23] first used nitrogen as both a spinning and cooling gas to perform long-term two-dimensional (2-D) DNP experiments at 90 K. Figure 1 shows a 2-D spectrum of a frozen solution of U-¹³C,¹⁵N-proline recorded with DNP at 5 T (a higher magnetic field than in earlier experiments). This was the first successful demonstration of the integration of DNP-based polarization enhancement with a standard 2-D SSNMR pulse sequence. These data involved enhancement of a solute in intimate contact with the bulk solvent (containing the radicals). More recent versions of this experiment have achieved ε ~ 200 (T. Maly, Massachusetts Institute of Technology, Cambridge, MA, USA, pers. commun.).

Fig. 1.

Spin diffusion spectrum of U-¹³C,¹⁵N-proline in 40 mM TEMPO and glycerol/water. The DNP enhancement is 9 at 5 T and a temperature of 90 K. Reproduced with permission from ref. 23. (Copyright 2002 American Chemical Society).

2.2 Macroscopic Particles and Aggregates

Rosay et al. [12] showed that nuclei inside a virus capsid, which are not in direct contact with the bulk solvent, can be efficiently polarized through DNP. These experiments demonstrated equal signal enhancements for ¹⁵N in the coat proteins (on the outside) and ³¹P nuclei in the deoxyribonucleic acid inside the capsid. These data indicated that ¹H spin diffusion can act as an efficient mechanism for the uniform transfer of polarization into macromolecular assemblies on the order of 6 nm in size. The virus capsid experiments were performed at 15 K in the absence of sample spinning, and with low mw power from a Gunn diode, resulting in a DNP enhancement of 26 for both ¹⁵N and ³¹P. This also demonstrated that polarizing the proton bath and then relying on proton spin diffusion allows the enhancement of many different nuclei, such as ³¹P, ¹⁵N, and ¹³C via cross polarization (CP) [25].

Recent MAS SSNMR/DNP experiments by van der Wei et al. [13] also established that ¹H spin diffusion allowed the highly polarized ¹H magnetization from DNP to penetrate into even larger domains devoid of radicals. This is important since one attractive application of DNP in the solid state is the study of nanocrystalline or fibrillar macroscopic aggregates of proteins or peptides. Since these polypeptide aggregates are of a finite size, such samples can involve a spatial separation of the compounds of interest from the frozen solvent matrix that contains the radicals acting as sources of electron polarization. As discussed above, earlier experiments demonstrated the ability to efficiently polarize the matrix and the molecules contained therein. Enhancement of the polypeptide signals inside macroscopic crystals is, however, dependent on the ability of the enhanced polarization to (i) cross the boundary between the matrix and the sample aggregates and (ii) the ability for the polarization to diffuse into the bulk of these aggregates.

These issues were directly addressed in DNP experiments performed on nanocrystalline aggregates made from a peptide fragment, GNNQQNY_7–13, originating from the yeast prion protein Sup35p. This peptide forms either nanocrystals or amyloidlike fibrils and has been studied by X-ray crystallography [26, 27] and solid-state NMR [28] with the goal of elucidating the nature of amyloid fibril structure. The crystals used in the DNP experiments were 100–200 nm wide and were shown to be impenetrable by the TOTAPOL biradicals used in the experiments. The crystals were prepared in the absence of the radicals and subsequently mixed with a standard DNP solvent system, designed to be highly deuterated as well as glass-forming due to the presence of glycerol. Hence, efficient DNP enhancement would require polarization to diffuse into the crystals (see Fig. 2). Indeed, it was found that the glycerol carbons in the frozen matrix were highly and rapidly enhanced (ε ~ 160 with a time constant of 7–8 s), whereas the peptide signals were enhanced less and more slowly (ε ~ 120 with a time constant of 15.5–17 s), as shown in Fig. 2b. These results were consistent with a transfer of polarization from the bulk solvent into the crystals via ¹H-¹H spin diffusion. The DNP enhancement allowed the rapid acquisition of a 2-D ¹³C-¹³C experiment as illustrated in Fig. 2c. The results suggest that sensitivity enhancement via DNP is in principle (and in practice) possible for heterogeneous, hydrated protein crystals as well as fibrils, and should be an essential contribution to these areas of biological solid-state NMR.

Fig. 2.

DNP experiments on [20% U-¹³C,¹⁵N-GNNQ]QNY nanocrystals in d₈-glycerol/D₂O/H₂O (60/30/10) with 10 mM TOTAPOL. a Illustration of heterogeneously mixed DNP sample of crystalline peptide and the DNP solvent matrix, based on the transmission electron microscopy data on GNNQQNY nanocrystals. Arrows illustrate the diffusion of the enhanced polarization from the matrix into the crystals, b Differential polarization enhancement buildup of peptide and matrix carbon signals. The signal intensities are normalized to the equilibrium off signal, c DNP-enhanced 2-D ¹³C-¹³C dipolar-assisted rotary resonance or radiofrequency-assisted diffusion correlation spectrum of the same sample. Adapted from and reproduced with permission ref. 13. (Copyright 2006 American Chemical Society).

2.3 Membrane Proteins: Bacteriorhodopsin

The most explicit demonstration of DNP in conjunction with SSNMR to address biologically relevant questions was recently performed on the membrane protein bacteriorhodopsin (bR) [14, 29]. bR is a 26.6 kDa, 248-residue membrane protein acting as a light-driven ion pump. Initial DNP experiments on bR performed by Rosay et al. [15] demonstrated an enhancement of 50 at 90 K and 5 T. Extending these experiments to 9 T, corresponding to 380 MHz proton frequency, provided sufficient resolution to gain high-quality 2-D spectra and DNP expedited data acquisition permitting experiments which would not be possible without DNP.

Figure 3a shows the clear improvement in signal-to-noise ratio that DNP provides in the active site of a membrane protein. The single ¹⁵N resonance of the Schiff base is barely visible above the noise in the nonenhanced spectrum even with 3.5 days of signal averaging, but can clearly be seen after only 30 min of acquisition time using DNP. Figure 3b shows cross-peaks between the Schiff base ¹⁵N and ¹³C-15 of the retinal chromophore. Four cross-peaks are observed where only two are expected, providing clear evidence for structural heterogeneity in the dark-adapted state of bR that has not been detected previously. Note also that Fig. 3b shows negligible, if any, broadening of the resonances in the active site of bR due to the conditions used for DNP. Extensive assignments of resonances in mixed photointermediates of bR further show the usefulness of the excellent sensitivity available using DNP (V.S. Bajaj et al., unpubl.).

Fig. 3.

a ¹⁵N MAS spectra of light-adapted ζ-¹⁵N-Lys-bR. Top: Spectrum acquired on a 317 MHz spectrometer using a 5 mm ZrO₂ rotor with a 160 ml sample volume, 10000 scans, 3.5 days (about 5000 min) of data acquisition, T = 200 K. Bottom: Spectrum acquired with DNP-250 GHz mw irradiation using a 4 mm sapphire rotor, 40 ml sample volume, T = 90 K, 384 scans, 30 min of data acquisition. The resonances from left to right are: protonated Schiff base ¹⁵N at 165 ppm, natural-abundance amide backbone at 130 ppm, natural-abundance guanidine-HCl at 80 ppm (only in the 380 MHz spectrum), six free ζ-¹⁵N-Lys signals at 50 ppm. ω_r/2π = 7 kHz. b 2-D nitrogen carbon correlation spectrum of dark-adapted bR recorded with 250 GHz DNP, showing heterogeneity which cannot be resolved in the 1-D nitrogen spectrum. Reprinted from ref. 14. (Copyright 2007, with permission of Elsevier).

3 Instrumentation

3.1 Probe Design

Performing modern SSNMR experiments with concurrent high-frequency mw irradiation for DNP required the development of several new pieces of instrumentation. MAS SSNMR necessitates both the mechanical rotation of the sample rotor in the kilohertz regime and the ability to apply strong B₁ fields at the nuclear and electron Larmor frequencies.

Generation of strong B₁ fields at the nuclear Larmor frequencies is usually accomplished with solenoid radio frequency (RF) coils. The coil and MAS apparatus complicate the design of a mw resonator cavity and hence limit the quality factor, Q. This contrasts to Q values in EPR resonators which are about 10³, whereas the Q for the mw circuit in our SSNMR DNP experiments is close to unity. The inside of the stator cavity is coated with a thin layer of silver, which reflects the microwaves and increases the Q slightly. The large Q available in EPR probes permits the use of lower-power microwaves (milliwatts) to create strong B₁ fields near the electron Larmor frequency. In our SSNMR DNP cavities, the lower Q value means there is a need for a much larger mw power. Both the use of gyrotron oscillators as a high-power mw source and the designs of corrugated waveguides needed for such DNP/SSNMR experiments will be discussed below.

In DNP experiments the microwaves can be introduced either along the axis of the MAS rotor [7] or perpendicular to the rotor axis [30] (see Fig. 4). Note that perpendicular irradiation together with sample rotation also exposes more of the sample to the microwaves, which have a limited penetration depth, leading to more complete polarization. Using a high-power mw source, rather than a resonance cavity structure, separates the requirements for spinning samples at kilohertz frequencies and cryogenic temperatures from creating a B₁ for the electrons strong enough to saturate the DNP transition. Advances in the last decade in probe technology and other hardware needed for cryogenic MAS have allowed stable spinning of the MAS rotor down to 85 K and ω_r/2π ~ 10 kHz. Using cryogenic nitrogen as the bearing and turbine gas [12] provides important advantages compared with systems employing a separate variable-temperature gas stream. Namely, the gradient of the sample temperature is smaller and it is easier to fit all of the necessary lines into the limited space available in the bore of the magnet. The high amount of flow needed to spin the sample also provides a high cooling capacity that far exceeds losses due to conductive, convective, and radiative heat transfer. This heat loss still must be minimized to achieve temperatures down to 80 K at the sample, while preventing ice formation in the RF tuning box. Fiberglass vacuum-jacketed cryogen transfer lines, plated stainless steel RF transmission line, fiberglass insulation, and a fiberglass and aluminum dewar thermally isolate the probe. RF transmission lines separate the cryogenic environment in the vicinity of the sample from the tuning elements located outside the magnet bore [31].

Fig. 4.

Drawings of a cryogenic SSNMR DNP probe, a 1, probehead; 2, cut-out of the vacuum dewar; 3, tuning elements of the RF circuit located in the box; 4, corrugated waveguide from gyrotron; 5, concave and flat mirrors to direct microwaves into the vertical waveguide; 6, vacuum-jacketed transfer lines for the bearing and drive cryogens. b Probehead for rotors with a diameter of 4 mm. 1, stator housing; 2, sample rotor within RF coil (at the magic angle); 3, metal mirror miter; 4, the inner conductor of the coaxial RF transmission line is corrugated on the inside and serves as an over-moded waveguide; 5, outer conductor of the RF coaxial line is stainless steel for thermal isolation but is coated with silver and gold for good electrical performance.

The bearing and drive pressure of the MAS nitrogen gas is regulated at room temperature with a Bruker MAS unit, after which it passes through a heat exchanger with a pressurized heat transfer can, allowing for continual filling and operation [32]. The cold cryogens next move through a series of vacuum-jacketed transfer lines, bayonet connections, and heaters for precise temperature control. Sapphire rotors that are nearly transparent to the higher than 140 GHz mw radiation are routinely spun at about 10 kHz and 85 K with this apparatus.

3.2 Gyrotron Oscillators

The high-power mw radiation required by the low Q of the sample cavity is generated with a gyrotron oscillator. Prior to the use of a gyrotron, there was a dearth of high-power sources operating in the 100–600 GHz regime. This fact more than any other has impeded the development of DNP experiments for magnetic fields used in contemporary high-resolution NMR experiments. In a gyrotron the electron beam is launched from an annular cathode and accelerated through the field of a strong superconducting magnet. The field profile is designed to compress the beam as it moves through the vacuum tube to a resonant cavity that converts the transverse kinetic energy from the helical motion of the electrons into microwaves. A quasioptical mode converter couples the radiation to the output window of the device. Details of the physics and engineering of gyrotrons have been described recently [33, 34].

Gyrotrons are appropriate for use with high-field DNP because they are fast-wave millimeter devices, differing from slow-wave sources that rely on structures that scale with the microwave wavelength and become prohibitively fragile for generation of high power levels at higher frequencies required for DNP. Gyrotrons employ a resonator that can be overmoded with dimensions larger than the operation wavelength, allowing for high power output for extended periods due to reduced thermal and ohmic losses in the resonator walls. Gyrotrons capable of generating watts of CW power at 140 GHz [20], 250 GHz [37] and 460 GHz [35] have been built for integration into DNP spectrometers. The availability of these sources enables DNP experiments to be performed in situ at high fields and avoids the necessity of shuttling.

3.3 Corrugated Transmission Lines

Transmitting the microwaves from the gyrotron to the sample in the probe with minimal loss and monitoring the mw power output is another challenge that has been addressed by Woskov et al. [36]. Fundamental mode waveguides have unacceptable insertion losses and do not couple to a free-space Gaussian beam that is used for quasioptical manipulation of the beam demanded by the physical geometric restrictions of the experiment. A corrugated overmoded waveguide with a cross-sectional diameter greater than the wavelength supports the efficient HE₁₁ mode. The HE₁₁ mode has a very low insertion loss and couples efficiently to a free-space Gaussian beam. A schematic diagram of the apparatus implementing such waveguides, mirrors, and metal miter bends is shown in Fig. 5b resulting in a minimal 0.8 dB power loss from the gyrotron to the rotor. A quartz directional coupler was also developed for use in our 250 GHz apparatus to monitor the forward and reflected power output of the gyrotron.

Fig. 5.

a Cross-sectional schematic of the cylindrically symmetric 460 GHz gyrotron tube, not shown to scale, indicating key components. Adapted from ref. 35. (Reproduced by permission of IEEE), b 250 GHz line layout for DNP experiments. Adapted from ref. 36. (Reproduced by permission of IEEE).

4 CE and Biradicals

One of the important experimental findings of our group that allows efficient high-frequency DNP is that the CE [38–42] mechanism together with the use of biradicals always leads to improved polarization enhancements when compared to thermal mixing (TM) [9, 43] and the solid effect (SE) [6]. All of these CW polarization schemes show an inverse magnetic field dependence of the observed enhancements. Since the SE depends on excitation of forbidden electron-nuclear transitions, the enhancements are inherently small and the mechanism shows a $\epsilon ~B_0^{-2}$ dependence, where B₀ is the external magnetic field. Therefore, this mechanism is not routinely used in our current DNP applications. DNP experiments based on the CE mechanism have a less pronounced field dependence $(\epsilon ~B_0^{-1})$ but still show an attenuated enhancement at increasing magnetic fields. However, the enhancements remain sufficiently large to permit many experiments that are otherwise impossible. Thus, as discussed in more detail below, the CE mechanism is the primary polarization mechanism exploited for biological DNP experiments at high magnetic fields (5 and 9 T).

4.1 DNP Mechanisms at High Magnetic Fields

Recently Hu [44] introduced a quantum mechanical description of the high-field DNP processes that have been used at Massachusetts Institute of Technology over the last decade [12, 14–18, 23, 45–47]. This theoretical treatment is different from the existing literature on DNP processes that relied on equations of motion that correspond to macroscopic quantities averaged over an ensemble of spins [9, 43, 48, 49]. The historical semiclassical approach, although suitable at low magnetic fields, is less appropriate for the current experiments at higher magnetic fields where the electron spin reservoir is inhomogeneously broadened due to dilute radical concentrations and the fact that the g-anistropy is large compared with the electron-electron dipole coupling. This new quantum mechanical description allowed the detailed explanation of the SE and CE mechanisms and, in particular, explanation of the improved CE-DNP transfer reported at high magnetic fields when using biradicals as polarizing agents [16, 17].

Considering both experimental results and this new theoretical description, we will now briefly discuss the three CW DNP mechanisms found in solid dielectrics. The SE [6], CE [38–42] and TM [9, 43] mechanisms are distinguished by the number of electrons involved: single, paired and extended networks of electron spins, respectively. Figure 6 shows the energy level diagrams corresponding to these three DNP processes. The dominant DNP mechanism can be determined by a direct comparison of the EPR line width δ of the paramagnetic polarizing species with the nuclear Larmor frequency, ω_I. When δ < ω_I, the polarization transfer is principally driven by the SE and involves a polarization transfer between a single electron and nuclear spin described by the following time-independent Hamiltonian [44]:

$${\mathscr{H}}_0^{SI}={\omega }_{0S}{S}_z-{\omega }_{0I}{I}_z+A{S}_z{I}_z+B{S}_z{I}_x,$$ (1)

where ω_0SS_z and ω_0II_z are the electron and nuclear Zeeman terms in the laboratory frame, and A and B are the secular and nonsecular parts of the hyperfine coupling interaction. This can be represented in the product spin bases (PSB) shown in Fig. 6a. The DNP effect relies on the nonsecular hyperfine coupling (last term of Eq. (1)) which by mixing the states |1〉 and |3〉 and the states |2〉 and |4〉 allows the mw irradiation to drive the DNP polarization transfer. Two resonant effects can be achieved when the mw frequency matches ω_0S + ω_0I or ω_0S − ω_0I, leading to a negative zero-quantum or a positive double-quantum enhancement, respectively. The mixing factor that describes the probabilities of the above transitions is proportional to ${\omega }_{0I}^{-2}$ as it arises from a second-order perturbation with respect to the spin interactions. Thus, the efficiency of the SE scales with ${\omega }_{0I}^{-2}$.

Fig. 6.

Quantum mechanical diagrams of the electron-nuclear transitions (dashed arrows) in the SE (a), CE (b) and TM mechanisms (c), which involve single, paired and multiple electron spins, respectively. Note that the probabilities of electron-nuclear transitions are always small in the SE but could be large in the CE and TM, especially when there is degeneracy between the states with alternating nuclear spin quantum numbers. Adapted from ref. 44.

In contrast to the SE, which involves magnetization transfer from a single electron, the other two mechanisms involve two (or more) electrons in close proximity with EPR frequencies that are separated by ω_0I. For a single (mono) radical, this can only occur if its EPR line width is large compared with the nuclear Larmor frequency (i.e., δ > ω_0I). This is illustrated in Fig. 7a for monomeric TEMPO as the polarizing agent: two (close) TEMPO molecules at appropriate orientations relative to the magnetic field have the required difference in resonance frequency. When these electrons are dipolar-coupled, irradiation at the resonance frequency of the first electron produces a simultaneous spin flip of both the second electron and the nucleus, yielding the generation of nuclear spin polarization (Fig. 7b). Under these conditions, the SE is actually reduced due to the overlap of the positive and negative DNP enhancements that cancel each other [50]. In the CE there are two participating electrons and a single nuclear spin, and there are now eight energy levels to consider (Fig. 6b). Mw irradiation can drive polarization transfer by saturating the transitions (dashed lines in Fig. 6). This transfer is made possible because of the coupling between states |2〉 and |7〉 (or states |3〉 and |6〉, if γ_I < 0), which is a consequence of the combined effect of the electron-electron and electron-nucleus interactions. The DNP effect is further maximized when the levels |2〉 and |7〉 become degenerate, i.e., when the matching condition |ω_0S1 − ω_0S2| ≈ ω_0I is fulfilled [44]. For a monomeric radical having a broad EPR spectrum, this condition is fulfilled when the different g-tensor orientations of the two electrons result in a frequency mismatch equal to the nuclear Larmor frequency. However, another important requirement is sufficient proximity of the electrons such that the electron-electron dipolar coupling can induce the mixing of states |2〉 and |7〉. Increasing the monomeric radical concentration is one way to achieve this, but as shown by Hu et al. [16], the use of biradicals (see Fig. 8 and below) as polarizing agents is a much more efficient way to achieve an efficient polarization transfer. The two unpaired electrons associated with the two radical moieties of a biradical correspond to the two electrons required for the CE and as shown by Hu et al. [51], a quantum mechanical treatment of the spin dynamics of an electron-electron-nucleus system allows one to understand in detail the improved DNP mechanism [44]. Note that the two electrons involved in the process need not be from a single type of radical. Recent work by Hu et al. [52] demonstrated the use of a mixture of two radicals, TEMPO and trityl, as DNP polarizing agents. This approach also provided a significant improvement in the DNP enhancement over using TEMPO by itself. This is due to the fact that the EPR spectrum of trityl is offset from the g₂₂ maximum of the TEMPO spectrum, aside from being much narrower (less anisotropic), by a difference that approximates the nuclear Larmor frequency. These features increase the number of radicals with the proper frequency separation and average interelectron distance and thus improves the DNP transfer via the CE mechanism.

Fig. 7.

a Illustration of the EPR spectrum of monomeric TEMPO nitroxide at 5 T. Note that the breadth of the spectrum is about 600 MHz and is large compared to that of the ¹H Larmor frequency (211 MHz). Arrows indicate the approximate frequencies of two electron spins e₁ and e₂, separated by ωI/2π, expected to participate in the CE/TM DNP enhancement process, b Illustration of the mw-driven three-spin process associated with TM or CE DNP, where two coupled electrons undergo an energy-conserving flip-flop process that leads to the enhanced nuclear spin polarization of nucleus n. c The molecular structure of the BTnE biradicals, where m is the number of ethylene glycol units that tether two nitroxide radicals (TEMPO). The dots represent the two unpaired electrons, whose displacement is approximated as the oxygen-oxygen distance, R_O-O. Reproduced with permission from ref. 47. (Copyright 2004 American Chemical Society).

Fig. 8.

Histogram of DNP enhancements (with error bars) in 4 mm (white) and 2.5 mm (black) rotors with TOTAPOL biradical, a series of BTnE biradicals, and monomeric TEMPO. The data illustrate that TOTAPOL yields the largest enhancement, especially when the mw penetration depth is optimal for 2.5 mm rotors. Reproduced with permission from ref. 17. (Copyright 2006 American Chemical Society).

The TM mechanism differs from the CE by the number of electron spins involved in the polarization transfer, namely, two electrons for the CE and multiple for TM, which also translates into an EPR spectrum that is mainly inhomogeneously or homogeneously broadened, respectively. The TM can be seen as an extension of the CE where couplings among electrons induce manifolds of states (see Fig. 6c). In TM, energy overlap between manifolds is required for maximizing the electron-nuclear transfer. However, TM requires a high concentration of paramagnets to achieve a homogeneously broadened spectrum and this, in turn, could lead to broadening of NMR resonances when the nuclei of interest are too close to the electron spins.

4.2 Biradicals

As pointed out in Sect. 4.1, the CE mechanism can be greatly enhanced with the use of biradicals as polarizing agents [47]. These new biradicals consist of two 2,2,6,6-tetramethylpiperidinyl-l-oxyl (TEMPO) radicals tethered by a poly-(ethylene glycol) chain (Fig. 7c), and referred to as BTnE, for bis-TEMPO-n-eth-ylene glycol, where n is the number of ethylene glycol units in the tether. The size of the electron-electron dipole coupling is directly controlled by the length of the chain and can therefore be chosen to optimize the DNP enhancement. The electron-electron couplings in the biradicals discussed here vary between 10 and 30 MHz as opposed to the about 0.3 MHz coupling present when monomeric TEMPO is present at the same electron concentration (~10 mM).

The DNP enhancement results obtained with different polarizing agents are summarized in Fig. 8. Note that the BTnE biradical polarizing agents yield a factor of about 4 larger signal intensities over those obtained with monomeric TEMPO. In addition, larger enhancements are obtained at significantly lower electron concentrations (40 mM for TEMPO and 10 mM for BTnE), thereby reducing the paramagnetic broadening present in the NMR spectrum. Finally, as can be seen in Fig. 8, within the BTnE series of biradicals a reduction of the tether length improves the observed DNP enhancement. Unfortunately, the BTnE series is sparingly soluble in H₂O-glycerol solutions used in cryoprotecting samples for DNP experiments These observations motivated the design, synthesis and characterization of the improved polarizing agent, l-(TEMPO-4-oxy)-3-(TEMPO-4-amino) propan-2-ol (TOTAPOL) (Fig. 9b) consisting of two TEMPO molecules tethered with a three-carbon chain [17] copiously soluble in aqueous media.

Fig. 9.

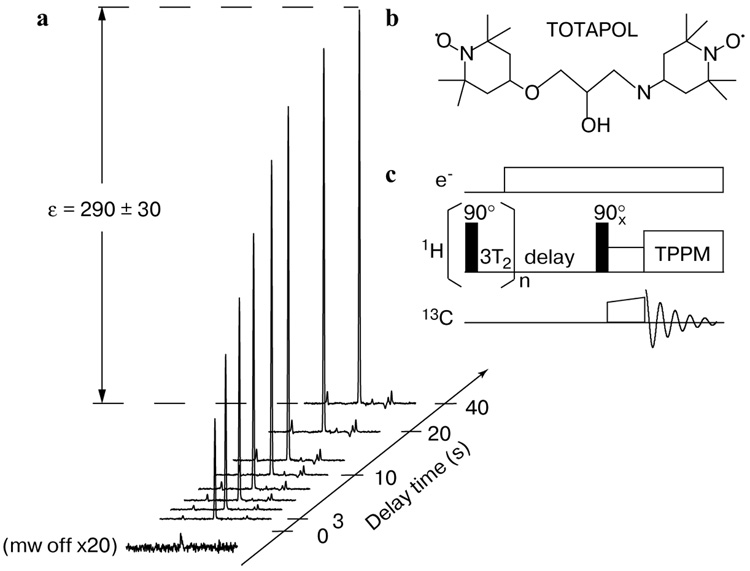
a Illustration of the growth of the nuclear polarization as a result of mw irradiation using the biradical TOTAPOL (b) as a polarizing agent. Integration of the spectral intensities with and without irradiation yields a ¹H enhancement of ε ~ 290 measured indirectly through the ¹³C CP signal using the pulse sequence shown in panel c. The measurements were performed on a sample of 3 mM TOTAPOL and 2 M ¹³C-urea in d₆-DMSO/D₂O/H₂O (60:34:6 w/w/w) at 90 K, 5 T, and ω_r/2π = 7 kHz MAS. The time constant associated with the growth is about 9 s, approximately the nuclear T₁ of the sample. Reproduced with permission from ref. 17. (Copyright 2006 American Chemical Society).

Figure 8 compares the DNP enhancement obtained with TOTAPOL (6 mM electron concentration) with results for the BTnE (n = 2, 3, 4) series and monomeric TEMPO (10 and 40 mM electron concentration, respectively). Reducing the number of atoms separating the two TEMPO moieties increases the electron-electron dipolar interaction and the observed enhancement. The enhancement is larger with TOTAPOL than with BT2E. The underlying reason for this result is partly due to the shorter electron-electron distance, but could also be related to differences in the electronic relaxation times of the two biradicals, or the relative orientations in which the two TEMPO moieties are frozen.

Figure 8 also shows different enhancements for rotors with a diameter of 4 and 2.5 mm. We attribute this to the penetration of the microwaves into the bulk of the sample and possibly the differential attenuation of the microwaves by the sapphire rotors with different wall thicknesses. For systems that are sample-volume-limited, the smaller rotor offers significant advantages in sensitivity. However, when this is not the case, the 4 mm system yields an improved signal-to-noise ratio, as even if the enhancement value is smaller, the increased volume still provides a stronger signal overall.

Figure 9 shows the DNP enhancement buildup obtained on a 2 M ¹³C-urea using TOTAPOL as the polarizing agent. The pulse sequence for DNP-enhanced ¹³C-CPMAS NMR experiments is shown in Fig. 9c. The ¹H polarization is initially saturated by a series of 90° pulses followed by a delay of 3T₂. Subsequently, mw irradiation is applied to dynamically polarize the ¹H’s or, in the absence of microwaves, the thermal-equilibrium polarization is allowed to develop. Finally, the ¹H polarization is transferred to ¹³C via CP and observed in the presence of two-pulse phase-modulation decoupling [53]. Figure 9 shows the resulting spectra for a range of mw irradiation periods, leading to an enhancement factor ε ~ 290 ± 30 for ¹H polarization determined by comparing the saturated NMR signals after a 40 s delay with and without microwaves. Note that the error for the enhancement factor was determined primarily by the uncertainty in measuring the intensity of the nonenhanced NMR signal.

Hence at 140 GHz mw frequency this yields a maximum enhancement of about 290, while the electron concentration is reduced by a factor of 6 from the typical level of 40 to 6 mM. Very importantly, TOTAPOL has hydroxyl and secondary amine moieties on the tether and these functional groups increase the solubility of the biradical in aqueous media so that it is compatible with a variety of biological systems where DNP experiments are currently performed.

5 New Perspectives

Previous sections have focused on MAS SSNMR experiments that have established DNP as a routine technique for improving sensitivity, but extending these experiments to even higher fields, solution NMR, and room temperature requires advancements in instrumentation and theory. This section is devoted to recent developments in solution DNP using an in situ temperature-cycling approach and coherent DNP transfers using pulsed methods.

5.1 Temperature-Jump Solution DNP

Solution-state DNP relies on completely different processes than the solid-state DNP mechanisms. In this case, none of the solid-state DNP methods, i.e., SE [6], CE [38–40] and TM [9, 43], can be used directly. The only available mechanism is the Overhauser effect [4, 5, 54] but its efficiency drops considerably at high magnetic fields. In particular, the Overhauser effect provides efficient polarization transfer for small molecules with rotational or translational correlation times of about 10⁻¹² s in low magnetic fields where the condition ω_Sτ_c < 1 is satisfied (ωs being the electron Larmor frequency and τ_c the correlation time). However, in the high-field regime commonly employed in modern NMR experiments (ω_S > 2π · 100 GHz) the rotational and translational spectral densities become vanishingly small. Thus, the Overhauser effect is no longer able to provide usable nuclear polarization enhancements.

With this in mind, Joo and coworkers [55] recently introduced an original solution to this problem in which they perform ¹H DNP at low temperature (ca. 90 K), and subsequently detect the solution-state NMR spectrum after rapidly melting the sample through in situ irradiation with an infrared laser. The experiment, referred to as temperature-jump DNP (TJ-DNP), can be recycled using the workflow diagram shown in Fig. 10a. The sample is cooled to 90 K and polarized in the solid state using a CE DNP mechanism with the recently introduced biradical TOTAPOL as the source of electron magnetization [17, 47]. The ¹H polarization is then transferred to low-γ spins via CP and the sample is melted in situ with an infrared laser pulse. The enhanced signal is finally observed in the presence of ¹H decoupling. The entire cycle can be repeated in situ and the signal averaging performed as in regular solution-state NMR experiments. Note that if the polarization step was performed at a lower temperature, a larger enhancement factor would be observed.

Fig. 10.

a Pulse sequence used in the TJ-DNP experiment. The samples are irradiated with 140 GHz microwaves at 90 K, polarizing the ¹H spins in the sample. Enhanced ¹H polarization is then transferred to ¹³C via CP. During the heating period using a 10.6 mm CO₂ laser, the ¹³C magnetization is stored along the z-axis of the rotating frame. The ¹³C spectrum is detected following a 90° pulse in the presence of WALTZ ¹H decoupling, b Experimental spectra obtained for U-¹³C-urea. Left, solid-state MAS spectrum produced after 40 s DNP time at 90 K (ε ~ 290); right, liquid-state spectrum with an enhancement ε^† ~ 400, after a 1.2 s melting period. Note that the DNP spectrum was acquired in a single scan, whereas the room-temperature spectrum required 256 scans, c ¹³C TJ-DNP NMR spectra of Na[1,2-¹³C₂,²H₃]-acetate in 60% ²H₈-glycerol and 40% water (80% ²H₂O/20% H₂O) after 40 s polarization and 1 s melting, d ¹³C TJ-DNP NMR spectra of [U-¹³C₆,²H₇]-glucose in H₂O after 30 s polarization time and 1.5 s melting period. Samples contained 3–5 mM TOTAPOL biradical polarizing agent, corresponding to 6–10 mM electrons. The TJ-DNP spectra (the top traces in each panel) were recorded with a single scan, while the room-temperature spectra were recorded with 128 (c) and 512 scans (d), respectively. Reproduced with permission from ref. 55. (Copyright 2006 American Chemical Society).

Figure 10b-d shows the TJ-DNP-enhanced ¹³C NMR spectra of ¹³C-urea, Na-[1,2-¹³C₂,²H₃]-acetate, and [U-¹³C,²H₇]-glucose. The top traces in Fig. 10 represent the TJ-DNP-enhanced spectra, whereas the bottom traces in Fig. 10 reflect the signal intensity obtained with ¹H-decoupled Bloch decays. Deuteration of the samples was employed in order to circumvent the ¹H-mediated ¹³C relaxation in the viscous solution phase. The enhancements observed in these spectra are ε^† ~ 400 for urea, ε^† ~ 290 for sodium acetate, and ε^† ~ 120 for glucose. Note that the enhancement ε^† is determined by the intensity of the DNP-enhanced signal relative to the signal due to the Boltzmann polarization at 300 K as this represents the relevant enhancement in the case of solution-state DNP experiments. This enhancement can be separated into two distinct contributions due to (i) the polarization gain due to the electron-nuclear polarization transfer and (ii) a relative polarization increase due to changes in the Boltzmann polarization at different temperatures. This implies that enhancements reported in the literature for solid-state and liquid-state experiments often differ by the factor (T_obs/T_mv), since for solution DNP experiments that include a melting step, there can be a large difference between the mw irradiation (T_mw) and the NMR measurement temperature (T_obs). For instance, Ardenkjaer-Larsen and co-workers [56] achieve an enhancement ε^† = 44400 by polarizing at 1.2 K, which corresponds to ε^† ~ 178 and (T_obs/T_mw) ~ 250. Their experiments reflect an alternate approach to achieve DNP in solution, where the polarization step takes place at low field and very low temperature, followed by dissolution and dilution of the sample with superheated water, and transfer to a higher field for detection. Note that this is in contrast with TJ-DNP where the melting occurs in situ, which allows efficient recycling of the experiment. Another noteworthy distinction is the polarization time in both approaches: ≥80 min in the experiment of Ardenkjaer-Larsen et al. [56] compared with typically 40 s for the TJ-DNP approach. This difference is due primarily to the fact that in the dissoluton experiment ¹³C is polarized directly, whereas in TJ-DNP the ¹H’s are first polarized and this polarization is transferred to ¹³C.

Figure 10 hence shows that significant signal enhancements in the range of 120–400 can be obtained for low-γ spins such as ¹³C and ¹⁵N using the TJ-DNP approach as long as the ¹³C T₁ is long compared with the melting period and sufficiently long in the solution phase. The resolution is not degraded by the presence of a paramagnetic polarizing agent: the ¹³C-¹³C J-coupling is resolved in the acetate spectrum (Fig. 10c).

The TJ-DNP experiment should clearly find a wide application in metabolic screening, a subject that is of intense interest in the pharmaceutical industry. Moreover the TJ-DNP experiment could be performed together with multidimensional fast acquisition techniques allowing acquisition of multidimensional experiments in a few seconds or even a fraction of a second [57]. Finally, TJ-DNP should be applicable on proteins and nucleic acids that are robust with respect to the freezing and thawing process. This is an area of current investigation.

5.2 Pulsed DNP

Although the CE mechanism provides large enhancements (ε ~ 10²), it requires relatively long polarization transfer times on the order of T_1n (nuclear spin-lattice relaxation time) and becomes less efficient as the B₀ field is increased (see Fig. 11b). The expected 1/B₀ dependence has recently been confirmed experimentally by comparing enhancements at 5 and 9 T. It is therefore important to investigate and develop different polarization DNP schemes in this high-field regime.

Fig. 11.

Energy level diagram comparing various polarization transfer schemes, a CP, b laboratory frame solid effect (LFSE), c NRF-SE, d DSSE. The polarization transfer is achieved when either allowed or forbidden transitions are irradiated (dashed lines). The highlighted terms represent interactions that mix eigenstates and allow RF/mw irradiations to drive the polarization transfer.

In the late 1980s three alternative DNP techniques were introduced at low magnetic fields: nuclear orientation via electron spin locking (NOVEL), the integrated solid effect (ISE) and the nuclear rotating frame (NRF)-DNP. These three DNP schemes rely on the use of coherent pulses (either RF or mw) and fall into the class of pulsed-DNP methods as opposed to the CW-DNP methods mentioned above (SE, CE, TM). In principle, they should be of interest for applications at high magnetic fields (11–20 T) currently used in biological NMR. More recently the dressed state solid effect (DSSE) was proposed as a fourth time domain DNP mechanism [58, 59].

The magnetic resonance community encountered a similar barrier for transferring polarization from protons to low-γ nuclei, the solution to which was a doubly rotating frame pulsed experiment now known as CP [60]. This experiment, introduced in 1973, consists of a double on-resonance irradiation and alleviates the field dependence problem. In conventional NMR-CP experiments involving I=1/2 nuclei, the RF fields are sufficiently strong that they dominate all other interactions in the Hamiltonian of the spin system. The entire NMR spectrum for both species can be efficiently excited and spin-locked. The Hartmann-Hahn matching condition is then met by matching the RF field strengths ω_1S = ω_1I, allowing an efficient, field-independent zero-quantum polarization transfer to occur [61]. This is illustrated in Fig. 11a.

The situation is however completely different for pulsed DNP experiments where the electron g-anisotropies and hyperfine couplings are of the order of several or tens of megahertz, whereas nuclear interactions and RF/mw fields are 1 to 3 orders of magnitude smaller. This leads to different polarization transfer mechanisms. The other major difference with SSNMR CP is that the number of nuclear spins to polarize is much larger than the number of electron spins (3–4 orders of magnitude) leading to small single-passage polarization transfer. Fortunately, the much shorter electron relaxation time T_1e/T_1n ~ 10⁻³–10⁻⁴ allows for a multiple contact experiment within the nuclear relaxation time T_1n, thereby accumulating nuclear polarization approaching the large ratio of the electron and ¹H γ-factors.

The first pulsed DNP experiment we discuss is NRF-DNP, the corresponding pulse sequence is shown in Fig. 12a. The principle of NRF-DNP was originally demonstrated in 1958 by Bloembergen and Sorokin [62] for a single crystal of CsBr in which the transverse Cs magnetization was built up by cooling the rare ¹³³Cs spins in the rotating frame with a ¹³³Cs spin-lock pulse, while irradiating the abundant ⁷⁹Br spins with an RF field of frequency ω = ω_Br ± γ_CsB₁^Cs. Wind and coworkers [63] performed the first NRF-DNP experiment at low field (B₀ = 1.4 T) to enhance the ¹H magnetization by irradiating electrons during a ¹H spin-lock pulse.

Fig. 12.

a NRF-DNP pulse sequence. The NRF-DNP enhancements are determined from a comparison with the laboratory frame signal obtained with a solid-echo pulse sequence and no mw irradiation or nuclear spin-lock, b Pulse sequence for the indirect detection of electron-nuclear CP. The electron spin echo intensity is monitored after an electron spin-lock and a refocusing π-pulse. The echo intensities of two sequences with and without RF pulses are subtracted and recorded as a function of the RF frequency, ω_RF. Reprinted from refs. 59 and 64. (Copyright 2000 and 2006, with permission of Elsevier).

In NRF the nuclear energy splitting decreases, which consequently improves the degree of eigenstate mixing between a single electron-nuclear (e-n) spin pair. This is implicit in Eq. (2) that gives the degree of dipolar mixing q_L and q_R in the laboratory and rotating frames, respectively:

$$\begin{array}{c}{q}_{\text{L}}=-\frac{3}{4}\frac{{\gamma }_S{\gamma }_1\hslash }{{\omega }_I^{\text{lab}}}\frac{1}{r^3}\text{sin}\theta \text{cos}\theta \text{exp}(-i\varphi ),\hfill \\ q_{\text{R}}=\frac{1}{4}\frac{{\gamma }_S{\gamma }_1\hslash }{{\omega }_I^{\text{rot}}}\frac{1}{r^3}{(1-3\text{cos}}^2\theta ),\hfill \end{array}$$ (2)

where γ_e and γ_n are the electron and nuclear gyromagnetic ratios, ћ is the Planck constant, ω_I is the nuclear Larmor frequency in either the laboratory or rotating frame, r is the electron-nuclear interspin distance, and θ and φ are the polar coordinates that specify the orientation of the dipole vector in the laboratory or rotating frame. The increase of nuclear eigenstate mixing in the NRF allows the mw irradiation to efficiently drive the polarization transfer to the nuclei during a relatively short combined RF and mw irradiation period (less than 100 ms).

Using this approach, Farrar et al. [64] reported a high-field (5 T) NRF-DNP ¹H single-shot enhancement ε of 0.89 for a frozen solution of 15 mM trityl radical in 40:60 water-glycerol at 11 K. While this value of the enhancement reflects an effective signal attenuation (compared to thermal equilibrium), the transfer is governed by a very small NRF spin-lattice relaxation time (T_1ρ = 27 ms), which thus allows signal averaging with a repetition rate orders of magnitude faster than in the CW-DNP experiments, especially at (very) low temperatures. The repetition rate is therefore not limited by the laboratory frame spin-lattice relaxation time T_1n, which is typically many minutes at 10 K for non-paramagnetically doped samples. The increased repetition rate allowed by the NRF-DNP experiment translates to a real-time signal enhancement of ε_t ~ 197, where ε_t is the ratio of the signal-to-noise ratio per square root unit time with and without mw irradiation. The NRF-DNP experiment allows one to leverage the increased sensitivity provided by low temperatures (since ε is close to 1), while avoiding the limitations of slower repetition times due to the very long nuclear spin-lattice relaxation times induced by the cryogenic temperatures for systems. Note that this is only valid if nuclear spin diffusion is not the rate-limiting process to polarize the bulk nuclei.

An important point to highlight is that this DNP experiment was performed with a low-power Gunn diode source (power at the sample, about 1–5 mW) and no resonant structure. Under the same experimental conditions, the NRF-DNP does indeed compare favorably with an optimized laboratory frame CE-DNP due to its faster recycling time and hence improved signal-to-noise ratio per square root unit time (${\epsilon }^{\text{rot}}/T_{1\mathrm{\rho }}^{1/2}=4.4$ for 15 mM trityl radical and ${\epsilon }^{\text{lab}}/T_{1\mathrm{n}}^{1/2}=1.7$ for 25 mM 4-amino TEMPO radical, respectively).

By rewriting the electron-nuclear Hamiltonian (see Eq. (1)) and the on-resonance RF irradiation, in the tilted NRF, one can understand the nature of the polarization transfer:

$${\mathscr{H}}_0^{SI}+{\mathscr{H}}_I^{\text{RF}}={\omega }_{0S}{S}_z-{\omega }_{1I}{I}_z+A{S}_z{I}_x.$$ (3)

From Eq. (3), it is clear that the secular term of the hyperfine coupling in the laboratory frame A is no longer secular with respect to the electron laboratory frame and NRF Larmor frequencies. In this experiment, the nonsecular hyperfine coupling has been neglected as ω_0I » B in the high-field regime considered in this review. Equation (3) shows that the secular hyperfine coupling A mixes the eigenstates in the nuclear tilted frame and allows the mw irradiation to drive the polarization transfer. By writing the mw irradiation in the tilted NRF, we obtain the matching condition for the NRF-SE (see Fig. 11c):

$${\omega }_{\text{mw}}={\omega }_{0S}\pm \sqrt{{(A/2)}^2+{\omega }_{1I}^2,}$$

where ω_mw represents the frequency of the mw irradiation.

In the limit of a weak RF field strength (ω_1I/2π ~ 100 kHz) compared with the hyperfine coupling to protons in trityl (about 1 MHz), the above expression simplifies to

$${\omega }_{\text{mw}}={\omega }_{0S}\pm A/2.$$ (4)

The NRF-DNP experiment (as is also indicated by Eq. (2)) is not dependent on the static magnetic field strength, suggesting that large DNP enhancements should be obtainable even at magnetic fields larger than 5 T. This definitely appears as a significant advantage over the laboratory frame DNP experiments, which all exhibit an inverse dependence with the B₀ magnetic field.

The second high-field pulsed DNP mechanism discussed was introduced in 2000 by Weis et al. [58, 59] as the dressed state solid effect (also referred to as electron-nuclear CP (e-NCP)) and explained as a SE mechanism in the electron dressed state (defined by the mw irradiation) [65, 66].

This experiment relies on a simultaneous mw spin-lock of the electron magnetization and an off-resonance RF irradiation of the protons that can be set to match the strong γB_1S electron Larmor frequency in the rotating frame. The interaction of the electron spin with the mw field is treated as an electron spin-dressed state. In contrast to the customary laboratory frame SE, it is possible to obtain the nuclear polarization with the DSSE even in the absence of nonsecular hyperfine coupling.

Efficient, selective excitation of forbidden dressed-state transitions (see Fig. 11d) generates the nuclear polarization in the nuclear laboratory frame on a timescale of microseconds, depending on the strength of the electron-nuclear coupling, the mw and RF irradiation, resulting in a repetition rate comparable to $T_{1e}^{-1}$, where T_1e is the electronic spin-lattice relaxation time. These frequencies fall into the RF range and are given by the following matching condition:

$${\omega }_{\text{rf}}=-{\omega }_{0I}\pm \sqrt{{(A/2)}^2+{\omega }_{1S}^2,}$$ (5)

where ω_rf, ω_0I, ω_1S and A stand for the RF field frequency, the nuclear Larmor frequency, the electron rotating frame Larmor frequency and the hyperfine coupling constant, respectively.

The pulse sequence of the DSSE experiment is displayed in Fig. 12b. The electron spin-echo intensity is monitored after an electron spin-lock and a refocusing π-pulse. The echo intensities of two sequences with and without RF pulse are subtracted and recorded as a function of the RF frequency ω_RF and thus represent an indirect detection of electron-nuclear CP. Experimental results obtained on a perdeuterated BDPA-d₂₁ radical in a protonated polystyrene matrix are shown in Fig. 13 using a 3 ms on-resonance spin-lock irradiation.

Fig. 13.

DSSE/e-NCP experiment on perdeuterated BDPA for various settings of the mw (ω_1S/2π ~ 1.75, 0.9 and 0.5 MHz) and RF field strengths (ω_1I/2π ~ 100 kHz at 350 W). The CP contact time was set to 3 µs. Reprinted from refs. 59 and 64. (Copyright 2006, with permission of Elsevier).

The EPR spectra display three lines representing the three dressed-state transitions. The positions of the outer peaks change with the mw power applied and converge towards the nuclear Larmor frequency ω_0I as the mw is decreased, which is in agreement with Eq. (5). The upper traces of Fig. 13 show the variation of the transferred polarization for two RF field strengths (50 and 350 W, ω_1I/2π ~ 100 kHz at 350 W) and a fixed mw field strength. A change in the RF power does not result in a detectable shift or broadening of the CP matching condition, which is expected from Eq. (4). However, a decrease in the signal intensity is observed upon reduction of the RF power, indicating that the polarization transfer is faster for larger RF fields, and a detailed analysis of the time evolution supports this observation [41].

6 Conclusions

We have reviewed experiments on a wide range of samples that demonstrate large NMR signal enhancements available using a common technique of polarizing the bulk nuclei with DNP and subsequent spin diffusion. In 2000 we reported enhancements of about 10 in MAS spectra recorded at 90 K. Subsequently we have improved that figure to 290 with advances in theory, polarizing agents and instrumentation. The pulsed methods and biradical polarizing agents discussed here, together with future instrument developments, represent an avenue for extending DNP of biologically relevant systems to even higher magnetic fields, and improving enhancements that approach the theoretical maximum of 657. These experiments should lay a foundation for conducting magnetic resonance experiments at higher rates and on systems that have heretofore been inaccessible due to low sensitivity.