Abstract
The forcibly launched spores of ascomycete fungi must eject through several millimeters of nearly still air surrounding fruiting bodies to reach dispersive air flows. Because of their microscopic size, spores experience great fluid drag, and although this drag can aid transport by slowing sedimentation out of dispersive air flows, it also causes spores to decelerate rapidly after launch. We hypothesize that spores are shaped to maximize their range in the nearly still air surrounding fruiting bodies. To test this hypothesis we numerically calculate optimal spore shapes—shapes of minimum drag for prescribed volumes—and compare these shapes with real spore shapes taken from a phylogeny of >100 species. Our analysis shows that spores are constrained to remain within 1% of the minimum possible drag for their size. From the spore shapes we predict the speed of spore launch, and confirm this prediction through high-speed imaging of ejection in Neurospora tetrasperma. By reconstructing the evolutionary history of spore shapes within a single ascomycete family we measure the relative contributions of drag minimization and other shape determinants to spore shape evolution. Our study uses biomechanical optimization as an organizing principle for explaining shape in a mega-diverse group of species and provides a framework for future measurements of the forces of selection toward physical optima.
Keywords: hydrodynamics, biological optimization, fungal spores
Many organisms have visible adaptations for minimizing drag, including the streamlined shapes of fast-swimming fish and of Mayfly nymphs that cleave to rocks in rapidly flowing streams, or the precisely coordinated furling of tulip tree leaves in strong winds (1). However, although drag minimization may improve some aspects of individual fitness, it is also clear that physiological and ecological trade-offs will constrain the evolution of body shape. Similarly, although signatures of optimization can be seen in diverse features of organism morphology (2), behavior (3), and resource allocation (4, 5), the strength of the force of selection for one physical optimum over another can not be readily quantified (6).
Most fungi grow on highly heterogeneous landscapes and must move between disjoint patches of suitable habitat. Sexual spores can be carried by air flows and allow dispersal between patches (7, 8). To reach dispersive air flows, spores of many species of ascomycete fungi are ejected from asci, fluid-filled sacs containing the spores (9). At maturity the turgor pressure within each sac climbs until a critical pressure is reached, whereupon a hole opens at the apex and spores are ejected (8). Spores must travel far enough from the originating fruiting body to enter dispersive air flows. In particular, it is necessary that they pass through a boundary layer of still air of thickness ∼1 mm that clings to the fungal fruiting body (10).
Multiple independently evolved adaptations enhance spore range in disparate fungal species. For example, appendages and mucilaginous sheathes promote spore cohesion during launch, increasing projectile mass but allowing spores to subsequently disassociate into small, easily dispersed fragments (7, 11), whereas the long thread-like spores of some Sordariomycete fungi are ejected slowly and may physically span the layer of still air before fully leaving the ascus (12). We consider how spores lacking these conspicuous adaptations may yet be shaped to maximize range.
We analyze an entire phylogeny of >100 such species for drag minimization. We use numerical optimization to construct drag-minimizing shapes over the range of flow speeds and sizes relevant to real spores. These drag-minimizing shapes are very different from the well understood forms of macrobodies such as man-made projectiles and fast-swimming animals (13). By comparing real spores with these optimal shapes we predict the speed of spore ejection, and then confirm this prediction through high-speed imaging of ejection in Neurospora tetrasperma.
A simple physical argument shows that the speed of ejection of unappendaged spores is itself insensitive to spore shape, size, or species identity. We can estimate the speed of a launched spore by noting that during ejection, the work of the turgor pressure (ΔpV, where V is the volume of a spore) is converted to kinetic energy, giving the spore a velocity
 |
which depends on the density, ρ≈1,200 kg·m−3 (7), of the spore but not on its shape or size. Furthermore, assuming that the ascus is inflated to the largest overpressure allowed by the concentration and activity of the osmolytes present (14), we expect Δp, and thus U0, to be conserved across all ascomycetes with explosive spore ejection.
The speed of ejection has not been directly measured for any singly ejected, unappendaged ascomycete spore, but is constrained by previous indirect measurements. The turgor pressure within a ripe ascus has been estimated to be Δp ≈ 0.08–0.3 MPa (16); from which Eq. 1 would give U0 = 10–20 m·s−1. Such pressure-based estimates give only upper bounds on U0, they neglect the friction between spore and ascus walls. Spore travel distances are similarly strongly affected by air flows but give a second set of upper bounds ranging between 9–35 m·s−1 (14, 17, 18). Nonetheless, although the value of U0 is not known, the assumption that launch speed is conserved among species with this mode of ejection is supported by Vogel's remarkable collection of launch speed data for a large range of plant and fungal projectiles (15).
Ingold (7) hypothesized that spores are shaped to maximize the speed of ejection by minimizing frictional losses within the ascus. We find no evidence of selection for such shapes: in the supporting information (SI) Appendix II we analyze a model for friction within the ascus and show that minimization of frictional losses favors oblate shapes. Such shapes are not seen in real spore shape data (see Fig. 3A).
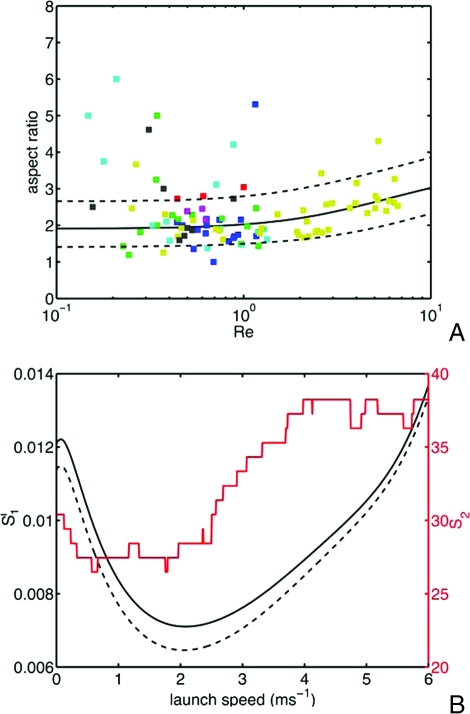
Fig. 3.
Forcibly ejected spore shapes across a phylogeny of 102 species. (A) Comparison of optimal shapes with real spores. Spore aspect ratio (length divided by width) is plotted against Reynolds number. Each point represents the average aspect ratio and size for a single species, color-coded by phylogenetic (sub)class. The black curve displays the optimal aspect ratio; species between the two dotted curves are within 1% of the minimum drag. Key to symbols: (blue) Pezizomycetes, (green) (Sordariomycetes) Sordariomycetidae, (red) (Dothideomycetes) Dothideomycetidae, (aqua) Leotiomycetes, (magenta) Eurotiomycetes, (yellow) (Lecanoromycetes) Ostropomycetidae, (black) (Lecanoromycetes) Lecanoromycetidae. (B) Inference of U0, using two measures of quality of fit. S1 (black curves, left axis) gives the sum of squared differences between optimal and real spore aspect ratios, averaged over bins in volumetric radius, and then between bins (the solid curve corresponds to bins of width 10 μm, and the dashed curve to bins of width 5 μm) and S2 (red curve, right axis) is the per cent fraction of species whose drag exceeds the minimum possible by > 1%. Both fits are consistent with a launch speed in the range 1-3.5 m·s−1. The optimal aspect ratio in A is obtained by using a consensus value from multiple quality-of-fit measures: U0 = 2.1 m·s−1.
With launch speed conserved, maximizing the spore range requires minimizing the ratio of drag to mass. To see this, balance the fluid drag -ζu, where u is the speed and ζ is the Stokes drag coefficient, which is approximately independent of speed for sufficiently small projectiles (10), against the inertia of the spore:
where x is the distance traveled and m is the spore mass. This formula can only be used to infer distance traveled from spore shape for the smallest spores (for which the Reynolds number, Re, defined below, is <1). Although there is no formula relating distance traveled to spore shape for larger spores (Re > 1), it is clear, nevertheless, that minimization of the drag-to-mass ratio will maximize the distance traveled by the spore during the early part of its trajectory. In the SI we describe the three assumptions necessary for computing and then minimizing the drag on an ejected spore.
Results and Discussion
Shapes that minimize the ratio of drag to mass can be efficiently computed by using algorithms developed for the design of airplane wings (19): our implementation iteratively modifies the projectile shape, at each iteration solving numerically for the flow field around the shape and then for an adjoint flow field to determine the shape perturbation that gives the largest possible reduction in drag. The algorithm for computing minimum drag shapes is described in ref. 20 and summarized in the Materials and Methods. Optimal shapes are parameterized by the Reynolds number Re ≡ U0a/ν, where ν is the kinematic viscosity of air, and a is the volumetric radius (the radius of a sphere with matching volume) of the spore. Assuming that U0 does not vary between species, the Reynolds number provides a dimensionless measure of the spore size. For example, U0 = 2 m·s−1 implies Re = a/(9μm). In Fig. 1, minimal drag shapes are displayed for Re ranging from 0.1 up to 10, and compared with real spore shapes.
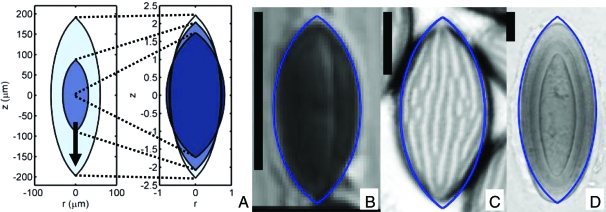
Fig. 1.
Real and drag-minimizing spore shapes. (A) Minimal drag shapes for Re = 0.1 (darkest), 1, 10 (lightest). The arrow points in the direction of flight and spores are axisymmetric about this direction. (Left) Spore dimensions are given in physical units (assuming U0 = 2.1 m·s−1). (Right) All spores are scaled to have equal volumes. The near fore-aft symmetry is not imposed (20). Comparison of minimal-drag shapes with Astrocystis cepiformis (B), N. crassa (C), Pertusaria islandica (D) spores. (Scale bar: 10 μm.) Like surface ornamentations (Fig. 2 and Table 1), rounding of spore apices only mildly increases drag. [B, reproduced with permission from ref. 38 (copyright 1998, British Mycological Society); C, reprinted from Experimental Mycology Vol 14, Glass NL, Metzenberg RL, Raju NB, Homothallic Sordariaceae from nature: The absence of strains containing only the a mating type sequence, 16 pp, 2008, with permission from Elsevier; D, reproduced with permission from ref. 39 (copyright 2006, British Lichen Society).
To determine whether the species shown in Fig. 1B are representative of ascomycetes with explosive ejection, we compared real spores with optimal shapes in over 102 species by using a previously created phylogeny of the phylum Ascomycota (21). Shape data were gathered from 77 species whose spores are launched forcibly and individually. We rejected species whose spores have adaptations such as appendages or septa, which may have different ejection dynamics (see SI Appendix, Section III). When possible, rejected species were replaced by species within the same genus lacking any such adaptations. To provide the greatest possible spread of spore sizes, additional large-spored species were added to our analysis until every 10-μm interval of volumetric radii contained at least five species.
We find that the drag on a spore can be calculated by approximating its shape by an ellipsoid of matching size and aspect ratio. This applies even to spores with pointed apices, or surface decorations such as warts, spines, or ridges, because at small Reynolds numbers such shape features do not strongly contribute to drag. Four of 102 species in our phylogenetic survey have decorated surfaces. To show the validity of the approximation, we compare directly the computed drag on one smooth-spored species and three species of exceptionally rugose spores with the computed fluid drag on the corresponding ellipsoids. Rugose spore silhouettes were traced from electron micrographs: an image of the sculpted species Aleuria aurantia was provided by J. Dumais and images of the ridged species Peziza baddia and of the coarsely warty Peziza vacinii were taken from ref. 22, whereas the silhouette of the smooth spored species Neurospora crassa was traced from a optical micrograph provded by N.B. Raju (see Fig. 2). The true spore shape was approximated by revolving the silhouette to form an three-dimensional body. The computed drag on the spore is compared with the drag on its approximating ellipsoid in Table 1. The shape approximation captures the drag on the spore with high (<1%) accuracy for smooth and rough spores, but is slightly less accurate for spores with coarse, dense warts such as P. vacinii. For these warty spores, the drag is more accurately approximated by an ellipsoid that completely encloses the spore and its surface ornamentation.
Fig. 2.
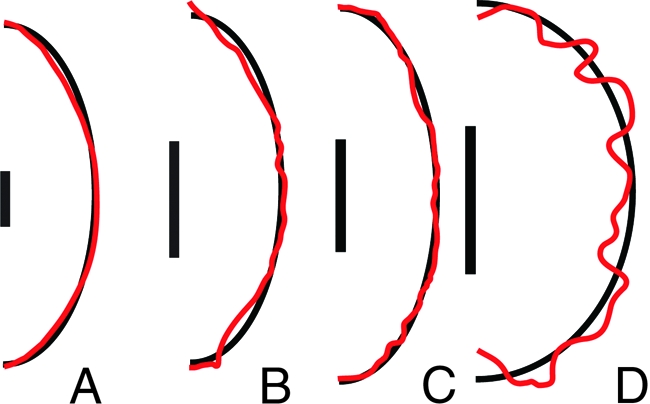
Silhouettes of highly rugose spores (red curves), traced from optical or electron micrographs and approximating ellipsoids (black curves) constructed to have the same volume and aspect ratio for N. crassa (A), A. aurantia (B), P. baddia (C), and P. vacinii (D). (Scale bar: 5 μm.) Although the approximating ellipsoids do not precisely capture the shape of the spore, they well-approximate the drag on the spore (see Table 1).
Table 1.
Comparison of the drag for real spore shapes with the drag on an ellipsoid having the same volume and aspect ratio, assuming launch speed U0 = 2.1 m·s−1
| Species | Spore drag, nN | Ellipsoid drag, nN | Error, % |
|---|---|---|---|
| Neurospora crassa | 4.03 | 4.04 | 0.3 |
| Aleuria aurantia | 1.73 | 1.73 | 0.3 |
| Peziza baddia | 2.05 | 2.04 | 0.6 |
| Peziza vacinii | 2.31 | 2.23 | 3.7 |
Fig. 3A compares the aspect ratio and Re data for the species in the phylogeny with optimal shapes. Species between the two dotted curves suffer no more than 1% more drag than the drag-minimizing shape. Seventy-three of 102 species from the phylogeny have drags within 1% of the optimum, and half of the species are within 0.46%, which corresponds to conforming to within 25% of the the optimal aspect ratio. This comparison requires us to assume a launch velocity U0, to convert between size and Re. Launch velocities in the range 2.1 (+1.4/−1.1) m·s−1 give good agreement of real and optimal shapes (Fig. 3B). Some of the dispersion of spore shape may result from certain species being optimized for speeds larger than this assumed U0.
Fig. 3A also shows clear upper and lower bounds on spore size. Both bounds follow from fluid mechanical constraints. Spores must exceed a minimum size for their inertia to carry them through a boundary layer of nearly still air clinging to the fruiting body: for a fruiting body of size L ≈ 1 mm, and wind speed Uwind = 20 cm·s−1 (24) we expect this boundary layer to have a characteristic thickness . Within the boundary layer air flow normal to the boundary, i.e., in the direction of launch of the spores, is very weak (23), so the air may be treated as still, for the smallest spores, Re ≪ 1 (if a = 1 μm, then Re ≈ 0.1), so the Stokes formula (Eq. 2) may be then be used to determine range. For the range to exceed the characteristic boundary layer thickness we obtain, on setting ζ ≈ 6πaη, a lower bound on spore size of a > 1.8 μm. This is comparable to the size of the smallest spores in the dataset (Graphostroma platystroma, a = 0.7 μm). However, spores that are too large are too heavy to be supported by the often quite weak air flows beyond the boundary layer. For the lift from an upward wind of speed Uwind = 20 cm·s−1 to exceed the spore weight , it is necessary that , which matches the size of the largest forcibly launched spores (Pertusaria melanchora, with a = 58 μm).
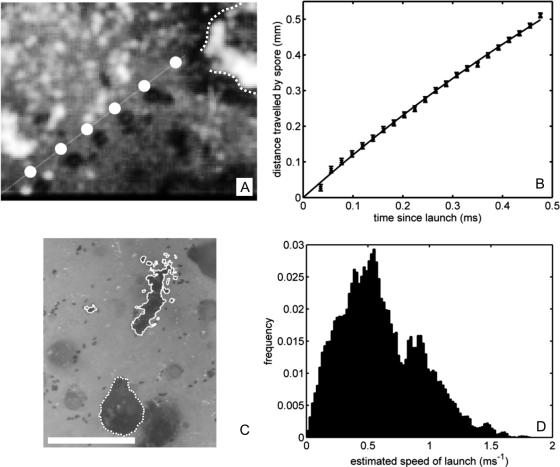
Because our fitted ejection speed is less than previous estimates based on pressure or spore range (8), we used high-speed imaging to directly measure U0 in laboratory cultures of N. tetrasperma (see Materials and Methods). One-sequence was captured (Fig. 4A) showing the trajectory of the launched spore. Fitting the spore trajectory to a Stokes drag model (Eq. 2), we find U0 = 1.24 ± 0.01 m·s−1 (Fig. 4B), well-matching our predicted ejection speed.
Fig. 4.
Experimental determination of spore ejection speed in N. tetrasperma. (A) Composite image of the flight of a N. tetrasperma spore at 63-μs intervals, including (slightly displaced) trajectory predicted from Eq. 2. The dotted curve shows the outline of originating perithecium. (B) Fit of spore trajectory (points) to Eq. 2; giving launch speed U0 = 1.24 m·s−1. (C) Spore piles (outlined by solid curves) surrounding the perithecium (dotted curve). (Scale bar: 0.5 mm.) (D) Inferred launch speeds from spore prints of N = 100 fruiting bodies.
By measuring the distances traveled by ejected spores we estimated the variability in launch speed among fruiting bodies. In contrast to previous range measurements (17, 18), we controlled for enhancement of range by air flows within the Petri dishes by measuring travel distances only for spores lying in piles (see Fig. 4C), which are likely to have followed identical trajectories. (By contrast, we expect spores whose ranges have been significantly augmented by random air flows to be scattered over the petri dish.) Supposing that U0 ≲ 2 m·s−1, so that Re ≲ 1, we used Eq. 2 to infer launch velocity, by taking ζ = 6πaψμ, where the shape factor ψ ≈ 0.95 for a spore of length 31 μm and width 15 μm (25), and the number of spores in a pile was estimated from its area on the substrate. Frequency counts of the launch velocities from 100 different perithecia are shown in Fig. 4D. Variation in both speed and angle of launch leads to large dispersion in the measured ranges, but the range of launch speeds lies within the fitted limits.
The effect of removing the selective constraint imposed by range maximization is well demonstrated by two divergent groups of fungi that lack spore ejection, but are nested within clades with forcible ejection. We focus on Sordariomycetes that are dispersed by insects or animals and discharge their spores as an oily cirrus, and on Pezizomycetes that produce closed hypogeous (underground) fruiting bodies. Representative genera for these groups are listed, respectively, in ref. 26 and (as the genus Geopora and family Tuberales) in ref. 27. We collected spore-shape data for the type species of each of these genera, and added two additional species per genus, either drawn from the references or randomly selected from the Cybertruffle taxonomic lists (28).
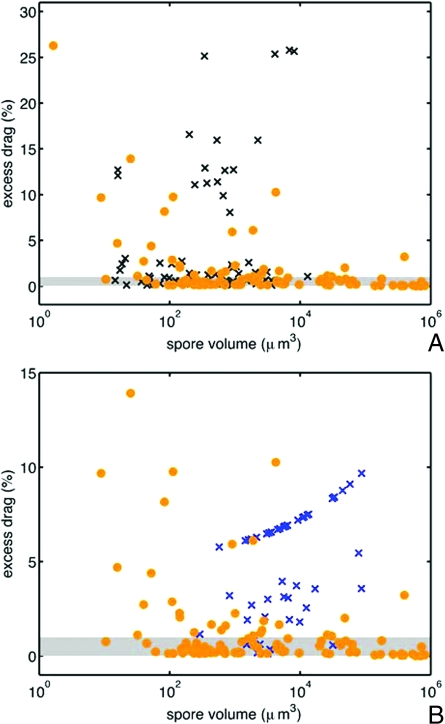
Spores from both groups of nonejected species have significantly larger mean drag (one-tailed Wilcoxon signed rank test P < 0.001) and fewer species within 1% of the drag minimum (ejected species, 73/102; insect dispersed group, 29/65; hypogeous group9/57) (see Fig. 5). The appearance of nonejected, spores with almost drag-minimizing shapes may result from the retention of an ancestral shape in the absence of selection for a new optimal shape; it is certainly for this reason that at least one species of hypogeous ascomycete (Geopora) still ejects its spores forcibly, albeit into the closed cavity of the fruiting body (29).
Fig. 5.
Ejected and nonejected spores. (A) Comparison of excess drag—the difference in drag between the real spore shape and the optimal shape of the same size—on logarithmic axes for forcibly ejected spores (·) and (×) insect-dispersed Sordariomycete spores. (B) Comparison of excess drag for forcibly ejected spores and hypogeous Pezizomycete spores (×). Species within the shaded region have drag-to-mass ratios within 1% of the optimal value. More than 75% of forcibly ejected spores, but <45% of insect dispersed spores and 16% of hypogeous spores have excess drag values below this bound. The axes have been rescaled in B, removing the ejected species G. platystroma from the plot window.
By considering the coevolution of spore size and shape over the reconstructed history of one family of fungi, we can determine the extent to which drag minimization, as opposed to other constraints, has controlled evolution of spore shape. The Pertusariaceae are a cosmopolitan medium-sized family of lichen species, most with forcibly ejected spores, and with the widest range of spore sizes of any ascomycete family (30-31).
We model the evolution of spore shape (aspect ratio αi) and size (represented by ui = log Rei) within each Pertusariacean lineage by a stochastic process:
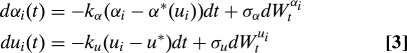 |
where dt is any scalar increment of genetic change. The first terms in the left-hand sides of Eq. 3 represent the force of selection for shapes with an optimal aspect ratio α*(u), and size u*, whereas dWtαi and dWtui are independent Wiener processes, representing the fluctuating contributions of genetic drift and other shape constraints (33). We apply the model to a two-gene phylogeny of 44 representative extant species (32). First, we find that differences in spore size and shape between species are uncorrelated with genetic distances estimated from the phylogeny (r2 < 1.0 × 10−3, Mantel test P = 0.09), suggestive of strong recent selection (see Materials and Methods). We therefore use shapes drawn independently from the invariant distribution of the stochastic process (Eq. 3) to fit the model to the real spore shape data and to obtain measures of the relative contributions of drag minimization and drift to shape evolution. In particular, we estimate σα2/2kα = 0.267, so that in practical terms selection has dominated drift to constrain spore aspect ratio to within ≈ 25% of the optimal value. Finally, by comparing the fit of the strong selection model with the fit from a drift-based reconstruction of the ancestral spore shapes (34) we confirm that the covariation of aspect ratio with size in the family is much more likely to have arisen by selection than by chance (36) (see Materials and Methods).
Materials and Methods
Calculation of Optimal Shapes.
Shapes of projectiles that minimize drag for prescribed Reynolds number and body volume were calculated by using a gradient descent algorithm, in which successive volume-preserving perturbations were made to the shape of a suboptimal projectile (20). At each iteration we calculated the change in fluid drag due to an arbitrary perturbation to the body boundary, and then inferred the optimal perturbation. Specifically, for a body, Ω, immersed in an infinite fluid domain, we calculate the effect of a small perturbation to the shape boundary, ∂Ω, on the drag-functional:
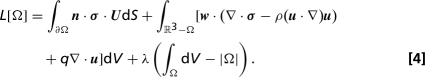 |
The first term of the of the functional represents the rate of working of the drag force on the body, the adjoint velocity (w) and pressure (q) fields are Lagrange multipliers that, respectively, enforce conservation of momentum and incompressibility in the surrounding fluid, and the Lagrange multiplier λ enforces volume conservation. Deformations to the boundary of the body are constructed as surface functions α(x) giving the local normal shift of the boundary from x to x + α(x)n. Provided that the adjoint fields satisfy an equation:
with ∇ · w = 0, subject to boundary conditions w = 0 on the boundary of the shape and w → −U in the far-field, then the corresponding small change in total drag on the body can be cast as a single integral over the unperturbed surface:
We can then write down the perturbation of the shape boundary that achieves maximum drag reduction while fixing the volume of the shape:
in which λ has been chosen to ensure that ∫∂Ω αdS = 0, so that the volume of the body is preserved. A parameter μ is introduced to parameterize the sequence of shapes that the body passes through to reach the drag minimum, giving an equation αn ≡ dx/dμ, which is integrated by using a low-order variable step-size routine (the Matlab function ode23). At each step the Navier–Stokes flow equations and adjoint Eq. 5 are solved numerically by discretizing the velocity and adjoint velocity field (u, w) by quadratic finite elements, and (p, q) by linear finite elements on an unstructured triangular mesh, and solving the discretized system by using COMSOL Multiphysics. Computation of optimal shapes is computationally costly, so we interpolate from the aspect ratio and drag data for exact optimal shapes at a small set of values of Re to intermediate values of Re, by approximating the minimum-drag body by the least-drag spindle formed by rotating the arc of a circle around the associated chord, and carrying out a single-parameter search over chord to width ratios (see SI Appendix I).
Measurement of Launch Speed.
Launch speed was directly measured in N. tetrasperma (Strain no. 614, obtained from the Fungal Genetics Stock Center), cultured in 10-cm-diameter Petri dishes in crossing medium at 1% sucrose concentration (37). Petri dishes were stacked, and the stacks laid in a container with a slotted lid, to control the direction of incident light, and illuminated for 10 min per day. On the ninth day of incubation cultures used for spore print photography were abraded with a cotton-tipped applicator to remove conidia and aerial mycelia. Photographs were taken 11 days after inoculation. Cultures used for high-speed imaging were deprived of light from the eighth day onward. High-speed imaging was carried out on the tenth day after inoculation. Petri dishes were righted, conidia removed, and ejection imaged at magnifications of up to 40×, and frame rates of up to 50,000 fps by using a Phantom v7 camera mounted on a Olympus SZX-ILLB2-100 dissecting scope. Even a small misalignment of initial trajectory and focal plane causes the spores to leave the plane of focus. However, 40 h of imaging sufficed to capture 30 ejection events and one focused sequence of images of a launched spore.
Comparative Methods.
We infer the relative strengths of drag minimization and drift as shape determinants by fitting the invariant distribution of the stochastic process (Eq. 3) to real spore shape data. Over the range of spore sizes covered by the Pertusariaceae (0.5 < log Re < 2.3), the optimal aspect ratio varies approximately linearly with u: α*(u) = α0 + α1u, where α0 = 2.02 and α1 = 0.38. Eq. 3 therefore defines an Ornstein–Uhlenbeck process with Gaussian invariant distribution (35), so that the spore shapes of tip species are independent random variables with expectation and covariance matrices
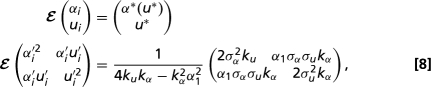 |
where we have defined α′i ≡ αi - E(αi) and u′i ≡ ui - E(ui).
Maximum likelihood estimates for each of the parameters in the model can then be extracted from the observed first and second moments of the species data. Four dimensionless parameters must be estimated, and we choose these to be u*, σα2/2kα, σu2/2ku and kα/ku (see SI Appendix, Fig. S4).
The statistical support for the hypothesis of evolution of spores under strong shape selection can be determined by comparing the fit to real spore shape data from model 3 with two other models for trait evolution: (i) a Brownian model (34), in which both u and α are unconstrained:
and (ii) a Ornstein–Uhlenbeck process in which α is unconstrained, but there is selection on the size variable u:
dWtαi,ui are independent Wiener processes, and t parameterizes the amount of genetic change from the common ancestor of the family. Distinct lineages co evolve from the ancestral state up until the time, t = tij of first divergence, so that shape and size data for the observed species have multivariate Gaussian distributions. Thus, if ti is the “age” of the the ith lineage then for Eq. 10:
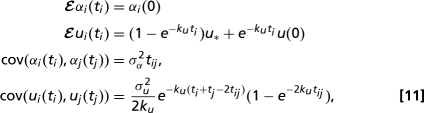 |
and the corresponding distribution for the pure Brownian process Eq. 9 can be obtained by setting ku = 0. A version of these formulae for the case when all lineages have the same ages (ti = tj for all i, j) is given in ref. 36. Note that genetic and phenotypic distances between tip species will become uncorrelated if and only if kuΔt ≫ 1, where Δt is the smallest genetic distance between any pair of species, i.e., in the presence of strong selection. We measure t in units of the average number of substitutions per base pair, in the two genetic locii used in ref. 32. σu,α2 therefore have units of base pairs per substitution. Fitting these models to the observed species data requires estimation of (i) four or (ii) six parameters: the drift strengths, σα,u2, the ancestral spore shape data [αi(0), ui(0)] and, in the case of process 10, the force of selection ku and optimal size u*.
The maximum likelihood estimators for all the parameters that feature in the three models are given in Table 2. The Akaike Information Criterion corrected for small sample sizes (AICc) allows the quality of fit of the three models to be compared (36), and shows that the strong selection hypothesis provides a significantly better fit to the real spore shapes data than either of the models in which there is no shape selection (last row of Table 2).
Table 2.
Parameter estimators and Akaike information criteria for shape evolution models fitted to spore shape data from the Pertusariaceae
| Strong selection | Weak selection | Size selection | |
|---|---|---|---|
| σα2/2kα | 0.267 | – | – |
| σu2/2ku | 0.278 | – | – |
| ku/kα | 0.127 | – | – |
| u* | 1.17 | – | 0.92 |
| ku (bp/sub.) | – | – | 10.02 |
| σα2 (bp/sub.) | – | 13.9 | 13.9 |
| σu2 (bp/sub.) | – | 6.50 | 9.30 |
| α(0) | – | 2.40 | 2.40 |
| u(0) | – | 1.21 | 2.24 |
| -2 log L | 119.70 | 131.81 | 128.50 |
| AICc | 128.95 | 141.07 | 143.30 |
Supplementary Material
Acknowledgments.
We thank Imke Schmitt, Jacques Dumais, and François Lutzoni for making their data available to us, Jacques Dumais, L. Mahadevan, Nicholas Money, Andrew Murray, Sheila Patek, Frances Trail, Dominic Vella, Howard Stone, and members of the Pringle lab for useful discussions and comments on the manuscript, and Ozymandias Agar for assistance with the spore launch imaging. This work was supported by fellowships from the Kodak-Eastman group and the Harvard University Herbaria (M.R.) and by additional support from the Harvard Materials Research Science and Engineering Center and National Science Foundation Division of Mathematical Sciences.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0805017105/DCSupplemental.
References
- 1.Vogel S. Life in Moving Fluids: The Physical Biology of Flow. 2nd Ed. Princeton: Princeton Univ Press; 1994. [Google Scholar]
- 2.Parkhurst D, Loucks O. Optimal leaf size in relation to environment. J Ecol. 1972;60:505–537. [Google Scholar]
- 3.Taylor GK, Nudds RL, Thomas ALR. Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature. 2003;425:707–711. doi: 10.1038/nature02000. [DOI] [PubMed] [Google Scholar]
- 4.Pyke G, Pulliam H, Charnov E. Optimal foraging: A selective review of theory and tests. Q Rev Biol. 1977;52:137–154. [Google Scholar]
- 5.Gilchrist M, Sulsky D, Pringle A. Identifying fitness and optimal life-history strategies for an asexual filamentous fungus. Evolution. 2006;60:970–979. [PubMed] [Google Scholar]
- 6.Parker GA, Smith JM. Optimality theory in evolutionary biology. Nature. 1990;348:27–33. [Google Scholar]
- 7.Ingold C. Fungal Spores: Their Liberation and Dispersal. Oxford: Clarendon Press; 1971. [Google Scholar]
- 8.Trail F. Fungal cannons: Explosive spore discharge in the Ascomycota. FEMS Microbiol Lett. 2007;276:12–18. doi: 10.1111/j.1574-6968.2007.00900.x. [DOI] [PubMed] [Google Scholar]
- 9.Buller A. Researches on Fungi. Vol. 6. New York: Longmans & Green; 1934. [Google Scholar]
- 10.Batchelor G. Introduction to Fluid Dynamics. Boulder, CO: C.U. Press; 1967. [Google Scholar]
- 11.Jones E. Form and function of fungal spore appendages. Mycoscience. 2006;47:167–183. [Google Scholar]
- 12.Ingold C. Spore Discharge in Land Plants. London: Oxford Univ Press; 1939. [Google Scholar]
- 13.Radhakrishnan V. Locomotion: Dealing with friction. Proc Natl Acad Sci USA. 1998;95:5448–5455. doi: 10.1073/pnas.95.10.5448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vogel S. Living in a physical world II. The bio-ballistics of small projectiles. J Biosci. 2005;30:167–175. doi: 10.1007/BF02703696. [DOI] [PubMed] [Google Scholar]
- 15.Vogel S. Living in a physical world III. Getting up to speed. J Biosci. 2005;30:303–312. doi: 10.1007/BF02703667. [DOI] [PubMed] [Google Scholar]
- 16.Fischer M, et al. New information on the mechanism of forcible ascospore discharge from Ascobolus immersus. Fung Gen Biol. 2004;41:698–707. doi: 10.1016/j.fgb.2004.03.005. [DOI] [PubMed] [Google Scholar]
- 17.Ingold CT, Hadland SA. The ballistics of Sordaria. New Phytol. 1959;58:46–57. [Google Scholar]
- 18.Trail F, Gaffoor I, Vogel S. Ejection mechanics and trajectory of the ascospores of Gibberella zeae (anamorph Fuarium graminearum) Fung Gen Biol. 2005;42:528–533. doi: 10.1016/j.fgb.2005.03.008. [DOI] [PubMed] [Google Scholar]
- 19.Mohammadi B, Pironneau O. Applied Shape Optimization for Fluids. Oxford: Oxford Univ Press; 2001. [Google Scholar]
- 20.Roper M, Squires TM, Brenner MP. Symmetry unbreaking in the shapes of perfect projectiles. Phys Fluids. 2008;20:093606. [Google Scholar]
- 21.Lutzoni F, et al. Assembling the Fungal Tree of Life: Progress, classification and evolution of sub-cellular traits. Am J Bot. 2004;91:1446–1480. doi: 10.3732/ajb.91.10.1446. [DOI] [PubMed] [Google Scholar]
- 22.Norman JE, Egger KN. Phylogeny of the genus Plicaria and its relationship to Peziza inferred from Ribosomal DNA sequence analysis. Mycologia. 1996;88:986–995. [Google Scholar]
- 23.Schlicting H. Boundary Layer Theory. New York: McGraw–Hill; 1960. [Google Scholar]
- 24.Deering R, Dong F, Rambo D, Money N. Airflow patterns around mushrooms and their relationship to spore dispersal. Mycologia. 2001;93:732–734. [Google Scholar]
- 25.Brenner H, Happel J. Low Reynolds Number Hydrodynamics with Special Application to Particulate Media. 2nd Ed. Leiden, the Netherlands: Martinus Nijhoff Publishers; 1973. [Google Scholar]
- 26.von Arx J, Figueras M, Guarro J. Sordariaceous ascomycetes without ascospore ejaculation. Beih Nova Hedwigia. 1988;94:1–104. [Google Scholar]
- 27.Ainsworth G, Sparrow F, Sussman A. The Fungi—An Advanced Treatise. 4A. Academic Press: New York; 1973. [Google Scholar]
- 28. [Last accessed January 28];Cybernome: The Nomenclator for Fungi and Their Associated Organisms. 2008 Available at: www.cybertruffle.org.uk/cybernome. [Google Scholar]
- 29.Burdsall HH., Jr Operculate asci and puffing of ascospores in geopora (tuberales) Mycologia. 1965;57:485–488. [Google Scholar]
- 30.Archer A. The Lichen genus Pertusaria in Australia. Bibl Lichen. 1997;69:1–249. [Google Scholar]
- 31.Dibben M. The chemosystematics of the Lichen genus Pertusaria in North America north of Mexico. Publications in Biology and Geology. Vol. 5. Milwaukee: Milwaukee Public Museum; 1980. [Google Scholar]
- 32.Schmitt I, Lumbsch H. Molecular phylogeny of the Pertusariaceae supports secondary chemistry as an important systematic character set in lichen-forming ascomycetes. Mol Phylogenet Evol. 2004;33:43–55. doi: 10.1016/j.ympev.2004.04.014. [DOI] [PubMed] [Google Scholar]
- 33.Hansen TF. Stabilizing selection and the comparative analysis of adaptation. Evolution. 1997;51:1341–1351. doi: 10.1111/j.1558-5646.1997.tb01457.x. [DOI] [PubMed] [Google Scholar]
- 34.Felsenstein J. Phylogenies and the comparative method. Am Nat. 1985;125:1–15. [Google Scholar]
- 35.Lemons DS. Introduction to Stochastic Processes in Physics. Baltimore: John Hopkins Univ Press; 2002. [Google Scholar]
- 36.Butler M, King A. Phylogenetic comparative analysis: A modeling approach for adaptive evolution. Am Nat. 2004;164:683–695. doi: 10.1086/426002. [DOI] [PubMed] [Google Scholar]
- 37.Westergaard M, Mitchell H. Neurospora V. A synthetic medium favoring sexual reproduction. Am J Bot. 1947;34:573–577. [Google Scholar]
- 38.Dulymamode R, Cannon PF, Peerally A. Fungi from Mauritus: Three Astrocystis species from Pandanus. Mycol Res. 1998;102(11):1325–1330. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.