Prediction of incommensurate crystal structure in Ca at high pressure

Abstract

Ca shows an interesting high-pressure phase transformation sequence, but, despite similar physical properties at high pressure and affinity in the electronic structure with its neighbors in the periodic table, no complex phase has been identified for Ca so far. We predict an incommensurate high-pressure phase of Ca from first principle calculations and describe a procedure of estimating incommensurate structure parameters by means of electronic structure calculations for periodic crystals. Thus, by using the ab initio technique for periodic structures, one can get not only reliable information about the electronic structure and structural parameters of an incommensurate phase, but also identify and predict such phases in new elements.

The continuous improvement of the high-pressure technique and the advances in the methods of characterization of materials under high pressure have opened new perspectives for materials physics community. The discovery of a series of phases for periodic table elements within the explored interval of pressures (1, 2) have stimulated an increased interest from both experimentalists and theoreticians to understand the unexpected behavior of simple elements under high pressure. Within the alkali and earth-alkaline metals, a series of complex structures at high pressure have been identified and, in particular, the complex phases of Ba-IV (3), Sr-V (4), Rb-IV (5), and K-III (6) have been determined as composite host-guest structures, which are incommensurate along the common axis of host and guest sub-lattices. The occurrence of such complex composite structures in a large number of elements and the robustness of these complex phases over a wide range of pressures and temperatures make the existence of composite incommensurate structures an intrinsic high-pressure phenomenon. Therefore, other elements may undergo similar high-pressure phase transitions. The nature of the transition to a composite structure is not completely understood yet, partly, because such an essential theoretical tool for describing the condensed matter as electronic structure calculations cannot be directly applied to study an incommensurate structure. However, one can perform first-principles calculations on commensurate analogues of an incommensurate phase and, indeed, such calculations can reproduce the phase transition sequence in close agreement with the experiment and provide reliable information about the electronic structure (7, 8). Ab initio calculations of Ba-IV commensurate analogue (7) suggest that the transition from a closed, packed structure at low pressure to a more open, complex structure at high pressure might be because of the transfer of electrons from free-electron like s-bands to more directional d-bands. In the Ba-IV phase, the sd-hybridization occurs between the orbitals of two nonequivalent Ba atoms: guest atoms with a more d-like character and host atoms with a more s-like character. Therefore, from the electronic structure perspective, the composite structure of the Ba-IV phase can be considered as a two-component intermetallic compound rather than a single element phase. These calculations also showed that the hcp phase is competitive with the pseudoBa-IV phase and one could expect that elements with the hcp structure because of partial sd-hybridized bonding might undergo a transition to a composite phase at high pressures. Indeed, the Sc-II phase, which was unknown for a long time, has been recently determined as an incommensurate host-guest structure, isostructural to Sr-V phase (9). The structural changes are accompanied also by drastic changes of the transport properties with pressure. Both Sr and Ba are superconductors at high pressure and the critical temperature T_C increases with pressure (10). The Sc-II phase was found to be superconducting (11) and recent observations show that T_C also increases monotonically with pressure (12). Following through the arguments given above, one can expect Ca to undergo a similar transition to a complex phase at very high pressures.

Ca shows an interesting and unique phase transition sequence from a closed, packed structure at ambient pressure to an open one at high pressures, namely, a face-centered cubic cF4 to a body-centered cubic cI2 transition at ≈19.5 GPa (13, 14), and a cI2 to a simple cubic cP1 phase transition at 32 GPa (14). This remarkable transition sequence was found to occur because of the same s-band to d-band electron transfer, and that at high pressures the valence band acquires a complete d-like character (15). It was also theoretically predicted that Ca might undergo a transition to the hexagonal closed, packed hP2 structure at pressure >112 GPa. Finally, superconductivity was observed in Ca >50 GPa (16) and the pressure dependence of T_C is positive up to 150 GPa. Recently new experimental data on Ca at high pressure were reported and two new high pressure phases of Ca were observed >113 GPa (17). The structure of these phases could not be resolved from the analysis of the diffraction picture; however, in a very recent metadynamics simulation based on ab initio calculation, two structures, which x-ray patterns match the experimental ones (18), were found. One structure, Ca-IV, is a tetragonal lattice, which consists of two helical chains along the c-axis, and another structure, Ca-V, is an orthorhombic lattice of four zigzag chains. However, the occurrence of an incommensurate complex phase at these pressures is not excluded, because in numerical simulations (18) periodic boundary conditions were imposed on the system. A recent low temperature study of Yabuuchi et al. (19) shows a significant increase of the superconducting transition temperature of Ca with pressure. At 160 GPa T_C reaches the record value for an element of 25 K. In the case of Ba, T_C reaches its maximum value in the Ba-IV phase (10), therefore we can expect a maximum of T_C in Ca to occur for a composite crystal structure.

In this article, we predict the existence of a stable Sc-II type incommensurate complex structure for Ca at high pressures from first-principles calculations. Our statement is based on the results of the ab initio calculation of several commensurate analogues of Sc-II structure and it is to our knowledge the first time that an incommensurate complex structure is predicted from the electronic structure calculations. Our results show that at pressure ≈122 GPa, Ca should undergo a structural phase transition from a Ca-V phase to an incommensurate I4/mcm(00γ) structure made of a tetragonal body-centered host and tetragonal C-face-centered guest sub-lattices.

Results and Discussion

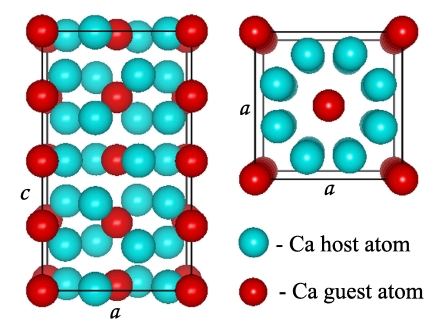
We have performed a study of Ca under hydrostatic pressure by means of the first-principles electronic structure calculations technique. We have calculated the total energy of experimentally observed and well determined structures, namely cF4, cI2, and cP1, of recently discovered phases Ca-IV tP8) and Ca-V (oC8), and of a set of commensurate analogues of I4/mcm(00γ). The true incommensurate structure I4/mcm(00γ) is composed of two tetragonal sub-lattices (1, host; 2, guest) with the same a lattice parameter but different values for the c lattice parameter, which ratio γ = c₁/c₂ is an irrational number. The host lattices is a body-centered tetragonal described by the symmetry group I4/mcm with atoms at Wyckoff position 8h(x,x + 1/2,0), and the guest lattice is a C-face-centered tetragonal with atoms at sites (0, 0, 0) and (1/2,1/2,0). We started our simulation of the incommensurate structure with a commensurate supercell consisting of three host cells and four guest cells corresponding to a commensurate complex structure with γ = c₁/c₂ = 4/3 (see Fig. 1). The overall structure is body-centered tetragonal described by the space group I4/mcm and contains 32 atoms at the following Wickoff positions: 4c (0, 0, 0), 4a(0,0,1/4), 8h(x,x + 1/2,0), and 16l(x,x + 1/2,1/3) .

Fig. 1.

Crystal structure of I4/mcm(00γ) commensurate analogue with γ = 4/3. The supercell is build up of 3 body-centered tetragonal cells with atoms at Wickoff position 8h(x,x + 1/2,0) (host), and 4 C-face-centered tetragonal cells with atoms at positions (0, 0, 0) and (1/2,1/2,0) (guest). The overall structure is a body-centered tetragonal lattice described by space group I4/mcm with 32 atoms at Wickoff positions 4c (0, 0, 0), 4a(0,0,1/4), 8h(x,x + 1/2,0), and 16l(x,x + 1/2,1/3). After structure optimization the positions of atoms in the host sub-lattice deviate from the initial one.

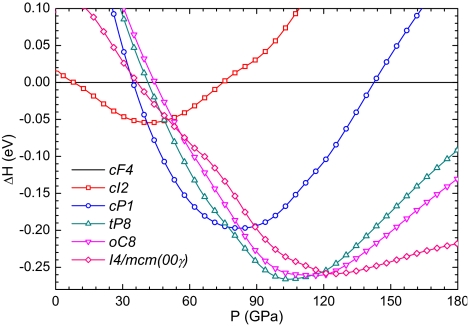
In Fig. 2 enthalpies of the cI2, cP1, tP8, oC8, and I4/mcm(004/3) phases relative to the enthalpy of the cF4 structure, stable at ambient conditions, are shown. At T = 0K the enthalpy H = H(V) describes the phase diagram and within a given range of pressures the phase with the lowest enthalpy is the stable one. Our calculations reproduce the phase sequence for the experimentally observed structures giving the values for transition pressures of ≈8 GPa and 40 GPa for the cF4 → cI2 and cI2 → cP1 phase transitions, respectively. One can notice that calculated cF4 → cI2 transition pressure does not agree well with the transition pressure determined from the experiment and previous calculations. Nevertheless, the values for the equilibrium volume V₀, bulk modulus B₀ and its derivative B′₀, which from our calculation are 42.19 ų, 17.46 GPa, and 3.14, respectively, are in close agreement with the corresponding experimental parameters of the equations of state (20). Calculated volume collapse ΔV/V of 1% and 7% at the cF4 → cI2 and cI2 → cP1 phase transitions, respectively, are also in good agreement with the experiment (14).

Fig. 2.

Phase diagram of Ca with respect to the enthalpy of cF4 phase. The incommensurate structure I4/mcm(00γ) is approximated by the γ = 4/3 analogue.

We reproduced also the results of Ishikawa et al. (18). At the pressure of 77 GPa the cP1 structure undergoes a transition to Ca-IV with a volume collapse of 3.5%, which in turn transforms >115 GPa into Ca-V phase with a volume collapse of 1%. We found that the structure of Ca-IV can be described by the space group No. 96 P4₃2₁2 with atoms occupying 8b site, rather than the space group No. 78 P4₃ with 2 sorts of atoms occupying 4a site. We also quenched the structure parameters of both Ca-IV and Ca-V phases at pressures below their stability range, because both phases tend to change their structures during the relaxation procedure. Again, the transition pressures are at variance with the experimental values from the x-ray diffraction studies (17). Simple cubic phase was found to be stable up to 109 GPa and the diffraction peaks attributed to the Ca-V were observed at 139 GPa. This discrepancy was noticed also by Ishikawa et al. (18) and has no reasonable explanation yet. However, if we consider the pressure dependence of the electrical resistance in figure 4 of ref. 19, the pressures at which the electrical resistance changes drastically are shifted to lower values with respect to the phase boundaries. These changes may correspond to the onset of the structural phase transition. One can also notice some feature at 90 GPa in the volume compressibility of Ca shown in figure 3 of ref. 17. Yabuuchi et al. (19) have emphasized that sample purity plays an important role in the determination of the electrical properties of Ca. This fact may be important also for the correct determination of the phase boundaries during the structural transformations. We should not exclude also the fact that the current implementation of the DFT uses an approximate expression for the exchange-correlation functional. Therefore, this issue requires further examination and enforces our statement that Ca is an extraordinary system at high pressures.

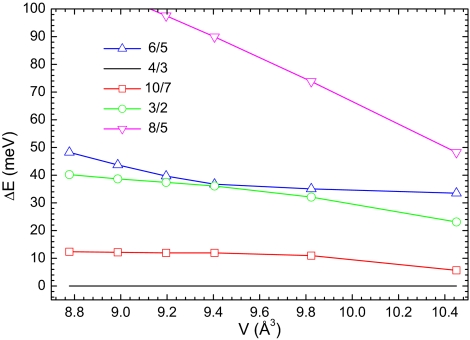
Fig. 3.

Total energies of various commensurate analogues with respect to the energy of γ = 4/3 commensurate supercell as a function of volume/atom. Symbols correspond to calculated points.

We can further see that predicted Ca-V phase is stable within a narrow interval of pressure and >122 GPa the commensurate analogue of Sc-II type structure becomes energetically more favorable. The calculated phase diagram of Ca strongly support the idea that at high pressure Ca should transform to a complex incommensurate structure Ca-VI.

If I4/mcm(00γ) is the superspace group of Ca-VI phase, is it then possible to determine the lattice parameter a, the incommensurate ratio γ, and the parameter x of the Wickoff position 8h from ab initio calculations? Because the total energy is a continuous function of the structural parameters, the energy of an analogue commensurate structure with a c₁/c₂ ratio close to the incommensurate one will approach the total energy of the true incommensurate structure. Therefore, total energy as a function of the c₁/c₂ ratio, E = E(c₁/c₂), should have a minimum for c₁/c₂ corresponding to the incommensurate ratio γ (21).

To estimate the incommensurate ratio of the I4/mcm(00γ) structure, we performed additional calculations for a set of commensurate supercells with γ = {6/5,10/7,3/2,8/5}, where the nominator stands for the number of guest cells and the denominator for the number of host cells, and interpolated polynomially the calculated values of energy. Structures with γ = {6/5,10/7,8/5} are analogous to that with γ = 4/3 and contain 26, 38, and 28 atoms, respectively. Structure with γ = 3/2 is a simple tetragonal supercells, which contain 22 atoms, and is described by the space group P4/mbm.

In Fig. 3 calculated energies of various commensurate structures with respect to the γ = 4/3 periodic supercell as a function of volume/atom are shown. We can see from Fig. 2 that the enthalpy difference between the commensurate analogue of the I4/mcm(00γ) structure with γ = 4/3 and the Ca-V structure becomes large than 20 meV >140 GPa. Therefore, according to the results shown in Fig. 3, two commensurate analogue structures with γ = 4/3 and γ = 10/7 are energetically more favorable than the Ca-V phase. Above 160 GPa, two other commensurate supercells with γ = 3/2 and γ = 6/5 also become energetically more favorable than the Ca-V structure. Thus, at high pressures we have a set of commensurate analogues, which approximate the incommensurate I4/mcm(00γ) structure with enthalpies lower than the enthalpy of the Ca-V structure. By fitting the calculated values of total energy of different commensurate analogues at a given volume with a smooth polynomial function, we can estimate the incommensurate ratio γ, which gives the minimum of the energy curve E = E(c₁/c₂) at this volume (21).

We also did an estimation of the internal parameter x of the Wyckoff position 8h. Because the considered model structure is an artificial approximation to the real incommensurate structure, one can expect that the imposed constraints of a periodic supercell will force atoms to deviate from the superstructure positions to mimic the incommensurate nature of that complex phase. The structure shown in Fig. 1 corresponds to the relaxed supercell at the volume/atom of 10.450 ų, which in our calculations corresponds to ≈138 GPa. It is build up of four guest cells with lattice parameter a = 5.7961 Å and c₂ = 2.4885 Å, but we cannot decompose host structure into the originally three body-centered unit cells. Host atoms still occupy the Wickoff positions 8h(x,x + 1/2,0) and 16l(x′,x′+1/2,z′), but with different values for internal parameters: x = 0.1445, x′ = 0.1480, and z′ = 0.3328. Therefore, for a given commensurate analogue at a given volume we calculated the average value of x in the supercell and then we fitted polynomially x¯ with respect to c₁/c₂. Finally, x¯ were estimated for γ(V). A similar fitting procedure was applied to estimate the lattice parameter a. Calculated values for pressure, lattice parameter, incommensurate ratio and the Wickoff parameter are summarized in Table 1.

Table 1.

Estimated values of pressure, lattice parameter, incommensurate ratio, and Wickoff parameter for Ca-VI I4/mcm(00γ) phase

V/atom, Å3	P, GPa	A, Å	γ	x
8.778	230	5.5285	1.3418	0.1477
8.987	213	5.5627	1.3405	0.1475
9.196	198	5.5943	1.3398	0.1472
9.405	185	5.6265	1.3379	0.1470
9.823	163	5.6924	1.3384	0.1465
10.450	138	5.7958	1.3592	0.1460

We did not speculate so far about the nature of the incommensurate phase because this subject goes beyond the purpose of this article. A preliminary study of the electronic structure of the commensurate analogue γ = 4/3 clearly shows that d-electrons play the essential role for an incommensurate structure to occur. We did not find a large difference between the site-projected partial density of states, that is, our incommensurate structure is unlikely to be an intermetallic compound, as suggested for Ba-IV structure (7).

Conclusions

To conclude, we performed first principle calculations of different phases of Ca at high pressures. Based on similarities of the physical properties and electronic structure between Ca and its neighbors in the periodic table of elements, we predict a new high-pressure phase Ca-VI, which is an incommensurate structure I4/mcm(00γ), isostructural to Sc-II and Sr-V. First, we approximated the incommensurate structure with a commensurate analogue γ = 4/3 and obtained that this phase becomes energetically more favorable >122 GPa than all known phases of Ca. Second, we did additional calculations for a set of commensurate structures and estimated structural parameters of the predicted incommensurate phase.

Methods

Ab initio simulations were done within the framework of the density functional theory DFT by using VASP and WIEN2k simulation packages. First, all considered structure were calculated and relaxed by using VASP (22, 23), which is a robust and highly efficient implementation of the projector augmented-wave (PAW) method (24). We used the generalized gradient approximation (25) to describe the electronic exchange and correlation effects, and Ca PAW potential with 3s²3p⁶4s² valence orbitals had been used. We used a plane-wave basis cut-off of 435 eV, sufficient to converge total energies to better than 1 meV per atom and safe to optimize the structure. A Ã-centered Monkhorst-Pack grid was used to sample the Brillouin zone (BZ) and for different phases an amount of k-points providing the same degree of convergence as the energy cut-off were generated in the irreducible BZ. For relaxation and total energy calculation we used the smearing method of Methfessel-Paxton and structures were relaxed until the Hellman-Feynman forces became less than 10−³ eV/Å. Second, all results were verified by additional calculations by using WIEN2k (26).