Kinetic model for lamellipodal actin-integrin ‘clutch’ dynamics

Abstract

In migrating cells, with especial prominence in lamellipodial protrusions at the cell front, highly dynamic connections are formed between the actin cytoskeleton and the extracellular matrix through linkages of integrin adhesion receptors to actin filaments via complexes of cytosolic “connector” proteins. Myosin-mediated contractile forces strongly influence the dynamic behavior of these adhesion complexes, apparently in two counter-acting ways: negatively as the cell-generated forces enhance complex dissociation, and at the same time positively as force-induced signaling can lead to strengthening of the linkage complexes. The net balance arising from this dynamic interplay is challenging to ascertain a priori, rendering experimental studies difficult to interpret and molecular manipulations of cell and/or environment difficult to predict. We have constructed a kinetics-based model governing the dynamic behavior of this system. We obtained ranges of parameter value sets yielding behavior consistent with that observed experimentally for 3T3 cells and for CHO cells, respectively. Model simulations are able to produce results for the effects of paxillin mutations on the turnover rate of actin/integrin linkages in CHO cells, which are consistent with recent literature reports. Overall, although this current model is quite simple it provides a useful foundation for more detailed models extending upon it.

Introduction

Dynamic adhesive interactions between a cell and its environmental substratum, such as underlying two-dimensional surfaces or surrounding three-dimensional matrices, are crucial to the phenomenon of cell migration.^1–4 These interactions appear to be highly regulated at both the cell front and the cell rear by signaling events operating via a combination of covalent modification and enzymatic cleavage processes^5–7 that help govern local balances between cytoskeletal contractile force and substratum traction.^8–10 In recent years, intense focus has been trained on the regulation of cell/substratum adhesive interactions involved in lamellipodial protrusion at the cell front, emphasizing the role of biophysical forces coupled with biochemical signaling in this regulation.^11–14

Productive lamellipodial (or filopodial) protrusions require stable attachment of the extended membrane to the proximal substratum,^15–17 which occurs by means of linkages between the polymerized actin cytoskeleton and integrin/matrix bonds involving complexes of myriad cytosolic proteins including α-actinin, vinculin, talin, zyxin, paxillin and focal adhesion kinase (FAK), among others.¹¹ Stable linkages of this sort enhance productive membrane protrusion by inhibiting the retrograde flow of actin polymers generated in the process of membrane extension,^18,19 corresponding to the ‘clutch’ hypothesis originally proposed by Mitchison and Kirschner.²⁰ Development of sophisticated techniques for dynamic molecular imaging in live cells has enabled elaboration of the clutch hypothesis in terms of specific components.^21,22 Using a combination of total internal reflection fluorescence microscopy and fluorescent speckle microscopy, Hu²² elucidated a topological hierarchy for the connector proteins in the linkage complexes between lamellipodial actin polymers and α_vβ3 integrin/fibronectin bonds in migrating PtK1 cells: α-actinin exhibiting predominantly coherent movement with actin polymers, vinculin and talin demonstrating slightly less coherence with moving actin, and FAK, zyxin and paxillin showing relatively more coherence with the immobile integrin. Employing spatio-temporal image correlation spectroscopy, Brown²¹ found a similar correspondence hierarchy for CHO cells migrating on fibronectin: α-actinin movement again was found to be most closely correlated with that of the polymerized actin, talin and vinculin slightly less correlated, and FAK and paxillin most closely correlated with immobile integrin (α5β1 in this case). Additionally, Brown²¹ showed that these quantitative correlations could be altered in the CHO cells by modifying the substratum fibronectin level, and that they are different for other cell types—3T3 and MEF mouse fibroblasts—compared to the CHO cells. Moreover, some molecular bases for the signaling regulation of these linkages are now being suggested, with paxillin a feature of central interest. Work by Nayal²³ has implicated p21-activated kinase (PAK)-mediated phosphorylation of the paxillin serine-237 site as important for modulating turnover of cell/substratum adhesions, within a feedback loop coupling adhesion to membrane protrusion by a mechanism likely involving myosin-II contractile force generation;²⁴ an ensuing study by Zaidel-Bar²⁵ obtained findings consistent with this implication.

Molecular details concerning the integration of biophysics and biochemistry in the coupling among cell/substratum adhesion, contractile force and signaling activities in the extending lamellipod will require intense investigation to sort out.^26,27 Nonetheless, a compelling argument exists for governance of lamellipod protrusion dynamics by a local balance between myosin-II-mediated contractile force and integrin-mediated traction,^10,14 regulated by an exquisite combination of negative feedback and positive feedback processes arising from the myosin-II-mediated force operating on the actin/connector-complex/integrin linkage.²⁴ This force operates negatively on the linkage by input of energy tending to increase the complex dissociation rate at one or another locus within the linkage;²⁸ at the same time, the same force can reduce breakage of the linkage by so-called “adhesion-strengthening.”²⁷ Because these opposing effects are nonlinear in nature, not only is the net outcome of the dynamic balance for any given cell/substratum situation unclear but also the effects of key molecular properties of special interest are not obvious. Thus, experimental studies involving molecular-level manipulations or interventions, such as the paxillin-mediated myosin activity modulation, are challenging to interpret and predict.

The goal of this present work, accordingly, is to offer a framework for analysis of the integrated negative/positive-feedback loops involved in myosin-II-mediated force-induced actin-integrin linkage dynamics and consequent membrane protrusion behavior underlying cell migration. Toward this goal, we develop an idealized and relatively simple mathematical model for actin-integrin linkages with an idealized “connector protein complex” serving as the intermediate. The precise identification of specific proteins within this complex is evaded for this initial study; following the hierarchies elucidated by Brown²¹ and by Hu,²² we can crudely associate α-actinin with the actin polymer, talin and vinculin as comprising major components of the connector complex, and roughly place FAK and paxillin more closely with the integrin/matrix bond. Clearly, one could expand this model to denote each of these proteins—and others—as explicit individuals exhibiting complicated inter-molecular interactions, if our current study offers sufficiently interesting results to motivate further efforts. With our simplified model here, we aim to determine the effects of key parameters governing actin-integrin linkage dynamics in manner consistent with experimental literature observations and capable of providing useful interpretation of current data and offering interesting predictions of prospective new experimental studies. We note that our work here is not concerned with the actin polymerization-mediated initial lamellipod protrusion, which has been beautifully examined by many other investigators (see, for example, the recent review by Mogilner²⁹), but instead with the adhesion-based dynamics that follow.

Results

Distinct parameter value ranges are obtained for different cell types.

In order to explore insights and predictions generated by our model (see Methods section) for the dynamic behavior of actin-integrin linkage during lamellipodial protrusion, we first needed to constrain the model parameter values in accord with experimental information. Even with the highly simplified model framework employed here, the parameters remain elusive to narrow specification because of the dearth of the necessary molecular-level measurements to date. Thus, we employed a strategy that permits trial parameter value sets to be selected initially from within plausible ranges estimated from previous literature (see Table 1), and then identifying appropriate sub-sets by selecting combinations randomly from within the plausible ranges and determining which combinations lead to simulation results that are consistent with experimental observations.³⁵ As our constraining experimental observations, we used recent data from speckle and spatio-temporal image correlation spectroscopy to study the lamellipodial adhesion dynamics in CHO cells and 3T3 cells.^21,22 These two cell types exhibit diverse behavior in terms of the correlation of movement of connector proteins (paxillin, FAK, talin) with that of actin filaments; in 3T3 cells this correlation is in the ∼60–80% neighborhood, while in CHO cells this correlation is in the ∼10–30% neighborhood. Matching the model simulation output for the steady-state fraction of “connector” (C) associated with actin (AC) as a crucial criterion (see Fig. 2) permits rejection of a large proportion of parameter value sets. For the CHO cells, an additional filter arose from requiring this correlation to increase with increasing number of integrin/fibronectin bonds (B), based on further observations by Brown²¹ (see Fig. 3). Finally, we required the parameter value sets to yield specific turnover rates for the adhesion linkages to be relatively high for CHO sets and relatively low for 3T3 sets, again consistent with the observations by Brown.²¹ The ultimate acceptable parameter value ranges are shown in Table 2. Importantly, only certain combinations of values within the acceptable ranges yield the appropriate behavior for one of these cell types. Using F₀ = 5 × 10⁻¹¹ N and f₁ = 10, fewer than 2% of randomly-selected parameter value sets (51 out of 3,000) meet the selection criteria for CHO behavior, and fewer than 4% of randomly-selected parameter value sets (96 out of 3,000) meet the selection criteria for 3T3 behavior.

Table 1.

Parameter value ranges from literature

Parameter	Value range	Source
Actin density	109–1012 cm-2 = 103–106 #/cell	Palecek 1999 (30)
Integrin receptor density	103–107 #/cell	Ward 1993 (41)
Kd	0.4–5 νM	Goldmann 2000 (42)
Koff	10−5–10 s−1	Palecek 1999 (30)
γ	10−1 to 1 nm	Palecek 1999 (30)
F	10−12 to 10−11 N	Li 2005 (26)
kb*T	4.1e–21 J
Cell area	102–104 νm2	Ward 1993 (41)

Figure 2.

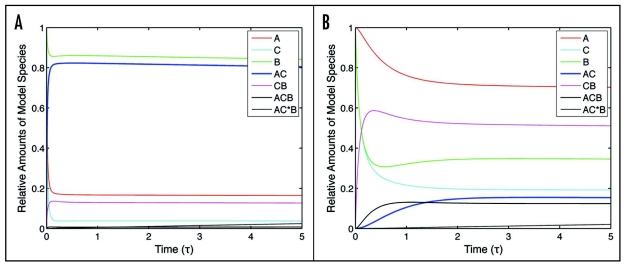
Transient plots of model species toward dynamic steady-state values. (A) One example set of 3T3 parameter values [Θ_AC = 100, Θ_actin = 10, Θ_CB = 10, Θ_base = 0.001, κ_actin = 1, κ_CB = 1, κ_base = 10, σΘ_f = 100] (B) One example set of CHO parameter values [Θ_AC = 0.01, Θ_actin = 1, Θ_CB = 10, Θ_base = 1, κ_actin = 1, κ_CB = 1, κ_base = 1, σΘ_f = 1].

Figure 3.

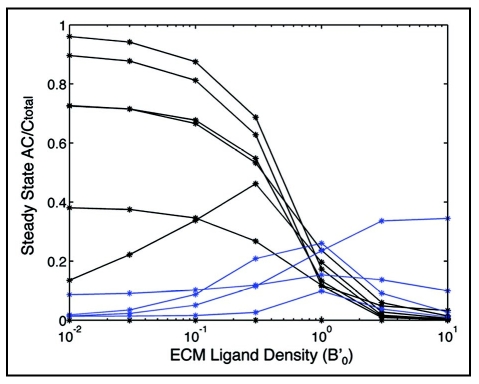
Fraction of connector protein(s) associated with rearward-moving actin filaments, for example sets of CHO parameter values, as it depends on substratum matrix protein level. Blue curves represent parameter sets in which rearward-moving connector protein(s) increases with increasing matrix protein level.

Table 2.

Parameter value ranges used in model simulations

Parameter	CHO	3T3
ΘAC	10−3 to 10−1	10−3 to 103
Θactin	1 to 103	10−3 to 103
ΘCB	10−1 to 103	10−3 to 103
Θbase	10−3 to 102	10−3 to 1
κactin (unloaded)	10−1 to 10	1−1 to 10
κbase (unloaded)	1 to 10	1−1 to 10
κCB	1−1 to 10	1−1 to 10
σΘf	1 to 102	1 to 102

For all subsequent model simulations, multiple parameter value sets were selected from these constrained cell type-associated sub-sets. This methodology did indeed generate diverse cell type-associated parameter value sets representing CHO behavior versus 3T3 behavior (see Table 2). 3T3 sets showed very little restriction in the range of possible values for each parameter. There were parameter sets that met all the 3T3 conditions with values in the entire range of 10⁻³ to 10³ for Θ_AC, Θ_actin and Θ_CB. The specific combination of parameter values was what determined the behavior. One exception was the specific formation rate constant of ACB from AC and B (Θ_base), which was always less than or equal to one for selected 3T3 sets. This is as we expect—in order for 3T3 sets to have a high level of AC, the rate at which AC is turned into ACB must be low. Parameter sets selected to meet CHO conditions showed less of a range of possible values for each parameter than the 3T3 sets. For CHO sets, the value for specific formation rate constant of AC from A and C (Θ_AC), were always in the low end of the sampled range, and values for the specific formation rate constant of ACB from CB and A (Θ_actin) were always in the high end of the sampled range. The possible ranges for Θ_CB and Θ_base were also slightly reduced for CHO sets. The reduction of possible parameter values for CHO sets seems to have arisen from the constraint of increasing levels of actin-associated connector complexes with increasing levels of initial B. The dissociation rate constants (κ_actin, κ_base and κ_CB), and the formation rate of AC*B (Θ_f), all show comparable ranges for both CHO and 3T3.

Effect of force on steady state actin-ECM linkages.

A central objective of this work is to examine the net effect of cell-generated contractile force on the number of linkages at dynamic steady-state. We examined values of F₀ between 10⁻¹³ and 10⁻⁹ N. For each validated parameter set, the system of model equations were numerically integrated over a long time at different values of initial force, F₀, to yield steady-state values of model species. We also calculate the steady-state value of the force being exerted on the linkages, which can be different from F₀ because of the feedback operating within the system.

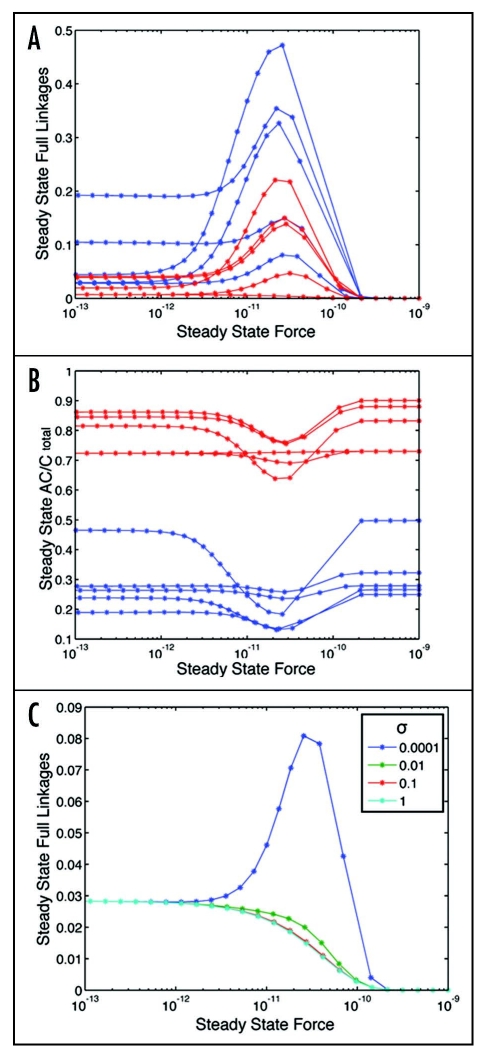
The number of full linkages at steady state is defined as the sum of the values of ACB' and AC*B'. The dependence of the number of steady-state linkages on the steady-state force per linkage is generally biphasic, as illustrated in Figure 4A for several example parameter sets of each cell type. This behavior is not surprising, because of the opposing effects of force on the linkages: force tends to promote linkage dissociation, due to the input of stress-induced energy, but at the same time force-induced adhesion strengthening renders this force-related dissociation more difficult to achieve. The dissociation effect is predicted to dominate at high force levels whereas the strengthening effect is predicted to dominate at low force levels. CHO parameter value sets often yield higher levels of steady-state full linkages than 3T3 parameter value sets. This derives from the selection of 3T3 sets to give 0.6–0.8 AC/C_total, which limits the amount of C that can make ACB or AC*B, whereas CHO parameter sets were selected to give 0.1–0.3 AC/C_total, which leaves more C available to form ACB or AC*B. The number of steady-stage linkages, produced here by our mathematical model, bears potentially alternative interpretations at this point. This quantity could represent the number of distinct adhesion sites in the lamellipodal region under consideration, or could represent the average size of these adhesion sites, or some combination thereof. Discriminating between these alternatives will require a more complicated model, incorporating additional species (e.g., identified aggregate sizes) and/or spatial distributions and/or stochastic effects. These considerations are worthy of further studies, motivated by the initial findings we obtain with our foundational model here.

Figure 4.

(A) Steady-state number of integrin/actin linkages as a function of force, for 3T3 (red) and CHO (blue) parameter value sets. (B) Steady-state fraction of connector protein associated with rearward-moving actin filaments as a function of force, for 3T3 (red) and CHO (blue) parameter value sets. (C) Effect of linkage reinforcement arising from adhesion-strengthening, with the magnitude of reinforcement as σ decreases from 1 to 0, on steady-state number of integrin/actin linkages for range of force levels. [Θ_AC = 0.01, Θ_actin = 10, Θ_CB = 1, Θ_base = 0.1, κ_actin = 0.1, κ_CB = 10, κ_base = 10, σΘ_f = 10].

Effect of force on steady-state correlation between connector proteins and actin.

We next examined the effect of force per linkage on the AC/C_total quantity, which had been used to select valid parameter estimates. Figure 4B shows the effect of force on this quantity for several example parameter sets of each cell type. For forces near 5 × 10⁻¹¹ N, 3T3 parameter value sets all fall within 0.6 to 0.8 AC/C_total while CHO parameter value sets fall within 0.1 to 0.3 AC/C_total, as this was one of the selection criteria that generated these sets. Most parameter value sets show the behavior of AC/C_total remaining fairly level over a broad range of F₀ around this base value. Some sets do yield values of AC/C_total that are changed from their target levels significantly; for some of the CHO parameter sets a dramatic increase in linkage-associated actin is predicted at high force levels.

Another interesting effect to examine is that of the linkage reinforcement due to adhesion strengthening, characterized by the value of σ in the dissociation rate constant for AC*B. Figure 4C shows that as σ approaches a value of 0 (very little dissociation of AC*B) from a value of 1 (dissociation rates of ACB and AC*B are equivalent), there arises a range of initial overall force values over which the total number of full linkages at steady state can increase substantially. This effect yields a biphasic behavior where the number of full linkages increases with force at low levels but decreases at high levels. The magnitude of this augmentation and reduction is amplified as σ becomes small.

Turnover rate increases with increasing force.

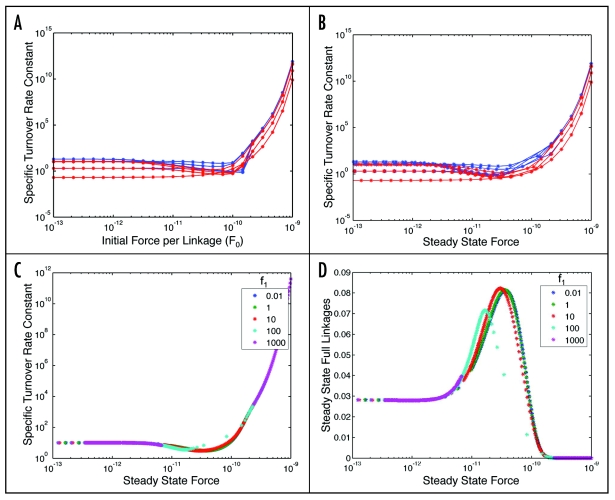
With an increased force applied to linkages, one might expect the linkages to become more dynamic and turn over more rapidly. Indeed, some experimental studies have shown that highly dynamic adhesions at the leading edge of cells exert higher traction forces than less dynamic adhesions.^36,37 Figure 5A and B show the predicted effect of force per linkage on specific turnover rate constant for several example parameter sets from each cell type; Figure 5A offers plots with respect to initial force, F₀, whereas Figure 5B provides plots with respect to steady-state force, exploring F₀ in the range 10⁻¹³ to 10⁻⁹ N. The specific turnover rate constant is found to be fairly level for steady-state forcesless than 10⁻¹¹ N, but to potentially increase sharply for values above this. The values of specific turnover rate constant for CHO parameter sets are generally higher than those for 3T3 parameter value sets, as expected from using this comparison as one of the parameter value set selection criteria.

Figure 5.

Specific turnover rate constant for integrin/actin linkages as a function of force, for 3T3 (red) and CHO (blue) parameter value sets. (A) plotted versus initial force, for f₁ = 10. (B) plotted versus steady-state force, also for f₁ = 10. (C) range of f₁ values. [Θ_AC = 0.01, Θ_actin = 10, Θ_CB = 1, Θ_base = 0.1, κ_actin = 0.1, κ_CB = 10, κ_base = 10, σΘ_f = 10]. (D) Steady state number of integrin/actin linkages as a function of force over a range of f₁ values. [Θ_AC = 0.01, Θ_actin = 10, Θ_CB = 1, Θ_base = 0.1, κ_actin = 0.1, κ_CB = 10, κ_base = 10, σΘ_f = 10].

An important effect to explore is that of paxillin-mediated myosin activity feedback, characterized by the value of f₁, on the relationship between force per linkage and specific turnover rate as shown in Figure 5C. At high values of f₁ (100 and above) the trend for a specific parameter set stays the same, but the steady-state forces are always low or high because of the feedback effects. Therefore, the values of specific turnover rate constant corresponding to intermediate steady-state forces are not observed. Similar behavior is predicted for the number of full linkages (Fig. 5D).

Turnover rate decreases as matrix-substrate density increases.

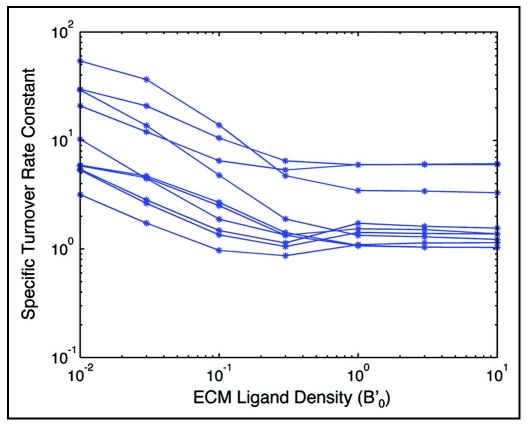
Another condition critically influencing cell migration is the density of the integrin adhesion ligand. In culture, for example, the density of fibronectin on the substrate has a large effect on cell migration.^21,38 Our model can predict the effect of different ECM ligand densities on factors essential to cell migration, such as specific turnover rate constant. In our model there is no species explicitly representing adhesion ligand, but the B species represents integrin receptors bound to a ligand and therefore encompasses ligand concentration as an increase in ligand concentration correlates to an increase in B. Figure 6 shows the relationship between specific turnover rate and the initial value of B' for 10 example CHO parameter sets. Each point was generated by numerically integrating the model equations over a long time with a different initial value of B'. F₀ was set to 5 × 10⁻¹¹ N, and f₁ was set to 10. At low values of initial B', the specific turnover rate constant of all parameter sets decreases sharply and levels off at values of initial B' of around 1. As increasing B' is analogous to increasing substrate ligand concentration experimentally, this result indicates that increasing substrate ligand concentration decreases the adhesion turnover rate.

Figure 6.

Specific turnover rate constant for integrin/actin linkages as a function of substratum matrix protein level (represented by B', normalized number of integrin/matrix bonds) for CHO parameter value sets.

Effect of paxillin-mediated myosin activity modulation on turnover rate.

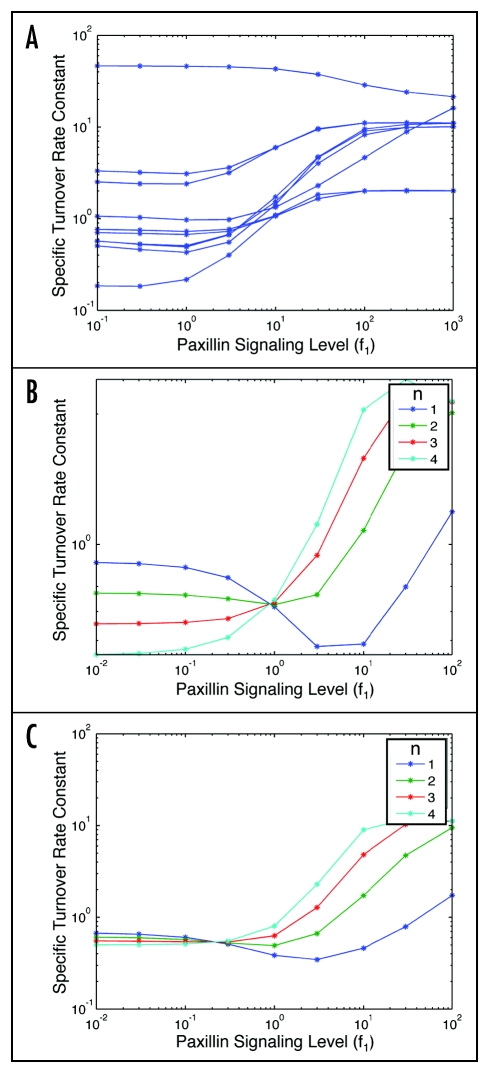
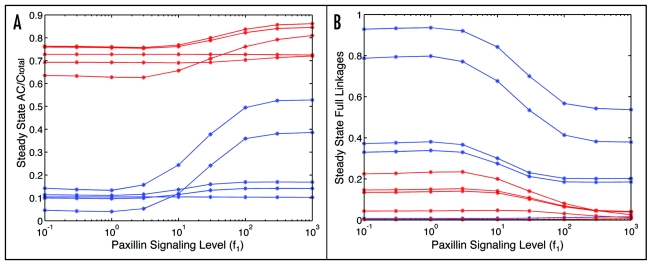
We were prompted by an additional, intriguing experimental literature report to analyze the effect of positive force feedback on specific turnover rate. Nayal²³ and Zaidel-Bar²⁵ have identified a regulatory mechanism of adhesion turnover involving phosphorylation of paxillin on any of several sites. Phosphorylation on any of these sites induces rapid adhesion turnover and interrupts adhesion maturation. One of these phosphorylations, at least, involves a feedback loop as p21-activated kinase (PAK) is responsible for the phosphorylation but also lies downstream in the pathway along with Rac and myosin-II activity.²³ In our model here we accordingly represent the paxillin-mediated effects in terms of a coefficient, f₁, characterizing the degree of negative modulation of myosin-based force (F) by signaling arising from adhesion linkages. Figure 7A plots the specific turnover rate constant versus f₁ for CHO cell parameter sets, and shows that for the majority of these sets the turnover increases with extent of paxillin-mediated myosin activity reduction, consistent with the Nayal²³ experimental observations. Of all the model parameters we explored with particular reference to this phenomenon, the force-dependency exponent for adhesion-strengthening (n) was noted to be especially significant. Figure 7B and C illustrate the effect of n on the behavior found in Figure 7A, for two example CHO parameter sets. Typically, for n > 1 the specific turnover rate constant is found to increase with increased f₁, whereas for n = 1 this effect is biphasic. It is conceivable that n = 1 remains a realistic value for this process, and that the f₁ value must reside on the higher end of the range depicted here in the CHO cells studied by Nayal.²³ We could, of course, use this paxillin mutant study to further constrain the feasible CHO cell type parameter sets in future work. Given the consistency of our parameter sets in current form with the comprehensive scope of experimental observations to date, however, two additional a priori predictions can be generated from the model as shown in Figure 8A and B. These plots show that we might expect the proportion of actin-associated connector proteins to increase and the number of full linkages to decrease, for stronger paxillin-mediated downmodulation of myosin-II activity.

Figure 7.

Effects of paxillin-mediated downmodulation of Myosin-II activity, increasing with f₁. (A) Steady-state turnover rate constant, n = 2. (B) Steadystate turnover rate constant, comparison of n = 1, 2, 3 and 4, for example CHO parameter sets. [Θ_AC = 0.1, Θ_actin = 1, Θ_CB = 1000, Θ_base = 0.1, κ_actin = 1, κ_CB = 1, κ_base = 1, σΘ_f = 1]. (C) A different example CHO parameter set [Θ_AC = 0.1, Θ_actin = 100, Θ_CB = 10, Θ_base = 1, κ_actin = 10, κ_CB = 0.1, κ_base = 1, σΘ_f = 10].

Figure 8.

Effects of paxillin-mediated downmodulation of myosin-II activity, increasing with f₁. (A) Steady-state number of full linkages. (B) Steady-state fraction of connector proteins associated with actin.

Discussion

The general objective of our modeling study here was to explore the behavior of integrin-actin linkage dynamics in the lamellipodal region of spreading or migrating cells, in terms of quantitative biochemical and biophysical properties of protein complexes that connect the cell force generating-cytoskeleton and the force-transmitting cell/substratum adhesion bonds. A more particular goal was to try to interpret recent experimental literature observations^22,23 of this behavior with respect to the ‘clutch’ hypothesis originally proposed by Mitchison and Kirschner.²⁰ Essentially, a plethora of cytoskeleton-associated proteins (including α-actinin, vinculin, talin, zyxin, paxillin and FAK among others) associate dynamically with polymerized actin, integrin-matrix bonds, and/or each other to differential degrees, serving to establish an actin-“connector”-integrin linkage that translates myosin-generated force into lamellipod retraction or stable adhesion (enabling subsequent cell body translocation)^24,25 depending on numerous parameters characterizing the myriad biomolecular interactions. While many interesting questions can be asked about this fascinating system, we have focused on a fairly narrow issue: what is the net outcome of the competing negative (force-enhanced dissociation) and positive (force-induced strengthening) influences of myosin-generated force acting on the actin-connector-integrin ‘clutch’, and how do key molecular properties govern this?

Because of the complexity inherent in this system, and the great uncertainty regarding precise mechanisms of the various individual molecular interactions, we chose to construct a highly idealized model with only three major components: actin polymers, integrin-matrix bonds and “connector” proteins. Thus, from the start we recognize that we do not incorporate specific information corresponding to any particular connector protein, nor the intricate detail surely present in the combinatorial interactions among them. Nonetheless, we submit that casting the critical concepts involved in this system in explicit mathematical formalism should offer a useful foundation for efforts by many laboratories in building larger, more sophisticated edifices to study one facet or another in more depth.

A feature of our approach that is crucial to note is our inability even for this greatly simplified model to ascertain unique estimates for most of the still-numerous parameter values, from either previous literature or direct experimental curve-fitting. Instead, we follow a procedure we have recently found useful in an analogous study on caspase dynamics in apoptotic cell death:³⁴ we used relevant experimental observations (in the present case, from the Brown²¹ and Hu²² studies of our central focus) to constrain parameter value sets, from within broad ranges taken as “reasonable” from previous literature, to those bearing resulting model simulation behaviors consistent with the observations. By doing so, we are able to reject more than 95% of the parameter value sets selected randomly from within the “reasonable” ranges, finding ∼50–100 feasible sets for each of two cell types (NIH3T3 and CHO) for which the Brown²¹ report provides quantitative data. Each of these “consistent” sets yields model simulation results consistent with experimentally observed behavior, but at the same time can produce diverse results for behaviors outside the constraining observations. (The unconstrained extrapolating results, obviously, offer a priori predictions for future experimental studies). One notion for interpretation of the various consistent sets is as possible alternative sets for the relevant cell population on average. A contrasting notion is that each, or at least some, of the various consistent sets could represent individual cells within the population, enabling different cells to exhibit non-identical behaviors—i.e., cell-to-cell “heterogeneity.”

We will not re-summarize all our findings described in the Results section again here, but will emphasize two especially interesting aspects. One is the potential for biphasic behavior in the dynamics of the actin-connector-integrin ‘clutch’, arising from the opposing negative and positive influences of myosin-generated force on the linkages (see Figs. 4, 5 and 7). Thus, the effect of modulating myosin force-related processes on the net stability-versus-lability of actin-integrin linkages is not straightforward to predict; i.e., a given molecular intervention (e.g., addition of an pharmacological inhibitor, or expression of a genetically-mutated version of a component) can in one cell type, or under one substratum condition, yield increased linkage stability whereas in another it would yield increased linkage lability. It has been found experimentally that the smallest adhesions form in dendritic actin and are tension independent.²³ During pauses of protrusion, tension increases and the adhesions grow and elongate; this occurs out of the dendritic actin and corresponds to a change to an association with actin filament bundles and myosin sensitivity. The resulting adhesions, therefore, grow in response to myosin-mediated stresses at the front of the cell, and consequently turn over more slowly.¹³ With increasing tension, these begin to slide and then disassemble. Thus, our model shows that we can expect to find a basic stress-induced effect that mediates adhesion site growth and another, related to clutch engagement properties, that mediates disassembly.

Related to this insight is the second point worth special emphasis in context of our model results: the effects of the paxillin mutants^23,25 and PAK mutations.²³ In our model, a greater extent of PAK-mediated phosphorylation of paxillin on S237 is represented by a larger value of f₁, diminishing myosin activity to a further degree. We are able to reproduce the increased rate of actin-integrin linkage turnover with most of the consistent CHO parameter value sets (see Fig. 7A), in accord with the Nayal observations. However, we found that successful comparison between model and experiment is especially sensitive to the value of n, the exponent characterizing the force dependence of myosin-mediated adhesion strengthening (see Fig. 7B and C). Accordingly, constraining our model predictions by the paxillin mutant observations could predict an important but currently unknown feature of adhesion strengthening.

Additional experimental studies can be envisioned for further testing of cell behavior associated with predictions from this model. The behavior predicted in Figure 8, for instance, could be examined for the current paxillin mutants, and mutation and/or knockdown approaches could be extended to other important connector components such as FAK and talin. Talin, in particular, could be an especially interesting component to probe due to its implication in adhesion strengthening,^38,39 which is incorporated into our model by the rate of creation of the reinforced AC*B. In these kinds of studies one could modulate key parameters in our model such as f₁, σ, force per linkage, and B'₀ (ECM ligand density), alone or in combination. Thus, we hope for continuing advance in this area of cell migration, with initial model foundation here serving usefully as a base for ongoing studies.

Methods

Model development.

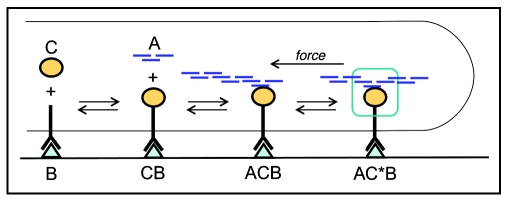
In the model, the molecules involved in forming linkages between the ECM and actin filaments are idealized to three key types of species: A, B and C; these species and their interactions are represented in Figure 1. Actin filaments are denoted A. B represents an integrin receptor bound to a ligand on the ECM. Following previous modeling efforts of this kind,^30,31 we simplify the system by assuming that total cell receptors and ECM ligand are in excess of the number of bonds formed, in order to omit conservation equations and associated nonlinearities for those species. C represents a linker complex approximating the many molecules known to bind to actin and/or integrin receptors in adhesions such as paxillin, talin, FAK, zyxin and vinculin. The three model species can combine to form complexes of actin and connector (AC), connector and base (CB), or a full link of actin, connector and base (ACB). A full linkage complex can also be reinforced through recruitment of reinforcing proteins leading to a strengthened complex (AC*B). Both types of full linkages, ACB and AC*B, can be dissociated into AC or CB, and likewise AC and CB can return to their respective non-complexed species.

Figure 1.

Schematic illustration of basis for mathematical model.

The time-dependent concentration of each of the model species in time is described by a differential equation containing terms for the formation and dissociation of the relevant species; these equations can be integrated to find concentrations of model species at steady state:

$$\begin{array}{l}\frac{\text{d[A]}}{\text{dt}}={\text{k}}_{\text{offAC}}[\text{AC}]-{\text{k}}_{\text{onAC}}[\text{A][C}]+{\text{k}}_{\text{offactin}}[\text{ABC}]-{\text{k}}_{\text{onactin}}[\text{CB}][\text{A}]+{\text{k}}_{\text{offA}}[\text{AC*B}]\\ \frac{\text{d[B]}}{\text{dt}}={\text{k}}_{\text{offCB}}[\text{CB}]-{\text{k}}_{\text{onCB}}[\text{C][B}]+{\text{k}}_{\text{offbase}}[\text{ACB}]-{\text{k}}_{\text{onbase}}[\text{B}][\text{AC}]+{\text{k}}_{\text{offB}}[\text{AC*B}]\\ \frac{\text{d[C]}}{\text{dt}}={\text{k}}_{\text{offAC}}[\text{AC}]-{\text{k}}_{\text{onAC}}[\text{A][C}]+{\text{k}}_{\text{offCB}}[\text{CB}]-{\text{k}}_{\text{onCB}}[\text{C}][\text{B}]\\ \frac{\text{d[AC]}}{\text{dt}}={\text{k}}_{\text{onAC}}[\text{A][C}]-{\text{k}}_{\text{offAC}}[\text{AC}]-{\text{k}}_{\text{onbase}}[\text{AC][B}]+{\text{k}}_{\text{offbase}}[\text{ACB}]+{\text{k}}_{\text{offB}}[\text{AC*B}]\\ \frac{\text{d[CB]}}{\text{dt}}={\text{k}}_{\text{onCB}}[\text{C][B}]-{\text{k}}_{\text{offCB}}[\text{CB}]+{\text{k}}_{\text{offactin}}[\text{ACB}]-{\text{k}}_{\text{onactin}}[\text{CB}][\text{A}]+{\text{k}}_{\text{offA}}[\text{AC*B}]\\ \frac{\text{d[ACB]}}{\text{dt}}={\text{k}}_{\text{onbase}}[\text{AC}][\text{B}]-{\text{k}}_{\text{offbase}}[\text{ACB}]+{\text{k}}_{\text{onactin}}[\text{CB][A}]-{\text{k}}_{\text{offactin}}[\text{ACB}]-{\text{k}}_{\text{f}}[\text{ACB}]\\ \frac{\text{d[AC*B]}}{\text{dt}}={\text{k}}_{\text{f}}[\text{ACB}]-{\text{k}}_{\text{offA}}[\text{AC*B}]-{\text{k}}_{\text{offB}}[\text{AC*B}]\end{array}$$ (1)

The effects of force on linkages are incorporated in the following manner. First, forces can affect linkages negatively by enhancing their dissociation. We assume that all bonds feel the effect of force equally and that the force increases the dissociation rate constants (k_offactin, k_offbase, k_offA, k_offB) as originally proposed by Bell:³²

$$k_{off}=k_{off}^{\text{0}}\exp \left(\frac{\gamma F}{k_{b}T}\right)$$ (2)

γ is the characteristic length of the binding c_left, F is the force per bond, k_b is the Boltzmann constant, and T is the absolute temperature. It is theoretically conceivable that catch bonds, for which the bond strength increases upon increasing force,³³ could be present in this system. However, previous evidence for catch bonds has been obtained mainly for cell/substratum interactions, centrally via selectin receptors, we will not consider their involvement in this current model.

Positive force feedback is incorporated based on the premise that signaling induced by myosin-mediated stress on integrin bonds leads to strengthening of the actin-ECM linkage. The forward reaction rate for ACB to the reinforced AC*B complex depends on the ACB concentration and contains a force term, such that the formation of AC*B ceases in the absence of myosin-mediated stress:

$$k_f={\sigma }_{kf}[ACB]{\left(\frac{\gamma F}{k_{b}T}\right)}^n$$ (3)

This expression represents the net effect of force-induced signals to enhance protein-protein docking interactions within the linkage complex. This effect has not been characterized quantitatively, so we employ a phenomenologically plausible form with first-order dependence on the number of bonds that are stressed by myosin-mediated force; the force effect might likely be linear, with n = 1 in this expression, but we permit more generality because of the lack of information concerning this process. σ_kf is a factor that characterizes the magnitude of force-induced complex reinforcement. The AC*B complex dissociates into AC or CB, but at a much lower rate than ACB dissociates. In principle there could be a purely biochemical step dissociating AC*B to ACB with rate constant k_r, but we will assume that this process is very slow on the time scale we are considering. The strengthened linkage can, however, still be broken in a force-induced manner, with the corresponding alternative dissociation rates for the break-up of AC*B taking the following form:

$$k_{offA}=\sigma k_{offactin}$$ (4a)

$$k_{offB}=\sigma k_{offbase}$$ (4b)

σ is a factor less than unity that characterizes how much stronger the complex is than the normal ACB complex. For values of σ near 1, the outputs are similar to a scenario without positive feedback. For values of σ that are much less than 1, the effect of positive feedback is more pronounced.

The myosin-mediated force on each linkage is also now appreciated to be negatively modulated by a feedback loop operating through linkage-mediated PAK phosphorylation of paxillin, leading to increased PAK-mediated inhibition of myosin activity. This is incorporated using a modulatory term diminishing F in manner dependent on the number of linkages:

$$F=F_0\left[1-\frac{f_1\left([ACB]+[AC*B]\right)}{1+f_1\left([ACB]+[AC*B]\right)}\right]$$ (5)

F₀ is the constitutive myosin-mediated force, and f₁ characterizes the modulatory PAK-Pax feedback loop. The denominator term yields saturation of the feedback loop effect in order to prohibit a negative force result, which obviously would be physically unrealistic.

Our model neglects receptor endocytosis and formation, secretion of ECM ligands and integrin and cytoskeleton transport. We also assume that each linkage is a single bond and not a cluster of many cross-linked complexes.

Model analysis.

The model equations can be scaled using the following dimensionless parameters:

$$\begin{array}{l}\begin{array}{ll}\tau ={\text{k}}_{\text{offAC}}\text{t}\hfill & {\Theta }_{\text{AC}}=({\text{k}}_{\text{onAC}}/{\text{k}}_{\text{offAC}}){[\text{A}]}_{\text{T}}\hfill \\ \text{A'}={\text{[A]/[A]}}_{\text{T}}\hfill & {\Theta }_{\text{CB}}=({\text{k}}_{\text{onCB}}/{\text{k}}_{\text{offAC}}){[\text{A}]}_{\text{T}}\hfill \\ \text{B'}={\text{[B]/[A]}}_{\text{T}}\hfill & {\Theta }_{\text{actin}}=({\text{k}}_{\text{onactin}}/{\text{k}}_{\text{offAC}}){[\text{A}]}_{\text{T}}\hfill \\ \text{C'}={\text{[C]/[A]}}_{\text{T}}\hfill & {\Theta }_{\text{base}}=({\text{k}}_{\text{onbase}}/{\text{k}}_{\text{offAC}}){[\text{A}]}_{\text{T}}\hfill \\ \text{AC'}={\text{[AC]/[A]}}_{\text{T}}\hfill & {\kappa }_{\text{actin}}={\text{k}}_{\text{offactin}}{}^0/{\text{k}}_{\text{offAC}}\exp (\gamma {\text{F/k}}_{\text{b}}\text{T})\hfill \\ \text{CB'}={\text{[CB]/[A]}}_{\text{T}}\hfill & {\kappa }_{\text{base}}={\text{k}}_{\text{offbase}}{}^0/{\text{k}}_{\text{offAC}}\exp (\gamma {\text{F/k}}_{\text{b}}\text{T})\hfill \\ \text{ACB'}={\text{[ACB]/[A]}}_{\text{T}}\hfill & {\kappa }_{\text{CB}}={\text{k}}_{\text{offCB}}/{\text{k}}_{\text{offAC}}\hfill \\ \text{AC*B'}=[\text{AC*B}]/{[\text{A}]}_{\text{T}}\hfill & {\kappa }_{\text{2A}}=\sigma {\text{k}}_{\text{offactin}}{}^0/{\text{k}}_{\text{offAC}}\exp (\gamma {\text{F/k}}_{\text{b}}\text{T})\hfill \\ {\Theta }_{\text{f}}={\sigma }_{\Theta \text{f}}[\text{ACB'}]{(\gamma {\text{F/k}}_{\text{b}}\text{T})}^{\text{n}}\hfill & {\kappa }_{\text{2B}}=\sigma {\text{k}}_{\text{offbase}}{}^0/{\text{k}}_{\text{offAC}}\exp (\gamma {\text{F/k}}_{\text{b}}\text{T})\hfill \end{array}\\ {\text{[A]}}_{\text{T}}\text{ is the total concentration of actin in the system.}\\ \text{These yield the following set of dimensionless equations:}\\ \frac{d\text{[A']}}{d\tau }=[\text{AC'}]-{\Theta }_{\text{AC}}[\text{A'][C'}]+{\kappa }_{\text{actin}}[\text{ACB'}]-{\Theta }_{\text{actin}}[\text{CB'}][\text{A'}]+{\kappa }_{\text{2A}}[\text{AC*B'}]\\ \frac{d\text{[B']}}{d\tau }={\kappa }_{\text{CB}}[\text{CB'}]-{\Theta }_{\text{CB}}[\text{C'][B'}]+{\kappa }_{\text{base}}[\text{ACB'}]-{\Theta }_{\text{base}}[\text{B'}][\text{AC'}]+{\kappa }_{\text{2B}}[\text{AC*B'}]\\ \frac{d\text{[C']}}{d\tau }=[\text{AC'}]-{\Theta }_{\text{AC}}[\text{A'][C'}]+{\kappa }_{\text{CB}}[\text{CB'}]-{\Theta }_{\text{CB}}[\text{C'}][\text{B'}]\\ \frac{d\text{[AC']}}{d\tau }={\Theta }_{\text{AC}}[\text{A'][C'}]-[\text{AC'}]-{\Theta }_{\text{base}}[\text{AC'][B'}]+{\kappa }_{\text{base}}[\text{ACB'}]+{\kappa }_{\text{2B}}[\text{AC*B'}]\\ \frac{d\text{[CB']}}{d\tau }={\Theta }_{\text{CB}}[\text{C'}][\text{B'}]-{\kappa }_{\text{CB}}[\text{CB'}]+{\kappa }_{\text{actin}}[\text{ACB'}]-{\Theta }_{\text{actin}}[\text{CB'}][\text{A'}]+{\kappa }_{\text{2A}}[\text{AC*B'}]\\ \frac{d\text{[ACB']}}{d\tau }={\Theta }_{\text{base}}[\text{AC'}][\text{B'}]-{\kappa }_{\text{base}}[\text{ACB'}]+{\Theta }_{\text{actin}}[\text{CB'}][\text{A}\text{'}]-{\kappa }_{\text{actin}}[\text{ACB'}]-{\Theta }_{\text{f}}[\text{ACB'}]\\ \frac{d\text{[AC*B']}}{d\tau }={\Theta }_{\text{f}}[\text{ACB'}]-{\kappa }_{\text{2A}}[\text{AC*B'}]-{\kappa }_{\text{2B}}[\text{AC*B'}]\end{array}$$ (6)

This set of equations was numerically integrated using MATLAB (The MathWorks, Norwich, MA). Initial conditions were set to one for A', B' and C', and zero for the rest of the species. Steady-state values were determined by integrating the system for reasonably long times (tau of 80 or 90—all species no longer changing). Explicit Runge-Kutta integration methods were used to numerically integrate the equations. When this became computationally intensive, a multi-step solver based on the numerical differentiation formulas was used. Figure 2A and B illustrate sample transient profiles of the normalized concentrations of each of the model species with respect to τ, for one example 3T3 cell parameter value set and one example CHO cell parameter value set, respectively. These example plots show that the system can at least approach near steady-state behavior on the time scale of τ ∼ 1 for both cell types; this is a typical result for the vast majority of feasible parameter value sets. Thus, steady-state results should generally have at least approximate utility for insight as long as t > (k_offAC)⁻¹, which is on the order of a few minutes for most of the feasible parameter value sets and thus in the realm of lamellipod extension and retraction time scales for fibroblast migration. Accordingly, we will use steady-state results to describe the parameter effects in our system.

Parameter value constraints.

Plausible ranges of estimates for most model parameters were found in the literature (see Table 1), and we reduced the breadth of these ranges by undertaking computational search for parameter combinations required to yield model outputs that match germane previously published experimental results. The initial force per linkage (F₀) was set at either 5 × 10⁻¹¹ or 5 × 10⁻¹² N. Roughly similar results were found for both, but most behaviors were more consistent with experimental observations for 5 × 10⁻¹¹ so our figures are plotted for this value (Suppl. Fig. can be provided for the 5 × 10⁻¹² value). We examined model behavior for various values of n (1–4), the force-dependence exponent for myosin activity modulation, and chose the value n = 2 because it represents the mildest force-dependence that consistently yields an increase in adhesion turnover rate constant with increasing paxillin-mediated signaling in accord with the experimental findings of Nayal²³ (as will be discussed later in the Results section).

The four theta parameters (Θ_AC, Θ_actin, Θ_CB, Θ_base) were each chosen randomly in the range from 10⁻³ to 10³ at order of magnitude intervals. The preexponential coefficients for the three kappa parameters (κ_actin, κ_CB, κ_base) were similarly sampled randomly in the range of 0.1 to 10, and the remaining σ_Θf parameter was sampled in the range of 1 to 100. For the purpose of parameter selection, f₁ was set to 10, which yields essentially complete myosin activity modulation. Within these ranges, approximately 200,000 potential combinations of parameter value sets exist; a random sampling of sets was conducted from among these for simulation purposes. (κ_2A and κ_2B could be specified in terms of κ_actin and κ_base, with value chosen to be σ = 0.0001 so it was unnecessary to randomly sample these parameters). Parameter value sets yielding steady-state model behavior consistent with experimental observations were determined (see Table 2) by the following procedure.

Observations of fluorescently labeled focal adhesion proteins have shown that connector proteins at the leading edge of cells are bound to actin at varying levels across different cell types and ECM ligand concentrations. Brown²¹ found that the connector proteins talin, vinculin, paxillin and FAK are bound to actin filaments about 70% of the time and that CHO cells on low concentrations of fibronectin had connector proteins associated with actin less than 30% of the time and the correlation of these proteins and actin increased on a higher concentrations of fibronectin. This result corresponds to the model output of the amount of total C found in the AC complex.

This is:

• AC/C_total = AC'/(C'+AC'+CB'+ACB'+AC*B')

Parameter sets were identified with the 3T3 condition when the steady-state value of AC/C_total was between 0.6 and 0.8. CHO parameter sets, in contrast, were identified by first selecting sets that met the condition of steady state AC/C_total between 0.1 and 0.3. All sets that did not meet these conditions were rejected for further study. Next, the remaining CHO parameter sets were screened for sets that showed increasing values for AC/C_total with increasing initial values of B' (a positive difference between AC/C_total at initial B' = 0.01 and AC/C_total at initial B' = 10). Figure 3 illustrates the varying behavior of CHO parameter sets with respect to increasing initial B', demonstrating that some sets were consistent with the experimental observation whereas some are not; we rejected for further study those that were not.

Next, both conditions (CHO and 3T3) were screened for appropriate turnover rate behavior using the surviving parameter sets. The rate at which linkages form and break apart, or turnover rate, is an important variable in cell migration. In our model, we defined the specific turnover rate constant as the rate of formation of full links (which is equal to the rate of dissociation at steady state) divided by the total number of full links:

$$\text{Specific turnover rate constant = }\frac{{\Theta }_{base}[AC\text{'}][B\text{'}]+{\Theta }_{actin}[CB\text{'}][B\text{'}]}{[ACB\text{'}]+[AC*B\text{'}]}$$

Extremely motile cells exhibit adhesions that turn over rapidly, whereas slower moving cells have adhesions that turn over less rapidly.³⁴ Therefore, the CHO parameter sets should exhibit the behavior of high specific turnover rate constants while the 3T3 parameter sets should have lower specific turnover rate constants. The 3T3 parameter sets were screened for values of specific turnover rate constants of less than 5 and CHO parameter sets were constrained likewise to specific turnover rate constants of greater than 1; all sets that conflicted with these requirements were rejected for further study.

Thus, we have constrained our parameter sets with multiple conditions, separately for the 3T3 cell type model and the CHO cell type model. For both cell type models, criteria we applied concerning: (a) the proportion of connector proteins associated with actin and (b) the turnover rate constants. For the CHO cell type model, an additional criterion was applied, that of increasing proportion of actin-associated connector proteins as the number of integrin/ECM bonds is increased. The combination of these conditions led to rejection of more than 95% of the parameter sets sampled randomly from within the original parameter value ranges.