Cytokine-induced Signaling Networks Prioritize Dynamic Range over Signal Strength

Abstract

Signaling networks respond to diverse stimuli, but how the state of the signaling network is relayed to downstream cellular responses is unclear. We modeled how incremental activation of signaling molecules is transmitted to control apoptosis as a function of signal strength and dynamic range. A linear signal input-response output relationship, with signaling dynamic range uniformly distributed across activation states, most accurately predicted cellular responses. When nonlinearized signals relay network activation to apoptosis, we observe catastrophic, stimulus-specific prediction failures. We develop a general computational technique, “model-breakpoint analysis”, to analyze the mechanism of these failures, identifying new time- and stimulus-specific roles for Akt, ERK and MK2 kinase activity, which were experimentally verified. We further show that hyperactive and hypoactive MK2 alleles provide stronger and weaker levels of signaling, respectively; however both reduce apoptosis compared to wildtype MK2 because of reduced dynamic range. Dynamic range is rarely measured in signal-transduction studies but our experiments based on model-breakpoint analysis indicate that it may be a greater determinant of cell fate than measured signal strength.

INTRODUCTION

Changes in cell behavior are determined by an interconnected set of proteins that actively transmits signaling information as a network (Irish et al., 2004; Jordan et al., 2000; Pawson, 2004). Modifications of the posttranslational state, enzymatic activity, or total level of key proteins can act as “molecular signals” that are relayed and interpreted to control cell function. The challenge of identifying which observed molecular signals determine a cell response is complicated, because many signaling proteins appear to send mixed or opposing messages. For example, the transcription factor nuclear factor-κB (NF-κB) is widely regarded as a prosurvival protein because nuclear relocalization and DNA binding upregulate expression of apoptosis inhibitors such as c-IAP2, Bcl-x_L, and c-FLIP (Karin and Lin, 2002). In response to DNA-damaging agents, however, nuclear NF-κB can promote cell death by recruiting histone deacetylases that silence anti-apoptotic genes (Campbell et al., 2004). Molecular signals can not only change their phenotypic meaning but also the relative importance of their message. Tumor cells, for instance, become addicted to chronically activated mitogenic pathways that are used only transiently in normal cells (Weinstein, 2002). Tools that could predict or explain such context-specific roles of molecular signals would be valuable for designing better-targeted therapies against disease (Blume-Jensen and Hunter, 2001; Miller-Jensen et al., 2007).

Many data-driven approaches exist for grouping, separating, or predicting outcomes based on complex quantitative patterns of signaling or gene expression (D'Haeseleer, 2005; Janes and Yaffe, 2006; Noble, 2006). The problem with all of them is that they cannot distinguish molecules that are mechanistically linked to a phenotype from biomarkers that are correlative but not causative (Sawyers, 2008). This difficulty can be avoided by creating models from datasets that consist of molecular signals with recognized but complicated roles in the outcome that is to be predicted (Janes et al., 2005; Miller-Jensen et al., 2007). The drawback is that one’s interpretation of such a model is biased toward the recognized roles of the molecular signals and away from more-surprising correlations with phenotype that could indicate new mechanisms. Data-driven models often identify hundreds of correlations in large datasets, making it impractical to perturb each one experimentally. Thus, an additional means for filtering correlation-based hypotheses is greatly needed.

Here, we develop a general approach, called “model-breakpoint analysis”, which involves globally perturbing the measurements used to build a data-driven model and then quantifying the loss of model accuracy. We altered signaling-network measurements by manipulating each molecular signal’s “dynamic range”, defined as the responsiveness of cell outcomes to incremental changes in signal activation. Dynamic range has been understudied, because signaling networks are typically measured in either their basal (minimum) or hyperstimulated (maximum) states (Irish et al., 2004; Janes et al., 2004; Natarajan et al., 2006; Wolf-Yadlin et al., 2006). This is despite the fact that intermediate network states, induced by sub-saturating stimuli, are more likely to be experienced physiologically.

Using two independent data-driven models (Janes et al., 2005; Kumar et al., 2007), we found, surprisingly, that perturbing dynamic range did not cause progressive declines in model accuracy. Rather, model predictions remained highly accurate until reaching a defined “breakpoint” where they failed catastrophically. Only a few molecular signals and stimuli turn out to be responsible for failed predictions at the breakpoint. This allowed us to reveal new, context-specific roles for molecular signals that were not prominent in the original models but were confirmed to be critical regulators nonetheless. In addition, our analysis suggested that a linear and uniform dynamic range of molecular signals is a generally important requirement for the control of cell phenotypes, which we directly demonstrate for the stress kinase MK2 based on a data-driven model of cytokine-induced cell death (Janes et al., 2005). We show that stimulus-dependent MK2 catalytic activity appears to have been optimized for dynamic range rather than signal strength to maximize the apoptotic response of cells to a diverse range of cytokines. Contrary to conventional thinking, we therefore conclude that the dynamic range over which signaling occurs is a greater determinant of cellular outcomes than either the basal or maximally inducible signal strength. As a general approach, model-breakpoint analysis is useful for extracting new biological mechanisms from large datasets and for identifying general principles about how signal-transduction networks transmit information to mediate downstream responses.

RESULTS

We started to explore how specific molecular signals control phenotypic outcomes by using a data-driven model of cytokine-induced apoptosis (Janes et al., 2005). This model is based on a dataset of 7980 measurements of molecular signals that are dynamically activated by combinations of tumor necrosis factor (TNF), which is a death stimulus, together with either epidermal growth factor (EGF) or insulin, which are survival stimuli (Janes et al., 2006). (See Supplementary Material.) Most proteins whose activities and levels were measured were causally implicated in cytokine signaling or apoptosis (Figure 1A), but how collective information from these pathways determines a cell’s decision to die or survive was unclear.

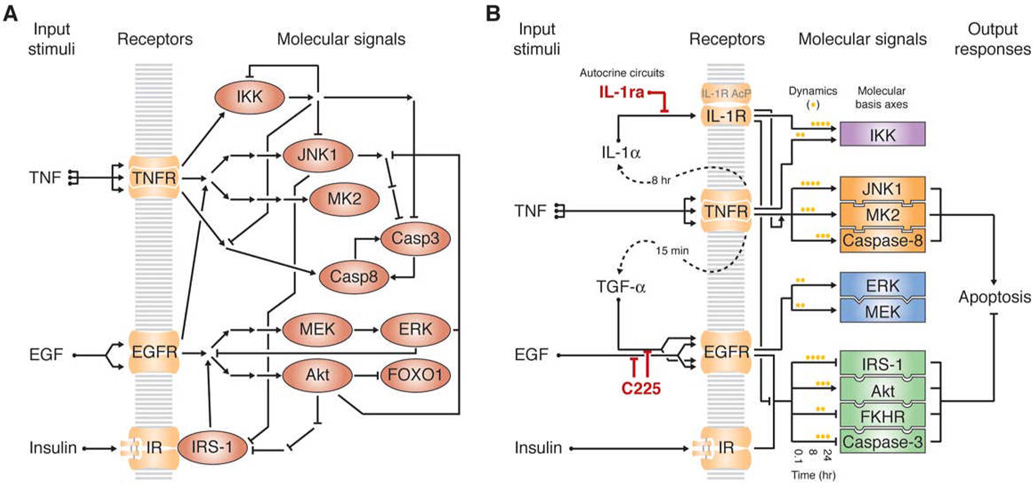
Figure 1. The TNF–EGF–insulin apoptotic-signaling network.

(A) Classic overview of the TNF–EGF–insulin network. Mechanistically connected activating signals are represented by arrows and inhibitory signals are shown by barred lines. Nodes corresponding to proteins whose activities we directly measured are shown as red ovals.

(B) Systems overview of the TNF–EGF–insulin apoptotic-signaling network. Dashed lines indicate the autocrine cascade activated by TNF (Janes et al., 2006). The two perturbations of the TGF-α and IL-1α autocrine feedback circuits (by C225 and IL-1ra, respectively) are highlighted in red. Intracellular signals (rectangles) are divided into groups (purple, orange, blue, green) based on linked statistical dependencies identified by a data-driven model. A stress-apoptosis group (orange) and a cell-survival group (green) contribute heavily to two molecular basis axes, defined by the first two principal components of the model, which together accurately predict apoptosis induced by TNF, EGF, and insulin (Janes et al., 2005). A subset of time-dependent signals from these groups, indicated by yellow dots, form the largest contributors to the molecular basis axes of the network.

After measuring the extent of cell death experimentally, we examined how the measured molecular signals could function together to control apoptosis by using partial least squares regression (Janes and Yaffe, 2006). This method combines a large number of experimentally measured signaling events (“variables” composed of time-derived signaling metrics; see Supplementary Material) into a smaller number of super-variables called principal components that are trained to predict cell-death outcomes.) The resulting data-driven model accurately captures the apoptotic responses induced by various TNF–EGF–insulin combinations (Janes et al., 2005), as measured by a “fitness function” that quantifies the predictive ability of the model (Gaudet et al., 2005) (see Supplementary Material).

The model also led us to recognize two previously unknown autocrine feedback loops involving transforming growth factor-α (TGF-α) and interleukin-1α (IL-1α) (Janes et al., 2006). Secretion of both of these cytokines was induced by TNF, and their autocrine stimulation played key roles in modulating the subsequent apoptotic response (Figure 1B). Importantly, the model accurately predicted the profound effects on TNF-induced signaling and apoptosis that resulted from blocking TGF-α (with the anti-receptor antibody C225) or blocking IL-1α (with the receptor antagonist IL-1ra) (Janes et al., 2005), despite neither of these autocrine factors being explicitly specified in the dataset. Thus, the accurate predictions of cell death after autocrine blockade are a stringent and independent validation of the model’s general predictive ability.

Perturbing dynamic range reveals context-specific model breakpoints

To examine how signaling activity influenced cell death, we manipulated the dynamic range of the measured signals computationally. We used mathematical functions that, when multiplied by the original dataset, maintained the minimum and maximum experimentally-determined values of signaling activity but dampened or amplified the intermediate values hyperbolically based upon a single nonlinearity parameter (Figures 2A and 2D; see Experimental Procedures). As the nonlinearity parameter (k) decreases, the effective dynamic range of each signaling molecule becomes compressed. We first investigated models where the signal output increased rapidly at low signaling and saturated at high signaling (Figure 2A). Saturation could occur biologically if, for example, the availability of a downstream effector were to become limiting when signal activation is high. As the nonlinearity parameter k was progressively decreased, the models showed a small gradual decline in their ability to predict apoptosis after TGF-α blockade with C225, followed by an abrupt drop in model performance when k = 0.8 (Figure 2B). Notably, predictive accuracy did not simply erode away with increasing saturation. Instead, the models tolerated some degree of saturation before reaching a catastrophic “breakpoint” where the accuracy fell dramatically. Surprisingly, this failure was specific to disruption of the TGF-α autocrine circuit; predictions of apoptosis induced with or without IL-1α blockade were unaffected (Figure 2B, 2C, Figure S1A, and data not shown; see Supplementary Material). This suggested that perturbing dynamic range causes non-global failures within a data-driven model that are treatment specific and thus context specific.

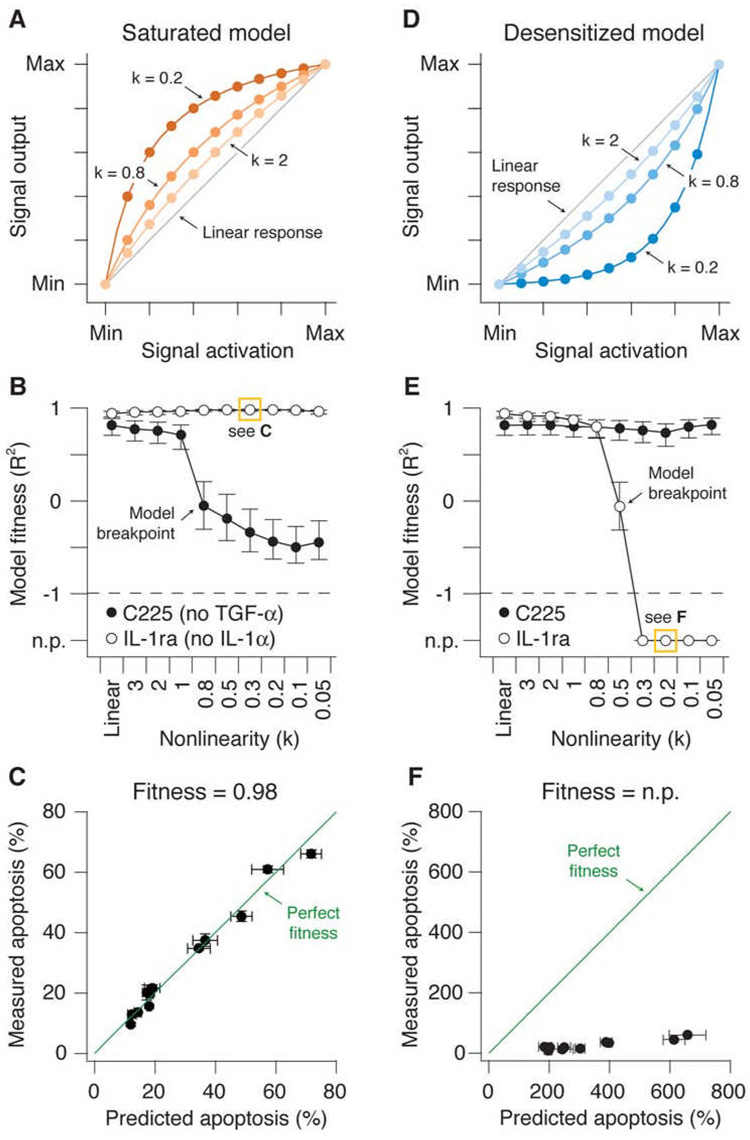
Figure 2. Selective failure of nonlinear models linking signal activation to signal output for predicting apoptosis.

(A) The saturation model with k = 2, 0.8, and 0.2 compared to the original linear model (Linear response, gray line). Signal output was amplified at low levels of signal activation and saturated at moderate to high levels of signal activation. For all k values, the minimum (Min) and maximum (Max) observed values for each signaling metric were preserved.

(B) Predictions of apoptosis after perturbation of the TGF-α autocrine feedback circuit with C225, or the IL-1α feedback loop with IL-1ra, in models with increasing saturation compared to the original linear model. The accuracy of predictions was quantified by model “fitness”, where a value of one is a perfect match between predicted and measured values. A specific data point boxed in yellow is further expanded in (C) as an example. The model breakpoint is indicated where catastrophic failure of the C225 prediction occurs.

(C) An example of good model fitness. Measured and predicted apoptosis are shown for the 12 apoptotic readouts corresponding to the TNF+IL-1ra condition and a saturated model with k = 0.3, highlighted in (B). Perfect model fitness (= 1) is shown in green as a reference.

(D) The desensitization model with k = 2, 0.8, and 0.2 compared to the original linear model (Linear response, gray line). Signal output was attenuated relative to true measured signal activation, particularly at low-to-moderate levels of activation. For all k values, the minimum (Min) and maximum (Max) observed values for each signaling metric were preserved.

(E) Predictions of apoptosis after perturbation of the TGF-α autocrine feedback loop with C225, or the IL-1α feedback loop with IL-1ra, in models with increasing desensitization compared to the original linear model. Model fitnesses quantifying the agreement between prediction and experiment were calculated as in (A). A specific data point boxed in yellow is further expanded in (F) as an example. The model breakpoint is indicated where catastrophic failure of the IL-1ra prediction occurs.

(F) An example of no prediction (n.p.). Measured and predicted apoptosis are shown for the 12 apoptotic readouts corresponding to the TNF+IL-1ra condition and a desensitized model with k = 0.2, highlighted in (E). Perfect model fitness (= 1) is shown in green as a reference.

For (B) and (E) model fitness is shown as the R² value ± 90% Fisher Z-transformed confidence intervals for the regression model: Measured apoptosis = Predicted apoptosis (see Experimental Procedures). For (C) and (F) data are shown as the central prediction ± crossvalidated standard error (s.e.) along the x-axis and the mean ± standard error of the mean (s.e.m.) of triplicate biological measurements along the y-axis. Apoptosis data are from four readouts measured by flow cytometry at three time points (Janes et al., 2005).

We next looked at desensitization. A reaction pathway could appear desensitized if, for example, multimerization of the activator were required for signal transmission to downstream effectors. A desensitization function was defined that warped the activation-output relationship similarly to the saturation function but in the opposite direction (Figure 2D; see Experimental Procedures). Models with increasing desensitization again showed drastically different accuracies in predicting the apoptotic response (Figure 2E). Here, the TGF-α perturbation and training-data predictions were completely accurate across all desensitization values, but now the quality of the apoptosis predictions following IL-1ra blockade dropped precipitously when k was below 0.8 (Figure 2E, 2F, Figure S1B, and data not shown). Once again, the models reached a sudden “breakpoint” where small changes in dynamic range caused a complete loss of predictive accuracy, suggesting that the models could accommodate a finite amount of desensitization of molecular signals before failing. Therefore, saturation and desensitization complement one another in their ability to reveal context-specific breakpoints in data-driven models (see Supplementary Material). Similar model breakpoints were observed with other types of data transformations (Figure S2) as well as with non-biological datasets (Figure S3), indicating that context-specific model breakpoints are a general property of data-driven models.

Model-breakpoint analysis identifies a TGF-α-specific role for early PI3K–Akt pathway in TNF-induced apoptosis

We sought to determine exactly which measurements in the dataset caused the TGF-α blockade predictions to fail during saturation and the IL-1α blockade predictions to fail during desensitization. We reasoned that this “model-breakpoint analysis” could provide context-specific insight into the function of signaling networks. Our first application of model-breakpoint analysis revealed a time- and treatment-specific role for the survival kinase Akt (see below).

We started by examining the structure of the failed saturation model when it had passed just beyond the breakpoint for accurately predicting the TGF-α perturbation (k = 0.8). The starting model required three principal components for optimal accuracy (Figure 3A). Saturating the model did not affect the number of components until the breakpoint was reached, when suddenly the third principal component was no longer statistically informative (Figure 3B and data not shown). If the failed saturation model was forced to contain three principal components, the resulting model now accurately predicted the TGF-α perturbation (Figure 3C). Conversely, when the third principal component was removed from the original model, prediction accuracy for TGF-α blockade decreased substantially. Together, the model results indicated that the third principal component was critical for quantitatively accurate predictions when autocrine TGF-α signaling was blocked with C225.

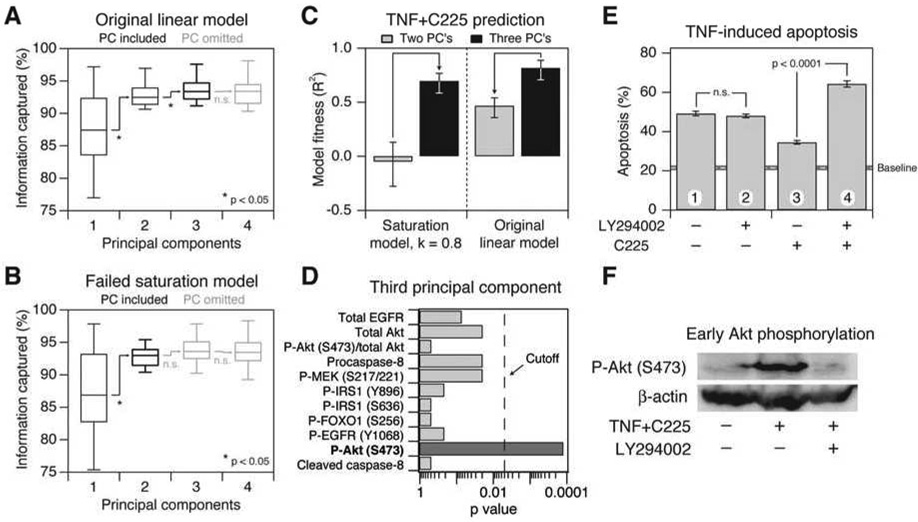
Figure 3. Failure of the saturation models involves loss of a principal component containing information from early Akt signaling.

(A and B) Box-and-whisker plots showing the increase in information captured for (A) the original linear model and (B) the saturation model as the number of principal components is increased from one principal component to four. The midline indicates the median crossvalidated variance captured across the 12 apoptotic outputs measured, the boxes indicate the 25^th and 75^th percentiles, and the error bars indicate the 10^th and 90^th percentiles. Significant increases in variance captured were assessed by a one-sided sign-rank test. Principal components that were included in the predictive model are shown in black, and principal components that were omitted are shown in gray.

(C) Changes in model fitness for the C225 prediction as the number of components for the saturation and linear models is changed from two principal components (gray) to three principal components (black). Model fitness is shown as R² value ± 90% Fisher Z-transformed confidence intervals for the regression model: Measured apoptosis = Predicted apoptosis (see Experimental Procedures).

(D) Akt signaling makes an important contribution to the third principal component when a two-component saturation model fails to predict apoptosis after TGF-α blockade. The statistical significance of any particular signal being over-represented in the top-30 metrics after inclusion of the third princpal component was examined by the binomial test (after correcting for multiple-hypothesis testing, a significance level [“Cutoff”] below 0.005 was required). Molecular signals are considered over-represented when significantly more metrics are observed in a list than would be expected by chance. See Table S1 for a complete list of molecular signals that contribute to the third principal component.

(E) Early inhibition of Akt phosphorylation affects TNF-induced apoptosis only in the context of TGF-α blockade by C225. HT-29 cells were pretreated for 1 hr with 10 µg/ml C225 in the presence or absence of 20 µM LY294002 where indicated and then stimulated with 5 ng/ml TNF for 24 hr. At 3 hr after TNF stimulation, LY294002 was washed out by replacing the medium with conditioned medium from TNF+C225-treated cells. Apoptosis was measured by cleaved caspase-3 staining and flow cytometry (Janes et al., 2005). Data are shown as the mean ± s.e.m. of triplicate biological measurements. The baseline apoptosis induced by mock stimulation ± s.e.m. (gray line) is indicated.

(F) Early TNF+C225-induced Akt phosphorylation is inhibited by LY294002. HT-29 cells were pretreated for 1 hr with 10 µg/ml C225 in the presence or absence of 20 µM LY294002 where indicated. Cells were then stimulated with 5 ng/ml TNF and Akt phosphorylation (P-Akt) was measured 15 min later by Western blotting with β-actin as a loading control.

The importance of the third principal component was surprising, because it provided only a small improvement in overall predictive power towards the training set in which no TGF-α blockade was performed (Figure 3A). Nevertheless, the sensitivity of the apoptosis predictions to inclusion of the third principal component suggested that some subtle-yet-critical information was being encoded, prompting us to look at its role in greater detail. When the third principal component was included, and the predictive accuracy of the saturation model was restored, we found that early measurements of Akt phosphorylation became more heavily weighted (Figure 3D). Therefore, model-breakpoint analysis of the saturation model led us to predict that early Akt signaling might be a critical signal for TNF-induced apoptosis when the TGF-α autocrine circuit is disrupted.

To test the context-specific role of early PI3K–Akt signaling, we performed timed-inhibitor experiments with LY294002, a reversible inhibitor of PI3K (Figure 3E and 3F). After TNF stimulation of C225-inhibited HT-29 cells, we observed strong phosphorylation of Akt at 15 min, which was blocked with LY294002 as expected (Figure 3F). In the absence of TGF-α blockade by C225, there was no change in apoptosis when LY294002 was present for the first 3–4 hours after TNF stimulation and then removed from the medium (Figure 3E, conditions 1 and 2), confirming earlier findings that early Akt signaling does not affect apoptosis induced by TNF alone (Janes et al., 2003). Strikingly, when PI3K–Akt was inhibited at early times in C225-treated cells, we observed a ~twofold increase in TNF-induced apoptosis compared to C225-treated cells in the absence of LY294002 (p < 10⁻⁴, conditions 3 and 4). These experiments show that early PI3K–Akt signaling makes an important anti-apoptotic contribution only when cells lack a functional TGF-α autocrine circuit. Therefore, by deemphasizing early Akt measurements through loss of a principal component, the breakpoint of the saturation model had correctly revealed a context-specific role of early Akt signaling in promoting cell survival.

Model-breakpoint analysis correctly distinguishes non-essential from essential signals for TNF-induced apoptosis and reveals a new regulatory mechanism for TNF-induced IL-1α signaling

Autocrine IL-1α is a potent prodeath stimulus downstream of TNF (Janes et al., 2006), but the relevant intracellular pathways upstream of IL-1α release or downstream of the IL-1 receptor that mediate this response are not known. We therefore performed model-breakpoint analysis on the desensitization model at the IL-1ra breakpoint (Figure 2E) to identify candidate regulators of IL-1α-mediated apoptosis. In contrast to the saturation breakpoint involving disruption of the TGF-α autocrine feedback circuit, we observed no change in the number of principal components at the model breakpoint for IL-1ra treatment (data not shown). This prompted us to search for changes within the principal components themselves.

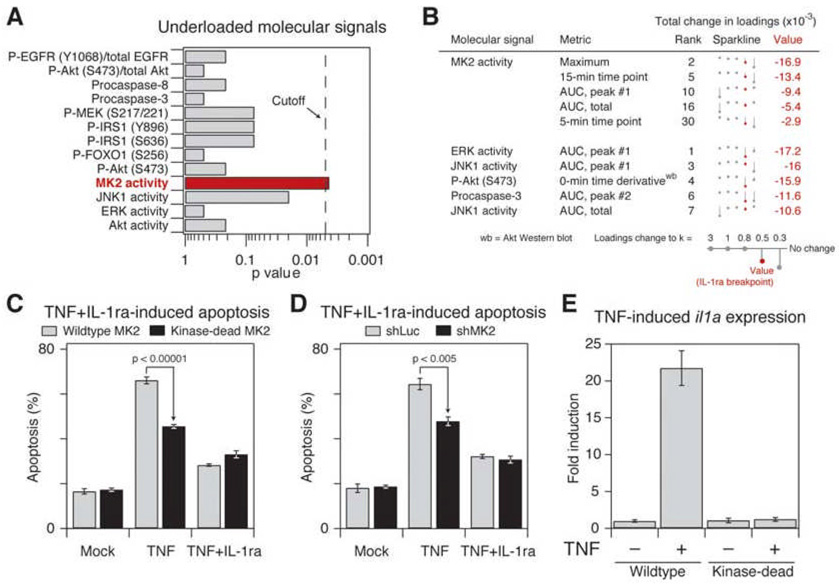
Each principal component consists of weighting factors, called “loadings”, which quantify how much each signaling metric contributes to that principal component (Janes and Yaffe, 2006; Martens and Martens, 2001). Signaling metrics with large positive or negative loadings values are very important for the principal component; conversely, molecular signals with loadings near zero play a negligible role. At the desensitization breakpoint, we found that some metrics decreased their weightings and thus became “underloaded”, whereas others increased their weightings and became “overloaded”. For prediction of apoptosis after autocrine IL-1α perturbation, we found that the underloaded metrics were critical for model performance and were therefore likely to be of high biological importance (Figures S4A and S4B, see below). By contrast, overloaded metrics were uninformative and thus possibly dispensable for apoptosis induced by IL-1α and TNF (Figure S4C and S4D).

Among the top-30 overloaded metrics in the failed desensitization model, we found that ERK activity was significantly over-represented (Figures 4A and 4B). The ERK pathway is widely regarded as prosurvival (Ballif and Blenis, 2001) (Figure 1A), but our analysis suggested that ERK signaling played a minimal role in promoting survival when autocrine IL-1α was blocked with IL-1ra (Figure 4A). To test the importance of ERK by experiment, we treated HT-29 cells with TNF+IL-1ra in the presence or absence of the MEK inhibitor, U0126. Despite complete inhibition of inducible ERK phosphorylation (Figure 4C), apoptosis mediated by TNF+IL-1ra was unchanged in the presence of U0126 (Figure 4D), indicating that ERK plays a negligible prosurvival role. Therefore, model-breakpoint analysis had correctly separated an ERK-activation epiphenomenon (Figure 4C) from the signals that actually control apoptosis (Figure 1B).

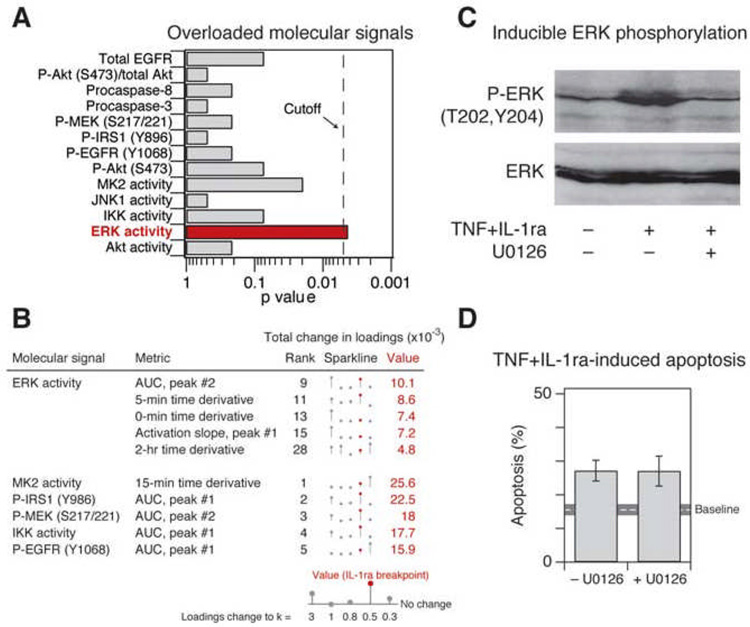
Figure 4. Overloaded signaling metrics highlight irrelevant signaling information from ERK activity.

(A) ERK activity is significantly over-represented among overloaded molecular signals in the desensitization model at the point of IL-1ra-prediction failure. Statistical significance of over-representation in the top-30 metrics was assessed as described in Figure 3D.

(B) Overloading of ERK activity metrics contributes to failure of the desensitization model to predict apoptosis after IL-1α blockade at the breakpoint (indicated in Figure 2E). All ERK activity metrics in the top 30 metrics with the largest positive change are shown, along with the top five metrics that are not derived from ERK activity. Overall rank is shown to the right of the metric description. Changes in total loadings are depicted by sparklines (Tufte, 2006) bounded by the range of the data. The value at which the apoptosis prediction by IL-1ra first fails is highlighted in red.

(C) TNF+IL-1ra induces ERK phosphorylation, which is inhibited by U0126. HT-29 cells were pretreated for 1 hr with 25 µM U0126 where indicated and then stimulated with 100 ng/ml TNF + 30 µg/ml IL-1ra for 15 min. ERK phosphorylation (P-ERK) was measured by Western blotting with total ERK levels used as a loading control.

(D) Inhibition of ERK activity by U0126 pretreatment does not affect TNF+IL-1ra-induced apoptosis. HT-29 cells were pretreated for 1 hr with 25 µM U0126 where indicated and then stimulated with 100 ng/ml TNF + 30 µg/ml IL-1ra for 24 hr. Apoptosis was measured by cleaved caspase-3 staining and flow cytometry (Janes et al., 2005). Data are shown as the mean ± s.e.m. of triplicate biological measurements. The baseline apoptosis induced by mock stimulation ± s.e.m. (gray line) is indicated.

We next examined the most-underloaded metrics, which were the direct cause of the desensitization breakpoint (Figure S4A). When model failure occurred, we found several measurements of MK2 activity among metrics with the largest reduction in total loadings (Figures 5A and 5B). To investigate the potential role of MK2 experimentally, we perturbed MK2 signaling by modestly overexpressing a kinase-dead MK2 that acts as a dominant negative (see Figure 6 below). Compared to cells expressing wild-type MK2 at similar levels, kinase-dead MK2 showed significantly decreased apoptosis in response to TNF (p < 10⁻⁶, Figure 5C). Importantly, the difference in TNF-induced apoptotic responses between cells expressing kinase-dead versus wild-type MK2 vanished when the Il-1α autocrine circuit was blocked by IL-1ra. Similar results were obtained with shRNA-mediated knockdown of endogenous MK2 in these cells (Figure 5D and Figure S5). These data indicate that functional MK2 signaling is quantitatively essential for normal apoptotic regulation via TNF-induced IL-1α signaling.

Figure 5. Failure of the desensitization model in the context of IL-1α blockade occurs by neglecting critical information from MK2.

(A) MK2 activity is significantly underloaded in the desensitization model at the point of IL-1ra-prediction failure. Statistical significance of molecular signals that become underloaded in the desensitization model immediately following the breakpoint was assessed as described in Figure 3D.

(B) All MK2 activity metrics in the top-30 metrics with the largest negative change at the point of model failure are shown, along with the top five metrics that are not derived from MK2 activity. Overall rank is shown to the right of the metric description. Changes in total loadings are depicted by sparklines (Tufte, 2006) bounded by the range of the data. The value at which the apoptosis prediction by IL-1ra first fails is highlighted in red.

(C and D) MK2 signaling is important for IL-1α-dependent responses to TNF. (C) Changes in TNF- and TNF+IL-1ra-induced apoptosis in HT-29 cells overexpressing wildtype or kinase-dead MK2. (D) Changes in TNF- and TNF+IL-1ra-induced apoptosis in HT-29 cells stably expressing an shRNA for MK2 (shMK2) or control hairpin (shLuc). HT-29 cells were stimulated with 100 ng/ml TNF + 30 µg/ml IL-1ra for 24 hr, and apoptosis was measured by cleaved caspase-3 staining and flow cytometry (Janes et al., 2005). Data are shown as the mean ± s.e.m. of sextuplicate or quadruplicate biological measurements. Note that loss of MK2 signaling decreases apoptosis only when the IL-1α feedback loop is present.

(E) MK2 signaling promotes sustained expression of il1a. HT-29 cells were stimulated with 100 ng/ml TNF for 1 hr and il1a mRNA levels measured by RT-qPCR. Data are shown as the mean ± s.e.m. of triplicate biological measurements.

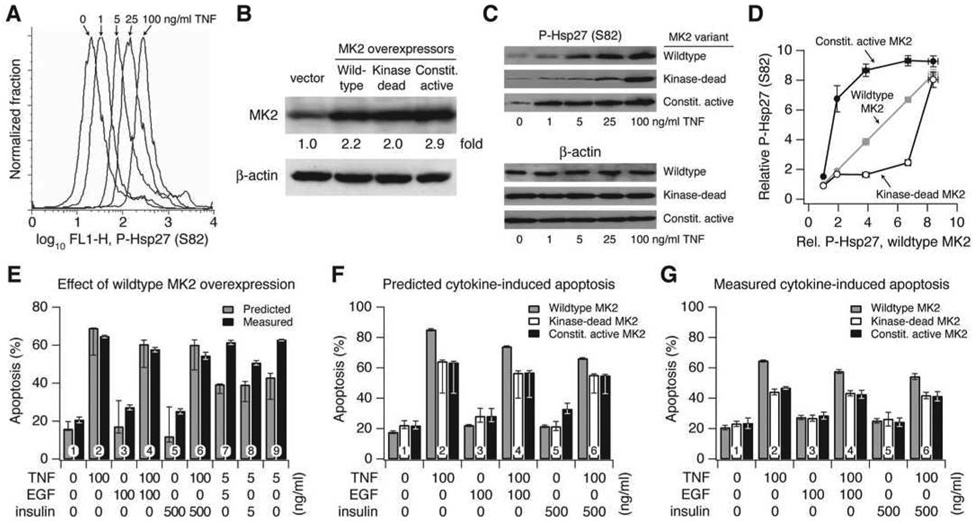
Figure 6. Prediction and experiment indicate that wildtype MK2 signaling provides an optimum dynamic range for TNF-induced apoptosis.

(A) Flow-cytometry profiles of HT-29 cells stimulated with the indicated TNF concentrations for 30 min and stained for P-Hsp27 levels showing a dose-dependent shift of the entire cell population, indicative of a uniform increase in MK2 activity.

(B) Overexpression of wildtype, kinase-dead, and constitutively active MK2 in HT-29 cells, which represent multiplicative, desensitized, and saturated model variants. Cells were transduced with retroviral vectors containing the indicated MK2 constructs, and MK2 overexpression was quantified by Western blotting and densitometry compared to vector control cells. β-actin was used as a loading control.

(C) HT-29 cells stably overexpressing wildtype, kinase-dead, and constitutively active MK2 were stimulated with the indicated TNF concentrations for 30 min, and P-Hsp27 was measured by Western blotting. β-actin was used as a loading control.

(D) Densitometry quantifying relative P-Hsp27 levels in the MK2 retrovirally transduced cells after TNF stimulation as a function of P-Hsp27 measured for the same TNF concentration in wildtype MK2 overexpressing cells.

(E) Comparison of measured and predicted apoptosis for HT-29 cells overexpressing wildtype MK2. Predictions closely matched experiments at high cytokine concentrations.

(F) Predicted apoptosis for HT-29 cells overexpressing wildtype, kinase-dead, and constitutively active MK2 at high cytokine concentrations. Wildtype predictions are re-plotted from (E) for comparison.

(G) Measured apoptosis for HT-29 cells overexpressing wildtype, kinase-dead, and constitutively active MK2 at high cytokine concentrations. Wildtype measurements are re-plotted from (E) for comparison.

For (E) and (F), predictions are shown as the central prediction ± range of eight ([E]) or five ([F]) crossvalidation runs. For (E) and (G), HT-29 cells were stimulated with the indicated cytokine combinations for 24 hr, and apoptosis was measured by cleaved casapase-3 staining and flow cytometry (Janes et al., 2005). Data are shown as the mean ± s.e.m. of triplicate biological measurements. Note that expression of either the kinase-dead or the constitutively active MK2 causes decreased apoptosis compared to expression of wildtype MK2.

Paradoxically, in the original model built on linear data, MK2 signaling contributes to TNF-induced apoptosis at early times, whereas signaling through the IL-1α feedback loop is not observed until somewhat later times (Janes et al., 2005; Janes et al., 2006). These observations raised the possibility that MK2 could be acting as a mediator that links TNF signaling to the IL-1α feedback loop. Early TNF-induced MK2 activation was unaffected by IL-1ra blockade (p = 0.2, Figure S6), suggesting that MK2 functions downstream of TNF but upstream of IL-1α.

TNF induces the transcription of many proinflammatory cytokines, including the il1a gene, via activation of IKK–NF-κB (Figure 1A) (Mori and Prager, 1996). TNF also activates the p38–MK2 pathway, where a major role of MK2 is to stabilize AU-rich element (ARE)-containing mRNA transcripts that are ordinarily degraded rapidly after transcription (Kotlyarov et al., 1999). We noted that the 3’ UTR of il1a contains two copies of an UUAUUUA(U/A)(U/A) consensus sequence implicated in destabilizing ARE-containing transcripts (Lagnado et al., 1994). We therefore hypothesized that early MK2 signaling could be providing an IL-1α-specific proapoptotic signal by stabilizing il1a transcripts and thereby allowing sustained IL-1α protein expression for subsequent release.

To test this prediction, il1a mRNA levels were measured following treatment of cells with TNF for 1 hr, a time when MK2 remains strongly activated but IKK–NF-κB signaling has returned to basal levels (Janes et al., 2006) (Figure S6). In cells expressing wild-type MK2, il1a transcript levels remained high 1 hr after TNF treatment (Figure 5E). By contrast, il1a levels in cells expressing kinase-dead MK2 had returned to baseline at 1 hr after TNF treatment. Thus, the proapoptotic role of early MK2 signaling appears to function through stabilization of il1a transcripts, thereby amplifying the magnitude of the prodeath IL-1α autocrine circuit induced by TNF.

Model-breakpoint analysis applies to other large-scale measurements of signal transduction

To test its general applicability, we applied model-breakpoint analysis to a second dataset of quantitative phosphoproteomic measurements that had been paired with phenotypic readouts of cell migration and proliferation in a mammary epithelial cell line (Wolf-Yadlin et al., 2006). In this study, 62 tyrosine-phosphorylated peptides were quantified at four time points shortly after stimulation of cells with EGF or the EGF-family ligand, heregulin. A data-driven model built on this 62-phosphopeptide signature was previously shown to capture the migratory and proliferative responses of cells stimulated with EGF or heregulin (Kumar et al., 2007). The starting model also correctly predicts the EGF- and heregulin-induced responses of cells engineered to express ~20-fold higher levels of the EGF receptor family member, ErbB2. The treatments involving ErbB2-overexpressing cells were not included in the initial model and therefore serve as an independent validation of its accuracy.

We observed a clear breakpoint for predicting the effects of ErbB2 overexpression when the phosphoproteomic data was desensitized (Figure S7A and S7B). At this breakpoint (k = 0.2), there was a significant enrichment in three phosphopeptides, which became undervalued in the model’s principal components (Figure S7C). Two of these phosphopeptides were in the scaffolding protein p130^Cas (Y234 and Y249), which is an important mediator of migration downstream of focal adhesion kinase (FAK) (Cary et al., 1998). The other phosphopeptide lies in the activation loop of ERK2 (T185Y187), which is widely known to be an important regulator of the G₁/S transition (Torii et al., 2006) and is also involved in migration of epithelial cells (Matsubayashi et al., 2004). Both ERK and p130^Cas have been identified as critical signaling proteins for mediating ErbB2-induced cell invasion of mammary adenocarinoma cells (Spencer et al., 2000). Taken together, we conclude that model-breakpoint analysis is a general tool that can derive unique biological insight from data-driven models that link signal transduction to cell phenotype.

MK2 dynamic range is more important for TNF-induced apoptosis than absolute signal strength

Maximum dynamic range was clearly essential for optimum model performance, but could dynamic range be similarly important for the function of individual signaling pathways within cells? We focused on MK2 catalytic activity as a prototypical molecular signal, because it had emerged as an important regulator of TNF-induced apoptosis through autocrine IL-1α (Figure 5). We first confirmed that MK2 activation was occurring uniformly in the entire cell population by using flow cytometry to analyze phosphorylation of its substrate, Hsp27 (P-Hsp27) (Stokoe et al., 1992). P-Hsp27 increased proportionally with TNF dose (Figure 6A), allowing us to use biochemical measurements of P-Hsp27 as an estimate of MK2 activity in vivo.

The dynamic range of MK2 signaling was experimentally perturbed by establishing stable lines of HT-29 cells expressing comparably low levels of wildtype, kinase-dead, or constitutively active MK2 (Figure 6B). Quantitative immunoblotting for P-Hsp27 showed that all cell lines displayed the expected hyperbolic increases in MK2 activity with TNF dose (Figure 6C and Figure S8). Compared to the responsiveness of cells overexpressing wildtype MK2, however, the kinase-dead and constitutively active mutants showed compressed dynamic range similar to the desensitization and saturation functions used in model-breakpoint analysis (Figure 6D, compare with Figures 2A and 2D). Thus, these MK2-overexpressing cells act as in vivo surrogates of linear (wildtype), desensitized (kinase dead), and saturated (constitutively active) signaling via the MK2 pathway.

We first assessed whether the model could capture the behavior of cells overexpressing wildtype MK2 at 2.2-fold above endogenous levels (Figure 6B). The overexpression was explicitly incorporated into the original linear model (in which MK2 was not overexpressed) by multiplying the pre-existing cytokine-stimulated MK2 time courses by 2.2. This simple approximation for proportional MK2 activation accurately captured the extent of apoptosis observed for all six combinations of high-dose TNF, EGF, and insulin (Figure 6E, conditions 1–6). We found that the model could not capture the extent of apoptosis induced by low-dose concentrations of TNF (conditions 7–9), likely due to a shift in TNF sensitivity. Specifically, overexpression of wildtype MK2 caused low-dose TNF treatments to induce apoptosis similarly to high-dose treatments (compare conditions 2 and 9, 4 and 7, and 6 and 8 in Figure 6E). We therefore examined the kinase-dead and constitutively active MK2 mutants only under high-dose TNF conditions, where the model accurately captured the apoptotic responses.

To model the kinase-dead and constitutively active MK2 mutants, we first quantified the overexpression of each MK2 variant (Figure 6B) and then applied the saturation and desensitization functions with k equal to 0.2 (Figures 2A and 2D) to mimic the activation profile of constitutively active and kinase-dead MK2, respectively (Figures 6C and 6D). Last, for both MK2 mutants, we challenged the model to predict how cytokine-induced apoptosis would be changed relative to wildtype-MK2 overexpression.

Surprisingly, the model predicted that both kinase-dead and constitutively active MK2 would decrease TNF-induced apoptosis relative to wildtype (Figure 6F). When apoptosis was measured experimentally, we found that the two MK2 mutants were significantly more resistant to TNF-induced apoptosis compared to wildtype (p < 0.05, Figure 6G), exactly as predicted by the model. Thus, both model and experiment support the nonintuitive conclusion that catalytic activity does not monotonically predict how MK2 influences cell death stimulated by TNF. Taken together, our application of model-breakpoint analysis to apoptotic signaling indicates that the network exists in a state of “optimal tuning” for signal transfer, which is achieved by maximizing the dynamic range of molecular signals rather than by interpreting absolute signal strength.

DISCUSSION

Here we describe a new method for quantitatively analyzing the link between signaling events and cellular responses. The technique starts with a data-driven model based on quantitative signaling measurements that are used by the model to predict cellular responses. The signaling dataset is progressively nonlinearized, and the model is then rebuilt from the nonlinear dataset. Eventually, the nonlinearization reaches a critical breakpoint where the model abruptly stops predicting cellular responses accurately. At this breakpoint, the reason for model failure is diagnosed by identifying which nonlinearized signals caused the failed model to be built incorrectly. The biological importance of these specific signals is then tested by experiment for their role in controlling the predicted cellular response. Together, model-breakpoint analysis can identify new mechanisms that would not have otherwise emerged from the data. Using model-breakpoint analysis, we further propose here that the control of cell phenotypes requires maximum dynamic range of the response-determining pathways within the cell.

The value of model-breakpoint analysis

Many “systems-biology” initiatives are actively compiling large-scale signaling measurements, and data-driven modeling is emerging as the first level of analysis for these datasets (Gaudet et al., 2005; Janes et al., 2005; Natarajan et al., 2006; Pradervand et al., 2006). Model breakpoints provide a next level of analysis by evaluating both the model performance as well as the data upon which it was based. One practical benefit of the nonlinearizations is that they gauge the sensitivity of the model predictions to experiments that are not quantitative. The saturated and desensitized relationships used to explore signal transmission could just as easily be used to simulate nonlinear assay readouts for the measured molecular signals. Our biochemical assays were painstakingly validated to be linear, quantitative, and reproducible (Gaudet et al., 2005; Janes et al., 2003). In retrospect, this optimization was crucial, because only minor nonlinearities in the data would have been sufficient to cause failed predictions of one or both of the autocrine perturbations. The results here explicitly indicate that the success of data-driven modeling is directly tied to the quality of the large-scale measurements (Janes and Yaffe, 2006). Model-breakpoint analysis is applicable to any quantifiable set of assays and can be used to benchmark their accuracy and consistency to help steer data-collection efforts. As large-scale signaling experiments are being pursued with increasing frequency (Albeck et al., 2006), it will be important to determine the extent of quantitative accuracy needed to analyze these data correctly. Indeed, applying model-breakpoint analysis to a phosphoproteomic dataset revealed several important phosphopeptides that were not emphasized in the authors’ preliminary and follow-up analyses (Kumar et al., 2007; Wolf-Yadlin et al., 2006).

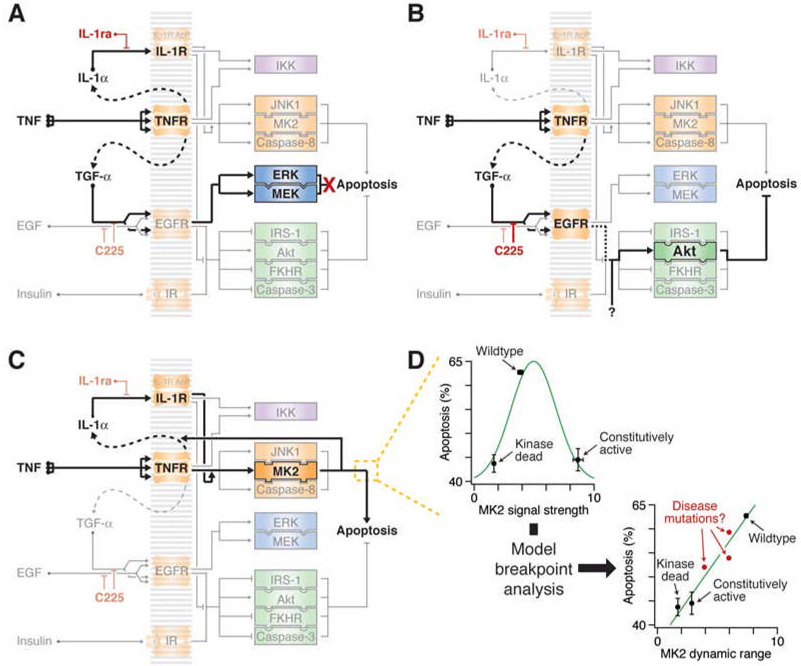
Second, we found that by examining where data manipulations cause sudden breakpoints in model accuracy, we can uncover unexpected, context-specific biological connections between individual molecular signals and apoptosis. For example, model-breakpoint analysis correctly showed that ERK signaling is not important in preventing TNF-induced apoptosis when autocrine IL-1α is blocked (Figure 7A), despite that ERK activity is among the most informative molecular signals for predicting apoptosis overall (Janes et al., 2005). Conversely, early Akt signaling does not normally send an effective anti-apoptotic message when cells are treated with TNF alone (Janes et al., 2005; Janes et al., 2003), but Akt emerges as a prominent apoptosis-determining signal when these same cells are treated with TNF and autocrine TGF-α is blocked (Figure 7B).

Figure 7. Context-specific and network-level mechanisms revealed by model-breakpoint analysis.

(A) MEK–ERK signaling is not involved in TNF-induced apoptosis.

(B) Early Akt activity sends a pro-survival signal when TNF-induced TGF-α autocrine signaling is blocked. An unknown activator of early Akt (“?”) must be critical for the pro-survival function.

(C) Wildtype MK2 signaling promotes TNF-induced apoptosis by stabilizing the autocrine IL-1α circuit.

(D) The dynamic range of MK2 is more predictive of its apoptotic contribution than MK2 signal strength. (Upper left) Apoptosis induced by 5 ng/ml TNF is plotted against MK2 signal strength as measured by P-Hsp27 in Figure 6C. Apoptosis increases then decreases with signal strength (green curve). (Lower right) Apoptosis induced by 5 ng/ml TNF is plotted against MK2 dynamic range as defined by the range of signal strengths where the slope of activation compared to wildtype MK2 is greater than or equal to one in Figure 6D. Apoptosis appears to increase proportionally with dynamic range (green curve). Disease mutations (red) may cause perturbations in dynamic range that fall between the wildype and the hyperactive-hypoactive alleles.

Part of the reason why context specificity is so puzzling is that it is has been challenging to find experimental conditions where such behavior can be easily revealed (Natarajan et al., 2006). Model-breakpoint analysis provides a tool for computationally interrogating context specificity without having to resort to brute-force screening of ligands and inhibitors. Obviously, the breakpoints of a data-driven model can only analyze the contexts of the stimulus conditions that are being predicted. We did not, for example, re-discover the context-specific, prodeath role of the IKK–NF-κB pathway (Campbell et al., 2004), despite having measured it, because we lacked treatment conditions in the dataset that involved DNA damage. This stresses the importance of proper experimental design when the goal is to build data-driven models that help reveal new biological mechanisms.

Dynamic range in signaling and disease

One surprising result from this study was the prediction and experimental verification that MK2 dynamic range is more critical for proapoptotic signaling than signal strength (Figure 7C and 7D). Retrospectively, the behavior of the different MK2 variants could be explained from the perspective of signal transmission. Unlike the predictions of TGF-α and IL-1α perturbation, which selectively required low or high levels of signal activation, our results indicate that the MK2 pathway uses its complete dynamic range. Overexpression of a dominant negative MK2 acts as a buffer for signal transmission, desensitizing the pathway such that only very strong activation events lead to productive output from the endogenous MK2. Conversely, a constitutively activated MK2 that has been stably incorporated provides a tonic, near-saturating level of signaling, which reduces the relative responsiveness of the endogenous MK2 to external stimuli. Only overexpression of the wildtype kinase, which both augments signal strength and maintains appropriate control of catalytic activity, maximizes the pro-apoptotic contribution of MK2 to TNF-induced signaling (Figure 7D and Figure S9).

Recent work has indicated that the fold change in activity of a signaling molecule (relative to its basal activity) is a greater determinant of cell-fate control than the absolute level of signaling (Miller-Jensen et al., 2006; Sasagawa et al., 2005). Because fold changes in activation are a direct reflection of the dynamic range in which phenotypic information is communicated, these data independently support our conclusions. Indeed, the reduction of effective dynamic range is our main explanation for the decrease in cytokine-induced apoptosis that we observed when cells express constitutively active MK2, a kinase whose function is mainly proapoptotic (Kotlyarov et al., 1999).

To test the predicted effect of nonlinear MK2 signaling, we chose to stably overexpress constitutively active or kinase-dead MK2 mutants and compare their behavior to wildtype MK2. We have found that such mutation-based approaches are more effective at nonlinearizing signal activation-output relationships than other techniques. RNA interference (RNAi) or wildtype overexpression, for instance, reduce or increase the induced level of signaling but do not affect the general linearity of dynamic range as a function of these levels (Figure S9). Discrepancies between RNAi- and dominant-negative-based perturbations of a signaling pathway have not been openly documented. However, we predict that differences should arise occasionally because these approaches affect dynamic range differently. For example, in our work, the small but significant increase in TNF+IL-1ra-induced apoptosis in cells overexpressing kinase-dead MK2 (Figure 5C) was not observed when MK2 levels were downregulated with an RNA hairpin (Figure 5D). An important function of MK2 is to stabilize AU-rich transcripts (Winzen et al., 1999), suggesting that dynamic range may be particularly important at the interface between signaling and gene expression.

Although complete gain- and loss-of-function mutations cause dramatic changes in signaling responsiveness, more subtle amino-acid changes (single-nucleotide polymorphisms, disease mutations, etc.) could alter dynamic range with pathophysiological consequences (Figure 7D). Our finding that cellular outcomes are highly sensitive to dynamic range suggests that mutant proteins should be characterized under conditions that capture a breadth of activation states. This is perhaps best achieved by inducing the network with diverse stimuli in a dose-dependent and combinatorial manner (Figure 6).

In general, computational models are most valuable when they provide new biological insight that can then be verified experimentally. Model-breakpoint analysis is a new method for hypothesis generation using pre-validated models. Model breakpoints are not mere computational anomalies but instead highlight previously unexplored aspects of a data-driven model that are biologically relevant. Just as it is no longer possible to comprehend signal-transduction networks by intuition alone (Jordan et al., 2000), we believe that models of networks cannot be fully grasped by mere inspection of their parameters or their predictions. Our study using model-breakpoint analysis suggests that dynamic range may be a particularly important criterion for the evolution of complex signaling networks.

EXPERIMENTAL PROCEDURES

See the Supplementary Material for a detailed description of standard experimental procedures and reagents.

Data-driven modeling

The signal-response datasets and partial least squares models of cytokine-induced apoptosis and EGF–heregulin-induced migration-proliferation have been described elsewhere (Janes et al., 2005; Janes et al., 2006; Kumar et al., 2007; Wolf-Yadlin et al., 2006). Additional details are available in the Supplementary Material.

Partial least squares modeling and model fitness

Application of partial least squares to biological data has been described in detail elsewhere (Janes et al., 2004; Janes and Yaffe, 2006). Before all analyses, the signaling and apoptosis matrices were variance scaled to nondimensionalize the different measurements. Model predictions were made via crossvalidation by leaving out one of the observations, and model uncertainties were calculated by jack-knifing (Efron and Tibshirani, 1993). To assess the accuracy of predictions, model fitness (R²) was calculated according to the following formula (Gaudet et al., 2005):

$$R^2=1-\left[\frac{{\displaystyle \sum _{i=1}^n{(\text{Predicted}}_i-{\text{Measured}}_i}{)}^2}{{\displaystyle \sum _{i=1}^n{{(\text{Predicted}}_i)}^2-\frac{{\left({\displaystyle \sum _{i=1}^n{\text{Predicted}}_i}\right)}^2}{n}}}\right]$$

where Predicted_i is the prediction of the i^th apoptotic output, Measured_i is the measurement of the i^th apoptotic output, and n is the total number of apoptotic outputs. An R² value of 1 indicates a perfect match between measured (x) and predicted (y) apoptosis values. As the R² value drops to zero and below, the comparison is better fit by the equation y = 0 than y = x. 90% confidence intervals for model fitness were calculated by the Fisher inversion.

Model-breakpoint analysis

All model-breakpoint analyses were performed on the apoptosis model after a 60° subspace rotation of the first two principal components to maintain consistency with earlier studies (Janes et al., 2005). Derivation of the saturation and desensitization functions is available in the Supplementary Text. For assessing relative variable importance, the information content of each signaling metric was assessed by its variable importance in the projection (VIP):

$${\mathit{\text{VIP}}}_k=\sqrt{\frac{K{\displaystyle \sum _{a=1}^A{w}_{\mathit{\text{ak}}}^2{\mathit{\text{SS}}}_a}}{{\displaystyle \sum _{a=1}^A{\mathit{\text{SS}}}_a}}}$$

where K is the total number of signaling metrics, w_ak is the weight of the k^th metric for principal component a, A is the total number of principal components, and SS_a is the sum of squares explained by principal component a (Wold, 1994). The change in total loadings between models a and b (Δp_a,b) was calculated according to the following formula:

$$\mathrm{\Delta }{p}_{a,b}={\displaystyle \sum _{i=1}^m(p_{b,i}-p_{a,i})}$$

where p_a,i and p_b,i are the scores for the i^th principal component of models a and b, and m is the total number of principal components. Signaling metrics were ranked by their largest positive and negative changes in total loadings, and the significance for each molecular signal among the top 30 metrics was assessed by the binomial test after the Bonferroni correction to adjust for multiple-hypothesis testing.

MK2 predictions

For wildtype MK2 predictions, the measured MK2 signaling time courses were multiplied by the fold overexpression (Figure 6B). MK2-signaling metrics were then re-extracted and input into the original linear model as test observations. For prediction of the MK2 mutants, an overexpression model was explicitly trained using measured apoptosis values for the wildtype MK2-overexpressing cells stimulated with saturating cytokines (Figure 6E, conditions 1–6). Mutant MK2 time courses were approximated by multiplying by the corresponding fold overexpression (Figure 6B), re-extracting metrics, and multiplying the metrics by the saturation or desensitization functions with k = 0.2. Similar results to Figure 6F were obtained when nonlinear functions were applied with k = 0.8 (data not shown).