Optimizing the Precision for Localizing Fluorescent Proteins in Living Cells by 2D Gaussian Fitting of Digital Images: Application to COPII-Coated Endoplasmic Reticulum Exit Sites

Abstract

An insight into the operation of molecular motors has already been obtained under in vitro conditions from single-molecule tracking of proteins. It remains to analyze the effects of these motors on the position and secretion of specific organelles in the environment of the cell. For this purpose, we have investigated the accuracy of a standard algorithm to enable the tracking of particles in live-cell microscopy. The results have been applied to an example study into the role of the microtubule-motor kinesin on the function of COPII-coated secretory-cargo exit sites forming part of the mammalian endoplasmic reticulum. These exit sites are marked with multiple EYFP-tagged proteins to produce bright fluorescent particles, and a demonstration of the motility of vesicles, under different conditions in the cell, is described here. It is essential to use a low-level expression of fluorescent protein-tagged cellular components to ensure faithful replication for the behaviour of endogenous protein. However, this leads to a lower ratio for the signal-to-noise than is desired for the sub-pixel tracking of objects in digital images. This has driven the present effort to develop a computational model of the experiment in order to estimate the precision for localization of a fluorescent particle. Our work gives a greater insight, than has been managed in the past, into the accuracy and precision of particle tracking from live-cell imaging under a variety of different conditions, and it takes into consideration the current standards in digital technology for optical microscopy.

I. Introduction

Computational algorithms for particle tracking in video images have been applied in different areas of science and technology for many years. However, the recent burst of research activity in the nanosciences is currently leading to a renewed interest in the analysis of diffraction-limited images. Although the resolution of an optical microscope is in the region of 0.2 to 0.4 μm (approx. λ/2, where λ is the wavelength of light), there is still a potential to reveal the detailed mechanics for a particle moving on the scale of a few nanometers using the same instrumentation.

Particle tracking in diffraction-limited images

Quantitative studies of particle dynamics are made possible through the use of charge-coupled devices (CCDs) to capture digital images in an optical microscope and there is a potential to determine the fine detail in the position and trajectory of particles that cannot be identified by visual inspection. Currently, this type of analysis for video images is central in a wide range of research activity and an example of the remarkable accuracy that can be achieved is found in ref. 1. In this work, the set of coordinates for the positions of micron-sized spheres in a colloidal suspension were found to within an accuracy of 10 nm in the focal plane and 150 nm in the depth of the image. It should be appreciated that the former value is less than both the diffraction limit of the optical microscope and the pixel dimensions in the CCD array (85nm, for the example in ref. 1). The data analysis involved a process of identifying intensity peaks in the image of the colloidal suspension and refining the estimate for the location of each origin to the brightness-weighted centroid of the pixels. The same methodology has been applied in other disciplines including single-molecule research. Traditionally, a quadrant photodiode had been the preferred choice of detector for monitoring the small displacements of single particles. However, a recent publication demonstrated that the relative performance of a CCD and a quadrant detector is comparable as long as the temporal resolution of the camera is acceptable2. The quadrant detector is indeed the only option for the study of fast dynamics for a single particle but the advantage provided by digital imaging is the possibility of performing a single measurement to obtain data for a large number of particles in the field of view. This latter property is particular useful for single-molecule studies because it enables statistical distributions to be rapidly obtained.

The interest in particle tracking from sequences of in vitro or in vivo fluorescence images derives from the possibility to obtain unique information on the structure and dynamics of individual molecules. In particular, the observation of single copies for a protein or DNA is essential to reveal features that would normally be obscured by ensemble averaging in bulk measurements. It is typically necessary to conjugate a natural or synthetic dye, or fluorescent bead, to the target molecule and the position of the tagged particle can then be located in a wide-field microscope. The dimensions of a molecular dye are below the diffraction limit for an optical microscope and, therefore, the measured fluorescence profile is identical to a point source (a symmetrical image spread across a small number of pixels, with a width of 200-400 nm). Tracking the position of a diffraction-limited particle with sub-pixel accuracy involves the exact localization of the origin for the fluorescence. However, there is an inherent uncertainty in the measured position due to the stochastic nature of photon counting in a quantum detector. There is additional noise in the digital output due to the conversion of light intensity into an electrical output from the CCD. Therefore, it is essential to provide a detailed validation of a methodology that is used to deduce the origin of the fluorescence; especially, for examples in which the accuracies in position are given to sub-pixel values. The validation must include a rigorous account of the statistical fluctuations in the image data from photon counting and CCD noise.

The emission intensity from biological specimens, notably live cells expressing fluorescent proteins, is also inherently low. Despite the low signal-to-noise in the digital images, it is still crucial that the expression levels of proteins tagged with fluorescent markers (such as GFP) are maintained at low levels to reflect, as close as possible, endogenous conditions. Electron multiplying (EM) CCDs are used in many microscopy systems and these have largely replaced the need for intensified (I) CCD cameras for low-light measurements. EM-CCDs are currently favoured for sensitive imaging due to the exceptionally-low noise introduced by the amplification of the incident light and because they do not suffer the problem of massive damage caused by brief over-illumination of intensified cameras. An I-CCD is needed in scientific applications that require nanosecond-gating for the detection of light emission but this is not relevant for the particle tracking in cell biology. It is the large noise in the digital output from signal amplification that is the reason that the use of an intensified camera should be avoided for the precise localization of fluorescent objects in video images. Therefore, our work is based on the use of an EMCCD. Although the pixel size in an I-CCD is typically larger than that in recent models of EM-CCD (24μm compared with 8-16μm), the extent of pixelation in fluorescence images is less critical in many experiments than the noise introduced by the amplification of the signal.

The majority of experimental workers report accuracies for particle positions based on the prior measurement, under the same conditions, of a sequence of fluorescence images from a rigidly-fixed source. This is indeed an important sample control but it will fail to identify a bias in the method of analysis. For example, the value of position obtained using a centroid-based algorithm would be biased to the centre of the image matrix at low values of the signal-to-noise3. In addition, the standard error in the mean (SEM) calculated from a sequence of images will not give an insight into the relative contributions of photon counting, thermal fluctuations and instrument noise to the resulting uncertainty in the measured position. A number of researchers have recognized that it is important to develop a detailed theoretical model for the experiments. It is then possible to obtain artificial profiles from computer simulations of a fluorescent particle3,4,5,6. The exact location of the origin will already be known in each computer simulation, but the same algorithms used for the analysis of real data are then applied to the artificial image. Thus, a theoretical estimate for the SEM can be obtained in the particle-tracking experiment. In ref. 3, this approach was used to make a detailed comparison of different tracking algorithms for fluorescent particles. Realistic images of different-sized objects were generated with Monte Carlo methods, and the bias and standard deviation of a large sample gave an insight into the accuracy for each of the tracking algorithms. In particular, this work has become an important reference for particle tracking of diffraction-limited images. Gross’s group have given a more detailed investigation of centroid and correlation-based methods suitable for the localization of particles with sizes above the diffraction limit4, and they have also used these methods to examine single-molecule data for labelled kinesin (as in our work, described here). Their work included the analysis of computer-generated images from both fluorescence and differential-interference contrast microscopes, and they examined the influence of different conditions and instrumentation for the tracking of large particles. The same motivation in ref. 3 and 4 has also been shared in further publications from other groups but in each case the work is related to a particular system or apparatus.

In this paper, we will describe our approach for modelling the diffraction-limited images of fluorescence from labelled molecules, tailored to in vivo studies of particle dynamics. This area has not been treated explicitly before and our analysis will bear a much greater relevance than the earlier treatments given in the literature. Our work is based on the recording of digital images using the most common approaches in live-cell microscopy and single-molecule detection. The computational model is useful for the design of new experimental strategies and enables an appreciation of the precision for in vivo tracking of fluorescent particles.

Molecular motors and secretory cargo export from the endoplasmic reticulum

The organization of mammalian cells is highly dependent on the function of the intracellular cytoskeleton and associated molecular motors. These motors define the direction and rate of movement of intracellular organelles and transport vesicles; thereby underlying the correct operation of multiple aspects of cell physiology and, in particular, the secretory pathway. This is of further importance in many disease states. A full understanding of the mechanistic basis for organelle position and secretion requires a thorough analysis of motor-protein function. One approach toward this goal is to analyze the effects of these motors on the position of specific organelles. Considerable work has focussed on the dynamics and mechanism of secretory cargo export from the endoplasmic reticulum (ER). This event is the first vesicular transport event in the mammalian secretory pathway and proceeds by the recruitment of a cytosolic-coat complex, COPII, to the ER membrane at specific sites known as export sites (reviewed in ref. 7). These sites are defined by the presence of COPII proteins that together assemble to drive the selection of secretory cargo from within the ER membrane and the deformation of the ER membrane to generate coated vesicles. Our previous work has shown that these sites couple to the dynein/dynactin machinery of the microtubule cytoskeleton8. In our recent work, we have determined the role of the microtubule motor kinesin on the function of secretory cargo exit sites that form part of the mammalian endoplasmic reticulum. These exit sites (ES) can be marked with EYFP-tagged Sec23A9. This protein lies at the heart of the COPII complex and provides a faithful marker of ERES localization in cells (see ref. 9). ERES undergo short range dynamic movements in cells and considerable evidence shows that these movements, and the broader function of ERES in accumulating and packaging secretory cargo, are microtubule dependent. ER-to-Golgi transport depends on the function of the dynein motor protein10 but some intriguing evidence exists that kinesin might also be involved11. Our goal has been to image the dynamics of ERES at a sub-pixel resolution in cells in which we perturb motor protein function by siRNA-mediated gene silencing. The full effect of the different conditions on the motility of ERES will be described in a future publication. The present paper will give an outline of these experiments and it will describe the theoretical model that we are using to validate the observations made from in vivo imaging of ERES. A key problem with this work is the inherent low signal-to-noise ratio owing to the necessity to express low levels of the protein marker, and the considerable background from either diffuse-distributed label or sample autofluorescence. Nevertheless, we are able to demonstrate tracking of the position for an exit site with a precision of ∼11 nm. This is sufficient to identify the movement of an ERES on a single microtubule filament inside a cell. We will also demonstrate the genuine possibility to measure the particle position to 4-6 nm; this would be suitable to reveal the discrete steps made by a motor protein. However, this would be concealed in our current experiments that directly measure ERES because they are complex amorphous structures and the discrete steps for the displacement of a motor protein are unlikely to be clearly seen as a corresponding displacement of the centre-of-mass for the ERES. Nevertheless, our analysis of data does point toward alternative strategies that would lead to a successful measurement of the position (at near-nanometre precision) for in vivo particles.

II. Overview of Experimental Studies

In this section, we will give an outline of our method for analysing a sequence of in vivo fluorescence images of EYFP-tagged marker proteins and illustrate the dynamics of ERES under different conditions in the cell.

Normal HeLa cells following transient gene expression of EYFP-Sec23A were studied using wide-field epifluorescence microscopy. The ERES are marked at numerous locations by multiple molecules of EYFP-Sec23A and they appear as bright particles above the background in fluorescence images of live cells. The digital pictures shown in this paper were obtained using an Improvision 3DM system with an inverted microscope (Olympus IX-81, 100× objective lens), 175W xenon lamp (Lambda DG-4, Sutter Instrument Company) and a Electron-Multiplied Charge-Coupled Device (EM-CCD, Hamamatsu C9100-12). There is not a benefit in the use of intense laser illumination to address the low signal-to-noise in the digital images of live cells expressing fluorescent proteins. A higher level of illumination will lead to more rapid photobleaching of fluorophores and prevent the tracking of a particle for a sufficient interval of time. We have not attempted to calibrate the microscope stage to find the exact (x, y)-coordinates for the position of each fluorescent particle. The important information for our studies is contained in the relative displacement of each particle compared with its initial position.

Finding the origin of a point source of fluorescence

A fluorescence image of a fixed cell is shown in fig. 1a. Symmetrical peaks are seen for small assemblies of EYFP-Sec23A marking each individual ERES. In each case, the dimensions of the particles are below the diffraction limit of the microscope and the spatial distribution is indistinguishable from a point source. The image should actually appear as a pattern of light and dark regions (known as an Airy disc) but this structure is not resolved in the fluorescence microscope due to a coarse pixelation and the presence of shot noise. Instead, the spatial distribution (or the point-spread function, PSF) is described with sufficient accuracy using a 2-dimensional Gaussian function, and the expected profile of the fluorescence for a total integrated intensity of N photons is given by:

$$\begin{array}{c}\langle I(x,y)\rangle =\frac{N}{2\pi s^2}{e}^{-({(x-x_0)}^2+{(y-y_0)}^2)∕2s^2}\hfill \\ \text{where}s=\frac{\Lambda }{2\sqrt{2\ln 2}}\hfill \end{array}$$ (1)

where x and y are the cartesian coordinates in the image plane, and the origin of the peak is (x₀, y₀). The standard deviation, s, is related to the full-width-half-maximum, Λ, of the PSF and, under 100× magnification, its value is similar to the pixel size, a, for images recorded by charge-coupled devices (CCD). Therefore, the expression in eq. 1 must be integrated to describe the spatial distribution of a point source in a digital image, and the expected profile of the fluorescence consisting of an array of i × j pixels is given by

$$\langle I(i,j)\rangle =\frac{N}{2\pi s^2}\underset{x_i-a∕2}{\overset{x_i+a∕2}{\int }}\underset{y_j-a∕2}{\overset{y_j+a∕2}{\int }}{e}^{-({(x-x_0)}^2+{(y-y_0)}^2)∕2s^2}dxdy$$ (2)

where x_i, y_j are the Cartesian coordinates for the centre of the pixel (i, j). The integral of a Gaussian can be given in terms of the error function (erf), and an analytical solution for the double integral is

$$\begin{array}{cc}\hfill \langle I(i,j)\rangle =& \frac{N}{4}\left\{erf\left(\frac{x_i+a∕2-x_0}{s\sqrt{2}}\right)-erf\left(\frac{x_i-a∕2-x_0}{s\sqrt{2}}\right)\right\}\hfill \\ \hfill \times & \left\{erf\left(\frac{y_j+a∕2-y_0}{s\sqrt{2}}\right)-erf\left(\frac{y_j-a∕2-y_0}{s\sqrt{2}}\right)\right\}\hfill \end{array}$$ (3)

In our work, we have treated the EYFP-Sec23A assembly as a single entity and we will in fact be determining the centre of brightest labelling of ERES by Gaussian fitting. Typical values for the full-width-half-maxima, Λ, of the PSFs for ERES (as seen in our digital images) are around 350nm; in this case, the standard deviation, s, is ∼150nm. We expect that the actual size of the particles in fig. 1a is not much less than this value for Λ and similar to the diffraction limit of the microscope. The location of the origin for the fluorescence can be determined accurately by identifying the values of x₀ and y₀ in eq. 3 that give the best possible fit with the measured profile, I(i, j), in the digital image. This is formally done using a mathematical algorithm for minimizing the function χ²,

$${\chi }^2=\sum _{ij}\frac{{(I(i,j)-\langle I(i,j)\rangle )}^2}{{{\sigma }_{ij}}^2}$$ (4)

and evaluating the least-squares difference between the measured and expected values of the intensity profile. In this case, the terms in the summation are each weighted by a factor equal to the inverse of the mean square noise (or variance), σ_ij². We use a numerical method applying the downhill simplex algorithm to obtain the parameters x₀, y₀, N and s in eq. 3 corresponding to a minimum value of χ². ^* The computer code is written in Fortran77 using the subroutine amoeba, developed by Press et al.12, for minimization of multiparameter functions. The fluorescence image obtained from an experiment is converted to an ASCII data file and read directly by the Fortran program. For each data point in the image file, an estimate of the root-mean-square (RMS) noise, σ_ij, is made using data for the noise characteristics of the CCD (as outlined below).

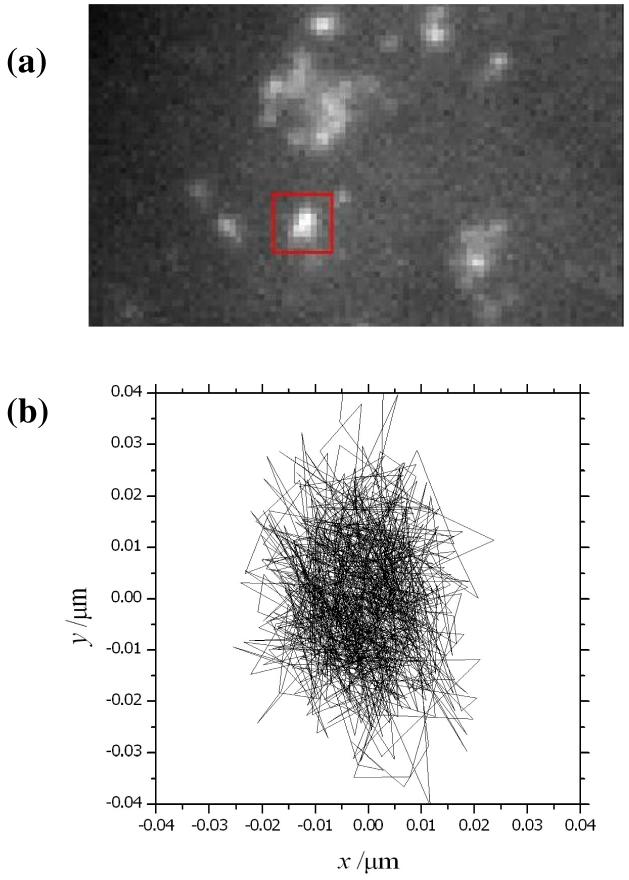
Figure 1.

(a) Image of a fixed HeLa cell following transient gene expression of EYFP-Sec23A using wide-field epifluorescence microscopy. The ERES are marked by the fluorescent-tagged proteins. (b) Experimental tracking of an individual ERES (highlighted by a red box) gives an estimate of the instrument precision under these conditions. The fluorescence emission from EYFP-Sec23 molecules was measured at 20.1195fps, and the location of the origin for the fluorescence was tracked in an overall sequence of 1000 frames

In vivo tracking data of ERES marked with EYFP-Sec23A

The data shown in fig. 1a is the 1^st fluorescence image in a sequence of 1000 frames measured for a fixed cell expressing EYFP-Sec23A. The trajectory shown in fig. 1b has been determined (as described above) from the coordinates (x₀, y₀) of the origin for the particle highlighted in the red box. The minimization of χ² using an integrated 2D Gaussian for the expected-intensity profile, 〈I (i, j)〉, was performed using a grid of 7 × 7 pixels centred on the element of highest intensity in eq. 6. Our tracking program adjusts the location of this grid after the origin has been found and this ensures that the PSF is centred during the analysis of each successive frame. The integration time for each image was 48ms and the capture rate was 20 fps. The position of the origin for the fluorescence is restricted to a region of 40×40 nm (the full range of the experimental data in fig. 1b). The actual standard deviation for the x- and y- displacement in the data from fig. 1b is 9 and 13 nm respectively. This measurement is an important control to identify the stability of the current instrument to vibrations and thermal fluctuations. In this paper, we will state that the instrument precision for the measurement of position is approx. ±11 nm based on the average value of the standard deviations given above. This precision would likely be considerably improved with better isolation of the microscope stage. The current experiments are performed on a standard optical table, resting on a workstation frame, and our apparatus does not have a very effective method for instrument isolation and vibration control. We believe that there is a potential for locating the origin of fluorescence from tagged proteins (using Gaussian fitting as in fig. 1) to much better than ±11 nm and this will be justified in the next section. This degree of precision is important for revealing the detailed mechanism of cellular processes driven by the displacement of motor proteins.

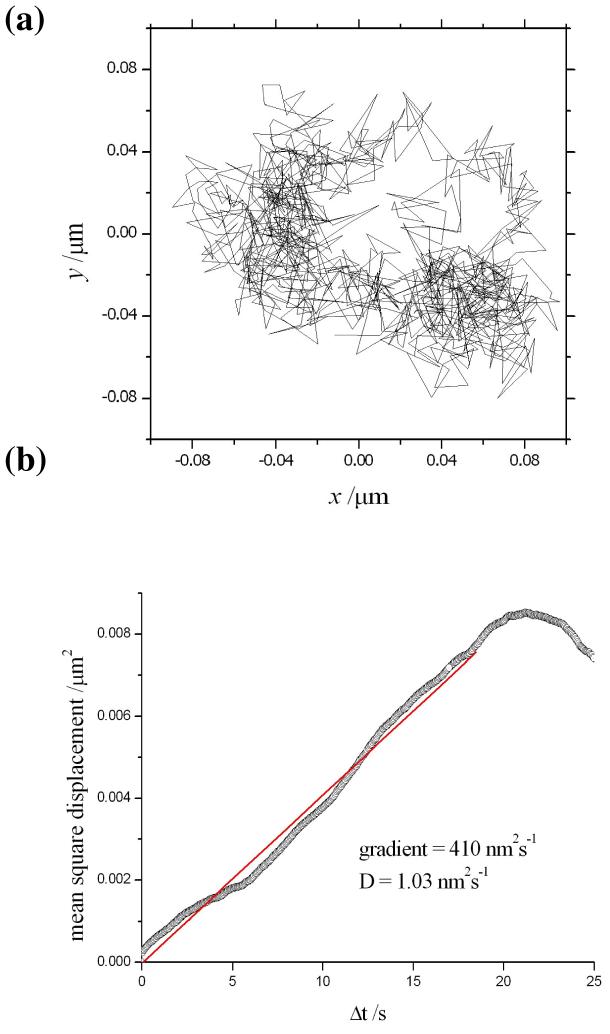
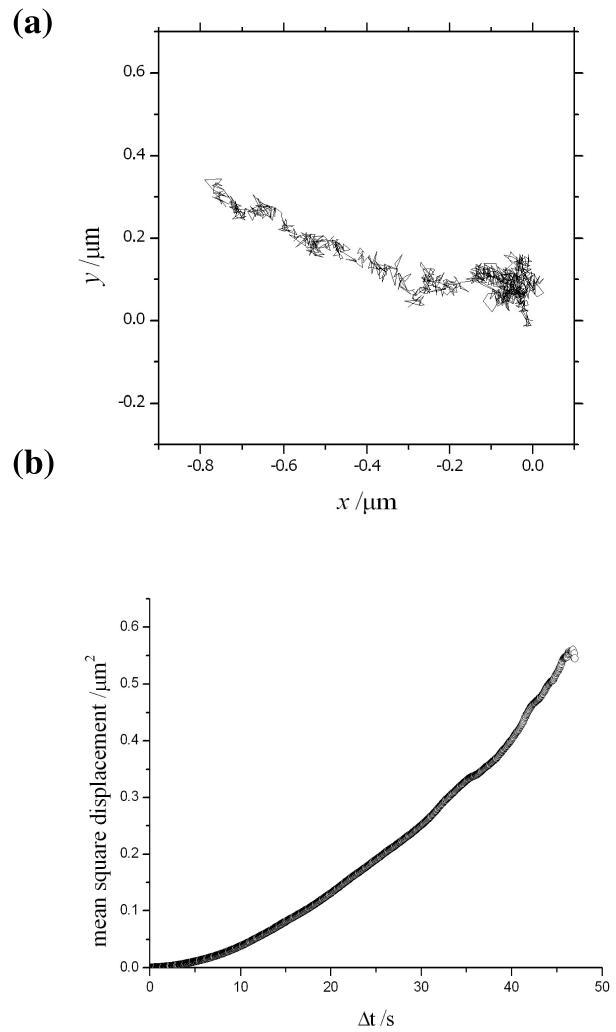
The motility of ERES in kinesin-1 suppressed HeLa cells was recorded under the same conditions and an example of the experimental data obtained from a single marker is illustrated in fig. 2a. In this case, the fluorescent-tagged object is seen to explore a wider cross-sectional area of 160×160 nm. This particular example was found to be representative of a large ensemble of particles measured in the images from wide-field microscopy. An interpretation in terms of Brownian motion accounts for the observed trajectory as demonstrated in the plot of the mean-square displacement against the time interval (see fig. 2b). The linear region up to 20 s is used to obtain an estimate for the diffusion constant of approx. 1.0 nm²/s. However, the trajectory of a single particle should not be used to make a general conclusion about the presence of either confined or directed motion under these conditions. A large distribution of trajectories is currently being analysed from a series of measurements and the results will be presented in a future publication. A contrasting trajectory is seen for the motility of ERES in normal HeLa cells (without suppression of kinesin-1) in fig. 3a. In this example, a much longer range of movement (∼800nm) is seen to take place along a linear track. Note that the cells were incubated with cytochalasin D to depolymerise actin filaments and allow this type of trajectory to be clearly seen. This has no effect on the motility of ERES and the directed movement along a microtubule is clearly demonstrated in the corresponding plot of the mean square displacement against the time interval in fig. 3b.

Figure 2.

(a) Experimental tracking of an ERES in kinesin-1 suppressed HeLa cells. (b) The mean-square displacement of the particle as a function of the time interval appears to suggest Brownian motion in the cell

Figure 3.

(a) Experimental tracking of an ERES in normal HeLa cells. (b) The mean-square displacement of the particle as a function of the time interval suggests that the motion is directed along the length of a microtubule.

We will now analyse the experimental data in more detail and, for illustration, use the example in fig. 2a representing a trajectory of a single ERES in kinesin-1 suppressed HeLa cells. The ERES are tagged with multiple EYFP-tagged protein molecules and, consequently, we observe a gradual decrease in the detected signal due to photobleaching of the fluorescent marker during the measurement of a sequence of frames. This is in contrast to the single-step events that occur in protein labelling with single molecules of dye. A theoretical model has indicated that as many as 600 COPII complexes are assembled in the self organization of ERES13. However, in our experiments, the expression level is low and the ratio of EYFP-Sec23 to endogenous EYFP is likely to be from 1:20 to 1:5 (estimated from immunoblotting). Therefore, it is expected that we are imaging of the order of 30-100 EYFP probes per particle in the initial frame of the sequence. The first and last images recorded (at times of 0.05s and 49.70s) for an example ERES in a sequence of 1000 frames are illustrated in fig. 4a. The pixel size of the CCD array is 16μm and pixel binning was not used in these images; therefore, the unit size is 160nm (with 100× magnification). It is informative to estimate the actual number of photons incident on the chip during the 48ms-integration time for each frame. This is done using the specifications supplied by the camera manufacturer for the (i) gain calibration, (ii) analog-to-digital conversion (ADC) factor and (iii) quantum efficiency. Note that the sensitivity setting indicated in the operating software for commercial EM-CCDs represents an arbitrary (uncalibrated) magnitude for the gain. Furthermore, the calibration of the sensitivity setting will differ amongst manufacturers and camera models. In our experiments, the actual gain was ×80 and this corresponded to a sensitivity setting of 140 for the Hamamatsu C9100-12. The ADC factor for the same model is 23 electrons per count (@ 14 bits per channel) and the quantum efficiency is ∼93%. The background level has been subtracted from each pixel using the average intensity observed around the periphery of the observation window shown in fig. 4a. This last step enables the number of incident photons from the fluorescent marker to be determined. In this example, the values ∼12,000 and 7000 photons are obtained for the first and last frames. The gradual decrease in the number of photons from the fluorescent marker results in a corresponding decline in the r² parameter during the sequence of measurement; i.e. from >0.98 to <0.97 as shown in fig. 4b^†.

Figure 4.

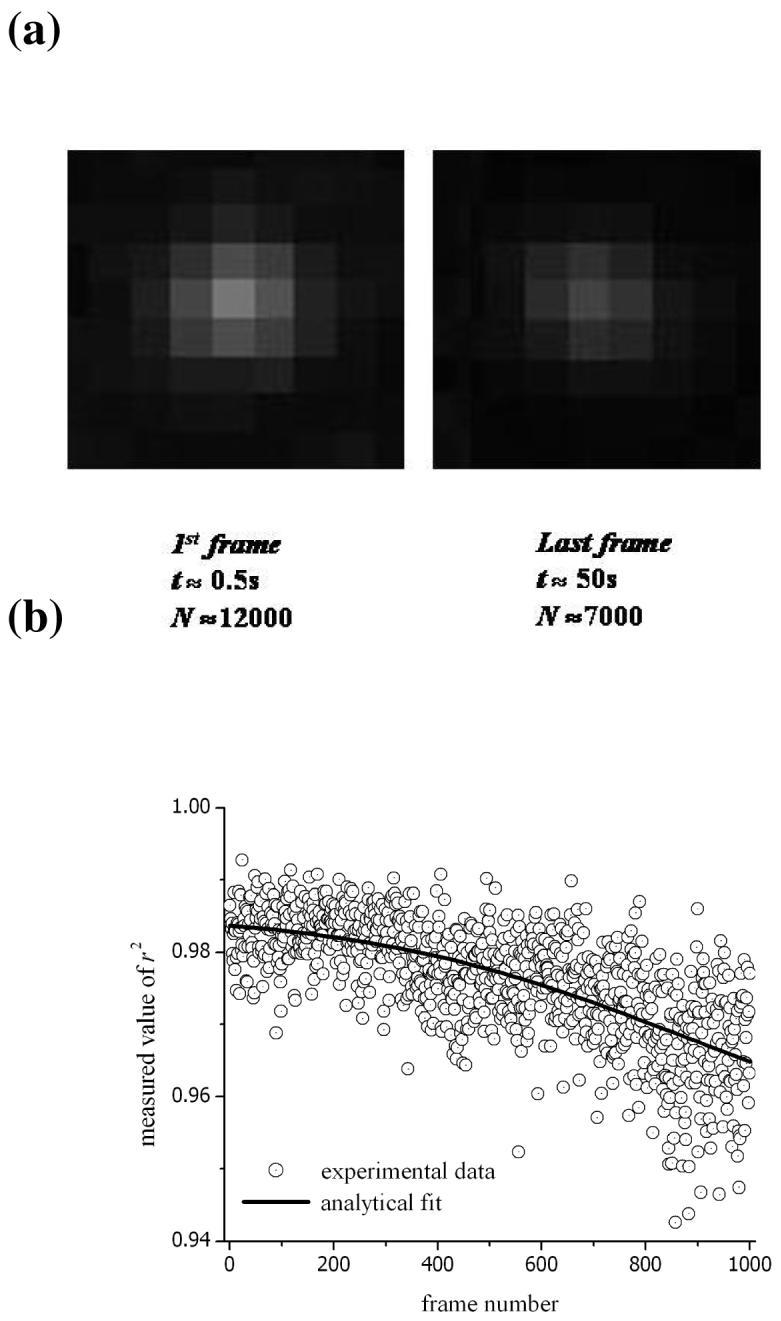
(a) The fluorescence-intensity profile for ERES labelled with EYFP-tagged proteins. The in vivo images are the first and last obtained in a sequence of 1000 frames. The experimental conditions are described in the main text. The images were generated by 12000 and 7000 incident photons (from fluorescence) collected during a 48ms integration time. (b) The r² parameter representing the goodness-of-fit was calculated for each frame.

The multiplication gain of ×80 used in our experiments is not the highest setting for the EM-CCD (this is ×255). However, this was found to be the optimal setting for particle tracking and, in section IV, the importance of using a moderate value for gain (rather than the maximum) will be explained. The background level of light incident on the CCD can be estimated using the same method as above. However, it is necessary to subtract the DC offset for the ADC. This value will be different for various models of camera (and it can sometimes be adjusted within the software). For the in vivo image used to obtain the data in fig. 2, we found a background of 400-500 photons per pixel in regions without large assemblies of EYFP-tagged proteins. It will be realised that this photon count is much higher than the typical charge in a CCD pixel that arises from the dark current during the image-capture time, and this is the reason that it has been neglected in the calculation of the photon levels in the background light. An estimate of the actual dark charge is given below. The important observation is that, in these examples, the background in fluorescence images of live cells is dominated by scattered light and non-localised fluorescence in the cell.

An overview of the sources of noise in digital images

The individual sources of noise in digital images obtained with CCDs are well understood and we can use this knowledge to obtain an estimate of σ_ij (as required for calculating χ² in eq. 4). We will start by giving an outline of the various contributions to the overall RMS noise (σ_ij) and these will be classified as either temporal or spatial. An approximate value for the signal-to-noise (SN) ratio in fig 4a will be obtained but a more detailed calculation of noise is described in a later section.

The temporal noise is normally dominated by shot noise, which is due to the stochastic properties for photon counting and charge accumulation in a CCD. It will include a component for the dark charge but, in this example, it can be shown to be negligible. The expected number of dark counts (in electrons per pixel), n_d, can be estimated using the empirical formula in equation 6​¹⁴.

$$\begin{array}{c}\hfill \langle n_d\rangle =2.5\times {10}^{15}\times I\times t\times A^2\times T^{3∕2}\exp (-E_g∕2kT)\hfill \\ \hfill E_g=1.1557-\frac{7.021\times {10}^{-4}\times T^2}{1108+T}\hfill \end{array}$$ (6)

where A is the area of a pixel in cm², I is the dark-current density at 300K in nA/cm² (typically, around 1 nA/cm²) t is the integration time for a single frame, T is the temperature in Kelvin, E_g(T) is the bandgap of silicon in eV and k is the Boltzmann constant (8.62×10^-5 eV/K). For our model of EM-CCD, the pixel area is 2.56×10^-6 cm² and it is operated at -50°C. For the integration time of 48ms used to obtain the digital images shown in fig. 4a, the expected dark count is less than 1 electron per pixel. The RMS dark noise can be estimated by assuming Poisson statistics for the generation of electronic charge, and it would have a value equal to the square root of the expected dark count per pixel. In comparison with the observed background of 400-500 photons per pixel, it is clear that the shot noise will be dominated by the amount of incident light on the CCD.

There is some value to be obtained in the calculation of the power-spectral density from the observed temporal fluctuations in the intensity of the fluorescence signal. The Fourier transform of the photon signal gives the intensity as a function of the different frequency components in the signal, and it is most important that the power spectral density is uniform in the region of frequencies corresponding to the integration time for the CCD (to minimize temportal noise). In the majority of cases, this will be frequencies around 100 to 10 Hz corresponding to integration times of 10 to 100ms (note that the integration times are slightly less than the period between successive frames in a video recording). Measurements from David Grier’s group have already demonstrated that the power-spectral intensity is uniform at low frequencies for typical molecular fluorophores15. There is a decline at higher frequencies attributed to inter-system crossing (singlet-to-triplet transitions) and the formation of dark molecular states but this will not be important for normal integration times in a CCD. A different behaviour is observed in the microscope images of quantum dots. In this case, the ‘blinking’ of these fluorescent particles leads to the presence of approx. 1/f noise and an increase in the power-spectral density at low frequencies15. The varying components of the Fourier series can result in much greater temporal noise in digital images of a quantum dot.

The spatial noise in digital images can arise from the non-uniformity in either the photo-response or dark current for different pixels in the CCD array. However, this can be neglected under the conditions of high background in live-cell microscopy. We have carefully considered the RMS readout noise using the specification provided by the manufacturer. Strictly, we should have paid some attention to the possible electronic artefacts or fluctuations in the intensity of the light sources. However, these should be minor in short sequences of images.

It is helpful to make an estimate of the signal-to-noise (SN) in the fluorescence images. This can be evaluated in a window around the area of maximum intensity for the particle. In the example from fig. 4a, this is an area of 5 by 5 pixels, and the arrival of photons from the fluorescent marker cannot be distinguished from the background noise outside this region on the CCD array. The SN is correctly given for the conditions in our experiment by the formula:

$$\mathrm{SN}=\frac{N}{F\sqrt{{{\sigma }_N}^2+{{\sigma }_B}^2}}\approx \frac{N}{F\sqrt{N+B}}\text{or}\frac{\sum _{ij}{n}_{ij}}{F\sqrt{\sum _{ij}(n_{ij}+b)}}$$ (7)

where the numerator and denominator represent the total signal and total noise respectively in the area of interest, and the summation on the right-hand side of the equation must be performed across the entire 5 by 5 window (as indicated above). n_ij is the number of fluorescent photons incident on the i^th, j^th pixel element and b is the number of photons from the background light incident on a single pixel (assumed to be uniform across the area of the window). The value of F is √2 and it is the noise factor associated with the gain register in the EM-CCD (more detail is given below, and a different value of F would be needed to describe the noise introduced by an intensified CCD). The estimation of the number of photons from the fluorescent marker (N) and the average background level (B) in the images from fig. 4a were outlined above. It should be appreciated that the value for the total noise in the denominator of eq. 7 is estimated by treating the counting of photons by the CCD with Poisson statistics.

Using the method outlined above, the SN is approx. 57 (for the 1^st frame) and 35 (for the last frame in fig. 4a). We are cautious about reporting these numerical values for the SN. This is because there are different estimates provided in the literature for the SN in fluorescence images that are quite comparable in terms of signal strength and noise to the results shown above. In most cases, an outline for the calculation of signal-to-noise is not given, and we are concerned that an unsuitable procedure is sometimes used. We would like to draw attention to a numbers of features in eq. 7: (i) the use of photon numbers for the signal to enable an estimate of the total noise using a treatment based on Poisson statistics (note that the noise cannot be represented by Poisson statistics on the counts measured from the ADC), (ii) the calculation of the total noise in the denominator is made using the sum rule for the photon noise and background noise, (iii) the SN is calculated across a user-identified window in the fluorescent images (in this example, 5 by 5 pixels) and the numerical value of SN depends on the size of the selected window, and (iv) the inclusion of the noise factor, F, for the gain in images recorded using an EM-CCD camera. Finally, the gain, G, of 80× used in these measurements gives a corrected readout error (σ_r/G) of 2 electrons at the input to the gain register (according to data from the manufacturer). Therefore, the read noise has been neglected in the estimate of the total noise used in eq. 7. Other commercial models of EM-CCD are expected to have similar specifications.

Despite the low signal-to-noise in the resulting images, it is still essential to use a low level expression of fluorescent protein-tagged cellular components. This will ensure that the behaviour of endogenous proteins are faithful replicated in the experiment; this has been demonstrated for Sec23A in ref. 9.

III Theoretical Analysis of the Tracking Algorithm & Discussion of the Data

Thus far, the discussion of the data has included the evaluation of actual counts for the number of photons incident on the detector, the dark noise in a CCD (eq. 6), and the expected noise in the output data (eq. 7). These calculations merely required an understanding of silicon technology and the quantum detection of light, and are broadly relevant in optical microscopy and imaging. In the instances that the manufacturer’s data for our actual model of EM-CCD (Hamamatsu, C9100-12) was used in a formula, it is entirely possible to substitute appropriate values from other manufacturers. In this section, we will analyse in more detail the tracking algorithm used to obtain the data in figs. 1b, 2b and 3b. The expected accuracy of Gaussian-fitted functions will be determined by using a theoretical model for the fluorescence images.

The theoretical work in this paper remains focussed on the use of an EM-CCD, and the analysis is applicable to the majority of modern imaging systems in cell biology. The Silicon-chip technology is universal for the gain register in models from different manufacturers, and the empirical equations given below are valid for any experimental setup using an EM-CCD. It is merely necessary to obtain the relevant calibration data from the manufacturer. The alternative to our theoretical approach requires the user to experimentally measure the various parameters such as gain, ADC factor and dark current at regular intervals of time. Although this is a more careful and rigorous method, it will be costly in terms of the time spent, the expertise needed and the additional equipment and standards required for accurate calibration. We recommend the procedure outlined in this paper as a practical guide to obtain precise data in a timely manner from a particle-tracking experiment.

Computational modelling

An estimate of the RMS noise for the measured signal intensity in each pixel, σ_ij, is given in the denominator of eq. 7. However, a more detailed consideration of this term will now be given and the associated probability distribution for the number of incident photons (n_ij) will be used to derive a theoretical model of the fluorescence profiles.

The RMS noise σ_ij contained terms for the stochastic properties of photon counting and instrument noise. In the shot noise, we should have included a contribution due to the dark current (and RMS dark noise) and, in the instrument noise, we should have accounted for the reset noise, clock-induced charge and readout error. It is reasonable to neglect the reset noise and clock-induced charge as the photon noise will dominate the uncertainty in the stored charge for the signal intensities observed in the majority of live-cell fluorescence images. In general, the background level in fluorescence images can be assumed to include the dark current because the statistics for the intensity fluctuations are exactly the same (see below); and, as shown in the previous section, the dark noise is usually negligible due to the much higher background in cell images. Thus, the RMS noise for the intensity of each pixel (i, j) can be simply expressed as

$${\sigma }_{ij}=f\{{\sigma }_p(i,j),G,{\sigma }_r\}$$ (8)

where σ_p is the photon noise (due to the signal, n_ij and background, b), G is the gain of the electron multiplier, and σ_r is the readout error of the CCD. The number of photons incident on each pixel, m_ij, will be described by Poisson statistics, and the photon noise is given by:

$$\begin{array}{c}{\sigma }_p(i,j)=\sqrt{m_{ij}}\hfill \\ m_{ij}=n_{ij}+b\text{and}N=\sum _{ij}{n}_{ij}\hfill \end{array}$$ (9)

as before, n_ij and b are the expected number of photons incident on each pixel that originate from the point source and the background respectively. The output from the gain register in an EM-CCD is accurately modelled using a gamma distribution (see ref. 16). This is described by the probability-density function shown below for an input into the gain register of m_ij electrons and an output consisting of Ω_ij electrons.

$$\begin{array}{c}p\left(x\right)=\frac{{\left(x\right)}^{k-1}}{(k-1)!{\theta }^k}\exp \left(-\frac{x}{\theta }\right)\hfill \\ \text{with}\theta =G-1+\frac{1}{m_{ij}},\hfill \\ k=m_{ij}\hfill \\ x={\Omega }_{ij}-m_{ij}+1\hfill \end{array}$$ (10)

This distribution has an expected value of Ω_ij equal to G× m_ij and a standard deviation equal to G×√ m_ij (for a fixed value of m_ij). However, this last value does not account for the uncertainty that already exists in the number of incident photon on the CCD, m_ij (see eq. 9). Nevertheless, it is possible to specify a standard deviation in the gain factor, σ_G, for the distribution in eq.10:

$${\sigma }_G(i,j)=\frac{1}{m_{ij}}\times G\sqrt{m_{ij}}=\frac{G}{\sqrt{m_{ij}}}$$ (11)

and the correct value for the standard deviation (or RMS noise) in the number of output electrons from the gain register, σ_Ω, can be obtained using the product rule:

$$\begin{array}{cc}\hfill {\sigma }_{\Omega }(i,j)& =G{m}_{ij}\sqrt{\frac{{\sigma }_G{(i,j)}^2}{G^2}+\frac{{\sigma }_m{(i,j)}^2}{{m_{ij}}^2}}\hfill \\ \hfill & =G\sqrt{2m_{ij}}=GF\sqrt{m_{ij}}\hfill \\ \hfill \text{with}F& =\sqrt{2}\hfill \end{array}$$ (12)

The readout error will lead to a normal distribution of intensity values for each pixel and a final expression for the RMS noise for the signal intensity is given by:

$${\sigma }_{ij}=\frac{1}{G}\sqrt{{\sigma }_{\Omega }{(i,j)}^2+{{\sigma }_r}^2}=\sqrt{F^2{m}_{ij}+{\left(\frac{{\sigma }_r}{G}\right)}^2}$$ (13)

A realistic intensity pattern for a point source was calculated by generating random deviates from the expected values given by eq. 3. This included (i) a Poisson distribution for photon noise, (ii) a gamma distribution for gain noise and (iii) a normal distribution for readout noise, as outlined above. This gives a more accurate model for the fluorescence images obtained from live cells than the theoretical data provided in earlier publications (i.e. refs. 3 to 6). In particular, we have found that it is essential to account accurately for gain noise associated with amplification in an EM-CCD. We believe that our work is the first, in the area of particle tracking, to use a realistic statistical distribution for the charge generated by electron multiplication in a CCD. Although the gamma distribution in eq. 10 is an approximate (empirical) formula, it has been shown in ref. 16 to give an excellent agreement with the measured input and output from the gain register. The same formula is suitable to be used in a theoretical treatment for any commercial EM-CCD (using the calibration data supplied by the manufacturer for the gain, G). Although the readout noise was neglected from eq. 7 to obtain an estimate of the signal-to-noise, it has been included in eq. 13 and our calculations of the intensity patterns for a point source. Nevertheless, the effect of the readout noise is vanishingly small (especially at higher values of gain).

The point-spread functions are simulated using a Fortran code incorporating subroutines developed by Press et al. in ref. 12 to give a sequence of psuedo random numbers and deviates with the appropriate probability distributions. The results from these calculations are described below and they have been used (i) to predict the likely precision for locating the origin of a particle from 2D Gaussian fitting and (ii) optimize the conditions in our experiments.

Accuracy and precision of fitted Gaussian functions to fluorescence images

In this section, we will give an insight into particle-tracking experiments using theoretical image data. The results will have a direct relevance to our work but they also have a broad importance in live-cell imaging and the same procedures can be used to investigate a wide range of specific experimental conditions.

As described in the introduction, it is possible to report accuracies for the origin of diffraction-limited objects (x₀, y₀) that are much less than the dimensions of a pixel in the digital images. The magnitude of the signal-to-noise ratio will determine the degree of uncertainty in the position. Selvin and co-workers have claimed an accuracy of 1.5 nm for the location of the origin in a digital image with unit dimensions, a, of 86nm17. These experiments used total-internal-reflection fluorescence microscopy (TIRFM) to observe single molecules of an organic dye. This technique involves the near-field imaging of a sample and it achieves an exceptional suppression of background light. Consequently, this degree of accuracy cannot be expected from the far-field images of live cells obtained in our measurements using an epifluorescence microscope. The reason that TIRF is an unsuitable technique for the present study is that it is restricted to events occurring within ∼100 nm of the surface of a coverslip. The resulting near-field images would fail to reveal the majority of ERES and the analysis would be limited to the periphery of the cell. More generally, it would also preclude the analysis of large numbers of other events happening further inside cells including the majority of endosomes, lysosomes, and melanosomes. Nevertheless, it has still been possible to use TIRF to outstanding effect in certain applications; for example, the lateral diffusion of membrane-bound molecules is measured in ref. 18.

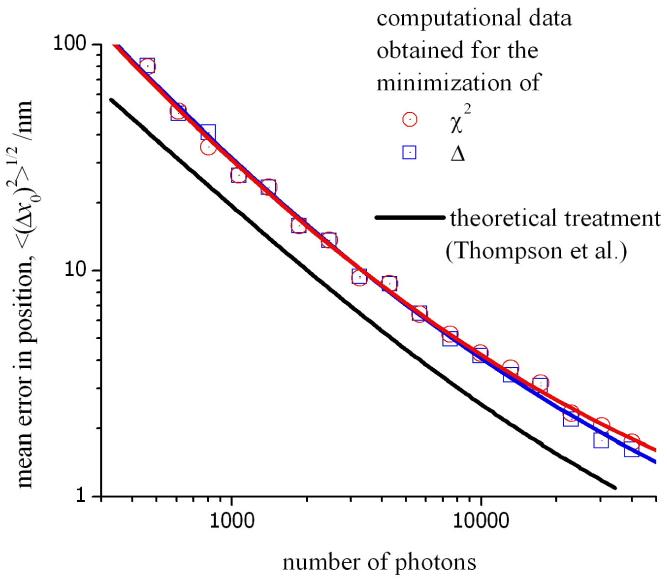
Thompson and co-workers have provided a theoretical treatment to estimate the uncertainty in the location of the origin from least-squares analysis6. They derived an expression for the mean error in each coordinate (see eq. 14) as a function of the signal intensity (or total number of photons, N) and the background noise, σ_b.

$${\langle {\left(\Delta x\right)}^2\rangle }^{1∕2}={\left(\frac{s^2+a^2∕12}{N}+\frac{8\pi s^4{{\sigma }_b}^2}{a^2{N}^2}\right)}^{1∕2}$$ (14)

This function has been plotted in fig. 5 (solid line) against the total number of photons, N, incident on the CCD. Appropriate values for the standard deviation of the PSF and background noise were used that are relevant to our experimental conditions. Note that the noise components arising from the gain of the multiplication register and the readout of the CCD, as well as the quantum efficiency of the detector, have been neglected from the theoretical values obtained from eq. 5. Therefore, this data must be regarded as a lower limit to the uncertainty in the position of the fluorescence origin. This is apparent in fig. 5 by comparing the solid black line with the computational data shown in red. The latter plot was obtained by generating a series of intensity profiles for a point source (with a known origin) and evaluating the mean error in the estimated value of x₀ obtained from minimization of χ². A realistic model of our experiments was achieved by using a random number generator to fix the location of the point source (at an intermediate value between pixels in the CCD) and then superimposing a noise on the fluorescence profile using the methods described above. The error in the position of the origin was determined for each of the intensity profiles generated in the model data and the results shown in fig. 5 represent the average of 100 calculations. For each intensity profile, a different set of coordinates were generated for the origin and a new sequence of random deviates was used. In addition, we have made a suitable correction to the theoretical data to account for the quantum efficiency of the detector (93%; see above). A larger mean error is found in the position of the origin compared with the theoretical values given by eq. 14.

Figure 5.

The mean error in the position of the origin measured using least-squares analysis. The solid line represents a theoretical treatment outlined in ref. 6. The data in red and blue are also theoretical results obtained in this work using a computational model for the measured intensity profile of a point source. The mean error in x₀ has been calculated by minimizing χ² (red) and Δ (blue) respectively; see main text for details.

Churchman et al. have pointed out that the estimated mean error, or accuracy, obtained in this type of calculation must be interpreted correctly19. In particular, that the mean error associated with Gaussian fitting represents the uncertainty in a single measurement of the particle position. The standard error in the measurement of displacement in a particle-tracking experiment from adjacent pairs of fitted Gaussian functions will actually be systematically larger than the values shown in fig. 5; and we refer the reader to ref. 19 for a detailed explanation.

The data in fig. 5 also shows that an accurate value of x₀ can be obtained by replacing the function χ² with an unweighted function for the sum of the square differences, Δ.

$$\Delta =\sum _{\mathit{ij}}{(\mathit{I}\left(i,j\right)-\langle \mathit{I}\left(i,j\right)\rangle )}^2$$ (15)

The trace shown in blue is the expected uncertainty in x₀ obtained by merely evaluating the least-squares difference between the measured and expected values for the intensity profile. The absence of a weight for each individual term in the summation is equivalent to stating that the RMS noise, σ_ij, is identical for each pixel. This is not a correct account of σ_ij (see above), however, it is shown in fig. 5 that the value of x₀ cannot be determined with a greater accuracy by minimising χ². Therefore, we have used the more direct method of least-squares analysis by minimising the value of Δ to locate the origin of fluorescence.

In ref. 3, Cheezum et al. have considered a number of different algorithms for particle tracking experiments including various centroid and correlation methods. We have not considered these other algorithms in the present paper. Nevertheless, they did observe that least-squares analysis involving the numerical fitting of a Gaussian function gave the most accurate results for small objects (less than the wavelength of light) and low values of signal-to-noise. This has also been the method of choice in experimental studies by the groups of Paul Selvin17, Richard Cherry20 and Gerhard Schütz21. However, it should be appreciated that Gaussian fitting is only suitable under conditions of uniform background across the PSF. A useful method for particle tracking under non-uniform conditions has been developed in ref. 5. This latter method is based on polynomial fitting to microscope images with a Gaussian-weight function and an excellent performance was obtained for model data. Nevertheless, the applicability of the results will be dependent on the actual topology of the background in any experiment. In our work, we merely discriminate against image data obtained from point sources in regions of non-uniform background, and we have not made an attempt to fit a functional form to the profile of the background light.

Optimization of Experimental Conditions

We performed a series of calculations to assist in the design of the experiments and justify the method of analysis used to interpret the measured data. A few important observations will be described below. In particular, the examples in this section will relate to (i) the grid size used for the least-squares fitting of a Gaussian function, (ii) the value of gain used for the EM-CCD in the fluorescence microscope, and (iii) the most suitable combination of magnification and pixel binning. In each case, the accuracy for the localisation of the position of a particle will be estimated.

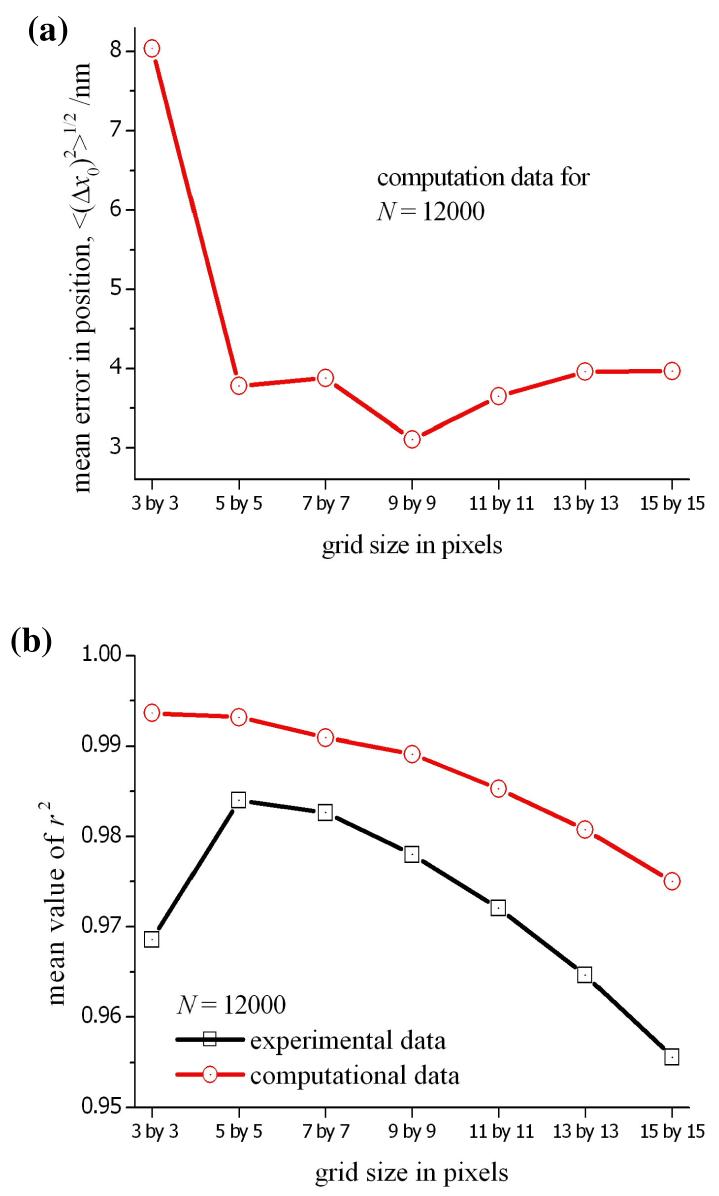
It is important to perform the least-squares analysis on a small grid to minimize the effect of a non-uniform background levels, but it is also necessary to include a sufficient number of data points to ensure an accurate fitting of the Gaussian function from eq. 3. As described above, we used a grid of 7 × 7 pixels (i.e. 49 data points) to obtain the data shown in figs. 1b,2b and 3b. The effect of grid size on the accuracy of the least-squares analysis is demonstrated by the series of calculations reported in fig. 6; where the mean error in x₀ for 100 different copies of the PSF is illustrated as a function of the grid size used in the least-squares analysis. As for the data reported in fig. 5, the PSFs are generated by the computational model using different origins and sequences of random deviates in each profile. It is clear from fig. 6a that below 5 × 5 pixels, an insufficient number of data points are available to precisely locate the origin of the PSF. Although the mean error in the value of x₀ does not appear to decrease as the grid size is increased above 5 × 5, this is not a correct reflection of the experimental conditions. Non-uniformity of the background is likely to lead to a much greater uncertainty in x₀ for a large grid and the deterioration in the quality of the fit to the computational data is still apparent in the value of r² shown in fig. 6b. The size of the grid was also varied in the least-squares analysis of the experimental data from fig. 2, and the resulting value of r² for the fitted Gaussian is also included in fig. 6b. Due to non-uniformity of the background, the decrease in r² is more pronounced than that seen in the computational data. However, in this example, the interpretation of r² must be made carefully as a higher value can actually be obtained using small numbers of data points in eq. 15. This is seen in the computational data for a grid of 3 × 3 pixels; the value of r² is high (>0.993), even though the mean error in x₀ at 8nm is also high.

Figure 6.

(a) The mean error in the position of the origin determined as a function of the grid size used in the least-squares analysis. The theoretical data was obtained using a computational model to generate realistic intensity profiles for the conditions in the experiment (see main text). Each data point is the mean error for 100 iterations using different coordinates for the origin and random deviates for the noise components. (b) The average value of r² obtained for each corresponding grid size in the least-squares fit.

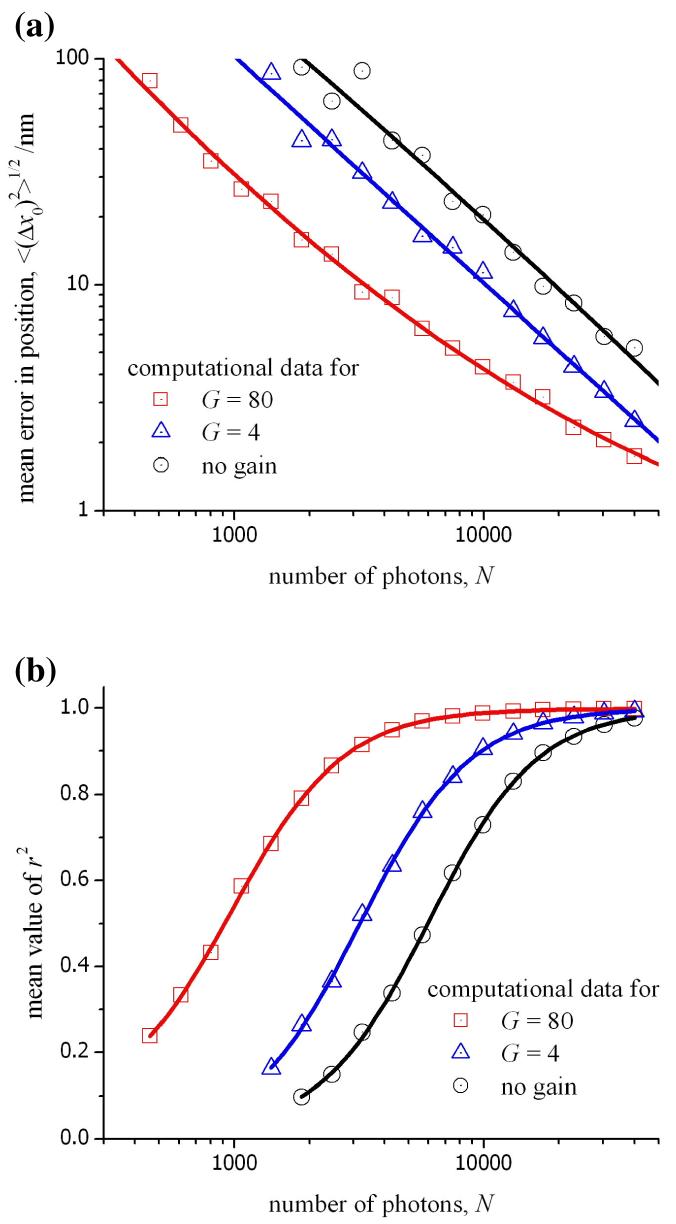
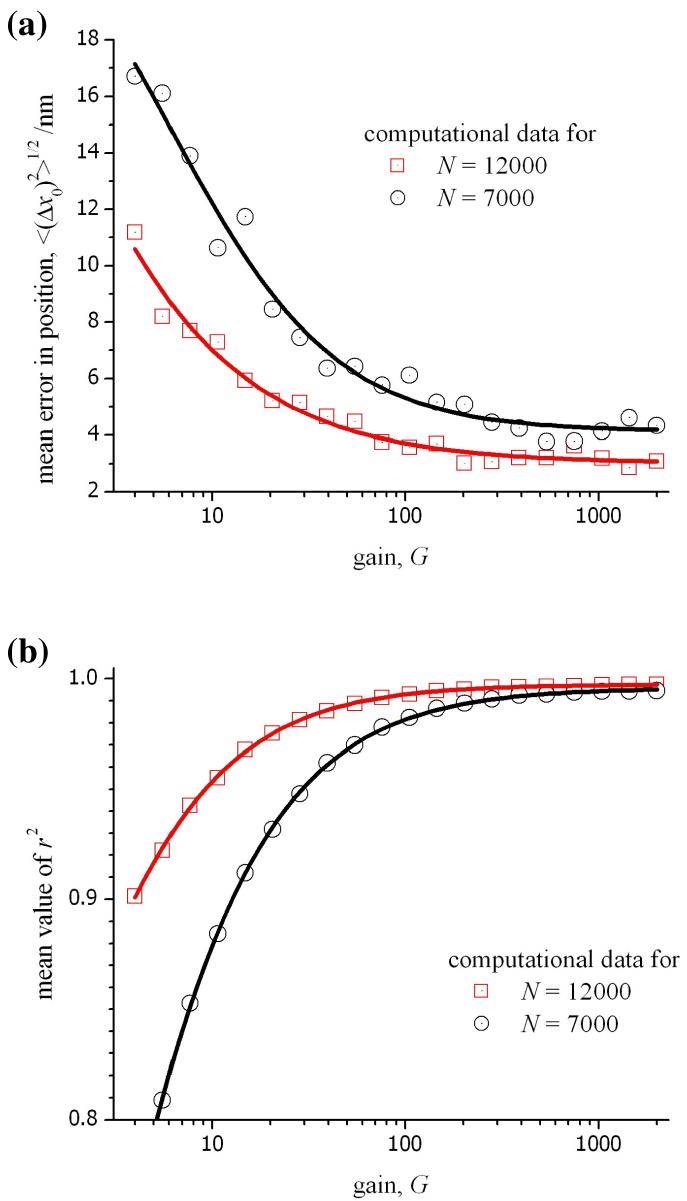
For low signal intensities, the benefit obtained for a high gain is a reduction in the ratio, σ_r/G, leading to a lower overall noise, σ_ij, for each pixel (see eq. 13). For high signal intensities, this is not the case as σ_r/G will be small in comparison with F²m_ij. In fact, the noise in an image obtained without the gain register would be less, and the factor F would be absent from eq. 13. We examined these different conditions by calculating intensity profiles for a point source from varying numbers of emitted photons and under a range of values for the gain of the EM-CCD. In each case, the remaining conditions in the calculation were fixed (see the caption for fig. 7). The data shown in this figure has been obtained using three different values for the multiplication gain; G = 1 corresponds to the direct readout from the signal register, G = 4 is the minimum setting for the gain register, and G = 80 represents the conditions used in the experiments. The overall magnitude of the readout noise is lower in the absence of electron multiplication (in this case for the Hamamatsu C9100-12 camera, σ_r = 17 electrons). However, the corrected readout noise, σ_r/G, has a value of 10 electrons for G = 4, and 2 electrons for G = 80 for the same instrument. It is seen in fig. 7a that the mean error in x₀ is lower for the higher gain with an improved Gaussian fit to the computational data indicated by a higher value of r² in fig. 7b. It is important to pay attention to the region in fig. 7 corresponding to values of N between 7000 and 12000 photons as these are typical values for signal intensities observed in our experiments (see fig. 4). In this region, the mean error in x₀ and the r² value for the 2D-Gaussian fit to the computation data is shown in fig. 8 as a function of the applied gain. In this case, it is quite clear that little benefit would be obtained by using a gain greater than 80× for an experimental measurement of a diffraction-limited object. The results in figs. 7 and 8 using the computational model are likely to be unrealistic for large values of either the number of photons or the gain because the response of the CCD will likely be non-linear as the full well capacity of each pixel is approached. It is for this reason that, in our experiments, the gain is not increased above 80×. Similar theoretical data can be obtained for any experimental conditions or other models of EM-CCD by incorporating the relevant data into the equations given above.

Figure 7.

(a) The mean error in the position of the origin determined as a function of the number of photons incident on the CCD. The theoretical data was obtained using a computational model for photon and instrument noise, and the mean was calculated from a sequence of 100 different profiles for the PSF (background: ∼430 photons per pixel, effective pixel size: 160nm, quantum efficiency: 93%, σ_r: 160 electrons, grid size: 7 × 7 pixels). (b) The average value of r² for the least-squares fit as a function of the number of photons.

Figure 8.

(a) The mean error in the position of the origin measured as a function of the gain for the CCD. The theoretical data was obtained using a computational model for photon and instrument noise, and the mean was calculated from a sequence of 100 different profiles for the PSF (see fig. 7 caption for more details). (b) The average value of r² for the least-squares fit as a function of the gain.

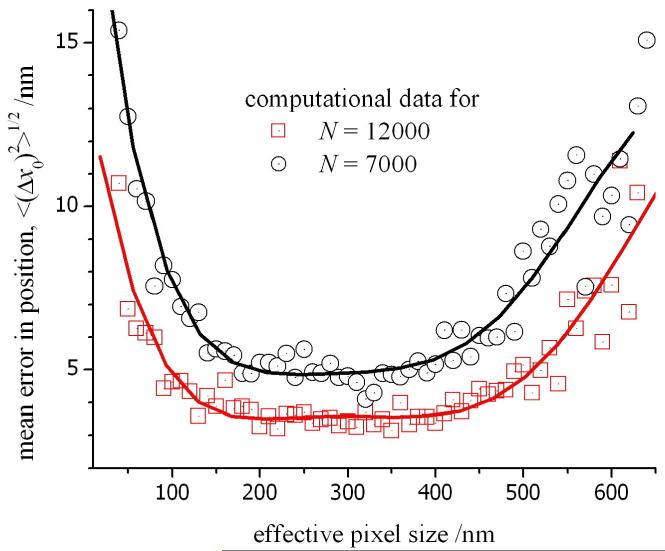
Finally, we examined the influence of the effective pixel size for the digital images on the accuracy for the locating the origin of a fluorescent particle. The effective pixel size (or unit size, a) is dependent on the actual dimension of each pixel, d, in the CCD, the factor for pixel binning, B, in the measured output and the magnification, M, of the microscope (a = d×B/M). The effective pixel size can be varied continuously by the addition of various lenses in the image path. However, it is not an advantage to use the smallest possible pixel size. Each element in the array will be exposed to fewer numbers of photon and the resulting Poisson noise in the output will exceed the signal intensity. This is evident in fig. 9 where the mean error in position begins to increase as the effective pixel size is reduced below 150 nm (for the examples of N = 7000 and 12000 photons). This is a crucial observation given that the latest generation of EM-CCD cameras have actual pixel dimensions from 5 to 8 μm. Using an objective lens with 100× magnification and, without pixel binning, the resulting unit size of 50 to 80 nm would lead to a larger error in the measured position of a fluorescent particle. In our experiment, the unit size is 160 nm and this corresponds to the flat region of the profile in fig. 9. This region of minimum error is constant up to unit sizes of around 450 nm where the fluorescence profile in an experimental image would be distributed over a grid of just 2×2 pixels. This observation accounts for the similar accuracies obtained for position measurements using a quadrant photodiode2. However, a CCD is favoured in live-cell microscopy due to the possibility of tracking multiple particles in a single image of a cell.

Figure 9.

The mean error in the position of the origin measured as a function of the effective pixel size, a. The theoretical data was obtained using a computational model for photon and instrument noise, and the mean was calculated from a sequence of 100 different profiles for the PSF (see fig. 7 caption for more details).

There will be a considerable degree of interplay between the various experimental parameters that is not completely covered by the theoretical data in figs. 6 to 9, and it is important to investigate the range of conditions relevant to a particular apparatus. Nevertheless, the treatment given above can be rapidly performed to assist in the optimization of any imaging system. Although the calculations depend on the reliability of the data provided by CCD manufacturers, we have found this information to be suitably reliable and has avoided the necessity to perform a rigorous and detailed calibration of the instrument.

IV. Conclusion

We have examined a standard algorithm for particle tracking in a sequence of digital images with low signal-to-noise, and identified the procedures to obtain the optimal precision for localization of fluorescent particles in living cells. Some example data for observing the motility of ERES under different conditions in the cell was presented. In a fixed HeLa cell, we measured an experimental precision of ∼11 nm for locating the position of a fluorescent-tagged ERES using 2D Gaussian fitting; indicating the current precision for our epifluorescence apparatus. This value is entirely sufficient for monitoring the movement of a particle along the length of a microtubule and example data that shows the directed motion of an ERES in a normal HeLa cell was also shown. Our theoretical treatment has indicated that it should still be possible to improve the precision of the instrument to locate the position of a particle to within 4-6 nm in a live cell. Although thermal fluctuation and vibrations of the microscope stage would need to be addressed to achieve this level, there is a potential to observe the step mechanism for in vivo displacement of motor proteins. However, in the majority of experiments, the current precision is sufficient for measuring the displacement of single particles or molecules in live cells, and it might be expected that this value of 11 nm would be near the limit of the uncertainty in the position of soft and deformable matter. In practice, an attempt to measure shorter distances might not be relevant in the majority of experiments as a result of the overall dimensions, non-uniform shape and orientation of the object. The development of a theoretical model of the experiment has been essential for the design and optimization of apparatus for precise tracking of particles, and we have provided a description of a methodology that is broadly relevant in live-cell microscopy.