Abstract
Specific rates of solvolysis at 25 °C for p-nitrophenyl chloroformate (1) are analyzed using the extended (two-term) Grunwald-Winstein equation. For 39 solvents, the sensitivities (l = 1.68±0.06 and m = 0.46±0.04) towards changes in solvent nucleophilicity (l) and solvent ionizing power (m) obtained, are similar to those previously observed for phenyl chloroformate (2) and p-methoxyphenyl chloroformate (3). The observations incorporating new kinetic data in several fluoroalcohol-containing mixtures, are rationalized in terms of the reaction being sensitive to substituent effects and the mechanism of reaction involving the addition (association) step of an addition-elimination (association-dissociation) pathway being rate-determining. The l/m ratios obtained for 1, 2, and 3, are also compared to the previously published l/m ratios for benzyl chloroformate (4) and p-nitrobenzyl chloroformate (5).
Keywords: Solvolysis, addition-elimination, association-dissociation, p-nitrophenyl chloroformate, chloroformates, Grunwald-Winstein equation, LFERS, leaving group effects
1. Introduction
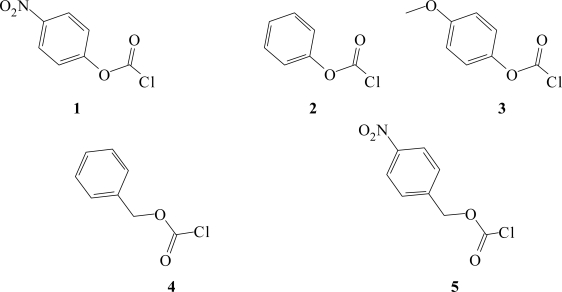
Chloroformates (Figure 1) [1, 2] have been extensively used to study substitution reactions involving the replacement of chlorine to an acyl carbon, as acid chlorides of the type RCOCl tend to react too fast for the kinetics to be followed by conventional techniques [3, 4]. An early survey [5] of the kinetics of solvolytic reactions including hydrolysis, suggested that nucleophilic substitution reactions of chloroformates [RO(CO)Cl] formally parallel those of other types of carboxylic acid esters. Due to an increased initial state stabilization [5–9] experienced with the insertion of an oxygen atom between the R group and the acyl carbon, it is possible to obtain information on the kinetics of the solvolysis process of a number of alkyl and aryl chloroformate esters by standard titrimetric methods.
Figure 1.
Molecular structures of p-nitrophenyl chloroformate (1), phenyl chloroformate (2), p-methoxyphenyl chloroformate (3), benzyl chloroformate (4), and p-nitrobenzyl chloroformate (5).
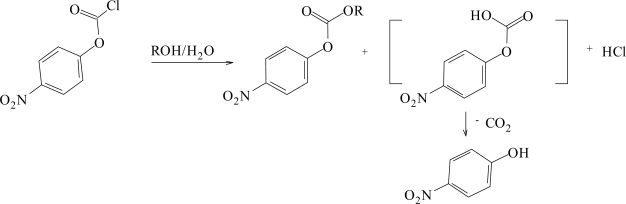
Chloroformate esters such as p-nitrophenyl chloroformate (1) have found increased use in the synthesis of aromatic polycarbonates for biomaterials [10], and in the present contribution its solvolyses expressed in Scheme 1, were conveniently followed at 25.0°C in ten fluoroalcohol containing solvents.
Scheme 1.
Alcoholysis of p-nitrophenyl chloroformate (1).
Sixty years ago the original Grunwald-Winstein equation (equation 1) was proposed [11] for the correlation of specific rates of solvolysis of initially neutral substrates reacting by an ionization (SN1 + E1) mechanism:
| (1) |
In equation (1), k and ko are the specific rates of solvolysis in a given solvent and in the standard solvent (80% ethanol), respectively, m represents the sensitivity to changes in the solvent ionizing power Y (initially set at unity for tert-butyl chloride solvolyses), and c is a constant (residual) term. It is now realized both that the scales are leaving-group dependent and that adamantyl derivatives provide better standard substrates, and for a leaving group X a series of YX scales are available [12].
For bimolecular (SN2 and/or E2) reactions [13], the correlation is extended (equation 2) to include a term governed by the sensitivity l to changes in solvent nucleophilicity (N):
| (2) |
Initially, Schadt, Bentley, and Schleyer [14] used methyl p-toluenesulfonate, to arrive at the NOTs scale. More recently NT scales based on the solvolyses of S-methyldibenzothiophenium ion [15] have been developed, in which the leaving group is a neutral molecule, which is little influenced by solvent change, and these values [15, 16] have become the recognized standards for considerations of solvent nucleophilicity. A problem with multiparameter equations, such as equation (2), is that strong covariances [17] are often observed between N and Y values, hence, Bentley’s group [18] favors the use of equation (1) rather than equation (2) in looking for weak nucleophilic assistance, because they claim that when multiparameter equations are employed, novel effects may not be detected because of the tendency to correlate all of the data moderately successfully. A recent review [19] from our laboratories, examined the development and uses of extended forms of the Grunwald-Winstein equation in a much greater detail than is presented in this manuscript.
During the past two decades, the Grunwald-Winstein equations (equations 1, 2) have emerged as powerful mechanistic tools that are utilized to understand solvolysis mechanisms in alkyl [20–28], alkenyl [29], and aryl [30–37] chloroformate esters. The published results corroborate recent suggestions [9, 19, 38, 39] that acid chlorides of monoesters of carbonic acid and of carboxylic acids tend to solvolyze with competing addition-elimination (with rate-determining addition) and ionization SN1 (assisted by nucleophilic solvation) pathways. The extended form of the Grunwald-Winstein equation (equation 2) has been applied successfully to the specific rates of solvolysis of phenyl chloroformate (2) [30, 36] and p-methoxyphenyl chloroformate (3) [36, 37] over the full range of solvents employed in these types of LFER studies. The reported [37] l value (bond making) of 1.60±0.05 and m value (bond breaking) of 0.57±0.05 for 2; and a value of 1.66±0.05 for l, and a m value of 0.56±0.03 for 3 [36, 37], are consistent with what one would expect for the addition step of an addition-elimination mechanism being rate-determining. In the present study, we have augmented previously published [32, 33] specific rates of solvolyses of p-nitrophenyl chloroformate (1) in order to analyze the contributions made by the excellent electron withdrawing nitro group which makes the carbonyl carbon more positive and thus more susceptible to nucleophilic attack. To better determine whether the nitro group manifests this electron withdrawing character we have extended the prior study [32, 33] by adding additional solvents having an appreciable fluoroalcohol component. Fluoroalchols have been shown to be extremely important, either as pure solvents or as components of binary mixtures, in studies leading to analyses in terms of Grunwald-Winstein equations [40–42].
2. Results and Discussion
To give additional specific rates of solvolysis of p-nitrophenyl chloroformate (1), five values in aqueous 2,2,2-trifluoroethanol (TFE), three values in aqueous 1,1,1,3,3,3-hexafluoro-2-propanol (HFIP), and two values in TFE-ethanol mixtures were measured at 25.0 °C. These specific rate values are reported in Table 1.
Table 1.
Specific rates of solvolysis (k) of p-nitrophenyl chloroformate (1), phenyl chloroformate (2), and p-methoxyphenyl chloroformate (3), in several binary solvents at 25.0°C and the solvent nucleophilicity (NT), and the solvent ionizing power (YCl) values, for the solvents.
| Solvent (%)a | 1; 105k(s−1)b | 2; 105k(s−1)c | 3; 105k(s−1)d | ||
|---|---|---|---|---|---|
| 97% TFE (w/w) | 0.113±0.008 | 0.0570±0.0030 | 0.0300±0.0013 | −3.30 | 2.83 |
| 90% TFE (w/w) | 8.87±0.28 | 1.15±0.08 | 0.825±0.032 | −2.55 | 2.85 |
| 80% TFE (w/w) | 56.8±0.4 | 7.02±0.28 | 8.63±0.24 | −2.22 | 2.90 |
| 70% TFE (w/w) | 153±1.5 | 17.4±1.3 | 15.2±0.6 | −1.98 | 2.96 |
| 50% TFE (w/w) | 438±44 | 63.5±3.0 | 52.6±2.8 | −1.73 | 3.16 |
| 90T-10E (v/v) | 8.82±0.17 | −2.67 | 2.33 | ||
| 80T-20E (v/v) | 45.5±0.7 | 2.43±0.21 | 3.52±0.13 | −1.76 | 1.89 |
| 90%HFIP (w/w) | 1.20±0.06 | 0.166±0.004 | 0.172±0.007 | −3.84 | 4.31 |
| 70%HFIP (w/w) | 83.8±0.9 | 10.5±0.3 | 7.58±0.22 | −2.94 | 3.83 |
| 50%HFIP (w/w) | 277±2 | 31.6±0.6 | 24.9±0.5 | −2.49 | 3.80 |
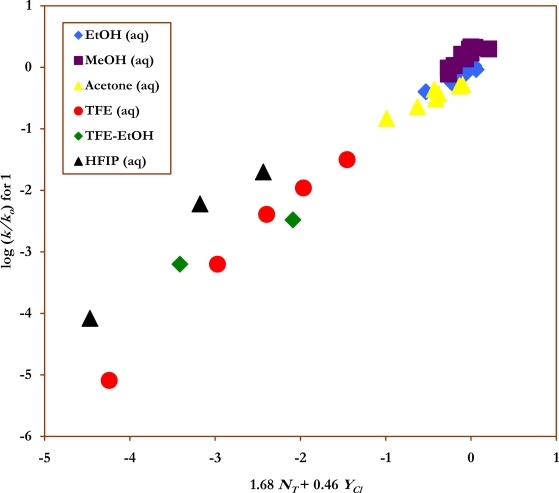
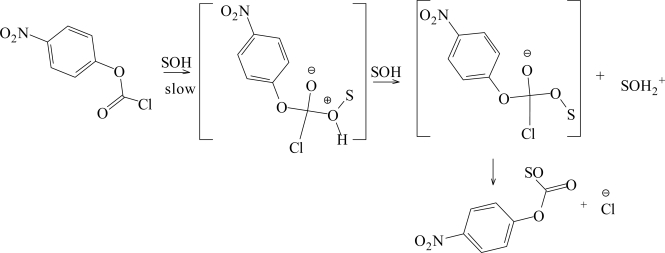
For the solvents listed in Table 1, the nitro group exerts a greater inductive electron withdrawing effect making the nucleophilic solvent attack at the electrophlic carbonyl carbon center easier, and accordingly the reported specific rates of solvolysis increase in the order; k (1) > k (2) ≈ k (3), indicating that a bimolecular type mechanism is in operation. In Table 2, the initial sensitivity values were obtained (l = 1.85±0.21 and m = 0.48±0.05) from the correlation analyses using just the previously studied data of 29 aqueous ethanol, aqueous methanol, and aqueous acetone mixtures [32, 33], together with NT values [16] and YCl values [42–44]. This multiple regression analysis using the extended Grunwald-Winstein equation (equation 2), gave a multiple correlation coefficient of 0.870, and an F test value of 41, suggesting that these results must be interpreted with considerable caution.The new data in ten solvents with appreciable fluoroalcohol content (Table 1) were then combined with the 29 literature values [32, 33]. For the 39 solvents, we obtained a good linear correlation with values of l = 1.68±0.06, m = 0.46±0.04, c = 0.074±0.08, 0.976 for the correlation coefficient, and 363 for the F-test value (Figure 2). With the application of equation 2, both the multiple correlation coefficient (from 0.870 to 0.976) and the F-test values (from 41 to 363), improved considerably on inclusion of the 10 fluoroalcohol data points from Table 1. These improvements illustrate the need for a good selection of solvents for a meaningful application of extended form of the Grunwald-Winstein equation. The observed l and m values are within the range previously observed for other reactions at acyl carbon which are believed to proceed by an addition-elimination (association-dissociation) mechanism shown in Scheme 2, with the addition step rate-determining [19, 20, 22–25, 27–39].
Table 2.
Correlationsa of the specific rates of solvolyses of 1, and a comparison with the corresponding specific rate values for 2 and 3 in identical solvents.
| Substrate | nb | ℓc | mc | cc | l/m | Rd | Fe |
|---|---|---|---|---|---|---|---|
| 29f | 1.85±0.21 | 0.48±0.05 | 0.14±0.05 | 3.85 | 0.871 | 41 | |
| 1 | 39g | 1.68±0.06 | 0.46±0.04 | 0.074±0.08 | 3.65 | 0.976 | 363 |
| 38h | 1.69±0.07 | 0.46±0.04 | 0.074±0.08 | 3.67 | 0.974 | 323 | |
| 2 | 38h | 1.59±0.07 | 0.54±0.03 | 0.16±0.08 | 2.94 | 0.972 | 299 |
| 3 | 38h | 1.58±0.06 | 0.57±0.04 | 0.17±0.07 | 2.77 | 0.974 | 320 |
a Using equation (2).
b Number of data points.
c With associated standard error.
d Correlation coefficient. e F-test value.
h Without 90T-10E; using identical solvents for the 38 data-point correlation of the specific rates of solvolysis of 1, 2, and 3.
Figure 2.
The plot of log (k/ko) vs. (1.68 NT + 0.46 YCl) for the solvolyses of p-nitrophenyl chloroformate (1) in pure and binary solvents at 25.0 °C.
Scheme 2.
Stepwise addition-elimination mechanism through a tetrahedral intermediate proposed for p-nitrophenyl chloroformate (1).
For a meaningful comparison of the extended Grunwald-Winstein results for the specific rates of solvolysis of 1, 2, and 3, at 25.0 °C reported in Table 2, it is important that the comparison is made in identical solvents. For 38 common solvents (90T-10E was excluded), results obtained are l = 1.69±0.07, m = 0.46±0.04, c = 0.074±0.08, R = 0.974, F-test = 323, for 1; l = 1.59±0.07, m = 0.54±0.03, c = 0.16±0.08, R = 0.972, F-test = 299, for 2; and l = 1.58±0.06, m = 0.57±0.04, c = 0.17±0.07, R = 0.974, F-test = 320, for 3. The l/m ratios decreased from a value of 3.67 for 1, to 2.94 for 2, and to 2.77 for 3. This trend implies an earlier transition state for the rate-determining addition step in 1, and the importance of general base catalysis decreases in going from 1, to 2 and 3. The importance of general-base catalysis in solvolyses of aryl chloroformates is indicated by large kinetic solvent isotope effects (KSIEs) in methanol and methanol-d (kMeOH/kMeOD). Unfortunately, there is an ambiguity regarding the value for p-nitrophenyl chloroformate, with values of 2.51±0.07 [45] and 2.10 [33] having been reported (the difference arises from a discrepancy between the kMeOD values). In one study, the value is higher than for other aryl chloroformates and, in the other, it is lower. Either value suggests, however, that general base catalysis is operating [28].
The l/m ratios of 2.96 for 2 and 2.80 for 3 previously reported [37] in 44 solvents, are very close to the values of 2.94 for 2, to 2.77 for 3 reported in Table 2 above for 38 solvents. The l/m ratios are important in two regards. They compensate for earlier and later transition states within otherwise very similar mechanisms and, if one is carrying out a direct logarithmic correlation of the specific rates for two compounds for which both solvent nucleophilicity and ionizing power effects are important, the requirement for a good linear correlation is a close similarity in the l/m ratios for the two substrates. For example, the similarity in l/m ratios for 2 and 3 suggest that a very good direct linear relationship exists between their specific rates of solvolysis, which was indeed the case in the excellent linear plot [37] of log (k/ko) values for 3 against those for 2 with a correlation coefficient of 0.998, F-test value of 9302, slope of 0.991±0.010, and intercept of 0.075±0.015. The larger differences in the l/m ratios of 3.67 for 1 and 2.96 for 2, are substantiated by the plot shown in Figure 3 of log (k/ko) values for 1 against those for 2, with a reduced correlation coefficient of 0.981, F-test value of 933, slope of 1.07±0.04, and intercept of –0.35±0.04.
Figure 3.
The plot of log (k/ko) for p-nitrophenyl chloroformate (1) against log (k/ko) for phenyl chloroformate (2) in pure and binary solvents at 25.0 °C.
For the 15 solvolyses considered [35] to be via addition-elimination for benzyl chloroformate (4), values were obtained of 1.95±0.16 for l, 0.57±0.05 for m, 0.16±0.15 for c, R of 0.966 and F-test value of 83. The l/m value reported of 3.42 for these 15 solvents, was essentially identical to the value of 3.50 obtained for p-nitrobenzyl chloroformate (5) in 19 solvents [35], where values of 1.61±0.09 for l, 0.46±0.04 for m, 0.04±0.22 for c, R of 0.975 and F-test value of 157 were obtained. The identical l/m ratios suggest the presence of a tighter rate-determining tetrahedral transition state, and that the importance of general base catalysis is very similar for benzyl and p-nitrobenzyl chloroformate esters.
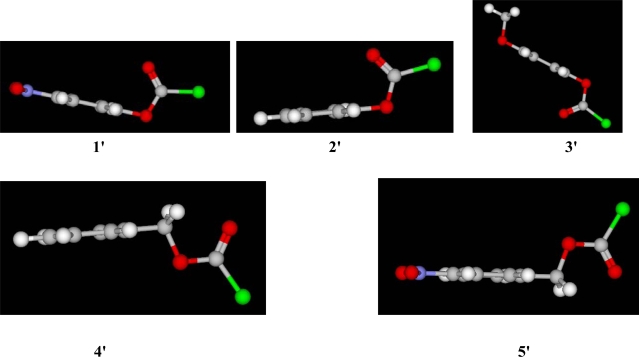
A visual inspection of the computed 3-D views shown in Figure 4, reveals the reason of the powerful inductive effect observed in 1. The planarity observed with the p-nitrophenyl group and its ether oxygen as shown in 1′ makes them linear, so that they can exert their full inductive ability, and this further substantiates the differences seen in the l/m ratios reported in Table 1 for 1, 2, and 3. The specific rate order [this work, 33–35] of k (1) > k (5) in all of the common solvents studied, is probably in part because the p-nitrobenzyl group twists out of the plane with its ether oxygen (as shown in 5′), and therefore is able to exert only a fraction of its possible inductive capability.
Figure 4.
3-D views for p-nitrophenyl chloroformate (1′), phenyl chloroformate (2′), p-methoxyphenyl chloroformate (3′), benzyl chloroformate (4′), and p-nitrobenzyl chloroformate (5′), computed using the KnowItAll® platform.
3. Conclusions
The extended Grunwald-Winstein equation is a versatile tool that can be effectively used to gauge solvent effects in solvolysis reactions. The presently reported analyses demonstrate that meaningful contributions associated with the extended Grunwald-Winstein treatment of 1 can result when an adequate selection of solvents with considerably different NT and YCl values are made available. The l and m parameters obtained for 1 are very similar to other chloroformate esters (such as 2, and 3) where the addition step of an addition-elimination pathway is rate-determining. The trends in the l/m ratios observed (Table 2) and observations from the 3D-views shown above, support our proposal of an earlier step-wise transition state for 1, and a decrease in the importance of general base catalysis in going from 1 to 2 and 3.
4. Experimental Section
The p-nitrophenyl chloroformate (Sigma-Aldrich, 96%) was used as received. Solvents were purified and the kinetic runs carried out as described previously [41]. A 0.6 <u>M</u> stock solution was made in acetonitrile (Sigma-Aldrich, 99.5%) and a substrate concentration of approximately 0.03 <u>M</u> in a variety of fluoroalcohols was employed. The calculation of the specific rates of solvolysis (first-order rate coefficients) were obtained when the conventional Guggenheim treatment [46] was modified [47] so as to give the infinity titer, which was then used to calculate for each run a series of integrated rate coefficients. The specific rates and associated standard deviations, as presented in Table 1, are obtained by averaging all of the values from, at least, duplicate runs.
Multiple regression analysis were carried out using the Excel 2007 package from the Microsoft Corporation, and the SigmaPlot 9.0 software version from Systat Software, Inc., San Jose, CA, was used for the Guggenheim treatments. Incorporating prior results [9] for the assigned position of the halogen in the ground-state structure of 2, the 3D-views presented in Figure 4 for the 5 molecules in this study were computed using the KnowItAll® Informatics System, ADME/Tox Edition, from Bio-Rad Laboratories, Philadelphia, PA. The KnowItAll® platform contains a 3-D molecular rendering program SymApps™ that uses a modified MM2 force field minimization module to convert 2-D structure drawings to 3-D images.
Acknowledgments
This research was supported by grant number 2 P2O RR016472-08 from the National Center for Research Resources (NCRR), a component of the National Institutes of Health (NIH). The grant was obtained under the leadership of the Delaware Biotechnology Institute, University of Delaware, and the authors sincerely appreciate their efforts. The authors also wish to acknowledge the helpful comments from and discussions with Dr. T. W. Bentley, Chemistry Group, Grove Building, School of Medicine, Swansea University, Wales, U.K.
References and Notes
- 1.Queen A. Kinetics of the Hydrolysis of Acyl Chlorides in Pure Water. Can. J. Chem. 1967;45:1619–1629. [Google Scholar]
- 2.Kivinen A. The Kinetics of the Solvolysis of Acid Chlorides. Acta Chem. Scand. 1965;19:845–870. [Google Scholar]
- 3.Bentley TW, Llewellyn G, McAlister JA. SN2 Mechanism for Alcoholysis, Aminolysis, and Hydrolysis of Acetyl Chloride. J. Org. Chem. 1996;61:7927–7932. doi: 10.1021/jo9609844. [DOI] [PubMed] [Google Scholar]
- 4.Ryu ZH, Lim GT, Bentley TW. Applications of Third Order Models in Solvolytic Reaction of Aliphatic Substituted Acyl Derivatives in 2,2,2-Trifluoroethanol-Ethanol Systems. Bull. Kor. Chem. Soc. 2003;24:1293–1302. [Google Scholar]
- 5.Kevill DN. Choloroformate Esters and Related Compounds. In: Patai S, editor. The Chemistry of the Functional Groups: The Chemistry of Acyl Halides. Wiley; New York: 1972. pp. 381–453. Chapter 12. [Google Scholar]
- 6.Matzner M, Kurkjy RP, Cotter RJ. The Chemistry of Chloroformates. Chem. Rev. 1964;64:645–687. [Google Scholar]
- 7.Kivinen A.Mechanisms of Substitution at the COX groupIn The Chemistry of the Functional Groups: The Chemistry of Acyl Halides Patai S.EdWiley; New York: 1972. Chapter 6177–230. [Google Scholar]
- 8.Satchell D. P.N. An Outline of Acylation. Quart. Rev. Chem. Soc. 1963;17:160–203. [Google Scholar]
- 9.Bentley TW. Structural Effects on the Solvolytic Reactivity of Carboxylic and Sulfonic Acid Chlorides. Comparisons with Gas-Phase Data for Cation Formation. J. Org. Chem. 2008;73:6251–6257. doi: 10.1021/jo800841g. [DOI] [PubMed] [Google Scholar]
- 10.Mikulec LJ, Puleo DA. Use of p-Nitrophenyl Chloroformate Chemistry to Immobilize Protein on Orthopedic Biomaterials. J. Biomed. Mater. Res. 1996;32:203–208. doi: 10.1002/(SICI)1097-4636(199610)32:2<203::AID-JBM8>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 11.Grunwald E, Winstein S. The Correlation of Solvolysis Rates. J. Am. Chem. Soc. 1948;70:846–854. [Google Scholar]
- 12.Bentley TW, Llewellyn G. Yx Scales of Solvent Ionizing Power. Prog. Phys. Org. Chem. 1990;17:121–158. [Google Scholar]
- 13.Winstein S, Grunwald E, Jones HW. The Correlation of Solvolyses Rates and the Classification of Solvolysis Reactions into Mechanistic Categories. J. Am. Chem. Soc. 1951;73:2700–2707. [Google Scholar]
- 14.Schadt FL, Bentley TW, Schleyer P.v.R. The SN2-SN1 Spectrum. 2. Quantitative Treatments of Nucleophilic Solvent Assistance. A Scale of Solvent Nucleophilicities. J. Am. Chem. Soc. 1976;98:7667–7674. [Google Scholar]
- 15.Kevill DN, Anderson SW. An Improved Scale of Solvent Nucleophilicity Based on the Solvolysis of the S-Methyldibenzothiophenium Ion. J. Org. Chem. 1991;56:1845–1850. [Google Scholar]
- 16.Kevill DN.Development and Uses of Scales of Solvent NucleophilicityIn Advances in Quantitative Structure-Property Relationships Charton M.EdJAI Press; Greenwich, CT: 1996. Vol. 181–115. [Google Scholar]
- 17.Wells PR. Linear Free Energy Relationships. Academic Press; New York: 1968. pp. 67–68. [Google Scholar]
- 18.Bentley TW, Garley MS. Correlations and Predictions of Solvent Effects on Reactivity: Some Limitations of Multi-Parameter Equations and Comparisons with Similarity Models Based on One Solvent Parameter. J. Phys. Org. Chem. 2006;19:341–349. [Google Scholar]
- 19.Kevill DN, D’Souza MJ. Sixty Years of the Grunwald-Winstein Equation: Development and Recent Applications. J. Chem. Res. 2008:61–66. [Google Scholar]
- 20.Kevill DN, Kyong JB, Weitl FL. Solvolysis-Decomposition of 1-Adamantyl Chloroformate: Evidence for Ion Pair Return in 1-Adamantyl Chloride Solvolysis. J. Org. Chem. 1990;55:4304–4311. doi: 10.1021/jo0207426. [DOI] [PubMed] [Google Scholar]
- 21.Koo IS, Yang K, Kang K, Oh HK, Lee I. Stoichiometric Solvation Effects. Product-Rate Correlation for the Solvolyses of Phenyl Chloroformate in Alcohol-Water Mixtures. Bull. Korean Chem. Soc. 1996;17:520–524. [Google Scholar]
- 22.Kevill DN, D’Souza MJ. Concerning the Two Reaction Channels for the Solvolyses of Ethyl Chloroformate and Ethyl Chlorothioformate. J. Org. Chem. 1998;63:2120–2124. [Google Scholar]
- 23.Kevill DN, Kim JC, Kyong JB. Correlation of the Rates of Methyl Chloroformate with Solvent Properties. J. Chem. Res. Synop. 1999:150–151. [Google Scholar]
- 24.Kyong JB, Kim YG, Kim DK, Kevill DN. Dual Pathways in the Solvolyses of Isopropyl Chloroformate. Bull. Korean Chem. Soc. 2000;21:662–664. [Google Scholar]
- 25.Kevill DN, D’Souza MJ. Correlation of the Rates of Solvolyses of n-Octyl Fluoroformate and a Comparison with n-Octyl Chloroformate Solvolyses. J. Chem. Soc. Perkin Trans. 2. 2002:240–243. [Google Scholar]
- 26.Kyong JB, Yoo J.–S, Kevill DN. Solvolysis-Decomposition of 2-Adamantyl Chloroformate: Evidence for Two Reaction Pathways. J. Org. Chem. 2003;68:3425–3432. doi: 10.1021/jo0207426. [DOI] [PubMed] [Google Scholar]
- 27.Kyong JB, Won H, Kevill DN. Application of the Extended Grunwald-Winstein Equation to Solvolyses of n-Propyl Chloroformate. Int. J. Mol. Sci. 2005;6:87–96. [Google Scholar]
- 28.Bentley TW, Harris HC, Zoon H-R, Gui TL, Dae DS, Szajda SR. Mechanisms of Solvolyses of Acid Chlorides and Chloroformates. Chloroacetyl and Phenylacetyl Chloride as Similarity Models. J. Org. Chem. 2005;70:8963–8970. doi: 10.1021/jo0514366. [DOI] [PubMed] [Google Scholar]
- 29.Ryu ZH, Lee YH, Oh Y. Stoichiometric Effects. Correlation of the Rates of Solvolysis of Isopropenyl Chloroformate. Bull. Kor. Chem. Soc. 2005;26:1761–1766. [Google Scholar]
- 30.Kevill DN, D’Souza MJ. Correlation of the Rates of Solvolysis of Phenyl Chloroformate. J. Chem. Soc. Perkin Trans. 2. 1997:1721–1724. [Google Scholar]
- 31.Koo IS, Yang K, Koo JC, Park J.–K, Lee I. Stoichiometric Solvation Effects. Part 4. Product–rate Correlations for Solvolyses of p-Methoxyphenyl Chloroformate in Alcohol–Water Mixtures. Bull. Korean Chem. Soc. 1997;18:1017–1021. [Google Scholar]
- 32.Koo IS, Yang K, Kang K, Lee I, Bentley TW. Stoichiometric Solvation Effects. Part 3. Product–rate Correlations for Solvolyses of p-Nitrophenyl Chloroformate in Alcohol–Water Mixtures. J. Chem. Soc. Perkin Trans 2. 1998:1179–1183. [Google Scholar]
- 33.Koo IS, Yang K, Kang K, Lee I. Transition-State Variation in the Solvolyses of para-Substituted Phenyl Chloroformates in Alcohol-Water Mixtures. Bull. Kor. Chem. Soc. 1998;19:968–973. [Google Scholar]
- 34.Park KH, Kyong JB, Kevill DN. Nucleophilic Substitution Reactions of p-Nitrobenzyl Chloroformate. Bull. Kor. Chem. Soc. 2000;21:1267–1270. [Google Scholar]
- 35.Kyong JB, Park B-C, Kim C-B, Kevill DN. Rate and Product Studies with Benzyl and p-Nitrobenzyl Chloroformates under Solvolytic Conditions. J. Org. Chem. 2000;65:8051–8058. doi: 10.1021/jo005630y. [DOI] [PubMed] [Google Scholar]
- 36.Kevill DN, Koyoshi F, D’Souza MJ. Correlation of the Specific Rates of Solvolysis of Aromatic Carbamoyl Chlorides, Chloroformates, Chlorothionoformates, and Chlorodithio-formates Revisited. Int. J. Mol. Sci. 2007;8:346–352. [Google Scholar]
- 37.D’Souza MJ, Reed D, Koyoshi F, Kevill DN. Consideration of the Factors Influencing the Specific Rates of Solvolysis of p-Methoxyphenyl Chloroformate. Int. J. Mol. Sci. 2007;8:788–796. [Google Scholar]
- 38.D’Souza MJ, Ryu ZH, Park B-C, Kevill DN. Correlation of the Rates of Solvolysis of Acetyl Chloride and α-Substituted Derivatives. Can. J. Chem. 2008;86:359–367. [Google Scholar]
- 39.Castro EA, Ruiz MG, Santos JG. Structure-Reactitvity Correlations in the Aminolysis of Aryl Chloroformates. Int. J. Chem. Kinet. 2001:281–287. [Google Scholar]
- 40.Kaspi J, Rappoport Z. Nucleophilicity and Ionizing Power in Binary Solvent Mixtures. Tetrahedron Lett. 1977:2035. [Google Scholar]
- 41.Kevill DN, Park B-C, Park K-H, D’Souza MJ, Yaakoubd L, Mlynarski SL, Kyong JB. Rate and Product Studies in the Solvolyses of N, N-Dimethylsulfamoyl and 2-Propanesulfonyl Chlorides. Org. Biomol. Chem. 2006;4:1580–1586. doi: 10.1039/b518129a. [DOI] [PubMed] [Google Scholar]
- 42.Kevill DN, Ryu ZH. Additional Solvent Ionizing Power Values for Binary Water – 1,1,1,3,3,3,-Hexafluoro-2-propanol Solvents. Int. J. Mol. Sci. 2006;7:451–455. [Google Scholar]
- 43.Bentley TW, Carter GE. The SN2-SN1 Spectrum. 4. Mechanism for Solvolyses of tert-Butyl Chloride: A Revised Y Scale of Solvent Ionizing Power based on Solvolyses of 1-Adamantyl Chloride. J. Am. Chem. Soc. 1982;104:5741–5747. [Google Scholar]
- 44.Kevill DN, D’Souza MJ. Additional YCl Values and Correlation of the Specific Rates of Solvolysis of tert-Butyl Chloride in Terms of NT and YCl Scales. J. Chem. Res. Synop. 1993:174–175. [Google Scholar]
- 45.Yew KH, Koh HJ, Lee HW, Lee I. Nucleophilic Substitution Reactions of Phenyl Chloroformates. J. Chem. Soc. Perkin Trans 2. 1995:2263–2268. [Google Scholar]
- 46.Frost AA, Pearson RG. Kinetics and Mechanism-a Study of Homogeneous Chemical Reactions. 2nd. Wiley; New York: 1961. pp. 49–50. [Google Scholar]
- 47.Kevill DN, Abduljaber MH. Correlation of the Rates of Solvolysis of Cyclopropylcarbinyl and Cyclobutyl Bromides Using the Extended Grunwald-Winstein Equation. J. Org. Chem. 2000;65:2548–2554. doi: 10.1021/jo991904+. [DOI] [PubMed] [Google Scholar]