Functional organization of the yeast proteome by a yeast interactome map

Abstract

It is hoped that comprehensive mapping of protein physical interactions will facilitate insights regarding both fundamental cell biology processes and the pathology of diseases. To fulfill this hope, good solutions to 2 issues will be essential: (i) how to obtain reliable interaction data in a high-throughput setting and (ii) how to structure interaction data in a meaningful form, amenable to and valuable for further biological research. In this article, we structure an interactome in terms of predicted permanent protein complexes and predicted transient, nongeneric interactions between these complexes. The interactome is generated by means of an associated computational algorithm, from raw high-throughput affinity purification/mass spectrometric interaction data. We apply our technique to the construction of an interactome for Saccharomyces cerevisiae, showing that it yields reliability typical of low-throughput experiments from high-throughput data. We discuss biological insights raised by this interactome including, via homology, a few related to human disease.

The collection of protein physical interactions present in a cell—the interactome—constitutes a cornerstone to systems biology, because it is at the most fundamental level at which it is still possible to perform an integrated analysis of a cell rather than just an isolated study of individual components (1). For a system's-level functional understanding of a cell, we suggest that modeling an interactome in terms of (i) predicted permanent (i.e., high-affinity) protein complexes and (ii) predicted specific transient (i.e., lower-affinity) interactions between such complexes and/or individual proteins, while discarding (iii) generic, predicted less-specific transient interactions is a sensible choice. This alternative falls in between a detailed structural characterization of each interaction (2) and a binary protein–protein pairwise-only reporting of interactions (3). The former of these two, the arguable system's-level functional relevance of the detail it provides aside, would certainly be hard to realize accurately in a large-scale fashion because of current experimental limitations. The latter of the two, because of its scalability, can be very useful as a first approximation but is ultimately less than ideal, because proteins do not work in a strict pairwise fashion (4) besides the fact that significant functional information can be lost under a purely on/off description of an interaction.

We developed an algorithm to construct an interactome as proposed above, based on raw data from high-throughput affinity purification, followed by mass spectrometric identification (AP-MS) assays (5–7). A key premise used is that, under ideal conditions, every protein member of a given complex, when used as a bait, should pull down every other protein in that same complex. Although this ideal is not attainable in practice because of a variety of experimental limitations, how close it comes to being fulfilled provides a measure of the certainty that a given group of proteins constitutes a complex in the cell. In this light, the problem becomes one of searching for sets of proteins that fulfill the above test to a specified minimum degree. Throughout the process, an appropriate statistical correction is made to account for proteins that tend to bind indiscriminately to other proteins and/or to the purification column itself and that, as such, could more easily fulfill the test by chance. Once a set of predicted complexes has been built, a set of predicted putative pairwise transient interactions between these complexes is assembled by submitting each pair of complexes to the less-stringent test of partially appearing together in a single pulldown assay. Now, from a functional perspective, transient interactions can usefully be approximately divided into 2 qualitatively distinct types, which we name here “wide-ranging” and “restricted.” The wide-ranging kind is associated with a protein/complex performing a standard function on many target proteins/complexes. An example of interactions of this type are those between a chaperone and its, potentially, hundreds of targets (8). The restricted kind of transient interaction occurs when 2 proteins/complexes come together in a more delimited functional context, for example a kinase-substrate transient interaction within a particular signaling pathway. Both kinds are of relevance, but because of their functionally distinct nature, they are best addressed separately, in particular so that, because of its pervasiveness, the wide-ranging kind does not occlude the restricted kind, as may be the case under the concept of hubs (9). In our interactome map, we attempt to screen out the wide-ranging types by excluding predicted transient interactions of complexes involved in more than a specified cutoff number of predicted transient interactions. With some arbitrariness, we settled on 8 interactions as a biologically reasonable choice for this cutoff. A detailed description of both the permanent complex prediction algorithm and the transient interaction prediction algorithm, is given in Materials and Methods.

Results and Discussion

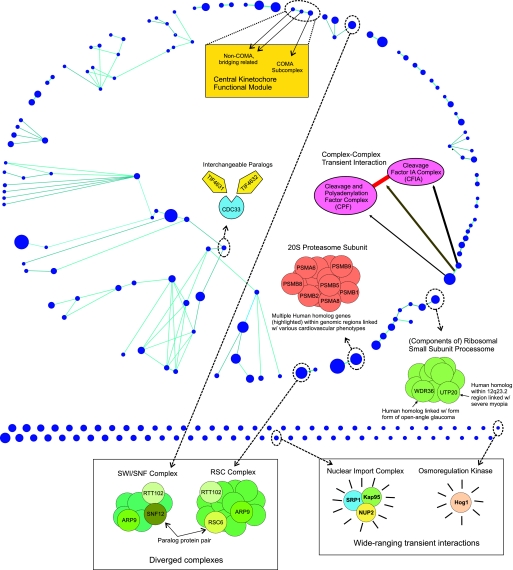
In this section, we apply our algorithms and rationale described above to assemble a Saccharomyces cerevisiae interactome. The experimental data source used is raw data from 3 large-scale AP-MS studies on S. cerevisiae (5–7). Using our complex prediction algorithm, we first build a set of predicted permanent complexes. We then go on to further organize the interactome in terms of restricted transient interactions between these complexes, leaving wide-ranging interactions as a separate class of its own. Before excluding wide-ranging interactions as prescribed, we enriched the set of predicted transient interactions with kinase-substrate literature-curated interactions (Kinase and phosphatase database (2007), accessible at www.proteinlounge/). We did so because phosphorylation interactions are clear examples of what we deem transient interactions, and a sizable curated set of such interactions was readily available (Kinase and phosphatase database (2007) accessible at www.proteinlounge/). The final interactome built in this fashion consists of 248 nodes (210 predicted multiprotein complexes and 38 single kinases) and 113 restricted transient interactions (65 predicted with our algorithm and 48 phosphorylation literature interactions) (Fig. 1). In addition, we will discuss a diversity of biological topics in the context of this yeast interactome in the process arguing for the quality of the predicted permanent complexes and for the fact that the proposed interactome organization is biologically sensible and useful. Throughout, Fig. 1 will serve as a go-to, summarizing figure, highlighting some of the biological issues and cases discussed.

Fig. 1.

S. cerevisiae interactome. Blue nodes represent 210 predicted multiprotein complexes and 38 kinases (node sizes proportional to complex sizes). Light blue represent 113 putative predicted restricted transient interactions between nodes (65 complex–complex predicted interactions and 48 kinase–substrate literature-based interactions). The network is laid out in Polar Map fashion (47, 48), with each topological module placed in a conical region with some blank space in between the modules. A diversity of biological issues and cases discussed throughout the main text are highlighted.

One complex and 1 kinase (HOG1) had more than the 8 cutoff number of predicted transient interactions, with those interactions being therefore classified as wide-ranging (Fig. 1). Subsequent examination showed this complex to be composed of 3 proteins, SRP1, KAP95, and NUP2, that are expected to transiently interact with many proteins/complexes in a function-nonspecific manner. These proteins are all involved in nuclear protein import and are known to interact with dozens of partners representing a broad range of functional categories (10, 11). This is exactly the sort of wide-ranging interaction that we wished to distinguish, one representing a standard function performed on many targets/complexes and that could occlude the role of more restricted interactions. Similarly, the protein kinase HOG1 is involved in a multitude of distinct cellular processes, including water homeostasis (12), arsenite detoxification (13), copper-resistance (14), hydrogen peroxide response (15), and adaptation to citric acid stress (16), among others.

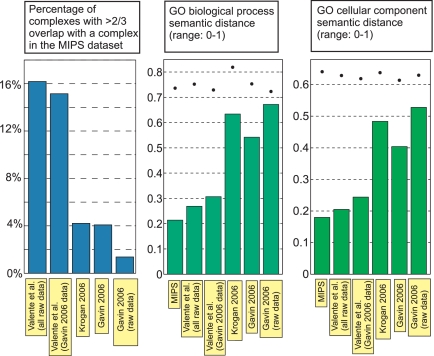
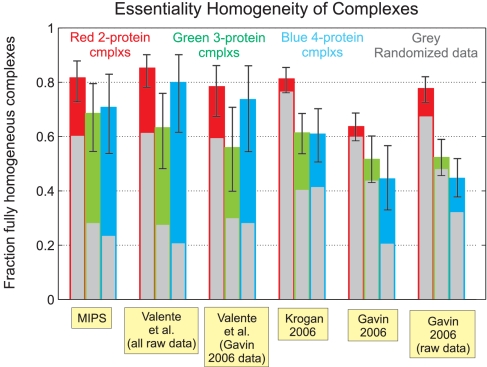
We assessed the quality of the interactome map via a number of distinct tests. First, we used a set of manually curated complexes from the MIPS database (17) [in a form further refined for accuracy by Lichtenberg et al. (18)] as a gold standard for comparison (Fig. 2). Second, because we were interested in comparing the reliability of our predicted complexes with that of the MIPS gold standard itself, we used a non-gold-standard-based measure, termed Semantic Distance (19). Semantic distance (range: 0 to 1) provides an automated measure of the distance among a complex's protein members with regard to annotation, in this case, based on the GO database Biological Process and Cellular Component annotations (20, 21) (Fig. 2). This test showed that the average Semantic Distance among proteins within each of our predicted complexes comes close to that for the gold-standard MIPS complexes. Furthermore, it is relevant to note that some of the GO database protein annotations and some of the MIPS dataset complexes may be based on the same literature source, artificially deflating, to an undetermined extent, the Semantic Distance within MIPS complexes. Seemingly, this should be most pronounced in the case of the Biological Process annotation. Defining a complex to be, in terms of essentiality, fully homogeneous if either (i) knockout of any one of its member proteins is lethal to the cell or (ii) no single member protein knockout is lethal; we present the fraction of such fully homogeneous complexes in a dataset as our third quality test (22, 23) (Fig. 3). A major advantage of this test is the apparent lack of significant hidden biases or sources of noise: The essentiality classification for most yeast proteins is reliable, and the test involves neither the use of a less-than-perfect gold standard nor comparisons based on annotations that are always subjective by nature. In this sense, the error bars shown in Fig. 3 likely constitute a correct, nonunderestimated assessment of the error associated with the test, an error that will decrease as the net number of predicted complexes increases in future studies. In this study, it is already worth noticing how the homogeneity above random (difference between the background colored bars and the respective foreground gray bars) of our predicted complexes is comparable with that of the MIPS complexes, for 2-, 3-, and 4-protein-sized complexes. Taken together with the Semantic Distance results, this leads us to conclude that the integration of our algorithm with the latest AP-MS high-throughput experimental techniques (6, 7) allows large-scale prediction of complexes with a reliability typical of low-throughput experiments.

Fig. 2.

Reliability of predicted complexes. Detailed legend: MIPS, the set of manually curated complexes from MIPS database (17), further refined for accuracy by Lichtenberg et al. (18) (199 complexes); Valente et al. (all data), our set of predicted complexes based on combined raw AP-MS data from refs. 5–7 (210 complexes); Valente et al. (Gavin 2006 data), our set of predicted complexes based on AP-MS Gavin 2006 (6) raw data only (165 complexes); Krogan 2006, the predicted complexes in ref. 7 (546 complexes); Gavin 2006, the predicted complexes in ref. 6 (491 complexes); Gavin 2006 (raw data), taking each raw pulldown in ref. 6 as a predicted complex, without computational treatment (1,751 complexes). Dots represent results under randomization of the respective datasets (standard deviation values smaller than dot size).

Fig. 3.

The fraction of complexes that are fully homogeneous in the sense that either (i) knockout of any one of their member proteins is lethal to the cell or (ii) no single member protein knockout is lethal. Analysis was performed separately for complexes of sizes 2, 3, and 4 to avoid size-related biases (no statistically significant data for larger-sized complexes was available). Error bar shows 90% confidence interval for the underlying homogeneity fraction (see Materials and Methods). Foreground gray bar shows expected homogeneity fraction under randomization of the respective data (see Materials and Methods). Dataset source references are as noted in Fig. 2.

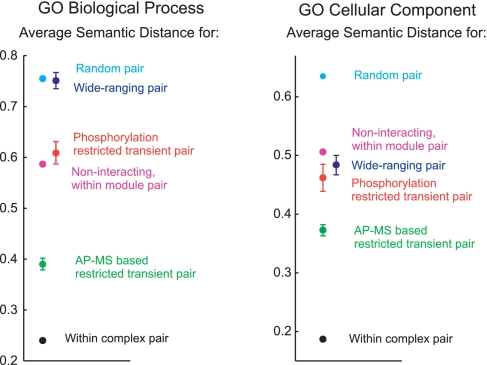
As noted earlier, upon building a set of permanent complexes, we extracted further information from the AP-MS raw data by building a set of predicted putative transient interactions between the permanent complexes (Fig. 1). Being of lower affinity, such interactions are naturally harder to discern, present-day literature data on transient complex–complex interactions being itself still comparatively sparse. This precludes a better net assessment of the reliability of the transient interaction predictions. Given also the lower stringency of this algorithm (vis-à-vis the complex prediction algorithm), we emphasize the greater uncertainty over the reliability of these predictions. Nonetheless, Semantic Distance tests show that for both the GO Biological Process and the GO Cellular Component annotations, the average Semantic Distance associated with the class of predicted restricted transient interactions is higher than the respective average for permanent complexes, although it is lower than the respective average for the class of predicted wide-ranging transient interactions (Fig. 4), consistent with expectations. As a concrete example, our method predicted a complex mainly comprising protein components of the cleavage and polyadenylation factor complex (CPF) to transiently interact with a complex mainly comprising protein components of the cleavage factor IA complex (CFIA) (Fig. 1). The CPF and CFIA complexes are both involved in the process of transcript poly(A) tail synthesis and maturation and are known to transiently interact as part of this process [see, for instance, Mangus et al. (24)].

Fig. 4.

Average Semantic Distance for pairs of proteins in different interaction classes. These were calculated as follows: Within complex pair-average Semantic Distance over all pairs of proteins A and B, where A and B are found in the same predicted permanent complex; AP-MS based predicted restricted transient interaction pair-average Semantic Distance over all pairs of distinct proteins A and B, where A and B are in distinct predicted complexes that interact via an AP-MS data-based predicted transient restricted interaction; Phosphorylation restricted transient interaction pair-as in the previous case, but where the restricted transient interaction is now based on a kinase–substrate literature-reported interaction; Wide-Ranging pair-average Semantic Distance over all pairs of distinct proteins A and B, where A and B are in distinct predicted complexes that interact via a transient interaction (either predicted or kinase–substrate literature-based) classified as wide-ranging; Noninteracting, within module pair-average Semantic Distance over all pairs of distinct proteins that belong to the same topological module but that do not fall within any of the cases above; Random pair-average Semantic Distance over all pairs of proteins present in the dataset. Assuming independence of the observed Semantic Distances for pairs in a given class, 95% confidence intervals for the predicted averages are shown (unless confidence interval is smaller than data point size). The presence of correlations means that these are underestimates of the true, hard to quantify errors (see Materials and Methods). The x axis placement of data points was chosen for the purpose of clarity.

In the past, S. cerevisiae underwent a whole-genome duplication event (25). A total of 22 paralog protein pairs originating at this single event fall within our interactome. In only 1 of these 22 pairs, do the 2 proteins appear in distinct complexes. This happens also to be the pair furthest apart in terms of protein sequence homology [as per Blastp (26) score]. From the other 21 within complex paralog pairs, 18 are viable–viable pairs (i.e., single knockout of either of the paralogs is viable), with the remaining 3 being viable–lethal pairs (i.e., one of the paralogs is essential). Genetic interactions (27) are reported in the SGD database (21) for 12 of the viable–viable pairs and for 1 of the viable–lethal pairs [a dosage rescue case of SEC24 by SFB2 (28)]. Note that the absence of reported genetic interactions for the other cases could be simply because of lack of testing. Altogether, this evidence points to a picture where 2 paralogs could remain similar enough to be redundant and used interchangeably in a complex (19 potential such cases); paralogs could evolve to having noninterchangeable roles, as evidenced by possession of distinct knockout phenotypes (with no known dosage rescue interaction), but still work within the same complex, as a reminiscence of their common evolutionary origin (2 potential such cases); paralogs could diverge to the point of acquiring roles within different complexes altogether (1 potential such case). This observed latter case, may conceivably illustrate the eventual functional divergence of a complex into 2 complexes with separate but still closely related functions: The 2 paralogs, SNF12 and RSC6, are found in 2 different complexes that, although distinct, are functionally related and share a subset of proteins in common (10) (Fig. 1). SNF12 is a component of the SWI/SNF complex, and RSC6 is a component of the chromatin structure-remodeling complex (RSC). Both of these complexes promote ATP-dependent remodeling of chromatin and thus serve to regulate gene expression (29). In contrast, the paralogs TIF4631 and TIF4632 may exemplify the prior case of paralogs that can be interchangeably used within a complex (Fig. 1). Both are individually nonessential, but together they form a synthetic lethal pair. They are predicted to be part of a complex whose remaining member, CDC33, is essential (Fig. 1). This opens the possibility that the complex is performing some critical role within the cell and that its functionality requires both CDC33 and either one of the two paralogs. We note that analysis and interpretation of protein evolutionary rates in the context of our assembled set of complexes may provide another interesting research direction (30, 31).

The full homogeneity with respect to essentiality of many of our permanent complexes (Fig. 3) hints that this property is oftentimes intrinsic to the complex and to its role rather than to its individual proteins. Likewise, certain pathologies may be more correctly assigned to an intrinsic malfunction of a complex as a whole, rather than to an individual or loose set of proteins (32–34). With this in mind, we lifted our yeast interactome to human via homology (35) and checked how known disease-associated genes and chromosomal loci relate to our interactome map. Interestingly, a number of cases potentially pointing in this direction were found. One complex provides an interesting example of 2, possibly related, phenotypes associated with the same complex (Fig. 1): A gene in this complex, WDR36, is known to cause a form of adult-onset primary open-angle glaucoma (36). This condition is associated with characteristic changes of the optic nerve head and visual field, often accompanied by elevated intraocular pressure. Also in this complex is UTP20, located at 12q23.2. This gene falls within a chromosomal region identified as linked to severe myopia (37) (the causative gene has not yet been identified). Severe myopia occurs primarily as a result of increased axial length of the eye (37), but it is known to be associated with glaucoma, cataracts, and other ophthalmologic disorders (38). Both WDR36 and UTP20 are known to be expressed in the retina and other tissues as well (36, 39). Another example of related phenotypes mapping to the same complex is provided by a complex containing the gene PSMA6 (Fig. 1). A specific variant of this gene is known to confer susceptibility to myocardial infarction in the Japanese population (40). A linkage to a related phenotype, susceptibility to premature myocardial infarction, has been reported at 1p36–34 (41) (again, no causative gene has yet been identified). This region includes PSMB2, another gene in the same complex. Linkage between various other cardiovascular phenotypes and genomic regions including genes from this complex have also been reported, e.g., linkage between familial atrial septal defect and 6p21.3 (42), a region that includes PSMB8 and PSMB9, genes that are also present in the complex.

There is by now accumulated evidence that protein complexes define a distinct, relevant scale of functional organization in the cell (4–7). Perhaps a subsequent higher-level scale of functional organization is provided by functional modules, or pathways, involving groups of complexes/proteins that transiently interact. As an attempt to probe for such hypothetical organization, we divide the interactome into topological modules that are dense in predicted restricted transient interactions (Fig. 1) (see Materials and Methods and refs. 43 and 47). Individually, the functional relevance of some modules is immediately apparent. For instance, 1 module consists of 3 complexes whose proteins are all clearly related: Each is a subunit of the central kinetochore, mediating the attachment of the centromere to the mitotic spindle. One of the complexes appears to comprise mainly proteins from the COMA subcomplex, a group of proteins that together bridge subunits in direct contact with DNA to those bound to microtubules (44). The other 2 complexes also comprise proteins with a similar bridging function, but these proteins are not members of the COMA subcomplex (45). With this modular breakdown, we have now organized the predicted interactome in terms of (i) permanent complexes, restricted (ii) AP-MS-based transient interactions and (iii) phosphorylation transient interactions, (iv) topological modules based on restricted transient interactions, and (v) wide-ranging transient interactions. Of note are the Biological Process distinct average Semantic Distances for these classes (Fig. 4), overall supporting this proposed structuring of the interactome. By comparison, regarding cellular component average Semantic Distances (Fig. 4), wide-ranging interactions are now comparable with phosphorylation-restricted transient interactions, with even AP-MS-based restricted transient interactions being now closer to both of these than to permanent complexes, unlike they were with regard to biological process. This is consistent with the more homogeneous nature, based on physical location, of all transient interactions, the distinction among these classes being fundamentally a functional one (in the sense defined by the Biological Process GO annotation). Another observed difference, is the now slightly-higher average Semantic Distance for modules than for all transient interaction types, even wide-ranging ones, which is consistent with modules being more physically extended over multiple cellular components. Nonetheless, given the combination of uncertainty in the different classes' average Semantic Distances (see comments in Fig. 4 and Materials and Methods) with the incompleteness and degree of inherent subjectivity of the GO annotations, collection of additional data will be necessary to confirm the biological relevance of organizing interactome data in the fashion we have put forward.

We introduced a mathematical algorithm that, when combined with the latest AP-MS high-throughput experimental techniques, provides, under a higher throughput setting, the reliability typical of traditional biochemical assays. The algorithm is ideally suited for large-scale AP-MS interactome mapping projects, because the reliability (with regard to both sensitivity and specificity) of its predicted complexes improves as the number of AP-MS assays performed increases (see Materials and Methods). A way to organize protein interaction data, essentially in terms of permanent complexes, transient restricted, and transient wide-ranging interactions, is also proposed in this article. We believe this proposed structuring is practical, biologically sensible, and appropriate for the level of detail that present-day high-throughput protein interaction assays provide. Hopefully, the ongoing improvement, both experimental and theoretical, on how to handle protein interactions on a global scale, will gradually help realize the full potential of genome-wide protein interaction maps.

Materials and Methods

Complex Prediction Algorithm.

Here, we describe the algorithm for predicting permanent complexes. We assume a set of pulldown assay data of the form a = {a, b, c, d}, meaning that protein a as a bait pulled down proteins a, b, c, and d. Given a set of proteins {p_i}, for each protein p in the set: Let P (“Possible”) be the number of baits in {p_i}, other than p, that produced nonempty pulldowns. Let S (“Seen”) be the number of those pulldowns where p was identified. If (i) for every protein in the set {p_i} the ratio S/P is well-defined, with S/P ≥ C_crit, where C_crit is a predefined threshold, and (ii) the set {p_i} is not a subset of a larger set satisfying the above condition, then the set {p_i} is defined as a permanent complex.

Note 1.

When >1 nonempty pulldown with a given bait b was performed (for example, because data from multiple datasets is being used), the contribution of these bait b pulldowns to the values S and P of another protein p in the same set {p_i} as b is determined as follows: P is still increased by 1. S is increased by the fraction of the multiple bait b assays that pulled down p. In this fashion, repeating the same pull downs multiple times provides a way to systematically increase the accuracy of the S/P ratios and hence, ultimately, the accuracy of the final complex predictions.

Note 2.

From both S and P calculated for a given protein p as prescribed above, a value D (“Discount”) is subtracted to further mitigate the effect of indiscriminate interactions. D is defined as the largest integer such that the probability of obtaining by chance a score S ≥ D for p is equal or larger than a prespecified threshold B_crit. This probability is calculated under a random model that uses the net data ratio (no. of baits with at least 1 assay that pulled down p/no. of baits with a nonempty pulldown) as the base probability that any given single assay pulls down p. For baits that had multiple assays in the dataset, a single assay is assumed in this random model.

Note 3.

The parameters C_crit and B_crit were set to 0.6 and 0.01, respectively, based on both the biological reasonableness of these values and on the overlap with the MIPS gold-standard reliability measure evaluation of other possible values. This evaluation showed that reliability was not very sensitive to the exact choice of C_crit and B_crit [see supporting information (SI)].

The problem of finding complexes now becomes the problem of finding sets of proteins that satisfy the above definition of a complex. This appears to be a computationally intractable problem, so here, we settled for a nonoptimal solution. We use the algorithm outlined below to search for complexes. It yields a local optimal list of complexes in the sense that no single protein addition to a complex in the list as well as no merging of any 2 complexes in the list could still satisfy criterion (i) above.

Step 1.

Take all proteins pulled down by a given bait as a “complex seed.” Check for satisfaction of main criterion (i) above for this set of proteins. If it is satisfied, then add this set to the list of potential complexes. If not, then prune the protein with the lowest S/P score in the set (arbitrarily choose one in case of a tie) and recheck for satisfaction of criterion (i). Repeat until a set satisfying (i) is found and hence can be added to the list of potential complexes or until there is only 1 protein left (in which case no potential complex was found from this seed). Repeat for all pulldown seeds, building in this fashion a list of potential complexes.

Step 2.

Test all possible pairs of proteins for satisfaction of criterion (i). Add the pairs that satisfy the criterion to the list of potential complexes.

Step 3.

Merge complexes in the list, whenever a merged complex satisfies criterion (i). Repeat until no 2 complexes in the list could be merged and still satisfy criterion (i). Note that the particular sequential order in which the merges are done could, in theory, lead to a different final list of potential complexes. An arbitrary merging order was chosen.

Step 4.

For each complex in the list, iteratively, consider every possible single protein addition, updating the complex by adding the protein to it if criterion (i) was still satisfied. Repeat until no further single protein addition is possible. Note that the particular order in which the proteins are tested could, in theory, lead to a different final list of potential complexes. An arbitrary testing order was chosen.

Step 5.

Alternate Steps 3 and 4 until neither step can further change the complexes in the list. Note that every complex in the final list satisfies criterion (i) and that no merging of any 2 complexes in it could still satisfy criterion (i).

Because of pulldown data biases and limitations originating in a diversity of factors, the above algorithm can spuriously yield what, in reality, is a single complex as a number of distinct predicted complexes that do not fully overlap. It proves valuable to submit the final list of predicted complexes above to a coalescence process, as described below. It is important to note that after the coalescence process, there is no longer a guarantee that the complexes in the list satisfy criterion (i).

Coalescence process:

Step 1.

Given a complex A and a smaller or equal-sized complex B, if at least 50% of the proteins in B are present in A, then add the remaining proteins in complex B to complex A (without eliminating complex B from the list), regardless of criterion (i). Every possible pair of complexes is subject to this process, in turn. Note that the particular order in which the pairs are tested could, in theory, lead to a different final list of complexes. An arbitrary testing order was chosen.

Step 2.

Complexes that are now subsets of larger complexes are eliminated from the list.

Step 3.

Repeat steps 1 and 2 until no further changes can be made.

Note 1.

The above-mentioned 50% threshold was chosen based both on the biological reasonableness of this value and on the overlap with the MIPS gold-standard reliability measure evaluation of a range of other possible values (see SI).

Restricted Transient Interaction Prediction Algorithm.

Consider 2 permanent complexes, A and B, as defined above. If a pulldown assay with bait p, where p is a member of A but not a member of B, contains strictly >50% of the proteins of A and strictly >50% of the proteins of B, then we define A and B to transiently interact. The set of transient interactions was constructed by checking every pulldown in the dataset and every pair of permanent complexes for satisfaction of the above criterion.

Phosphorylation Transient Interactions.

To our 65 AP-MS-based predicted complex–complex transient interactions, we added 48 kinase–substrate restricted transient interactions curated from the literature (Kinase and phosphatase database (2007) accessible at www.proteinlounge/) (an additional 9 interactions involving the HOG kinase were classified as wide-ranging). For kinase or substrate proteins that were members of one of our predicted complexes, we took the transient interaction to involve the respective complex. Note that an additional 81 kinase–substrate literature-curated interactions present in the same database (Kinase and phosphatase database (2007) accessible at www.proteinlounge/) were not used in this work because they did not involve any protein present in our 210 predicted-complexes dataset.

Overlap with MIPS Complexes.

Given 2 complexes, their fractional overlap is defined as (no. of protein species common to both complexes/net no. of protein species in the 2 complexes). For example, if complex A = {a, b, c} and complex B = {b, c, d}, then their overlap is 2/4.

In the Gavin 2006 raw dataset (6), only pulldowns where at least 1 protein other than the bait was identified were considered.

Semantic Distance Between 2 Genes.

To calculate the Semantic Distance between 2 genes (or respective proteins), we follow the method of Lord et al. (19), except that we treat “is-a” and “part-of” edges equivalently. Details are given in the SI.

Semantic Distance Within Complexes in Fig. 2 Plot.

In Fig. 2, we employ the following procedure to ensure that differences on the typical complex size on different datasets do not lead to biases that would prevent a valid comparison among the different datasets average Semantic Distances.

The Semantic Distance of a complex is the average Semantic Distance of all of the pairwise combinations of protein members of that complex. The Semantic Distance of a dataset is calculated by

1. Separately calculating the mean Semantic Distance for all complexes of each given size.

2. Averaging the different complex sizes average Semantic Distances.

Note 1.

Complexes containing any proteins without the relevant GO annotation were excluded from the respective Semantic Distance calculation.

Note 2.

Semantic distances were calculated only for complexes of size up to and including 6 because of the statistically small number of complexes beyond this size.

A base random case Semantic Distance was calculated for each dataset (dots in Fig. 2). This was done by

1. Randomizing the dataset via a large number of pairwise protein permutations among the complexes.

2. Calculating this randomized dataset Semantic Distance as described above.

Note.

Standard deviations were determined for the randomized dataset Semantic Distances by repeating the above process 50 times for each dataset, and they were smaller than the data point size in Fig. 2.

Essentiality Homogeneity of Complexes (Fig. 3).

Colored bar.

For each dataset and complex size, the underlying Fraction of Fully Homogeneous Complexes whence the observed data were drawn is estimated in a Bayesian (46) fashion, assuming a prior probability uniform in the [0,1] interval. The statistical mode (no. of fully homogeneous complexes observed/no. of total complexes observed) is reported in the main bar. The error interval reports the 90% confidence interval for this underlying fraction.

Gray bar.

The expected homogeneity under randomization of the data (the foreground gray bar) is calculated based on the net fraction of lethal protein appearances (i.e., the same protein species appearing in 2 different complexes is counted twice for purposes of calculating this lethal fraction) on complexes of the size in question, for the given dataset. For example, for complexes of size 3, if 0.4 of the protein appearances in complexes of size 3 in the dataset are essential proteins and 0.6 are nonessential, then it is expected for 0.4³ + 0.6³ = 0.28 of the complexes to be fully homogeneous with respect to essentiality (because the complex could be “fully homogeneous lethal” or “fully homogeneous viable”).

Throughout, complexes where the essentiality of every member protein was not known were excluded from the analysis.

No statistically significant data were available for complexes of sizes larger than those reported.

Semantic Distances in Fig. 4 Plot.

In each case, the confidence interval for the average Semantic Distance is calculated by assuming a Gaussian distribution for its predictor X (via the Central Limit Theorem), hence leading to a 95% confidence interval of the form (X − 1.96^σ−$\sqrt{n}$, X + 1.96^σ−$\sqrt{n}$), where n is the number of pairs tested, and σ is approximated by the observed sample standard deviation. This confidence interval estimate assumes independence of the observed pair Semantic Distances in a given interaction class. However, in reality, correlations of multiple kinds are present (e.g., the Semantic Distances for the pairs of proteins (A, B) and (A, C) are not independent in general, because of having protein A in common). This makes the error bars in Fig. 4 underestimate the true, hard to quantify errors.

Human Interactome via Homology Matching.

An homologous human version of the yeast interactome was obtained by matching each yeast protein to its human inparalog proteins, as per the Inparanoid database (35).

Interactome Modular Division.

The “Q-modularity” algorithm of Clauset et al. (43, 47, 48) was applied to clustering the network of transient interactions. In this algorithm, the basic criterion for selecting the partition into modules is that the fraction of within-module transient interactions is maximized with respect to a base random case.