Waltzing α-helices

Proteins are 30% α-helices, which, together with β-sheets and loops, self-assemble into specific topological arrangements that make biologically active 3-dimensional structures. The α-helix has another important feature: it is capable of folding autonomously (1). Despite the apparently simpler structure, α-helix formation is governed by the same physical principles as protein folding, and recruits a similar array of interactions for its stabilization, including hydrogen bonds, electrostatics, dipole–dipole, and hydrophobic interactions (2). Furthermore, isolated α-helices display very complex conformational behavior. All of these properties have made the α-helix an excellent test lab for protein-folding research. From such efforts we now understand the factors that determine α-helix stability (3) and the timescales and mechanism of α-helix formation (4). New nanosecond laser-induced temperature-jump techniques can detect the kinetics of individual residues within the α-helix (5), producing exciting data with which to refine our understanding of helix formation. However, what has been missing is a technique to detect the complex motions that should take place in the nanosecond timescale in isolated α-helices. In an article appearing in a recent issue of PNAS, Fierz et al. (6) describe the application of the contact formation ultrafast kinetic technique to monitor nanosecond conformational fluctuations in α-helices at equilibrium conditions. The method promises to directly report on previously unobserved and important conformational processes of already formed α-helical segments, such as motion resulting from helix melting at one end and growth at the other.

In the theoretical description of α-helix formation, already developed in the late 1950s (7), short helical segments are thought to be highly unstable and thus relatively slow to form, whereas growth into longer helices is both more favorable and much faster. Pioneering experiments on very long nonnatural homopolymers quickly followed (8), but it took another 2 decades to develop the tools to study short protein-like α-helices. The discovery of the first protein segment capable of forming helix structure on its own (1) and the development of simple design principles to produce short helical peptides resulted in extensive experimental characterization of α-helix stability (3). From these experiments, we learned that nucleation is only slightly unfavorable. In other words, helix formation is weakly cooperative, resulting in complex distributions of helical segments of different size and position along the peptide sequence. Such empirical data from hundreds of designed and natural peptides were introduced into nucleation–elongation models producing a theory with real predictive power, demonstrating that the general principles behind α-helix stability were well understood (9).

Helix kinetics studies followed on. The timescales of α-helix formation were among the first phenomena measured with ultrafast folding techniques, most notably the laser-induced temperature jump (10, 11). The overall timescale for the relaxation between coil and helices was discovered to be hundreds of nanoseconds (10, 12). Analysis with a kinetic nucleation–elongation model demonstrated consistency between T-jump kinetic experiments and the nucleation barrier required for the equilibrium data, and estimated an elementary rate of helix propagation of 1–4 ns per residue (12). Kinetic theory made another intriguing prediction. In addition to the overall relaxation corresponding to motion over the nucleation barrier, there should be a fast process corresponding to interconversion among preformed helical segments. The fast process would arise from packets of propagation-shortening events and thus should take longer than the 1- to 4-ns single-residue rotations, but shorter than the overall equilibration with the coil. The problem is that this fast process was not observed in infrared (10) nor in fluorescence (12) T-jump experiments. The underlying kinetic complexity of helix formation became apparent when laser T-jump experiments were combined with infrared detection of single residues by using specific isotopic labeling (5, 13). But again, detailed theoretical analysis, this time including the complete description of α-helix stability and accounting for helix breaking and merging, showed that such complexity was expected for helix kinetics at the residue level (14). At this point, it seemed that we had a complete quantitative understanding of both stability and kinetic mechanism of α-helix formation.

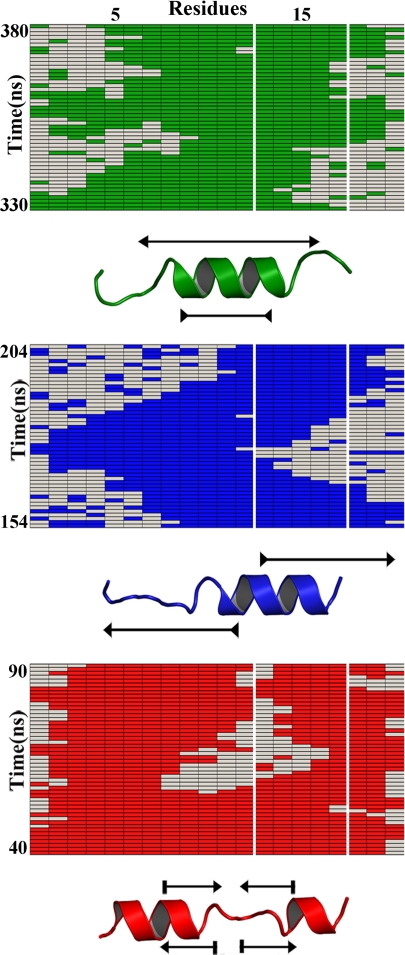
However, the diffusive phase corresponding to interconversion among helical segments has remained an unresolved issue. A way to obtain mechanistic insight about this process is to examine the distribution of single molecule trajectories obtained from stochastic kinetic simulations (see Fig. 1). The simulations reveal the conformational motions that helical peptides undergo at equilibrium. These helical motions are incredibly rich, but can be grouped into 3 main categories: (i) stretching–shrinking in which helical segments grow and melt from both ends (green in Fig. 1); (ii) sliding from one end of the molecule toward the other (blue in Fig. 1); and (iii) splitting–merging between a long helix and 2 shorter segments (red in Fig. 1). Importantly, all 3 modes have essentially the same timescale, which is predicted to be ≈50 ns according to the elementary rates for addition and subtraction of helical residues obtained from previous laser T-jump experiments (see ordinate for the 3 trajectories in Fig. 1). Stretching–shrinking and sliding modes are found much more frequently at the molecule ends, whereas the splitting–merging mode is less common and is preferentially seen in the middle. These “waltzing” helical motions observed at equilibrium will also occur while a protein is folding and may also be related to the function of proteins.

Fig. 1.

Stochastic kinetic simulations of α-helix formation in a 20-residue peptide according to nucleation–elongation theory. The rectangles show 50-ns segments showcasing the 3 basic helix motions: green, stretching-shrinking; blue, sliding; red, splitting-merging. The white vertical frame represents a 5-residue observation window in the Fierz et al. experiment. In principle, the experiment monitors the average time the 5 residues stay in helical conformation (green, blue, or red), or in the coil conformation that allows contact between the 2 probes (uncolored). The simulations, which are performed with single residue rotation rates estimated from T-jump experiments, are nicely consistent with the Fierz et al. results (6). These simulations also highlight that fully exploiting this exciting technique will likely require precisely determining the probe-to-probe contact probability of the rather common conformations with helix and coil residues within the observation window (e.g., the 330- to 345-ns segment in the green simulation).

“Waltzing” helical motions observed at equilibrium will also occur while a protein is folding.

How can these theoretical predictions be tested experimentally? The question takes us back to Fierz et al. (6) and the ultrafast contact-formation technique applied to study α-helix dynamics (15). In the Fierz et al. version of the experiment, 2 fluorophores are placed close in sequence but off register in the helix structure, for example, 6 residues apart (6), and then their rate of close contact is determined from triplet-triplet energy transfer measurements. Because in a peptide with high helical content (e.g., 70%) the contact should only occur when the helix breaks in between, the rate of contact formation becomes coupled to the local helical motions at equilibrium. In this way the measurement can report the transient presence of coil gaps in between the 2 probes (e.g., uncolored stretches within the white-framed window in Fig. 1). Some technical issues still need to be sorted out, such as what specific peptide conformations allow contact between the fluorophores, or how placing large aromatic groups in the middle of the molecule affects the helix dynamics. However, the great advantage of this technique is its essentially nonperturbative character. In this regard, it is tantalizing that the rates for addition and removal of 5-residue helical segments extracted by Fierz et al. from their data (≈40–60 ns) are in very close agreement with the timescales predicted by theory parameterized with the T-jump experiments (Fig. 1). The agreement strongly strengthens the Fierz et al. microscopic interpretation that the contact formation rate acts as a reporter of local helix motions, and suggests that the possibility of watching α-helices waltz is finally at our fingertips.