Culling experiments demonstrate size-class specific biomass increases with mortality

Abstract

Size-selective mortality inevitably leads to a decrease in population density and exerts a direct negative effect on targeted size classes. But density and population size structure are also shaped by food-dependent processes, such as individual growth, maturation, and reproduction. Mortality relaxes competition and thereby alters the dynamic interplay among these processes. As shown by the recently developed size-structured theory, which can account for food-dependent individual performance, this altered interplay can lead to overcompensatory responses in size class–specific biomass, with increasing mortality. We experimentally tested this theory by subjecting laboratory fish populations to a range of size-selective mortality rates. Overall, the results were in agreement with theoretical predictions. Biomass of the juvenile size class increased above control levels at intermediate adult mortality rates and thereafter declined at high mortality rates. Juvenile biomass also increased when juveniles themselves were subjected to intermediate mortality rates. Biomass in other size classes decreased with mortality. Such biomass overcompensation can have wide-ranging implications for communities and food webs, including a high sensitivity of top predators to irreversible catastrophic collapses, the establishment of alternative stable community states, and the promotion of coexistence and biodiversity.

Whenever mortality of individuals in natural populations increases due to more intense predation (1–3) or human exploitation (4, 5), total population density can be expected to decline. In addition to this direct and obvious effect, surviving individuals experience higher per capita resource availability and thus decreased competition among one another. As an indirect but inevitable side effect, mortality relaxes food-dependent regulation mechanisms, which limit population density and biomass turnover, thereby altering the dynamic interplay of these processes. Survivors may grow and mature faster or reach higher fecundities, for example (6). These indirect effects of mortality can affect the recruitment of individuals to and their distribution over different life-history stages or size classes (6–8). For example, in his classical experiments with blowflies, Nicholson (9) showed that under strong adult competition, an increase in adult mortality more than doubled the densities of immature stages. Furthermore, in the case of intense larval competition, adult density even increased when the adult stage itself was subjected to increased mortality (9). Several other experimental studies have subsequently found similar positive responses to mortality in the density of particular life-history stages (10–12).

A recently developed theory that accounts for size structure and food-dependent individual growth, maturation, and reproduction suggests that these experimentally observed stage-specific overcompensatory responses to mortality may be general and robust phenomena, because they occur in a variety of mathematical models that differ in complexity and the extent to which size-structure, food-dependent individual performance, and size-dependent processes are accounted for (13–18). The mechanisms of biomass overcompensation were revealed most clearly in an analysis of a stage-based extension (17) of the model of Yodzis and Innes (19). Which life-history stage or size-class exhibits biomass overcompensation depends on the mode of population regulation (14, 17). With strong adult competition, population density and biomass turnover are more regulated (i.e., limited) by the population reproduction rate rather than by its maturation rate. In this case, adults dominate the population and make up the largest part of its biomass. Furthermore, reproduction responds more strongly to competition relaxation. Thus, an increase in mortality will especially decrease the high adult density, but will indirectly lead to a proportionally larger increase in population reproduction due to increased individual fecundity than in maturation and, consequently, to an overcompensatory increase in biomass of the nonregulatory, juvenile stage. In contrast, with strong juvenile competition, increases in mortality lead primarily to increases in population maturation rate due to faster individual growth, and thus to an overcompensation in adult biomass (17). Under both modes of population regulation, overcompensation is reflected in a hump-shaped relationship between stage-specific biomass and mortality, because very high mortality inevitably decreases the biomass of all stages (17).

More generally, biomass overcompensation occurs in nonregulatory life-history stages— those stages in which individual performance is not strongly limited by competition and consequently do not impose a bottleneck on population density and biomass turnover (13–15, 17). The outflow from these nonregulatory stages will not respond much when mortality relaxes competition among survivors, and the increased inflow into these stages is likely to translate into a net increase in biomass density (14, 17).

Mortality is generally size-selective (4, 20), which can have subtle consequences for biomass redistribution (15, 17). Increased mortality of a nonregulatory stage only indirectly decreases density and thus competition in the regulatory stage, while also directly and negatively affecting the density in the nonregulatory stage. For example, under reproduction regulation, the indirectly increased biomass of juveniles through increased adult fecundity is offset by the mortality imposed on the juveniles. This weakens the overcompensatory response (15, 17), which consequently reaches its maximum at lower mortality rates (13, 17) compared to when the regulatory stage is subjected to mortality. In the latter case, competition in the regulatory stage is relaxed directly, and the biomass overcompensation in the nonregulatory stages is more pronounced, because these stages are affected only by the indirect, positive consequences of the increased mortality (17). Most importantly, overcompensation in stage-specific biomass due to a size-selective mortality imposed by natural enemies may have wide-ranging community-level consequences. Predators feeding selectively on a nonregulatory stage can “cultivate” their own resource by feeding on them and hence increase their own performance. This positive feedback can manifest itself as an Allee effect for the predator population (13–16). In contrast, predators feeding selectively on a regulatory stage can increase the biomass in other prey stages and thereby allow other predators to invade (18).

Here we experimentally investigated whether increased size-selective mortality can indeed lead to the biomass redistribution patterns and positively hump-shaped relationship between size class–specific biomass and mortality predicted by size-structured theory. We subjected laboratory populations of a small poeciliid fish (Heterandria formosa) to a range of mortality rates that targeted either small juveniles (referred to simply as “juveniles” hereinafter) or adults. Based on theory (13–15, 17) and experimental data suggesting that fish populations in general are reproduction-regulated (21), we expected to find that population biomass was dominated by adult biomass (prediction I; Table 1). We further expected to see a positive response of juvenile biomass to mortality for both mortality regimes (prediction II). We expected this overcompensation to be weaker (prediction III) and to occur at a lower mortality (prediction IV) when juveniles were targeted compared to when adults were targeted. Finally, we expected adult biomass to decrease monotonically with both adult and juvenile mortality (prediction V), but to a smaller extent under the latter regime (prediction VI).

Table 1.

Comparison between theoretical predictions and experimental observations for the features of the biomass–mortality relationship for a reproduction-regulated population in response to adult and juvenile mortality

	Feature of biomass–mortality relationship	Prediction		Observation
		Adult mortality	Juvenile mortality	Adult mortality	Juvenile mortality
I	Biomass in controls dominated by	Adult biomass	Adult biomass	+	+
II	Positively hump- shaped for	Juvenile biomass	Juvenile biomass	+	+
III	Magnitude of overcompensation	Strong	Weak	+ (22.7%)	+ (11.5%)
IV	Occurrence of overcompensation at	Higher mortality	Lower mortality	+ (0.015 day−1)	+ (0.008 day−1)
V	Monotonic decrease in	Adult biomass	Adult biomass	+	—*
VI	Rate of biomass decrease	High	Low	+	+†

Plus signs indicate agreement between theoretical predictions and experiment, and minus signs indicate discrepancy. Values in brackets were estimated from fitted models.

*Nonrecruit biomass declined continuously with juvenile mortality.

^†Adult biomass–juvenile mortality relation was compensatory over the entire range of mortality rates imposed here.

Results

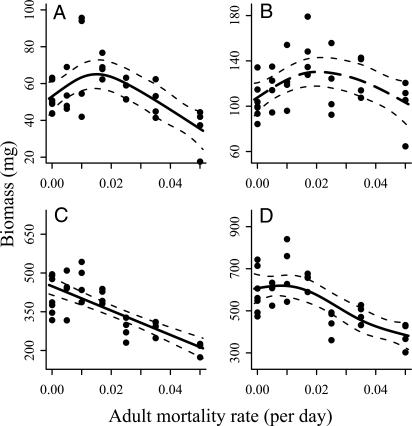
The population size structure was dominated by adult biomass, especially under nonharvested control conditions (Figs. 1 and 2). We found that adult mortality led to an increase in juvenile biomass at intermediate mortality rates, only to decrease below control values at higher mortality rates (Fig. 1A; Table 2A). The estimated maximum overcompensation amounted to a 22.7% difference [(bootstrap 95% confidence interval (CI), 14%–162%] between the juvenile biomass in controls and the estimated hump, which occurred at a mortality rate of 0.015 day⁻¹ (bootstrap 95% CI, 0.011–0.028 day⁻¹). A similar positively hump-shaped relation between biomass and mortality also was observed for the intermediate size class, consisting of large juveniles, referred to as “nonrecruits” hereinafter (Fig. 1B; Table 2A). The biomass of adults decreased monotonically with adult mortality (Fig. 1C; Table 2A). Total biomass exhibited an initial compensatory response at low adult mortality, but decreased rapidly thereafter with further increases in adult mortality (Fig. 1D; Table 2A). Furthermore, the relative proportion of large females to total females and the relative number of large males to total males decreased with adult mortality [regressions, F_1,29 = 12.5 (P = .001) and F_1,29 = 15.2 (P < .001), respectively; supporting information (SI) Fig. S1A and B].

Fig. 1.

Biomass of different size classes as a function of adult mortality: (A) juvenile biomass, (B) nonrecruit biomass, (C) adult biomass, and (D) total biomass. Each dot represents the estimated long-term average biomass of a replicate (n = 31). Solid lines represent the fitted and selected models (see Table 2). The regression was only marginally significant for nonrecruits, as indicated by the long-dashed line. The thin-dashed lines give the approximate 95% CIs. Note that the ordinate axes differ between panels and do not include 0.

Fig. 2.

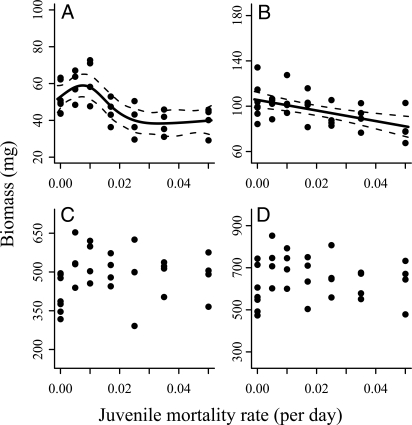
Biomass of different size classes as a function of juvenile mortality. Same notations as in Fig. 1; n = 31.

Table 2.

Summary of statistics and results from the model fitting and selection procedure for biomass for each size class and mortality scenario

Size class	Model	P value	Estimated df*	GCV†	AIC†	Adjusted R2
(A) Adult mortality
Juveniles	Smoother	.004	2.69	3.16	250	0.36
	Linear	.017		4.19	259	0.10
Nonrecruits	Smoother‡	.082	2.24	4.37	283	0.20
	Linear	.971		5.43	290	−0.03
Adults	Smoother	<.001	1	11.4	349	0.59
	Linear	<.001		11.4	350	0.59
Total	Smoother	<.001	3.73	0.03	367	0.53
	Linear	<.001		0.03	375	0.40
(B) Juvenile mortality
Juveniles	Smoother	.001	4.09	1.72	226	0.48
	Linear	<.001		2.1	232	0.31
Nonrecruits	Smoother	.098	1	0.02	249	0.26
	Linear	.001		0.02	249	0.26
Adults	Smoother	.209	3.31	17.5	368	0.12
	Linear	.571		18.62	371	−0.02
Total	Smoother	.380	1.16	17.18	378	−0.03
	Linear	.793		17.19	378	−0.03

Statistics for selected models are given in bold. P values are for smoothing terms and slopes for GAM and linear regression models, respectively.

*Estimated df for the smoothing term as provided by the fitting procedure. These should not be to close to 1 or the maximum df possible (here 6).

^†GCV scores are for GAMs with and without (= linear) smoothing terms for mortality rate, whereas AICs are for GAMs with smoothers and standard linear models (= linear). The lower the GCV score, the better the model performance. GAMs without smoothing terms are here essentially standard linear models, so the both comparisons select the same models.

^‡Marginally significant.

Juvenile biomass also increased when mortality targeted juveniles. The overcompensatory hump was weaker, with an estimated effect of 11.5% (bootstrap 95% CI, 0.06%– 50%), and occurred at a lower mortality than for adult mortality (at 0.008 day⁻¹; bootstrap 95% CI, 0.001–0.018 day⁻¹) (Fig. 2A; Table 2B). In contrast to the adult mortality scenario, nonrecruit biomass decreased monotonically with juvenile mortality (Fig. 2B; Table 2B). No significant trends in adult and total biomass were observed over the range of juvenile mortalities studied (Fig. 2 C and D; Table 2B). Furthermore, the relative proportion of large females to total females increased with juvenile mortality, whereas no such relationship was found for males [regressions, F_1,29 = 5.4 (P = .027) and F_1,29 = 2.3 (P = .143), respectively; Fig. S1C and D].

Discussion

The biomass redistribution pattern that we report here is congruent with theoretical predictions for reproduction-regulated populations, that is, when adults constitute the regulatory stage (14, 17). In contrast, the inverse patterns expected under maturation regulation would be highly inconsistent with our data. First, we found a dominance of adult biomass over juvenile biomass in the control (prediction I), along with increasing juvenile biomass with increasing adult and juvenile mortality (prediction II). The fit between expectations and observations even included detailed aspects of the biomass redistribution pattern (13, 15, 17), because the juvenile biomass increase was weaker (prediction III) and occurred at lower mortality levels with juvenile mortality than with adult mortality (prediction IV). The only deviation from the predictions was the lack of a significant decrease in adult biomass for the juvenile mortality scenario (prediction V). One explanation for this discrepancy is that this theoretical prediction was based on a population model that did not include adult growth in body size (17). Adult H. formosa, particularly females, grow substantially after maturation; between the time of maturation and attainment of maximum length, body weight can increase by a factor of ≈10 for females and 3 for males. Correspondingly, we found that the relative proportion of large females increased with juvenile mortality, indicating an increased food-dependent individual growth under decreased competition that compensated for adult biomass loss due to decreased maturation inflow. This trend was not observed for males, likely because of the size-dimorphism between the sexes. In contrast, the relative numbers of both large females and large males decreased with adult mortality as they were removed from the populations. The weaker response in adult biomass to juvenile mortality compared with adult mortality is in line with prediction VI. The cost of juvenile mortality was instead paid by the intermediate size class consisting of large individuals, likely resulting from a decreased inflow from the juvenile size class due to the experimental removal of juveniles.

Positive effects of mortality on stage-specific densities have been reported previously in empirical studies of blowflies (9, 11), soil mites (12), Daphnia (10), and guppies (22). This wide taxonomical range in which overcompensation has been observed suggests that biomass overcompensation is a common phenomenon, likely due to the ubiquity of size-structure and food-dependent growth, maturation, and reproduction in natural populations (23). These studies support the recently developed size-structured theory that accounts for these features (13–18). Our findings for H. formosa provide a more complete test of this theory, including the demonstration of a hump-shaped relationship between size class–specific biomass and mortality and the effects of different size-selective mortalities.

Structured theory predicts that life-history stage-structure and food-dependent individual performance can have far-reaching consequences for the stability and dynamics of whole food webs. The biomass redistribution and overcompensation in prey populations due to the consumption pressure of predators is at the core of these community-level effects (13–16, 18). Predators that feed on the prey size class that exhibits overcompensation can increase their own resource abundance and establish a positive feedback between predator density and predator ecological performance (13–16). But this positive feedback also makes the predator prone to catastrophic collapses (13, 15, 16), because decreasing consumption mortality of prey due to declining predator density leads to an accumulation of prey biomass in size classes inaccessible to the predator, thereby enhancing the predator's decline (17). On the community level, this process manifests itself as an Allee effect in the predator and establishes alternative stable community states with and without the predator (13–16), because the altered prey biomass distribution makes the collapse of the predator irreversible. Indeed, many commercially exploited stocks of predatory fish have rapidly and drastically declined after decades of overfishing (5) and also have shown a lack of recovery (24). These observed collapses in overharvested top predators have been accompanied by changes in prey fish populations that are in line with biomass overcompensation. For example, following the collapse of the northwest Atlantic cod stock, the total biomass of the main forage fish capelin increased (25), whereas capelin mean size, individual performance, and body conditions deteriorated (26–29), indicative of intensified competition. The remaining cod individuals also have low body conditions (30), indicating a lower availability of vulnerable prey fish size classes. Similar observations come from the Baltic Sea, which also has seen a drastic decline in the cod stock. This decline is associated with an increased density of cod's major prey, sprat, which has experienced declines in individual growth and total population fecundity (31, 32). These observed changes in the state of the prey populations are all in congruence with an Allee effect in cod due to prey overcompensation, but are somewhat inconsistent with alternative explanations for the lack of recovery (32).

The fact that imposing mortality on prey can redistribute the prey biomass to the benefit of the predator suggests—seemingly counterintuitively—that thinning of the prey population may aid the recovery of a collapsed predator population by increasing the resource availability for the predator (13). The applicability of this management strategy has recently been demonstrated experimentally in a natural lake community with Arctic char as prey and brown trout as predator, where the latter had effectively gone extinct (33). After a massive removal of Arctic char biomass, relaxed competition among char led to accelerated individual growth and, most importantly, increased biomass of small char, the size class on which brown trout feed. The brown trout population subsequently recovered and has since persisted by controlling the char size distribution and “cultivating” its own prey (33).

Finally, predators feeding on the regulatory prey stage decrease their own resource but can increase the biomass in other, nonregulatory stages. This may facilitate size-selective predators feeding on these overcompensatory stages, whose successful invasion and persistence thus will depend on the beneficial biomass redistribution in the common prey caused by the presence of the first predator (18). If the facilitating predator goes extinct, then the prey biomass distribution will change, causing the secondary predators to go extinct as well. Such facilitation may explain the paradox of the commonly observed coexistence of several consumers on a single prey population (34) even under equilibrium conditions and the cascading effects of keystone predator extinctions that reverberate through the food web with consequential ecosystem-wide transitions (35, 36). Thus, biomass overcompensation can be an important factor in promoting and explaining biodiversity or food web complexity and stability.

Materials and Methods

Natural History.

H. formosa is a viviparous poeciliid fish native to ponds and streams on the coastal plains of southeastern United States, where it feeds on small invertebrates and algae (37). Length at birth is 5–6 mm. In males, maturation starts at a length of 10–11 mm with the development of a gonopodium and is completed at a length of 12 mm with the formation of a hook at the tip of this fin. Males reach a maximum length of about 18 mm. In females, maturation of females begins at a length of 8–10 mm with the appearance of a black dot on the anal fin. Full reproductive functionality is reached at 14 mm with the complete development of ovaries. Females reach a maximum length of about 36 mm. Females simultaneously carry embryos of different developmental stages (37). Under unlimited food conditions, females give birth to litters of 1–7 juveniles every 7–21 days (38). Average age at first reproduction for females is 7 weeks (39). The numbers of offspring and litters and the intervals between litters are food-dependent (40). Otholith samples indicate that males and females live for about 90 and 120 days in the field, respectively (J. Travis, personal communication).

Experimental Setup and Stocking.

The experiment was performed at Umeå University between March 2006 and October 2007. A total of 56 aquaria, each with a volume of 80 L, were set up in a semicirculation system with a total water exchange of 20 L h⁻¹. We used well water supplied by the local municipality, warmed to 25 °C and salted to 5 g L⁻¹ as protection against ectoparasites. The use of a biofilter, an activated carbon filter, and a UV filter ensured good water quality. The light regime was 14 h light and 10 h dark. To provide refuges, 4 loosely packed balls of green plastic threads (55.2 g ± 2.0 SD) were placed in each aquarium, 2 on the surface and 2 on the bottom. Between August and November 2005, each aquarium was stocked twice with a total of 25 randomly chosen adults of each sex. During the experiment, the fish were fed a mixed diet of pellets, delivered by automatic microfeeders (9.45 ± 0.41 mg per feeding, 4 × 2 feedings per day), and volumetrically quantified Artemia salina nauplii (2 × 5 mL/week). Before the experiment, the system was medicated with a malachite green/formaldehyde solution against protozoan parasites and with a bactericide.

Treatments.

Mortality regimes targeted either adults or small juveniles, with 6 mortality levels for each mortality regime. Replication was 4-fold. Controls were replicated 8 times. Juvenile mortality was imposed on juveniles < 9 mm long. Adult mortality was sex-explicit and targeted male individuals > 12 mm long and female individuals > 14 mm long. Treatments were randomly assigned to aquaria. Per capita mortality rates of 0.0 (controls), 0.005, 0.01, 0.017, 0.025, 0.035, and 0.05 day⁻¹ were imposed for both regimes. Mortality was imposed weekly and performed by hand netting the appropriate numbers of individuals. A coin flip determined whether or not an individual was removed. The actual numbers removed were based on the previous census and calculated as follows:

This quantity was 1–10 individuals for the lowest mortality rate and 2–52 individuals for the highest mortality rate in juveniles, and 2–10 individuals for the lowest mortality rate and 3–52 individuals for the highest mortality rate in adults. The numbers were distributed as evenly as possible over the subsequent 4 weeks. In April 2007, all adult and 4 juvenile mortality treatments were terminated, leaving the 8 controls and the replicates of the juvenile mortality treatments with mortality rates of 0.01 and 0.05 day −¹, respectively.

Sampling, Measurements, and Maintenance.

Sampling was done every 28th day. The entire population of an aquarium was captured by repeated hand netting until no individual could be seen on visual inspection. The fish were sorted into females, males, and juveniles, then placed in a transparent bowl and photographed. Individuals were counted and measured on a computer screen. Length was measured from the tip of the snout to where the cone-shaped, pigmented body merges into the straight, transparent tail fin. Measurements were transformed into dry weight biomass using internal standards and sex-specific length–weight regressions. During samplings, the aquarium walls were scraped, debris was removed, and the thread balls were rinsed. The feeders were cleaned and refilled every fourth week. Conductivity, pH, temperature, and oxygen were measured after each sampling in each aquarium. Dead individuals were removed at least every working day.

Calculations and Statistical Analyses.

One control replicate showed a consistently and conspicuously higher pH (Δ_temporal = 0.12; P < .001) than all other replicates and thus was excluded from any further analysis. No further biologically significant differences between replicate aquaria were found in abiotic water parameters (see SI Text and Fig. S2 for details).

We divided each population into the following size classes: juveniles (individuals < 9 mm long), adults (males > 12 mm long and females > 14 mm long), and nonrecruits (all others). Based on this classification, we calculated stage-specific and total biomass for each sampling. We fitted models of the form log(y) = M + a · e ^{(−b · time)}, log(y) = M · (1-e ^{(−b · time)}), and log(y) = M to the time series, with M being either the function asymptote or simply the intercept. Data were log-transformed to stabilize the variance and to account for the multiplicative character of population-level processes. We extracted the value of exp(M) of the best performing model as assessed using the Akaike information criterion (AIC). This procedure allowed us to obtain M as a measure of the asymptotic long-term average biomass of a size class that represents equilibrium instead of transient conditions and that also accounts for potential transient increases or decreases in biomass of a given stage due to harvesting and overcompensatory responses. This approach is valid because our theoretical predictions about the long-term biomass (Table 1) hold for nonequilibrium systems as well (see SI Text and Fig. S3 for details). The qualitative results and the conclusions were robust to alternative methods of calculating the long-term biomass average and the specific statistical analysis (see SI Text for details).

To check for curvilinear relationships between mortality rates and estimated long-term average biomass, we fitted generalized additive models (GAMs) to the extracted data using penalized iterative reweighted least square estimation. The models were represented by penalized thin plate regression splines and were of the form biomass_size-class = a + s(mortality), with s indicating the nonparametric smoother spline function as implemented by the mgcv package in R (41, 42). We compared the performance of the GAMs with that of standard linear regression models of the form biomass_size-class = a + b · mortality as null models. Standard diagnostic plots revealed reasonably well-behaved residuals. Occasionally, heteroscedasticity required the specification of a nonconstant variance (43). Model selection was based on the significance of the nonparametric part (smoother spline) and slope for GAMs and linear models, respectively, the degrees of freedom used up by smoothing parameter estimation and the AIC. Nonsignificant models were disregarded. P values for GAMs were obtained by unpenalized regression, because penalized regression does not account for model selection uncertainty, and thus the associated P values tend to be nonconservative (41). GAMs with estimated df close to 1 were simplified by replacing the smoothing function with a parametric linear term, essentially rendering the simplified GAM to a standard linear model. This model simplification was accepted if it resulted in a drop of the generalized cross validation (GCV) score of the GAM (41). Among the remaining models, we selected those with lower AICs (see SI Text for information on robustness of the results).

For juvenile biomass under both harvesting scenarios, we extracted the mortality rate at which the maximum overcompensation occurred and the relative difference between this mortality and the control. We used stratified nonparametric bootstrapping with 1,000 iterations to assess the variance of these characteristics (44). Because the previous analysis provided evidence of a nonlinear relationship between mortality and juvenile biomass, we restricted the bootstrap to models exhibiting such a relationship by excluding models with a linear relationship.

We calculated the ratio of large females (> 20 mm) to total female abundance and the ratio of large males (> 15 mm) to total male abundance for each replicate and sampling, and then averaged over time with the initial sampling excluded. After performing arcsine transformation to account for the proportional character of these data, we regressed the data over mortality rates using standard linear models (see also Fig. S1).

The α-level used was 0.05 unless indicated otherwise. All computations and statistical analyses were performed in R 2.7.0 using the stats, mgcv, gam, and nlme packages (42).

Ethical Statement.

The experimental design and the use of vertebrates were in accordance with institutional standards and were approved by the Swedish Animal Welfare Organization (Dnr A 95–04).