Direct interaction of flagellin termini essential for polymorphic ability of flagellar filament

Abstract

We report the structures of flagellar filaments reconstituted from various flagellins with small terminal truncations. Flagellins from Salmonella typhimurium strains SJW1103 (wild type), SJW1660, and SJW1655 were used, which form a left-handed supercoil, the L- and R-type straight forms, respectively. Structure analyses were done by electron cryomicroscopy and helical image reconstruction with a help of x-ray fiber diffraction for determining precise helical symmetries. Truncation of either terminal region, irrespective of the original flagellin species, results in a straight filament having a helical symmetry distinct either from the L- or R-type. This filament structure is named Lt-type. Although the local subunit packing is similar in all three types, a close comparison shows that the Lt-type packing is almost identical to the R-type but distinct from the L-type, which demonstrates the strong two-state preference of the subunit interactions. The structure clearly suggests that both termini are located in the inner tube of the concentric double-tubular structure of the filament core, and their proper interaction is responsible for the correct folding of fairly large terminal regions that form the inner tube. The double tubular structure appears to be essential for the polymorphic ability of flagellar filaments, which is required for the swimming–tumbling of bacterial taxis.

Molecular events behind the swimming–tumbling pattern of bacterial motility involve polymorphic transitions of normally left-handed supercoiled flagellar filaments into a right-handed form (1) upon quick reversal of motor rotation that drives the filament (2–4). The polymorphic mechanism of the filament has been modeled assuming two-state subunit conformations (5–7), but not been fully understood because of the limited resolution of available structural data that show only the outer shape of subunits and distribution of axially aligned bundles of α-helices in the core (8–10).

The supercoiled forms of bacterial flagellar filaments are thought to be constructed from a mixture of two distinct subunit conformations of flagellin arranged in a regular manner, while all the subunits are chemically identical (5). There are two types of straight filaments with distinct helical symmetries, one called the L-type, in which the 11 protofilaments are tilted to the left, and the other called the R-type, with the protofilaments tilted to the right (11). Flagellin mutants from SJW1660 (the L-type) and SJW1655 (the R-type) can be copolymerized to form different types of supercoiled filaments, depending on the mixing ratio (12). Therefore, the two conformations of the flagellin mutants are thought to be representing the two that coexist in the supercoiled filaments.

Flagellin from Salmonella typhimurium is composed of 494 amino acids (13). About 65 residues of the NH₂ terminal and 44 of the COOH terminal are disordered in monomeric form (14) but well folded in the filament (15), which indicate their roles in assembly regulation mechanism to suppress spontaneous polymerization of flagellin under physiological conditions. Although there is no direct evidence, indirect evidence has suggested that these terminal regions contribute to the core part of the filament, which occupies about half of the filament diameter of 230 Å and has a concentric double tubular structure (9, 10).

The role of the disordered terminal regions in filament formation, stability, and polymorphism has been studied by using proteolytic fragments of flagellin with terminal deletions of different sizes (16). Polymerization could be induced even when most of the disordered terminal regions were removed, although the filaments were much less stable. The most dramatic effect observed was that truncation of only a few residues from wild-type flagellin resulted in straight filaments upon polymerization and loss of polymorphic ability.

Taking advantage of the straight form of the filaments reconstituted from terminally truncated flagellins, we carried out structure analysis of these filaments to find out the location of the termini and their roles in the polymorphic ability of the intact filaments. The simplest interpretation of the results is that both termini are located in the inner tube of the concentric double tubular structure of the filament core, and their direct interaction is responsible for the proper folding of fairly large terminal regions that form the inner tube. Strong preference of the subunit interactions in the outer tube to be in one of the two states is also demonstrated, and its implication for the polymorphic mechanism is discussed.

MATERIALS AND METHODS

Preparation of Filaments of Flagellins with Terminal Truncations.

Flagellins were isolated from a wild-type strain, SJW1103, and two mutant strains, SJW1660 and SJW1655, and purified as described (14). Fragments of flagellins with small terminal truncations were prepared by limited proteolysis of monomeric flagellins and purified by ionic exchange column chromatography (16). The F-(1–486) fragments, which lack the 8 COOH terminal residues, were prepared from all three types of flagellin, while the F-(20–494) fragment, which is deprived of the NH₂ terminal 19 residues, was made from SJW1655 flagellin. Filaments were reconstituted by adding appropriate concentrations (0.2–0.5 M) of (NH₄)₂SO₄ to solutions containing the truncated flagellins, as described (16).

Electron Cryomicroscopy and Helical Image Reconstruction.

The experimental procedure of electron cryomicroscopy, including the preparation of frozen hydrated samples, is fully described in ref. 9. Electron micrographs were taken at a magnification of ×50,000 with a JEOL model JEM-3000SFF (300 kV) electron microscope equipped with a cryo-stage cooled to 4 K with liquid helium (17) and a field emission electron source (18). The defocus levels were within the range from 2 to 5 μm. The helical image reconstruction procedure fully described in ref. 9 was used in the exactly same way, including correction for the contrast transfer function. The data out to 12-Å resolution were included for calculating the density maps and radial density distribution.

X-Ray Fiber Diffraction.

Well-oriented filament sols were prepared as described (19). Filament sols prepared by centrifugation at 10,000 × g for 15 h were made into a liquid crystalline state in the solution containing 30 mM NaCl and 50 mM glycine-acetate (pH 5.0). After further centrifugation of the sols in capillary tubes at 2000 × g for 20 h, the sols were placed in a superconducting magnet with a 13.5 Tesla magnetic field for 2 to 3 days. X-ray fiber diffraction patterns were recorded as described (19), using a rotating anode x-ray generator (Rigaku, Tokyo), a Ni-coated double mirror optics (Rigaku), and Imaging Plate (Fuji). The layer-line spacings and intensity distributions were obtained by a data processing procedure using the two-dimensional angular deconvolution method, as partially described in ref. 19, and these data were used only to determine the helical symmetries of the filaments.

RESULTS AND DISCUSSION

Helical Symmetry of the Filaments of Truncated Flagellins.

Studying the structures of filaments of flagellins with the COOH terminal eight residues truncated [F-(1–486)] from strains SJW1103 (wild type), SJW1660 (L-type), and SJW1655 (R-type) by electron cryomicroscopy, it turned out that the symmetries of these filaments were different either from the L- or R-type, but all were the same irrespective of the original flagellin. Truncation of 19 residues from the NH₂ terminal of SJW1655 flagellin [F-(20–494)] also resulted in the same symmetry. Fourier transforms of filament images demonstrate it clearly, as shown in Fig. 1. The somewhat poor quality of the Fourier transforms in Fig. 1 C–F is caused by significantly lower mechanical stability of the filaments of truncated flagellins compared with the intact filaments, for which the Fourier transforms are shown in Fig. 1 A and B. Flagellins with larger truncations also yielded filaments of the same symmetry (data not shown).

Figure 1.

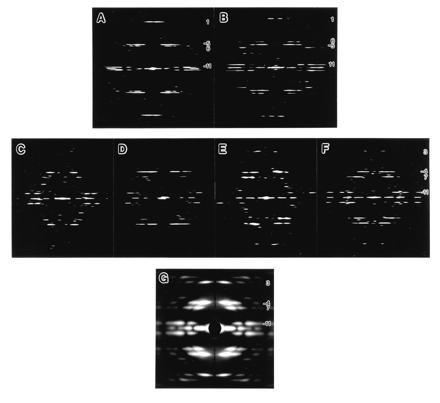
Computed Fourier transforms and x-ray diffraction pattern of various reconstituted filaments. (A–F) Computed Fourier transforms of electron cryomicrographs of frozen hydrated filaments: (A) SJW1660 (the L-type), (B) SJW1655 (the R-type), (C) F-(1–486) of SJW1103 (wild type), (D) F-(1–486) of SJW1660, (E) F-(1–486) of SJW1655; and (F) F-(20–494) of SJW1655. (G) X-ray fiber diffraction pattern from an oriented filament sol of SJW1655 F-(1–486). For all the figures, the data out to about 20-Å resolution are shown. The order of Fourier–Bessel component (or helical start number), n, of each layer line is indicated on the right side. In the Fourier transforms of the L- and R-type (A and B), relative layer-line intensities and the order of Fourier–Bessel component are strongly correlated because the local subunit packing is similar to each other, and this makes it easy to identify the order. Therefore, the difference in helical symmetry between the two, such as the tilt of the 11-start helix, can be roughly identified from the axial positions of the major layer lines. If the strong layer line, n = −5, is above the relatively weaker layer line, n = 6, the 11-stranded protofilaments are tilted to the left, or vice versa. The larger the distance between the two layer lines, the larger the tilt angle (see also Fig. 2 B and C). This relation is also valid in the Fourier transforms of the filaments of truncated flagellins (C–F), except that some of the Fourier–Bessel components have slightly different orders: e.g., n = 1 of the L- and R-type is 3; n = −5 is −4; n = 6 is 7; and so on. This indicates that the local packing and orientation of the subunits are more or less preserved also in the filaments of truncated flagellins.

In Fig. 1 C–F, the diffraction patterns indicate that the longitudinal protofilaments are tilted to the left in contrast to the R-type (Fig. 1B), but the tilt angle is larger than that of the L-type (Fig. 1A). Although the overall layer-line pattern is similar to that of the L-type, there is a small but clear shift of the radial peak positions of the layer-line intensity distributions. We carefully checked the peak positions and phase residuals between the near and far sides to find out the order of Fourier–Bessel component (or helical start number) of each layer line. More accurate radial peak positions were obtained from the x-ray fiber diffraction pattern shown in Fig. 1G. They are listed in Table 1, from which the Bessel orders of the major layer lines were unambiguously determined. The filament radius is the same as those of the L- and R-type, and the radial peak position of the layer line labeled −11 is unchanged, showing that this filament also has 11 protofilaments. However, the other Bessel orders are changed: from −5 to −4, from 6 to 7, and from 1 to 3. The layer-line spacings were measured from the x-ray diffraction pattern and the helical symmetry was determined by building the reciprocal lattice using these Bessel orders. The helical lattice parameters are listed in Table 2. We call this the “Lt” type symmetry, where “L” stands for the left-handed 11-start helix and “t” for truncated flagellin.

Table 1.

Radial positions of the first peaks of the layer-lines

Type	G−11/G11	G7/G6	G−4/G−5	G3/G1
Lt	0.0195  (0.0195)	0.0135  (0.0134)	0.0090  (0.0091)	0.0075  (0.0082)
Parity	Odd	Odd	Even	Odd
R	0.0195	0.0120	0.0110	0.0035

Layer-lines are specified by G_n, where n indicates the Bessel order. Radial peak positions were measured on x-ray fiber diffraction patterns and are listed in Å⁻¹ unit. The errors are ±0.0003 Å⁻¹ at most. The structurally corresponding Fourier–Bessel components are listed in the same column for the Lt- and R-type and they are indicated in the top row as Lt-type/R-type. Parity indicates the phase difference between the near and far side of the layer line and it is even when the difference is close to 0° and odd when close to 180°. Since the helical symmetry of the R-type is well established, the radial peak positions of the Lt-type layer lines are calculated from those of the R-type layer lines, taking into account the Bessel order of each layer line, and listed in parenthesis. The close match between the observed and calculated radial positions and phase parities confirms that the deduced symmetry of the Lt-type is correct. Only for G₃, the difference between the observed and calculated radial positions is relatively large, probably because of the significant difference in the subunit orientations with respect to the filament axis between the Lt- and R-type structures, but the peak position calculated for G₂ is 0.060, which is twice further than that for G₃. 

Table 2.

Helical symmetries and cylindrical surface lattice parameters

Type	Subunits/turn	daxial-rise	d−11(d11)	d3(d1)	d−4(d−5)	d7(d6)
Lt	3.6435  ±  0.0003	4.684	51.80	51.88	33.41	39.64
L	5.5148  ±  0.0005	4.772	52.51	51.50	35.56	37.95
R	5.4699  ±  0.0002	4.700	51.79	51.91	33.79	39.33

The second column, Subunits/turn, is the number of subunits per one turn of the one-start (left-handed) helix for the Lt-type and one-start (right-handed) helix for the others, where the significant numbers are the deviation from 3.6667 (=11/3) for the Lt-type and those from 5.5000 (=11/2) for the L- and R-type, which are the numbers of subunits/turn when the 11-start helical lines are exactly parallel to the filament axis. These deviations reflect the tilt angles of the 11-start helices. The estimated error of subunits/turn is relatively large for the L-type, because the layer-line interval is relatively small compared to the layer-line width by the direct beam size. The deduction of the data listed in this table will be described in detail elsewhere. The next column, d_axial-rise, is the axial distance of the subunits and the experimental errors are ±0.005 Å for all of them, which is mainly due to the errors in the specimen-film distances (±0.1%). The other columns are distances from one subunit to neighbors on the cylindrical surface lattices along helical lines specified by the subscripts. The parameters within parentheses are for the L- and R-type except that d₁₁ is for the R-type. These distances are calculated from the values in columns two and three for the surface lattices at the radius of 45 Å. All distances are in Å unit. 

Comparison of Three-Dimensional Structures.

Three-dimensional structures of the Lt-type filaments as well as the L-type were deduced by helical image reconstruction, exactly in the same way as described for the structure analysis of the R-type filament by Mimori et al. (9). Helical image reconstruction of all four filaments of truncated flagellins (three with COOH terminal truncation and one with NH₂ terminal truncation) produced almost identical density maps except for small differences around the filament axis. The reconstructed images in a solid surface representation are shown in Fig. 2, which compares the Lt-, L-, and R-type filaments. In Fig. 2, the filament structure of F-(1–486) of SJW1103 represents those of the four Lt-type filaments.

Figure 2.

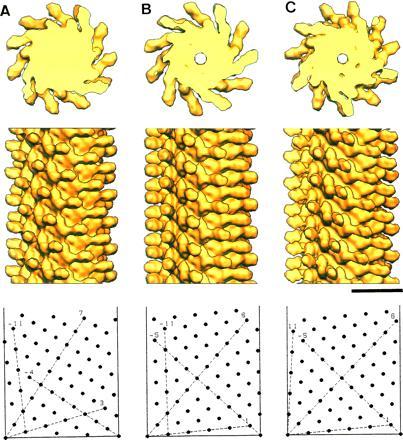
Solid surface representation of the reconstructed density maps. F-(1–486) of SJW1103 (A), SJW1660 (B), and SJW1655 (C). (Top) Axial view of 50-Å-thick cross sections showing 11 subunits in two turns of one-start helix. (Middle) Side view of 300-Å-long segments. (Bottom) Helical lattice showing subunit packing arrangements at the radius of 45 Å, where the radial density distribution of the outer tube has its peak (see Fig. 3C). The data out to 12-Å resolution are included for calculating the density maps. The numbers of averaged filament images for reconstruction are 20, 14, and 16, and average phase residuals of individual images to the reference images are 17 (±4), 21 (±7), and 14 (±3) degree, for A, B, and C, respectively. (Bar = 100 Å.)

In the structures of all three filaments, there are no obvious differences in the shapes of outer projections and short vertical column densities that are directly attached to the densely packed core, while the subunit orientations seem to be slightly different according to the different tilt angles of the protofilaments. The local subunit packing relations are also similar to one another.

Because the two conformations of the mutant flagellin subunits of the L- and R-type filaments shown in Fig. 2 B and C, respectively, are thought to represent the two that coexist in the supercoiled filaments, the small difference between them indicates that the conformational change involved in polymorphism is a rather small one. The close packing of axially aligned α-helices in the filament core (8–10) and the nature of the local lattice conversion (see Fig. 4B) suggest that the probable conformational change involved in the polymorphic transition would be a distinct mutual shift of these α-helices by about 2.5 Å along the protofilament, and the subunit rotation within a cylindrical surface plane assumed in the polymorphic model by Calladine (6, 7) would be rather unlikely. In any case, these two lattices are interconvertible to each other by a continuous twisting deformation of the cylindrical surface lattice around the axis, except for the small but distinct difference in the intersubunit distance along the protofilament.

Figure 4.

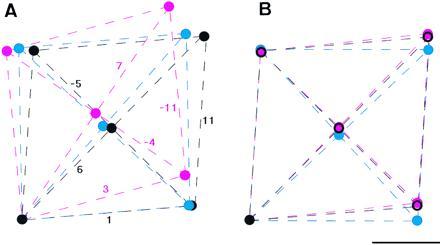
Comparison of the local subunit packing of the three different helical symmetries. (A) Local lattices of the Lt-, L-, and R-type are superimposed with the filament axis vertical. (B) Lattices are tilted so that the lattice lines representing the protofilaments (the 11-start) are superimposed. Lines and circles are colored red for the Lt-type, blue for the L-type, and black for the R-type. The lattices are drawn on the cylindrical surface at the radius of 45 Å, which corresponds to the radial position of the center of the outer-tube structure shown in Fig. 3. The lattice parameters were calculated from the helical symmetries (Table 1), which were obtained from the layer-line spacings in the x-ray fiber diffraction patterns (the diffraction pattern of the Lt-type is in Fig. 1G; data not shown for the L- and R-type). (Bar = 20 Å.)

However, the Lt-type symmetry could only be produced by the following operation involving a discontinuous transformation on either the L- or R-type: first open up the tubular structure at an interface of any two protofilaments, then deform the tube so that the protofilament on the right at the interface slides down by one subunit relative to the one on the left, and close the tube. Similar relations within a group of lattices have been found in the polyhead tubes of bacteriophages (20) and the carbon nanotubes (21). This transformation may be called a reconstructive transformation as opposed to a displacive one between the L- and R-type filaments, in the similar way as discussed by Moody (22) for the contraction of bacteriophage tail sheath.

Structural Difference in the Inner Core.

The difference between the subunit structures of intact and truncated flagellins can be found in the axial views (Fig. 2 Top). The L- and R-type filaments have the central channel with a diameter of about 30 Å, which is necessary for subunit transport to the distal end for in vivo filament elongation, whereas the Lt-type filament lacks the channel.

At a higher contour level in wire-frame representation of the maps in Fig. 3, while the R-type filament from SJW1655 (Fig. 3A), which represents the filament structures of intact flagellins, shows a concentric double tubular structure in the core, the filament of F-(1–486) of SJW1103 (Fig. 3B), which represents the filament structures of truncated flagellins, has only the outer tube remaining intact; the inner-tube structure is destroyed and the mass roughly corresponding to the inner tube is found around the filament axis. The radial density distributions in Fig. 3C show the difference clearly.

Figure 3.

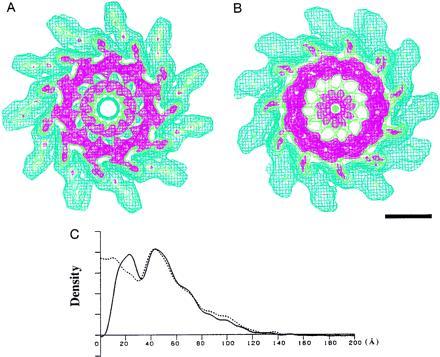
Wire frame representation of the density map of the filaments showing higher contour levels and their radial density distributions. (A) SJW1655. (B) F-(1–486) of SJW1103. Both maps are axial views of 50-Å-thick cross sections. Color coding of contour lines indicates density levels of 1.0, blue; 1.8, green; 2.1, red. The contour lines in blue approximately cover the correct molecular volume. (Bar = 50 Å). In A, the contour lines in red show a concentric double-tubular structure in the core of the filament, which is a common feature of all the intact filaments of supercoiled, the L- and R-type straight forms. In B, the density corresponding to the inner tube moved toward the axis, while the other part remained unchanged. (C) Radial density distributions of the filaments of intact and truncated flagellins. The solid line represents the density distribution of SJW1655, and the dotted line represents that of F-(1–486) of SJW1103.

Because of the large conformational change of the inner tube, we could not precisely locate the truncated terminal portions. It is, however, very likely that both termini are located in the inner tube, and a direct interaction of the termini is essential for the formation of the inner tube, because removal of a small segment from either terminal results in the disruption of the inner-tube structure.

From the analyses of the volume (9) and mass (19) of each domain, subunit domains of the inner and outer tubes were estimated to contain about 70 and 190 residues, respectively. The 70 residues of the inner-tube domain seem to be within the 65 NH₂ terminal and 44 COOH terminal residues that are disordered in the monomeric form, because they are not correctly folded in the absence of the either terminal. Then, the rest of the disordered terminal regions, only about 40 residues, is part of the outer-tube domain, which means that almost 80% of the outer-tube domain is already folded in the monomeric state. This suggests that the initial step of polymerization involves subunit interactions at this preformed part of the outer-tube domain, which would result in the folding of the 40 residues to complete the outer-tube formation, and then the direct terminal interaction triggers the folding of the inner-tube portion. This highly cooperative nature of the folding appears to play an important role in the regulation mechanism of polymerization, by which monomers alone do not spontaneously polymerize in the cell body, but are able to polymerize at the distal end of the filament, where a large portion of the disordered terminal regions are expected to be folded.

The Structural Relevance to the Polymorphic Ability.

The polymorphic ability is lost in the Lt-type filaments (16). This indicates that the presence of the inner tube is essential for the polymorphic ability of the intact filaments. However, the major subunit interactions in the outer tube alone are able to sustain the ability of polymerization in its nearly correct form, because the local subunit packing in the Lt-type filament is similar to the intact filaments.

Local subunit lattices on the cylindrical surface at the radius of 45 Å are drawn in Fig. 4A. This radius corresponds to the outer tube, where the major subunit interactions are found in all the filament structure. Although the helical symmetries by numbers look quite different as listed in Table 2 and the operation to convert the L- or R-type symmetry to the Lt-type is a reconstructive transformation as mentioned above, the local subunit packing of the Lt-type is rather similar to the L- and R-type (Figs. 2 and 4A). This operation requires either a deformation of subunit shape or local twist at subunit–subunit interface, but a relatively small one suffices.

To compare the three lattices directly, those in Fig. 4A were rotated about the point at the left bottom, so that the nearly axial 11-start helical lines are superimposed. As shown in Fig. 4B, the local subunit arrangement of the Lt-type is almost identical to the R-type, but clearly different from the L-type. The subunit–subunit distances listed in Table 2, in particular the ones along the 11-start, also indicate that, in the outer-tube region, the subunit interactions of the Lt- and R-types are almost identical, while the one in the L-type is distinct from them. Thus, the third conformation of flagellin found in the Lt-type filament is not a distinct one. Even in the absence of the inner-tube structure, flagellin subunits still prefer to be in one of the two conformations that are presumably the base for flagellar polymorphism.

The overall lattice difference of the Lt-type compared with the R-type appears to be produced by a small twist of a subunit against its neighbor about the circumferential axis at the outer-tube radius. This small twist, however, results in an axial displacement of about 8 Å between inner-tube domains neighboring along the one-start helix. This can be correlated with the absence and presence of the terminal interaction in the Lt- and R-type structure, respectively, which suggests a strong intersubunit nature of the terminal interaction along the one-start helix.

Another concern about the difference in the three types of subunit packing would be an even smaller rotation of the subunit relative to its neighbors, which is caused by different tilts of the protofilaments to the filament axis. All these relative rotations and twists, however, seem to occur without deforming the cylindrical surface lattices at the outer-tube radius, which is demonstrated by the almost identical lattice parameters of the Lt- and R-type. Also in the model lattices for supercoiled filaments (6, 7), the protofilaments take 10 different tilt angles between the two in the L- and R-type, and yet the subunit interactions are in either one of the two states. This means that those rotated and twisted subunit packing modes are quasi-equivalently related and only nonequivalent ones are produced by the mutual shift along the protofilament as shown in Fig. 4B.

From the heptad repeats found in the terminal sequences of the flagellar axial proteins, an intersubunit α-helical coiled–coil formation was suggested for the axial subunit interactions, which would explain the very high cooperativity along the protofilament important for polymorphism (23). This is quite possible because the axially aligned coiled–coils occupy a significant part of the filament core (8–10). The intersubunit terminal interaction found in the present study could be part of this interlocking coiled–coil structure. However, it remains to be confirmed by the atomic resolution structure.

Although the truncated flagellins alone form the Lt-type straight filaments, it has been shown that they form coiled filaments when the intact helical filaments are used as seeds for reconstitution (16). This means that, although the subunit interactions at the outer tube alone show strong preference for one of the two states, these interactions can also take the other state under the influence of external perturbations. According to the domain–sequence assignment (9, 19), the mutation sites of flagellins from the strains SJW1660 and SJW1655 (13) are in the outer-tube domain, and yet these mutations do not affect the symmetry of the filament being Lt-type in the absence of the inner-tube structure. Thus, in a sense, the Lt-type subunit packing may be considered to be the most relaxed state of the outer-tube domain interactions, without having any strain from the terminal interactions to form the inner tube. The role of the inner-tube structure seems that it produces some strain on the outer-tube domain interactions to modulate the free energy profile of the two-state transition, which determines the stable form of the filament among the possible polymorphic forms.