Red blood cell adhesion on a solid/liquid interface

Abstract

Red blood cells (RBCs), previously fixed with glutaraldehyde, adhere to glass slides coated with fibrinogen. The RBC deposition process on the horizontal glass surface is investigated by analyzing the relative surface covered by the RBCs, as well as the variance of this surface coverage, as a function of the concentration of particles. This study is performed by optical microscopy and image analysis. A model, derived from the classical random sequential adsorption model, has been developed to account for the experimental results. This model highlights the strong influence of the hydrodynamic interactions during the deposition process.

Adhesion of proteins, bacteria, and cells to solid surfaces plays an important role in many biological phenomena. In particular, in recent years much work has been devoted to the adhesion process of red blood cells (RBCs) on various materials, generally coated with plasma proteins (1–4), to compare specific and nonspecific adhesion (1), to describe the influence of a flow or a shear rate on the adhesion efficiency (2–5). The influence of others factors, such as the nature of the surface and of the protein coating (6–9), or the ionic strength of the suspension (10), has also been tested.

The RBC is one of the easiest obtainable and controllable cells, and studies with this type of cell should contribute to the elucidation of the mechanism of adhesion, the problems of biocompatibility, and the mechanism of cardiovascular and thromboembolic diseases. In the present work, we use an original approach that compares experimental results and modeling to find general laws governing the deposition process of RBCs or of similarly shaped, but nonspherical, particles, on a glass surface.

For cells at rest on a surface, the gravitational potential energy is currently equal to or greater than the thermal energy, with the consequence that gravity is an important factor especially during the transport through the liquid in static deposition experiments (11). For RBCs, the characteristic potential energy ΔU corresponding to a vertical displacement of the center of mass by 1 μm (the typical thickness of a RBC being 2 μm) is about 13 times the thermal energy at 300 K (excess density, 0.06 g·cm⁻³; volume, 90 μm³). The trajectory of a particle in the fluid should therefore be approximately a vertical line, at least until it is in the vicinity of the adsorbing surface already covered with previously deposited particles, where the hydrodynamic interactions may tend to repel the moving particle from those at rest on the surface. Moreover, our microscopical observation did not reveal any diffusion at the surface after adhesion. We are thus dealing with an irreversible adhesion process that cannot be described by the usual tools developed in statistical physics and devised for systems at equilibrium.

The problem of the irreversible adhesion or adsorption of particles has attracted much efforts aimed notably at the modeling of the experimental configurations of particles formed at a solid/liquid interface. Various models describing the irreversible adhesion of spherical or ellipsoidal colloidal particles depositing on a surface were developed especially during the past decade (12–16). All of these models share the common feature that they exclude mutual overlaps of the deposited particles, even though they are disks, for instance. In particular, the well-known random sequential adsorption (RSA) model (12, 13) leads to the immediate rejection of any deposition trial leading to overlapping particles (excluded volume effect). More recently, the ballistic deposition model (14, 15) was proposed to account for the influence of a strong gravitational force experienced by adhering spherical particles. In this model, also, a particle that cannot touch the adsorbing surface, eventually after rolling over preadsorbed particles, is rejected from the system.

Nevertheless, neither the RSA model nor the ballistic deposition model can account for the deposition of RBCs on a solid surface, because the particles are not globular, cannot roll over preadsorbed ones, and lead to overlaps. One of the goals of this paper will be to extend these models to the deposition process of erythrocytes on a collector. We will propose a new model that, on the basis of a few simple assumptions, will account for the coverage by RBCs (considered as disks) once all of them have settled, as well as for the fluctuation of the coverage on the collector. This model provides a phenomenological description of the effect of hydrodynamic interactions, which are long range interactions, whereas the ultimate adhesion to the surface is favored by short range interactions between the RBC membrane and the adsorbed fibrinogen (1).

In the next section, we shall describe the experimental procedure, notably the adhesion of the RBCs to a glass slide and the image processing of the pictures obtained by optical microscopy. Then the experimental results are given, followed by an elaboration of the model and to the computer simulation. The comparison between the simulation results and the experimental data, as well as the physical meaning of the parameters introduced in the model, will also be discussed. Finally, some concluding remarks will be given.

MATERIALS AND METHODS

Fresh human blood samples, with EDTA as anticoagulant, are centrifuged at 1300 × g for 10 min to separate RBCs from plasma. The cells are then fixed with glutaraldehyde (2.5%, vol/vol), which preserves their original shape and renders them rigid, placed 30 min at 4°C with agitation, centrifuged at 550 × g for 10 min, and washed twice in Sorensen buffer (pH 7.35) (Fig. 1). After appropriate dilution in Sorensen buffer, the total number of RBCs in the aliquot is determined with a particle counter (Technicon H2 System; Bayer Diagnostics, Puteaux, France). They are stored at 4°C and used before a period of 15 days. Before use, the cells are again diluted at the desired concentration in a 1 mM NaCl solution (pH 4).

Figure 1.

RBCs after fixation with glutaraldehyde. (Scanning electron microscope, ×3150.)

The experiments are carried out in a sedimentation cell of height h = 4 mm consisting of plane parallel Plexiglas walls and connected to a flow system to allow suspension injections (17). Two microscope slides are fixed with Parafilm sheet (American National Can, Greenwich, CT) at the top and the bottom of the cell. The slides are previously cleaned for 20 min in a KOH/ethanol solution, abundantly rinsed with deionized water, and air dried.

Before injection of the RBCs, the sedimentation cell is coated with human plasma fibrinogen (Cohn fraction I, purity > 92%; Sigma) which serves to bind irreversibly the RBCs to the substrate. Fibrinogen diluted in a 100 mM NaCl solution at a concentration of 1 g·liter⁻¹ is injected in the sedimentation cell and is adsorbed during 2.5 h. Then, nonadsorbed proteins are removed by two successive rinsings with NaCl solutions (100 and 1 mM, respectively). To avoid the dilution of the RBC suspension during injection, the sedimentation cell is first emptied before it is filled with the RBC suspension. This latter is quickly injected in the sedimentation cell positioned vertically to prevent the deposition of the RBCs on the slides during injection. Finally, the sedimentation cell is moved to its horizontal position and the RBCs settle during ≈1 h, the time needed for all the cells to reach the bottom slide. No rinsing is performed once all the erythrocytes are deposited. This experiment is repeated for a series of cell concentrations, C_RBC, of the injected suspension, with C_RBC ranging from 152 up to 3741 erythrocytes/mm³.

An inverted optical microscope (Axiovert 10; Zeiss) is used for the observation of deposited RBCs (magnification, 10 × 32). The pictures are taken by a charge-coupled device (CCD) camera (type 4710 CCIR monochrome; Cohu, San Diego) and digitalized with an 8-bit flash analogue-to-digital converter. Then, they are stored in a 256 × 256 element pixel memory array of 8 bits (Matrox; Dorval, PQ, Canada) installed in a computer equipped with an image processing software (Visilog; Noesis, France). About 100 independent pictures of area a = 24791 μm² are taken from the whole adsorbing glass surface of area A (A ≫ a) for each concentration. Ideally, it would be interesting to count the number of RBCs on each picture to determine the coordinates of their geodesic centers and to estimate the area they cover. However, due to both irregular shape and overlaps, these data are difficult to obtain. Instead we measure, by means of a semiautomated image processing, the relative area η covered by the RBCs on each of ν pictures (i.e., the area covered divided by the area a of one picture), and derive the mean relative area 〈n〉, as well as the variance σ_η² of these areas. It must be stressed that during the image processing a threshold procedure is used. Because the RBCs located in different layers that might form during the sedimentation appear with different grey levels, it was possible by the image analysis to retain only those located in contact with the glass slide. In addition, the mean area 〈πR²〉_b of a deposited isolated RBC was determined for each batch of RBCs, R being the radius of a RBC assimilated to a disk of area 〈πR²〉_b.

EXPERIMENTAL RESULTS

Because all RBCs initially present in the suspension eventually adsorb, the average number 〈n〉 of RBCs deposited on one picture is equal to a × h × C_RBC. If the RBCs are deposited without overlapping, they would cover a relative area equal to

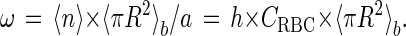1

In fact, due to overlaps, the relationship between ω and 〈η〉 is not linear over the whole RBC concentration range investigated. For small concentrations, however, 〈η〉 is equal to ω because overlaps occur seldom there, and in any case 〈η〉 ≤ ω (Fig. 2a).

Figure 2.

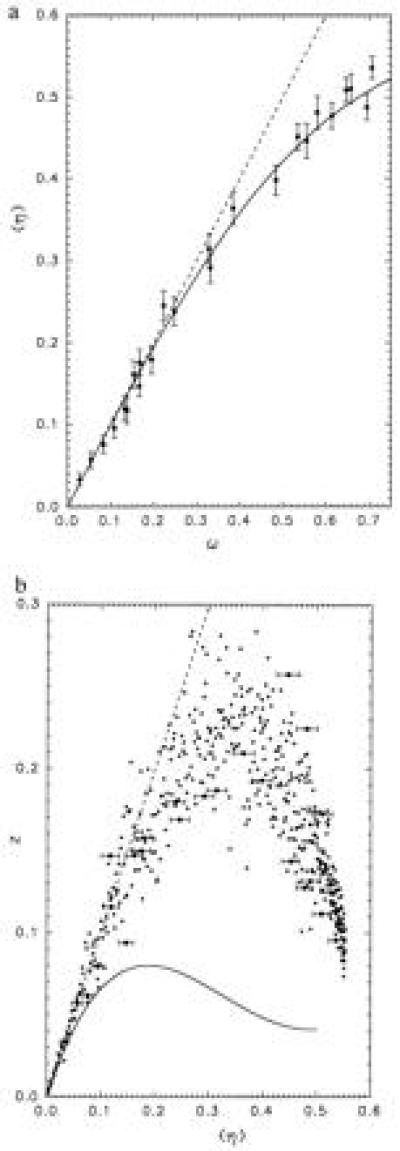
(a) Average coverage 〈η〉 as a function of the coverage ω which would be obtained if no overlap between particles occurred. In the absence of overlaps the data points would align on the dashed line. The error bars on the experimental data (•) represent ±1 SD. The solid line corresponds to the simulation with the parameter combination δ/R = 1.2, f = 0.88, which leads to M² ≈ 0.28. (b) Normalized variance z of the relative covered area η as a function of the mean coverage 〈η〉. If the system obeyed the binomial law, z would equal 〈η〉 everywhere (- - -). Experimental data (•). Results of the simulation (○) for the same parameter values as in a. The solid line represents the normalized variance which would be obtained with the RSA model.

In the following, we shall also use a normalized relative area variance z defined by (18, 19):

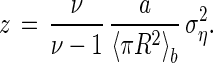2

In the particular case of the independent deposition of particles in a system consisting of ν subsystems (in the present context each picture is a subsystem), without overlap and without rejection, it is easy to verify that z = 〈η〉 = ω, which corresponds to a system governed by the binomial law from the statistical point of view. Fig. 2b shows the experimental data for z as a function of 〈η〉 (filled dots). In spite of the scattering of the measured data, it appears that for the smallest values of 〈η〉, z is in fact approximately equal to 〈η〉. However, as 〈η〉 increases, z deviates from the binomial relation, as could be expected, reaches a maximum, and falls off. It can be noted that, qualitatively, this behavior resembles that of the RSA model (12) developed for nonoverlapping disks. Nevertheless, z is higher than its RSA counterpart (18) because in the present process no rejection occurs during the deposition. Then, no homogenization mechanism can take place.

MODEL AND DISCUSSION

The RBCs are represented by monodisperse disks of radius R. They are initially located in a homogeneous suspension. We assume that they settle independently one from each other and admit that they adsorb near from the vertical projection of their starting point while overlapping eventually with one or more already adsorbed particles. All particles, including the overlapping ones, participate to the deposition history, even though only the particles directly in contact with the surface are finally taken into account to determine the apparent covered area and its fluctuation. In addition, it is likely that the hydrodynamic interactions tend to drive an incoming RBC away from any preadsorbed one. Hence, the deposition of a RBC on the top of another one is quite improbable, at least at low to intermediate coverages of the collector. This is equivalent to a lateral sliding which tends to minimize the mutual overlappings. However, this lateral displacement is necessarily limited because the RBCs are more dense than the liquid and are therefore pulled down by their own weight. According to these remarks, the deposition model contains two free parameters, δ and f. It may be stressed that the model deviates strongly from the former ones (notably from the RSA and the ballistic deposition model) that do not account for overlaps. The nonoverlapping hypothesis is in fact justified in most experiments, because generally spherical particles are used as model particles. Then, up to a high coverage, a particle hitting another one rolls down to the surface. Only when several particles form a trap can an incoming particle be prevented from touching the surface if the gravitational force renders the escape probability vanishingly small over the duration of the experiment.

To deposit on the average 〈n〉 particles on ν identical subsurfaces out of a large surface, a total number of N particles (N = ν〈n〉) are distributed over the ν subsurfaces. Periodic conditions are applied to the edges of these subsurfaces. For each new particle, a random impact point is chosen a priori with each of its coordinates (x_i, y_i) drawn from an uniform distribution defined on the interval [0, c[, where c = 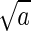. If the incoming RBC has no common point with any of the preadsorbed ones it is permanently fixed at this place. On the contrary, if the incoming particle interacts (i.e., overlaps) with one or several preadsorbed particles, a minimum area search procedure is started. It consists of evaluating the overlap area of the new particle with the preadsorbed particles in many points uniformly distributed over a disk of radius δ centered at the initial impact point. This first parameter, δ, is related to the finite range of the lateral sliding mentioned above. The number of probe points is fixed to 200[(δ/R)/0.8]² on the basis of preliminary tests that showed that the resulting 〈η〉 and z become stable if a sufficiently dense scanning is performed. The new particle is finally fixed at the point of lowest total overlap area.

The area measurements are performed with the help of a fine mesh grid. Each mesh is a square of side length taken as the unit of length (u), small if compared with the size of the RBCs represented by disks of radius R = 10 u. Accordingly each of the ν adsorbing surfaces has an area of 174724 u².

At the end of the deposition, the average number of particles 〈n〉 is converted to the dimensionless number ω (Eq. 1). Then the covered area increment f corresponding to each particle is evaluated, taking into account its chronological order of arrival on the collector. This second parameter, f, is defined by f = Δη/(πR²/a), where πR²/a represents simply the relative area covered by an isolated disk, and Δη represents the true increment of the relative covered area due to the deposition of the new particle (obviously 0 ≤ f ≤ 1). For a given value of f, only the particles contributing to an increase Δη equal to at least fπR²/a to the coverage η are included in the computation of η. Indeed, a particle that contributes an amount to the coverage smaller than a fixed value of f must be located on the top of one or, more probably, several preadsorbed particles. It would then be eliminated by the threshold procedure during the image analysis. Thus, for a given δ, we can obtain 〈η〉 as a function of ω, and z as a function of 〈η〉, for a series of values of f, and compare them to the corresponding experimental data.

A large number of pairs (δ,f) were used to find the optimal solution (see Appendix) as far as the comparison between experiments and model is concerned (Fig. 3). The best overall result was obtained for δ/R ≈ 1.2 and f ≈ 0.88, which corresponds to a goodness-of-fit index M² ≈ 0.28 (Fig. 2). As to the computation of z, it may be emphasized that the noise, predicted by the simulation, based on a sample of 100 covered surfaces (equivalent to the sample of experimental pictures), is practically equal to the dispersion of the measurements, although the model disregards most of the uncertainty sources involved in the true experiment—e.g., those due to the dilution of the original suspension. Furthermore, for each value of δ/R, one can search the value f_m of f, such that the combination (δ,f_m) leads to the smallest possible value M_m² of M² for this particular value of δ (Fig. 4). If we define the region of the acceptable solutions by M² < 0.56 (i.e., twice the minimum found), we obtain 0.95 ≤ δ/R ≤ 1.45.

Figure 3.

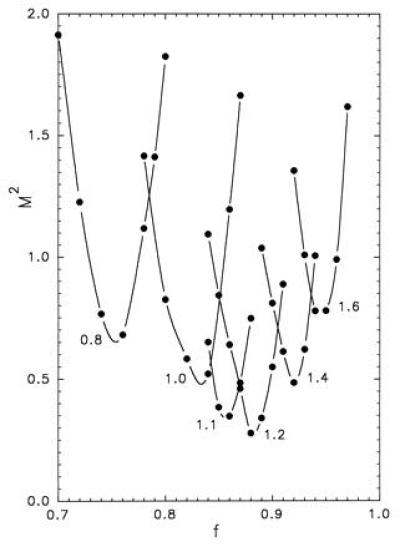
Values of the goodness-of-fit index M² resulting from the simulation (•) as a function of the parameter f, for different values of δ/R = 0.8, 1.0, 1.1, 1.2, 1.4, and 1.6 as indicated by the label on each of the six curves. The lines connect the data points corresponding to the same value of δ/R for the sake of clarity.

Figure 4.

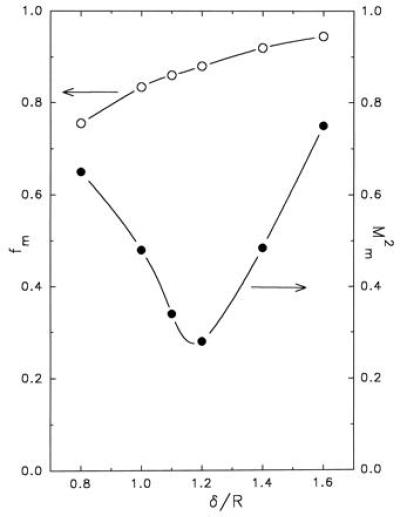
Representation of the minimum value M_m² of M² (•) and corresponding value f_m of the parameter f (○) as a function of δ/R.

Thus, the model confirms that the lateral deviation of the RBCs from their vertical deposition position exists and is of the order of R. This suggests that in spite of the relatively large density difference between the particles and the liquid, the hydrodynamic interactions of an incoming RBC with its neighbors at the surface is strong enough to induce a significant drift force. This latter repels the new particle from any other already located at the surface. The geometrical net effect of this mechanism is to reduce the overlap areas or, conversely, to maximize the number of contact points between the RBC and the adsorbing surface. However, the gravitational force limits the range of this lateral sliding. Therefore a new RBC cannot systematically avoid the overlap with another particle; in this respect the hydrodynamic interactions become gradually inefficient when the coverage increases. The resulting increase of the number of overlapping RBCs, hence the increasing probability for them to have no contact point with the surface, is accounted for by the second parameter, f. It must be pointed out that this parameter is directly related to the experimental method of analysis of the covered surfaces and does not reflect the actual deposition mechanism. In other words, the physics of the process is entirely depicted by the model with the unique parameter δ.

CONCLUSION

This paper presents experimental results on the adhesion of RBCs to glass slides. The relative area covered by the RBCs once settled on silica slides, as well as the variance of the coverage from one region of the collector to another one, were measured by means of an image processing system for a series of concentrations of the suspension initially containing the RBCs. The analysis of the experimental results clearly reveals that the RBCs deposit more or less independently at low concentrations, but overlap more and more when the concentration increases.

A new model, derived from the random sequential adsorption model, was proposed, aimed at the interpretation of the experimental results. This model consists in the random deposition of monodisperse circular RBCs, with the possibility of a rearrangement at the surface that minimizes the overlap area with neighboring particles. This model contains only two free parameters: the distance over which the RBCs can deviate from their vertical trajectory at the surface while adsorbing, and the minimal contribution they must bring to the coverage to be taken into account in the image analysis procedure. Numerical simulations showed that the coverage, as well as the spatial fluctuation of the coverage, could effectively be reproduced on the basis of this simple two-parameter model. Thus, it may be concluded that the model permits to explain the most pertinent features of the deposition of disk-like particles on a flat surface after sedimentation in a liquid, and to stress the importance of the hydrodynamic interactions during the deposition stage. However, it may be emphasized that the numerical value of the parameters depends a priori on the particular experiment to be modeled. This means explicitly that the values δ/R ≈ 1.2 and f ≈ 0.88 derived from the present experimental observations should not be taken as “universal” values.

Appendix

The quality of the agreement (goodness-of-fit) between the simulated data and the experimental data is quantified for each of the curves 〈η〉 versus ω and z versus η by calculating the sum of the squared differences between the measured and the simulated values, provided that the simulated data are previously smoothed by means of a polynomial of degree 4, of the form x + a₂x² + a₃x³ + a₄x⁴, where x stands for either ω or 〈η〉. In this way, we obtain the quantities M²(〈η〉) and M²(z), respectively. From these expressions, we derive finally a resulting sum of squares, M², by:

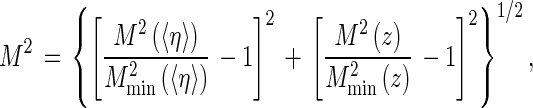A1

where “min” means the smallest term out of a series of values. The index M² serves to select the best (δ,f) combinations.