Interhemispheric Integration of Visual Processing during Task-Driven Lateralization

Abstract

The mechanisms underlying interhemispheric integration (IHI) remain poorly understood, particularly for lateralized cognitive processes. To test competing theories of IHI, we constructed and fitted dynamic causal models to functional magnetic resonance data from two visual tasks that operated on identical stimuli but showed opposite hemispheric dominance. Using a systematic Bayesian model selection procedure, we found that, in the ventral visual stream, which was activated by letter judgments, interhemispheric connections mediated asymmetric information transfer from the nonspecialized right to the specialized left hemisphere when the latter did not have direct access to stimulus information. Notably, this form of IHI did not engage all areas activated by the task but was specific for areas in the lingual and fusiform gyri. In the dorsal stream, activated by spatial judgments, it did not matter which hemisphere received the stimulus: interhemispheric coupling increased bidirectionally, reflecting recruitment of the nonspecialized left hemisphere. Again, not all areas activated by the task were involved in this form of IHI; instead, it was restricted to interactions between areas in the superior parietal gyrus. Overall, our results provide direct neurophysiological evidence, in terms of effective connectivity, for the existence of context-dependent mechanisms of IHI that are implemented by specific visual areas during task-driven lateralization.

Introduction

The nature of hemispheric specialization is an old enigma. One particularly vexing question is how the brain integrates processes that are lateralized to opposite hemispheres (Johansson et al., 2006). Studies of patients with callosal lesions (Gazzaniga, 2000) and of healthy volunteers (Hellige, 1990) imply that even closely related tasks can rely on different mechanisms of interhemispheric integration (IHI). For example, controlling the focus of spatial attention and identifying spatial locations are joint subprocesses of many visuospatial tasks, yet they show strikingly different dependencies on callosal integrity (Holtzman et al., 1981). This complexity calls for computational models of IHI that account for context- and task-dependencies (Hellige, 1990; Liederman, 1998). The challenge is to test such models, directly and quantitatively, for the human brain: given a particular lateralized task, which candidate mechanism of IHI best explains the measured neural responses?

A powerful characterization of integration mechanisms in neural systems is through “effective connectivity” (i.e., the causal influences that system elements exert over one another) (Friston, 1994; Horwitz et al., 1999). Specifically, to better understand IHI, one needs anatomically precise models that specify how individual connections change with cognitive context (task requirements and/or stimulus properties). Given the reciprocal nature of callosal connections and the ensuing complexity of interhemispheric models, this approach was previously hampered by methodological limitations (but see McIntosh et al., 1994).

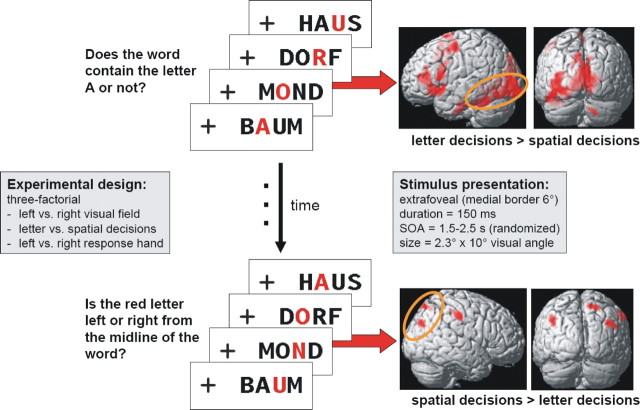
Recently, dynamic causal modeling (DCM) was introduced as a new approach to inferring effective connectivity from functional magnetic resonance imaging (fMRI) data (Friston et al., 2003). In a single-subject analysis, we previously demonstrated the usefulness of DCM for complex interhemispheric models (Stephan et al., 2005). Here, we report an extended analysis of a group of subjects (see Fig. 1), combining DCM with Bayesian model selection (BMS), to reanalyze fMRI data from a novel paradigm that probes IHI during two inversely lateralized tasks, a letter decision (LD) and a spatial decision (SD) task, using identical and peripherally presented visual stimuli (see Fig. 1). An fMRI study by Stephan et al. (2003) found that LD activated the left ventral stream of the visual system, whereas SD activated the right dorsal stream (Ungerleider and Mishkin, 1982; Merigan and Maunsell, 1993).

Figure 1.

Summary of the experimental design and SPM results. For details, see Materials and Methods and supplemental material (available at www.jneurosci.org). The right part of this figure shows the results of an analysis with SPM2 (p < 0.05, whole-brain cluster-level corrected): despite identical stimuli, strong task-dependent lateralization of activity was found. In particular, letter decisions activated the left ventral stream of the visual system, whereas spatial decisions activated the right dorsal stream (ellipsoids).

In this paradigm, IHI could be explained by three well established theories of interhemispheric interactions: asymmetric information transfer, interhemispheric inhibition, and hemispheric recruitment. These theories predict different patterns of interhemispheric effective connectivity as a neurophysiological signature of IHI (for details, see Discussion). We investigated which theory best described IHI (1) in the ventral stream of the visual system during letter judgments and (2) in the dorsal stream during spatial judgments, and (3) which visual areas were at all involved in IHI during our tasks. A total of 64 candidate DCMs was fitted for each subject; from these, BMS determined optimal models of IHI in ventral and dorsal streams (see Fig. 1). Our results suggest that, for the particular paradigm studied, IHI is characterized by asymmetric information transfer between lingual gyrus (LG) and fusiform gyrus (FG) in the ventral stream and by hemispheric recruitment in the dorsal stream, involving the superior parietal gyrus.

Materials and Methods

Experimental design and data acquisition

Figure 1 summarizes the most important aspects of the experimental design and stimulus presentation. The central idea of this paradigm is to apply two tasks requiring language and visuospatial processes, respectively, to peripherally presented stimuli that contain both language and spatial features. The stimuli were concrete, high-frequency German nouns, each consisting of four letters. In each stimulus either the second or third letter was red, whereas all other letters were black. During an LD task, the participants indicated by button press whether the word contained the target letter “A” or not. During an SD task, they indicated by button press whether the single red letter of the word was located left or right from the midline of the word. A total of 16 right-handed male adult subjects were scanned on a 1.5 T Siemens (Erlangen, Germany) Sonata scanner. All details of experimental design and data acquisition can be found in the study by Stephan et al. (2003) and in supplemental material (available at www.jneurosci.org).

Construction of statistical parametric maps

The results previously reported by Stephan et al. (2003) were obtained using the software package SPM99. To enable the application of DCM and BMS, we reanalyzed the data using SPM2 and adopted a slightly different preprocessing strategy. For this reason, the activation maps shown in Figure 1 are slightly different from those published in the study by Stephan et al. (2003). Briefly summarized, the present analysis of the fMRI data comprised the following steps. For each subject, after discarding the first five images, the remaining 700 images were realigned to correct for head movements, spatially normalized to the MNI (Montreal Neurological Institute) template brain, smoothed spatially with a three-dimensional Gaussian kernel of 8 mm full-width at half-maximum, and resampled, resulting in 3 × 3 × 3 mm voxels. The data were then modeled voxelwise, using a general linear model (GLM) that included all combinations of task, visual field, and response hand, plus effects of no interest (instruction periods and realignment parameters to account for motion-related variance). The data were high-pass filtered (cutoff, 1/128 s) to remove low-frequency signal drifts. A first-order autoregressive model was used to remove serial correlation in the data. Contrast images were created for each subject and entered separately into voxelwise one-sample t tests (df = 15), implementing a random effects analysis. The statistical threshold was set at p < 0.05 at the cluster level (with a standard voxel level cutoff of p < 0.001), whole-brain corrected for family-wise errors using Gaussian random field theory (Poline et al., 1997).

Dynamic causal modeling

DCM is an established model of neural system dynamics that has been methodologically evaluated by several studies (Friston et al., 2003; Penny et al., 2004a,b; Lee et al., 2006) and has found numerous applications (Mechelli et al., 2003; Bitan et al., 2005; Haynes et al., 2005; Stephan et al., 2005; Smith et al., 2006). Given some measured regional fMRI time series, DCM enables one to infer the connectivity between the neural sources that give rise to these regional measurements. The basic idea is to estimate the parameters of a reasonably realistic neural model such that the predicted regional blood oxygen level-dependent (BOLD) signals, which result from converting the modeled neural dynamics into hemodynamic responses, correspond as closely as possible to the observed BOLD signals. Importantly, DCM models how the neural dynamics are shaped by experimentally controlled manipulations (i.e., external inputs u) that enter the model in two different ways. Inputs can elicit responses through direct influences on specific regions [“driving inputs” (e.g., sensory inputs)] or they can change the strength of coupling among regions [“modulatory inputs” (e.g., task effects or learning)]. This distinction represents an analogy, at the level of neural populations, to the concept of driving and modulatory afferents in studies of single neurons (Sherman and Guillery, 1998).

Mathematically, DCM is based on a bilinear model of neural population dynamics that is combined with a hemodynamic model describing the transformation of neural activity into predicted BOLD responses (Buxton et al., 1998; Friston et al., 2000). The “hidden” neural dynamics (i.e., not directly observed by fMRI) are modeled by the following bilinear differential equation:

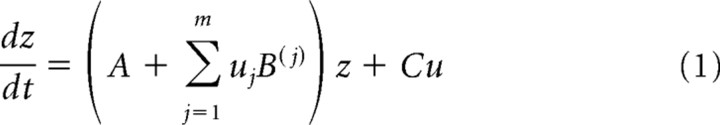Here, z is the state vector (with each state variable representing the population activity of one region in the model), t is continuous time, and u_j is the jth input to the modeled system (i.e., some experimentally controlled manipulation). In this state equation, the A matrix contains the “intrinsic” or “fixed” connection strengths between the modeled regions, and the B⁽¹⁾… B^(m) matrices represent the context-dependent modulation of these connections (e.g., by task) as an additive change. Finally, the C matrix represents the strengths of direct (driving) inputs to the modeled system (e.g., sensory stimuli). Note that all parameters correspond to rate constants of the modeled neurophysiological processes and are thus in units of 1/second (hertz).

For any given set of parameter values, the neural state equation can be integrated, and the resulting neural dynamics transformed into predicted BOLD signals, using a well established hemodynamic model (Friston et al., 2000). Combining the neural and hemodynamic state equations into a joint forward model, DCM uses Bayesian inversion to determine the posterior densities of the parameters (Friston et al., 2003). Under Gaussian assumptions (Laplace approximation), these densities can be characterized in terms of their maximum a posteriori (MAP) estimates and their posterior covariances.

Practical implementation of DCM in this study

Choice of areas and time series extraction.

The definition of areas was informed by the results of the conventional SPM analysis (for details, see Results). DCMs are fitted to subject-specific BOLD time series. Because the exact locations of activated areas vary over subjects, a general challenge is to define the elements of the modeled system (and thus the extracted time series) such that models are comparable across subjects. Here, we ensured comparability across subjects by requiring that the extracted time series met a combination of anatomical and functional criteria (for details, see supplemental material, available at www.jneurosci.org). Given these criteria, we were able to extract time series for the four-area dorsal stream model in 13 of the 16 subjects and for all other models in 12 of the 16 subjects (for the coordinates of all regions in all participants, see supplemental Tables S2 and S3, available at www.jneurosci.org as supplemental material). In the remaining four subjects, one of the areas in the model could not be defined because of the lack of an activation that met our criteria. These subjects therefore had to be excluded from the DCM analysis.

Definition of anatomical connections.

Meta-analyses of primate connectivity data have shown that intrahemispheric connections between visual areas are almost always reciprocal (Kötter and Stephan, 2003). Also, macaque (Zeki, 1970; Van Essen et al., 1982; Abel et al., 2000) and human (Van Valkenburg, 1913; Clarke and Miklossy, 1990; Van Essen et al., 1995) visual areas, with the notable exception of area V1, possess rich reciprocal callosal connections with their homotopic counterparts in the opposite hemisphere. Given these empirical facts, we assumed (1) reciprocal intrahemispheric connections and (2) reciprocal interhemispheric connections between homotopic areas in our model, except for the cuneus (CUN) in the dorsal stream model. The reason for omitting interhemispheric connections between left and right CUN was that an anatomical evaluation of our SPM results by means of a probabilistic cytoarchitectonic atlas (Eickhoff et al., 2005) indicated that activated CUN voxels were likely located in V1 (for details, see supplemental material, available at www.jneurosci.org). However, the assumption of absent interhemispheric connections at the level of CUN was checked in subsequent models that did include these interhemispheric connections (supplemental Tables S7, S13, available at www.jneurosci.org as supplemental material) and was found to be appropriate.

Definition of driving inputs.

We modeled the peripheral stimulus presentation by allowing all stimuli to directly induce activity in contralateral LG (ventral stream model) or contralateral CUN (dorsal stream model), respectively, regardless of task. These areas showed a main effect of visual field in the SPM analysis (for details, see supplemental material, available at www.jneurosci.org). Because each stimulus lasted for only 150 ms, these inputs were represented as trains of events (δ functions).

Definition of modulatory inputs.

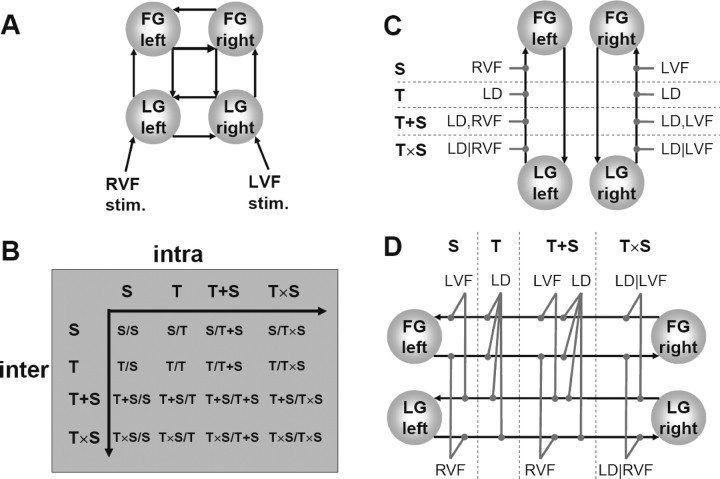
The above choices of regions, connections, and driving inputs resulted in the construction of basic models for the ventral and dorsal stream (Fig. 2A shows the basic model for the ventral stream). The final and critical step was to extend these models by modulatory inputs that change connection strengths as a function of the relevant experimental factors (i.e., task demands and visual field of stimulus presentation). Any given connection in the model could be influenced by four potential modulatory causes: the connection strength could depend (1) only on the visual field of stimulus presentation (the S model, for stimulus-dependent), (2) only on whether a specific task is performed or not (T model, for task-dependent), (3) on both the task and the visual field, but independently of each other (the T+S model), or (4) on both the task and the visual field, but in a conditional manner (i.e., the connection strength is only modulated by task if the stimulus was presented in a particular visual field) (the T×S model). These possibilities equally exist for interhemispheric and the intrahemispheric connections. We performed an exhaustive model comparison, systematically comparing all combinations of how interhemispheric and intrahemispheric connections could be changed as described above (Fig. 2B). Figure 2, C and D, exemplifies how combinations of the LD task and left/right visual fields yield 16 ventral stream models; analogous combinations, using SD as task, were chosen for the dorsal stream. However, we initially constrained the combinations by only allowing for modulation of the forward intrahemispheric connections. This constraint was subsequently evaluated in additional models (supplemental Tables S7, S13, available at www.jneurosci.org as supplemental material) and found to be appropriate. Overall, this combinatorial approach resulted in 64 different DCMs per subject (16 DCMs each for the four-area and six-area models of both the ventral and dorsal stream). We generally refer to any specific models by first listing the modulation of the interhemispheric and then that of the intrahemispheric connections (compare Fig. 2B). For example, T/S is the model in which interhemispheric connections are modulated by the task and the intrahemispheric connections are modulated by the stimulus properties (i.e., visual field). All modulatory inputs were modeled as boxcar inputs of 24 s duration.

Figure 2.

A, Basic structure of the four-area ventral stream model, comprising the reciprocally connected LG and FG in both hemispheres. Because of the nonfoveal stimulus presentation, stimuli in RVF and LVF drive contralateral LG activity. During the instruction periods, bilateral visual field input was provided for 6 s; this was modeled as a boxcar input affecting LG in both hemispheres (not shown here). The basic four-area model for the dorsal stream, comprising cuneus and superior parietal gyrus in both hemispheres, was constructed in an analogous manner (see Materials and Methods and Fig. 6). B–D, Schema of how 16 variants of the ventral stream model (B) were constructed by systematically combining four different types of modulatory inputs for intrahemispheric (C) and interhemispheric (D) connections. The strength of a connection could depend (1) only on the visual field of stimulus presentation (the S model, for stimulus-dependent), (2) only on whether a specific task is performed or not (T model, for task-dependent), (3) on both the task and the visual field, but independently of each other (the T+S model), or (4) on both the task and the visual field, but in a conditional manner [i.e., the connection strength is only modulated by task if the stimulus was presented in a particular visual field (the T×S model)]. These possibilities equally exist for interhemispheric and the intrahemispheric connections. However, we initially constrained the combinations by only allowing for modulation of the forward intrahemispheric connections. This constraint was subsequently evaluated in additional models and found to be appropriate (see Results). Overall, this combinatorial approach resulted in 64 different DCMs per subject (16 DCMs each for the four-area and six-area models of both the ventral and dorsal stream). Models are generally referred to by first listing the modulation of interhemispheric connections, followed by the modulation of intrahemispheric connections (B). Analogous model variants were constructed for the dorsal stream, using SD as task.

DCM uses a gradient ascent procedure on the log posterior to compute MAP estimates (Friston et al., 2003). Given the relatively complex connectivity of our models, we took two steps to ensure convergence and validity of the parameter estimates. First, we used an extended version of the original DCM estimation scheme as described by Friston et al. (2003), using a Fisher scoring scheme with Levenburg–Marquardt regularization in the expectation maximization algorithm. This proved to ensure a robust behavior of the gradient ascent scheme. Second, in an associated methodological study (K. E. Stephan and K. J. Friston, unpublished observations), we performed a systematic series of simulations to test whether the structure of our models, in particular the multiple occurrence of identical modulatory inputs, could (1) influence the results from the BMS procedure and/or could (2) lead to systematic bias in the sense that modulatory parameters of interest were overestimated. For the models presented here, we investigated this issue using simulations and found that even at high levels of noise (1) BMS reliably chose the correct model and that (2) comparisons of modulations of interhemispheric connections were not biased.

Bayesian model selection

Assessing model goodness is a central theme in statistics. Importantly, neither can one make statistical inferences about “absolute” model fit nor is model fit the only criterion to take into account when comparing models. As for the first point, all inferential statements about “model fit” or “variance accounted for” are relative to some null or reference model [e.g., R² values in regression models (Kleinbaum et al., 1988) or χ² tests in structural equation modeling (SEM) (Penny et al., 2004b)]. Concerning the second point, model fit is a monotonic function of model complexity; overly complex models, however, will overfit the data and show inferior generalizability (Pitt and Myung, 2002).

In this study, we used BMS to decide which DCM was optimal. BMS not only takes into account the relative fit of competing models but also their relative complexity (number of free parameters, functional form). It rests on the so-called “model evidence” [i.e., the probability p(y|m) of the data y given a particular model m] (Raftery, 1995). Usually, the model evidence cannot be determined analytically; therefore, approximations are needed. For DCM, two suitable approximations are the Bayesian information criterion (BIC) and Akaike information criterion (AIC) (Penny et al., 2004a). These two approximations are both biased but in opposite ways: BIC tends to prefer simpler models, whereas AIC tends to favor more complex models. This can lead to disagreement between the two approximations about which model should be favored. The general convention, to which we also adhere in this paper, is that, for any pairs of models m_i and m_j to be compared, a selection is only made if AIC and BIC concur. The decision is then based on that approximation which gives the more conservative Bayes factor (BF) as follows:

An established convention is to prefer one model over another if the BF is >3 (“positive evidence”) (Raftery, 1995).

When determining the optimal model for a group of individuals by BMS, it is likely that the optimal model will vary to some degree across subjects. Because model comparisons from different individuals are statistically independent, a group Bayes factor can be computed by multiplying the individual Bayes factors (where k is an index across subjects) (Stephan and Penny, 2006) as follows:

For each subject of our group, we first performed pairwise comparisons between all models and then computed the group Bayes factors (GBFs) across subjects. However, GBFs can be misleading in the presence of strong outliers. Therefore, we additionally evaluated the number of comparisons for which the BF passed the threshold for positive evidence for either of the compared models. These numbers give a “positive evidence ratio” (PER), which serves as a complementary measure of which model is optimal at the group level (Stephan and Penny, 2006).

Second-level analysis of model parameters

Once the best model was identified, the next step was to find which of the modeled processes were expressed consistently across subjects. We performed a classical second-level (between-subject) inference by applying a one-sample t test to the corresponding MAP estimates from the individual DCMs. We performed these tests separately for each parameter of the fixed connections, modulatory changes of connections, and driving inputs of the optimal model. We adopted a conservative procedure by using two-sided t tests and a statistical threshold of p < 0.05, with Bonferroni's correction within each parameter class. This is analogous to the typical method for inference in conventional neuroimaging analyses [i.e., correcting for multiple comparisons within (but not across) several chosen statistical contrasts].

General methodological remarks

Before presenting the modeling results in detail, a few general methodological comments may be helpful. First, our models are agnostic to whether interhemispheric interactions are mediated through the corpus callosum or through other commissural tracts. However, this is neither critical for the definition of our models nor for the conclusions we draw from them. Second, our modeling results are not confounded by differences in task difficulty because the tasks were carefully matched for error rates (see Results). Third, in our factorial design, the experimental factors (visual field, task, and response hand) were altered in a blocked manner. Such a design differs from traditional behavioral paradigms in lateralization research that mostly use randomized visual field presentation to (1) minimize eye movements away from fixation and (2) prevent attentional bias to contralateral visual space during prolonged stimulation of one hemisphere (Klein et al., 1976). In this study, we verified good fixation by online monitoring of eye movements using an infrared video system (Stephan et al., 2003). Also, we controlled for potential effects of attentional bias by ensuring that the visual field of stimulation was perfectly balanced across all conditions of our factorial design. Generally, for studying lateralized processes with fMRI, blocking the visual field has three advantages: (1) for difficult tasks like ours, error rates can be kept at acceptable levels, (2) the statistical power of the fMRI analysis is considerably higher, and (3) whereas sustained covert spatial attention during a blocked design is not asymmetrically implemented in the brain (Tootell et al., 1998; Yantis et al., 2002), randomizing the visual field requires the subjects to engage continuously in attentional reorienting, a process that is known to induce activity lateralized to the right hemisphere (Corbetta and Shulman, 2002). The last point highlights that blocked versus randomized stimulation may lead to different mechanisms of stimulus processing; this should be kept in mind when comparing the results of the present study to previous studies that used randomized visual field stimulation.

Finally, please note that we explicitly focus on investigating IHI in separate ventral and dorsal streams models. The reason for this is that the conventional analysis based on the GLM (Fig. 1) showed a fairly clean separation between activations induced by letter judgments (confined to the ventral stream) and activations induced by spatial judgments (restricted to the dorsal stream). GLMs and DCMs are tightly linked in that they are both generative models of the same observed data, albeit differing in the explanations offered for how these observations were caused [Stephan (2004), compare his Figs. 2, 4]. Critically, the definition of any DCM depends on the results of a preceding GLM analysis that localizes those system elements (i.e., brain areas) in which the experimental manipulations led to significant changes in BOLD signal. These local signal changes can subsequently be explained mechanistically by a DCM in terms of connections between the system elements and their modulation by experimental factors. In our case, the results of the GLM analysis (Fig. 1) suggested that it would be more appropriate to investigate IHI in separate ventral and dorsal streams models rather than constructing a large joint model. We verified this in an additional analysis in which we combined ventral and dorsal stream models into a joint model and tested, using BMS, whether one should include or exclude connections between the two streams. We found that treating ventral and dorsal stream models as separate networks was clearly more appropriate for the present paradigm (GBF > 10¹⁵) (for details, see supplemental material, available at www.jneurosci.org). We therefore report only the results from separate ventral and dorsal stream models in this article.

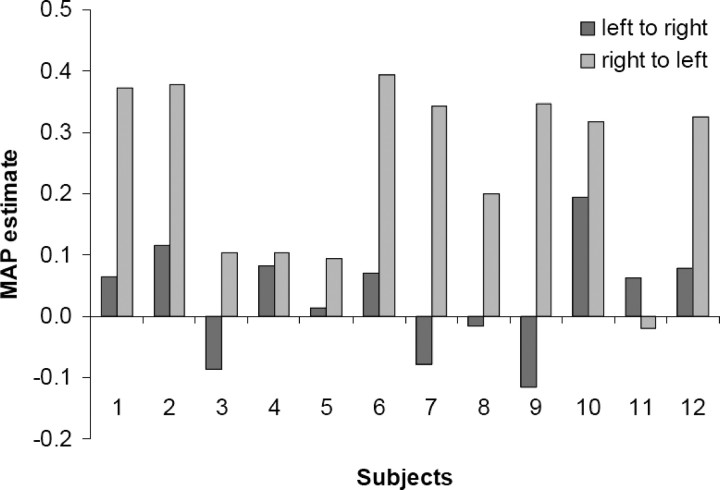
Figure 4.

MAP parameter estimates (y-axis) for modulation of interhemispheric connections between left and right LG by letter decisions conditional on visual field (LD|VF) in all subjects (x-axis). Dark gray, Modulation of left→right connection; light gray, modulation of right→left connection. The consistent asymmetry across subjects is obvious and highly significant (p = 0.0007). Compare Figure 3 and supplemental Table S5 (available at www.jneurosci.org as supplemental material).

Results

Behavioral results

The tasks were designed to be of comparable difficulty as indexed by error rates. Indeed, ANOVA of the behavioral responses during scanning demonstrated similar error rates between tasks (letter decisions, 8.5 ± 1.0%; visuospatial decisions, 10.4 ± 2.0%; p > 0.196). However, the participants needed more time for letter decisions (686 ± 21 ms) than for visuospatial judgments (612 ± 28 ms) (p < 0.001). For both error rates and reaction times, neither the main effects of visual hemifield or hand nor any of the interactions between the three factors were significant (Stephan et al., 2003).

Construction of DCMs based on statistical parametric maps

In this study, we reanalyzed the data by Stephan et al. (2003) using SPM2 to enable the application of DCM and BMS. To motivate the construction of our DCMs, we briefly summarize task-dependent activations in visual areas as obtained from the SPM analysis. All results described in this section are reported at p < 0.05, whole-brain cluster-level corrected with a standard p < 0.001 voxel-level cutoff.

Despite physically identical stimuli and matched task difficulty, a comparison of LD and SD tasks resulted in strongly lateralized activation patterns (Fig. 1; supplemental Table S1, available at www.jneurosci.org as supplemental material). Contrasting LD versus SD, we found left-lateralized activations in several visual areas of the ventral stream, particularly in left FG, left middle occipital gyrus (MOG), and bilateral LG (Figs. 3, 5). This is in good accordance with other studies of letter processing (for review, see Jobard et al., 2003). In the opposite contrast, SD versus LD, right-lateralized activations were found in dorsal stream areas [i.e., right superior parietal gyrus (SPG) and bilateral posterior angular gyrus (PAG)] (see Fig. 6). An additional activation in right anterior parietal cortex (supramarginal and postcentral gyri) (Fig. 1) substantially overlapped with somatosensory area 2 [according to a probabilistic cytoarchitectonic atlas (Eickhoff et al., 2005)] and can thus not be regarded as a purely visual region.

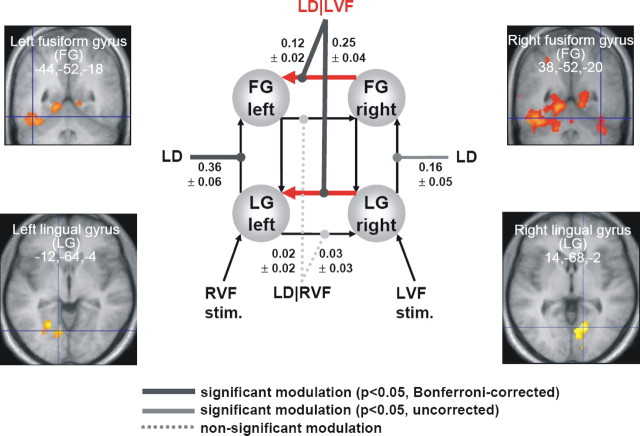
Figure 3.

Summary of the group results for the optimal four-area ventral stream model (T×S/T). This model indicates that interhemispheric connections are modulated by the LD task but conditional on the visual field of stimulation (LD|VF). Furthermore, there is a highly significant asymmetry in the strength of interhemispheric modulations (see Results). This indicates asymmetric information transfer from the nondominant right to the dominant left hemisphere (red arrows). The average modulatory parameter estimates ± SEs are shown alongside the modulatory inputs. Dark gray, Significant effects surviving Bonferroni's correction; light gray, significant effects not surviving Bonferroni's correction; dotted lines, nonsignificant effects (for details, see supplemental Table S5, available at www.jneurosci.org as supplemental material). For clarity, this figure shows only the modulatory parameters; the values of all other parameters can be found in supplemental Table S6 (available at www.jneurosci.org as supplemental material). The insets display the results from the random effects SPM analysis together with the group coordinates of the regions included in the model. Activations in left and right LG and left FG are shown at a threshold of p < 0.05, cluster-level corrected (with p < 0.001, voxel-level cutoff). Left and right LG activations are additionally masked by the main effect of visual field (RVF > LVF and LVF > RVF, respectively). The right FG activation is displayed at an uncorrected threshold of p < 0.01.

Figure 5.

Summary of the group results for the optimal six-area ventral stream model (T×S/T). As in the four-area model (Fig. 3), interhemispheric connections are modulated by the LD task, but conditional on the visual field of stimulation (LD|VF). This modulation is strongly asymmetric for LG and FG interhemispheric connections (see Results), indicating asymmetric information transfer from the nondominant right to the dominant left hemisphere (red arrows). Notably, however, interhemispheric connections of MOG did not exhibit any significant modulation (compare supplemental Table S9, available at www.jneurosci.org as supplemental material). For abbreviations and conventions, see Figure 3.

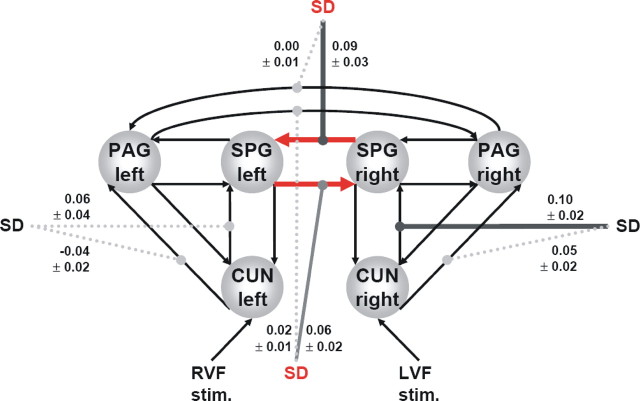
Figure 6.

Summary of the group results for the optimal four-area dorsal stream model (T/T). Interhemispheric connection strengths were bidirectionally modulated by SDs, regardless of the visual field of stimulation. This task-dependent modulation symmetrically increased interhemispheric connections of SPG (supplemental Table S11, available at www.jneurosci.org as supplemental material). This connectivity pattern in the dorsal stream fits the predictions by the hemispheric recruitment theory. For conventions, see Figure 3. The insets display the results from the random-effects SPM analysis together with the group coordinates of the regions included in the model (p < 0.05, cluster-level corrected, with p < 0.001, voxel-level cutoff; CUN activations are additionally masked by the main effect of task, LD > SD).

Based on these results, we constructed a basic four-area ventral stream model for the LD task that comprised LG and FG in both hemispheres (Fig. 2A). The peripherally presented visual stimuli entered the system by directly affecting contralateral LG (note that LG showed a significant main effect of visual field) (Fig. 3, insets). The induced activity was then allowed to spread along reciprocal intrahemispheric connections between LG and FG and reciprocal interhemispheric connections between left/right LG and left/right FG. From this basic model, 16 variants (Fig. 2B) were created by allowing that intrahemispheric (Fig. 2C) and interhemispheric connections could independently be modulated by one of four potential causes (Fig. 2D) (for more details on the construction of model variants, see Materials and Methods). Specifically, the strength of a connection could depend (1) only on the visual field of stimulus presentation (the S model, for stimulus-dependent), (2) only on whether a specific task is performed or not (T model, for task-dependent), (3) on both the task and the visual field, but independently of each other (the T+S model), or (4) on both the task and the visual field, but in a conditional manner (i.e., the connection strength is only modulated by task if the stimulus was presented in a particular visual field) (the T×S model). We generally refer to any specific models by first listing the modulation of the interhemispheric and then that of the intrahemispheric connections (compare Fig. 2B). Another 16 variants of a six-area ventral stream model, which additionally included MOG bilaterally (see Fig. 5), were constructed according to the same principles.

For the dorsal stream, an equivalent procedure was adopted, although the basic connectivity layout was slightly different (for details, see Materials and Methods). Here, we initially focused on connections between left and right SPG because this area has previously been implicated in IHI during visuospatial tasks (Iacoboni and Zaidel, 2004). Because the SD versus LD contrast did not activate any early visual area, we lacked an input site where stimuli would enter the system. We therefore complemented the dorsal stream model by a “neutral” input area (i.e., a subpart of the CUN) (see Fig. 6). Bilaterally, this area showed no significantly different activation between LD and SD tasks (p > 0.05, uncorrected) but responded to visual stimuli in a hemifield-specific manner (p < 0.05, corrected). Sixteen variants of this basic four-area dorsal stream were constructed by allowing for context-dependent modulation of connection strengths, following the same principles used for construction of the ventral stream models (compare Fig. 2). An extended six-area dorsal stream model additionally included PAG in both hemispheres, giving rise to further 16 model variants. For details of how individual time series were extracted, see supplemental material (available at www.jneurosci.org).

DCM: ventral stream

Comparing all 16 variants of the four-area ventral stream model across all subjects by BMS, the optimal model was found to be the T×S/T model (see Materials and Methods and Fig. 2B). According to this model, interhemispheric connections were modulated by the LD task but conditional on the visual field (VF) of stimulus presentation (LD|VF), whereas intrahemispheric connections depended on the LD task alone. Supplemental Table S4 (available at www.jneurosci.org as supplemental material) shows the subject-specific Bayes factors for comparing the T×S/T model with the other 15 models and the resulting group Bayes factors. Across the group, the evidence for the optimal T×S/T model was approximately eight times higher as that of the second-best model (T/T×S), and the PER was 3:1. The results from the statistical group analysis, implemented as one-sample t tests of the modulatory parameters from the optimal T×S/T model, are summarized by Figure 3. Supplemental Table S5 (available at www.jneurosci.org as supplemental material) lists the estimates of the modulatory parameters for all subjects individually and the statistical results. Note that DCM parameters correspond to rate constants of the modeled neurophysiological processes and are thus given in hertz (see Materials and Methods).

The analysis of the optimal T×S/T model showed that right→left interhemispheric connections were significantly strengthened during LD whenever the stimulus was presented in the left visual field (LVF) and was thus initially received by the right hemisphere (Figs. 3, 4): the average rate constants for the modulation of the right→left interhemispheric connections by LD|LVF were 0.25 ± 0.04 Hz (right LG→left LG; p = 0.0001) and 0.12 ± 0.02 Hz (right FG→left FG; p = 0.0006), respectively. These effects were strong, corresponding to an increase in connectivity by a factor of 2.3 (LG) and 3.0 (FG) compared with the fixed (intrinsic) connection strengths (supplemental Table S6, available at www.jneurosci.org as supplemental material) and surviving Bonferroni's correction for multiple comparisons. Notably, this modulation of interhemispheric connections was highly asymmetric, with modulatory effects being virtually absent for the left→right connections. Both at the level of LG and FG, this asymmetry was highly significant (p = 0.0007 and p = 0.0047) (supplemental Table S5, available at www.jneurosci.org as supplemental material) and consistently expressed across subjects (Fig. 4). Together, these findings match exactly the predictions from the information transfer hypothesis (see Discussion): stimulus information is transferred from the nonspecialized to the specialized hemisphere, but only when the LD task is required and the stimulus information is presented to the nonspecialized hemisphere.

Three things remain to be mentioned about the four-area model. Intrahemispheric LG→FG connections were also strengthened, although by LD alone, and particularly in the left hemisphere (Fig. 3). Second, neither the fixed connection strengths nor the strengths of direct inputs showed any significant hemispheric asymmetries (supplemental Table S6, available at www.jneurosci.org as supplemental material). This emphasizes the notion that the ventral stream network is symmetric per se and that hemispheric differences are induced by the specific demands of the LD task. Finally, to test the basic assumptions underlying our models, we constructed and fitted additional variants of the basic structure of the T×S/T model for each subject. The first variant modeled additional changes in connection strengths by SD as well (i.e., interhemispheric connections were modulated by both LD|VF and SD|VF), and intrahemispheric connections were modulated by both LD and SD. The second alternative model allowed for a modulation of the backward (FG→LG), instead of the forward, intrahemispheric connections. A third alternative included a modulation of both forward (LG→FG) and backward (FG→LG) intrahemispheric connections. BMS indicated that none of these alternative models came close to the T×S/T model: the group Bayes factors in favor of the T×S/T model were larger than 10¹², 10⁵⁸, and 10⁸, respectively (supplemental Table S7, available at www.jneurosci.org as supplemental material). Finally, an additional model comparison was performed to address a reviewer's concern whether interhemispheric connections between left and right LG exist in the human brain and should therefore be part of the model (see Discussion). Comparing the original T×S/T model against one without interhemispheric connections between left and right LG, we found the former to be superior (group Bayes factor >10⁸). Together, these results confirmed that our initial choice of the basic model structure (Fig. 2) was sensible.

An extended six-area model of the ventral stream, which additionally included left and right MOG, gave very similar results (Fig. 5). The BMS procedure confirmed the same model (i.e., T×S/T) to be optimal. Although the group Bayes factor was marginally in favor of the similar T×S/T+S model (group BF = 0.798), this was attributable to a single outlier subject (supplemental Table S8, available at www.jneurosci.org as supplemental material). In fact, in 10 of 12 subjects, the T×S/T was strongly preferred (with one subject showing no clear difference between the two models), resulting in a PER of 10:1. The statistical group analysis of the T×S/T model parameters replicated all results from the four-area model [compare Figs. 3, 5, and supplemental Tables S5, S9 (available at www.jneurosci.org as supplemental material)]. Again, we found a strongly asymmetric modulation of interhemispheric connections: right→left connections were significantly increased by LD|VF (LG, 0.20 ± 0.04 Hz, p = 0.0003; FG, 0.07 ± 0.02 Hz, p = 0.0012), whereas the corresponding modulation of left→right connections was significantly weaker (LG, p = 0.0019; FG, p = 0.0121). The other findings from the four-area model (stronger LD-modulation of the LG→FG connection in the left hemisphere, symmetric intrinsic connections and driving inputs) were also replicated. Importantly, no significant modulations were observed for interhemispheric connections between left and right MOG (right→left, 0.01 ± 0.01 Hz; p = 0.1605; left→right, 0.00 ± 0.01 Hz, p = 0.9725). Given this result, we focus on the four-area model as a sufficient representation of IHI in the ventral stream throughout the rest of this article.

DCM: dorsal stream

BMS among all 16 variants of the four-area dorsal stream model across all subjects indicated that the T/T model was optimal (Figs. 2B, 6; supplemental Table S10, available at www.jneurosci.org as supplemental material). According to this model, both intrahemispheric connections and interhemispheric connections between left and right SPG were modulated by the SD task alone, regardless of the visual field of stimulation. Supplemental Table S10 (available at www.jneurosci.org as supplemental material) reports the subject-specific Bayes factors for comparing the T/T model with all other models. Across the group, the evidence for this model was ∼10⁷ times higher as that for the second-best model (T/T×S), and the PER was 3:1. The statistical group analysis of the optimal model showed that interhemispheric SPG connections were significantly strengthened by the SD task in both directions (Fig. 6; supplemental Table S11, available at www.jneurosci.org as supplemental material), with average rate constants of 0.22 ± 0.06 Hz (right→left; p < 0.0018) and 0.15 ± 0.06 Hz (left→right; p < 0.0160). These modulations, corresponding to an increase in connectivity by a factor of 1.9 (right→left) and 2.9 (left→right), respectively, compared with the fixed (intrinsic) connection strengths alone (supplemental Table S12, available at www.jneurosci.org as supplemental material), were not significantly different from each other (p = 0.2073). This connectivity pattern (i.e., symmetric enhancement of interhemispheric connections by task demands alone) matches the predictions from the hemispheric recruitment hypothesis (see Discussion): regardless of which hemisphere initially receives the stimulus during the SD task, it increases its connectivity with the opposite hemisphere to recruit additional processing resources.

There are three more interesting aspects of the four-area dorsal stream model. Intrahemispheric CUN→SPG connections were also strengthened by SD alone. This effect was significant in the right hemisphere (0.16 ± 0.04 Hz; p = 0.0017), but not in the left hemisphere (0.11 ± 0.07 Hz). Second, as for the ventral stream model, neither the fixed connections nor the direct inputs showed any significant hemispheric asymmetries (supplemental Table S12, available at www.jneurosci.org as supplemental material). Third, we tested the validity of the assumptions underlying the dorsal stream model by fitting five additional DCM variants for each subject and comparing these alternatives against the optimal T/T model. The first three alternatives were analogous to the alternative models tested for the ventral stream model (see above) [i.e., (1) additional modulation of all connection strengths by LD; (2) modulation of the backward (SPG→CUN), instead of the forward (CUN→SPG), intrahemispheric connections; and (3) modulation of both forward and backward intrahemispheric connections]. Two additional alternative models asked whether (4) an inclusion of interhemispheric connections between left and right CUN and (5) an additional modulation of these connections by SD would give a better model. The BMS procedure showed that all of these alternative models were inferior to the T/T model (supplemental Table S13, available at www.jneurosci.org as supplemental material). As with the ventral stream model, these additional comparisons corroborated our basic model structure.

The six-area dorsal stream model additionally included left and right PAG (Fig. 7). As with the four-area model, the BMS procedure found the T/T model to be optimal. The evidence for this model was ∼2.8 × 10⁴ times higher as that of the second-best model (T/T×S) (supplemental Table S14, available at www.jneurosci.org as supplemental material). The statistical group analysis of the T/T model parameter estimates replicated all results from the four-area model (supplemental Table S15, available at www.jneurosci.org as supplemental material). In particular, we again found a symmetric increase in SPG interhemispheric connections during SD (right→left, 0.09 ± 0.03 Hz, p = 0.0063; left→right, 0.06 ± 0.02 Hz, p = 0.0129; nonsignificant difference, p = 0.1746). However, no significant modulatory effects were found for the interhemispheric connections between left and right PAG (right→left, 0.00 ± 0.01 Hz; p = 0.9009; left→right, 0.02 ± 0.01 Hz, p = 0.1745). Given this finding, the rest of this article focuses on the four-area model as a sufficient representation of IHI in the dorsal stream.

Figure 7.

Summary of the group results for the optimal six-area dorsal stream model (T/T). As in the four-area dorsal stream model (Fig. 6), interhemispheric connection strengths were bidirectionally modulated by spatial decisions, regardless of the visual field of stimulation. This task-dependent modulation symmetrically increased interhemispheric connections of SPG, but not of PAG. Compare with supplemental Table S15 (available at www.jneurosci.org as supplemental material) and see Figure 3 for conventions.

Discussion

A mechanistic understanding of IHI is important, not only for basic neuroscience, but also for clinical disorders related to hemispheric specialization (e.g., neglect, aphasia, or schizophrenia) (Woodruff et al., 1997; Shkuro et al., 2000; Corbetta and Shulman, 2002). IHI strongly depends on cognitive context, such as the task performed and the stimuli processed. Models of IHI are needed that account for this context dependency, particularly during lateralized tasks (Hellige, 1990; Liederman, 1998). Testing such models experimentally, however, is challenging. Despite the importance of callosal lesions studies, their interpretation can be difficult (e.g., because of plastic reorganization of brain function). Coherence analyses based on EEG can be useful (Schack et al., 2003) but suffer from low anatomical resolution. Invasive recording studies (Engel et al., 1991; Kiper et al., 1999) cannot usually be performed in humans and only sample a few locations.

Models of effective connectivity in neuroimaging could overcome these problems. However, a challenge is that IHI models are usually complex because of the reciprocal nature of interhemispheric connections and the multiple pathways by which the hemispheres can interact. For example, SEM is problematic in this situation because the parameters required often outnumber the observed covariances (McIntosh and Gonzalez-Lima, 1994; Penny et al., 2004b). One can constrain reciprocal connections to be identical (Rowe et al., 2002) or constrain the fitting procedure (McIntosh et al., 1994), but neither is optimal. This may explain the lack of IHI studies that combine modeling and neuroimaging. An exception is McIntosh et al. (1994), who used two right-hemispheric tasks engaging ventral and dorsal visual streams, respectively. Whereas the activation pattern was surprisingly symmetric for both tasks, SEM demonstrated asymmetries of interhemispheric connections, with right-to-left connections being positive and stronger during both tasks.

Currently, three major theories of IHI exist, which predict different patterns of interhemispheric connectivity during lateralized tasks with lateralized inputs, as in our paradigm. The first theory is based on the notion of “information transfer” (Poffenberger, 1912). It has been investigated in animals (Bures and Buresova, 1960), by studies of split-brain patients (Pollmann and Zaidel, 1998; Funnell et al., 2000; Gazzaniga, 2000; Corballis et al., 2003), and in healthy volunteers (Marzi et al., 1991; Brown and Jeeves, 1993). A broadly accepted proposal is that, given a particular lateralized task, information transfer should be asymmetrically enhanced from the nonspecialized to the specialized hemisphere to ensure most efficient processing (Nowicka et al., 1996; Endrass et al., 2002; Barnett and Kirk, 2005) (but see Larson and Brown, 1997). In terms of effective connectivity, this hypothesis predicts that connections toward the dominant hemisphere should be positive and significantly stronger than connections away from it. Furthermore, this task-dependent increase in connectivity should be particularly pronounced when stimulus information is initially only available to the nondominant hemisphere (e.g., by presenting a visual stimulus in the periphery of the contralateral hemifield). In summary, the concept of information transfer predicts an asymmetric modulation of interhemispheric connections by task, but conditional on the visual field of stimulus presentation.

A second account of IHI concerns the functional balance between hemispheres. Kinsbourne (1970) proposed “interhemispheric inhibition,” mediated by mutual inhibition between homotopic brain regions, as a general principle of brain function. From this view, specialization of one hemispheric is equivalent to its being superior in suppressing the opposite hemisphere. Although interhemispheric inhibition has been found mainly in the context of motor (Ferbert et al., 1992; Meyer et al., 1995) and visuospatial tasks (Kapur, 1996; Vuilleumier et al., 1996; Fink et al., 2000; Hilgetag et al., 2001), Kinsbourne (1970) suggested that it might underlie all lateralized processes, including language. Recent studies also implicated it in nonspatial visual processing (Walsh et al., 1998; Sack et al., 2005). Although different variants of this theory use somewhat different concepts of “inhibition” (Chiarello and Maxfield, 1996), most models predict that interhemispheric connection strengths should be negative in both directions (Hilgetag et al., 1999; Levitan and Reggia, 2000). This does not necessarily mean, however, that two areas that affect each other by interhemispheric inhibition necessarily show decreased activity: regional activations can coexist with interhemispheric inhibition if other (e.g., intrahemispheric) inputs to the areas of interest are positive and dominant in magnitude.

A third major theory of IHI concerns “hemispheric recruitment”: when is it advantageous to restrict information processing to a single hemisphere or to distribute the computational load across both hemispheres? Extending pioneering work on limited hemispheric processing capacities (Hellige and Cox, 1976; Liederman, 1986), Banich and colleagues showed in behavioral experiments that hemispheric recruitment occurs as a function of computational complexity and attentional demands of the task performed (Banich, 1998; Belger and Banich, 1998; Weissman and Banich, 2000; Passarotti et al., 2002). They conjectured that, if the neural resources in the hemisphere receiving a stimulus are insufficient for optimal processing, the benefits of distributing processing load across both hemispheres should outweigh the costs of transcallosal information transfer. Given a sufficiently demanding task, hemispheric recruitment also occurs during lateralized tasks, even when the dominant hemisphere receives the stimulus (Belger and Banich, 1998). Banich and colleagues predicted that hemispheric recruitment necessitates a tight coordination of processes in both hemispheres and that this should be reflected by a bidirectional and task-dependent increase in interhemispheric connectivity (Banich, 1998; Weissman and Banich, 2000).

Here, we have demonstrated how one can disambiguate among different candidate mechanisms of IHI for a given lateralized task, using DCM and BMS. Our modeling approach gave three main results. First, in the ventral stream, interhemispheric connections were asymmetrically modulated by letter processing but conditional on the stimulated VF (Figs. 3, 5): right→left connections alone significantly increased during LD, but only with LVF stimulation. This is exactly the connectivity signature predicted by the information transfer hypothesis for a left-lateralized task. This asymmetric modulation of connectivity was observed for LG and FG, but not MOG. According to the model, MOG activation during LD is caused through its intrahemispheric connections with LG and FG. We therefore conclude that MOG is not a key structure for IHI in letter processing. Second, in the dorsal stream, interhemispheric connections were bidirectionally modulated by spatial decisions, regardless of the stimulated VF (Figs. 6, 7). This is the connectivity signature predicted by the hemispheric recruitment hypothesis. As in the ventral stream model, the contextual modulation of interhemispheric connections was spatially specific: it was found for SPG, but not PAG. These results concur with the findings of Iacoboni and Zaidel (2004), who identified the right SPG as a key structure in IHI during a visuomotor paradigm. Third, in all our models, neither the fixed (intrinsic) connection strengths nor the strengths of LVF/RVF inputs showed any asymmetries (supplemental Tables S6, S12, available at www.jneurosci.org as supplemental material). Instead, as described above, it is the specific task requirements that dynamically reconfigure connection strengths. This emphasizes the context dependence of IHI and relates it to other cognitive processes in which connectivity changes mediate contextual effects (Büchel et al., 1999; Kastner and Ungerleider, 2000; McIntosh, 2000; Fries et al., 2001). It follows that the IHI mechanisms identified by the present study are probably not invariant properties of ventral and dorsal streams but are specific for the particular paradigm used. For other tasks, different mechanisms might be used by the two streams (for example, see Hilgetag et al., 2001). The approach presented here introduces a general procedure, based on DCM and BMS, how the most likely mechanism of IHI during a specific cognitive task can be determined.

The structure of the optimal ventral and dorsal stream models differed with regard to the existence of interhemispheric connections at the level of the input areas. This was a deliberate choice, because human postmortem tracing studies indicated that V1 (CUN in the dorsal stream model) lacks callosal connections, whereas V2 (LG in the ventral stream model) is connected callosally (see Materials and Methods). Although these findings are not yet convincingly replicated by diffusion tensor imaging (DTI) (Dougherty et al., 2005), this is likely attributable to the lower sensitivity of DTI compared with anatomical studies. Nevertheless, we tested the validity of our assumptions about anatomical connectivity in additional models. Both removal of connections between left and right LG in the optimal ventral stream model and inclusion of connections between left and right CUN in the optimal dorsal stream model decreased model goodness (for details, see Results). This emphasizes that the different mechanisms embodied by ventral and dorsal stream models are not attributable to invalid assumptions about the connectivity of the input-receiving areas, but are caused by the specific task requirements.

Together, our results provide direct neurophysiological evidence, in terms of effective connectivity, for asymmetric information transfer and hemispheric recruitment in ventral and dorsal streams, respectively, during a paradigm inducing task-driven lateralization. Furthermore, we have clarified the role of specific visual areas for IHI: LG and FG (but not MOG) are critical for IHI during letter processing, and SPG (but not PAG) during visuospatial processing. We hope that this study will be a useful starting point for future investigations of IHI in the human brain using dynamic system models of functional imaging data.