Dynamic cerebral autoregulation during repeated squat-stand maneuvers

Abstract

Transfer function analysis of spontaneous oscillations in blood pressure (BP) and cerebral blood flow (CBF) can quantify the dynamic relationship between BP and CBF. However, such oscillation amplitudes are often small and of questionable clinical significance, vary substantially, and cannot be controlled. At the very low frequencies (<0.07 Hz), coherence between BP and CBF often is low (<0.50) and their causal relationship is debated. Eight healthy subjects performed repeated squat-stand maneuvers to induce large oscillations in BP at frequencies of 0.025 and 0.05 Hz (very low frequency) and 0.1 Hz (low frequency), respectively. BP (Finapres), CBF velocity (CBFV; transcranial Doppler), and end-tidal CO₂ (capnography) were monitored. Spectral analysis was used to quantify oscillations in BP and CBFV and to estimate transfer function phase, gain, and coherence. Compared with spontaneous oscillations, induced oscillations had higher coherence [mean 0.8 (SD 0.11); >0.5 in all subjects at all frequencies] and lower variability in phase estimates. However, gain estimates remained unchanged. Under both conditions, the “high-pass filter” characteristics of dynamic autoregulation were observed. In conclusion, using repeated squat-stand maneuvers, we were able to study dynamic cerebral autoregulation in the low frequencies under conditions of hemodynamically strong and causally related oscillations in BP and CBFV. This not only enhances the confidence of transfer function analysis as indicated by high coherence and improved phase estimation but also strengthens the clinical relevance of this method as induced oscillations in BP and CBFV mimic those associated with postural changes in daily life.

continuous measurements of cerebral blood flow (CBF) velocity (CBFV) using transcranial Doppler (TCD) have shown that CBFV is affected by dynamic perturbations in blood pressure (BP) considered to lie within the “autoregulatory range” (2, 10, 28, 41). Transfer function analysis of spontaneous oscillations in BP and CBFV quantifies this dynamic pressure-flow relationship of the cerebral circulation and has suggested that cerebral autoregulation is more effective at low compared with high frequencies (the “high-pass filter” effect) (7, 8, 10, 27, 39). However, this method may be limited by the relatively small magnitude of spontaneous oscillations. Also, assessment of dynamic cerebral autoregulation based on spontaneous changes in BP and CBFV exhibits substantial individual variability under most experimental conditions (27, 33). In addition, coherence between these oscillations at low frequencies (<0.07 Hz) generally is low (<0.5), and thus it is uncertain whether the quantification of the transfer function is statistically reliable (39) and whether oscillations in CBFV and BP are causally related (12). In practice, most studies exclude data with coherence < 0.5 for analysis, which can amount to one-third of all collected measurements (16, 22).

Squatting followed by standing produces dramatic changes in BP (31). In daily life comparable maneuvers occur frequently, e.g., when standing up after tying shoelaces or picking up something from the floor, and these maneuvers are often accompanied by symptoms of light-headedness suggestive of cerebral hypoperfusion. When such squat-stand maneuvers are performed repeatedly, large and periodic changes in BP and CBFV are created (3). Thus the magnitude of these changes is representative of daily life challenges for cerebral autoregulation.

We conducted this study to address the following hypotheses: 1) oscillatory changes in BP and CBFV at specific low frequencies (0.025, 0.05, and 0.1 Hz) can be induced with repeated squat-stand maneuvers, thus creating relatively narrow-band but high-amplitude signals; and 2) with increased correlation between BP and CBFV, and reduced signal to noise, transfer function assessment of dynamic cerebral autoregulation at the low and very low frequencies would be improved, associated with reduced variability in phase and gain estimates.

METHODS

Subjects.

We studied eight healthy young subjects (4 men), age 30 yr (SD 4), weight 72 kg (SD 18), systolic/diastolic BP 114 (SD 5.4)/70 mmHg (SD 8.7). These subjects were free of known disease, used no medication, and did not smoke.

Ethical approval.

The study complies with the standards set by the latest revision of the Declaration of Helsinki and was approved by the Institutional Review Boards of the University of Texas Southwestern Medical Center and Presbyterian Hospital of Dallas. All participants provided informed consent in writing.

Instrumentation.

BP was measured in the finger by photoplethysmography (Finapres, Ohmeda, Madison, WI). We and others have shown that this method reliably assesses dynamic changes in beat-to-beat BP that correlate well with intra-arterial recordings and can be used to quantify the dynamic pressure-flow relationship of the cerebral circulation (29, 39, 40). The servo-reset mechanism was turned off during data collection for a maximum of 5 min to allow uninterrupted data recording (25). Intermittent BP was also measured in the arm by electrosphygmomanometry (SunTech Medical, Morrisville, NC), with a microphone placed over the brachial artery and the Korotkoff sounds gated to the electrocardiogram (ECG). The arm pressure was used to verify the accuracy of the finger pressure recordings throughout the experiment.

CBFV was obtained in the middle cerebral artery (MCA) by TCD ultrasonography. This technique allows noninvasive and repeatable estimates of changes in CBF on a beat-to-beat basis. A 2-MHz Doppler probe (DWL Elektronische Systeme) was placed over the temporal window and fixed at a constant angle and position with a custom-made individually shaped mould. End-tidal CO₂ (ETCO₂) was monitored with a nasal cannula using capnography (Criticare Systems, Waukesha, WI). In addition, arterial saturation (pulse-oximetry) and three-lead ECG were registered.

Experimental procedures.

All experiments were performed in the morning, at least 2 h after a light breakfast and 12 h after the last caffeinated beverage or alcohol, in a quiet, environmentally controlled laboratory with an ambient temperature of 22°C. After at least 10 min rest in sitting position, 5-min segments of BP and CBFV data were recorded during spontaneous respiration. These data were used for spectral analysis of spontaneous oscillations in BP and CBFV. Next, repeated squat-stand maneuvers were performed. After careful instruction and practice, participants were coached into performing these maneuvers at a frequency of 0.025 Hz (20-s squat followed by 20 s standing up), 0.05 Hz (10-s squat, 10-s stand), and 0.1 Hz (5-s squat, 5-s stand) for 5 min each, separated by 10 min of recovery between the maneuvers. During these maneuvers, subjects were instructed to keep normal breathing and to avoid a Valsalva-like maneuver.

Data processing.

The analog finger BP and Doppler CBFV signals were sampled simultaneously at 100 Hz (Multi-Dop X2, DWL). Real time beat-to-beat mean values of pressure and velocity were calculated as waveform integration of the sampled pressure and velocity signal within each cardiac cycle, divided by the corresponding pulse interval and stored for off-line analysis. Beat-to-beat changes in mean BP and CBFV were aligned with the time of R wave peaks of the ECG and linearly interpolated, then resampled at 2 Hz to convert the unequally spaced beat-to-beat time series to a uniformly spaced time series for spectral and transfer function analysis. The time series were detrended with third-order polynomial fitting and then subdivided into 128-point segments (64 s) with 50% overlap for spectral estimation. This process resulted in eight segments of data for the segment periodogram average, with a spectral resolution of ∼0.0156 Hz. In this way, each segment contains at least one full period of oscillations at the lowest frequency (0.025 Hz) and up to six full periods of oscillations at the frequency of 0.1 Hz. Fast Fourier transforms were implemented with each Hanning-windowed segment and averaged to calculate the autospectrum of BP and CBFV. This analysis was repeated after adjustment of the window length to the cycle length of the squat-stand maneuvers, to the effect that each window contained three cycles. Because this did not alter transfer function estimates, the described standard window lengths were used for both spontaneous and induced oscillations. Breath-to-breath values for ETCO₂ were linearly interpolated and resampled at 2 Hz, and spectral analysis was performed to estimate the variability in ETCO₂. Respiratory frequency was obtained from spectral analysis of continuous recording of CO₂ waveforms.

Transfer function estimation.

Estimation of transfer function gain, phase, and coherence function was based on the cross-spectral method (39). Transfer gain quantifies how changes in BP are transmitted into CBFV; a lower gain suggests that oscillations in CBFV in response to changes in BP are either buffered by active changes in cerebrovascular resistance out of phase with changes in BP (dynamic autoregulation) (16, 19, 20) and/or by increases in steady-state cerebrovascular resistance (38). The phase spectrum describes the temporal relationship between changes in BP and CBFV at different frequencies (7, 8, 16). Finally, estimates of coherence function quantify to what extent changes in CBFV are linearly correlated with changes in BP.

Transfer function analysis for spontaneous oscillations was carried out in the three frequency domains: very low frequency (VLF; 0.02–0.07 Hz), low frequency (LF; 0.07–0.2 Hz), and high frequency (HF; 0.2–0.35 Hz) (39). Because we wished to make comparisons, the oscillations induced by repeated squat-stand maneuvers were analyzed in the same frequency domains as used for spontaneous oscillations: squat-stand maneuvers at 0.025 and 0.05 Hz were analyzed in the VLF domain (0.02–0.07 Hz); 0.1-Hz maneuvers were analyzed in the LF domain (0.07–0.2 Hz).

For induced oscillations, we also performed the analysis around each of the three evoked frequencies. Thus 0.025-Hz maneuvers were analyzed in the range 0.02–0.06 Hz, and 0.05-Hz maneuvers were analyzed in the range 0.03–0.08 Hz in all subjects. The 0.1-Hz maneuvers were analyzed in the range 0.08–0.14 Hz in seven subjects and 0.11–0.17 Hz in one subject with the peak at 0.14 Hz. Transfer function gain, phase, and coherence did not differ significantly between the choices of the frequency bands. Therefore, we will only report the results based on the same frequency ranges as used for spontaneous oscillations.

Statistical analysis.

Comparisons between baseline and squat-stand maneuvers and between different frequencies were performed using ANOVA for repeated measures. The data for BP, CBFV, heart rate (HR), and CO₂ had a normal distribution (Kolmogorov-Smirnov test), and repeated-measures ANOVA with Bonferroni posttest for multiple comparisons if P < 0.05 was applied. Normal distribution could not be assumed for the data for spectral power, transfer function gain, phase, and coherence. Therefore, the nonparametric Friedman test with Dunn posttest was applied. Statistical significance was set at P < 0.05. Data are presented as means (SD).

RESULTS

Hemodynamics effects of squat-stand maneuvers.

Large oscillations in BP and CBFV were observed at all three frequencies of repeated squat-stand maneuvers (Figs. 1–3). There was a low intersubject variability in the frequency induced by the repeated squat-stand maneuvers, determined from the peak of the BP and CBFV power spectra: maneuvers at 0.1 Hz induced a peak at 0.11 Hz in seven subjects and 0.14 Hz in one subject; maneuvers at 0.05 and 0.025 Hz induced peaks, respectively, at 0.047 and 0.031 Hz in all eight subjects. Table 1 shows that the mean values of BP, HR, ETCO₂ and respiratory frequency did not change significantly due to the repeated squat-stand maneuvers, despite the increased oscillation amplitude. Fluctuations in ETCO₂ were slightly enhanced during these maneuvers (Table 2).

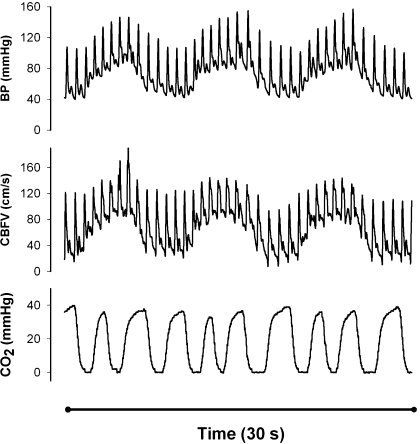
Fig. 1.

Effects of the repeated squat-stand maneuvers on mean arterial blood pressure (BP), cerebral blood flow velocity (CBFV), and respiration. Raw waveform data from a representative individual during repeated squat-stand maneuvers at 0.1 Hz (5-s squat, 5-s stand) are shown. CO₂, CO₂ waveform (capnography); CBFV, transcranial Doppler; BP, mean arterial BP (Finapres). The graph starts with 5 s squatting, leading to increases in BP and CBFV, followed by 5 s standing, causing reductions in BP and CBFV. A total of 30 s is displayed, showing 3 full cycles of the maneuvers. Note that despite strong hemodynamic effects, there is no distortion of waveforms.

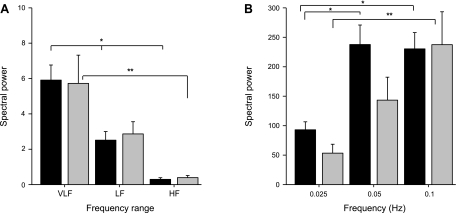
Fig. 3.

Spectral power of BP and CBFV for spontaneous and induced oscillations. A: spectral power of spontaneous oscillations in BP (in mmHg²; black bars) and CBFV [in (cm/s)²; gray bars]. Bars represent group mean and SE. VLF, very low frequency band (0.02–0.07 Hz); LF, low-frequency band (0.07–0.2); HF, high-frequency band (0.2–0.35 Hz). Statistical comparisons were made using Friedman test with Dunn posttest. *P < 0.001 (BP); **P = 0.005 (CBFV). B: spectral power of BP (black bars) and CBFV (gray bars) during oscillations induced by periodic squatting at 3 frequencies: 0.025 and 0.05 Hz (VLF range) and 0.1 Hz (LF range). Note the different y-axis scale (factor 30) for spectral power compared with A. *P = 0.001 (BP). **P = 0.014 (CBFV). Differences in spectral power between spontaneous and induced oscillations were highly significant (P < 0.0001).

Table 1.

Main hemodynamic parameters during the different tests

	Rest	Periodic Squatting			P Value
		0.025 Hz	0.05 Hz	0.1 Hz
BP, mmHg	84 (8)	90 (9)	86 (9)	90 (3)	0.18
CBFV, cm/s	55 (13)	53 (8)	52 (9)	55 (11)	0.24
HR, beats/min	69 (15)	84 (17)	88 (17)	90 (17)	0.1
ETCO2, Torr	38 (3)	38 (3)	38 (4)	40 (3)	0.08
Resp frequency, Hz	0.29 (0.07)	0.31 (0.07)	0.34 (0.05)	0.28 (0.07)	0.34

Values are means (SD) during each test. BP, blood pressure (Finapres); CBFV, cerebral blood flow velocity (transcranial Doppler); HR, heart rate; ETCO₂, end-tidal CO₂ (capnograph); Resp frequency, respiratory frequency (spectral analysis of the CO₂ waveform). P values, repeated-measures ANOVA.

Table 2.

Effect of squatting maneuvers on variability in ETCO₂

	Rest	0.025 Hz	0.05 Hz	0.1 Hz	P Value
VLF, Torr2	0.38 (0.18)	1.92 (1.60)*	2.15 (1.38)*	1.69 (1.10)	0.003
LF, Torr2	0.19 (0.07)	0.97 (1.37)	0.79 (0.52)	2.41 (1.45)*	0.0002
HF, Torr2	0.02 (0.02)	0.18 (0.25)	0.15 (0.10)	0.50 (0.17)*	0.0005

Values are means (SD). Power spectrum (PS) of variability of ETCO₂ (PS_ETCO2) in very low frequency (VLF; 0.02–0.07 Hz), low frequency (LF; 0.07–0.2 Hz), and high frequency (HF; 0.2–0.35 Hz) are compared across the 4 different conditions [resting conditions and repeated squat-stand maneuvers at 3 different frequencies (0.025, 0.05, and 0.1 Hz)]. For example, PS_ETCO2 in the LF band is significantly higher in repeated squat-stand maneuvers at 0.1 Hz compared with rest. P values, repeated-measures ANOVA (Friedman test).

^*Dunn posttest, P < 0.05 vs. Rest.

Magnitude of induced oscillations.

The repeated squat-stand maneuvers at 0.025 and 0.05 Hz resulted in, respectively, 15-fold and 40-fold increases in BP spectral power (compared with spontaneous VLF oscillations), while at 0.1 Hz, a 100-fold increase occurred relative to spontaneous LF oscillations (Fig. 3). These augmented oscillations in BP led to 10-, 20-, and 100-fold increases in CBFV spectral power at 0.025, 0.05, and 0.1 Hz, respectively. Thus increases in CBFV oscillations were relatively smaller than increases in BP oscillations at 0.025 and 0.05 Hz but not at 0.1 Hz, indicating more effective damping at the lower frequencies (Fig. 3B). As expected this was corroborated by lower gain in these frequencies (Fig. 4).

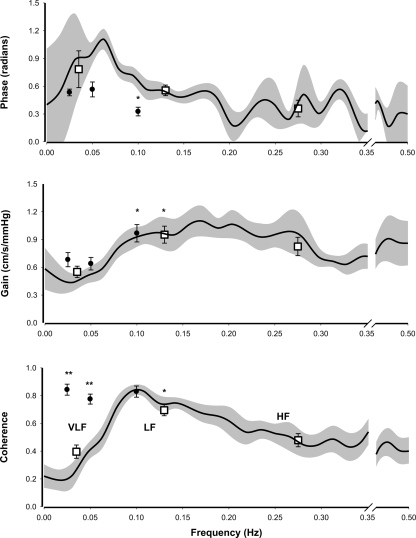
Fig. 4.

Transfer function analysis of spontaneous and induced oscillations. Group results of transfer function analysis of spontaneous oscillations (resting conditions) and oscillations induced by repeated squat-stand maneuvers at 3 different frequencies. The background plots are frequency distribution graphs, obtained from spontaneous oscillations, of mean (black line) and SE (gray area) phase, gain, and coherence plotted against oscillation frequency. Squared boxes represent mean (SE) phase, gain, and coherence within the 3 frequency bands VLF, LF, and HF (see Fig 2). For comparison, results obtained from repeated squat-stand maneuvers are plotted as black dots (mean and SE) at their respective frequencies (0.025, 0.05, and 0.1 Hz). Statistical comparisons were made using Friedman test with Dunn posttest. *P < 0.05 for differences between frequency bands within each group. **P < 0.05 for differences between the 2 groups (spontaneous oscillations vs. induced oscillations).

Transfer function gain, phase, and coherence.

Figure 4 summarizes transfer function gain, phase, and coherence in the frequency domains of VLF, LF, and HF for spontaneous oscillations and for oscillations induced at 0.025, 0.05, and 0.1 Hz by the repeated squat-stand maneuvers. For comparison, these parameters are superimposed on the frequency plots of transfer function gain, phase, and coherence for spontaneous oscillations. Coherence between BP and CBFV was much higher for repeated squat-stand maneuvers than for spontaneous oscillations, with values > 0.6 for all subjects (range: 0.61–0.96). Specifically, coherence was 0.4 (SD 0.13), 0.7 (SD 0.11), and 0.5 (SD 0.13) at VLF, LF, and HF for spontaneous oscillations vs. 0.8 (SD 0.11), 0.9 (SD 0.07), and 0.9 (SD 0.06) at 0.025. 0.05, and 0.1 Hz for induced oscillations, respectively. Despite the poor coherence at the very low frequencies for spontaneous oscillations, there was consistency between the estimates of gain from spontaneous and induced oscillations. At VLF, gain was 0.6 cm·s⁻¹·mmHg⁻¹ (SD 0.16) for spontaneous vs. 0.7 (SD 0.22) and 0.6 cm·s⁻¹·mmHg⁻¹ (SD 0.19) at 0.025 and 0.05 Hz for induced oscillations, respectively. At LF, gain was 1.0 cm·s⁻¹·mmHg⁻¹ (SD 0.24) for spontaneous vs. 1.0 cm·s⁻¹·mmHg⁻¹ (SD 0.27) at 0.1 Hz for induced oscillations (all nonsignificant). Note that variability of the gain estimates was comparable.

Findings for phase were different. For spontaneous oscillations, VLF phase was 0.8 radians (SD 0.53). For repeated squat-stand maneuvers, phase was 0.5 (SD 0.10) and 0.6 radians (SD 0.23) at 0.025 and 0.05 Hz, respectively (P = 0.4). LF phase was 0.6 radians (SD 0.15) for spontaneous and 0.3 radians (SD 0.13) for induced oscillations at 0.1 Hz (P = 0.01). HF phase for spontaneous oscillations was 0.4 radians (SD 0.24). Estimations of phase from induced oscillations at 0.025 and 0.05 Hz had less interindividual variability (mean 0.6 radians, range 0.2–1.0, associated with a coherence of 0.8) compared with spontaneous oscillations (mean 0.8 radians, range 0.1–1.9, associated with a coherence of 0.4). Considering gain and phase together, for induced oscillations, estimates at 0.025 and 0.05 Hz were comparable. Gain increased and phase decreased from these VLF frequencies to LF at 0.1 Hz as with spontaneous oscillations in line with high-pass filter properties of the dynamic pressure-flow relationship of the cerebral circulation (Fig. 4).

DISCUSSION

There are several new findings in this study. During repeated squat-stand maneuvers at three specific frequencies of 0.25, 0.05, and 0.1 Hz, large oscillatory changes in BP and CBFV were generated around each of these frequencies. Increases in oscillations in BP and CBFV led to an increase in coherence in the VLF range and improved estimations of transfer function phase. Estimation of transfer function gain yielded identical results with spontaneous and induced oscillations. The “high-pass filter” behavior of the dynamic pressure-flow relationship, deduced from these augmented and causally related oscillations in BP and CBFV, fits the model based on analysis of spontaneous oscillations. These findings show that the large oscillations in BP and CBFV induced during repeated squat-stand maneuvers not only provided strong and physiologically relevant hemodynamics perturbations, but also led to improved estimation of transfer function to assess dynamic cerebral autoregulation at the very low frequencies.

Previous studies have induced repeated oscillations in BP and CBFV in order to advance the understanding of dynamic pressure-flow relationship of the cerebral circulation (1, 3, 4, 7, 15, 16, 40). In one of the first studies describing the clinical application of the phase relationship between BP and CBF, Diehl et al. (7) used periodic breathing to induce sinusoidal oscillations at 0.1 Hz (6 breaths/min). Forced breathing carries the risk of altering arterial CO₂, which affects CBF. This technique cannot be used to induce oscillations at frequencies much lower than 0.1 Hz. Augmented oscillations have also been induced by repeated head-up tilt to 45° (<2 s) with a period of 10 s (16) and to 60°, at frequencies between 0.07 and 0.25 Hz (13). The purpose of the former study was to investigate the phase relationship between BP and cerebrovascular resistance, in order to explain the phase lead of CBFV to BP in studies of autoregulation. Compared with spontaneous oscillations, coherence between BP and CBFV was increased by these maneuvers. A disadvantage of this technique was the uncertain effect of the gravitational force on cerebral perfusion pressure when going from supine to tilt (16). Cyclic thigh cuff compression and release were used to induce oscillatory changes in BP and CBF at a single frequency of 0.033 Hz (1). On average, BP increased by ∼10 mmHg during cuff compression and decreased by ∼6 mmHg during cuff release. However, continuous recordings did not reveal clearly discernible sinusoidal changes in BP and CBFV in response to cyclic changes in cuff pressure (1). Oscillatory lower-body negative pressure (OLBNP) has been applied to create oscillations in BP and CBFV (4, 15, 40). This technique has important limitations in that changes in pressure of lower-body negative pressure (LBNP) chambers may not transfer immediately and effectively into changes in BP with increases in oscillatory frequencies (15). In addition, LBNP pressures that were high enough to be effective in generating large BP and CBFV oscillations are poorly tolerated by subjects (4). Despite these technical difficulties, Hamner et al. (15) have applied OLBNP to induce oscillations in BP and CBFV at the frequencies of 0.03, 0.05, and 0.1 Hz, with the purpose of increasing low-frequency coherence. Even at a maximum change of LBNP pressure from zero to −40 mmHg and at the most effective frequency of 0.05 Hz, spectral power of BP and CBFV increased only by a factor of 10 and 5 (15). Of note, 14 of 36 LBNP trials in nine subjects still had coherence < 0.3 at the frequencies of 0.03 and 0.05 Hz, indicating the limitations of using OLBNP to generate large and coherent low-frequency changes in BP and CBFV (15).

Rationale for using repeated squat-stand maneuvers.

Sharpey-Schafer (31) described the strong hemodynamics changes provoked by a squat-stand maneuver. Briefly, squatting induces a rapid but transient rise in BP with its peak after about 2–3 s. The increase in BP has been attributed mainly to a sudden increase in cardiac output from increased venous return from the lower limbs (21). The reduction in BP during standing up has been attributed to a combination of reduction in peripheral vascular resistance and a reduction in cardiac output due to rapid translocation of central blood volume to the lower limbs (37). We observed large and coherent oscillations in BP and CBFV, induced by repeated squat-stand maneuvers at three distinct frequencies. These results demonstrated that low-frequency transient changes in CBFV occur in response to dynamic changes in arterial pressure that should lie within the “autoregulatory range.”

Different frequencies induced oscillations with different magnitude.

Oscillations in BP at 0.05 and 0.1 Hz were much larger than at 0.025 Hz. A likely explanation is that at 0.025 Hz, baroreflex sympathetic control of BP would have sufficient response time to counteract dynamic changes in BP (9). Conversely, large oscillations in BP at 0.05 and 0.1 Hz may be compounded by cardiovascular resonance in response to external perturbations to BP (14, 36). The frequencies of 0.05 and 0.1 Hz of repeated squat-stand maneuvers in this study are close to the baroreflex resonance frequencies observed in humans (14, 36).

LF coherence.

LF coherence (<0.07 Hz) was increased in all subjects. Low coherence may indicate that changes in CBFV are relatively independent of changes in BP and thus may reflect an intact cerebral autoregulation, while increases in coherence have been interpreted to reflect impairment of autoregulation (10). Could the higher coherence indicate that autoregulation was less efficient for the large hemodynamic changes during the repeated squat-stand maneuvers? Given that transfer function gain was not different from spontaneous oscillations, a similar degree of damping for the much stronger induced oscillations in BP makes this very unlikely (19). We propose that the increased coherence reflects improved “signal-to-noise ratio” for induced oscillations. Finally, it can be speculated that the high coherence for induced oscillations may reflect nonlinear synchronization or entrainment of the two oscillatory systems (BP and CBFV) with periodic external stimuli, similar to what has been observed in other biological regulator systems (23).

Transfer function phase and gain.

Phase estimates at the VLF frequencies from spontaneous oscillations had large interindividual variability; this most likely results from the low coherence, since phase for augmented oscillations in BP and CBFV, associated with higher coherence, showed considerably less interindividual variability. Decreases in phase with increases in frequency confirmed observations based on spontaneous oscillations under resting conditions that phase shift is larger at the VLF than the LF frequencies. Phase for induced oscillations at the VLF of 0.025 and 0.05 Hz [mean value of 0.6 radians (SD 0.23)] was slightly lower than that from spontaneous oscillations [0.8 radians (SD 0.53)]. However, this difference is not statistically significant. In addition, the improved signal-to-noise ratio may lead to improved accuracy of phase estimation at the VLF for induced oscillations. Consistent with these findings, observations in studies using enhanced oscillations found a phase lead of CBFV of 0.6–0.8 radians in the VLF region < 0.07 Hz (3, 4, 15).

LF phase for induced oscillations was lower than for spontaneous oscillations. The underlying mechanism for this difference is not clear. It is possible that increases in shear stress in the cerebral blood vessels associated with the enhanced BP and/or CBFV oscillations may alter cerebrovascular tone, leading to a reduction in phase under these conditions (5).

Transfer function gain was similar for spontaneous and induced oscillations even though coherence was low for spontaneous oscillations [0.4 (SD 0.13)] at frequencies below 0.07 Hz. These findings suggest that, compared with phase, estimation of gain is less affected by the magnitude of BP and CBFV oscillations and by low coherence.

The characteristics of transfer function gain and phase in the present study, under conditions of augmented oscillations in BP and CBFV, extend observations of the “high-pass filter” characteristics of dynamic cerebral autoregulation (15). The consistency of transfer function gain and phase estimates between spontaneous and augmented changes in BP and CBFV suggests that for each specific frequency, CBFV changed in proportion with changes in BP, revealing linear dynamic system properties (35). Given that BP and CBFV spectral power during repeated squat-stand maneuvers was substantially higher than for spontaneous oscillations (10- to 100-fold), linear transfer function analysis can be applied in a wide range of changes in BP and CBFV. Of note, for induced oscillations, even though the pattern of higher phase and lower gain for VLF than for LF frequencies is consistent with a high-pass filter, the pattern of phase and gain within VLF is not. A slight decrease in gain and increase in phase from 0.025 to 0.05 Hz (Fig. 4) is not consistent with the characteristics of a typical first-order high-pass filter, which would suggest increases in gain and decreases in phase with an increase in frequency from 0.025 to 0.05 Hz. These observations indicate the presence of high-order (>1) regulatory mechanisms for cerebral hemodynamics.

ETCO₂ during repeated maneuvers.

Fluctuations in ETCO₂ were enhanced slightly during repeated squat-stand maneuvers (Table 2). Considering that CBF changes 3% for each Torr change in ETCO₂, the spectral power of these fluctuations translates into fluctuations in CBFV with a maximum of 2.5%, which is small relative to the >20% of change induced by BP. Moreover, the repeated body movements may introduce artifacts in capnography registration of the CO₂ waveform, which do not affect mean ETCO₂ estimation but could cause overestimation of fluctuations. We did not find a temporal relationship between fluctuations in ETCO₂ and oscillations in BP or CBFV.

Study limitations.

Repeated squat-stand maneuvers can be considered as aerobic exercise. Thus these maneuvers per se may modulate the dynamic pressure-flow relationship of the cerebral circulation. Specifically, performing these maneuvers may lead to brain activation (for motor and cognitive control), which in turn may elevate regional CBF (26). It is, however, unlikely that these increases in regional CBF would be periodic in response to the frequencies of squat-stand maneuvers. In addition, increases in CBF due to brain activation are small relative to the large changes induced by oscillations in BP. Thus the effect of brain activation during squat-stand maneuvers on the estimation of phase and gain, if anything, should be minimal. In line with this argument, moderate- to high-intensity aerobic exercise did not alter dynamic cerebral autoregulation (24).

Finally, flow velocity in the MCA is determined by CBF and by the diameter of the MCA. Therefore, changes in CBFV reflect changes in CBF only if the MCA diameter is constant. During acute, moderate changes in BP, MCA diameter showed <4% change (11, 30). This suggests that small changes in MCA diameter cannot be excluded. This would have the following effects on our data. Vasoconstriction during an increase in BP overestimates the associated rise in CBF. Conversely, vasodilatation induced by a decrease in BP overestimates the reduction in CBF. Collectively, these effects, if they did occur, would overestimate transfer function gain but would not affect phase, as this parameter is not affected by the amplitude but by the timing of the oscillations. In a similar vein, pressure-induced passive changes in diameter would underestimate changes in CBFV and thus transfer function gain, but not phase.

Clinical significance.

In clinical practice, the consequences of sudden changes in BP are frequently encountered in patients complaining of feeling light-headed or dizzy when standing up, and in patients evaluated for unexplained falls or syncope. Diagnostic evaluation generally focuses on BP measurements, with the inexplicit assumption that a reduction beyond a certain defined cut-off value (e.g., 20 mmHg systolic) induces cerebral hypoperfusion. However, dynamic cerebral autoregulation mediates the consequences of BP changes on CBF and therefore plays an important role in determining the clinical consequence of hemodynamic instability. Quantification of dynamic cerebral autoregulation has provided insight in these syndromes (34) and in other clinical conditions such as stroke (18, 34) and hypertension (17, 22) and will be important to investigate in Alzheimer's disease (6, 32).

Conclusions.

We have demonstrated that large and coherent oscillations in BP and CBFV at the low frequencies of 0.025, 0.05, and 0.1 Hz can be induced by repeated squat-stand maneuvers. This study succeeded in inducing high-amplitude oscillations in the low frequencies, in combination with high coherence, thereby allowing confident comparisons of the behavior of dynamic cerebral autoregulation in low vs. high frequencies. The magnitude of these hemodynamics changes as well as the maneuvers through which they are induced arguably are representative of the daily physiological challenges put to cerebral autoregulation, such as orthostatic hypotension. Phase estimates at the low frequencies below 0.07 Hz were substantially improved by the augmented BP and CBFV oscillations. We conclude that addition of these maneuvers to an analysis based on spontaneous oscillations enhances the information obtained from transfer function analysis and may be an important step toward its translation and implementation in clinical medicine where patients are able to perform these maneuvers.

GRANTS

This study was supported in part by the Kelly King Foundation and by National Institutes of Health Grant P30-AG-12300.

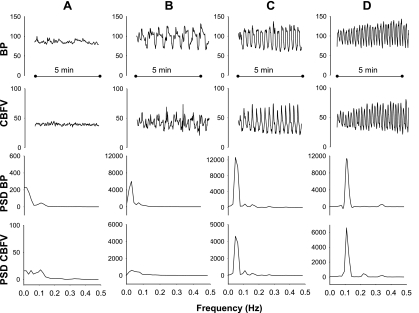
Fig. 2.

Spectral analysis of hemodynamic changes under resting conditions and during repeated squat-stand maneuvers. Data from 1 subject, showing beat-to-beat variability in BP and CBFV (top), and results of spectral analysis of these data (bottom). PSD, power spectral density. A: resting condition (spontaneous oscillations). B: oscillations induced by squat-stand maneuvers at 0.025 Hz. C: oscillations induced at 0.05 Hz. D: oscillations induced at 0.1 Hz.