Role of NADH/NAD⁺ transport activity and glycogen store on skeletal muscle energy metabolism during exercise: in silico studies

Abstract

Skeletal muscle can maintain ATP concentration constant during the transition from rest to exercise, whereas metabolic reaction rates may increase substantially. Among the key regulatory factors of skeletal muscle energy metabolism during exercise, the dynamics of cytosolic and mitochondrial NADH and NAD⁺ have not been characterized. To quantify these regulatory factors, we have developed a physiologically based computational model of skeletal muscle energy metabolism. This model integrates transport and reaction fluxes in distinct capillary, cytosolic, and mitochondrial domains and investigates the roles of mitochondrial NADH/NAD⁺ transport (shuttling) activity and muscle glycogen concentration (stores) during moderate intensity exercise (60% maximal O₂ consumption). The underlying hypothesis is that the cytosolic redox state (NADH/NAD⁺) is much more sensitive to a metabolic disturbance in contracting skeletal muscle than the mitochondrial redox state. This hypothesis was tested by simulating the dynamic metabolic responses of skeletal muscle to exercise while altering the transport rate of reducing equivalents (NADH and NAD⁺) between cytosol and mitochondria and muscle glycogen stores. Simulations with optimal parameter estimates showed good agreement with the available experimental data from muscle biopsies in human subjects. Compared with these simulations, a 20% increase (or ∼20% decrease) in mitochondrial NADH/NAD⁺ shuttling activity led to an ∼70% decrease (or ∼3-fold increase) in cytosolic redox state and an ∼35% decrease (or ∼25% increase) in muscle lactate level. Doubling (or halving) muscle glycogen concentration resulted in an ∼50% increase (or ∼35% decrease) in cytosolic redox state and an ∼30% increase (or ∼25% decrease) in muscle lactate concentration. In both cases, changes in mitochondrial redox state were minimal. In conclusion, the model simulations of exercise response are consistent with the hypothesis that mitochondrial NADH/NAD⁺ shuttling activity and muscle glycogen stores affect primarily the cytosolic redox state. Furthermore, muscle lactate production is regulated primarily by the cytosolic redox state.

during the transition from rest to exercise, the metabolic requirement of mammalian skeletal muscle for ATP synthesis can increase over 100-fold, while ATP concentration only decreases marginally (61). To maintain ATP homeostasis, the pathways of ATP synthesis must be activated rapidly to match the rate of ATP utilization (43, 44). Anaerobic glycolysis in cytosol and oxidative phosphorylation in mitochondria provide most of the ATP used during exercise; in both processes, NADH and NAD⁺ interconversions take place (5). These reducing equivalents not only participate in reduction-oxidation reactions as cosubstrates but also play important roles in metabolic regulation in both cytosol and mitochondria (2, 5, 19, 77, 88, 91). Specifically, NADH produced in glycolysis is utilized in reactions catalyzed by lactate dehydrogenase (LDH) (82) or transported to the mitochondria for oxidation in the electron transport chain (37) to maintain the redox states (NADH/NAD⁺) in cytosol and mitochondria. However, the inner mitochondrial membrane is impermeable to NADH and NAD⁺, so effective transport of these species between cytosol and mitochondria is accomplished via specialized shuttle systems (e.g., malate-aspartate or glycerol-3-phosphate), which contribute to nonequilibrium distribution of NADH and NAD⁺ between cytosol and mitochondria (79, 84, 100). These largely distinct redox states in cytosol and mitochondria play different roles in metabolic regulation (38, 103, 105). Regulation of skeletal muscle metabolism requires that NADH and NAD⁺ concentrations ([NADH] and [NAD⁺]) in each domain be related by coupled reaction and transport processes. With significantly increased metabolic rates during exercise, it is crucial to maintain the balance of [NADH] and [NAD⁺] between cytosol and mitochondria (66).

At present, no reliable methods exist to measure redox states (NADH and NAD⁺ or NADH/NAD⁺ ratio) distinctly in cytosol and mitochondria or their transport fluxes in vivo (50). Commonly used indirect measurements of steady-state values for NADH/NAD⁺ are based on the equilibrium relationships of LDH in cytosol (84) and glutamate dehydrogenase in mitochondria (100) and may not reflect accurately the situation in vivo (50). Consequently, the specific roles of cytosolic and mitochondrial NADH/NAD⁺ on the regulation of energy metabolism in skeletal muscle during exercise have not been elucidated quantitatively. Specifically, two current issues have not been resolved with respect to skeletal muscle energy metabolism during exercise: 1) whether the shuttling activity of NADH and NAD⁺ is activated, and 2) whether lactate dynamics depend on the mitochondrial NADH/NAD⁺, which is related to mitochondrial oxygen consumption and oxygen availability.

In silico studies using validated computational models at the whole organ level can provide a complementary approach to in vivo experimental studies to investigate quantitatively the dynamic responses of NADH and NAD⁺ and corresponding control mechanisms during exercise of skeletal muscle. For this purpose, a physiologically based computational model of skeletal muscle energy metabolism is presented, which distinguishes capillary blood, cytosolic, and mitochondrial domains. The model also incorporates distinct capillary blood-cytosolic and cytosolic-mitochondrial transport processes together with key metabolic pathways of skeletal muscle energy metabolism (i.e., glycolysis, lipid metabolism, creatine kinase, TCA cycle, and oxidative phosphorylation). In addition, the model accounts for the macroscopic reversibility of the associated biochemical reactions. First, the model is validated with available experimental data on skeletal muscle energetics during ischemia and exercise. The model is then applied to analyze the role of mitochondrial NADH/NAD⁺ shuttling activity and intracellular glycogen stores on skeletal muscle energy metabolism during exercise.

The underlying hypothesis is that during the transition from rest to exercise, the cytosolic redox state is more sensitive to metabolic disturbance than the mitochondrial redox state. This hypothesis was tested by simulating skeletal muscle metabolic responses during moderate intensity exercise [60% maximal O₂ consumption (V̇o_2max)] with different transport (shuttling) rates of reducing equivalents (NADH and NAD⁺) between cytosol and mitochondria and different intracellular glycogen concentrations. The model simulations of exercise response are consistent with the hypothesis that the cytosolic redox state is much more sensitive to the changes in mitochondrial NADH/NAD⁺ shuttling activity and intracellular glycogen stores than the mitochondrial redox state. Furthermore, muscle lactate production is regulated primarily by the cytosolic redox state.

METHODS

Model Development

Dynamic mass balances.

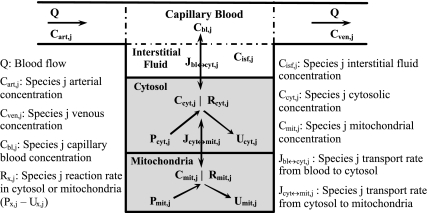
The governing dynamic mass balance equations are based on a model structure for skeletal muscle that distinguishes blood, cytosolic, and mitochondrial domains (Fig. 1). The capillary blood and tissue interstitial fluid (ISF) domains are assumed to be in phase equilibrium with each other so that the chemical species concentrations in these two domains can be considered equal, and the two domains can be referred to as the “blood” domain. The dynamic mass balance of a chemical species “j” in the blood domain has the following general form:

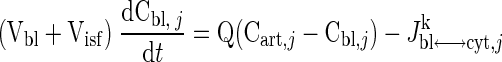(1)

where C_art,j is the arterial species concentration; C_bl,j is the capillary blood species concentration (equal to the venous species concentration, C_ven,j); V_bl + V_isf is the total effective volume of blood and ISF domains; Q is the regional blood flow; and J_bl↔cyt,j^k is the net mass transport flux of species j between blood and cytosol associated with passive (k = p) or facilitated (k = f) transport. Similarly, the dynamic mass balances of the species j in cytosol and mitochondria are given by

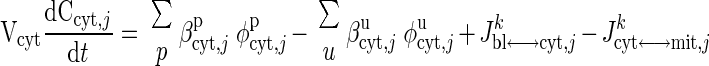(2)

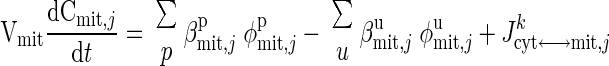(3)

where C_x,j (x = cyt, mit) is the species concentrations in cytosol or mitochondria; V_x (x = cyt, mit) is the effective volume occupied by cytosol or mitochondria; φ_x,j^p and φ_x,j^u are the reaction fluxes that produce and utilize species j in cytosol or mitochondria, respectively (Fig. 2), and β_x,j^p and β_x,j^u (x = cyt, mit) are the corresponding stoichiometric coefficients; and J_cyt↔mit,j^k is the net mass transport flux of species j between cytosol and mitochondria.

Fig. 1.

Schematic diagram of the structure of the model for blood-tissue cell exchange and cellular metabolism in skeletal muscle. The compartments are assumed to be perfectly mixed, and the capillary blood and tissue interstitial fluid (ISF) domains are assumed to be in phase-equilibrium with each other so that C_isf,j = C_bl,j = C_ven,j for any chemical species j. The tissue cells domain is further compartmentalized into the cytosolic and mitochondrial domains with the chemical species having distinct dynamics in these 2 subcellular domains. A total of 9 species [glucose (Glc), lactate (Lac), pyruvate (Pyr), alanine (Ala), free fatty acid (FFA), glycerol (Glr), CO₂, O₂, and H⁺ (protons)] undergo blood-cytosol exchange, and 11 species [Pyr, fatty acyl-CoA (FAC), CoA, reduced nicotinamide adenine dinucleotide (NADH), oxidized nicotinamide adenine dinucleotide (NAD⁺), ATP, ADP, inorganic phosphate (P_i), CO₂, O₂, and H⁺] undergo cytosol-mitochondria exchange.

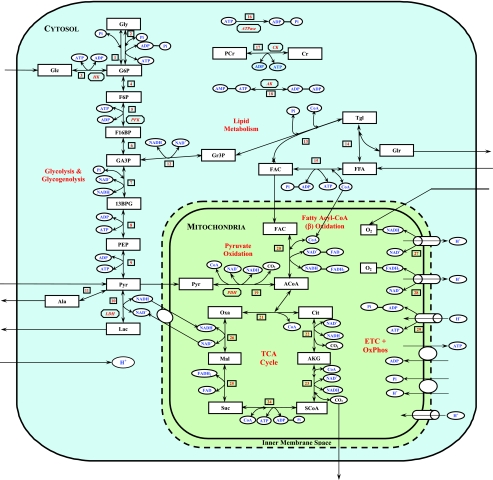
Fig. 2.

Schematic diagram of biochemical pathways depicting various chemical reactions and species involved in the cellular metabolism of skeletal muscle. The reactions and species are further compartmentalized into the cytosolic and mitochondrial reactions and species. Gly, glycogen; G6P, glucose-6-phosphate; F6P, fructose-6-phosphate; F16BP, fructose-1,6-biphosphate; GA3P, glyceraldehyde-3-phosphate; 13BPG, 1,3-biphosphate glycerate; PEP, phosphoenolpyruvate; Gr3P, glycerol-3-phosphate; Tgl, triglycerides; ACoA, acetyl-CoA; Cit, citrate; AKG, α-ketogluterate; SCoA, succinyl-CoA; Suc, succinate; Mal, malate; Oxa, oxaloacetate; CoA, coenzyme-A (free); PCr, phosphocreatine; Cr, creatine; FADH₂, reduced flavin adenine dinucleotide; FAD, oxidized flavin adenine dinucleotide; CK, creatine kinase; AK, adenylate kinase; HK, hexokinase; PFK, phosphofructokinase; LDH, lactate dedrogenase; PDH, pyruvate dehydrogenase. ETC+OxPhos, electron transport chain plus oxidative phosphorylation.

The derivations of dynamic mass balance equations for O₂ and CO₂, which have several special components (23, 26), are presented in Appendix A of Supplemental Materials. (Supplemental data for this article is available online at the American Journal of Physiology-Cell Physiology website.) Specific dynamic mass balance equations for all chemical species are presented in Appendix B of Supplemental Materials. Steady-state flux relationships are obtained by setting the time derivatives of these mass balances to zero. Under resting conditions, special conditions apply that can be used to simplify these steady-state flux relationships (Appendix C, Supplemental Materials).

Transport fluxes.

The interdomain species transport may be passive or carrier mediated (facilitated). The net transport flux of species j between domains x and y for passive diffusion is

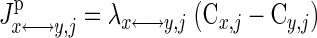(4)

and for facilitated transport (Appendix D, Supplemental Materials) is

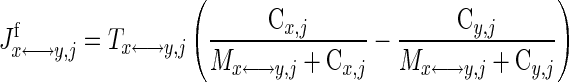(5)

where λ_x↔y,j is the effective permeability-surface area product for passive diffusion; T_x↔y,j is the maximal transport rate for facilitated transport; and M_x↔y,j is the corresponding Michaelis-Menten (MM) constant. In this study, the model considers passive and facilitated blood-cytosol transport of glucose, pyruvate, lactate, free fatty acid (FFA), alanine, glycerol, O₂, CO₂, and protons and cytosol-mitochondria transport of O₂, CO₂, pyruvate, fatty acyl-CoA, CoA, P_i, ATP, ADP, NADH, NAD⁺, and protons. Facilitated transport between blood and cytosol is assumed for glucose, pyruvate, lactate, and FFA (18, 47, 54, 106). Facilitated transport between cytosol and mitochondria is assumed for pyruvate, fatty acyl-CoA, CoA, P_i, and protons.

In skeletal muscle, the apparent transport of NADH from cytosol to mitochondria in exchange for NAD⁺ occurs through the malate-aspartate shuttle and glycerol phosphate shuttle via oxidative-reductive reactions and enzymatic transporters (29, 72). The ATP-ADP exchange between cytosol and mitochondria depends on the adenine nucleotide translocase (ANT), an antiporter on the mitochondrial inner membrane (29, 72). In this study, the effective transport (exchange) fluxes of NADH for NAD⁺ and ATP for ADP across the mitochondrial inner membrane are represented by phenomenological equations (104, 105), which depend on the compartmental redox states (RS = NADH/NAD⁺) and phosphorylation states (PS = ATP/ADP):

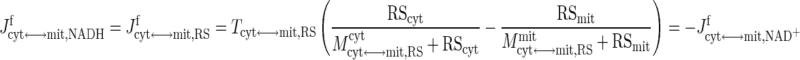(6)

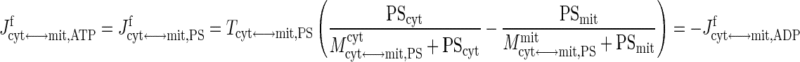(7)

where T_cyt↔mit,j are the maximal transport rate parameters and M_cyt↔mit,j^cyt and M_cyt↔mit,j^mit are the corresponding MM constants. Note that these transport flux expressions involve two distinct MM parameters, since these flux expressions characterize antiporters. The phenomenological MM parameters include the effect of mitochondrial membrane potential (ΔΨ).

Metabolic fluxes.

The present model differs significantly from our previous models of cardiac and skeletal muscle energy metabolism (26–28, 102–105) in that the biochemical reactions governing energy metabolism (Fig. 2) are assumed to be reversible with their fluxes satisfying Haldane relationships. For a multisubstrate, multiproduct enzymatic reaction, the net reaction flux in the direction of product formation is derived from a simplified one-step binding model with reversible enzyme kinetics (87) (Appendix E, Supplemental Materials):

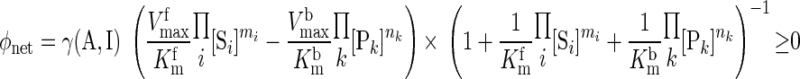(8)

where γ(A, I) represents a controller function that accounts for the effects of other regulators (activators, A, or inhibitors, I) of the reaction; [S_i] and [P_k] denote concentrations of substrates and products and m_i and n_k are the corresponding stoichiometries; and K_m^f and K_m^b are the MM constants for forward and backward reactions and V_max^f and V_max^b are the corresponding maximal reaction rates. The flux-concentration relationship for each metabolic reaction is given in Appendix F of Supplemental Materials.

Several metabolic reaction fluxes are regulated by specific activators (A) and inhibitors (I). The effects of such regulators are accounted for by modifying the reaction fluxes appropriately:

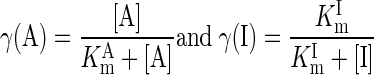(9)

where K_m^Ctrl = K_m^A or K_m^I is the K_m value for the controller A or I. The activation control applies to reactions involving 1) C_cyt,AMP/C_cyt,_ATP with glycogen phosphorylase, 2) C_cyt,AMP with phosphofructokinase, 3) C_cyt,F16BP (fructose-1,6-biphosphate) with pyruvate kinase, and 4) C_mit,ADP/C_mit,ATP with pyruvate dehydrogenase, citrate synthase, and aconitase; the inhibition control applies to the hexokinase reaction where C_G6P (glucose-6-phosphate) is an inhibitor (Appendix F of Supplemental Materials). For reactions that do not have special controllers, γ = 1.

Thermodynamic constraints.

Each reaction flux must satisfy thermodynamic constraint based on the entropy inequality (11–13):

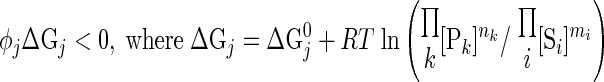(10)

where ΔG_j is the transformed reaction (Gibbs) free energy associated with the reaction flux j and ΔG_j⁰ is the standard reaction (Gibbs) free energy; R is the universal gas constant; and T is the absolute temperature. Furthermore, at thermodynamic equilibrium (ΔG_j = 0 and φ_j = 0), each reaction flux must satisfy the Haldane relationship:

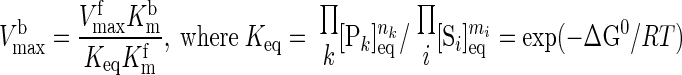(11)

K_eq is the apparent equilibrium constant of the reaction. With this thermodynamic constraint, the reaction flux expression (Eq. 8) simplifies to

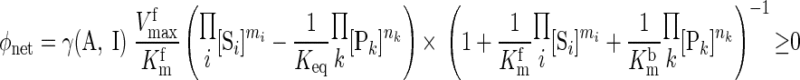(12)

Incorporation of protons in reaction rates.

In this model, the effect of protons is incorporated with specific reaction fluxes in each domain. We assume facilitated transport of protons between blood and cytosol and between cytosol and mitochondria according to Eq. 5. The reaction equilibrium coefficients (K_eq), which are functions of pH (3), affect the V_max parameters (Eq. 11), which affect the reaction fluxes (Eq. 8). We defined modified equilibrium constants for cytosolic and mitochondrial reactions (K_eq,cyt and K_eq,mit) for use in the dynamic reaction fluxes:

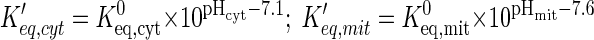(13)

where 7.1 is pH in the cytosolic domain at rest and 7.6 is pH in the mitochondrial domain at rest; K_eq,cyt⁰ and K_eq,mit⁰ are reaction equilibrium constants in cytosol and mitochondria at rest.

Protons are also transported in and out of the mitochondrial matrix via the redox-linked proton pumps located on the electron transport chain and via proton leak (Fig. 2). The proton effluxes and influxes via proton pumps are governed by the fluxes of oxidative phosphorylation and ATP synthesis (Reactions 27, 28, and 29, Appendix F, Supplemental Materials). The proton leak flux is represented by a phenomenological equation following Zhou et al. (60, 105):

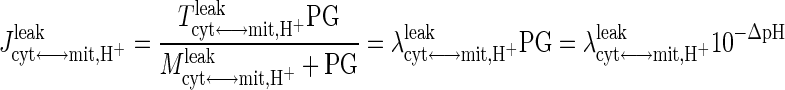(14)

where Tcyt↔mit,H+leak is the maximal H+ leak rate coefficient and Mcyt↔mit,H+leak is the corresponding MM parameter; PG = Ccyt,H+/Cmit,H+ = 10−(pHcyt − pHmit) = 10−ΔpH is the H+ gradient across the inner mitochondrial membrane; λcyt↔mit, H+leak = Tcyt↔mit, H+leak/Mcyt↔mit,H+leak is the effective H+ leak rate coefficient when Mcyt↔mit,H+leak ≫ PG; and Jcyt↔mit,H+leak,0 = 10φO2↔H2O, NADH0 + 6φO2↔H2O,FADH20 − 3φADP↔ATP0 is the effective H+ leak flux at normal, resting steady state (Appendix C, Supplementary Materials).

Parallel activation mechanism in response to exercise.

The basic assumption to simulate skeletal muscle energy metabolism during exercise is that the transport and reaction fluxes can be activated in parallel (26, 55, 57, 59, 102, 103). The activation factors associated with the transport and reaction fluxes can be incorporated in the flux expressions.

In skeletal muscle, recruitment of muscle fibers during the transition from rest to exercise increases active muscle volume (V_mus), blood flow (Q), and oxygen utilization (U_O2). In this model, we assume that the work rate (WR) changes from one steady state to another exponentially with a very short time constant, which is an approximate step change. Each physiological muscle variable Γ ∈ (V_mus, Q, U_O2) is assumed to change as a linear function of WR (53, 82). After a step increase in WR at time t₀, the muscle variables (V_mus, Q, and U_O2) increase exponentially with a time constant τ_Γ (distinct for each muscle variable Γ, Table 1):

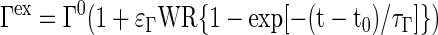(15)

where ɛ_Γ is an exercise enhancement coefficient that depends on the muscle variable Γ (Table 1). When WR = 0, or at rest (t ≤ t₀), the muscle variable is Γ⁰.

Table 1.

Miscellaneous physiological parameter values in the computational model of skeletal muscle energy metabolism

Parameter	Definition	Value	Reference
Vmus	Volume of active muscle (at rest)	5.0 kg wet weight	Estimated
Vbl + Visf	Volume of capillary blood + tissue interstitial fluid	0.2Vmus	Calculated
Vcyt	Volume of cytosol	0.72Vmus	Calculated
Vmit	Volume of mitochondria	0.08Vmus	Calculated
Q	Muscle blood flow at rest for 2 legs	0.9 l/min	1, 76
Qisch	Muscle blood flow during ischemia for 2 legs	0.18 l/min	Estimated
ɛVmus	Exercice enhancement coefficient of muscle volume	0.004 W−1	78
ɛQ	Exercise enhancement coefficient of blood flow	0.0556 W−1	8
ɛUO2	Exercise enhancement coefficient of O2 consumption rate	0.166 W−1	8
τVmus	Time constant of muscle volume change in response to exercise due to capillary recruitment	0.4 min	Correlated
τQ	Time constant of blood flow change in response to exercise	0.5 min	30
τUO2	Time constant of O2 consumption rate change in response to exercise	0.4 min	Correlated
τTbl↔cyt, τλbl↔cyt	Time constant of blood-cytosol transport rate coefficients in response to exercise	0.5 min	Correlated
τTcyt↔mit, τλcyt↔mit	Time constant of cytosolic-mitochondrial transport rate coefficients in response to exercise	0.4 min	Correlated
τVmax	Time constant of metabolic flux rate coefficients in response to exercise	0.4 min	62, 63
βcyt	Buffering capacity in cytosol (for protons)	6.65 mmol/pH	Correlated
βmit	Buffering capacity in mitochondria (for protons)	25 mmol/pH	9, 25, 60
CIMM	Capacitance of the inner mitochondrial membrane	6.75E−3 mmol/mV	9, 25

Activation mechanisms associated with exercise responses can be represented by phenomenological expressions for a subset of rate parameters Ω ∈ (λ, T_max, V_max) of the transport and metabolic fluxes linearly related to WR:

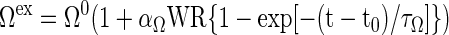(16)

where the activation coefficient α_Ω depends on the specific external effector (e.g., the effects of Ca²⁺, catecholamine, or hormones). The time constant τ_Ω, related to cellular processes, is usually smaller than the time constant τ_Γ for a muscle variable change (Table 1).

Simulation and Parameter Estimation Strategy

Database.

The information needed to simulate metabolic responses to exercise includes effective domain volumes, blood flow, chemical species concentrations, transport fluxes, and metabolic fluxes under resting steady-state conditions. From the literature, some model parameters, including the domain volumes, can be evaluated (Table 1). The volume of tissue cells (V_tis = V_cyt + V_mit) is related to the volume of cytosol as V_cyt = 0.9V_tis. Also, average species concentrations in the tissue cells at rest (C_tis,j⁰) are obtained from the literature (Table 2). These average values are converted from a dry weight (dw) basis to a wet weight (ww) basis using the formula C_ww = C_dw/4 (76). To relate cytosolic and mitochondrial species concentrations of the model to tissue species concentrations from experiments, we make a wet weight mass balance:

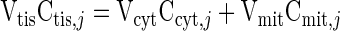(17)

In addition, we specify the cytosolic and mitochondrial mass fractions of each cellular species (Table 2) according to

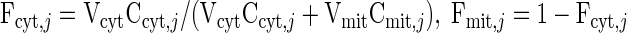(18)

Consequently, the resting steady-state species concentrations in the cytosol and mitochondria can be estimated (Table 2).

Table 2.

Species concentrations in muscle tissue cells from the literature and their compartmentalization (distribution) into cytosol and mitochondria at normal, resting steady-state conditions

Species	Tissue Cells (100%)		Cytosol (90%)		Mitochondria (10%)
	Concentration, mmol/kg cell ww	Reference	Mass, %	Concentration, mmol/kg Cytosolic ww	Mass, %	Concentration, mmol/kg Mitochondrial ww
Glc	0.5	34, 35, 48, 76	100	0.5556	0	0
Pyr	0.05	34, 35, 48, 75	95	0.0528	5	0.025
Lac	0.78	34, 35, 48, 76	100	0.8667	0	0
Ala	1.3	17, 45, 83	100	1.4444	0	0
Glr	0.065	74, 76, 94	100	0.0722	0	0
FFA	0.45	74, 76, 94	100	0.50	0	0
CO2 (F)	N/A	24	N/A	1.403 (46 mmHg)	N/A	1.525 (50 mmHg)
O2 (F)	N/A	24	N/A	0.0338 (25 mmHg)	N/A	0.027 (20 mmHg)
H+	N/A	80	N/A	10−7.1+3 (pHcyt = 7.1)	N/A	10−7.6+3 (pHcyt = 7.6)
Gly	95.0	35, 74, 76, 83, 94	100	105.56	0	0
G6P	0.25	48, 74, 76, 84	100	0.2778	0	0
F6P	0.044	39, 40, 48	100	0.0486	0	0
F16BP	0.06	39, 40, 48	100	0.0667	0	0
GA3P	0.08	64	100	0.0889	0	0
13BPG	0.08	64	100	0.0889	0	0
PEP	0.0049	64	100	0.00539	0	0
Tgl	15.0	46, 52, 75	100	16.667	0	0
Gr3P	0.15	48, 67	100	0.167	0	0
FAC	0.0035	94, 97	95	0.00369	5	0.00175
PCr	21.0	35, 75, 76, 83	100	23.333	0	0
Cr	10.5	35, 75, 76, 83	100	11.667	0	0
ATP (T)	6.2	48, 74–76	86	5.924	14	8.68
ADP (T)	0.8	48, 74–76	2	0.0178	98	7.84
AMP (T)	0.04	48, 74–76	100	0.0444	0	0
Pi	2.75	39, 75	95	2.903	5	1.375
CoA	0.02	45, 74, 76	80	0.0178	20	0.04
NADH	0.05	39, 75, 83, 84	0.5	0.2778E−3	99.5	0.4975
NAD+	0.45	39, 75, 83, 84	30	0.15	70	3.15
ACoA	0.002	45, 74, 76	0	0	100	0.02
Cit	0.095	34, 35, 75, 83	0	0	100	0.95
AKG	0.0125	34, 35, 75, 83	0	0	100	0.125
SCoA	0.125	34, 35, 75, 83	0	0	100	1.25
Suc	0.095	34, 35, 75, 83	0	0	100	0.95
Mal	0.095	34, 35, 75, 83	0	0	100	0.95
Oxa	0.0024	34, 35, 75, 83	0	0	100	0.0024
FADH2	0.024	105	0	0	100	0.24
FAD	0.212	105	0	0	100	2.12

The tissue cell species concentrations (mM or mmol/kg tissue cell ww, where ww denotes wet weight) are converted from the literature data (mmol/kg tissue cell dw, where dw denotes dry weight) by multiplying a factor of 0.25 kg tissue cell dw/kg tissue cell ww (76) (for unit density, kg ww = liter and mmol/kg ww = mmol/l = mM). The cytosolic and mitochondrial species concentrations are calculated from the tissue cell species concentrations according to their approximate volumes of distributions and mass fractions. The mass fractions are set to have reasonable compartmentalized species concentrations and mass action ratios consistent with available information from the literature: C_cyt,Lac/C_cyt,Pyr = 16.4, C_cyt,NAD+/C_cyt,NADH = 540, C_mit,NAD+/C_mit,NADH = 6.3, C_cyt,PCr/C_cyt,Cr = 2, C_cyt,ATP/C_cyt,ADP = 333.2, C_mit,ATP/C_mit,ADP = 1.11, K_LDH = (C_cyt,Lac/C_cyt,Pyr) × (C_cyt,NAD+/C_cyt,NADH) = 8856, K_CK = (C_cyt,Cr/C_cyt,PCr) × (C_cyt,ATP/C_cyt,ADP) = 166.6, and K_AK = (C_cyt,ADP)²/(C_cyt,ATPC_cyt,AMP) = 1.2E−3. N/A, not applicable; pH_cyt, cytosolic pH. CO₂ (F), and O₂ (F), free CO₂ and O₂; ATP (T), ADP (T), and AMP (T), total ATP, ADP, and AMP. See legend to Fig. 2 for species definitions.

To determine the resting steady-state concentration of species j in venous blood (Table 3), we use the reported uptake-release rate (UR_j⁰) and arterial blood species concentration (C_art,j⁰):

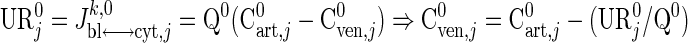(19)

Table 3.

Blood species concentrations and muscle tissue cells uptake-release rates from the literature at normal, resting steady-state conditions

Species	Cart, mM	Cven, mM	UR Rate, mmol/min	Reference
Glc	5.0	4.7833	0.195	17, 35, 52, 76
Pyr	0.075	0.0617	0.012	17, 35, 52, 76
Lac	0.5	0.6	−0.09	17, 35, 52, 76
Ala	0.25	0.322	−0.065	17, 34, 35
Glr	0.04	0.0489	−0.008	52, 76, 94, 95
FFA	0.7	0.619	0.073	52, 76, 94, 95
CO2 (T)	23.405	25.5	−1.885 (−41.66 ml/min)	17, 35, 52
CO2 (F)	1.22 (40 mmHg)	1.33 (43.61 mmHg)	N/A	23, 24
O2 (T)	9.235	6.548	2.418 (54.0 ml/min)	17, 35, 52
O2 (F)	0.135 (100 mmHg)	0.049 (36.32 mmHg)	N/A	23, 24
H+	10−7.4+3 (pHart = 7.4)	10−7.32 + 3 (pHven = 7.32)	−7.25E−6	Calculated

A resting blood flow of 0.9 l/min corresponding to the 2-leg quadriceps femoris muscle is used to calculate the venous species concentrations (C_ven) from the arterial species concentrations (C_art) and uptake-release (UR) rates or arteriovenous differences. pH_ven, venous pH. Some of UR rates are tuned further to satisfy the physiological constraints below. UR_CO2 = J_bl↔cyt,CO2^p = J_{cyt↔mit,CO2}^p = −(φ_Pyr↔ACoA + φ_Cit↔AKG + φ_AKG↔SCoA) = −(6UR_Glc + 3UR_Pyr + 3UR_Lac + 3UR_Ala + 3UR_Glr + 16UR_FFA), RQ = −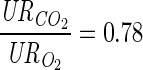, UR_O2 = J_bl↔cyt,O2^p = J_cyt↔mit,O2^p = 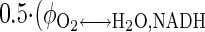+ 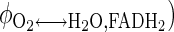= 6UR_Glc + 2.5UR_Pyr + 3UR_Lac + 2.5UR_Ala + 3.5UR_Glr + 23UR_FFA

URH+ = Jbl↔cyt,H+f = Jcyt↔mit,H+f − 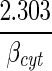Ccyt,H+ (+φGlc↔G6P + φF6P↔F16BP + φGA3P↔13BPG − φPEP↔Pyr−φPyr↔Lac + 3φTgl↔Glr − φGA3P↔Gr3P + 2φFFA↔FAC + φATP↔ADP − Jcyt↔mit,H+leak), Jcyt↔mit,H+f = − 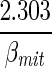Cmit,H+ (φPyr↔ACoA + 7φFAC↔ACoA + φACoA↔Cit + φMal↔Oxa − φO2→H2O,NADH − φADP↔ATP).

Estimation under steady-state conditions.

Resting steady-state flux balances provide physiological constraints for estimating model parameters associated with blood-cytosol and cytosol-mitochondria transport fluxes as well as cellular reaction fluxes. From the steady-state species mass balances in the capillary blood, cytosol, and mitochondrial domains, we find

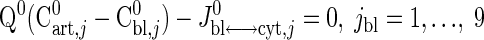(20a)

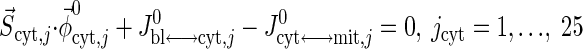(20b)

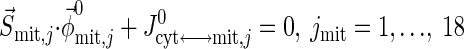(20c)

where S→_x,j (x = cyt, mit) is the stoichiometry vector and φ→_x,j⁰ (x = cyt, mit) is the corresponding reaction flux vector involving the species j. Values of Q⁰, C_art,j⁰, and C_bl,j⁰ from the literature (Table 3) are used to solve Eq. 20a for J_bl↔cyt,j⁰ and vice versa. Next, using Eqs. 20b and 20c, we evaluate the reaction fluxes φ_cyt,j⁰ and φ_mit,j⁰ and transport fluxes J_cyt↔mit,j⁰ sequentially (Appendix C, Supplemental Materials), the values for which are presented in Tables 3–5.

Table 5.

Metabolic reaction standard Gibbs free energies, flux rates at resting steady-state, flux rates at end of exercise, and the corresponding activation coefficients during exercise

Metabolic Reactions	ΔG0, kJ/mol	ϕ0, mmol/min	ϕee, mmol/min	αφex, W−1
1. Glycogen synthase	−31.626	0.25	0.2063	0
2. Glycogen phosphorylase	−4.404	0.25	0.720	0.512
3. Hexokinase	−24.41	0.195	19.345	0
4. Phosphoglucose isomerase	3.18	0.195	5.999	0.235
5. Phosphofructokinase	−23.24	0.195	6.009	0.235
6. Aldolase + TPI	30.7	0.195	6.029	0.235
7. GA3P dehydrogenase	1.21	0.382	12.06	0.235
8. Phosphoglycerate kinase	−5.85	0.382	12.057	0.235
9. Pyruvate kinase	−28.89	0.382	12.056	0.235
10. Lactate dehydrogenase	−23.9	0.09	1.0994	0
11. Alanine aminotransferase	−20.0	0.065	0.0056	0
12. Lipases	−5.0	0.008	0.0241	0
13. Gr3P dehydrogenase	−50.07	0.008	0.0071	0
14. Acyltransferase	−30	0.008	0.271	0
15. ACoA synthetase	−32.5	0.097	223.15	0.0193
16. ATPase	−36.03	11.5115	−0.0062	0.166
17. Adenylate kinase	0.0	0.0	0.253	0
18. Creatine kinase	−12.5	0.0	0.1022	0
19. Pyruvate dehydrogenase	−38.64	0.239	8.908	1.030
20. β-Oxidation	−1097.12	0.073	0.293	0.0141
21. Citrate synthase	−36.61	0.823	11.238	0.0797
22. Isocitrate dehydrogenase	2.18	0.823	11.234	0.0797
23. AKG dehydrogenase	−37.08	0.823	11.234	0.0797
24. SCoA synthetase	1.26	0.823	11.233	0.0797
25. Succinate dehydrogenase	−3.62	0.823	11.234	0.0797
26. Malate dehydrogenase	28.83	0.823	11.238	0.0797
27. Complex I + III + IV	−224.84	3.503	55.594	0.253
28. Complex II + III + IV	−156.79	1.334	13.276	0.253
29. ATP synthase	36.03	10.758	208.39	0.0365

The standard Gibbs free energies (ΔG⁰; compiled from Ref. 4) provide the equilibrium constants (K_eq) for metabolic reactions for use in Haldane constraints. The resting metabolic reaction flux rates (ϕ⁰ at steady state; ϕ^ee at the end of exercise, t = 15 min) are based on a flux balance analysis at resting steady-state (Appendix C, Supplemental Materials). The activation coefficients (α_ϕ^ex) are determined from the optimal parameter estimation procedure using the data from muscle exercise experiments. The superscript ex denotes exercise, and ee denotes the end of exercise. TPI, triosephosphate isomerase.

The resting steady-state transport fluxes (J_bl↔cyt,j⁰, J_cyt↔mit,j⁰) are used to evaluate the transport rate coefficients (λ, T_max). With the values of these fluxes and resting steady-state species concentrations from Tables 2 and 3, we estimate the passive transport rate coefficients λ_x↔y,j from Eq. 4. To evaluate the facilitated transport coefficients T_x↔y,j, we set the values of M_bl↔cyt,j from the literature and M_cyt↔mit,j to the corresponding species cytosolic or mitochondrial concentrations at resting steady-state values from Tables 2 and 3. With the species concentrations, MM parameters (M_bl↔cyt,j, M_cyt↔mit,j), and transport fluxes (J_bl↔cyt,j⁰, J_cyt↔mit,j⁰), we solve for T_x↔y,j from Eq. 5. The transport fluxes at resting steady-state and the corresponding transport parameter estimates are summarized in Table 4. These parameter estimates are invariant and apply to all model simulations.

Table 4.

Optimal model parameter values for the interdomain transport fluxes between blood and cytosol and between cytosol and mitochondria determined using the optimal parameter estimation procedure

Species	Blood-Cytosol Passive or Carrier-Mediated (Facilitated) Transport Fluxes and Parameters
	λbl↔cyt, ml/min	Tbl↔cyt, mmol/min	Mbl↔cyt, mM	Jbl↔cyt(0), mmol/min	Jcyt↔mit,ee mmol/min	αbl↔cytex, W−1
Glc	N/A	0.411	2.5	0.195	0.401	0.0151
Pyr	N/A	1.513	1.0	0.012	−0.043	0.00044
Lac	N/A	2.217	5.0	−0.09	−1.1	0.0033
Ala	0.0579	N/A	N/A	−0.065	−0.0723	0
Glr	0.3432	N/A	N/A	−0.008	−0.0082	0
FFA	N/A	1.491	1.0	0.073	0.257	0.0244
CO2	25.818	N/A	N/A	−1.885	−31.37	0.242
O2	158.327	N/A	N/A	2.42	24.43	0.242
H+	N/A	5.84E−5	4.78E−5	−7.25E−5	−8.39E−5	0.0556

Species	Cytosol-Mitochondria Passive or Carrier-Mediated (Facilitated) Transport Fluxes and Parameters
	λcyt↔mit, ml/min	Tcyt↔mit, mmol/min	Mcyt↔mit, mM	Jcyt↔mit(0), mmol/min	Jcyt↔mitee, mmol/min	αcyt↔mitex, W−1
O2	358.30	N/A	N/A	2.42	34.43	0.242
CO2	15.45	N/A	N/A	−1.8885	−31.37	0.242
Pyr	N/A	1.338	0.0528	0.239	8.91	0.166
FAC	N/A	0.777	0.00175	0.073	0.292	0.0452
Pi	N/A	64.856	1.375	11.582	219.6	0.132
CoA	N/A	0.38	0.04	−0.073	−0.289	0.166
ATP/ADP	N/A	34.745	666.367*	−11.582	−219.6	0.132
			0.554*
NADH/NAD+	N/A	0.384	0.00062*	0.284	10.938	0.192
			15.794*
H+	N/A	1.06E−4	2.51E−05	2.75E−5	6.5E−4	0.166
H+ leak	3.402	N/A	N/A	10.76	10.82	0

The transport parameters (λ, T_max, M_m) are obtained using the data from resting steady-state and muscle ischemia experiments, and the transport flux activation parameters during exercise (α_j) are obtained using the data from muscle exercise experiments. The resting blood-cytosol species transport fluxes satisfy J_bl↔cyt = UR = Q(C_art − C_ven) at resting steady-state conditions. The resting cytosol-mitochondria species transport fluxes J_cyt↔mit are based on a flux balance analysis at resting steady-state conditions (Appendix C, Supplemental Materials). The superscript ex denotes exercise, and ee denotes the end of exercise. An asterisk denotes the antiporter, so the transport flux is characterized by two M_m values.

The reaction parameters (K_m^f, K_m^b, K_m^Ctrl, V_max^f, V_max^b) are estimated to fit the model outputs to the available dynamic data on muscle ischemia (48). For this dynamical parameter estimation procedure, preliminary estimates (initial guesses) of the reaction rate coefficients (V_max^f, V_max^b) are obtained using Eqs. 11 and 12. This requires the values of resting steady-state metabolic flux rates (φ_cyt,j⁰, φ_mit,j⁰) and standard Gibbs free energies (ΔG_cyt,j⁰, ΔG_mit,j⁰) of the metabolic reactions (Table 5) as well as the species concentration values (Table 2). Also, we assume K_m^f ≈ Σ_i[S_i]_rest^m_i, K_m^b ≈ Σ_j[P_j]_rest^n_j, and K_m^Crl = [Ctrl]_rest, where Ctrl is A (activator) or I (inhibitor).

Estimates using ischemic response data.

From in vivo studies of ischemia (∼80% blood flow reduction) in humans, muscle tissue concentrations of many chemical species have been measured (48). The optimal parameter estimates of the reaction parameters (K_m^f, K_m^b, K_m^Ctrl, V_max^f, V_max^b) are obtained (Table 6) by minimizing the sum of squared differences between the relative concentrations from experimental data [C_j^data(t_i)] and corresponding model outputs [C_j^mod(t_i)]:

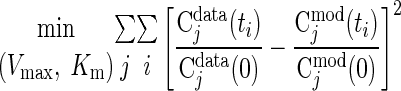(21)

where

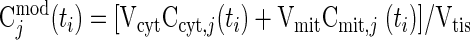(22)

The resting steady-state flux-concentration relationships serve as equality constraints. As inequality constraints in the minimization, we specified upper and lower bounds on all parameters values to keep them in a feasible domain that is positive. Furthermore, the thermodynamic inequality constraint (Eq. 10) and Haldane equality constraint (Eq. 11) are incorporated into the optimization procedure to reduce the number of unknown model parameters. This type of constraint-based, large-scale parameter estimation procedure was established previously (28).

Table 6.

Optimal model parameter values for metabolic reaction fluxes determined from the optimal parameter estimation procedure using the data from muscle ischemia experiments

Metabolic Reactions	Vmaxf, mmol/min	Vmaxb, mmol/min	Kmf	Kmb	KmCtrl
1. Glycogen synthase	2.78E+01	9.45E−07	1.74E+04	1.58E+02	0
2. Glycogen phosphorylase	2.54E−01	3.50E+06	3.06E−03	2.93E+05	1.87E−05
3. Hexokinase	5.90E−01	4.34E−12	3.29E+00	3.93E−07	2.78E+01
4. Phosphoglucose isomerase	1.12E+00	5.33E−01	2.78E−01	4.86E−02	0
5. Phosphofructokinase	1.76E+00	5.56E−11	2.88E−01	9.42E−08	9.35E−02
6. Aldolase + TPI	2.67E+00	3.30E−01	6.67E−01	7.90E−02	0
7. GA3P dehydrogenase	1.15E+00	7.37E−08	3.87E−02	1.96E−09	0
8. Phosphoglycerate kinase	1.19E+00	4.07E−02	1.58E−03	3.19E−02	0
9. Pyruvate kinase	1.22E+00	3.36E−02	7.61E−09	3.13E−01	2.67E−03
10. Lactate dehydrogenase	9.76E+44	7.20E−03	1.17E+23	1.30E−15	0
11. Alanine aminotransferase	1.97E−01	1.83E−03	5.28E−02	1.44E+00	0
12. Lipases	2.40E−02	7.43E−19	1.67E+01	4.52E−15	0
13. Gr3P dehydrogenase	2.49E−02	9.35E−04	1.96E−09	2.51E−02	0
14. Acyltransferase	3.11E−02	7.09E−03	8.42E−09	2.73E−04	0
15. ACoA synthetase	2.91E−01	1.54E−19	3.12E−01	6.21E−14	0
16. ATPase	2.75E+01	3.29E−11	5.92E+00	1.04E−05	0
17. Adenylate kinase	2.00E+02	4.01E−02	1.32E+02	3.18E−05	0
18. Creatine kinase	2.00E+02	6.65E+00	2.97E−04	2.07E+01	0
19. Pyruvate dehydrogenase	1.00E+00	9.47E−12	3.15E−03	3.81E−07	3.61E−01
20. β-Oxidation	1.47E−01	7.84E−189	4.67E−04	6.00E−06	0
21. Citrate synthase	3.46E+00	1.18E−09	4.80E−04	9.55E−07	3.61E−01
22. Isocitrate dehydrogenase	3.52E+00	6.53E−02	2.99E+00	9.48E−02	3.61E−01
23. AKG dehydrogenase	2.47E+00	2.12E−05	1.58E−02	9.48E−01	0
24. SCoA synthetase	2.50E+00	2.50E−02	1.35E+01	3.30E−01	0
25. Succinate dehydrogenase	2.48E+00	1.74E−02	2.01E+00	2.28E−01	0
26. Malate dehydrogenase	2.47E+00	1.91E−06	2.99E+00	3.00E−07	0
27. Complex I + III + IV	1.05E+32	1.64E−03	2.05E−06	3.15E+00	0
28. Complex II + III + IV	1.59E+19	8.43E−07	3.94E−02	2.12E+00	0
29. ATP synthase	1.79E−08	3.49E+00	2.71E−04	8.68E+00	0

As shown in Appendixes E and F, Supplemental Materials, each reversible metabolic reaction flux expression contains 4 kinetic parameters (5 if an additional control mechanism is incorporated) constrained by Haldane relationships (thermodynamic constraints) and resting steady-state flux-concentration relationships.

Estimates using exercise response data.

The next step is to estimate the activation coefficients α_Ω, Ω ∈ (λ, T_max, V_max), using data from studies of the metabolic responses of normal humans to exercise (15-min steady-state cycling at moderate intensity). The physiological enhancement coefficients ɛ_Γ, Γ ∈ (V_mus, Q, U_O2), and time constants τ_Ω and τ_Γ associated with exercise can be evaluated directly from the experimental data (Table 1) (8, 78). We assume that the values of the transport parameters (λ, T_max, M_m) and reaction parameters (V_max, K_m) are the same as those determined from the ischemia estimation. From exercise studies, tissue concentrations of many chemical species and blood-cytosol transport fluxes are available for comparison.

The exercise activation coefficients α_Ω may be positive or zero. The reactions that are not activated (α_Ω = 0) during exercise include hexokinase, glycogen synthase, glycerol-3-phosphate dehydrogenase, acyltransferase (triglyceride synthesis) (82), lipase, lactate dehydrogenase (LDH) (49, 84), creatine kinase (CK) (93), adenylate kinase, alanine aminotransferase (31, 32), and proton leak (51). The subset of activation coefficients most likely to be positive were determined based on the key cellular reaction fluxes associated with exercise. The same values of α_Ω > 0 were assigned according to subgroups with the same reaction pathway: glycolysis from fructose-6-phosphate (F6P) to pyruvate, TCA cycle, and oxidative phosphorylation. In addition to the exercise activation coefficients associated with reaction fluxes (Table 5), activation coefficients are also associated with the transport fluxes (Table 3).

The optimal estimates of these activation coefficients are those that give the best least-squared fit of the model-simulated outputs to the available species concentration and transport flux data during exercise with the objective function defined by

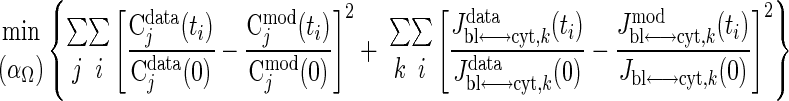(23)

where C_j^mod(t_i) is determined using Eq. 22. For practical implementation, we restrict the values of activation coefficients to the interval (0.01, 10). The data consist of tissue concentrations for glycogen and ATP (76); glucose, G6P, F6P, pyruvate, and lactate (74); tissue NADH/NAD⁺ (75), phosphocreatine (PCr), and creatine (Cr) (98); and transport fluxes of lactate and glucose (76).

Numerical methods.

The mathematical model of skeletal muscle energy metabolism consists of a large system of nonlinear, stiff, ordinary differential equations and a large number of nonlinear, algebraic flux equations. Numerical solution of this stiff, initial-value problem was accomplished with a robust, implicit integrator, DLSODES (http://www.netlib.org/odepack). Optimal parameter estimation was implemented using the generalized reduced gradient (GRG2) algorithm (65) (http://www.maxthis.com/Grg2ug.htm). This nonlinear optimization algorithm, designed for optimization of large-scale systems, incorporates both equality and inequality constraints, which are essential for this ill-posed, under-determined system (28).

RESULTS

Metabolic Responses to Ischemia and Reperfusion

Comparisons to experimental data.

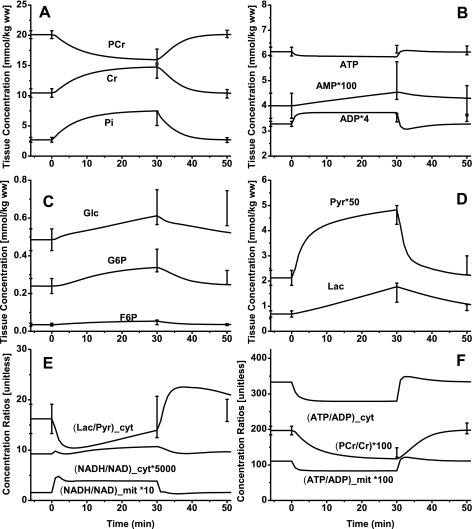
Comparisons of model-simulated outputs to the available in vivo experimental data on muscle ischemia and recovery in humans are shown in Fig. 3. These comparisons provide a basis for model validation and for obtaining optimal estimates of many model parameters. Model simulations correspond to most experimental data after 30 min of ischemia followed by 15 min of reperfusion (recovery) (Fig. 3, A–D). The change in cytosolic lactate-to-pyruvate concentration ratio ([Lac]/[Pyr]) is consistent with the change in cytosolic redox state but not with the change in mitochondrial redox state (Fig. 3E). However, the change in [PCr]/[Cr] ratio is proportional to the change in both cytosolic and mitochondrial phosphorylation state (Fig. 3F).

Fig. 3.

Model-predicted dynamic responses of PCr, Cr, and P_i (A), ATP, ADP, and AMP (B), Glc, G6P, and F6P (C), Lac and Pyr (D), (Lac/Pyr)_cyt, (NADH/NAD⁺)_cyt, and (NADH/NAD⁺)_mit (E), and PCr/Cr, (ATP/ADP)_cyt, and (ATP/ADP)_mit (F) in muscle tissue cells (where cyt and mit indicate cytosolic and mitochondrial ratios, respectively) during the resting, ischemia, and recovery periods with a blood flow reduction level of ∼80% and their comparison to the available experimental data (48). The lines represent the model simulation results with the symbols representing the experimental data points (means ± SD). The responses were computed using the estimated optimal parameter values with the ischemia protocol of −5 to 0 min of resting, 0 to 30 min of ischemia, and 30 to 50 min of recovery. The muscle blood flow Q is reduced as a step from 0.9 l/min at rest to Q_isch = 0.18 l/min at the onset of ischemia and returned to 0.9 l/min at the onset of recovery. The species concentrations in muscle tissue cells were calculated based on the volume-average formula: C_tis = (V_cytC_cyt + V_mitC_mit)/V_tis (see text for definitions).

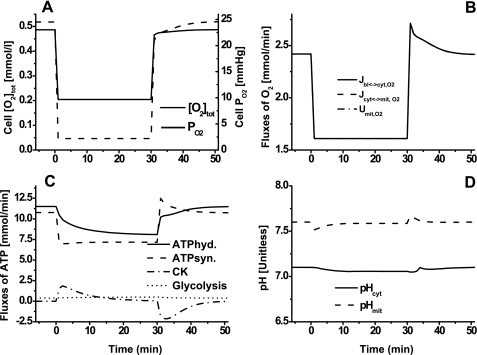
Metabolic characteristics and energetic aspects.

Model simulations of cellular total O₂ content, cellular O₂ uptake and consumption rates, primary reaction rates associated with the consumption and production of ATP, and cytosolic and mitochondrial pH changes during ischemia and reperfusion are shown in Fig. 4. In response to ischemia, cellular total O₂ content decreased considerably (Fig. 4A), whereas cellular O₂ uptake and consumption rates decreased by only ∼35% (Fig. 4B); the differences between O₂ uptake and consumption rates were too small to be evident. During ischemia, ATP hydrolysis rate decreased ∼30%, while ATP synthesis rate decreased ∼35%. Creatine kinase (CK) rate increased from 0 to ∼1.6 mmol/min during the transition from rest to ischemia and then decreased gradually to 0; this trend of CK was reversed during the transition from ischemia to reperfusion. The transient deficit in ATP during ischemia and recovery was mostly matched by the ATP supply from the CK ATP buffer reaction. The ATP supply via glycolysis/glycogenolysis (ATP deficit − ATP supply from CK reaction) during ischemia and recovery was almost constant, indicating that glycolysis/glycogenolysis is not a major source of ATP supply during ischemia; ATP synthesis via oxidative phosphorylation is still the major source of ATP supply during ischemia. Although pH changes were small, mitochondrial pH decreased more than cytosolic pH during ischemia (Fig. 4D).

Fig. 4.

Model-predicted dynamic responses of cellular total O₂ content (O_{2 tot}) and O₂ partial pressure (Po₂) (A), cellular O₂ uptake (J_bl↔cyt,O2), mitochondrial O₂ uptake (J_cyt↔mit,O2), and mitochondrial O₂ consumption (U_mit,O2) (B), ATP consumption via ATP hydrolysis, ATP production via ATP synthesis, ATP production via CK, and ATP production via glycolysis (C), and cytosolic and mitochondrial pH (D) during the resting, ischemia, and recovery periods with a blood flow reduction of ∼80%. The responses were computed using the estimated optimal parameter values with the following ischemia protocol: if (t < 0 min|t > 30 min), then Q = 0.9 l/min, else Q = Q_isch = 0.18 l/min, as detailed in the legend to Fig. 3.

Metabolic Responses to Moderate Intensity Exercise

Metabolic characteristics and energetic aspects.

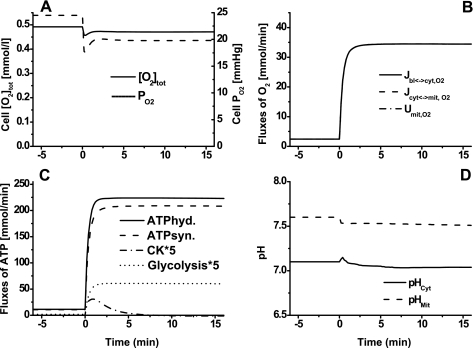
Model simulations of cellular total O₂ content, cellular O₂ uptake and consumption rates, primary reaction rates associated with the consumption and production of ATP, and cytosolic and mitochondrial pH changes during moderate intensity exercise (60% V̇o_{2 max}) are shown in Fig. 5. The energetic aspects of metabolic characteristics of skeletal muscle to increased energy demand are evident from these model simulations. Although cellular total O₂ content decreased very little (Fig. 5A), cellular O₂ uptake and consumption rates increased 36-fold (Fig. 5B), indicating that O₂ supply to skeletal muscle during moderate intensity exercise was not limited. The reaction rates of ATP hydrolysis and ATP synthesis increased ∼20-fold. Although ATP production by glycolysis increased ∼30 fold, ATP synthesis linked to oxidative phosphorylation still accounted for ∼90% of ATP supply during exercise (Fig. 5C). The CK reaction rate increased during the transition from rest to exercise and then decreased gradually to zero. Both cytosolic and mitochondrial pH decreased slightly during the moderate intensity exercise period (Fig. 5D).

Fig. 5.

Model-predicted dynamic responses of cellular O_2tot and Po₂ (A), J_{bl↔cyt, O2}, J_{cyt↔mit, O2}, and U_mit,O2 (B), ATP consumption via ATP hydrolysis (hyd), ATP production via ATP synthesis (syn), ATP production via CK, and ATP production via glycolysis (C), and cytosolic and mitochondrial pH (D) during the moderate intensity exercise [60% maximal O₂ consumption (V̇o_2max)] period. The responses were computed using the estimated optimal parameter values.

Effects of Mitochondrial NADH/NAD⁺ Shuttling Activity

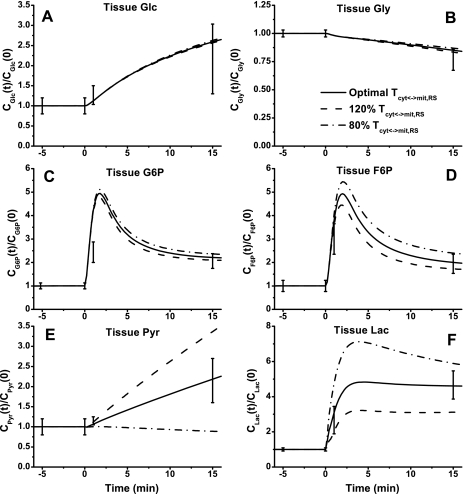
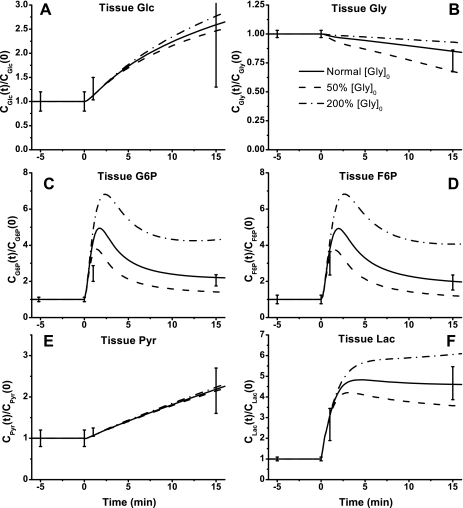
The dynamic metabolic responses of skeletal muscle to moderate intensity exercise (60% V̇o_{2 max}) depend on NADH/NAD⁺ shuttling activity between cytosol and mitochondria. This is simulated by changing the apparent transport rate coefficient T_cyt↔mit,RS^ex at the onset of exercise (Figs. 6–9). With the optimally estimated value of this rate coefficient, model outputs correspond well to the available experimental data. In response to exercise, glucose concentration ([Glc]) increased ∼150% and glycogen concentration ([Gly]) decreased ∼16% (Fig. 6, A and B). Although a 20% change of T_cyt↔mit,RS^ex had little effect on the responses of [Glc] and [Gly], it had noticeable effects on [G6P] and [F6P] dynamics corresponding to the experimental data (Fig. 6, C and D). At the onset of exercise, [G6P] and [F6P] increased nearly fivefold and then decreased to ∼100% higher steady-state levels (biphasic behavior). Whereas [Pyr] changed linearly with time over the entire period of exercise, [Lac] reached a maximum value within a few minutes (Fig. 6, E and F). The responses of [Pyr] and [Lac] were effected greatly by T_cyt↔mit,RS^ex. With the lower value of T_cyt↔mit,RS^ex, [Pyr] decreased a little, whereas [Lac] increased sevenfold to a maximum level. With the higher value of T_cyt↔mit,RS^ex, [Pyr] increased more than threefold, whereas [Lac] reached a lower plateau.

Fig. 6.

Model-predicted dynamic responses of Glc (A), Gly (B), G6P (C), F6P (D), Pyr (E), and Lac (F) in muscle tissue cells to moderate intensity exercise (60% V̇o_{2 max}) and to variations in mitochondrial NADH/NAD⁺ transporter (shuttling) activity parameter (T_cyt↔mit,RS) and their comparison to the available experimental data (Glc, G6P, F6P, Pyr, and Lac obtained from Ref. 74; Gly obtained from Ref. 76). The lines represent the model simulation results with the symbols representing the experimental data points (means ± SD). The responses were computed using the optimal parameter estimates. The species concentrations (mmol/kg wet weight or mM) in the muscle tissue cells were calculated based on the volume-average formula: C_tis = (V_cytC_cyt + V_mitC_mit)/V_tis and were normalized with respect to the resting species tissue cell concentrations: [Glc]_cl,0 = 0.5 mM (A), [Gly]_cl,0 = 95.0 mM (B), [G6P]_cl,0 = 0.25 mM (C), [F6P]_cl,0 = 0.044 mM (D), [Pyr]_cl,0 = 0.05 mM (E), and [Lac]_cl,0 = 0.78 mM (F).

Fig. 9.

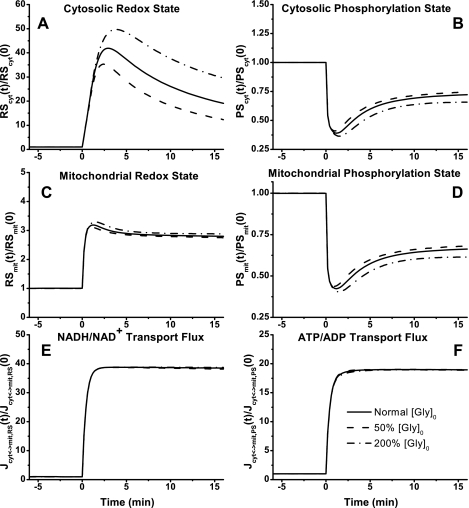
Model-predicted dynamic responses of cytosolic redox state (NADH_cyt/NAD⁺_cyt, RS_cyt) (A), cytosolic phosphorylation state (ATP_cyt/ADP_cyt, PS_cyt) (B), mitochondrial redox state (NADH_mit/NAD⁺_mit, RS_mit) (C), mitochondrial phosphorylation state (ATP_mit/ADP_mit, PS_mit) (D), mitochondrial NADH/NAD⁺ transport (shuttle) flux (J_cyt↔mit,RS) (E), and mitochondrial ATP/ADP transport flux (J_cyt↔mit,PS) (F) to moderate intensity exercise (60% V̇o_{2 max}) and to variations in mitochondrial NADH/NAD⁺ transporter (shuttling) activity parameter (T_cyt↔mit,RS). The responses were computed using the optimal parameter estimates. Experimental data for these key state variables were not available in the literature for comparison. These state variables were normalized with respect to their resting values: [RS]_cyt,0 = [NADH]_cyt,0/[NAD⁺]_cyt,0 = 0.00185 (A), [PS]_cyt,0 = [ATP]_cyt,0/[ADP]_cyt,0 = 332.2 (B), [RS]_mit,0 = [NADH]_mit,0/[NAD⁺]_mit,0 = 0.159 (C), [PS]_mit,0 = [ATP]_mit,0/[ADP]_mit,0 = 1.11 (D), J_{cyt↔mit,RS,0} = 0.284 (E), and J_{cyt↔mit,PS,0} = 11.58 (F).

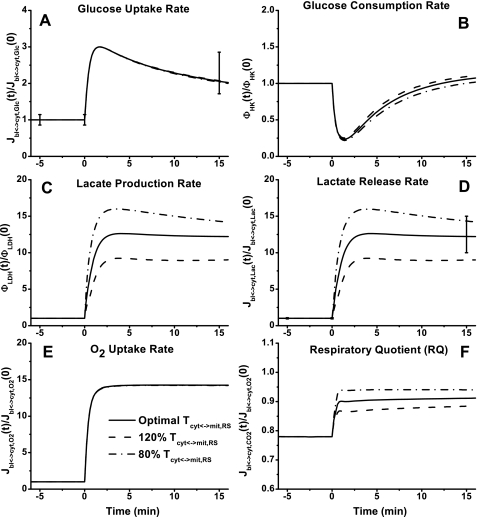
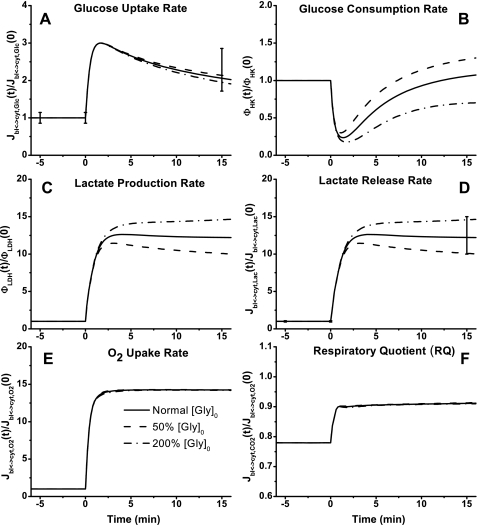
Model simulations of the rates of glucose uptake and consumption that show biphasic behaviors were essentially independent of the T_cyt↔mit,RS^ex changes (Fig. 7, A and B). However, their trends were distinct; glucose uptake rate first increased and then decreased to an ∼100% higher steady-state value, whereas glucose utilization rate first decreased and then increased to its baseline level. At the onset of exercise, lactate production and release rate increased ∼12-fold to a plateau at the optimal value of T_cyt↔mit,RS^ex and increased even more with a lower T_cyt↔mit,RS^ex value (Fig. 7, C and D). At the onset of exercise, O₂ uptake rate increased ∼14-fold to a plateau (Fig. 7E), whereas the respiratory quotient (RQ = −J_bl↔cyt,CO2/J_bl↔cyt,O2) increased from ∼0.78 to ∼0.91. The change of T_cyt↔mit,RS^ex had no effect on the rate of O₂ uptake and a modest effect on the value of RQ (Fig. 7F).

Fig. 7.

Model-predicted dynamic responses of glucose uptake (J_bl↔cyt,Glc) (A), glucose consumption (φ_HK) (B), lactate production (φ_LDH) (C), lactate release (J_bl↔cyt,Lac) (D), O₂ uptake (J_bl↔cyt,O2) (E), and respiratory quotient (RQ = −J_bl↔cyt,CO2/J_bl↔cyt,O2) (F) in muscle tissue cells to moderate intensity exercise (60% V̇o_{2 max}) and to variations in mitochondrial NADH/NAD⁺ transporter (shuttling) activity parameter (T_cyt↔mit,RS) and their comparison to the available experimental data (76). The lines represent the model simulation results with the symbols representing the experimental data points (means ± SD). The responses were computed using the optimal parameter estimates. The transport and reaction fluxes (mmol/min) were normalized with respect to the resting transport and reaction fluxes: J_{bl↔cyt,Glc,0} = 0.195 mmol/min (A), φ_HK,0 = 0.195 mmol/min (B), φ_LDH,0 = 0.09 mmol/min (C), J_{bl↔cyt,Lac,0} = 0.09 mmol/min (D), and J_bl↔cyt,O2,₀ = 2.42 mmol/min (E).

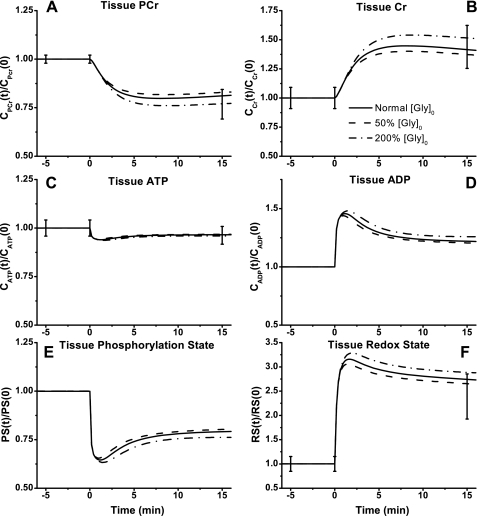
Model-simulated responses of high-energy phosphate metabolites to moderate intensity exercise showed some changes with T_cyt↔mit,RS^ex (Fig. 8, A–D). Similar to the experimental data, [PCr] decreased ∼20% and [Cr] increased ∼40%. Simulations showed that these reached new steady states within 5 min of onset of exercise (Fig. 8, A and B). Tissue-averaged [ATP] decreased only by ∼5%, and [ADP] showed a biphasic response with a ∼25% increase at steady state (Fig. 8, C and D). Tissue-averaged phosphorylation state (ATP/ADP) decreased by ∼20%, and redox state (NADH/NAD⁺) doubled at the optimal value of T_cyt↔mit,RS^ex (Fig. 8, E and F).

Fig. 8.

Model-predicted dynamic responses of PCr (A), Cr (B), ATP (C), ADP (D), phosphorylation state (ATP/ADP, PS) (E), and redox state (NADH/NAD⁺, RS) (F) in muscle tissue cells to moderate intensity exercise (60% V̇o_{2 max}) and to variations in mitochondrial NADH/NAD⁺ transporter (shuttling) activity parameter (T_cyt↔mit,RS) and their comparison to the available experimental data (PCr and Cr obtained from Ref. 98; RS obtained from Ref. 75). The lines represent the model simulation results with the symbols representing the experimental data points (means ± SD). The responses were computed using the optimal parameter estimates. The species concentrations (mmol/kg wet weight or mM) in the muscle tissue cells were calculated based on the volume-average formula C_tis = (V_cytC_cyt + V_mitC_mit)/V_tis and were normalized with respect to the resting species tissue cells concentrations: [PCr]_cl,0 = 20 mM (A), [Cr]_cl,0 = 10.5 mM (B), [ATP]_cl,0 = 6.2 mM (C), [ADP]_cl,0 = 0.8 mM (D), [PS]_cl,0 = ([ATP]/[ADP])_cl,0 = 7.75 (E), and [RS]_cl,0 = ([NADH]/[NAD⁺])_cl,0 = 0.111 (F).

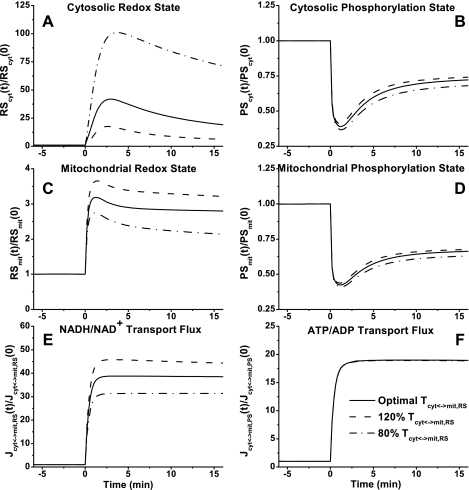
In cytosol and mitochondria, the model-simulated dynamic responses of NADH/NAD⁺ were significantly different, whereas those of ATP/ADP were quite similar (Fig. 9, A–D) during moderate intensity exercise. With the optimally estimated value of T_cyt↔mit,RS^ex, NADH/NAD⁺ increased ∼20-fold in cytosol (Fig. 9A) and only ∼3-fold in mitochondria (Fig. 9C), whereas ATP/ADP decreased by only ∼30% in both cytosol and mitochondria (Fig. 9, B and D). Although T_cyt↔mit,RS^ex had significant effect on NADH/NAD⁺ and its transport flux, it had little effect on ATP/ADP and its transport flux (Fig. 9, E and F).

Effects of Muscle Glycogen Stores

The model-simulated effects of halving or doubling glycogen storage level on skeletal muscle energy metabolism during moderate intensity exercise (60% V̇o_{2 max}) are shown in Figs. 10–13. The [Glc] and [Gly] responses were changed little (Fig. 10, A and B), but the [G6P] and [F6P] responses were varied considerably in a biphasic manner (Fig. 10, C and D). With changes in glycogen storage contents, tissue [Pyr] did not vary, but tissue [Lac] increased or decreased noticeably (Fig. 10, E and F). The glycogen storage effects were negligible on glucose uptake rate but not on glucose consumption rate (Fig. 11, A and B). The effects on lactate production and release rates increased or decreased to the same extent consistent with the experimental data (Fig. 11, C and D). The O₂ uptake and RQ were not affected by the glycogen storage changes (Fig. 11, E and F). Glycogen stores also had little effect on high-energy phosphate metabolites, tissue phosphorylation state, and tissue redox state (Fig. 12, A–F). Except for cytosolic NADH/NAD⁺, changes of glycogen stores had little effect on mitochondrial NADH/NAD⁺ and cytosolic and mitochondrial ATP/ADP dynamics and corresponding transport rates (Fig. 13, A–F).

Fig. 10.

Model-predicted dynamic responses of Glc (A), Gly (B), G6P (C), F6P (D), Pyr (E), and Lac (F) in muscle tissue cells to moderate intensity exercise (60% V̇o_{2 max}) and to variations in the initial level of muscle glycogen store ([Gly]₀) and their comparison to the available experimental data. The other details are the same as those described in the legend to Fig. 6.

Fig. 13.

Model-predicted dynamic responses of RS_cyt (A), PS_cyt (B), RS_mit (C), PS_mit (D), J_cyt↔mit,RS (E), and J_cyt↔mit,PS (F) to moderate intensity exercise (60% V̇o_{2 max}) and to variations in [Gly]₀. The other details are the same as those described in the legend to Fig. 9.

Fig. 11.

Model-predicted dynamic responses of J_bl↔cyt,Glc (A), φ_HK (B), φ_LDH (C), J_bl↔cyt,Lac (D), J_bl↔cyt,O2 (E), and RQ (F) in muscle tissue cells to moderate intensity exercise (60% V̇o_{2 max}) and to variations in [Gly]₀ and their comparison to the available experimental data. The other details are the same as those described in the legend to Fig. 7.

Fig. 12.

Model-predicted dynamic responses of PCr (A), Cr (B), ATP (C), ADP (D), PS (E), and RS (F) in muscle tissue cells to moderate intensity exercise (60% V̇o_{2 max}) and to variations in [Gly]₀ and their comparison to the available experimental data. The other details are the same as those described in the legend to Fig. 8.

DISCUSSION

Model Distinctions

The goal of this study was to develop a physiologically based mathematical model of cellular metabolism in perfused skeletal muscle that simulates metabolic responses to moderate intensity exercise (∼60% V̇o_2max) and provides the mechanistic basis for addressing key questions with respect to the mechanisms of metabolic regulation in contracting skeletal muscle. For this purpose, the model distinguishes metabolic processes occurring in capillary blood, cytosol, and mitochondria and incorporates distinct transport processes between these domains. The model accounts for proton handling and considers the coupled energy controller pairs ATP-ADP and NADH-NAD⁺ as cosubstrates. The model differs significantly from our previous models of cardiac and skeletal muscle cellular metabolism (26–28, 102–105) in that the biochemical reactions governing cellular metabolism are considered reversible with their fluxes satisfying Haldane relationships (thermodynamic constraints). Furthermore, the model differs from other published models of skeletal muscle cellular metabolism (55, 56, 59, 60, 64, 69, 96, 101) in that the model incorporates the primary substrates (glucose and FFAs) together with key metabolic pathways of cellular metabolism (glycolysis, lipid metabolism, CK, TCA cycle, and oxidative phosphorylation). A key feature of the model is its ability to simulate blood and tissue responses, which are routinely measured in experimental studies, as well as to predict dynamic intracellular species concentrations and reaction rates, which cannot be measured with the currently available experimental techniques. Specifically, the model simulations can address key questions with respect to metabolic changes that occur during the transition from rest to exercise: 1) what are the roles of mitochondrial NADH/NAD⁺ transport (shuttling) activity and intracellular glycogen stores on skeletal muscle energy metabolism?; 2) how sensitive are the distributions of NADH and NAD⁺ or NADH/NAD⁺ (redox state) in cytosol and mitochondria to changes in mitochondrial shuttling rates of reducing equivalents and intracellular glycogen stores?; and 3) what is the relationship between lactate production and redox states of cytosol and mitochondria?

Model Validation

The essence of model validation is to show that a single set of model parameter values can generate model simulations corresponding to multiple measured tissue metabolite concentrations at different time points and under distinct experimental conditions. First, optimally estimated model parameter values were obtained by minimizing an objective function that includes model simulations of available experimental metabolic responses to muscle ischemia and reperfusion (48) (Fig. 3). Physiological (resting steady-state flux-concentration relationships) and thermodynamic (entropy inequalities and Haldane relationships) constraints are applied to reduce the number of unknown parameters for estimation. This type of constraint-based, robust parameter estimation procedure for large-scale in vivo metabolic systems was recently established (27, 28). Next, to simulate metabolic responses to moderate intensity exercise (60% V̇o_{2 max}), the parallel activation hypothesis was incorporated in the model with non-zero activation coefficients for specific reaction and transport fluxes. This approach has been applied in other in silico studies (26, 55, 57–60, 68, 103) and has experimental justification (21, 22). Although activation mechanisms have yet to be definitively determined, contraction-related factors (e.g., Ca²⁺) and hormones (e.g., epinephrine) are likely to play important roles in metabolic activation during exercise. Such kinds of factors can act on both reactions and transport processes in skeletal muscle (15, 19, 20, 22, 33, 41, 66, 70, 71, 85, 92, 98). Given the lack of sufficient in vivo experimental data, the current model simply defines phenomenological activation relationships and coefficients for reaction and transport fluxes. The parameter values associated with the activation mechanisms were optimally estimated (Tables 4 and 5), which gives the best fit of the model-simulated outputs to the available experimental data on exercise in humans (74–76, 98) (Figs. 6–13). Specifically, with the optimally estimated activation coefficients, model simulations corresponded closely to the measurements of tissue concentrations of glycolytic intermediates (Figs. 6 and 10), glucose uptake and lactate release (Figs. 7, A–D, and 11, A–D), and high-energy phosphates and tissue redox state (Figs. 8, A–C and F, and 12, A–C and F). Elimination of any of the activation coefficients resulted in model simulations that were not in good agreement with the experimental data. With this validated model of skeletal muscle cellular metabolism, model simulations of exercise responses were used to predict effects of the apparent cytosol-mitochondria NADH/NAD⁺ transport (shuttling) activity and the muscle initial glycogen stores.

Model Simulations of Skeletal Muscle Energetics

Healthy skeletal muscle is characterized by a capacity (metabolic flexibility) to utilize lipid and carbohydrate fuels and to transition between them when facing discontinuities in both supply of and demand for energy. Model simulations of ischemia-reperfusion and exercise showed that [ATP] is maintained nearly constant (ATP homeostasis) under these physiological conditions (Figs. 3B, 8C, and 12C). Furthermore, the metabolite concentrations do not vary significantly, whereas the metabolic fluxes change severalfold under these conditions. This suggests that the effects of mass action associated with the metabolite concentration changes on metabolic reaction fluxes are limited.

In response to ischemia, because of the reduced blood flow and O₂ supply to mitochondria, the intracellular O₂ content decreased considerably (Fig. 4A). ATP synthesis via oxidative phosphorylation decreased by ∼35%, which indicates that mitochondrial function in skeletal muscle during ischemia was impaired. On the other hand, during the transition from rest to exercise, model simulations showed that O₂ consumption of skeletal muscle increased by ∼35-fold (Fig. 5B), and ATP hydrolysis rate and ATP synthesis rate, as well as other reaction fluxes associated with ATP, increased markedly (Fig. 5C). As an important index of metabolic status of skeletal muscle, RQ of skeletal muscle increased from ∼0.78 at rest to ∼0.91 at the end of exercise (Figs. 7F and 11F), which indicates that skeletal muscle turned to carbohydrate oxidation during exercise. In conditions of either ischemia or exercise, ATP synthesis via oxidative phosphorylation still accounted for most of the ATP supply (Figs. 4C and 5C), although the relative increase of glycolytic rate was much higher than ATP synthesis rate in exercise (Fig. 5C). Therefore, under the well-oxygenated condition of moderate intensity exercise (Fig. 5A), mitochondria still can play the primary role in energy supply in the contracting muscle.

Metabolic Responses of Redox States During Exercise

The reducing equivalents (NADH, NAD⁺) and corresponding redox state (NADH/NAD⁺ ratio) function as important metabolic regulators in mammalian tissue (7, 100). These reducing equivalents are strictly regulated via specific reactions and shuttling between cytosol and mitochondria. Because the inner mitochondrial membrane is impermeable to NADH and NAD⁺, they have different concentrations in cytosol and mitochondria and correspondingly different redox states (100). Current in vivo experimental studies with skeletal muscle provide only sparse tissue-averaged concentrations of reducing equivalents. Since the dynamic changes of NADH and NAD⁺ in cytosol and mitochondria in human skeletal muscle have not been measured during exercise, model simulations provide an alternative way to quantitatively investigate the dynamics of redox states during exercise and the associated mechanisms of metabolic regulation.

An important prediction from this modeling study is that the cytosolic redox state is much more sensitive to the apparent mitochondrial NADH/NAD⁺ transport (shuttling) activity than the mitochondrial redox state. The distinct sensitivities of redox states between cytosolic and mitochondrial domains can be first attributed to the nonuniform distributions of reducing equivalents (Table 2). Since the pool size of NADH in the cytosolic domain is much smaller than that in mitochondria, changes of the reaction and transport rates have greater effect in the cytosol. Moreover, more buffering of the reducing equivalents by other reactions occurs in mitochondria. In cytosol, reactions of reducing equivalents are mainly involved in the production by glyceraldehyde-3-phosphate dehydrogenase and consumption by LDH. In mitochondria, NADH can be produced in pyruvate dehydrogenase, β-oxidation, and TCA cycle and consumed by oxidative phosphorylation with the excess NADH transported from cytosol. This model can help to evaluate these differences quantitatively (Tables 4 and 5). At resting steady state, ∼75% of the NADH produced in the cytosol was transported to the mitochondria; in contrast, the same NADH-NAD⁺ transport flux accounted for only ∼9% of the total NADH formation in the mitochondria. After 15 min of exercise, ∼90% of the NADH produced in the cytosol was transported to the mitochondria, but this flux contributed to only ∼24% of the total rate of NADH formation in the mitochondria. These differences indicate that changes in the transport rate of reducing equivalents between cytosol and mitochondria affect more the cytosolic redox than the mitochondrial redox state. As a result, a 20% fluctuation in the NADH-NAD⁺ transport rate coefficient had a marked effect only on the cytosolic NADH/NAD dynamics during exercise.

In skeletal muscle, the exchange of reducing equivalents between cytosol and mitochondria occurs via specialized shuttle systems (16, 72), which maintain distinct redox states in these subcellular compartments. Whereas the mitochondrial redox state is maintained fairly stable during metabolic perturbations, the cytosolic redox state may change severalfold. This difference in dynamic behavior when perturbed may be a design characteristic associated with the highly specific roles the redox states play in these compartments.

In mitochondria, the primary organelle for ATP supply in skeletal muscle, the redox state regulates the relative contributions of carbohydrate and lipid oxidation for ATP synthesis and controls the rate of TCA cycling (19, 29, 36). As the primary electron donor, the mitochondrial redox state can affect the rate of oxidative phosphorylation (19, 36). Therefore, an abnormal mitochondrial redox state can negatively affect the rate of ATP synthesis. Especially during exercise, ATP production rate must be activated substantially to meet the required energy demand. Model simulation of the exercise responses showed that the mitochondrial redox state increased (3-fold) rapidly and reached a new steady state (Fig. 9C), which primarily determined the response of the tissue-averaged redox state (Fig. 8F).

On the other hand, cytosolic redox state played a far less important role in the regulation of energy supply of skeletal muscle during exercise. In moderate intensity exercise, although the relative increase of ATP production by glycolysis was much larger than the relative increase of ATP synthesis in oxidative phosphorylation (Fig. 5C), ATP synthesized by oxidative phosphorylation still could match as high as ∼90% ATP turnover rate (Fig. 5C). Changes in the glycolytic reaction rate associated with mitochondrial NADH/NAD⁺ shuttling had little effect on energy metabolism in exercising skeletal muscle (Fig. 8) due to the relatively small portion of ATP produced in glycolysis. The NADH/NAD⁺ shuttling did affect [Pyr] and [Lac] responses (Fig. 6, E and F). These simulations indicate a close relationship between lactate production and the cytosolic redox state (Figs. 7C and 9A) and support the concept of local regulation of lactate production in exercising skeletal muscle (105). This differs from the idea that lactate accumulation in exercising skeletal muscle is due to tissue hypoxia (81). Furthermore, the cytosolic redox state may be an index or signal of the capacity of mitochondria in the processing of pyruvate. If pyruvate produced in glycolysis was beyond the capacity, for example, in exercise, the highly increased cytosolic redox state could stimulate the conversion of pyruvate into lactate due to the near-equilibrium characteristics of LDH. In simulations when mitochondrial NADH/NAD⁺ shuttling was blocked, [Lac] further increased and [Pyr] returned to its resting level (Fig. 6, E and F). In summary, our in silico studies suggested that cytosolic and mitochondrial redox states had remarkably different sensitivity responses to the change of NADH/NAD⁺ transport coefficient during exercise, and the differences corresponded to different regulatory roles of redox states in cytosol and mitochondria.

Activation of Transport Activity for Reducing Equivalents

From in vivo isotopic and NMR measurements in canine cardiac muscle (73), it was reported that NADH transport rate from cytosol to mitochondria decreased significantly in response to an increased workload. In other words, the NADH/NAD⁺ transport rate was inhibited at a high rate of energy expenditure. In contrast, from in vitro experiments with vascular smooth muscle (7), it is apparent that contractile function was reduced and lactate was accumulated when the malate-aspartate shuttle (or apparent NADH/NAD⁺ transport rate) was inhibited. When activity of shuttle-related enzymes was measured in cytosol and mitochondria (aspartate aminotransferase and malate dehydrogenase), type I (slow twitch) fibers exhibited higher shuttle enzyme levels with exercise (86). In this case, the capacity of the shuttle systems to transport NADH into mitochondria increases during exercise. A case report of a human subject with malate-aspartate shuttle defect (42) indicated that the exercise response of this individual was accompanied by 1) rapid PCr decrease with abnormally slow recovery, 2) delayed transport of P_i into mitochondria, and 3) accumulation of phosphomonoester (G6P), which is consistent with our model simulations of the reduced NADH/NAD⁺ transport rate (Fig. 6C).

Overall, these experimental studies support the hypothesis that activation NADH/NAD⁺ shuttling occurs in exercising skeletal muscle. In model simulations, activation NADH/NAD⁺ shuttling had remarkable effects on glycolytic intermediates (Fig. 6, C–F) and cytosolic redox state (Fig. 9A). The effects of reducing equivalent transport between cytosol and mitochondria during exercise reflected an active stimulus of a shuttle mechanism during exercise; otherwise, cytosolic metabolism would be impaired by blockage of mitochondrial NADH/NAD⁺ transport. Whether Ca²⁺ or hormones associated with muscle contraction are involved in shuttle activity to increase mitochondrial NADH/NAD⁺ transport rate during exercise is under investigation (66, 85, 92). Regardless of the specific mechanisms, model simulations predicted that the rate of NADH transport into the mitochondria in exchange of NAD⁺ must be increased (activated) sufficiently during exercise to avoid the abnormal fluctuation of skeletal muscle metabolism. This conclusion is also supported by other in silico studies (99).

Effect of Muscle Glycogen Stores

Under pathological conditions or with special diets, glycogen stores in skeletal muscle at rest can differ significantly. Model simulations show the effect of various levels of glycogen storage on the metabolic responses of skeletal muscle to exercise. Sensitive to glycogen storage levels were dynamic responses of glycolytic metabolite concentrations (Fig. 10, C, D, and F) and cytosolic redox state (Fig. 13A) but not phosphate-energy metabolites and redox state in mitochondria (Figs. 12, A–D, and 13D). Furthermore, compared with the glycolytic cascade, intermediates in TCA cycle changed little with glycogen stores (simulations not shown). These simulations were consistent with experimental studies that showed no significant changes in TCA intermediates with altered initial glycogen content (6, 89).

With respect to short-term exercise, the level of muscle glycogen stores does not have much effect on energy metabolism (Fig. 12) but can influence the glycolytic rate and induce the changes of intermediate concentration by mass action (Fig. 10). These effects relate to the cytosolic processes but not mitochondrial processes (Fig. 13, C and D). Therefore, these results were consistent with the results obtained by disturbing mitochondrial NADH/NAD⁺ transport during exercise and provided extra evidence that redox states and reactions in cytosol and mitochondria had different sensitivities to metabolic disturbances. In addition, [Lac], but not [Pyr], was remarkably affected by the muscle glycogen stores. Whereas lactate is associated only with LDH reaction in regulation of the cytosolic redox state, pyruvate is involved in numerous transport and reaction processes that provide a buffering effect on pyruvate and make pyruvate more stable than lactate (Fig. 10E). These simulations are also consistent with other exercise-response studies on human subjects with low or high glycogen storage (90). In these studies, the change in pyruvate level was negligible, but lactate increased ∼2.6-fold (17.0 ± 6.2 mM for low glycogen vs. 60.8 ± 6.5 mM for high glycogen) at the end of exercise.

Model Limitations and Future Developments

Computational modeling of metabolic responses of skeletal muscle to physiological stresses (e.g., hypoxia, ischemia, and exercise) is intended to quantitatively elucidate regulatory mechanisms. Although more detailed mechanisms can be included, these cannot be effectively validated without appropriate in vivo experimental data. With the availability of additional data, the model could incorporate and test alternative mechanisms of the glycerol phosphate and malate-aspartate shuttles for NADH and NAD⁺ between cytosol and mitochondria. Furthermore, the model could incorporate the ANT located on the inner mitochondrial membrane to represent the transport of ATP and ADP between cytosol and mitochondria. In addition, the model could incorporate detailed coupled transport mechanisms relating protons and other metabolites (e.g., proton-lactate cotransporter on the plasma membrane and proton-phosphate cotransporter on the inner mitochondrial membrane) and detailed mechanisms of oxidative phosphorylation and ATP synthesis. Other key regulatory species may be needed to test hypotheses related to the quantitative regulation of fuel selection during exercise (e.g., malonyl-CoA reduces the transport rate of fatty acyl-CoA into mitochondria by inhibiting carnitine palmitoyl transferase 1).

A limitation of the present model is that the model does not account for blood flow heterogeneity and fiber type distributions associated with skeletal muscle cellular metabolism. Specifically, the capillary blood domain is considered to be spatially lumped, and the advective-diffusive transport of chemical species in capillary blood is ignored. Such compartmental modeling may not account for situations where important gradients of chemical species exist (e.g., due to distinct metabolic characteristics associated with different fiber types). In skeletal muscle, where the blood flow is highly heterogeneous due to complex capillarization and fiber type distributions, more than 70% of arterial oxygen is extracted from the blood before it leaves the microcirculation (14). High extraction results in large intracellular and intravascular gradients of oxygen and other nutrients. Therefore, the well-mixed assumption may not be valid, and compartmental modeling may not account for the heterogeneity of oxygen transport and consumption in different fiber types. These issues can be addressed through spatially distributed modeling of oxygen transport and consumption, coupled with other substrates and CO₂ (10, 24). Specifically, to investigate the effects of spatial locality on metabolic responses to muscle ischemia and exercise, one will require spatially distributed models involving tissue-capillary units arranged in parallel and representing different muscle fiber types.

Concluding Remarks

The mathematical model developed in this work can simulate metabolic responses of skeletal muscle to ischemia and moderate intensity exercise. The model not only simulates the available in vivo experimental data but also predicts metabolic responses (e.g., transport and reaction fluxes) for which no data exist. The model simulations by perturbing the transport rate of NADH/NAD⁺ (shuttling) between cytosol and mitochondria and muscle glycogen storage level during exercise supported the hypotheses that transport process of reducing equivalents has to be activated during exercise, cytosolic redox state is much more sensitive than mitochondrial redox state, and lactate production is locally regulated by the cytosolic redox state.

GRANTS

This work was supported in part by National Institutes of Health (NIH) Grant GM66309 and National Aeronautics and Space Administration Grant NNJ06HD81G from the Johnson Space Center. R. K. Dash was partially supported by NIH Grant HL072011.