Circuits Generating Corticomuscular Coherence Investigated Using a Biophysically Based Computational Model. I. Descending Systems

Abstract

Recordings of motor cortical activity typically show oscillations around 10 and 20 Hz; only those at 20 Hz are coherent with electromyograms (EMGs) of contralateral muscles. Experimental measurements of the phase difference between approximately 20-Hz oscillations in cortex and muscle are often difficult to reconcile with the known corticomuscular conduction delays. We investigated the generation of corticomuscular coherence further using a biophysically based computational model, which included a pool of motoneurons connected to motor units that generated EMGs. Delays estimated from the coherence phase–frequency relationship were sensitive to the width of the motor unit action potentials. In addition, the nonlinear properties of the motoneurons could produce complex, oscillatory phase–frequency relationships. This was due to the interaction of cortical inputs to the motoneuron pool with the intrinsic rhythmicity of the motoneurons; the response appeared more linear if the firing rate of motoneurons varied widely across the pool, such as during a strong contraction. The model was able to reproduce the smaller than expected delays between cortex and muscles seen in experiments. However, the model could not reproduce the constant phase over a frequency band sometimes seen in experiments, nor the lack of around 10-Hz coherence. Simple propagation of oscillations from cortex to muscle thus cannot completely explain the observed corticomuscular coherence.

INTRODUCTION

Recordings from primary motor cortex (M1) commonly show oscillations at around 10 and 20 Hz (Conway et al. 1995; Halliday et al. 1998; Murthy and Fetz 1992). Similar oscillations are present in the electromyogram (EMG) of forearm and intrinsic hand muscles during a sustained contraction (Baker et al. 1997; Conway et al. 1995; Halliday et al. 1998; McAuley et al. 1997). However, although oscillations around 20 Hz are coherent between cortex and muscles, most studies fail to find corticomuscular coherence at 10 Hz (Baker et al. 1997, 2003; Conway et al. 1995; Halliday et al. 1998; Kilner et al. 2000; Salenius et al. 1997). The studies that do find approximately 10-Hz coherence (Gross et al. 2002; Marsden et al. 2001; Ohara et al. 2000; Raethjen et al. 2002) use a variety of methods, making them hard to compare. Baker et al. (2003) showed that both frequency ranges are effectively carried down the corticospinal tract that, in primates, makes monosynaptic connections with motoneurons (Porter and Lemon 1993). The lack of corticomuscular coherence at about 10 Hz is therefore a puzzling enigma. Baker et al. (2003) argued that the failure of motoneurons to phase-lock to cortical inputs at 10 Hz could be explained only if some neural system actively cancelled these inputs. This could be advantageous in the reduction of physiological tremor, which has a dominant frequency peak at 8–12 Hz (Marsden et al. 2001; Randall and Stiles 1964; Stiles and Randall 1967).

Although the existence of close to 20-Hz corticomuscular coherence is well documented, the phase of this coherence has proved more controversial. Straightforward conduction of oscillations from cortex to motoneurons over fast corticospinal pathways should produce a linear phase–frequency relationship, with a slope related to the conduction delay (Rosenberg et al. 1989). In many cases the band of significant coherence is too narrow to determine a meaningful phase–frequency relationship. Where coherence phase has been examined, some subjects show a linear phase–frequency relationship, whereas for others phase is constant (Halliday et al. 1998; Riddle and Baker 2005).

Estimates of the corticomuscular conduction delay can be obtained using transcranial magnetic stimulation (TMS). Following a TMS pulse applied over M1, an EMG response in hand muscles occurs with an onset latency of roughly 21 ms (Rothwell et al. 1991). Riddle and Baker (2005) noted that the latency to the peak of response, rather than its onset, was probably the more relevant variable to compare with delays estimated from the corticomuscular coherence phase; for human hand muscles and surface EMG recordings, this gives a delay closer to 30 ms. In subjects showing a linear phase–frequency relationship, the slope of the best-fit line implied a delay of about 10 ms for the hand (Riddle and Baker 2005). Salenius et al. (1997) triggered averages of sensorimotor magnetoencephalograms from the onset of motor unit potentials in EMG; this method yielded a time lag of 33 ms to the hand. Ohara et al. (2000) calculated the cross-correlogram between an electroencephalogram (EEG) and an EMG and measured the lag of the peak. This yielded a delay estimate from motor cortex to a forearm muscle of 10 ms.

We decided to investigate the generation of corticomuscular coherence in more detail using a biophysically based computational model. In this study, we present results from a model that includes conduction of oscillations from the cortex to motoneurons and from there to muscle. We show that complex, nonlinear phase–frequency relationships can be generated as a consequence of motoneuron properties, explaining some of the previous experimental findings. A companion paper examines the possible role of feedback connections.

METHODS

Overview of model

The model builds on a model that we previously published (Baker and Lemon 1998), consisting of a pool of realistic motoneurons that receive common input from the motor cortex (Fig. 1 A). EMG and force are simulated from the firing of the motoneurons. By simulating these population recordings, which are typically measured experimentally, we were able directly to compare results from our simulations with experimental estimates of corticomuscular coherence.

FIG. 1.

A: schematic of the model. B: waveform of motoneuron excitatory postsynaptic potential (EPSP). C: dependence of motoneuron firing rate on rate of excitatory synaptic input for motoneurons (MNs) 1 (top curve), 60, 100, and 177 (bottom curve). D: example raw data output from the model.

Motoneuron model

The motoneuron model, based on a previously published model (Booth et al. 1997), includes both somatic and dendritic compartments and eight active conductances found in mammalian motoneurons [soma: g_Na, g_K(DR), g_Ca-N, g_K(Ca), g_Na-P; dendrite: g_Ca-L, g_Ca-N, g_K(Ca)], each with Hodgkin–Huxley style kinetics. The values of g_K(Ca) were 3.136 and 0.69 mS/cm² for the somatic and dendritic compartments. respectively. In an addition to the model of Booth et al. (1997), we included a sodium persistent inward current (PIC) in the soma with kinetics chosen to fit data from Li and Bennett (2003). In contrast to the noninactivating calcium PIC, following a depolarization the sodium PIC has a rapid inactivation lasting for about 1 s, after which a steady sodium current persists indefinitely (Li and Bennett 2003). The maximum conductance of the sodium PIC was set to 0.1 mS/cm².

Each motoneuron received excitatory common input from a cortical source. This number of inputs arriving per 0.2-ms time step was modeled as white Gaussian noise with a mean and variance of 0.5. The mean was set equal to the variance to mirror the properties of Poisson-distributed inputs. This is equivalent to each motoneuron receiving 2,500 impulses/s. The unitary excitatory postsynaptic potential (EPSP) from a corticomotoneuronal connection is from 25 to 100 μV in amplitude (Asanuma et al. 1979) and the compound EPSP from pyramidal tract stimulation can be ≤10 mV in size (Fritz et al. 1985; Porter and Lemon 1993), suggesting at most 100–400 fast corticospinal inputs project to each motoneuron. Corticospinal cells fire at close to 20 Hz during steady holding, when oscillations are greatest (Baker et al. 2001; Davies et al. 2006). The chosen value of 2,500 cortical inputs per second per motoneuron is thus approximately at the lower end of the range expected from published data. In some simulations, the cortical input was modeled as colored Gaussian noise, with peaks at 8–12 and 18–30 Hz, to simulate the cortical oscillations seen experimentally (Conway et al. 1995; Kilner et al. 2000).

Each motoneuron also received an independent input that was independent both from the common input and also from the independent input to all other motoneurons. Independent inputs were modeled as white Gaussian noise, with mean equal to the variance. The level of the mean was adjusted with reference to preliminary simulations to produce a force output at the desired percentage of maximal voluntary contraction (MVC). At 5% MVC, the ratio of cortical input to independent input was 1:3.2 for simulations that included PICs and 1:9 for those without.

The time course shape of synaptic conductances was modeled as an α-function

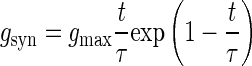(1)

where g_max is the maximum conductance and τ is the rise time (Baker and Lemon 1998). Unitary synaptic conductances added to produce the total synaptic conductance (g_t-syn) in the dendrite. The reversal potential for the synaptic conductance was set to 0 mV (Baker and Lemon 1998). The values of τ and g_max (0.03 ms and 0.0065 mS/cm², respectively) were chosen to produce an EPSP (Fig. 1B) in the somatic compartment with a rise time of 1 ms and a peak of 100 μV (Asanuma et al. 1979).

The properties of motoneurons vary continuously across the motoneuron pool, such that units generating the smallest twitch tension are recruited first (Zajac and Faden 1985). Bakels and Kernell (1993) showed that an orderly variation in motoneuron membrane properties underlies this. In this model, orderly recruitment was simulated by changing the ratio of the soma surface area to total surface area. The parameter P in the model of Booth et al. (1997) determines the proportion of the dendrite membrane potential allowed to activate the motoneuron. The first motoneuron to be recruited (MN1) was assigned P₁ = 0.1. Simulations were then run of this motoneuron model in receipt of different levels of total synaptic input, which allowed the construction of a curve of output firing rate versus synaptic input rate (Fig. 1C). It should be noted that the motoneurons began tonically firing at around 8 Hz, as described experimentally (Milner-Brown et al. 1973). For inputs just below the level required to achieve this, occasionally membrane noise led to a threshold crossing and an isolated spike. The calculated rate (estimated as spike count divided by simulation time) was then nonzero. However, this situation is very different from regular tonic firing. The steep initial section of the curves in Fig. 1C thus reflects the transition from occasional isolated spikes to true tonic firing.

The model of Wani and Guha (1975) was used to determine the firing rate of the first motoneuron (MN) when the jth was just recruited. The strength of total synaptic input needed to make MN1 fire at this rate was then determined from the input–output curve. P_j was then adjusted until the jth motoneuron fired at the minimum recruitment firing rate with this level of input. The procedure was repeated for all motoneurons, which resulted in estimates of P that increased exponentially with recruitment number. Adjusting P in this way does not reflect the processes that determine recruitment order in real motoneurons, but was a convenient means to match the rates across the pool to those predicted by the model of Wani and Guha (1975). In the resulting motoneuron pool, the afterhyperpolarization (AHP) varied in amplitude from 7.2 to 9.1 mV below threshold. The time taken for the AHP to reach half-maximum ranged from 17.2 to 18.1 ms. These decay times correspond with exponential time constants of 24–26 ms, in keeping with previous models of motoneurons (Matthews 1997).

Motor units

The motoneuron pool consisted of 377 neurons (Baker and Lemon 1998; Wani and Guha 1975). Following the firing of each motoneuron, a peripheral motor unit produced a motor unit action potential (MUAP) and twitch tension. The peripheral conduction delay for the jth motoneuron was given by (11 + 2j/377) ms, which accounted for the slightly faster conduction velocity of the higher-threshold motoneurons (Baker and Lemon 1998). MUAPs were used as in our previous publication (Baker and Lemon 1998); these are designed realistically to reflect the MUAPs that would be measured from a human hand muscle using surface recordings. Twitch tensions were simulated as alpha functions (similar to Eq. 1); the rise time and amplitudes varied across the pool as specified for the first dorsal interosseous muscle by the model of Wani and Guha (1975).

EMG was simulated by linear summation of the MUAPs from all active motor units. By contrast, the summation of single twitch tensions to generate total output force has been demonstrated to have several nonlinearities. Twitches summate more effectively at low spike rates, generating a sigmoidal dependence between rate and force (Rack and Westbury 1969). Fuglevand et al. (1993) developed a model to incorporate these nonlinearities in force production. In this model the motor unit force was multiplied by a gain g that depended on the unit's twitch contraction time T and the interspike interval (ISI) as follows

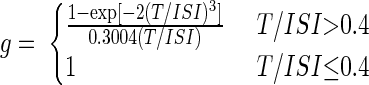(2)

Figure 1D shows example raw data produced by the model.

Model simulation

The model was implemented in the MATLAB environment (The MathWorks, Natick, MA), using the MATLAB Distributed Computing Toolbox and Engine to run multiple simulations simultaneously on a 16-processor computer cluster. Differential equations governing motoneuron membrane potential were solved using the exponential integration scheme (MacGregor 1987), with a time step of 0.2 ms.

Analysis

All analysis proceeded along lines similar to those normally used for experimental data. Simulated EMGs were full-wave rectified. Signals were split into 0.8192-s-long (4,096 sample points) disjoint segments before calculating power spectra, coherence, and coherence phase using formulas given in full in Baker et al. (2006). Power spectra were normalized as described in Witham and Baker (2007). Significant limits were determined as described in Baker et al. (2006). Phase 95% confidence limits (shown as error bars on plots) were determined according to Rosenberg et al. (1989). Linear regression analysis was used to fit lines to the linear segments of the phase–frequency plot; dividing the slope of fitted lines by 2π yielded the associated delay estimate, in seconds.

RESULTS

Corticomuscular coherence

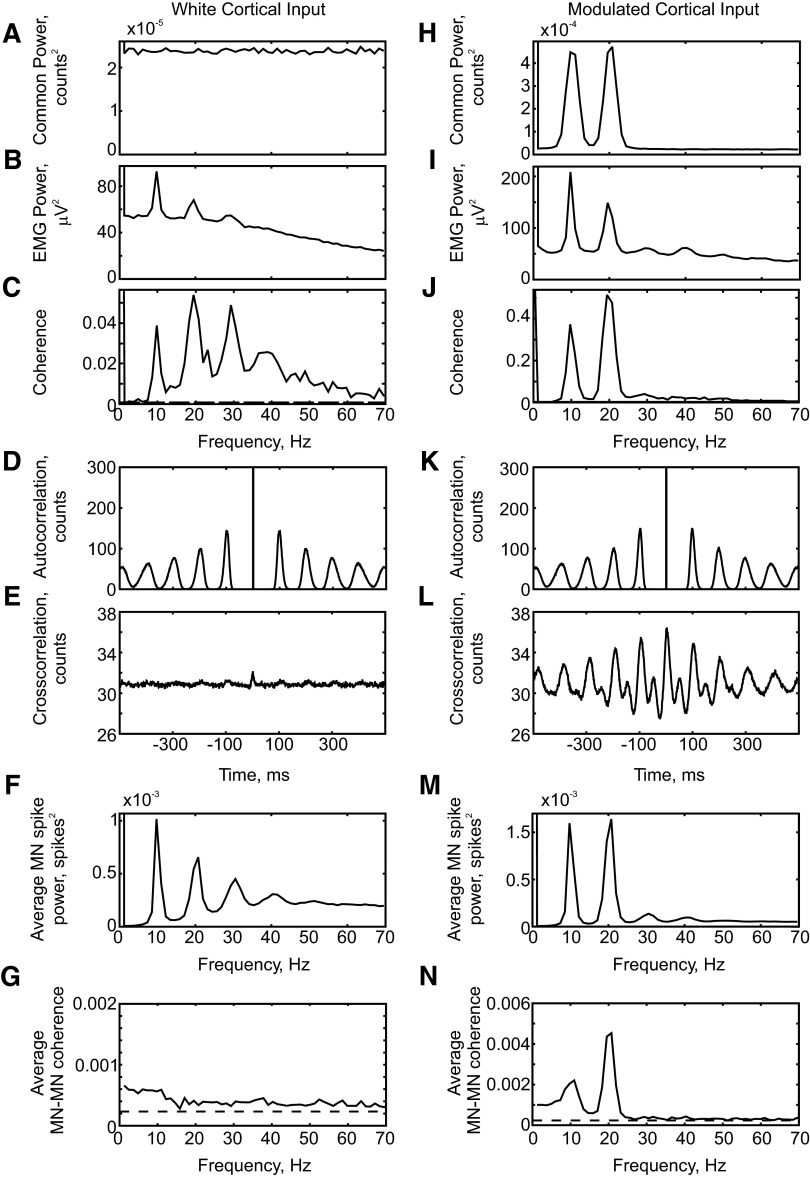
The model was simulated to determine the properties of corticomuscular coherence that would result from simple feedforward propagation of oscillations from the cortex to the motoneurons. A contraction strength of 5% MVC was simulated (involving activity in 177 motoneurons; based on Wani and Guha 1975) because this corresponds to the weak forces commonly used to investigate corticomuscular coherence experimentally in man. Although it is difficult to assess the strength of contraction as a percentage of MVC in animal studies, these also usually use weak contractions for which 5% MVC probably represents a reasonable estimated level. Figure 2 A shows the power spectrum of the cortical input; this was flat, since the cortical input was generated as white noise. The EMG power, however, revealed peaks at 10, 20, and 30 Hz (Fig. 2B). Although coherence between cortical input and EMG was significant over the entire frequency range (2–70 Hz), there were clear peaks at approximately 10, 20, and 30 Hz, with coherence values of 0.039, 0.054, and 0.049, respectively (Fig. 2C).

FIG. 2.

Results from simulations (4,017 s) using white-noise cortical inputs (A–G) and a cortical input modulated to produce spectral peaks at 10 and 20 Hz (H–N). A and H: power spectrum of cortical input. B and I: power spectrum of rectified electromyogram (EMG). C and J: coherence between cortical input and rectified EMG. D and K: motoneuron spike autocorrelation, averaged over all cells in the motoneuron pool. E and L: cross-correlation between motoneuron spikes, averaged over all possible pairs of motoneurons in the pool (E was smoothed using a Gaussian kernel, width 0.5 ms). F and M: power spectrum of the population spike activity of the motoneurons. Bin width of 1 ms in time domain plots. G and N: average coherence between motoneuron spike trains (averaged over 100 pairs of motoneurons, chosen at random).

Since the motoneuron pool in this simulation was driven by inputs with a white power spectrum, the source of the peaks in the EMG power spectrum must be the motoneurons themselves. Figure 2D shows the sum of the autocorrelation histograms of each motoneuron's spike output. The motoneurons fired fairly regularly (coefficients of variation of interspike intervals from 9 to 10%) and the mean rate varied only slightly across the pool (from 8.4 to 10.2 Hz). This resulted in a clear periodicity to the summed autocorrelation, with peaks close to multiples of 100 ms. Figure 2E shows the sum of all possible cross-correlation histograms computed between motoneuron cell pairs. A small narrow central peak is visible, similar to that seen experimentally (Datta and Stephens 1990); in addition, the periodicity in the motoneuron discharge causes weak oscillatory synchronization, visible as small side peaks at multiples of 100 ms. As a consequence of the periodic motoneuron discharge and the oscillatory synchrony between unit pairs, the power spectrum of the total motoneuron spiking shows peaks at 10 Hz and its harmonics (Fig. 2F). This is similar to the rhythmicity detected in the EMG power spectrum, although the relatively broad motor unit action potentials cause some smearing of oscillations in the EMG compared with the motoneuron spike train and less pronounced power spectral peaks (in Fig. 2, compare B with F). The interaction of an afterhyperpolarization with the spiking threshold represents an important nonlinearity of motoneuron behavior, leading to regular firing. This generates a periodic output and peaks in the corticomuscular coherence from a white cortical input.

Experimentally, we know that motor cortex generates oscillations at roughly 10 and 20 Hz that are propagated down the corticospinal tract (Baker et al. 1997, 2003; Conway et al. 1995; Halliday et al. 1998; Murthy and Fetz 1992; Witham and Baker 2007). To test the effects of driving motoneurons with nonwhite input, the cortical input was modulated in the frequency domain to have 10- and 20-Hz peaks in a further simulation (Fig. 2H), while leaving the independent input to the motoneurons unchanged. Much larger peaks at about 10 and 20 Hz were generated in both the EMG power spectrum (Fig. 2I) and the corticomuscular coherence (Fig. 2J). A small peak at about 30 Hz remained in the coherence, which was similar in size to that seen with unmodulated cortical input (peak height 0.040).

Introducing modulation of the cortical input left the summed autocorrelations of motoneuron spiking remarkably unchanged (Fig. 2K, compared with Fig. 2D). The most important impact on the motoneurons was to increase the extent of oscillatory synchronization between cell pairs, visible as large side peaks in the summed cross-correlation of Fig. 2L (compare with Fig. 2E). The increased oscillatory cross-correlation produced larger peaks at 10 and 20 Hz in the power spectrum of summed motoneuron spiking, similar to the increases at these frequencies in the EMG power spectrum (Fig. 2M).

It is hard to determine what level of modulation of the colored noise at about 10 and 20 Hz would be realistic. Although there are data on how well single corticospinal cells represent cortical oscillations (Baker et al. 2003), the modulation of the population spiking will depend on precise details of the size of the population and the extent of common noise (Baker et al. 2003). Using the levels shown in Fig. 2H, corticomuscular coherence at about 20 Hz peaked at 0.51, which is larger than most experimentally reported values. By contrast, the average coherence between pairs of motoneuron spike trains was 0.0045 at 20 Hz (Fig. 2N). Motor unit coherence in experimental studies is generally higher than this (Farmer et al. 1993; Semmler et al. 2004), although similar coherence values have also been reported (Semmler et al. 2004, Fig. 1E). This suggests that the magnitude of modulation used is approximately correct. However, little account should be taken of the precise values of the measures in Fig. 2, H–N because these could be altered by changing the bandwidth or the relative magnitudes of the 10- and 20-Hz modulation.

Figure 2G shows the motor unit coherence for white cortical input that is much smaller and has no clear peaks than for modulated common input (Fig. 2N). This agrees with a previous modeling study by Farmer et al. (1993), which suggested that white cortical inputs do not produce peaks in motor unit coherence, but that such peaks are most likely due to periodicities in common inputs to motoneurons.

The results from this simple model make it clear that corticomuscular coherence represents a complex interplay between nonlinearities introduced by intrinsic properties of motoneurons and periodicity in the descending input. Importantly, these simulations predict that corticomuscular coherence at about 10 Hz should be comparable to that seen at about 20 Hz (Fig. 2M). This does not fit with experimental data, where 10-Hz coherence is weak or absent, suggesting that the model lacks an important component of the neural circuitry involved.

Corticomuscular coherence phase

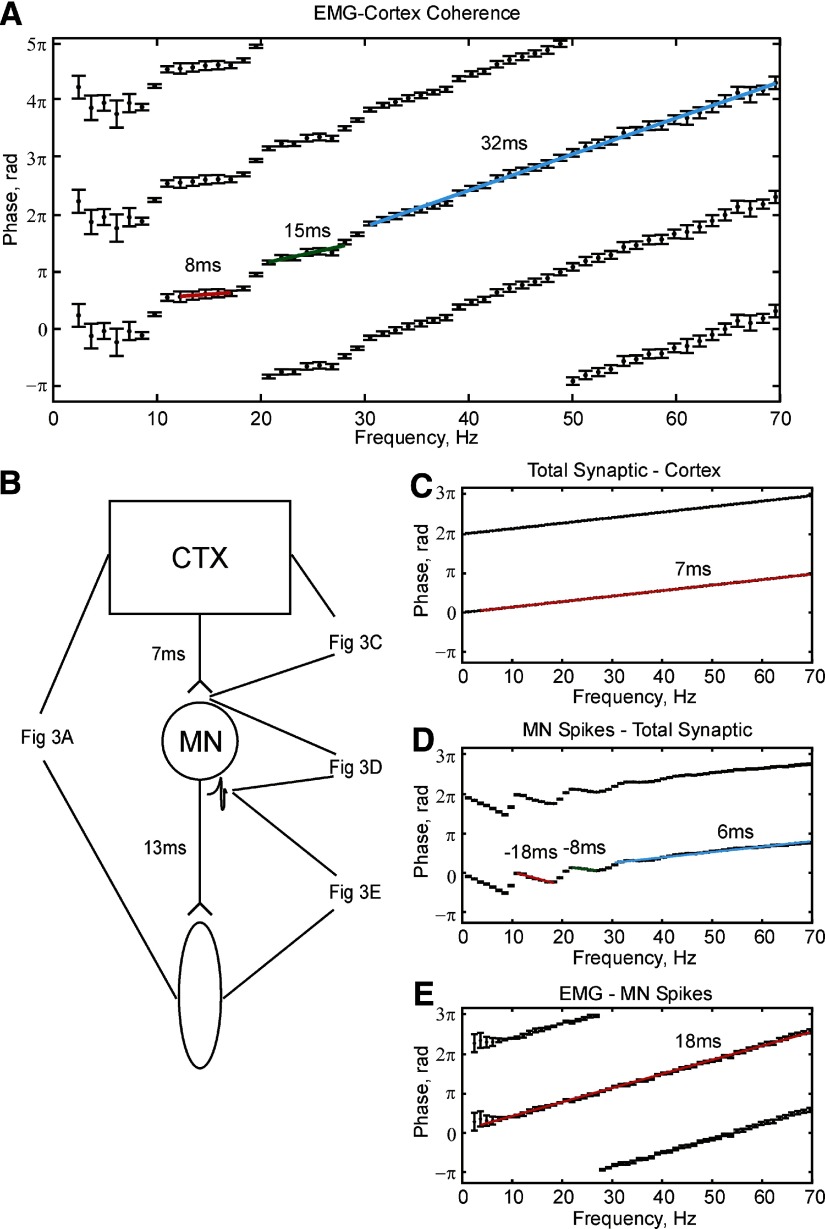
Figure 3 A shows the phase of corticomuscular coherence determined from the model investigated in Fig. 2, for cortical inputs with a white spectrum. The model was constructed to incorporate conduction delays from cortex to muscle of nearly 21 ms, comparable to those measured experimentally. A positive slope in Fig. 3A indicates that the cortex leads the EMG. It is apparent that a single straight-line fit does not adequately explain the phase–frequency relationship. The colored lines overlaid on the graph show linear regression fits to sections of the phase spectrum. The slope of these lines implied delays of 8 ms for the 11- to 18-Hz band, 15 ms for the 20- to 27-Hz band, and 32 ms for the 30- to 70-Hz band.

FIG. 3.

Phase–frequency relationships calculated from the coherence between different outputs of the simulation. Signal pairs are denoted “output signal–reference signal”; a positive slope indicates that the output signal lags the reference. Error bars indicate 95% confidence limits on phase. A: cortical input–EMG coherence phase. B: schematic of the model showing the signals analyzed in each panel of the figure. C: coherence phase for total synaptic input–common input. D: population motoneuron spikes–total synaptic input to motoneurons. E: EMG, population MN spikes. Simulation was 4,017 s long.

To understand the generation of these delay measures, we measured the coherence phase between various stages of the signal propagation from cortex to motoneuron (Fig. 3B). Coherence phase measured between the cortical activity and total synaptic input to the motoneuron showed a perfect linear relationship (Fig. 3C), with an implied slope of 7 ms. This exactly matched the conduction delay for transmission in the corticospinal axon, incorporated within the model.

The coherence between the total synaptic input to the motoneuron pool and the summed motoneuron spiking showed a much more complex phase–frequency relationship (Fig. 3D). In the 10- to 20-Hz band, there was a linear region with negative slope, indicating that motoneuron spikes appear to lead its inputs by 18 ms. From 21 to 27 Hz a smaller advance of 8 ms was seen. Between 30 and 70 Hz the line had a positive slope, implying a 6-ms delay.

For coherence between summed motoneuron spiking and EMG, the phase–frequency relationship was linear over a wide frequency range. The slope indicated that EMG is delayed from motoneuron spikes by 18 ms.

When the delays measured between individual stages of the network were summed, they closely approximated the overall delays estimated for corticomuscular coherence.

Input–output phase relationships for the motoneuron pool

Two aspects of the coherence phase–frequency relationship for the motoneuron pool (Fig. 3D) are unexpected. First, over some frequency ranges the best-fit line had a negative slope, suggesting a predictive spiking mechanism. Matthews (1997) showed, using both experiment and modeling, that motoneurons could introduce a phase advance between their spiking and their inputs. The size of this effect depended on the firing rate. The peak phase advance was roughly 90° when firing at about 9 Hz; this reduced to around 57° at 10 Hz. The present results probably reflect similar processes; for a more detailed account of the phase advance generated by motoneurons see Baldissera et al. (1984).

Second, the coherence phase appeared to oscillate with frequency, rather than showing a simple linear dependence. To understand this better, we computed a peristimulus time histogram of spikes from the motoneuron pool, triggered by the total synaptic inputs to the motoneuron pool, illustrated in Fig. 4A. The motoneuron pool impulse response consists of a facilitation (duration 8.8 ms) and a subsequent period of reduced firing probability. Kirkwood and Sears (1982) showed that the response of a cell to a synaptic input could be well represented by a mixture of the EPSP waveform and its derivative. The long duration of the peak in this instance indicates a dominant contribution from the EPSP time course; this is expected where the level of membrane noise in the responding cell is large compared with the EPSP, as in this case (Kirkwood and Sears 1982). The suppression following the peak reflects the refractory period of the motoneurons; cells that fire in the peak will not fire again shortly afterward (Perkel et al. 1967).

FIG. 4.

A: cross-correlation histogram of MN spikes triggered by synaptic inputs, averaged over the entire motoneuron pool. B: coherence computed between a white-noise input signal and an output signal formed by convolution with the impulse response function in A. C: coherence phase estimated from this procedure (black), overlaid on the MN phase response determined from the model (blue, equivalent to Fig. 3D). D: like A, but on a longer timescale, showing small later-period components of the cross-correlation (smoothed with a Gaussian kernel, 0.5-ms width). E: coherence spectrum calculated for this impulse response, showing peaks due to band-pass filtering action. F: phase response calculated from this response (black), overlaid on model phase as in C. Simulation length was 4,000 s (black) and 4,017 s (blue).

We sought to investigate how the impulse response function of Fig. 4A would translate into coherence and phase spectra. Accordingly, we generated a random waveform as zero-mean Gaussian white noise (signal 1). This was then convolved with the function shown in Fig. 4A and independent Gaussian white noise was added (signal 2). Figure 4B shows the resulting coherence spectrum calculated between signal 1 and signal 2. The impulse response acted as a band-pass filter. Figure 4C presents the phase spectrum of the coherence between signals 1 and 2 (black points). The phase spectrum observed between motoneuron input and output from the simulations is overlaid in blue. The impulse response estimated in Fig. 4A produced a monotonically increasing phase spectrum, which poorly matched that determined from the simulations at low frequencies.

The reason for this discrepancy can be understood from examining the impulse response function of the motoneuron pool on a longer timescale (Fig. 4D). Although this is dominated by the initial peak, subsequent smaller peaks are visible at a spacing of close to 100 ms. These arise from the regular discharge of the motoneurons that are all firing at rates close to 10 Hz. Figure 4E shows the coherence spectrum produced from this impulse response function—there were now clear peaks at 10 and 20 Hz. The impulse response function thus passes some frequencies of input more effectively than others. Figure 4F presents the coherence phase spectrum. This now exhibited oscillations in phase, rather than a monotonic relationship, and well matched the phase spectrum seen in the simulations.

We conclude that the nonlinear change of corticomuscular coherence phase with frequency seen in Fig. 3A results from the periodicity of firing of the motoneurons.

Phase delay between motoneuron spiking and EMG

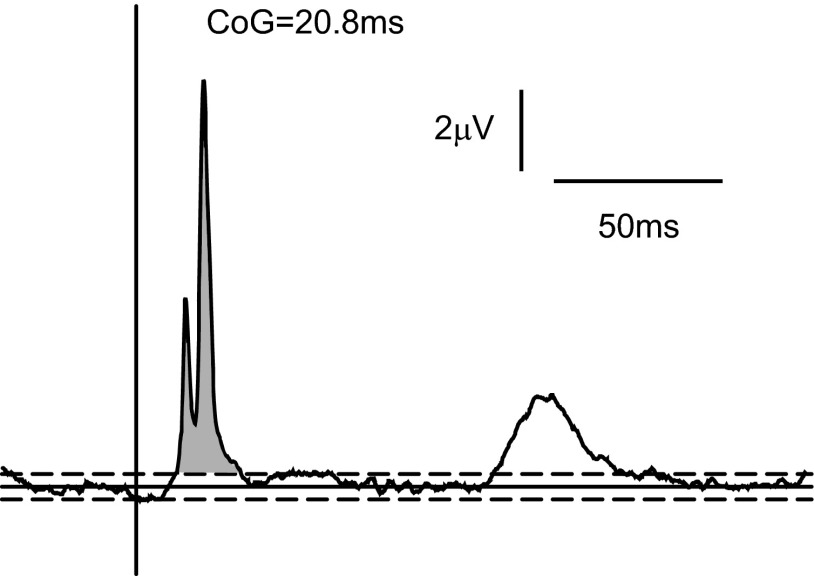
The model was constructed to include a minimum conduction delay from motoneurons to the muscle of 11 ms, with a maximum of 2-ms dispersion across the different motor axons. By contrast, the delay measured from the coherence phase between motoneuron spikes and EMG was around 18 ms (Fig. 3E). To understand this discrepancy, a spike-triggered average (STA) of the rectified EMG was constructed, triggered by the motoneuron spikes (Fig. 5). The onset latency of the peak in the STA was 13.6 ms, close to the expected neural conduction time. However, coherence analysis will not be sensitive to the onset latency, but to an “average” latency of the whole response. The center of gravity of the peak in Fig. 5 (shaded area) had a latency of 20.4 ms, close to the delay estimated from the coherence phase. The peripheral delay estimated using coherence is thus sensitive not only to the neural conduction time, but also to the duration of the motor unit action potentials. This was previously suggested by Riddle and Baker (2005).

FIG. 5.

A: spike-triggered average (STA) of the rectified EMG compiled using spikes from all motoneurons in the pool. Horizontal lines show the pretrigger baseline ±2SDs. The center of gravity (CoG) was calculated for the primary STA peak (shaded).

Effects of changing motoneuron pool properties

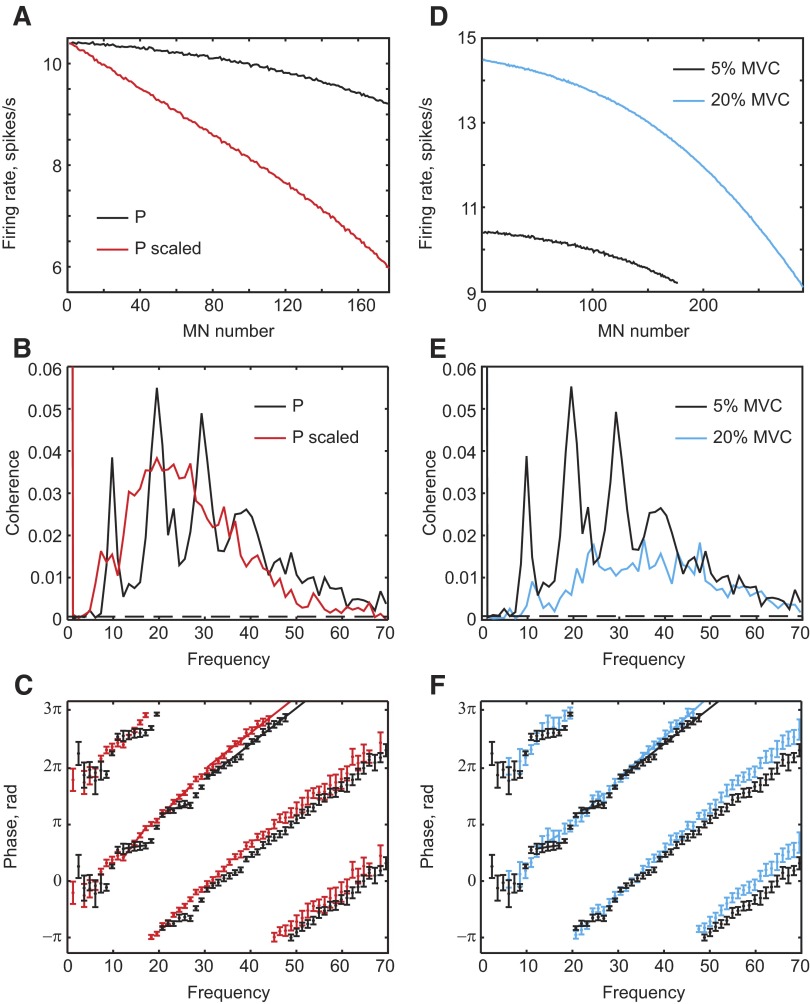
At the contraction strength of 5% MVC modeled so far, all cells in the motoneuron pool fired at very similar rates. We demonstrated earlier that this leads to oscillatory subpeaks in the motoneuron pool impulse response function. As a consequence, broadband input produces corticomuscular coherence with clear peaks (Fig. 2C) and the coherence phase varies in an oscillatory manner with frequency (Fig. 3A). It might be expected that a model with a more heterogeneous motoneuron pool would not show such effects. In this model, the parameter P represents the ratio of somatic to dendritic area. We normally determined P across the motoneuron pool so that the cells fired at the rates predicted by the model of Wani and Guha (1975) (Fig. 6 A, black line). To generate a more heterogeneous pool with greater rate variation, we scaled P, which we did by multiplying each value of P by a gain factor. The gain factor increased linearly across the motoneuron pool from 1 to 1.93 for motoneurons 1 to 177, respectively. This resulted in the rates changing across the pool as illustrated by the red line in Fig. 6A. Although, originally, rates varied only between 8.4 and 10.2 Hz, this change produced rates from 6.0 to 10.2 Hz across the pool. The independent input was kept the same, producing a smaller contraction strength. The narrow peaks in corticomuscular coherence observed in the original model (Fig. 6B, black line) were abolished by this procedure (Fig. 6B, red line). In addition, the oscillations in the phase spectrum (Fig. 6C, black) were removed in the altered model. Phase now varied linearly with frequency, with a slope implying a delay of 34 ms (Fig. 6C).

FIG. 6.

A: firing rate vs. motoneuron number at a contraction strength of 5% maximal voluntary contraction (MVC), for the standard model (black) and one where the parameter P has been rescaled to produce greater variation across the motoneuron pool (red). Corticomuscular coherence (B) and corticomuscular coherence phase (C), for the 2 simulations. D–F: plots similar to those of A–C, but for the comparison of contraction strengths of 5% MVC (black) and 20% MVC (blue). Simulation length was 8,034 s for all plots.

A more natural way to increase the variation in firing rate across the motoneuron pool is to increase the contraction strength. Results from a simulation that produced 20% MVC are shown in Fig. 6, D–F (blue lines). This effectively changed the rate variation across the pool (Fig. 6D). As for Fig. 6, B and C, when the motoneuron pool became more heterogeneous, the narrow coherence peaks were reduced (Fig. 6E) and the coherence phase was linearized (Fig. 6F).

In Fig. 6B the overall amount of coherence has not been reduced; instead it has been made broad with less prominent peaks. Changing the contraction strength also made the coherence broader with flatter peaks, but the overall amount of coherence was decreased. This is because more independent input is needed to achieve a contraction strength of 20%, which decreases the signal-to-noise ratio. The independent input was the same for the models in Fig. 6A, explaining why the amount of coherence did not change.

The introduction of peaks in the coherence spectrum and the oscillatory phase–frequency profiles occur when the firing rates are narrowly distributed across the motoneuron pool. Increasing the rate dispersion led to a more linear response to the white cortical input. At 5% MVC the motoneuron firing rates varied between 8.4 and 10.2 Hz. These values are consistent with experimental data from Milner-Brown et al. (1973), which estimates that motor units in the first dorsal interosseous increase their firing rate by 1.4 impulses/s per 100 g increase in force. However, some authors suggest a higher spread of firing rates (8–16 Hz) at 5% MVC (Bigland and Lippold 1954). This situation resembles the spread of firing rates in the present simulation at 20% MVC (Fig. 6, D–F), which still shows significant coherence peaks at 10 and 20 Hz for a white-noise input; these peaks were even larger if modulated cortical input was used (data not illustrated). Oscillations are thus still being passed effectively through this circuit despite the different dispersion of motoneuron firing rates.

Role of persistent inward currents in motoneurons

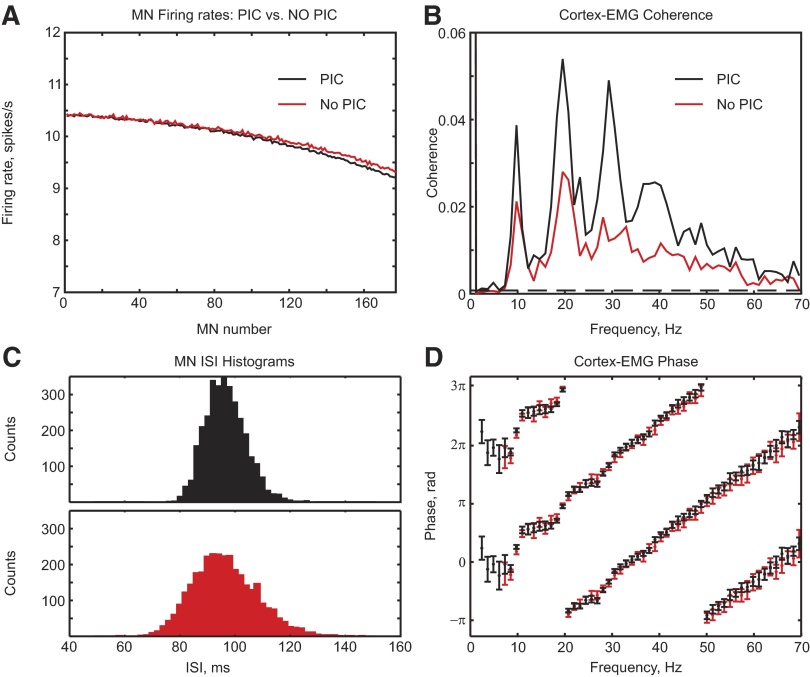
One feature of the present model is that it uses a realistic representation of the motoneurons, including sodium and calcium PICs (Li and Bennett 2003; Li et al. 2004a,b). Once activated, these currents allow the motoneurons to continue firing with less synaptic input. To investigate the impact of PICs on corticomuscular coherence, the model was simulated with these conductances disabled. To maintain a contraction strength of 5% MVC, a larger rate of independent input to motoneurons was required in this reduced model (8 kHz with PICs vs. 22.9 kHz without). We have seen that the dispersion of motoneuron firing rates can change both the coherence and its phase. Figure 7 A shows that the motoneurons have similar firing rates with and without PICs (Fig. 7A), indicating the success of the increased synaptic input at maintaining firing in the no-PIC simulation. The effect on corticomuscular coherence is shown in Fig. 7B; removing PICs reduced the coherence amplitude, but the location of the subpeaks was similar. The increased independent input required in the absence of PICs meant that the cortical input to the motoneuron was a smaller fraction of the total than when PICs were able to contribute to the current driving the motoneurons to fire. The reduced signal-to-noise ratio in the motoneuron inputs led to the reduction in coherence.

FIG. 7.

A: firing rates of individual motoneurons for the standard model (black) and a model in which persistent inward currents (PICs) were removed from the MNs (red). B: corticomuscular coherence. C: interspike interval (ISI) histograms from one MN. D: corticomuscular coherence phase for these 2 stimulations. Simulation length was 4,017 s.

Although the location of the coherence peaks without PICs is similar, the peak near 30 Hz decreased more than those near 10 and 20 Hz. Activation of PICs allowed the motoneuron to maintain its firing rate when the synaptic input was decreased. This produces a less regular firing rate in motoneurons without PICs (Fig. 7C). The average coefficient of variation of the ISIs of the motoneurons was 9.4% with PICs and 11.9% without PICs. This decrease in regularity without PICs produces smaller harmonics in the MN spike power at about 30 Hz and thus coherence at close to 30 Hz is reduced. Removing the PICs left the coherence phase unchanged (Fig. 7D). Aside from the reduced overall coherence, PICs seemed to affect corticomuscular coherence rather little.

DISCUSSION

Corticomuscular coherence

In this study, we have shown that a realistic computational model can reproduce many of the features of corticomuscular coherence seen experimentally. Most of the model parameters were not free, but constrained by the detailed knowledge of the motor system available from the literature. One important finding is that, using realistic values for these parameters, corticomuscular coherence was present at levels roughly in accord with experimental measurements.

Studies that work with massed activity, such as EEGs, local field potentials (LFPs), or EMGs, often make the implicit assumption that neural communication dynamics will be simple—for example, that phase–frequency relationships will be no more complex than a linear dependency indicating a fixed conduction delay. However, the considerable body of literature on single-cell electrophysiology points to a rich repertoire of response properties, in which the effect of an input critically depends on how it interacts with the intrinsic properties of the cell (Matthews 1997; Poliakov et al. 1997). The present work is an attempt to relate these well-known single-cell properties to the effect they will have on massed activity measures.

The model we describe here leads to several novel conclusions relevant to corticomuscular coherence. First, we show that even if inputs from the cortex to motoneurons are spectrally white, corticomuscular coherence may have distinct peaks produced by resonance between the input and the intrinsic rhythmicity of the motoneurons. It has been known for some time that the autocorrelation of a responding cell could produce secondary features in the cross-correlation histogram with another cell from which it receives input (Perkel et al. 1967). At the level of EMG, the heterogeneity of firing across the motoneuron pool also plays an important role (Fig. 6), which can be altered by strength of contraction (Fig. 6D). Different muscles also grade force using firing rate or recruitment of new units to different extents (Wani and Guha 1975), which will have an important influence on how similar motoneuron firing rates are across the pool at a given level of contraction.

Motoneurons in these simulations fired regularly with a coefficient of variation (CoV) of the ISIs around 9–10%. This regular firing produced the strong near 10-Hz periodicity in the motoneuron autocorrelations, contributing to the strong 10-Hz coherence peaks. Experimentally, interval CoV for motoneurons can be as low as 10%, but tends to be higher, at around 20% (Enoka et al. 1989; Johnson et al. 2004; Mottram et al. 2005). This would still be sufficiently regular to produce 10-Hz coherence, but the peak would probably be smaller and broader. Higher CoVs would also reduce the size of the coherence peaks at around 20, 30, and 40 Hz because these are due to the harmonics of the strong 10-Hz periodicity. Although the specific firing properties of the motoneurons probably play a role in determining the size and shape of the corticomuscular coherence peaks, they cannot account for the absence of corticomuscular coherence close to 10-Hz seen in most experiments.

Second, this model has shown that the phase of corticomuscular coherence is generated by several interacting factors that are not usually considered in this context. These include the full duration of the EPSP in the motoneuron (rather than just its rise time) and the width of the motor unit action potential (Figs. 3 and 5). In addition, the same resonant properties that led to peaked coherence spectra in response to white-noise input can lead to oscillations in the coherence phase (Fig. 4).

The result of all of these considerations is that, for the model considered here (appropriate for human hand muscles), corticomuscular coherence phase for frequencies around 20 Hz can show a linear dependence on frequency, with a slope indicating a delay of between 8 and 15 ms (Fig. 3A). If the nature of the contraction strength or muscle properties mean that firing rate differs substantially across the motoneuron pool, then a linear relationship implying a delay of about 32 ms will result (Fig. 7). Experimentally, corticomuscular coherence has variously been reported with linear phase–frequency relationships implying delays of 10 (Riddle and Baker 2005) or 16 ms (Mima et al. 2000). It is probable that these various findings can be reconciled with predictions of the present model. However, other studies have reported that corticomuscular coherence phase shows no dependence on frequency in some subjects (Halliday et al. 1998; Riddle and Baker 2005). This cannot be explained by the present model, in which coherence phase varied with frequency for all the configurations tested. Riddle and Baker (2005) proposed that both feedforward and feedback (afferent) pathways contribute to corticomuscular coherence. The companion paper investigates this suggestion in more detail by including afferent feedback in the computational model.

Most components of the system studied here were simulated using biophysically based models; however, by contrast we chose to represent the cortical activity as Gaussian white noise. This had the benefit of simplicity and allowed us to characterize the response to an input that was well defined in the frequency domain. It is known that LFP recordings do reflect population oscillations in single units with high fidelity, although there is a phase shift of π/2 between the LFP and the unit activity (Baker et al. 2003; Soteropoulos and Baker 2006; Witham et al. 2007). The general conclusions of the present study are thus likely to be unaffected by this simplification because we have focused on the slope of the phase–frequency relationship, rather than the absolute phase of coherence. Mima et al. (2000) noted that the coherence phase–frequency spectrum was best represented by a “constant phase plus constant delay” model. The constant phase offset probably partly reflects the transformation between spiking activity and LFP.

The phase of corticomuscular coherence has a complex relationship with the underlying circuitry producing it. This simple model can explain some but not all of the experimental results; it makes clear the critical role of motoneuron dynamics, which cannot be ignored in interpreting experimental coherence measurements.

GRANTS

This work was funded by the Wellcome Trust and a Medical Research Council studentship to E. R. Williams.