Reversal of Bimanual Feedback Responses With Changes in Task Goal

Abstract

We show that fast bimanual coordinative feedback responses can be reversed with changes in task goals. Participants moved a flexible virtual object across a finish line with an upward movement of both hands. In one condition, the middle of the object had to be aligned with a spatial goal at the end of the movement. In the second condition, the object had to be kept at a specific length. During the movement, a velocity-dependent force field was applied randomly to one of the hands to the left or to the right. Depending on the task condition, the unperturbed hand showed fast feedback corrections, either in or against the direction of the force field on the other hand. In the object-length condition we found evidence for a mixture of task goals: early in the movement the correction of the unperturbed hand was aimed at stabilizing object length; later in the movement, the correction reversed direction to reach a symmetric body posture in the end of the movement. The observed differences in feedback responses between task conditions also influenced the covariance structure of unperturbed movements and the adaptation when a specific force field was applied repeatedly to one of the hands. The results are congruent with the notion that coordination is established flexibly through a representation of the task-relevant controlled variables, rather than through a direct interaction between motor commands.

INTRODUCTION

When a part of our body is perturbed, our reflexes lead to local feedback corrections around that joint. However, we also show feedback responses with other, not directly perturbed body parts. Here these responses are called coordinative feedback responses. For example, a perturbation to the thumb can elicit a reflex reaction in the toe, if the thumb perturbation threatens postural stability (Marsden et al. 1981). These coordinative feedback responses appear to be “smart”; they reflect knowledge of the internal dynamics of the limb (Kurtzer et al. 2008), the relative position of the limbs in external space (Baldissera and Esposti 2005), and correctly anticipate the reaction forces coming from objects that are being manipulated (Wing et al. 1997).

Whereas prior studies have demonstrated the flexibility of coordinative feedback responses to changes in the physical dynamics of the body or the environment, we ask here how flexibly these responses adapt to changes of the task goal under identical physical conditions. We have recently shown an example of such flexibility (Diedrichsen 2007): when participants move two separate cursors to two separate visual targets, and one hand is perturbed by a velocity-dependent force field, feedback corrections are observed only in the perturbed hand. However, if participants move one single cursor, presented at the average position of the two hands, feedback corrections are observed in both hands: the unperturbed hand helps to correct for the other hand's perturbation.

We have argued that this coordinative feedback response reflects the optimal solution to a task-dependent cost function: in the one-cursor task the goal is reached when the single cursor is brought to the target. It does not matter whether one hand veers too far to the left or to the right, as long as the other hand compensates in the opposite direction by an equivalent amount. Given this additional degree of freedom, the best solution is to distribute the feedback correction across the two arms.

Alternatively, coordinative feedback responses may arise from a misperception of force: In the normal world objects are never purely visual and, when held bimanually, always transmit forces between the two hands. Therefore the presentation of the visual object may have induced the erroneous perception that a force applied to one hand is also transmitted to the other hand. The observed coordinated feedback corrections and subsequent adaptation of both hands would then be a consequence of this misperception, rather than an adaptive task-dependent change.

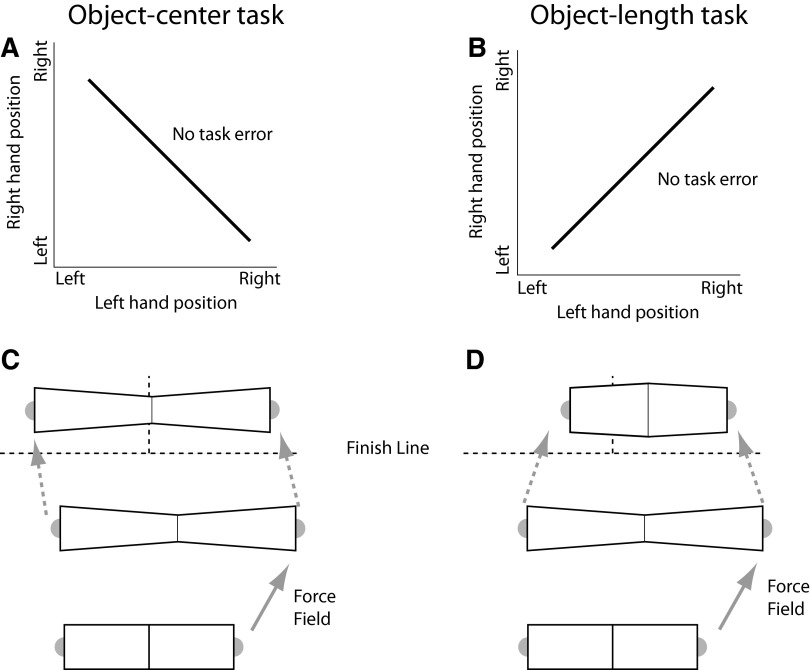
Here we dissociate the two explanations. The task-goal hypothesis makes the prediction that if the task goal is changed such that the task-relevant dimension is reversed, we should observe a reversal of the direction of the coordinative feedback response. We therefore designed a task in which participants made upward-reaching movements with both hands to transport a flexible virtual object across a finish line. The object was presented visually between the two hands, but could not be felt haptically. In the object-center condition (Fig. 1A), participants had to align the middle of the object at the end of the movement with a vertical reference line in the center of the screen. In this case, the length of the object (i.e., the distance between the two hands) was without relevance. In the object-length condition, participants had to ensure that the object length was constant. Here, the absolute position of the object at the end of the movement was task irrelevant. We then applied a force field to one of the hands during the movements. If feedback corrections reflect task goals, we predict corrections of the unperturbed hand to be in opposite directions for the two tasks (Fig. 1, C and D). However, if the observed feedback responses reflect a misinterpretation of the source of the perturbation, the feedback responses should not reverse.

FIG. 1.

Experimental task. A flexible object is visually presented between the 2 hands (gray spheres). The task is to move the object across the finish line. In the object-center condition (A, C) the middle of object has to be aligned to the center of the screen (dashed vertical line). In the object-length condition (B, D) the object has to be close to the original length. When the 2 hands are too far apart, the object was drawn out into an hourglass-figure shape (C, top), whereas when the hands were too close together, the object was compressed and started to bulge out (D, top). The line in A and B indicates the line of solutions with zero task-relevant error.

In experiment 1 we test these predictions by randomly perturbing either hand. Consistent with the task-goal hypothesis we observed a complete reversal of the initial fast response of the unperturbed hand. We then asked whether this reversal would also be present in the adaptation to a constant force field (experiment 2).

METHODS

Participants

Sixteen volunteers participated in the experiments, 8 in each experiment. Two of the participants were self-reported left-handers (average laterality index = −86; Oldfield 1971); all other were right-handers (average laterality index = 70.5). The average age was 24.7 ± 8.4 yr; 11 of the 16 participants were female. All procedures were approved by the ethics committee of the School of Psychology, Bangor University.

Apparatus

The participants made bimanual reaching movements while holding onto a robotic device (Phantom 3.0; SensAble Technologies, Lincoln, RI) with each hand. They tightly grasped the styli at the end of the robotic arms. Movements were executed in the natural workspace in an upward and slightly forward direction on a frontoparallel plane that was tilted 20° from vertical. The robotic devices simulated a soft spring (150 N/m) to assist the participants in keeping their hands on this plane. Participants leaned against a horizontal crossbar that provided postural stability to the upper body. They viewed the visual scene on a three-dimensional (3D) calibrated stereo-display that consisted of a liquid crystal display monitor for each eye and a system of two mirrors. The mirrors prevented the participants from seeing their hands and the locations of the styli were displayed throughout the experiment as two spheres with 8-mm radius.

An object was visually presented between the two hands. The object was 3D, with a square-shaped profile. The sides of the object were formed by two squares of 1.5 × 1.5 cm. The middle of the object had a square profile with the size depending on the length of the object. When the hands were exactly 12 cm apart, the object took the shape of a cuboid (Fig. 1, C and D, bottom row). When the two hands were further apart, the object adopted the shape of an hourglass (Fig. 1C, top row), with the middle becoming thinner than 1.5 cm. When the two hands were closer together, the object started to bulge out (Fig. 1D, top row). The thickness of the object in the middle varied between 0 and 3 cm, with a logistic dependence on the distance of the hands. The object could be translated and rotated freely by movements of the hands.

Procedure

Participants started a trial by moving both cursors into the visually indicated starting locations, 6 cm on either side of the sagittal midline. On starting, the object was presented, together with a horizontal finish line located on the movement plane 10 cm above the starting locations. Participants were instructed to move the object fast across the finish line and stop immediately behind it. In the object-center task the center of the object had to be aligned with the middle of the workspace, indicated by a line that extended 6 cm upward from the finish line. In the object-length task the length of the object at the end of the movement had to be within a certain range (see following text) of the desired length of 12 cm.

On some trials, a velocity-dependent force field (Shadmehr and Mussa-Ivaldi 1994) was applied to one of the hands. The robotic device pushed the arm in the lateral direction with a force that depended linearly on the upward velocity of the hand along the movement plane with a proportionality constant of 4 N·m⁻¹·s⁻¹. The force field was switched on throughout the trial and, given its velocity dependence, could be detected only once the hand started moving.

To be accepted as correct, movements had to fulfill both speed and accuracy criteria. First, the average peak movement speed of the hands needed to exceed 50 cm/s and the movement time (MT) had to be below an upper limit of 650–800 ms. Movement times were measured from the first moment the speed was >2 cm/s until the speed dropped again to <2 cm/s for ≥60 ms. The MT criterion was set based on the performance of the participant in the training blocks. When one of these requirements was not met, the object turned blue, indicating too slow a movement; otherwise, the spatial accuracy was evaluated. In the object-center task, the center had to be within 0.25–0.5 cm of the vertical goal line. In the object-length task, the length of the object had to be within 0.4–1.0 cm of the required length of 12 cm. When the spatial criterion was met, a point was awarded to the participant; otherwise, the object exploded visually. The spatial thresholds for the two task conditions were adjusted separately such that the average rate of rewarded movements was about 40%.

Experiment 1

Experiment 1 consisted of a training block and two sessions. In a training block of 64 trials participants got acquainted with the object and task. In this block, they had to move the object across the finish line within the MT cutoff, both to align the center of the object with the vertical reference line and to keep the object at the correct length. No force fields were applied in this block.

This was followed by a first session of eight blocks of 64 trials in either the object-length or object-center condition. In half of these trials no force field was presented. In the other half, a velocity-dependent force field (see Procedure) was applied either to the left or to the right hand, either to the left or to the right direction. In half of the trials, visual feedback about the location of the hands and the object was withdrawn during the movement and presented again only after the movement was completed. In the other half of the trials, visual feedback was continuously provided. Thus over the course of the one session, a particular feedback (2 possibilities) × force field condition (4 possibilities) was repeated 32 times. A second session was conducted 1–3 days after the first session. In this session participants performed eight blocks of the other task condition.

Experiment 2

In experiment 2, participants started the experiment with a practice block in the object-center and in the object-length tasks. No force fields were applied during these two blocks. After practice, participants performed eight adaptation runs, each consisting of 120 trials. Each run comprised 20 trials of null field, followed by 80 trials, in which a clockwise or counterclockwise force field was applied either to the left or to the right hand. We inserted 16 catch trials randomly chosen from these 80 trials, where no force field was applied.

Every participant performed each of the eight possible runs (two task conditions × two hands that the force field could be applied to × two force field directions) in a counterbalanced order. The first four adaptation runs were performed in the first 1-h session; the second four runs were performed in a separate session, 1–2 days after the first one.

RESULTS

Experiment 1

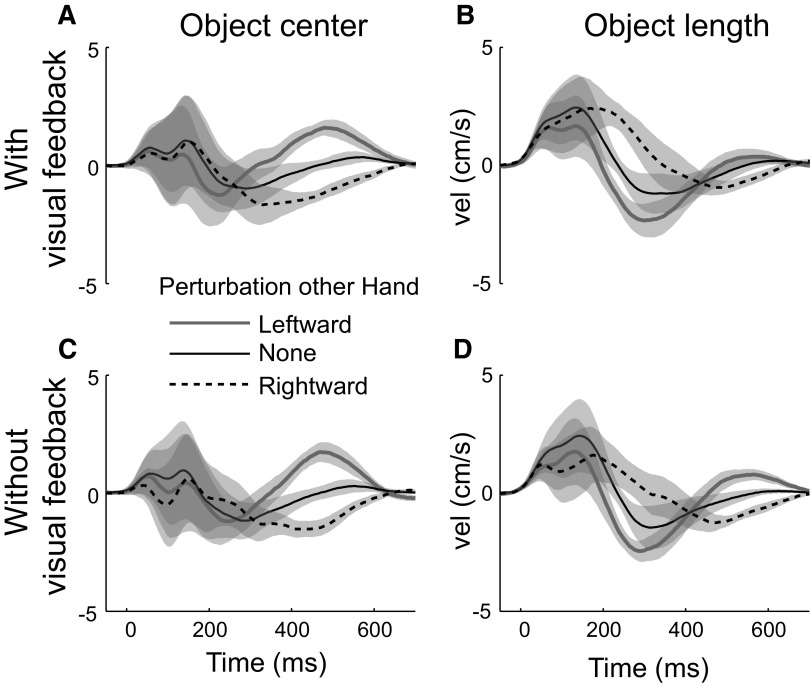
If coordinative feedback corrections are dependent on task goals, we would expect that the two hands would show feedback corrections in the same spatial direction for the object-center task, but in opposite directions in the object-length task. Figure 2 shows the average lateral velocity of the unperturbed hand, aligned to the start of the movement, when the other hand is perturbed leftward, rightward, or not at all. In the object-center condition, the unperturbed hand responded with a correction against the direction of the force field applied to the other hand. In the object-length condition, this early response was reversed: now the unperturbed hand responded with a correction in the direction of the force field. Furthermore, the on-line correction on the unperturbed hand was not different when visual feedback was present (Fig. 2, A and B) or absent (Fig. 2, B and D). Thus the early feedback response of the arm switched with changed task demands.

FIG. 2.

Lateral velocity of the unperturbed hand in experiment 1, when the other hand is perturbed leftward (gray), rightward (dashed), or not at all (solid black). A positive velocity indicates a movement to the right. Results are shown for trials with visual feedback (top row) or without visual feedback. Results are averaged across hands. The initial positive deflection in the object length task is caused by the tendency of most participants to move slightly to the right in this condition [t(7) = 2.282, P < 0.056].

Closer inspection of Fig. 2 revealed a somewhat more complex picture than a simple reversal. First, the onset of the correction in the object-center condition appeared to occur later than in the object-length condition. To determine the onset of the correction, we tested when the difference between the lateral velocities of the unperturbed hand started to differ at a significance level of P < 0.05 for leftward and rightward force fields. This test was performed for both hands of each participant, separately for each task condition. In the object-center condition the average onset was 313 ms (SD 78 ms) after movement start and in the object-length task 197 ms (SD 25 ms) [t(7) = 3.764, P = 0.007]. No significant differences in the onset or size of the correction were found when comparing left and right hands.

Second, in the object-length condition the lateral velocity reversed toward the end of the movement (Fig. 2, C and D), about 480 ms after movement start. At this point, the unperturbed hand started moving against the perturbation and into the same direction as the simultaneous correction of the other hand. As a result the middle of the object was returned toward the middle of the workspace. On average the distance of the object center from the midline was 5 mm in the object-length task and 3 mm for the object-center task. In comparison, the average error in the object length was 8 and 20 mm, respectively, in the object-length and the object-center conditions. Thus it seems that although the length of the object was not taken into account for control in the object-center condition, the end position of the object was an important variable for control in the object-length condition.

We have recently shown that coordinative feedback responses also changed the covariance structure of unperturbed movements (Diedrichsen 2007). Specifically, we found that when the two hands control a single cursor, the lateral movement endpoints were negatively correlated: when one hand ended the movement too far to the left, the other hand would compensate by stopping further to the right. This accumulation of variance along the task-irrelevant dimension can be explained by a model in which the coordinative feedback responses of both hands correct for the independent motor noise of each hand. In the object-center condition, where the task-irrelevant dimension is oriented as in the one-cursor task (Fig. 1A), we therefore should expect a negative correlation between the lateral movement endpoints for the two hands. Congruent with this prediction, the average correlation between the horizontal positions of the hands at the end of unperturbed movements was r = −0.50 in the object-center condition. Although this correlation did not fully reverse (r = −0.15) in the object-length condition, the correlations were significantly more positive than those in the object-center condition [t(7) = 4.617, P = 0.002].

Other than these significant changes in feedback correction, the mean movements were roughly comparable between the two task conditions. Movement times (680 ms, SD = 50 ms) were statistically equivalent for the two task conditions [t(7) = −0.33, P > 0.5] and similar with or without visual feedback [t(7) = −0.16, P > 0.5]. Only the average peak speed was faster in the object-center (72 cm/s) than that in the object-length condition (65 cm/s); however, this difference did not reach significance [t(7) = 2.20, P = 0.062].

In sum, we observed a reversal of the early feedback response on the unperturbed hand with the task goal. The reversal, however, was not fully symmetric. In the object-length condition, the feedback correction reversed in the end phase of the movement, canceling out some of the earlier response.

Experiment 2

We now turn to the question of how coordinative feedback responses influence adaptation to a constantly applied force field. In an earlier study (Diedrichsen 2007) we found that when a force field was applied to one hand, the other hand also adapted after a number of movements: it changed the initial movement direction against the direction of the force field and in the direction of its own coordinative feedback response. A similar finding should therefore be expected for the structurally equivalent object-center condition. For the object-length condition, however, there are two possibilities. If adaptation is driven by the initial phase of the feedback correction, then the adaptation should fully reverse; however, if adaptation is driven by the signal that indicates the contribution of the unperturbed hand to the correction across the whole movement, we may expect no bilateral adaptation in the object-length condition because the late response cancels out much of the earlier initial correction.

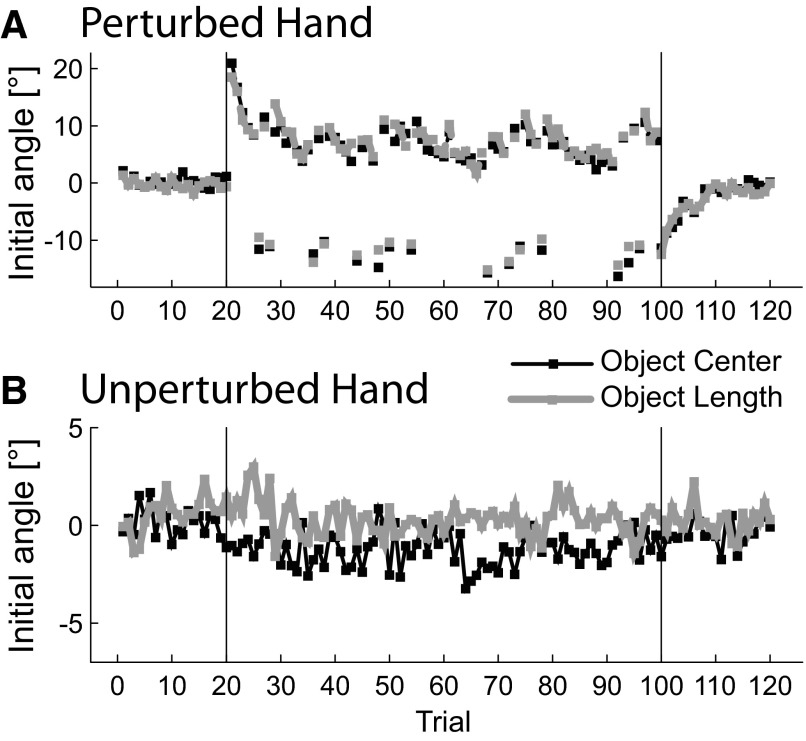
We therefore applied a force field in a constant direction to one of the hands for 80 trials. During this phase, adaptation on the perturbed hand was rapid and reached asymptote after the first 20 perturbed trials (Fig. 3A). Initial direction errors, in the opposite direction, were observed on interspersed catch trials. This adaptation was not significantly different between task conditions.

FIG. 3.

Results of experiment 2. A: initial angle of the perturbed hand and the unperturbed hand (B) as a function of trial, averaged across hands and force field directions. A force field was applied between trial 21 and trial 99 (vertical lines). Single trials with initial errors in the direction opposite to the force field (negative) are catch trials.

Of main interest in this experiment was the adaptation of the unperturbed hand (Fig. 3B). In the object-center task, we indeed observed a change of the initial direction of the unperturbed hand. Depending on whether the force field was leftward or rightward, the unperturbed hand changed its initial direction by 2.5° [t(7) = 2.504, P = 0.041]. In noncatch trials this difference accumulated to a 6-mm difference at the end of the movement. Interestingly, this amount of difference is equivalent to the average size of correction in the random perturbation paradigm in experiment 1.

In contrast to the object-center condition, no such adaptation was observed in the object-length condition: the average change was −0.5° [t(7) = 0.513, P = 0.62]. It therefore appears that not the initial correction, which fully reversed, but rather the total correction, which was close to zero in the object-length condition, may have served as the teaching signal for the adaptive change.

DISCUSSION

In sum, we clearly showed that the early coordinative response of the unperturbed arm is dependent on the task goal. When the task goal is to move the middle of the object to a certain location, the unperturbed hand quickly corrects against the direction of the perturbation on the other hand. When the task goal is to keep the length of the object constant, the unperturbed hand corrects in the direction of the perturbation.

These findings have parallels to some earlier work on long-latency postural reflexes. In an elegant series of experiments, Marsden and colleagues (1981) had participants make movements with the left wrist against a load, while standing freely. Using a step motor, they perturbed the wrist by either increasing or decreasing the load during the movement and measured the early postural reflex response in the other arm. In one task condition, the right hand held on to the edge of the table. When the left wrist was stretched away from the body, the right biceps increased its activity to stabilize the body by pulling in the opposite direction. The change in muscle activity began before any kinematic perturbation could be recorded at the right shoulder, arguing it was driven by an internal coordinative feedback response. In a second task condition, the participant held a freely movable object that needed to be stabilized in the right hand—a situation similar to holding a full teacup. In this condition, a stretch of the left wrist flexors led to increased activity in the right triceps, which prevented movement of the cup, again before any mechanical perturbation had been transmitted through the body. Thus as in our experiment, task requirements completely reversed the direction of the initial coordinative feedback response. In contrast to our task, the responses here were necessitated by a physical postural perturbation of the freestanding body. In our case, the need to coordinate arose from the task instruction alone, without any physical link between the hands and with the upper body supported.

Coordinative feedback responses can be understood as the optimal solution to a task-dependent cost function (Diedrichsen 2007). Specifically, if we assume that the nervous system estimates the state of the task-relevant controlled variables, here either the length of the object or the width, then the control policy, the function that translates a state estimate into motor commands, takes a particularly simple form: the motor commands to each limb then depend on the state of the limb and the state of the task-relevant controlled variable, but are independent of the state of the other limbs. Congruent with this notion, a number of studies have shown that changes in visual consequences of actions are a powerful determinant of the way movements are coordinated (Mechsner et al. 2001; Swinnen et al. 1993). Extending this notion, we show here clearly that the change in coordination does not depend on the presence of the actual visual feedback per se. Rather the anticipated changes in the task-relevant controlled variables dictate movement coordination (Prinz 1990).

Because the task requirements are mirror-reversals of each other (Fig. 1, A and B), the hypothesis of task-dependent feedback correction would have predicted that the unperturbed hand would show exactly mirror-symmetric responses in the object-length and the object-center conditions, although this was not the case. First, the onset of the coordinative feedback correction was significantly earlier in the object-length condition. This may reflect a tendency of the nervous system to prefer mirror-symmetric movements (Kelso 1984; Swinnen 2002), such as the corrections in the object-length condition, over movements in the same spatial direction, such as the corrections in the object-center condition. This propensity of mirror-symmetric corrections may also be caused by automatic anticipatory postural adjustments in one arm in response to movements in the other (Baldissera et al. 2008).

Second, in the object-length task, we found a reversal of the on-line correction of the unperturbed hand toward the end of the movement. This reversal, together with the simultaneous correction of the perturbed hand, brought the object back closer to the midline, although the absolute position of the object was not task relevant. We hypothesize that this response may reflect a hierarchy of goals. Early in the movement, the main task goal is to keep the length of the object constant. Toward the end of the movement, a symmetric hand position may become an important goal. This may be explained by several reasons. First, although we supported the upper body of the participants with a crossbeam, asymmetric body positions necessitate slight tension in the postural muscles of the trunk and may be more uncomfortable. Participants therefore may have been trying to maximize their end-state comfort (Rosenbaum et al. 1996; Weiss et al. 2007). Alternatively, a symmetric end position may have been preferable because it may allow a better estimation of object length.1 No matter the underlying reason, the reversal of the feedback correction appears to reflect an interaction of two implicit task goals that differ in their importance across the time course of the action: object length and the achievement of a symmetric end position.

A similar asymmetry between the object-length and object-center conditions was found in the endpoint correlation in unperturbed movements. The uncontrolled manifold hypothesis (Domkin et al. 2002; Latash et al. 2002) or, equivalently, the minimal intervention principle (Todorov 2004; Todorov and Jordan 2002), predicts that the nervous system should minimize output variance along the task-relevant dimension, whereas variance along the task-irrelevant dimension (line in Fig. 1, A and B) would be allowed to accumulate. In the object-center condition, a strong negative correlation of movement endpoints was indeed observed. However, in the object-length condition, the correlation did not fully reverse, but approached zero, again congruent with a mixture of feedback strategies.

A similar observation was made in experiment 2, where we studied sustained adaptation to a constant force field. In the object-center condition, the unperturbed hand changed its initial direction to point against the force field, as observed earlier in the equivalent one-cursor condition (Diedrichsen 2007). Again, this behavior did not full reverse; in the object-length condition, there was no significant change of the initial direction of the unperturbed hand. It thus appears that the endpoint of the movement rather than the initial correction (which was roughly symmetric across task conditions) served as the signal that drove the adaptation of the unperturbed hand.

In sum, our findings clearly show that coordinative feedback responses are task dependent and not caused by a misassignment of the force field to the wrong hand, induced by a visual linkage between the hands. Furthermore, we found that the feedback response in one of the task conditions reversed during the time course of the movement. This may reflect optimization of two different goals: object length and end-state comfort. These changes in coordinative feedback policy are congruent not only with accompanying changes in the structure of variability in the movements, but also with the adaptation to constant force fields.

GRANTS

This work was supported by Biotechnology and Biological Sciences Research Council Grant BB/E009174/1 and National Science Foundation Grant BSC 0726685.