Comparing Areas under the Receiver Operating Characteristic Curves: The Potential Impact of the “Last” Experimentally Measured Operating Point

Abstract

This commentary reviews a specific issue related to the selection of the analytical tool used when comparing the estimated performance of systems under the receiver operating characteristic (ROC) paradigm. This issue is related to the possible impact of the last experimentally ascertained ROC data point in terms of highest true positive and false positive fractions. An example of a case where the selection of a specific analysis approach could affect the study conclusion from being non-significant (p=0.75) for parametric analysis and significant (p=0.003) for the non-parametric analysis is presented, followed by recommendations that should help avoid misinterpretation of the results.

Currently, observer performance studies are routinely performed for the assessment and comparison of technologies and practices and the area (AUC) under the receiver operating characteristic (ROC) curve is the most frequently used summary index when comparing different modalities (1–5). In the medical imaging field conclusions resulting from important pivotal studies are often made based on the assessment of differences between areas under estimated ROC curves that include substantial portions near which no experimental data lie. Hence, in most instances, it would be preferable to assess differences between partial AUCs (6, 7). Unfortunately, the large variability frequently associated with these studies would necessitate extremely large sample sizes to enable demonstration of significant differences between partial AUCs, making this approach impractical in many situations. As a result, we continue to do the best we can under the circumstances, namely estimate the differences between the AUCs and assess the significance level of these differences, if any.

A variety of parametric and non-parametric approaches have been developed to make statistical inferences based on AUC in experiments that are performed under the ROC paradigm (8–17). An implicit assumption in all of these approaches is that even if the estimated AUCs are not precise in absolute terms, the comparison of two or more AUCs on a relative scale is frequently valid regardless of the analytical approach taken to estimate the individual ROC curves being compared. All of the methods employed to date extrapolate (or more precisely interpolate, depending on how one considers the sensitivity = 1, specificity = 0 point) from the last experimentally ascertained ROC point (we term here an “operating point”) to the upper right hand point (i.e., the sensitivity, 1-specificity coordinate (1, 1)) in the ROC domain. The parametric and the non-parametric approaches do it quite differently and the specific methodological approach depends on the actual analytical tool being used (14, 18, 19). However, fundamentally the non-parametric approach, which is solely data driven, (i.e., no underlying assumption regarding the distribution of the data) extends the ROC curve in a linear way from the last experimental point to the point (1, 1) in the ROC domain.

In a recent publication (20) a comparison was made among two paired ROC curves and showed the differences not to be statistically significant when using the parametric approach, but when using the non-parametric approach the differences were statistically significant. This motivated a look into the possible reasons for such a discrepancy in that there may be a fundamental problem not adequately recognized previously, that may have caused it.

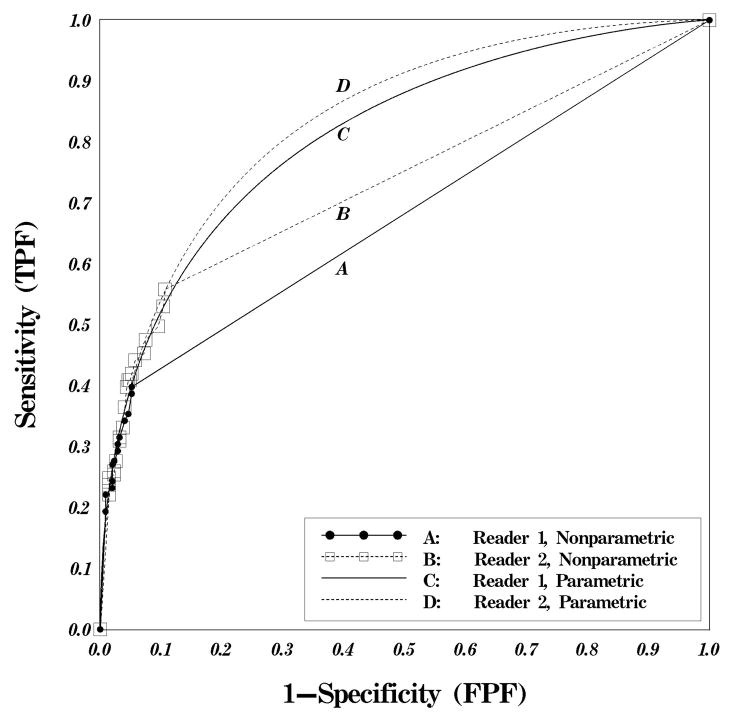
The question posed in this commentary is whether or not the last experimentally ascertained operating point could affect study conclusions and how? To address this question an example of two ROC datasets with the experimental points associated with each noted, is presented. This example is based on a sample of 348 actually negative and 181 actually positive cases interpreted by two readers under a paired design (Figure 1).

Figure 1.

Four ROC curves generated by parametric and nonparametric approaches using a dataset of two readers interpreting the same cases. Areas under parametric fit of the ROC curves are 0.81±0.065 and 0.83±0.034 for readers 1 and 2, respectively (p=0.75). The AUCs corresponding to the nonparametric approach are 0.68±0.025 and 0.74±0.024 for readers 1 and 2, respectively (p=0.003).

The problem:

Assume an ROC curve describing an experiment where the curves being compared are estimated by two similar curves under the parametric model but in one mode the experimental data extend beyond the last experimental point of the other (Figure 1). In this figure, the parametric approach (21) was used to fit the datasets of the two readers interpreting the same set of 529 cases during an ROC type study. Note that in many instances, whether the actual parametrically fitted curves are the same or only similar in overall shape would not affect the primary issue we are addressing. As can be seen from the two types of curves, the parametric approach extends the curve to the point (1, 1) in a totally different manner than the non-parametric approach. The parametric approach extrapolates (actually interpolates) the performance curve between the last experimentally ascertained operating point and the point (1, 1), namely the right upper corner of the ROC domain, under the assumption that the adopted parametric model provides a good approximation throughout the domain. Namely, the estimated parameters of the curve are assumed to be valid beyond the region in which experimental data are truly available. On the other hand, the non-parametric approach assumes a random decision making beyond the region for which experimental data are available. As a result, the computed AUC is clearly dependent on the approach taken and, most important to this discussion, the last actually measured operating point. The fact is that there is nothing in the experimental design itself that would force the experimentally ascertained points to either have the same specificity or the same sensitivity, or both. Reviews of our own studies suggest that this is not always the case. For example, Figure1 shows a very small difference in the parametric estimates of the AUCs between the two readers (AUC1 – AUC2 = 0.02, or 0.81 ± 0.065 and 0.83 ± 0.034, which is not significant (p = 0.75 using ROCKIT9.B (21)). At the same time the non-parametric estimates of the AUCs for the two readers are 0.68 ± 0.025 and 0.74 ± 0.024 for reader 1 and reader 2, respectively, or a statistically significant difference (p=0.003) using the approach of Delong et al (15). More important perhaps, the difference between the two curves is quite visible on the plot. In some situations it can be easily envisioned that the actual performance estimates as a result of one type of analysis (e.g. parametric) are the reverse of the other type (e.g. non-parametric) and this is more likely to occur in the case of crossing curves under the parametric model. This could lead to totally different (and sometimes opposing) study conclusions.

Figures 1 and 2 in the paper by Glueck et al. (20) are a clear demonstration that this could occur even when the data from different modes are not represented by very similar curves. For example, the two curves related to film mammography alone and the combined mode (film, digital, or both) in that study yielded AUCs equal to 0.83 and 0.89, respectively (actual difference 0.056, p=0.07), under the parametric model (Table 2 in reference 20), and visually these are reasonably similar. The difference in AUC increased to 0.073 (0.78 and 0.85, respectively) under the non-parametric model (Table 3 in reference 20) which was significant (p=0.008). Visually these curves look notably different as well. The reason we mention the results in the paper by Glueck et al. (20) is that in this study, indeed the use of the non-parametric method had a statistically different outcome than the parametric method (i.e., reject versus fail to reject the hypothesis of equality of the AUCs).

Discussion

We have shown that in the case of non-parametric analyses of AUC differences the last experimentally ascertained operating point can significantly affect AUC estimates in a manner that could result in different study conclusions as compared with the AUC estimates derived when using the parametric approach. It is very important that investigators plot the actual experimentally ascertained data and view these data together with the ROC fitted plots before making conclusions based on one type of analysis or the other. Providing a parametric fitted curve without the actually ascertained points being presented may be difficult to interpret (2). If partial AUC is of interest, the investigators should make sure that experimentally ascertained data points cover the range of false positive fraction (FPF) of interest to avoid these possible effects, as well. Some of these issues have been discussed in a recent review article by Wagner et al. (22). As statisticians frequently consider the use of non-parametric approaches to analyzing ROC type experiments, investigators should be cognizant of the possible effect described here.

Note that this commentary addresses issues related to ROC methodology and the use of the AUC as a summary index under the ROC paradigm but some of the concepts described here may be similarly relevant to experiments performed under the Free Response ROC paradigm (FROC), as well. However this topic is beyond the scope of this commentary. In addition, the issue discussed here is frequently not a problem in assessment of the performance of technology alone (e.g. computer-aided detection -CAD) because the experimental data generated by CAD systems are frequently well distributed along the complete FPF axis (23, 24).

We believe that, in general, when the last operating points are not the same in terms of actually measured sensitivity, the higher the slope of the performance curve at the last experimentally ascertained data points (i.e., at low false positive rates) the larger the likelihood that differences in AUC will be different for the non-parametric analysis than the parametric analysis. This may or may not result in different conclusions for the study based on the two analyses. It is truly not clear which of the two approaches is the one that should be routinely used. Since it is not known how the performance curve truly behaves beyond the last experimental operating point, arguments in support of either approach could be made. However, it could be reasonably argued that the parametric approach is more likely to represent how the curve should behave in the extrapolated region given that the estimated performance curve does not exhibit a “hook”. By “hooking” we mean that the fitted curve is concave upward in the considered region. When “hooking” occurs it is unlikely to represent the actual behavior of human observers.

Under the bi-normal ROC model, whenever the variance for the negative and positive cases in the set is not the same, which is very frequently the case, curve hooking can occur, as can be seen in published performance (1). This problem has been addressed to a large extent in newer parametric models (18, 19), but whenever the experimental data are predominantly in the low false positive region (left corner of the ROC domain) it is harder to judge the quality and “actual performance plausibility” of the complete curve. In addition, the price for a “properly-looking” extrapolation could be high sensitivity to the bi-normal model assumptions. It has been demonstrated that even in the case of “bi-normally-looking” curves that are formally not bi-normal ROC curves, inferences made based on the bi-normal ROC model can be highly sensitive to the actual location of the last experimentally ascertained operating point (25).

In summary, the issue discussed here is more likely to be important when the parametrically estimated AUC is very high (e.g. >0.9) and when observers tend to be more decisive in their observations (26). We believe that when indeed most experimental points are in the low false positive region one has to plot and carefully assess the quality of the curves. If the last experimentally ascertained operating points for the modalities being compared are substantially different in terms of true or false positive fractions one should justify the actual approach taken (e.g., parametric) and discuss (mention) the potential implication had the other approach (e.g., non-parametric) been taken.