The optimal burst of mutation to create a phenotype

Abstract

Mutagenesis is commonly applied to genes and genomes to create novel variants with desired properties. This paper calculates the level of mutagenesis that maximizes the appearance of favorable mutants, assuming that the mutagenesis is applied in a single episode. The downside of mutagenesis is that a substantial fraction of mutations will destroy gene/genome function. The upside of mutagenesis is the production of beneficial mutations, but the desired phenotype may require that 1, 2 or more beneficial mutations be present simultaneously (the phenotype dimensionality). The optimum level of mutagenesis is sensitive to both properties. In the simplest model, the mutation optimum occurs when number of lethal equivalents per genome equals the phenotype dimensionality, a result first derived by Mundry and Gierer (1958). This level of mutation is shown to be an upper bound for the optimum in various extensions of the model, and the recovery of mutants is also reasonably tolerant to deviations from the optimum.

Mutation is fundamental in evolution. It is essential for adaptation but also creates a burden of deleterious effects that can impede adaptation. Most efforts to understand the evolution of mutation rates assume that mutation is ongoing, that whatever the rate, the same level of mutation will happen generation after generation, at least until the rate evolves to some other value that is then perpetuated (Chao et al., 1983; Sniegowski, 1997; Sniegowski et al., 1997; Taddei et al., 1997; Giraud et al., 2001; Radman et al., 2000; Shaver et al., 2002). An alternative perspective is to consider the evolutionary effect of a pulse of mutation, an elevation of the mutation rate that disappears after one episode. There has been far less attention to the evolutionary consequences of mutation pulses, perhaps because they seem unnatural. Nonetheless, mutation pulses are used in industrial attempts to create novel molecules (Shafikhani et al., 1997; Drummond et al., 2005; Rowe et al., 2003), and they may also operate in nature, as when a cell induces an error prone DNA polymerase for repair (Tompkins et al., 2003) or during biofilm progression (Boles et al., 2004).

There is a substantial empirical literature on the effect of mutation pulses from chemical mutagens or radiation, the oldest literature addressing primarily viruses, dating from an era just after the discovery of DNA structure (see below). A seemingly universal observation is that the surviving viral fraction declines exponentially with time of exposure, hence that log survival declines linearly. Viral survival is measured as the ability to produce a plaque or some other visible disturbance that stems from a single infecting virus. More recent studies have assayed retention of function in proteins as a function of numbers of mutations; strict exponential decay with increasing numbers of mutations is not typically observed (Drummond et al., 2005; Daugherty et al., 2000; Shafikhani et al., 1997).

The empirical results raise some interesting theoretical questions. One set of questions addresses the biological basis for the shape of the mutation-survival curve, its log linearity and slope. This question has been investigated both empirically and theoretically for individual proteins, but not as yet for whole genomes. A separate set of questions concerns the production of beneficial mutants by mutation pulses: what level of mutation maximizes the production of beneficial mutants, and how much better is the optimum pulse than alternatives? This latter question is the focus of this study. An old result is re-derived, and its generality is evaluated in several ways.

The surviving fraction

As noted above, viruses exposed to a mutagen show log-linear survival over time. For the bacteriophage T7, the log linearity has been shown to operate to a surviving fraction of 10⁻¹⁴ (Scearce and Masker, 1987). In most studies, entire virions have been exposed, but in a few studies, only the naked viral genomes have been exposed (Scearce and Masker, 1987; Mundry and Gierer, 1958), so the data are consistent with changes to the viral genome rather than to other virion components. Log-linearity is also observed for repair-deficient bacteria exposed to UV exposure (although not for repair-competent bacteria, Morton and Haynes, 1969). Given log linearity, the surviving fraction (S) can be represented as an exponential decay,

$$S={\mathrm{e}}^{-\beta t},$$ (1a)

where t is time of exposure (Mundry and Gierer, 1958). The number of individuals surviving the mutagenesis is NS, where N is the population size exposed to mutagenesis, so NS < 1 will extinguish the entire population with a single pulse (on average).

Relationship (1a) motivates a useful interpretation. We suppose that the mutagen induces mutations at a constant rate per time of exposure. After an exposure, the average number of mutations per genome is U̅, a quantity that increases linearly with exposure time (U̅ = Cβt). For now, we assume that these mutations are base changes and are the only effect of the mutagen. A fraction L of all mutations are lethal, and a genome dies if it receives one or more lethal mutations. Thus,

$$S={\mathrm{e}}^{-\overline{U}L}.$$ (1b)

In this manifestation of survival, the surviving fraction of the population is the Poisson fraction that escapes lethal mutations (Shafikhani et al., 1997; Bershtein et al., 2006; Bloom et al., 2007). Log-linear survival across changes in U̅ requires that L be constant. The assumptions underlying (1b) are more restrictive than those for (1a), but they will be relaxed below.

Although many of the early studies reported survival of complete genomes, recent work has considered the ’survival’ or retention of function in proteins whose genes are exposed to mutagenesis. The data on protein survival typically violate strict log-linearity with U̅, at least for low mutation rates (Wilke et al., 2005; Bloom et al., 2005, 2007; Bershtein et al., 2006). A further distinction between the survival functions used here and some of those applied to protein survival is that the functions here are based on rates or the average number of mutations per genome/gene. Some protein survival functions are based on the actual number of mutations in the genome (e.g., Bloom et al., 2007; Charlesworth, 1990). When a population is exposed to an average of U̅ mutations, a distribution of genomes/genes with 0, 1, 2, and higher numbers of mutations will result, and the survivors will be disproportionately represented in these different classes. A survival function based on averages does not generally follow the same form as a survival function based on actual numbers of mutations.

The optimal mutation rate in a single pulse

In many settings, we are interested in the appearance of novel phenotypes (”successes”), such as resistance to drugs and pesticides, an ability to metabolize unnatural chemical substrates, host range expansion, or the ability to cause pathogenesis. A basic question is the level of a mutational pulse maximizing the appearance of the phenotype. A successful mutant genome must satisfy two criteria: it must not carry any lethals, and it must have the required number of beneficial mutations to produce the phenotype (denoted D, for phenotype dimensionality). If a single mutation can achieve the phenotype (D = 1), then the fraction M of the exposed population that consists of successful mutants satisfies

$$M=(1-{\mathrm{e}}^{-\overline{U}b}){\mathrm{e}}^{-\overline{U}L},$$ (2)

where b is the fraction of all mutations that will produce the phenotype. Log-linear survival has been assumed for now. Note that, if many different mutations can each produce the phenotype, their combined rate can be incorporated into a single b, or each can be assigned its own function. If two mutations are required simultaneously to produce the phenotype (D = 2), then

$$M=(1-{\mathrm{e}}^{-\overline{U}{b}_1})(1-{\mathrm{e}}^{-\overline{U}{b}_2}){\mathrm{e}}^{-\overline{U}L},$$ (3)

where b₁ and b₂ allow for the possibility that two different classes of mutations are required together to produce the phenotype. Extensions to larger values of D are straightforward.

To calculate the optimum, it is convenient to approximate 1 − e^−U̅b as U̅b, which neglects terms of order (U̅b)² and higher and thus is valid for small U̅b. Applying this approximation to (2), differentiating with respect to U̅, and setting the derivative equal to 0, we obtain

$$\widehat{\overline{U}}L=1,$$ (4a)

where the hat indicates an optimum value. The general result is

$$\widehat{\overline{U}}L=D.$$ (4b)

In words, the optimum level of a mutation pulse is such that the average number of lethal equivalents per genome matches the phenotype dimensionality, i.e., the number of mutations needed to produce the phenotype. This result is half a century old, by a somewhat less explicit derivation (Mundry and Gierer, 1958; Gierer and Mundry, 1958).

To achieve this optimum empirically, the only quantity required is the phenotype dimensionality, D. One merely mutates so that the surviving fraction is e^−D (37% if D = 1, 14% if D = 2). It will be shown below that this result is sensitive to various assumptions, and for many violations, a surviving fraction higher than e^−D obtains at the optimum.

In contrast to the generality of the surviving fraction at the optimum, the fraction of successful phenotypes at the optimum depends on several parameters and is especially sensitive to the unknown beneficial mutation rate, b:

$$\widehat{M}\approx {\left(\frac{\widehat{\overline{U}}b}{\mathrm{e}}\right)}^D={\left(\frac{Db}{\mathrm{e}L}\right)}^D,$$ (5)

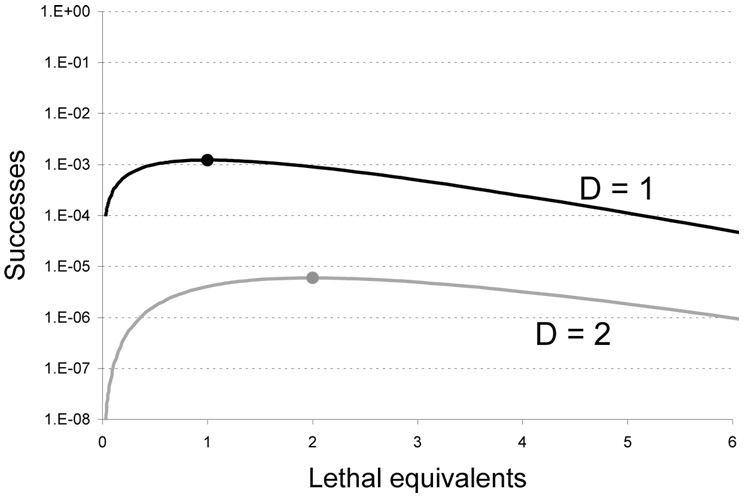
allowing that the b’s in different classes are all the same when D > 1. Thus the surviving fraction at the optimum is not a useful measure of the fraction of successful phenotypes. The fraction of successes may be relatively high at the optimum for small dimensionalities but will generally decrease by orders of magnitude with each increase in the phenotype dimensionality unless b is large (Fig. 1). As noted above, the successes from different beneficial mutations can be lumped into one curve or be divided into curves specific to each beneficial mutation identity. If there are (say) six different mutations, each of which yields the desired phenotype, there would be six parallel curves, with relative heights determined by the ratios of the b_i.

Figure 1.

Absolute level of mutant phenotypes arising from a single mutational pulse. The black curve represents the case in which the phenotype can be produced by single mutations (D = 1); the gray (lower) curve is for a phenotype requiring two mutations simultaneously (D = 2). As expected, the 2-mutant phenotype is several logs rarer than the 1-mutant phenotype. Optima are indicated with filled circles. Drawn for b = 0.001 and L = 0.3; for the gray curve, b₁ = b₂. The two curves would be shifted higher (lower) by increasing (decreasing) b.

These results are considerably more general than as framed in model (1b). Although L was defined as a lethal ‘fraction’ of mutations, there is no requirement that the lethals be comprised of any particular type of mutation, such as base changes, or that they even be a subset of the U̅ mutations. Lethal mutations need not even be mutations at all if the mutagen impairs viability by inactivating virion proteins and other non-nucleic acids needed for infection. The model underlying (2) merely describes the fractions of individuals in two categories as a function of exposure to some environment: survivors and individuals receiving beneficial mutations. Hence the mathematical calculations are indifferent to whether lethals are base changes, strand breaks, or effects on the non-genetic components of a viral particle - L and b are each rates in proportion to U̅. The only requirement for this optimum is that the average number of lethal equivalents per genome (UL) change in proportion to the average number of beneficial mutations per genome (Ub), although these two effects also need to be independent of each other. The calculations of Mundry and Gierer (1958) were framed in terms of time of exposure, which is a more accurate representation of the data from those chemical mutagenesis studies than is an assumed mutation rate.

Violations of log-linear decay

It is possible to calculate the optimum for survival functions other than exponential decay, as when the lethal rate L is not independent of genomic mutation rate. For the small U̅b approximation, the optimum generally obeys

$$\frac{dS}{d\overline{U}}=-D\frac{S}{\overline{U}},$$ (6)

where S is treated as an arbitrary function of U̅. Whereas log-linear survival survival ensured that there was a single optimum, use of an arbitrary survival function allows the possibility that a value satisfying (6) may not be a global optimum. Even so, it is easily seen from (6) that the optimum is sensitive to both the slope and the height of the survival function. A change in either the slope or the position of the function will affect the optimum. In what follows, D = 1 is assumed.

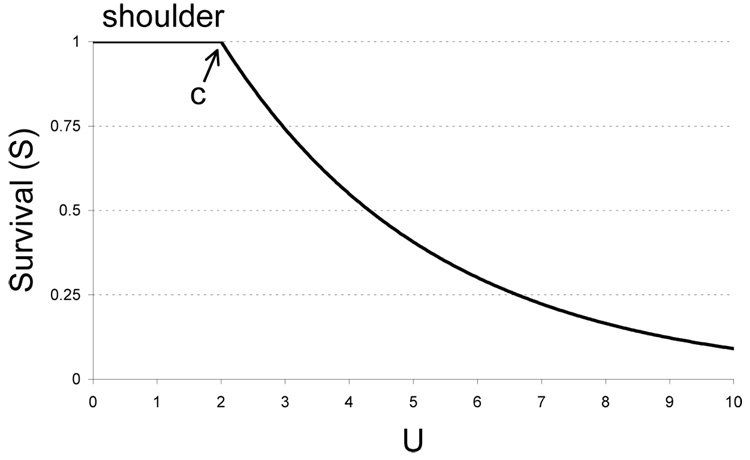
As one example of a non-exponential survival curve, consider a ’shoulder,’ as exhibited by some proteins (Bloom et al., 2005, 2006, 2007) and by bacterial survival after exposure to UV light (Morton and Haynes, 1969). A shoulder is characterized by a slow decay of survival (functionality) at low levels of mutation, often up to 1 or 2 mutations, but exponential decay beyond. For proteins, a shoulder is thought to arise from high thermostability, such that 1 or 2 destabilizing mutations can be tolerated, but beyond those, additional destabilizing mutations destroy folding and thus destroy function (Bloom et al., 2005, 2006, 2007). How will a shoulder affect the optimum? An extreme shoulder can be approximated as a simple translation of exponential decay:

$$S=\{\begin{array}{ll}1,\hfill & \text{for}\overline{U}\le c\hfill \\ {\mathrm{e}}^{-L(\overline{U}-c)},\hfill & \text{for}\overline{U}>c\hfill \end{array}$$ (7)

(Fig. 2). Thus, survival exhibits exponential decay only after genomes have been exposed to an equivalent of c mutations on average. Actual shoulders are not at, as here, but this model will suit our purposes.

Figure 2.

Survival function with a shoulder out to c = 2 followed by exponential decay. Drawn for L = 0.3. Shoulders observed in empirical data are not horizontal but exhibit a shallow decay.

To solve for the optimum, we confine ourselves to the part of the survival curve beyond the shoulder, U̅ > c. The successful mutant fraction is only slightly different from that in (2):

$$M=(1-{\mathrm{e}}^{-\overline{U}b}){\mathrm{e}}^{-L(\overline{U}-c)}=\left[\left(1-{\mathrm{e}}^{-\overline{U}b}\right){\mathrm{e}}^{-\overline{U}L}\right]{\mathrm{e}}^{Lc},$$ (8a)

with straightforward extension to the D > 1 cases. Using the small U̅b approximation, the optimum is the same as in (4):

$$\widehat{\overline{U}}L=D,$$ (8b)

which can be seen from the fact that the only difference between (8a) and (2) is in the factor e^Lc, which does not depend on U̅. For D = 1, this optimum obtains as long as the shoulder does not extend too far, i.e., when Lc ≤ 1. For larger values of c (Lc > 1), condition (8b) specifies a mutation rate that falls inside the shoulder, and the optimum then is simply U̅̂ = c, the maximum amount of mutation before the onset of any lethality.

From the equivalence of (8b) and (4b), it would appear that the shoulder has no effect on the optimum when Lc < 1. This similarity of results is misleading, however, because the surviving fraction differs at the two optima. The surviving fraction at the optimum with a shoulder is e^−D+Lc, higher by a factor of e^Lc than before. Thus, in contrast to the strict exponential decay model, the fraction of survivors at the optimum cannot be determined without knowledge of the parameters L and c (they can be determined if the survival curve is known).

Other forms of deviations from log linearity can be considered. One general form is

$$S={\mathrm{e}}^{-{\overline{U}}^{\beta }L}$$ (9a)

(Wilke and Adami, 2001; Wilke et al., 2003). If β = 1, the curve is exponential, whereas if β > 1, the curve decays faster than exponential, slower than exponential if β < 1 (β will generally be close to 1). This function has been used to represent survival for exact numbers of mutations, but we use it here for averages merely as a form that has desired properties. The optimum for this model is

$$\widehat{\overline{U}}=\frac{1}{{(L\beta )}^{\frac{1}{\beta }}}.$$ (9b)

which implies an optimal number of mutations less than $\frac{1}{L}$ if β > 1 and greater than $\frac{1}{L}$ if β < 1.

Another form of non-linearity is a quadratic function, ln(S) = −U̅L − δU̅ ² (with δ small). This function has also been proposed for exact numbers of mutations (Charlesworth, 1990; Bloom et al., 2007) but used to fit average numbers (Bershtein et al., 2006), as we assume here. The optimum U̅̂L is approximately $1-\frac{2\delta }{L^2}$, thus shifted to less than 1 if the log survival curve drops faster than linear and shifted above 1 if the log survival curve bows upward. Both models of deviations from log-linear survival thus yield similar qualitative effects on the optimum. Derivations below return to the assumption of log-linear survival, however.

Effect of initial frequencies

The foregoing results assume an absence of beneficial mutations in the pool to be mutated. If instead beneficial mutations are present at an overall frequency of p prior to mutagenesis, the counterpart to equation (2), which assumes D = 1 and log-linear survival, is

$$M=(1-p)(1-{\mathrm{e}}^{-\overline{U}b}){\mathrm{e}}^{-\overline{U}L}+p{\mathrm{e}}^{-\overline{U}L}.$$ (10a)

Using the small U̅b approximation, the optimum becomes

$$\widehat{\overline{U}}L=1-\frac{Lp}{b(1-p)}.$$ (10b)

Thus, the previous result is obtained with a correction term. For p > 0, the correction term is always positive, so the effect of an initial frequency of beneficial mutations is to reduce the optimum toward zero. When $p\ge \frac{b}{L+b},$ no pulse of mutation can improve the incidence of successful phenotypes. Beyond this point, the lethal effect of mutagenesis removes the existing beneficial mutants faster than mutagenesis replaces them.

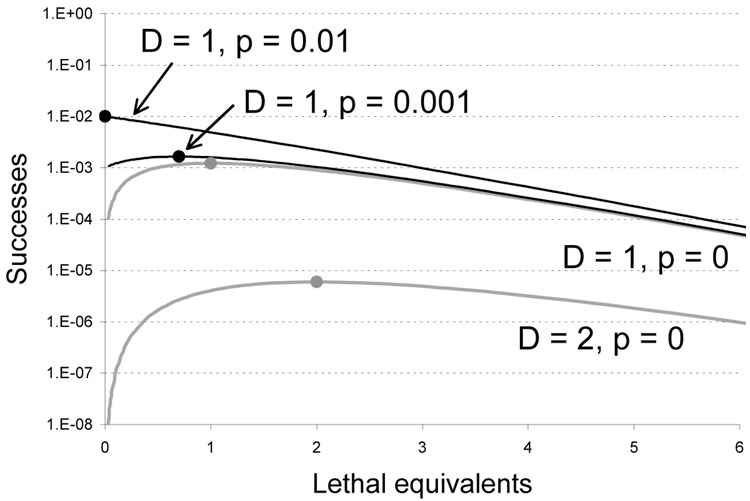
The effect of initial frequencies on the absolute level of successes is illustrated in Fig. 3. The main difference is observed at low mutation levels. When beneficial mutants are absent in the initial pool, they can be produced only by mutagenesis. Thus the curves for p = 0 drop to 0 when no mutagenesis is applied. In contrast, if mutants are present prior to mutagenesis, the curve intersects the vertical axis at their initial value of p.

Figure 3.

Effect of initial frequencies on recovery of beneficial mutants. Both gray curves (lower) assume the strict absence of mutant phenotypes before mutagenesis, whereas the black curves (upper) are drawn for mutant phenotypes present initially (D = 1; p = 0.001, D = 1; p = 0.01). The main effect of having mutants initially present occurs at low levels of mutagenesis, and the optimum is shifted toward or to 0. The optima are shown as circles on their respective curves. Otherwise as in Fig. 1.

The case of D = 2 is more complicated because there are two mutational classes to consider: two beneficial mutation rates, (b₁; b₂) and two initial frequencies, (p₁; p₂). However, assuming b₁ = b₂ and p₁ = p₂, the same correction is obtained:

$$\widehat{\overline{U}}L=2-\frac{Lp}{b(1-p)},$$ (11)

again using the small U̅b approximation.

The magnitude of initial frequencies found in a population will depend on many biological details. For a population grown up for n generations from a single individual who lacked beneficial mutations (e.g., a plaque or colony) and assuming small b, the frequency of successes prior to mutagenesis (p) will increase initially as ≈ nU̅_gb, leading to a correction term in (10b) and (11) of approximately nLU̅_g, where U̅_g is the intrinsic genomic mutation rate per generation. With the estimate of U̅_g = 0.003 for organisms with DNA genomes (Drake et al., 1998), the correction would be small enough to ignore if the organisms were grown only long enough to make a stock for mutagenesis (n ≤ 15 for viruses, n ≤ 30 for bacteria). For viruses with RNA genomes, the correction could be substantial even after a few cycles of growth, because viral RNA genomic mutation rates are near unity (Drake et al., 1998).

Deleterious, non-lethal mutations

Mutant individuals that have the correct phenotype will often carry deleterious mutations that impair their performance but do not abolish function (referred to henceforth simply as ”deleterious” mutations and understood to be non-lethal). Following a single mutational pulse, these mutations will occur at an average of U̅d per genome, where d is the fraction or rate of mutations that are deleterious. If U̅d is on the same order as U̅L, then a reasonable fraction of successful genomes will be free of deleterious mutations when U̅̂L = 1 (e^U̅d ≈ e⁻¹ = 0.37 will be free of deleterious mutations), but most successes will carry at least one. The incidence of deleterious mutations is amplified for the D = 2 case, because the optimum calls for twice the level of mutagenesis as in the D = 1 case.

For most purposes, deleterious mutations will be undesirable, either because they reduce fitness or reduce performance. How can they be avoided? There are two solutions: either reduce their incidence or eliminate them after the fact. To reduce their incidence, one merely reduces the level of mutagenesis. The optimum pulse for avoiding both lethals and deleterious mutations is given by (4) if L is replaced with L + d (assuming that L + d is constant across changes in U̅). Again, the optimum is less than one lethal equivalent per genome for D = 1 and may be approximately one lethal equivalent when D = 2.

Avoiding non-lethal, deleterious mutations is most feasible for the D = 1 case, but knowing the exact surviving fraction at the optimum presents difficulties. Whereas it is often practical to estimate L from survival curves when U̅ is known, there is no corresponding way to estimate d; the VSV study of single mutations estimated d as 0.3 (versus L = 0.4; Sanjuan et al., 2004), but that approach is labor intensive. So one could merely guess the fraction d, apply mutagenesis, and look for genomes with single mutations. Avoiding deleterious mutations becomes more problematic with D = 2 because the optimum is shifted to a higher value of U̅, hence a higher level of deleterious mutations. An alternative and possibly simpler solution is merely to obtain a successful mutant genome, which will be carrying beneficial mutations and possibly deleterious ones, create recombinants of the various mutations within its genome, and assay them for phenotype. Even simpler is to outgrow the population of successful mutants to reduce the frequencies of those carrying deleterious mutations, but this approach does not guarantee a genome free of deleterious mutations if there is wide variance in beneficial effects.

Sensitivity of the optimum

How sensitive is the production of successful mutants to deviations from the optimum? Some calculations give insight to this problem, where we assume D = 1. Using the small U̅b approximation and assuming an absence of beneficial mutations prior to mutagenesis, the second derivative of M in (2) is −Lbe⁻¹ at the optimum. The magnitude of this curvature is necessarily affected by the absolute magnitude of successes, so a more meaningful number is the 2nd derivative scaled relative to the height of the curve at the optimum: −L². Thus, the relative curvature depends only on the lethal fraction, at least when single mutations create the phenotype. The optimum is most sensitive when the lethal fraction is high.

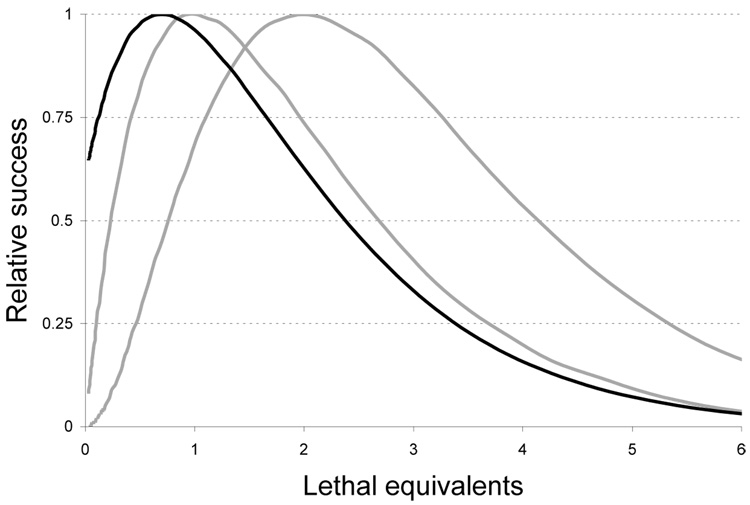
The ratio of M̂ at the optimal U̅̂ to the value of M for some alternative level of mutation is shown in Fig. 4. Three different curves are illustrated: 1-dimenional phenotypes, 2-dimensional phenotypes, and 1-dimensional phenotypes when mutants are initially present. Since each curve is scaled relative to its maximum, they are easily compared. Although each curve shows a clear maximum corresponding to the optimum, there is considerable breadth to the curves. For the 1-mutation case (leftmost gray), the relative success of half the optimal pulse is 80%; the relative success of twice the optimal pulse is 75%. Differences of this magnitude would only be evident in large samples. Thus, not knowing whether the mutant phenotype requires 1 or 2 mutations simultaneously, or whether mutants were initially present would not appear to make a profound difference. It would su_ce to apply a couple values of lethal equivalents, say 0.5 and 1.5, to cover a wide spectrum of possibilities. And of course, the foregoing sections provide several reasons that the optimum will be shifted to less than D lethal equivalents.

Figure 4.

Relative successes in 1-mutation phenotypes (D = 1; p = 0, leftmost gray), 2-mutation phenotypes (D = 2, rightmost gray) and 1-mutation phenotypes when mutants are present initially (D = 1, p = 0.001, black). Drawn for b = 0.001 and L = 0.3; for D = 2, b₁ = b₂. Curves for D = 1 and D = 2 were shown in Mundry and Gierer (1958) and Gierer and Mundry (1958), implicitly assuming p = 0.

Discussion

Random mutagenesis of genes and genomes is widely used to enhance the recovery of desired phenotypes when the nature of the mutations causing the phenotypes is unknown (PubMed lists over 4,000 papers in response to a search on ’random mutagenesis’). Mutagenesis has the beneficial effect of increasing the number of desired mutations but also decreases the number of viable genomes, so the phenotype can be observed only when a genome has both acquired the necessary beneficial mutations and avoided lethal ones. The purpose here has been to calculate the optimum level of random mutagenesis amid these opposing effects and to evaluate the robustness of the optimum to various violations of the basic model.

In contrast to the usual approach to understanding mutation rate optimality, the approach here assumes that mutation is administered in a single episode in which only its average (U̅) can be controlled, with death rate L and beneficial mutation rate b per mutation. If D beneficial mutations are required in the same gene/genome to produce the desired phenotype, the optimum is to mutate the population so that the average number of lethal equivalents per genome equals D, a result due to Mundry and Gierer (1958) and Gierer and Mundry (1958). This result makes several assumptions, however: (i) strict exponential decay of survival with increasing mutation rate (or equivalently, constancy of the lethal fraction, L); death need not be due to mutations per se, however; (ii) independent occurrence of lethal and beneficial mutations; mutations follow a Poisson distribution; (iii) an absence of beneficial mutations prior to mutagenesis; (iv) the mutation spectrum does not change with the mean number of mutations; and (v) beneficial mutations are rare among all the mutations created by mutagenesis. For many violations of these assumptions, the Mundry and Gierer optimum U̅̂ is shown to achieve greater mortality that should be applied. Modest deviations from these optima should be tolerable in most applications (of half a lethal equivalent, or so).

The optimum exhibits generality in the fraction of the population killed but not in the fraction of successes at the optimum. The fraction of successes is

$${\left(\frac{bD}{L\mathrm{e}}\right)}^D,$$

whose magnitude depends heavily on the beneficial fraction, b, for a given D (since L will tend to operate in a small range at least for certain types of proteins - see below). Thus, if either of two distinguishable mutations leads to the desired phenotype, with b₁ = 0.01 and b₂ = 0.0001, the maximum will occur at the same U̅ for both (U̅̂L = 1), but successes with mutation 1 will be 100 times more abundant than successes with mutation 2. Consequently, experimental efforts to increase b or decrease L may have a far bigger impact on increasing the numbers of successes than will adherence to the optimum level of mutagenesis.

Restrictions imposed by the genetic code and the inherent excess of transitions in most mutation processes will normally bias the spectrum of mutations obtained, especially at the amino acid level. Broadening the mutation spectrum will thus increase the incidence of some beneficial mutations, possibly decrease others, without necessarily changing L (recall that lethality may be due to mutations per se or other causes). If L does not change, the optimum will still sit at the same level of killing regardless of the mutation spectrum used, but the abundances of different classes of beneficial mutations will change. However, merely broadening the spectrum of mutations will not necessarily make any of the beneficial classes abundant, whereas efforts to greatly increase b may have profound effects.

A method sometimes used to increase b is to target mutations to residues likely to improve function (Miyazaki and Arnold, 1999); by avoiding mutations in unproductive parts of the genome/protein, the effect is to increase the fraction of beneficial mutations. Another method widely used to generate functional proteins uses recombination among diverged but functional molecules (Rowe et al., 2003; Stemmer, 1994b,a; Minshull and Stemmer, 1999). The use of pre-existing variants from functional molecules is tantamount to decreasing L. Perhaps the most exciting method proposed for enhancing recovery of mutants with new functions is to apply mutagenesis to a molecule exhibiting enhanced thermostability (Bloom et al., 2006). It appears that this approach allows recovery of beneficial mutations that would otherwise disrupt protein folding and abolish function. From one perspective, this approach uses a system that violates the independence of lethal and beneficial mutations. From a different perspective, the approach could be accommodated in this framework for the case of D = 2, in which one of the beneficial classes consists of mutations that enhance thermostability so that classes providing new functions can be realized. The effect of starting with a highly thermostable molecule is the to reduce the dimensionality to D = 1.

The fraction of lethal mutations (L for those models in which mutations are the only source of lethality) has been measured for several proteins and one viral genome. For a set of 70 randomly-generated point mutations evaluated singly in the RNA virus VSV, L was estimated as 0.4 (as a fraction of all mutations; Sanjuan et al., 2004). However, we have no idea of the lethal fraction for the vast majority of viruses, nor whether the observed log-linear decay following chemical mutagenesis even represents base changes. The ubiquity of exponential survival curves for viruses exposed to mutagens contradicts the data on proteins, because protein survival curves typically exhibit a shoulder. However, mutagens often have strong inactivating effects on DNA as well as inducing base changes (e.g., Freese and Freese, 1964), so it is plausible that the exponential decay of exposed viral genomes is due largely to inactivation effects rather than to base changes.

In studies of mutational effects on proteins, the usual approach has been to assay protein function when the number of mutations is measured directly. Survival curves are thus a function of base changes, and a lethal fraction is estimated as a proportion of total base changes. Protein lethal fractions are heterogeneous, commonly near 0.3 (subtilisin, DNA glycosylase, lac repressor; Guo et al., 2004; Shafikhani et al., 1997), but as high as 0.6 (for an antibody, Daugherty et al., 2000; Drummond et al., 2005) and with lows of 0.12 and 0.03 (for T4 lysozyme and an RNAse; calculated by Guo et al., 2004, from other studies). (These lethal fractions have been converted into per nucleotide change, whereas the lethal fractions for proteins are more commonly given per amino acid change.) The average lethal fraction per nucleotide for a genome would be the average across all essential proteins, weighted by their sizes, and be discounted by the sizes of non-essential proteins. The lethal fraction for a genome would also include the values for non-coding regions.

A shoulder in the survival curve indicates that the lethal fraction changes with the numbers of mutations, specifically that the lethal fraction increases with the number of mutations. Thus, the lethal fraction calculated from single mutations, as in some of the above studies, will underestimate the lethal fraction at high mutation rates. In some studies, the lethal fraction was deliberately calculated beyond the shoulder (Bloom et al., 2007).

The models here indicate how to maximize the number of 'successes' for a given spectrum of mutations. The optimum maximizes the number of successes of each type of mutation, assuming that each type is independent of the others. With industrial applications, there are other optimality criteria that may be preferred, such as maximizing the diversity or number of different of successes in a library (Drummond et al., 2005). It would also be feasible to calculate the specific number of mutations per gene/genome (instead of the average) that maximized the number of successes, a method that would obviously require knowing the sequences of each of the mutants in the library. A higher dimensional problem is to consider the optimal 'schedule' of mutation during population outgrowth (Kepler and Perelson, 1995). It is thus important to define the goal of a mutagenesis study before choosing a method to enhance success.

Two early studies of viruses observed the frequencies of mutant ”successes” as a function of lethal equivalents. Mundry and Gierer (1958) (presented in abbreviated form in Gierer and Mundry (1958)) plotted relative success rate from nitrous acid exposure of intact tobacco mosaic virus virions (one treatment) and naked RNA genomes (3 treatments) and compared the data to curves for D = 1 and D = 2. The virus was infected into tobacco leaves, and necrotic lesions were counted as the successful phenotype (as opposed to chlorotic lesions, which is normal for the virus). Of four treatments, the maxima occurred at U̅L = 1 for two and U̅L = 2 for the other two. As the assays/phenotypes were the same, the maxima should have coincided in all four cases. Several other data deviated moderately from the curves as well, but absolute numbers were not provided, so a statistical fit of these points is not possible. Tessman (1959) exposed virions of ϕX174 to nitrous acid and counted host range mutants on plates of mixed-host lawns. The maximum showed a broad peak from approximately one half to nearly two lethal equivalents, and a four-fold elevation above background at this peak. Thus, both studies are broadly consistent with the maximum at U̅L = 1 and further confirm the approximate equivalence of success levels within at least half a lethal equivalent.

Treatment of the bacterium Chlostridium acetobutylicum with the mutagen EMS and scored for ampicillin resistance showed a success rate curve that did not match the models here (Lemmel, 1985). The success curve behaved much like a step function, with a low frequency of successes up to 80% kill, and then a 10X jump at just above 80% kill. It is not clear how to reconcile those results with the theory, unless ampicillin resistance is being physiologically induced by the EMS (in which case, not compatible with the processes assumed by the models here).

Mutagenic PCR (polymerase chain reaction) is often used to create libraries of mutated genes. PCR mutagenesis violates some of the assumptions critical to the models presented here (Sun, 1995; Drummond et al., 2005). In contrast to chemical mutagenesis methods, PCR mutagenesis is limited to base changes (or at least, other types of changes are omitted from the libraries). The difficulty with PCR is that mutation accumulation is hierarchical, so copies produced early have fewer mutations than those produced late. Since the early products are retained no matter how long (and hence, no matter how 'mutagenic') the reaction, the distribution has a wider variance than Poisson, and the fraction of survivors does not follow e^−U̅L. This hierarchical distribution also destroys the independence of mutations between individual genomes. The optimum under PCR mutagenesis was calculated by Drummond et al. (2005) but is not easily compared to the optima here because different criteria were used. The maximum was calculated over library size and number of PCR cycles and showed no simple rule, and it is not immediately clear what the effect of PCR mutagenesis would be for the optimum criterion used in the present study. Indeed, it appears from Drummond et al. (2005) that the spectrum of beneficial mutations increases as the mean U̅ increases, which is not the case in the present models; here, only the abundances changed with the mean (and stochastic effects were ignored). This difference is obviously important to the optimum. Nonetheless, preliminary simulations of a PCR-based hierarchical mutation process otherwise corresponding to the model in section (2) suggest that the optimum in equation (4) is reasonably accurate (data not shown).

In the simplest model, the optimum mutation pulse depends only on the fraction of the population killed. In some cases, this quantity may be unknown. When mutating a non-functional gene to restore function, for example, some mutations will likely be incompatible with function, but their lethal effects cannot be known until the function has been restored.

A pulse of mutation has different properties than continuous mutation, and the optimum for one does not translate to the other. In particular, the population might not even survive if the mutation rate that optimizes a pulse was applied every generation (Bull et al., 2007). Long term exposure to mutation accumulates non-lethal, deleterious mutations; this accumulation occurs because of the continued input of mutation, and it can progressively lower fitness over time (Kimura and Maruyama, 1966; Johnson, 1999).

The results here are easily administered in an applied context, as when generating a large library of mutants. Might an organism adopt a pulse strategy when faced with a hostile environment? If the lethal fraction was relatively invariant across environments, then a strategy matching U̅̂L = D could be achieved merely as a fixed number of new mutations in the genome (or any portion of a genome) after a single episode of error prone replication. Furthermore, some infrequently used polymerases that are error prone could provide a mechanism to do so (Bull et al., 2001; Tompkins et al., 2003). While such a mechanism seems unprecedented, it should be possible to test whether bacteria behave in the appropriate fashion when challenged with harsh environments. This possibility harkens to the ”directed mutation” controversy (Cairns et al., 1988; McKenzie et al., 2001; McKenzie and Rosenberg, 2001; Andersson et al., 1998; Hendrickson et al., 2002), although in this instance, the mutations are not ”directed.” Such a model will no doubt prove much easier to advocate than to demonstrate.