Composition and Decomposition in Bimanual Dynamic Learning

Abstract

Our ability to skillfully manipulate an object often involves the motor system learning to compensate for the dynamics of the object. When the two arms learn to manipulate a single object they can act cooperatively, whereas when they manipulate separate objects they control each object independently. We examined how learning transfers between these two bimanual contexts by applying force fields to the arms. In a coupled context, a single dynamic is shared between the arms, and in an uncoupled context separate dynamics are experienced independently by each arm. In a composition experiment, we found that when subjects had learned uncoupled force fields they were able to transfer to a coupled field that was the sum of the two fields. However, the contribution of each arm repartitioned over time so that, when they returned to the uncoupled fields, the error initially increased but rapidly reverted to the previous level. In a decomposition experiment, after subjects learned a coupled field, their error increased when exposed to uncoupled fields that were orthogonal components of the coupled field. However, when the coupled field was reintroduced, subjects rapidly readapted. These results suggest that the representations of dynamics for uncoupled and coupled contexts are partially independent. We found additional support for this hypothesis by showing significant learning of opposing curl fields when the context, coupled versus uncoupled, was alternated with the curl field direction. These results suggest that the motor system is able to use partially separate representations for dynamics of the two arms acting on a single object and two arms acting on separate objects.

Introduction

The ability to predict and compensate for object dynamics is a fundamental feature of our motor system. Such dynamic learning has been extensively studied by applying state-dependent force fields to the arm. When exposed to a novel force field, subjects initially cocontract to minimize the effect of the field (Thoroughman and Shadmehr, 1999; Franklin et al., 2003; Milner and Franklin, 2005), and then eventually learn to compensate predictively for the expected force (Shadmehr and Mussa-Ivaldi, 1994). Although subjects can rapidly learn a single force field, when subsequently exposed to a force field that applies forces in the opposite direction, interference is usually observed (Brashers-Krug et al., 1996; Caithness et al., 2004). In marked contrast to this unimanual sequential interference, opposing force fields can be learned bimanually, without interference, if each is simultaneously applied to one of the arms (Tcheang et al., 2007). Moreover, having learned a force field with only one arm, there is some transfer of the learning to the other arm, although the coordinate system of such transfer is under debate (Criscimagna-Hemminger et al., 2003; Malfait and Ostry, 2004). These studies suggest that there may be separate representations for the dynamics experienced by each arm that partially overlap.

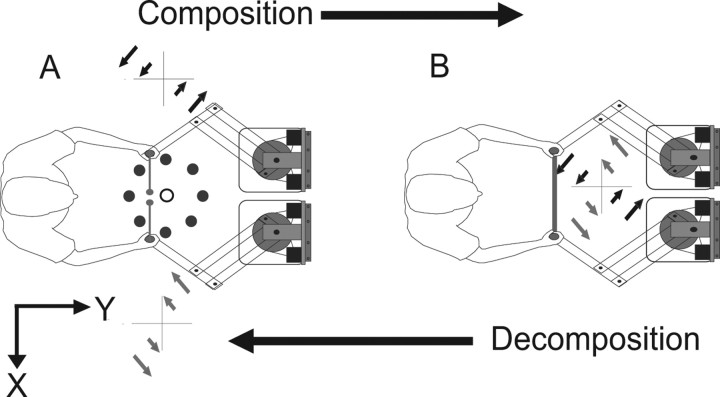
In these previous studies, the experience of each arm was independent of the other arm. However, when we act on real world objects bimanually, the object can induce coupling between the arms. Therefore, when the two arms act on a single object, they can act cooperatively and share the control of the dynamics of the object. When the two arms simultaneously act on separate objects, each can learn independently to control the dynamics of its own object. Here, we use two robotic interfaces to apply force fields to the two arms. A velocity-dependent curl field was used to simulate the dynamic properties of an abstract virtual object. The two robots could be operated uncoupled so that each hand was free to move within its own force field and thus simulate a separate object in each hand (Fig. 1A). Alternatively, to simulate the two hands acting together on a single object, the robot handles could be linked together using a simulated spring with both hands acting within a single force field (Fig. 1B) (see Materials and Methods). We examined how learning in one context transferred to the other. In a first experiment, subjects initially experienced orthogonal components of a clockwise curl field applied to each arm independently (uncoupled fields) (Fig. 1A). They then experienced a coupled force field that was the sum of the two orthogonal components (a clockwise curl field) (Fig. 1B). Finally, they transitioned back to the original uncoupled fields. Similarly, we examined the transition from a coupled field to uncoupled fields. Based on the results of these experiments, which showed rapid transitions between coupled and uncoupled contexts, we hypothesized that the representations of dynamics between the two contexts can be partially independent. To test this hypothesis further, we examined whether the context of coupled versus uncoupled could allow opposite curl fields to be learned (Fig. 2).

Figure 1.

Composition and decomposition experiments. In the uncoupled phase (A), the hands were unlinked and orthogonal curl field components were applied to each arm. The task involved making out-and-back movements with two cursors (displayed as the small filled circles with lines attached to the hand positions) from a central home position (shown as the unfilled circle) to one of eight targets (shown as the gray filled circles). In the coupled phase (B), the same task was performed, but the arms were linked with a stiff virtual spring and the arms experienced a full curl field.

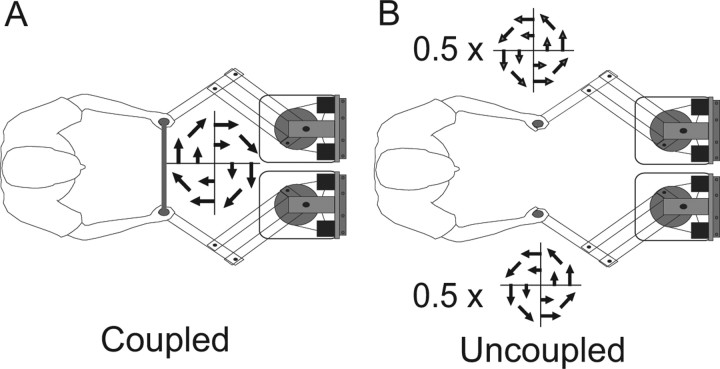
Figure 2.

Curl field switching experiments. Center out-and-back movements were performed and the direction of the curl field could be switched between batches to investigate interference in dynamic learning. In a coupled condition (A), the hands were linked with a stiff virtual spring, and both hands acted together on a curl field. In an uncoupled condition (B), each arm was unlinked and experienced a half-strength curl field.

Materials and Methods

A total of 45 right-handed subjects who were naive to the aims of the experiment took part in the study after providing written informed consent. The protocol was approved by a local ethics committee and all subjects completed an Edinburgh handedness questionnaire.

Experiments were performed using two custom-built back-drivable, planar robotic manipulanda that exhibit low mass at the handle (Körding et al., 2004). Optical encoders allowed the position of the handle of the vBOT to be sampled at 500 Hz and torque motors allowed translational forces to be updated at the same rate. Each vBOT was fitted with a force transducer (Nano 25; ATI) mounted below the handle to measure the applied translational forces. A planar virtual reality projection system was used to overlay images of targets and cursors in the plane of the movements of the vBOTs, and subjects were prevented from viewing their arm directly. Subjects were seated in front of the apparatus and held one robot handle in each hand.

All the experiments consisted of out-and-back movements to eight 1.0 cm radius circular targets equally spaced around a 10 cm radius circle with the start position (1.5 cm radius) at the center. The start position was in the midsagittal plane and located ∼30 cm below the eyes and 30 cm in front of the subjects' chest. To prevent the handles from colliding, each handle controlled a 0.5 cm radius cursor that was offset 10 cm from the position of the handle: the right hand controlled a cursor 10 cm to its left and vice versa (Fig. 1A). The right and left hands controlled red and green cursors, respectively, and virtual lines were drawn from the handle position to its corresponding cursor to indicate which hand controlled which cursor.

To initiate a trial, subjects had to place both cursors within the start position and maintain both cursor speeds <0.1 cm s⁻¹. After a 0.5 s delay, a target appeared at a pseudorandom location and a tone indicated that the subject should move out to the target and then back to the start position. The subjects were required to achieve this with both hands within 600 ms and were warned if their movements were too slow.

Dynamics simulation

During each movement, state-dependent forces could be applied by the vBOTs to the hands. The forces experienced by each hand could arise from two distinct mechanisms. Forces could arise because of movement in a velocity-dependent force field (see below). In the uncoupled context, these were the only forces present. In the coupled context, in addition to the velocity-dependent force field, forces could arise because of linkage between the hands. This linkage was generated by a stiff virtual spring that joined the handles together, simulating the hands acting on the ends of a single solid object such as a bar, which could translate but could not rotate. Specifically, we simulated a two-dimensional stiff spring that acted between the handles with a spring constant of 3000 N m⁻¹. In the coronal plane, the spring had a resting length of 20 cm and resisted any movement that changed this interhand separation. In addition, in the sagittal plane, the spring had zero resting length, thereby minimizing separation of the hands in this direction. This simulated the handles being attached to the opposite ends of a 20 cm bar that could be translated but not rotated. When both the velocity-dependent force field and the stiff spring were acting at the same time, it was as though subjects were holding two ends of a bar that was being perturbed by a velocity-dependent force field.

To prevent abrupt forces being generated on the introduction of coupling, the magnitude of the forces generated by the robots was limited to 5 N until the force generated by the spring was <5 N, at which point the full simulation was initiated and the force was then limited to 40 N. In the uncoupled condition, the handles were free to move independently.

Experiment 1

Composition–decomposition.

Experiment 1 involved 23 subjects. Subjects performed batches of 11 trials that consisted of movements to each of the eight targets as well as three catch trials to targets at −45, 0, and 45° (Fig. 1A shows the axes; 0° being straight ahead and positive angles are clockwise). Within each batch, target directions were presented in a pseudorandom order. During a catch trial, a channel was simulated between the starting handle location and the target (Scheidt et al., 2000), which had stiff walls (6000 N/m). Catch trials allowed an assessment of learning in terms of the force subjects exerted into the channel wall while minimizing any disruption to learning. In the catch trials during the coupled condition, the component of the forces generate by the spring perpendicular to the channel was set to zero to allow assessment of each arm independently.

The first group (eight subjects) completed a familiarization phase (10 batches) in which they made uncoupled movements in the absence of any force field (null field). Subjects were then exposed to 20 batches in which separate force fields (uncoupled) were applied to each hand. Each hand experienced a velocity-dependent force field. For the right hand, the force direction was always aligned with 45° (or in the opposite direction at 225°) and the forces (F_x^R, F_y^R) depended on the right-hand velocity (ẋ_R, ẏ_R) as follows:

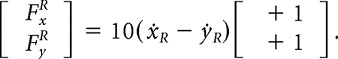For the left hand, the force direction was always at −45° (or in the opposite direction at 135) and the forces (F_x^L, F_y^L) depended on the left-hand velocity (ẋ_L, ẏ_L) as follows:

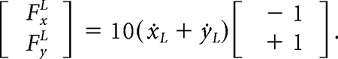The total force experienced by the two hands (F_x = F_x^R+F_x^L, F_y=F_y^R+F_y^L)as a function of the hand velocities [assuming similar velocities for both hands (ẋ_R ≈ ẋ ≈ ẋ_L, ẏ_L ≈ ẏ ≈ ẏ_R)] is as follows:

Therefore, across both hands, there was a typical velocity-dependent curl field, although each hand only experienced one component and the two components are an orthogonal decomposition of the full field in the +45 and −45° directions.

After 20 batches, subjects had their hands coupled by the stiff spring and each hand experienced the full curl field for another 20 batches. Finally, the hands were once again uncoupled for 10 batches and the subjects experienced the same curl field components as initially.

Decomposition–composition.

The second group of nine subjects was run in a similar paradigm except that after familiarization they experienced the coupled task first, followed by uncoupled and finally the coupled task again. As a measure of performance, for each trial we took the maximum perpendicular deviation of the hand path on the outward movement from the straight line path between the hand's start location and the center of the target. We chose this in preference to measures of positional error relative to the target for two reasons. First, maximum perpendicular deviation tends to reflect early feedforward compensation, whereas measures of target error include substantial feedback effects. Second, even when subjects generate highly looped movements, and therefore have not learned the dynamics, feedback allows them nevertheless to pass close to the target on the inward portion of the movement.

To assess the role of specific compensation for the force field, as opposed to a nonspecific cocontraction, catch trials were used in which a virtual channel constrained movements to a straight line path to the target. On these trials, the perpendicular force into the channel wall at peak velocity of the outward movement was used as a measure of predictive compensation.

Decomposition–composition control.

Based on the result from the decomposition experiment, we ran an additional decomposition experiment on an additional six subjects. This was identical with the decomposition experiment except that during the uncoupled task the curl field was decomposed so that each arm experienced a curl field with identical dynamics but of one-half the original strength. Again, the sum of what the arms experienced remained the same in both coupled and uncoupled contexts.

Experiment 2: curl field switching

This paradigm was used to examine whether subjects could learn opposing curl fields based on the context of whether the hands were coupled or uncoupled and 28 new subjects participated.

Subjects were randomly assigned to one of four groups. All subjects performed batches of nine trials, with one trial to each of the eight targets and either an additional field trial at 0° (first one-half of the experiment) or a catch trial at 0° (second one-half of the experiment).

The first group (eight subjects) performed 10 familiarization batches with the hands uncoupled and with no field. The group then alternated between a counterclockwise curl field applied with the hands coupled and two clockwise curl fields applied to each hand while they were uncoupled. In the coupled condition, the field was as follows:

and in the uncoupled conditions, each hand experienced the opposite (clockwise) curl field with one-half the strength as follows:

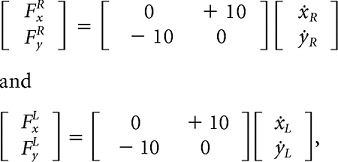so that the total force experienced by the hands was matched between the two conditions. Subject initially experienced the coupled condition for 10 batches and then the uncoupled for 10 batches. This was then repeated with the context changing every 10 batches until subjects had completed a total of 130 batches with the field. Therefore, in total, subjects performed 1260 trials.

The second group (eight subjects) performed the same paradigm except that the hands were always uncoupled, but again the direction of the field changed every 10 batches. The third group (eight subjects) performed the same paradigm except that the hands were always coupled (including in the familiarization phase), but again the direction of the field changed every 10 batches. The fourth group (four subjects) performed only coupled trials, and in this group the direction of the curl field remained counterclockwise throughout.

The same measures of performance were used as in the first experiment. We were interested in the ability to rapidly switch between the two fields and therefore examined the first batch of each block of 10 batches over the course of learning.

Results

Subjects found the task straightforward. Each hand was offset by a 10 cm translation from its cursor (to prevent the hands colliding). However, such visuomotor translations are very simple to learn, and by the end of the preexposure phase subjects were accurate with their movements.

For the three field composition experiments, we examined whether the arms moved with similar speeds. To do this, we calculated the differences in peak velocity between the left and right hands for the outward portion of the movement. This showed a nonsignificant difference between the peaks speeds for both the preexposure (mean ± SD, 3.26 ± 4.0 cm/s), coupled (0.51 ± 1.12 cm/s), and uncoupled (1.12 ± 5.66 cm/s) conditions.

Composition–decomposition

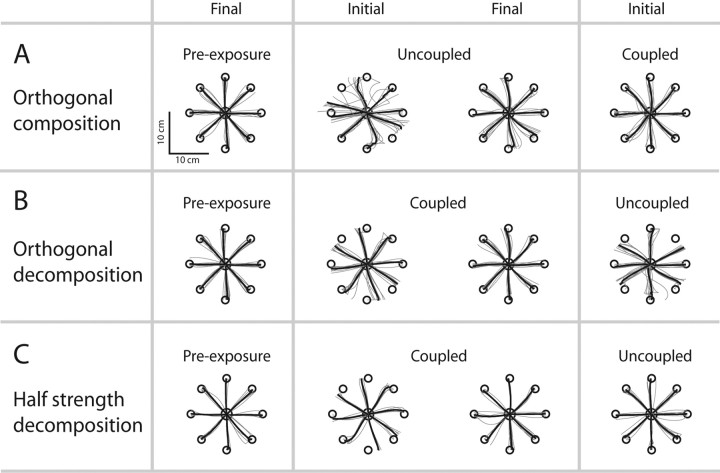
By the end of the familiarization phase, subjects made approximately straight line movements out to the target and back (Fig. 3A, final preexposure). On the introduction of the curl field components to each hand (uncoupled), the trajectories were perturbed (Fig. 3A, initial uncoupled). The perturbation depended on the particular component applied; the left hand experienced no force perturbation for movement along the −45° axis, and the right hand similarly experienced no perturbations for movement along the +45° axis. Hence the trajectories remained approximately straight for these directions. However, in the orthogonal direction, the perturbation was greatest leading to trajectories with large deviations from a straight line. After 20 batches, the trajectories became straighter and were comparable with movements in the null field of the familiarization phase (Fig. 3A, final uncoupled). On transition to the coupled condition, the trajectories remained relatively straight (Fig. 3A, initial coupled).

Figure 3.

All individual subject and mean outward right-hand paths at different stages of the experiment. To enable the mean to be calculated, each trajectory has been truncated to the shortest outward path across the subjects. A–C, Shown are the trajectories for the composition, decomposition, and decomposition control paradigms, respectively.

To quantify learning, we measured the maximum perpendicular deviations [maximum perpendicular errors (MPEs)] from a straight line to the target for each hand in the outward part of the movement (Fig. 4A,B). We performed a repeated-measures ANOVA on the MPE with factors of arm (left and right) and epoch (six categorical levels: the last batch of the null field, the first and last batch of the initial uncoupled field, the first and last batch of the coupled field, and the first batch of the final uncoupled field; that is, batches 10, 11, 30, 31, 50, and 51). This showed a significant main effect of epoch (F_(6,42) = 40.6; p < 0.001), but no significant effect of arm. We performed five planned comparisons (below) averaging over the arms and applied Bonferonni's correction for tests of significance.

Figure 4.

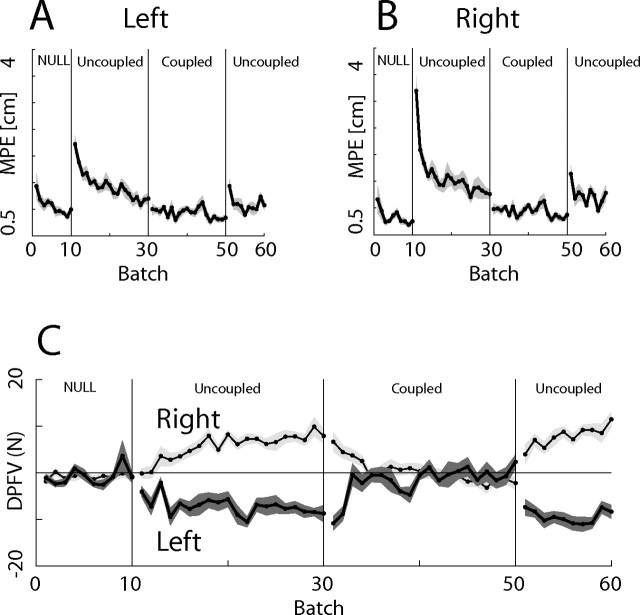
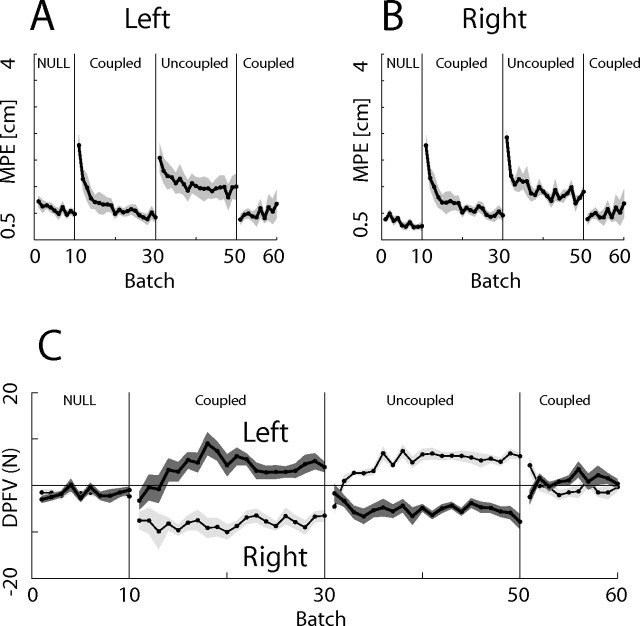
Results for the composition–decomposition experiment. A, B, Shown are the MPEs for the left and right hands, respectively, illustrating the effect of switching between uncoupled and coupled contexts. The shading shows SE across subjects. C, DPFV during catch trials for the two arms.

During the familiarization phase, the MPE decreased to 0.87 cm as subjects learned to perform the task and compensate for the low-inertia intrinsic dynamics of the vBOTs. On the introduction of the two orthogonal components of the uncoupled curl field, one to each arm, the MPE increased to 2.7 cm (p < 0.001, comparison of batches 10 and 11). Over the course of the next 20 batches, the MPE decreased significantly to 1.23 cm (p < 0.001, comparison of batches 11 and 30).

After each hand had separately learned a component of the curl field, the two hands were coupled and exposed to the sum of the component fields, that is, a full curl field. For the first batch in the coupled field, the MPE (0.99 cm) was not significantly different from the previous uncoupled batch. Over the course of 20 additional batches, the final error of 0.86 cm did not change significantly (comparison of batches 31 and 50). Finally, the hands were once again uncoupled and exposed to the same orthogonal components as before and the error rose significantly on the first uncoupled batch to 1.53 cm (p < 0.001, comparison of batches 50 and 51). A comparison of the final batch of the initial uncoupled field and the first batch of the final uncoupled field (batches 30 and 51, respectively) showed that the MPE was not significantly different.

To examine each arm's contribution to the task, catch trials were interspersed within the field trials. For these trials, each hand was constrained to move in a channel (Scheidt et al., 2000), and as a measure of the contribution of each arm, we calculated the force exerted by the hand perpendicular to the direction of movement at the peak velocity [force at peak velocity (FPV)] of the outward movement. We wanted to assess the extent to which each hand generated forces specific to the uncoupled component of the force field compared with the coupled field. For the uncoupled fields, a specific adaptation would mean a large FPV for one of the 45° directions (in which the force would be maximal) and a low FPV for the orthogonal direction (in which the force would be close to zero). Conversely, for the full curl field, the FPV should be similar for both directions. Therefore, we developed a differential measure, which was the (signed) difference in FPV between the +45 and −45° catch trials [difference in FPV (DFPV)]. This should be close to zero if the arm is producing similar forces in each direction, whereas a nonzero value of DFPV implies that the arm is generating different forces in each direction. Because a zero DFPV could also arise if cocontraction was used, over the coupled phase in which the DFPV was close to zero, the mean peak force generated by the right and left hands in the catch trials was computed. These values were significantly different from zero (one-tailed t test; p < 0.001) with means of 5.9 ± 1.5 and 4.0 ± 1.5 N for the left and right hands, respectively, demonstrating predictive compensation.

For statistical testing, we inverted the DFPV for the right hand so that a positive DFPV would indicate specific adaptation. However, for the figures, for clarity, we left the DFPV as defined above.

Figure 4C shows the DFPVs for both arms. In the initial uncoupled field, the DFPV became progressively more nonzero, suggesting that each arm was learning to compensate for its specific force field. When the arms were coupled, the DPVF fell to close to zero, suggesting the arms repartitioned their learning so that each arm contributed similarly to each direction. Finally, when the arms were once again uncoupled, the DFPV rapidly increased, suggesting that once again the arms were each compensating for their specific force field.

We performed repeated-measures ANOVA on the DFPV with factors of arm (left and right) and epoch. Because there are few catch trials per batch, we averaged the catch trials from two consecutive batches within a condition so that there were five categorical levels of epoch: the last batches of the null field (9 and 10), the last batches of the uncoupled field (29 and 30), the first (31 and 32) and last (49 and 50) batches of the coupled field, and the first batches of the final uncoupled field (51 and 52). This showed a significant main effect of epoch (F_(4,28) = 22.4; p < 0.001), but no significant effect of arm. We performed five planned comparisons (below) averaging over the arms and applied Bonferonni's correction to test for significance.

Before the introduction of the field, the hands generated little force into the channels (−0.90 N). On the introduction of the uncoupled field, each arm learned to compensate for its field, and after 20 batches the forces generated by the arms had significantly increased (p < 0.001) by an average of 9.6 N. This shows that subjects had learned to specifically compensate for the force field, rather than applying a nonspecific cocontraction strategy.

When the arms were then coupled, there was initially no significant change in the DFPV (batches 29 and 30 compared with 30 and 31). However, after 20 batches, the DFPV had reduced significantly (batches 29 and 30 compared with 49 and 50; p < 0.001), showing that the hands had repartitioned the task so that they contributed more equally for different directions. On the reintroduction of the uncoupled field, there was a rapid significant increase in the DFPV (batches 49 and 50 compared with 50 and 51; p < 0.004) and the new DFPVs were not significantly different from the final sharing in the uncoupled context (29 and 30 compared with 50 and 51).

Results from this experiment imply that the compensation learned in the uncoupled condition for separate orthogonal components of a field could immediately transfer to the full-field coupled condition.

Decomposition–composition

At the end of familiarization phase, subjects made relatively straight trajectories (Fig. 3B, final preexposure). On introduction of the coupled curl field components to each hand, trajectories were perturbed (Fig. 3B, initial coupled). In this case, the trajectories were similarly perturbed in all directions, because the field acted symmetrically. Again, after 20 batches, the trajectories approximated those from the final preexposure phase (Fig. 3B, final coupled). However, after adapting to this coupled condition, trajectories once again became perturbed on transition to the uncoupled condition (Fig. 3B, initial uncoupled).

Similar effects on error were seen for the group of subjects who first experienced the coupled curl field and then transitioned to the uncoupled orthogonal components of the curl field (Fig. 5 A–C). A repeated-measures ANOVA on the MPE with factors of arm (left and right) and epoch (batches 10, 11, 30, 31, 50, and 52) showed a significant main effect of epoch (F_(5,40) = 30.5; p < 0.001), but no significant effect of arm. Again, we performed five planned comparisons (below) averaging over the arms and applied Bonferonni's correction to test for significance.

Figure 5.

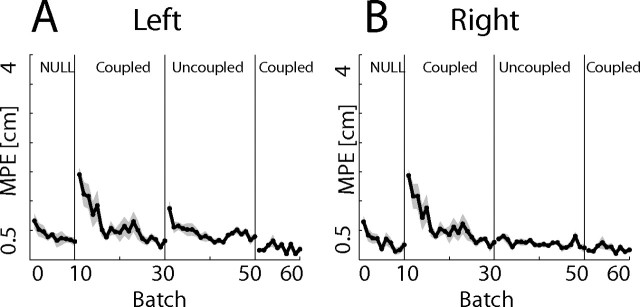
Results for the decomposition–composition experiment. A, B, Shown are the MPEs for the left and right hands, respectively, illustrating the effect of switching between coupled and uncoupled contexts. Shading shows SE across subjects. C, DPFV during catch trials for the two arms.

On the introduction of the coupled curl field, the MPE increased from 0.87 to 2.3 cm (p < 0.001). Over the course of the next 20 batches, the MPE decreased significantly to 0.93 cm (p < 0.001). After the hands had learned to jointly move in a single coupled curl field, the hands were uncoupled and exposed to two separate orthogonal components of the curl field. For the first batch in the uncoupled field, the MPE (2.3 cm) increased significantly (p < 0.001) from the previous coupled batch. Over the course of 20 additional batches, the error fell significantly to 1.4 cm (p < 0.001, comparison of first and last batch in uncoupled field). Finally, the hands were once again coupled and the error fell significantly on the first coupled batch to 0.88 cm (p = 0.006). A comparison of the final batch of the initial coupled session and the first batch of the final coupled session showed that the MPEs were not significantly different.

As before, we performed a repeated-measures ANOVA on the DFPV (Fig. 5C), with factors of arm (left and right) and epoch. This showed a significant main effect of epoch (F_(4,32) = 44.1; p < 0.001) and a marginally significant effect of hand (F_(1,8) = 6.5; p = 0.035). We performed five planned comparisons (below) averaging over the arms and applied Bonferonni's correction for test of significance.

Before the introduction of the field, the hands generated little force into the channels (0.27 N on last batches). On the introduction of the coupled force field after 20 batches the force generated by the arms was significantly higher (p = 0.001) and had increased by an average of 5.3 N. When the arms were then uncoupled, there was initially a decrease in the DFPV (batches 29 and 30 compared with 30 and 31; p < 0.001). However, after 20 batches, the DFPV had increased significantly (batches 29 and 30 compared with 49 and 50; p < 0.001). On the reintroduction of the coupled field, there was a rapid decrease in the DFPV, which was significant (batches 49 and 50 compared with 50 and 51; p < 0.001), and the new DFPV was also significantly different from the final DFPV in the previous coupled phase (p < 0.001; 29 and 30 compared with 50 and 51). When the DFPV was close to zero, the mean peak force generated by the right and left hands in the catch trials over the final coupled phase was computed. These values were significantly different from zero (one-tailed t test; p < 0.001) in both cases, with means of 5.8 ± 1.7 and 4.5 ± 2.0 N for the left and right hands, respectively, indicating predictive compensation.

Results from this experiment imply that the compensation learned in the coupled condition did not immediately transfer to the orthogonal components used in the uncoupled condition.

Decomposition–composition control

To determine whether the differential effects described above were simply the result of transitioning between coupled and uncoupled conditions, we ran an additional experiment. Subjects initially learned a full-strength curl field in the coupled condition, but this time were exposed to half-strength full curl fields in the uncoupled condition, rather than the orthogonal components used previously. Figure 3C shows the right hand paths for the outward portion of the movement of key phases in the experiment. On initial introduction of the coupled curl field (Fig. 3C, initial coupled), trajectories were symmetrically perturbed and after 20 batches the trajectories became straighter. This time after adapting to the coupled condition, on transition to the uncoupled condition trajectories remained quite straight (Fig. 3C, initial uncoupled).

Figure 6 shows the MPE for this group of subjects. A repeated-measures ANOVA on the MPE with factors of arm (left and right) and epoch (batches 10, 11, 30, 31, 50, and 52) showed a significant main effect of epoch (F_(5,25) = 51.0; p < 0.001) and a significant effect of arm (F_(1,5) = 29.7; p = 0.003) as well as a significant interaction (F_(5,25) = 4.6; p = 0.004). We performed a planned comparison for each arm between batch 30 (last coupled batch) and 31 (first uncoupled batch). For the first batch in the uncoupled field, the MPE for the left arm increased significantly by 0.55 cm from 0.82 to 1.37 cm (p < 0.05), whereas the MPE for the right hand did not change significantly (from 0.80 to 0.86 cm). In contrast, in the experiment in which the coupled field was decomposed into two orthogonal components, this average increase over the arms was 1.4 cm.

Figure 6.

Results for the decomposition–composition control experiment, using decomposition into half-strength full curl fields. A, B, Shown are the MPEs for the left and right hands, respectively, illustrating the effect of switching between coupled and uncoupled contexts. The shading shows SE across subjects.

This shows that the lack of transfer found in the previous experiment was not attributable to transition between coupled and uncoupled conditions but rather attributable to the specific field decomposition used. Together, these results show that subjects cannot decompose a field arbitrarily when moving from coupled to uncoupled contexts. However, the ability of subjects to rapidly relearn the uncoupled fields suggests that they retain knowledge obtained during their initial exposure to it. This rapid relearning therefore suggests that the motor system may be able to use partially separate representations when it is advantageous to do so.

Alternating field experiment

Results of the previous experiments that showed rapid transitions between coupled and uncoupled contexts suggested that the representations in these two contexts were at least partially separate. To examine the potential for separate representations associated with the coupled and uncoupled contexts, we exposed subjects to alternating fields.

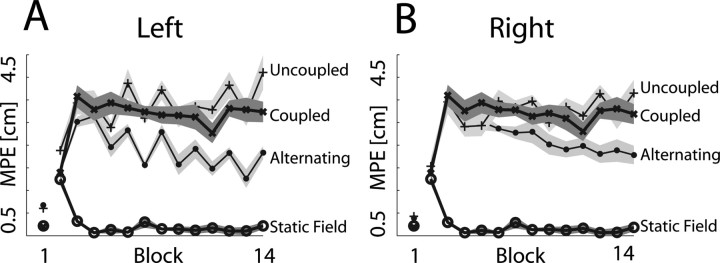
Subjects were exposed to curl fields, which switched between clockwise and counterclockwise directions every 10 batches. Each batch contained nine movements, and therefore subjects performed 90 trials for each field direction before switching. Three separate groups of subjects were exposed to alternating fields with the hands always uncoupled (Fig. 7A), always coupled (Fig. 7B), or with the coupled–uncoupled context switching with the fields (Fig. 7C). In each case, the errors increased on initial expose to the first field. Moreover, on subsequent exposure to the alternating fields, errors were always larger because of interference. Subjects adapted well to each exposure of a given field, as illustrated in Figure 7. Their ability to rapidly switch between the fields was examined by analyzing the average performance over the first batch after a switch (Fig. 8). The errors were high throughout the experiment when the hands were either always uncoupled (Fig. 8, plus signs) or coupled (Fig. 8, crosses). In contrast for the group in which the context switched with the fields, errors decreased progressively over the experiment (Fig. 8, filled circles). However, error in this case was still higher than the control condition in which the hands were always coupled and the field direction remained unchanged over the duration of the experiment (Fig. 8, open circles).

Figure 7.

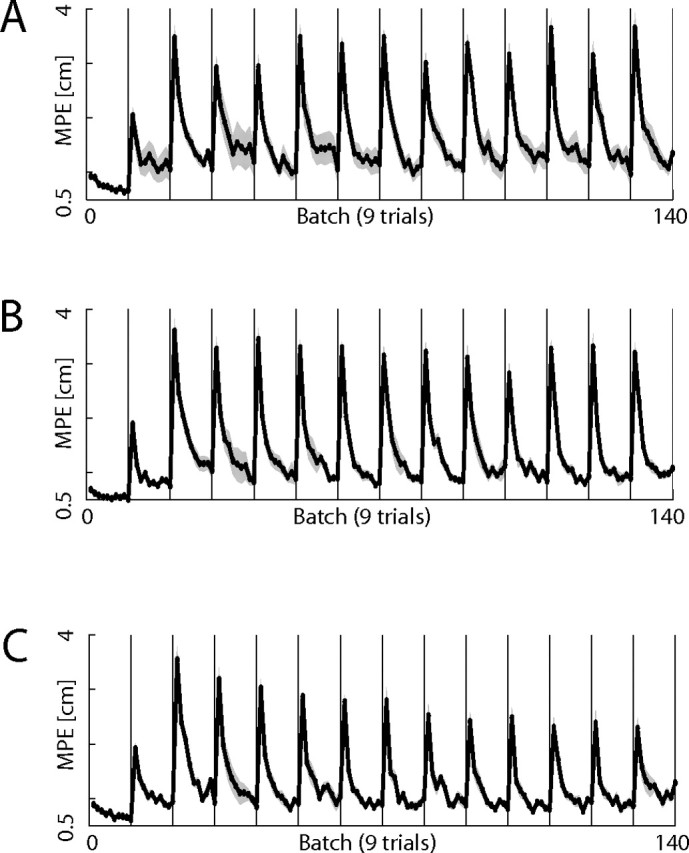
Results for the curl field switching experiments. A–C, Shown are the MPEs of the right hand over each batch in the uncoupled, coupled, and alternating conditions, respectively. Error bars show 1 SE on the mean across the subjects.

Figure 8.

Results for the curl field switching experiments. A, B, Shown are the MPEs over the first batch after switching for the left and right hands, respectively. Error bars show 1 SE on the mean across the subjects.

The catch trials were used to examine whether subjects were adapting to the force field by predictive compensation or by cocontraction. The mean absolute peak force generated by the right hand in the catch trials in each of the two last blocks, were calculated for each of the three alternating conditions. These were highly significantly (p < 0.001) different from zero in all cases with means of 4.8 ± 1.5, 3.7 ± 0.6, and 4.5 ± 1.1 N for the alternating, uncoupled, and coupled conditions, respectively.

To examine learning, we calculated, for each subject, the change in error from the mean error of the first batch of the third and fourth blocks and the corresponding error of the last two blocks (13th and 14th). We chose the third and fourth blocks because these were the first that could show both retrograde and anterograde interference effects and we took the mean over two blocks to average out any difference between clockwise and counterclockwise fields. We performed a repeated-measures ANOVA on this measure of learning with a between-subject factor of group (uncoupled, coupled, and alternating) and within-subject factors of hand (left and right). There was a significant main effect of group (F_(2,21) = 12.0; p < 0.001), but the effect of hand was not significant. Planned comparisons (Bonferonni-corrected) between the groups showed that the uncoupled and coupled groups did not differ significantly in their learning (both had a nonsignificant change in MPE of −0.18 and 0.21 cm, respectively) but that the alternating groups showed significantly more learning (significant change in MPE of −1.0 cm; p < 0.001) than both the coupled (p < 0.011) and the uncoupled (p < 0.001) groups. Thus, only in the alternating condition was significant learning observed and this group showed a significantly better performance than the groups in which the context did not change. Nevertheless, their performance was not as good as subjects who experienced a single field direction throughout the experiment (in the coupled condition) (Fig. 8A,B, open circles).

Discussion

We have investigated how dynamic learning transfers between the two arms acting on a single dynamic object (coupled) versus the two arms acting on its own separate object (uncoupled). When each arm was exposed to an orthogonal component of a curl field (uncoupled), we observed learning in both arms. This ability of the two arms to learn two force fields in an uncoupled condition agrees with recent results that show no interference when the two arms independently learn two force fields (Tcheang et al., 2007). In this previous study, each arm experienced full curl fields, which were either the same or opposite directions in extrinsic space. In both conditions, neither interference nor facilitation was observed. In the current study, we show that each arm is able to simultaneously learn a single orthogonal component of a force field. Moreover, in the composition experiment, we investigate how learning these separate components subsequently transfers to a condition in which the hands are coupled together and experience a full curl field.

When the context of the two arms changed so that they experienced a coupled field that was the sum of these two components, that is, a full curl field, the errors remained low. This suggests that, despite the change in context, subjects could continue to produce compensation for each arm appropriately. An analysis of the catch trials showed that initially the left and right arms were primarily responsible for compensating for the perturbing forces appropriate for the components of the curl fields that they had originally learned. Although such a strategy led to low errors, over time the contributions of the two arms became similar, suggesting that this is a preferable control strategy. In general, an equal contribution of the two arms to produce a set force both reduces the energy consumed (assuming energy use scales supralinearly with force) and also reduces the variability that arises because of signal-dependent noise (assuming each arm has an independent source of noise).

When subjects transitioned back to the two original uncoupled fields, there was an increase in error, which fell rapidly as the arms once again readapted to compensate separately for their component of the curl field. Although repartitioning of the forces generated by each arm was slow on transferring from uncoupled to coupled, it was fast when transferring back to the uncoupled condition. This rapid transition suggests that representations of dynamics for uncoupled and coupled contexts may be partially independent.

In a decomposition experiment, we investigated how learning a full curl field with the hands coupled subsequently transfers to a condition in which the hands are uncoupled and experience separate orthogonal components of the field. In this case, there was a lack of transfer between the two conditions. In addition, the solution found by the arms for the initial coupled condition was different from the equivalent condition in the composition experiment, although the final coupled condition was similar. This suggests that previous exposure to the uncoupled condition may have influenced the solution to the subsequent coupled condition in both composition and decomposition experiments.

In a variant of the decomposition experiment, we investigated whether the initial lack of transfer was attributable to the particular fields rather than the coupled versus uncoupled context. In this case, we examined transfer from a full curl field with the hands coupled to two half-strength curl fields with the hands uncoupled. If the lack of transfer in the first decomposition experiment was attributable to the change in coupled to uncoupled contexts, we would similarly see no transfer in this control experiment. The results clearly showed transfer, suggesting that it is not the transition from coupled to uncoupled that led to the previous lack of transfer, but the form of the field decomposition. When learning in the coupled condition, there are many ways in which each arm could contribute to the solution, and it is unlikely that the partitioning chosen naturally by subjects would match the decomposition to orthogonal components used in these experiments. In contrast, in the uncoupled condition, each arm is required to fully compensate for its particular field, and the sum of these compensations when combined is appropriate for the coupled condition.

This suggests that, when the fields are decomposed such that each arm can simply continue to generate the same forces, the motor system can continue to use the same representation. Importantly, this is not evidence against the ability of the motor system to use separate representations for coupled and uncoupled contexts. Crucially, when the fields are decomposed such that each arm cannot simply continue to generate the same forces, the motor system appears to use separate representations. To test this hypothesis, we examined the learning of opposing curl fields. If partially separate representations exist, it should be possible to learn opposing force fields if each is associated with a different context, coupled or uncoupled (Brashers-Krug et al., 1996; Caithness et al., 2004). When the context was kept fixed (either coupled or uncoupled) and the field direction switched every 90 trials, there was no significant learning consistent with previous studies showing interference. However, when the two fields were each associated with a different context (coupled or uncoupled), we found significant learning of the opposing fields despite the fact that there were minimal changes in the arms configuration between these two conditions (Gandolfo et al., 1996). In addition, the decrease in error over trials (Fig. 8) was almost linear, suggesting that additional learning may have occurred with additional trials. However, the duration of the experiment was limited by how long we could expect our subjects to generate bimanual movements in a force field. It is therefore an open question how low the asymptote would be for this learning curve. The ability to learn opposing fields when each is associated with a different coupling context between the arms suggests that there may be separate representations for two arms acting on a single object versus two arms acting separately on different objects.

Previous studies have focused on a variety of issues related to bimanual interactions. A key finding is the well documented symmetry bias seen in rhythmical movement of contralateral body parts, including the arms (Kelso, 1984; Swinnen et al., 1998). These studies show that, even without physical coupling, there is a bias for the arms to move either symmetrically or antisymmetrically, and at high frequencies only symmetrical movements are stable. In our task, movements of the two arms were always in the same direction in Cartesian space and therefore contained both symmetric and antisymmetric movements across different directions. However, we used speeds that were easy for the subjects to achieve, and therefore they were not limited by symmetry bias.

Several studies have explored behavior in which the movement of one arm affects the other to investigate predictive control during bimanual movements. These studies have shown that, when one hand acts on the other, there is a precise predictive response (Massion, 1992; Blakemore et al., 1998; Bays and Wolpert, 2006). A recent study examined a task in which both hands had to act on a single object to control a cursor that mapped various forces on the object to cursor motion (Johansson et al., 2006). This task examined the precise coordination of the two hands and showed that one hand is used as the main manipulator (the prime mover) while the other hand assists. Moreover, the allocation of which hand is prime mover is task dependent. These studies all involve one hand acting on another or on an object with simple dynamics. In contrast, in the current study, both arms acted to control a single dynamic object.

Dynamic learning experiments have shown that the dominant and nondominant arms may have different roles (Gandolfo et al., 1996; Sainburg and Kalakanis, 2000; Bagesteiro and Sainburg, 2002). For example, dominant arm joint torques were better coordinated for reaching movements than for the nondominant arm (Bagesteiro and Sainburg, 2002). Several studies have explored how learning novel dynamic with one arm transfers to the other and show that field compensation learned in the dominant arm will partially transfer to the nondominant one (Bagesteiro and Sainburg, 2002; Criscimagna-Hemminger et al., 2003; Wang and Sainburg, 2004). More recently, there has been interest in generalization in dynamic learning between the two arms that shows that there is transfer from the dominant to nondominant arm during learning of velocity-dependent force fields (Criscimagna-Hemminger et al., 2003). Another recent study compared the transfer of dynamic learning to the nondominant arm with either bimanual training or unimanual training of only the dominant arm and found similar transfer in both cases (Burgess et al., 2007). However, it has been suggested that such bimanual generalization may be the result of cognitive mechanisms and that a slow introduction of the force field prevented transfer from occurring (Malfait and Ostry, 2004). In addition to transfer of learning from one arm to the other, the current study shows differential transfer between different bimanual contexts.

A recent study examined dynamic learning with reaching movements of the left hand in a force field while the right hand either remained stationary or moved simultaneously (but without any field applied to it) (Nozaki et al., 2006). Their results suggest partially separate representations of dynamics for bimanual and unimanual movements. For example, when training was unimanual, they found that, if subjects washed out aftereffects during bimanual movement, the aftereffects remained when they returned to unimanual movements. In our study, all movements were bimanual and thus correspond to one context in the study by Nozaki et al. (2006). In a similar manner, we find evidence for separate representations within the bimanual context for movements that act on a single object versus movements that act on two separate objects. The results of Nozaki et al. (2006) support neurophysiological studies of bimanual and unimanual arm movements. Donchin et al. (1998) examined the activity of cortical neurons involved in coordination between the limbs. They found that most neurons in M1 showed specific activity to bimanual movements that was quite distinct to their activity during unimanual movements. Our results suggest that this population of bimanual neurons may be further segregated into different movement contexts.

In summary, our results from examining decomposition and composition of dynamic learning between the arms suggest that, when required to learn different dynamics in coupled and uncoupled contexts, the motor system can use partially separate representations and can thereby rapidly switch between previously learned contexts. Moreover, in the extreme case of exposure to alternating opposing force fields, the context of coupled and uncoupled allows significant learning. These results suggest that the representations of dynamics for these two bimanual contexts can become partially independent, which would predict that there may be separate neural representation for two arms acting on a single object compared with two arms acting on two separate objects.