Abstract
Full genome sequences of prokaryotic organisms have led to reconstruction of genome-scale metabolic networks and in silico computation of their integrated functions. The first genome-scale metabolic reconstruction for a eukaryotic cell, Saccharomyces cerevisiae, consisting of 1,175 metabolic reactions and 733 metabolites, has appeared. A constraint-based in silico analysis procedure was used to compute properties of the S. cerevisiae metabolic network. The computed number of ATP molecules produced per pair of electrons donated to the electron transport system (ETS) and energy-maintenance requirements were quantitatively in agreement with experimental results. Computed whole-cell functions of growth and metabolic by-product secretion in aerobic and anaerobic culture were consistent with experimental data, and thus mRNA expression profiles during metabolic shifts were computed. The computed consequences of gene knockouts on growth phenotypes were consistent with experimental observations. Thus, constraint-based analysis of a genome-scale metabolic network for the eukaryotic S. cerevisiae allows for computation of its integrated functions, producing in silico results that were consistent with observed phenotypic functions for ≈70–80% of the conditions considered.
Systems biology is commonly viewed as a four-step procedure (1–3): (i) the enumeration of the biological components that make up the biological process of interest, (ii) the reconstruction of the network of interactions among these components, (iii) the in silico simulation of the network function, and (iv) the comparison of computed network properties with actual phenotypic observations. A wealth of available biological data for Saccharomyces cerevisiae (4–7) led to the establishment of the first genome-scale reconstruction of the metabolic network in a eukaryotic cell (8). The initial completion of the first two steps of the systems biology procedure for yeast metabolism has been achieved. Steps iii and iv have not yet been carried out for a eukaryotic organism.
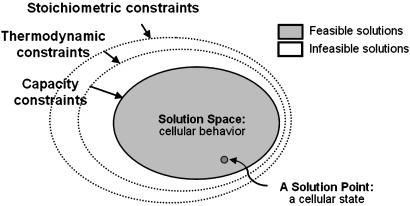
Integrated functions of reconstructed metabolic networks can be determined in silico by using a number of analytical approaches (9–11). The relatively young constraint-based approach differs fundamentally from the more traditional kinetic theory-based approaches in that it is not aimed at finding the solution or behavior of the network under certain conditions but rather at eliminating solutions (behaviors) that the network cannot exhibit (Fig. 1). By using this approach, a network of interactions is successively constrained by defining the stoichiometry of the interacting components, the direction of network reactions, and the maximum allowable throughput. In this way, candidate solutions to the network equations are systematically eliminated by the successive application of the governing constraints, i.e., stoichiometry, thermodynamics, and maximal enzymatic rates (12). One thus can define the range of capabilities of the reconstructed network and then, through the use of optimization procedures, calculate the “best” solution within the allowable range (13–15). If the network has evolved to produce this best or optimal function, then an agreement is obtained between experimentally determined behavior and the in silico computations (16).
Fig. 1.
Constraint-based modeling approach. The governing physicochemical constraints, such as stoichiometric, thermodynamics, and reaction-rate capacity constraints, confine the possible phenotypic outcome of a cellular network (12). Physiologically feasible cellular states or the “solution points” lie within the constrained solution space and are indicated as “feasible solutions.” Any states excluded by the physicochemical constraints are “infeasible” and cannot be attained by the cell. Optimization tools such as linear programming then can be used to determine an optimal solution within the allowable range of cellular capabilities.
The constraint-based approach provides an appropriate simulation platform for studying the overall phenotypic behavior for S. cerevisiae. A tremendous amount of experimental data has been and continues to be generated for S. cerevisiae (17–19). A number of databases have been dedicated to store and update yeast experimental data sets, and several mathematical models are available that use kinetic information to capture cell behaviors (20–23). Limited availability of kinetic information restricts such models to a subset of the whole cell. The constraint-based approach is not limited by the availability of the kinetic data and thus can capture the complex content of the whole cell by using the existing genomewide knowledge and maximally used high-throughput data on yeast.
The constraint-based approach (12–15) has been productively used to study the properties of genome-scale reconstructions of bacterial metabolic networks including Haemophilus influenzae (24), Escherichia coli (25), and Helicobacter pylori (26). Here we apply this approach to the recently reconstructed genome-scale S. cerevisiae metabolic network (8) to compute the properties of a eukaryotic cell and compare them to experimental observations.
Methods
Reconstructed Metabolic Network. The reconstruction procedure has been described in detail (8). Briefly, genomic, biochemical, and physiological information was used to construct a metabolic reaction network for S. cerevisiae. Genomic information was used to identify the ORFs in the genome and their associated proteins, biochemical information was used to assign biochemical functions to the identified enzymes, and physiological information was used to fill in the gaps in metabolic pathways and formulate the biosynthetic composition of the cell. The reconstructed network accounts for 708 unique metabolic ORFs, ≈16% of the assigned ORFs in the S. cerevisiae genome (7). The network includes a total of 1,175 biochemical reactions, of which 124 are mitochondrial, 702 are cytosolic, and 349 are transport reactions across the plasma and mitochondrial membranes. The metabolic network contains a total of 584 unique metabolites, which are distributed among different compartments: 559 are in the cytoplasm, 164 are in the mitochondria, and 121 are extracellular. The complete model is available at www.cpb.dtu.dk/models/yeastmodel.html and http://systemsbiology.ucsd.edu/organisms/yeast.html.
In Silico Computations. The metabolic capabilities of the S. cerevisiae network were calculated by using flux balance analysis and linear optimization (14, 15, 27). For growth simulations, biomass synthesis (i.e., production of biosynthetic components at the physiological level) was selected as the objective function to be maximized, and optimization was done subject to stoichiometric, limited thermodynamics, and reaction capacity constraints by using established procedures (13–15). Optimization problems were solved by using the commercially available package LINDO (Lindo Systems, Chicago).
In Silico Number of ATP Molecules Produced per Pair of Electrons Donated to the Electron Transport System (ETS) (P/O) Calculation. The P/O ratio, or ATP yield of respiration, is a measure of the efficiency of oxidative phosphorylation in energy metabolism. The P/O ratio is calculated as the relative amount of ATP molecules produced per pair of electrons donated to the ETS. The theoretical value of the P/O ratio for S. cerevisiae is 1.5 (28), i.e., 18 ATP molecules per 12 pairs of electrons transferred via the ETS. The in silico P/O ratio was calculated by determining the maximum number of ATP molecules produced through the ETS per consumed molecule of glucose by using the reconstructed model (maximizing ATP production in the S. cerevisiae model grown on one molecule of glucose yields YATP,max = 12.5 ATP molecules that are generated via the ETS). The in silico P/O ratio thus was calculated as the ratio of the maximum in silico ATP yield over total electron pairs transferred to the ETS.
Energy Requirement for Biomass Formation. The amount of ATP required for biomass formation, i.e., growth-associated ATP requirement, was calculated by summing the ATP needed for the formation of precursor metabolites [9.89 mmol of ATP/grams dry weight (gDW)], for polymerization of macromolecules (23.92 mmol of ATP/gDW), and the model-based ATP requirement to meet the biomass yield of 0.51 gDW/g glucose (29) in an aerobic glucose-limited continuous culture (35.36 mmol of ATP/gDW).
Chemostat Growth Simulation. In a continuous culture, growth rate is equivalent to the dilution rate and kept at a constant value. Calculations of the continuous culture of S. cerevisiae were performed by fixing the in silico growth rate to the experimentally determined dilution rate and minimizing the glucose uptake rate. This formulation is equivalent to maximizing biomass production given a fixed glucose uptake value and was used to simulate a continuous-culture growth condition.
Results
The in silico model can be used to assess network properties such as the P/O ratio and energy maintenance costs and to compute whole-cell functions. The efficiency of aerobic respiration is measured by the P/O ratio. Experimental studies of isolated mitochondria have shown that S. cerevisiae lacks site I proton translocation (28). Consequently, estimation of the maximum theoretical or “mechanistic” yield of the ETS alone gives a P/O ratio of 1.5 for oxidation of NADH in S. cerevisiae grown on glucose (28). However, based on experimental measurements, it has been determined that the net in vivo P/O ratio is ≈0.95 (28). This difference is generally attributed to the use of the mitochondrial transmembrane proton gradient needed to drive metabolite exchange (such as the proton-coupled translocation of pyruvate) across the inner mitochondrial membrane. In the reconstructed network, which contains no proton leakage, 12.5 molecules of ATP are generated via the ETS. As complete oxidation of glucose leads to donation of 12 electron pairs (10 NADH and 2 FADH2) to the electron transport chain, the in silico P/O ratio is 1.04 for oxidation of NADH and FADH2 during growth on glucose, i.e., 12.5/12 = 1.04, agreeing well with the measured value without including any proton leakage. The network-based computation systemically accounts for all the steps required to import and export compounds from the mitochondria, computing a net overall P/O ratio.
Cells require energy for both growth- and non-growth-associated activities (29). The energy requirement for the formation of biomass has been measured experimentally for S. cerevisiae, and reported values range from 62.5 to 71.4 mmol of ATP/gDW (29, 30). A network-based calculation procedure of the growth-associated energy requirement has been developed (31), and when applied to the reconstructed S. cerevisiae network, a value of 69.2 mmol of ATP/gDW was computed (see Methods), which falls in the range of experimentally determined values. Energy required for precursor metabolite formation and macromolecule polymerization can be calculated from the biosynthetic composition of the cell. The model-based ATP requirement is entirely network-dependent and was derived from the in silico calculations.
The reconstructed metabolic network of S. cerevisiae can be used to represent whole-cell functions by placing simultaneously all growth and maintenance demands on the network (14, 15). These demands include the production of all the biomass components in the appropriate physiological proportion (8) while meeting both growth-associated (69.2 mmol of ATP/gDW) and non-growth-associated (1 mmol of ATP/gDW per h) energy requirements (30, 32). The in silico representation of all metabolic demands on the reconstructed map can be used simultaneously for analyzing, interpreting, and predicting the phenotypic behavior of S. cerevisiae, such as in anaerobic and aerobic culture and during metabolic growth shifts.
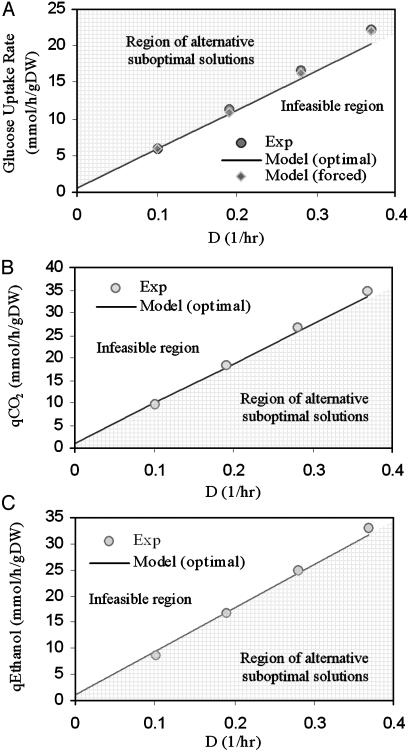
Optimal growth properties of S. cerevisiae were computed under anaerobic glucose-limited continuous culture at dilution rates varying between 0.1 and 0.4 h-1 (see Methods). The computed by-product secretion rates then were compared with the experimental data (33). The calculated uptake rates of glucose and the production of ethanol, glycerol, succinate, and biomass were in good agreement with the independently obtained experimental data (Fig. 2, and Fig. 5 and Table 2, which are published as supporting information on the PNAS web site) and, as for E. coli (34), lie at the edge of the allowable solution range. The relatively low observed acetate secretion rates were not predicted by the in silico model. The in silico analysis of the reconstructed network indicates that the release of acetate does not improve the optimal solution of the network, most likely because of the absence of kinetic and regulatory constraints. It is possible to constrain the in silico model further to secrete acetate at the experimental level and recompute an optimal solution under these additional constraints. This calculation results in values that are closer to the measured glucose uptake rates (Fig. 2 A). This procedure is an example of an iterative data-driven constraint-based modeling approach, by which the successive incorporation of experimental data is used to improve the in silico model (12, 35) without the addition of rigorous analytical tools and complex information. Besides the ability to describe the overall growth yield, the model allows further insight into how the metabolism operates at a more detailed level. From analysis of the metabolic fluxes at anaerobic growth conditions, the flux through the glucose-6-phosphate dehydrogenase is found to be 5.32% of the glucose uptake rate at a dilution rate of 0.1 h-1, which is consistent with the experimentally determined value (6.34%) for this flux when cells are operating with fermentative metabolism (33).
Fig. 2.
Anaerobic glucose-limited continuous culture of S. cerevisiae. (A) Utilization of glucose at varying dilution rates in anaerobic chemostat culture. The data point at the dilution rate of 0.0 is extrapolated from the experimental results. The shaded area (i.e., the infeasible region) contains a set of stoichiometric constraints that cannot be balanced simultaneously with growth demands. The model produces the optimal glucose uptake rate for a given growth rate on the line of optimal solution [Model (optimal)]. The imposition of additional constraints drives the solution toward a region in which more glucose is needed (i.e., region of alternative suboptimal solution). At the optimal solution, the in silico model does not secrete acetate. The maximum difference between the model and the experimental points is 9% at the highest dilution rate. When the model is forced to produce acetate at the experimental level [Model (forced)], the glucose uptake rate is increased and becomes closer to the experimental values (e.g., the 9% error is reduced to 1%). (B and C) Secretion rate of anaerobic by-products in chemostat culture. The highest difference between the model and the experimental data points is associated with glycerol production at the highest dilution rate for a value of 28% (Table 2). The ethanol secretion rate differences can be explained by a partial evaporation of ethanol in the experiments. Exp, experimental; q, secretion rate; D, dilution rate.
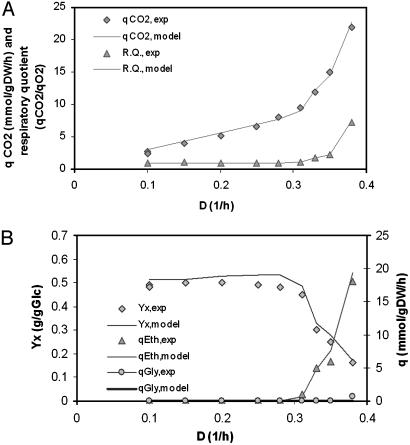
Optimal growth properties of S. cerevisiae were computed under aerobic glucose-limited continuous culture, where the Crabtree effect plays an important role. The Crabtree effect refers to alcoholic fermentation under aerobic conditions and occurs when the dilution rate in sugar-limited chemostat cultures exceeds a critical value that depends on the strain (29). The molecular mechanisms underlying the Crabtree effect in S. cerevisiae are not known. The regulatory features of the Crabtree effect (36), however, can be included in the in silico model as an experimentally determined (37) growth-rate-dependent maximum oxygen uptake rate (38). With this additional constraint, the in silico model makes quantitative predictions about the respiratory quotient, glucose uptake, ethanol, CO2, and glycerol secretion rates under aerobic glucose-limited continuous conditions (Fig. 3, and Fig. 6 and Table 3, which are published as supporting information on the PNAS web site). In addition, the capabilities of the reconstructed network to quantitatively predict experimental observations of growth in S. cerevisiae extends to metabolic by-product yields, specific growth rate, and specific substrate uptake rates under both batch culture and chemostat culture by using various carbon sources (e.g., glucose, galactose, and ethanol) and oxygenation conditions (i.e., aerobic and anaerobic conditions) (Tables 4 and 5, which are published as supporting information on the PNAS web site), demonstrating the utility of the model in a wide range of conditions.
Fig. 3.
Aerobic glucose-limited continuous culture of S. cerevisiae. (A) Biomass yield (YX) and secretion rates of ethanol (Eth) and glycerol (Gly). The only data point not predicted by the model is the glycerol production at the highest dilution rate: D = 0.38 h-1.(B)CO2 secretion rate (qCO2) and respiratory quotient (R.Q.; qCO2/qO2) of the aerobic glucose-limited continuous culture of S. cerevisiae. Exp, experimental.
A whole-genome in silico representation of an organism has the capability to predict the phenotypic consequences of gene deletions from the genome (25, 26). The impact of single-gene deletions on growth was analyzed by simulating growth on a synthetic complete medium containing glucose, amino acids, and purines and pyrimidines, where the reaction corresponding to the deleted gene was removed. The in silico results were compared with experimental results as supplied by the Saccharomyces Genome Database (5). For central metabolism, growth was predicted under various experimental conditions (Table 1), and 81.5% (93 of 114 cases) of the in silico predictions were in agreement with in vivo phenotypes. In all cases the disagreements could be explained by known regulatory mechanisms, illustrating that deviations of the model predictions from experimental data will generally point to the existence of specific regulatory structures. In a more detailed study (39), in 87.8% of all considered cases (526 of 599), the in silico prediction was in qualitative agreement with experimental results.
Table 1. Impact of gene deletions on growth in S. cerevisiae.
| Defined complete Glc
|
Defined minimal Glc
|
Defined minimal Ace
|
Defined minimal Eth
|
||
|---|---|---|---|---|---|
| Gene | (in silico/in vivo) | (in silico/in vivo) | (in silico/in vivo) | (in silico/in vivo) | Refs. (for minimal media) |
| ACO1 | (+/+) | (—/—) | 44 | ||
| CDC19* | (+/—) | (+/—) | 45 | ||
| CIT1 | (+/+) | (+/+) | 46 | ||
| CIT2 | (+/+) | (+/+) | 46 | ||
| CIT3 | (+/+) | ||||
| DAL7 | (+/+) | (+/+) | (+/+) | (+/+) | 47 |
| ENO1 | (+/+) | ||||
| ENO2† | (+/—) | (+/—) | |||
| FBA1‡ | (+/—) | (+/—) | |||
| FBP1 | (+/+) | (+/+) | (—/—) | 48, 49 | |
| FUM1 | (+/+) | ||||
| GLK1 | (+/+) | ||||
| GND1§ | (+/—) | (+/—) | |||
| GND2 | (+/+) | ||||
| GPM1¶ | (+/—) | (+/—) | |||
| GPM2 | (+/+) | ||||
| GPM3 | (+/+) | ||||
| HXK1 | (+/+) | ||||
| HXK2 | (+/+) | ||||
| ICL1 | (+/+) | (+/+) | 50 | ||
| IDH1 | (+/+) | (+/+) | 51 | ||
| IDH2 | (+/+) | (+/+) | 51 | ||
| IDP1 | (+/+) | (+/+) | 52 | ||
| IDP2 | (+/+) | (+/+) | 52 | ||
| IDP3 | (+/+) | ||||
| KGD1 | (+/+) | (+/+) | 53 | ||
| KGD2 | (+/+) | (+/+) | 53 | ||
| LPD1 | (+/+) | ||||
| LSC1 | (+/+) | (+/+) | (+/+) | 54 | |
| LSC2 | (+/+) | (+/+) | (+/+) | 54 | |
| MAE1 | (+/+) | (+/+) | (+/+) | 45 | |
| MDH1 | (+/+) | (+/+) | (+/—) | 55 | |
| MDH2 | (+/+) | (+/—) | (+/—) | 55 | |
| MDH3 | (+/+) | ||||
| MLS1 | (+/+) | (+/+) | (+/+) | (+/+) | 47 |
| OSM1 | (+/+) | ||||
| PCK1 | (+/+) | ||||
| PDC1 | (+/+) | (+/+) | 56 | ||
| PDC5 | (+/+) | (+/+) | 56 | ||
| PDC6 | (+/+) | (+/+) | 56 | ||
| PFK1 | (+/+) | (+/+) | 57 | ||
| PFK2 | (+/+) | (+/+) | 57 | ||
| PGI1‡, ∥ | (+/—) | (+/—) | 58 | ||
| PGK1‡ | (+/—) | (+/—) | |||
| PGM1 | (+/+) | (+/+) | 59 | ||
| PGM2 | (+/+) | (+/+) | 59 | ||
| PYC1 | (+/+) | (+/+) | (+/—) | (+/—) | 60 |
| PYC2 | (+/+) | ||||
| PYK2 | (+/+) | (+/+) | (+/+) | 45, 55 | |
| RKI1 | (—/—) | ||||
| RPE1 | (+/+) | ||||
| SOL1 | (+/+) | ||||
| SOL2 | (+/+) | ||||
| SOL3 | (+/+) | ||||
| SOL4 | (+/+) | ||||
| TAL1 | (+/+) | (+/+) | 61 | ||
| TDH1 | (+/+) | ||||
| TDH2 | (+/+) | ||||
| TDH3 | (+/+) | ||||
| TKL1 | (+/+) | (+/+) | 61 | ||
| TKL2 | (+/+) | ||||
| TPI1‡, ** | (+/—) | ||||
| ZWF1 | (+/+) | (+/+) | 61 |
Growth on different media was considered, including defined complete medium with glucose (Glc) as the carbon source, and minimal medium with Glc, ethanol (Eth), or acetate (Ace) as the carbon source.
+/—, growth/no growth.
The isoenyzme Pyk2p is glucose repressed and cannot sustain growth on glucose
ENO1 plays central role in gluconeogenesis whereas ENO2 is used in glycolysis (66)
Model predicts single deletion mutant to be (highly) growth retarded
Gnd1p accounts for 80% of the enzyme activity. A mutant deleted in GND1 accumulates gluconate-6-phosphate, which is toxic to the cell (62)
The isoenzymes Gpm2p and Gpm3p cannot sustain growth on glucose. They show residual in vivo activity only when they are expressed from a foreign promoter (65)
Different hypotheses exist for why Pgilp-deficient mutants do not grow on glucose, e.g., the pentose phosphate pathway in S. cerevisiae is insufficient to support growth and cannot supply the EMP pathway with sufficient amounts of fructose-6-phosphate and glyceraldehydes-3-phosphate (64)
Growth of single deletion mutant is inhibited by glucose (63)
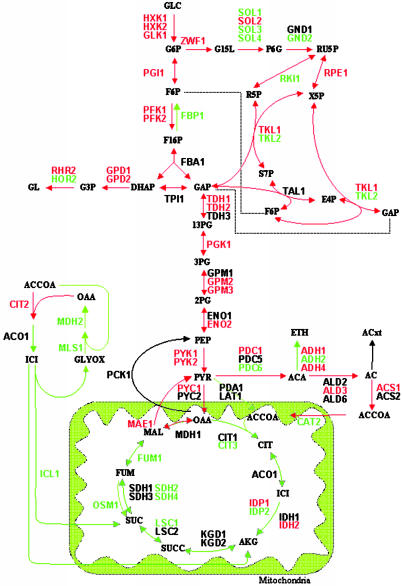
The in silico model was used to simulate the outcome of expression-profiling experiments during metabolic shifts. The computed changes in the flux maps then were compared on a qualitative basis (i.e., up or down) with experimentally determined mRNA expression profiles. Two metabolic shifts were considered: (i) aerobic-to-anaerobic glucose-limited continuous cultures (40) and (ii) a shift from respiro-fermentative growth on glucose to aerobic growth on ethanol (41), referred to as diauxic shift. The qualitative changes in calculated flux levels and experimentally determined transcription levels of the corresponding genes correlated in ≈58% for the central metabolic reactions (26 of 45; Table 6, which is published as supporting information on the PNAS web site) and 49% of all cases (215 of 436; Table 7, which is published as supporting information on the PNAS web site), including all the internal and transport reactions in anaerobic/aerobic glucose-limited continuous study. For the diauxic shift, the qualitative comparison between transcription and flux levels agreed in 61% of the central metabolic reactions (27 of 44 cases) (Table 8, which is published as supporting information on the PNAS web site).
By using the mRNA expression changes as additional biological constraints, flux changes during metabolic shifts were reexamined. Constraining the internal fluxes in both metabolic shifts improved the correlation between expression levels and flux changes to 78% for the central metabolic reactions (35 of 45 cases; Fig. 4 and Table 9, which is published as supporting information on the PNAS web site) and 63% for all cases (275 of 436; Table 10, which is published as supporting information on the PNAS web site) in anaerobic/aerobic glucose-limited continuous study and 84% (37 of 44 cases; Fig. 7 and Table 11, which are published as supporting information on the PNAS web site) in the diauxic shift study.
Fig. 4.
Gene expression and metabolic shift in anaerobic/aerobic glucose-limited continuous culture. The gene names in red and green have a higher and lower mRNA expression level, respectively, compared with the original condition. Red and green arrows correspond to an increase and decrease in flux activity, respectively. The changes in flux levels correlate qualitatively with changes in transcription levels in 78% of the investigated cases (35 of 45) and in 84% of the cases (37 of 44) during diauxic shift (Fig. 7, which is published as supporting information on the PNAS web site).
Discussion
Taken together, the results show that it is possible to compute whole-cell functions for eukaryotic cells based on genome-scale reconstruction of the underlying biochemical reaction networks. The constraint-based procedure used to evaluate the functions of the genome-scale yeast metabolic map gives a number of accurate predictions of cellular functions. However, there are also false predictions. These failure modes are of great interest because they point out incomplete parts of the reconstruction, and, as experience has shown, they guide us in focusing the iterative model-building process (12, 35). Furthermore, because of the absence of regulatory and kinetic constraints, many equivalent alternative optimal solutions are often available that contain the same objective value but differ in the internal flux values. Such alternative optimal solutions can be determined by using mixed-integer linear programming (42). Gene expression profiles can allow the best solution set to be identified among all possible equivalent sets that mixed-integer linear programming enumerates by providing transcriptional regulatory constraints. Imposing transcriptional regulatory constrains reduces the solution space and eliminates the physiologically infeasible flux distributions.
Unlike genome-sequencing projects that have a well defined endpoint, the in silico model-building procedure at the genome scale is an iterative and ongoing process during which the content of a model grows, and thus the scope of properties that can be computed widens. The 13-year history of building models for E. coli demonstrates this iterative model-building process (43). Importantly, the in silico model-building procedure in this way provides a framework for the integration of an expanding number of heterogeneous data types. The in silico computation of cellular functions from reconstructed networks allows for study of the relationship between environmental and genetic factors and how they come together to produce cellular phenotypes. These capabilities will be important in our quest to mathematically model and computer-simulate complex biological functions, which represents a fundamental goal of in silico biology.
Supplementary Material
Acknowledgments
We thank Drs. Mats Åkesson, Patrick Fu, and Jeremey Edwards for valuable discussions. We also thank the Whitaker Foundation for their support through the Graduate Fellowships in Biomedical Engineering (to I.F.), and support from National Science Foundation Grants MCB98-73384 and BES98-14092 and National Institutes of Health Grant GM57089. Research on Functional Genomics within the Center for Process Biotechnology is supported by the Danish Biotechnology Instrument Center.
Abbreviations: ETS, electron transport system; P/O, number of ATP molecules produced per pair of electrons donated to the ETS; gDW, grams dry weight.
References
- 1.Ideker, T., Galitski, T. & Hood, L. (2001) Annu. Rev. Genomics Hum. Genet. 2, 343-372. [DOI] [PubMed] [Google Scholar]
- 2.Nielsen, J. & Olsson, L. (2002) FEMS Yeast Res. 2, 175-181. [DOI] [PubMed] [Google Scholar]
- 3.Huang, S. (2002) Drug Discov. Today 7, S163-S169. [DOI] [PubMed] [Google Scholar]
- 4.Strathern, J. N., Jones, E. W. & Broach, J. R. (1982) The Molecular Biology of the Yeast Saccharomyces: Metabolism and Gene Expression (Cold Spring Harbor Lab. Press, Plainview, NY).
- 5.Cherry, J. M., Adler, C., Ball, C., Chervitz, S. A., Dwight, S. S., Hester, E. T., Jia, Y., Juvik, G., Roe, T., Schroeder, M., et al. (1998) Nucleic Acids Res. 26, 73-79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mewes, H. W., Frishman, D., Guldener, U., Mannhaupt, G., Mayer, K., Mokrejs, M., Morgenstern, B., Munsterkotter, M., Rudd, S. & Weil, B. (2002) Nucleic Acids Res. 30, 31-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Costanzo, M. C., Crawford, M. E., Hirschman, J. E., Kranz, J. E., Olsen, P., Robertson, L. S., Skrzypek, M. S., Braun, B. R., Hopkins, K. L., Kondu, P., et al. (2001) Nucleic Acids Res. 29, 75-79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Forster, J., Famili, I., Fu, P. C., Palsson, B. O. & Nielsen, J. (2003) Genome Res. 13, 244-253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fell, D. (1996) Understanding the Control of Metabolism (Portland Press, London).
- 10.Reich, J. G. & Sel'kov, E. E. (1981) Energy Metabolism of the Cell: A Theoretical Treatise (Academic, London).
- 11.Heinrich, R. & Schuster, S. (1996) The Regulation of Cellular Systems (Chapman & Hall, New York).
- 12.Palsson, B. O. (2000) Nat. Biotechnol. 18, 1147-1150. [DOI] [PubMed] [Google Scholar]
- 13.Varma, A. & Palsson, B. O. (1994) Appl. Environ. Microbiol. 60, 3724-3731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bonarius, H. P. J., Schmid, G. & Tramper, J. (1997) Trends Biotechnol. 15, 308-314. [Google Scholar]
- 15.Edwards, J. S., Ramakrishna, R., Schilling, C. H. & Palsson, B. O. (1999) in Metabolic Engineering, eds. Lee, S. Y. & Papoutsakis, E. T. (Dekker, New York).
- 16.Ibarra, R. U., Edwards, J. S. & Palsson, B. O. (2002) Nature 420, 186-189. [DOI] [PubMed] [Google Scholar]
- 17.Raamsdonk, L. M., Teusink, B., Broadhurst, D., Zhang, N., Hayes, A., Walsh, M. C., Berden, J. A., Brindle, K. M., Kell, D. B., Rowland, J. J., et al. (2001) Nat. Biotechnol. 19, 45-50. [DOI] [PubMed] [Google Scholar]
- 18.Lee, T. I., Rinaldi, N. J., Robert, F., Odom, D. T., Bar-Joseph, Z., Gerber, G. K., Hannett, N. M., Harbison, C. T., Thompson, C. M., Simon, I., et al. (2002) Science 298, 799-804. [DOI] [PubMed] [Google Scholar]
- 19.Kellis, M., Patterson, N., Endrizzi, M., Birren, B. & Lander, E. S. (2003) Nature 423, 241-254. [DOI] [PubMed] [Google Scholar]
- 20.Rizzi, M., Baltes, M., Theobald, U. & Reuss, M. (1997) Biotechnol. Bioeng. 55, 592-608. [DOI] [PubMed] [Google Scholar]
- 21.Vaseghi, S., Baumeister, A., Rizzi, M. & Reuss, M. (1999) Metab. Eng. 1, 128-140. [DOI] [PubMed] [Google Scholar]
- 22.Chen, K. C., Csikasz-Nagy, A., Gyorffy, B., Val, J., Novak, B. & Tyson, J. J. (2000) Mol. Biol. Cell 11, 369-391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hynne, F., Dano, S. & Sorensen, P. G. (2001) Biophys. Chem. 94, 121-163. [DOI] [PubMed] [Google Scholar]
- 24.Edwards, J. S. & Palsson, B. O. (1999) J. Biol. Chem. 274, 17410-17416. [DOI] [PubMed] [Google Scholar]
- 25.Edwards, J. S. & Palsson, B. O. (2000) Proc. Natl. Acad. Sci. USA 97, 5528-5533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schilling, C. H., Covert, M. W., Famili, I., Church, G. M., Edwards, J. S. & Palsson, B. O. (2002) J. Bacteriol. 184, 4582-4593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Varma, A. & Palsson, B. O. (1994) Bio/Technology 12, 994-998. [Google Scholar]
- 28.Verduyn, C., Stouthamer, A. H., Scheffers, W. A. & van Dijken, J. P. (1991) Antonie Leeuwenhoek 59, 49-63. [DOI] [PubMed] [Google Scholar]
- 29.Verduyn, C. (1991) Antonie Leeuwenhoek 60, 325-353. [DOI] [PubMed] [Google Scholar]
- 30.Verduyn, C., Postma, E., Scheffers, W. A. & van Dijken, J. P. (1990) J. Gen. Microbiol. 136, 405-412. [DOI] [PubMed] [Google Scholar]
- 31.Varma, A., Boesch, B. W. & Palsson, B. O. (1993) Appl. Environ. Microbiol. 59, 2465-2473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stouthamer, A. H. (1979) Microbiol. Biochem. 21, 1-48. [Google Scholar]
- 33.Nissen, T. L., Schulze, U., Nielsen, J. & Villadsen, J. (1997) Microbiology 143, 203-218. [DOI] [PubMed] [Google Scholar]
- 34.Edwards, J. S., Ibarra, R. U. & Palsson, B. O. (2001) Nat. Biotechnol. 19, 125-130. [DOI] [PubMed] [Google Scholar]
- 35.Covert, M. W., Schilling, C. H. & Palsson, B. (2002) ASM News 68, 529. [Google Scholar]
- 36.van Dijken, J. P., Weusthuis, R. A. & Pronk, J. T. (1993) Antonie Leeuwenhoek 63, 343-352. [DOI] [PubMed] [Google Scholar]
- 37.Overkamp, K. M., Bakker, B. M., Kötter, P., van Tuijl, A., de Vries, S., van Dijken, J. P. & Pronk, J. T. (2000) J. Bacteriol. 182, 2823-2830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Covert, M. W., Schilling, C. H. & Palsson, B. (2001) J. Theor. Biol. 213, 73-88. [DOI] [PubMed] [Google Scholar]
- 39.Forster, J., Famili, I., Palsson, B. O. & Nielsen, J. (2003) OMICS 7, 193-202. [DOI] [PubMed] [Google Scholar]
- 40.ter Linde, J. J., Liang, H., Davis, R. W., Steensma, H. Y., van Dijken, J. P. & Pronk, J. T. (1999) J. Bacteriol. 181, 7409-7413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.DeRisi, J. L., Iyer, V. R. & Brown, P. O. (1997) Science 278, 680-686. [DOI] [PubMed] [Google Scholar]
- 42.Phalakornkule, C., Lee, S., Zhu, T., Koepsel, R., Ataai, M. M., Grossmann, I. E. & Domach, M. M. (2001) Metab. Eng. 3, 124-137. [DOI] [PubMed] [Google Scholar]
- 43.Reed, J. L. & Palsson, B. O. (2003) J. Bacteriol. 185, 2692-2699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Gangloff, S. P., Marguet, D. & Lauquin, G. J. (1990) Mol. Cell. Biol. 10, 3551-3561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Boles, E., Jong-Gubbels, P. & Pronk, J. T. (1998) J. Bacteriol. 180, 2875-2882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kim, K. S., Rosenkrantz, M. S. & Guarente, L. (1986) Mol. Cell. Biol. 6, 1936-1942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hartig, A., Simon, M. M., Schuster, T., Daugherty, J. R., Yoo, H. S. & Cooper, T. G. (1992) Nucleic Acids Res. 20, 5677-5686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gancedo, C. & Delgado, M. A. (1984) Eur. J. Biochem. 139, 651-655. [DOI] [PubMed] [Google Scholar]
- 49.Sedivy, J. M. & Fraenkel, D. G. (1985) J. Mol. Biol. 186, 307-319. [DOI] [PubMed] [Google Scholar]
- 50.Smith, V., Chou, K. N., Lashkari, D., Botstein, D. & Brown, P. O. (1996) Science 274, 2069-2074. [DOI] [PubMed] [Google Scholar]
- 51.Cupp, J. R. & McAlister-Henn, L. (1992) J. Biol. Chem. 267, 16417-16423. [PubMed] [Google Scholar]
- 52.Loftus, T. M., Hall, L. V., Anderson, S. L. & McAlister-Henn, L. (1994) Biochemistry 33, 9661-9667. [DOI] [PubMed] [Google Scholar]
- 53.Repetto, B. & Tzagoloff, A. (1991) Mol. Cell. Biol. 11, 3931-3939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Przybyla-Zawislak, B., Dennis, R. A., Zakharkin, S. O. & McCammon, M. T. (1998) Eur. J. Biochem. 258, 736-743. [DOI] [PubMed] [Google Scholar]
- 55.McAlister-Henn, L. & Thompson, L. M. (1987) J. Bacteriol. 169, 5157-5166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Flikweert, M. T., Van Der Zanden, L., Janssen, W. M., Steensma, H. Y., Van Dijken, J. P. & Pronk, J. T. (1996) Yeast 12, 247-257. [DOI] [PubMed] [Google Scholar]
- 57.Clifton, D. & Fraenkel, D. G. (1982) Biochemistry 21, 1935-1942. [DOI] [PubMed] [Google Scholar]
- 58.Clifton, D., Weinstock, S. B. & Fraenkel, D. G. (1978) Genetics 88, 1-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Boles, E., Liebetrau, W., Hofmann, M. & Zimmermann, F. K. (1994) Eur. J. Biochem. 220, 83-96. [DOI] [PubMed] [Google Scholar]
- 60.Wills, C. & Melham, T. (1985) Arch. Biochem. Biophys. 236, 782-791. [DOI] [PubMed] [Google Scholar]
- 61.Schaaff-Gerstenschlager, I. & Zimmermann, F. K. (1993) Curr. Genet. 24, 373-376. [DOI] [PubMed] [Google Scholar]
- 62.Schaaff-Gerstenschlager, I. & Miosga, T. (1997) in Yeast Sugar Metabolism, Zimmermann, F. K. & Entian, K.-D., eds. (Technomic Publishing, Lancaster, PA), pp. 271-284.
- 63.Ozcan, S., Freidel, K., Leuker, A. & Ciriacy, M. (1993) J. Bacteriol. 175, 5520-5528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Boles, E. (1997) in Yeast Sugar Metabolism, Zimmermann, F. K. & Entian, K.-D., eds. (Technomic Publishing, Lancaster, PA), pp. 81-96.
- 65.Heinisch, J. J., Muller, S., Schluter, E., Jacoby, J. & Rodicio, R. (1998) Yeast 14, 203-213. [DOI] [PubMed] [Google Scholar]
- 66.Müller, S. & Entian, K.-D. (1997) in Yeast Sugar Metabolism, Zimmermann, F. K. & Entian, K.-D., eds. (Technomic Publishing, Lancaster, PA), pp. 157-170.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.