Contribution of climate-driven change in continental water storage to recent sea-level rise

Abstract

Using a global model of continental water balance, forced by interannual variations in precipitation and near-surface atmospheric temperature for the period 1981–1998, we estimate the sea-level changes associated with climate-driven changes in storage of water as snowpack, soil water, and ground water; storage in ice sheets and large lakes is not considered. The 1981–1998 trend is estimated to be 0.12 mm/yr, and substantial interannual fluctuations are inferred; for 1993–1998, the trend is 0.25 mm/yr. At the decadal time scale, the terrestrial contribution to eustatic (i.e., induced by mass exchange) sea-level rise is significantly smaller than the estimated steric (i.e., induced by density changes) trend for the same period, but is not negligibly small. In the model the sea-level rise is driven mainly by a downtrend in continental precipitation during the study period, which we believe was generated by natural variability in the climate system.

Sea-level variation is an integrator and indicator of global climate variation. Although the rate of 20th-century sea-level rise is uncertain (1), during the past decades the global mean sea level has been rising at a rate that is still debated, but that might be as large as 1.5–2 mm/yr (2). Recognized factors that have contributed to the 20th-century (specifically, 1910–1990) sea-level rise (3) include thermal expansion caused by warming of the oceans (0.3–0.7 mm/yr), melting of glaciers (0.2–0.4 mm/yr), mass imbalances of Greenland and Antarctica, including a long-term readjustment since the last glacial maximum and a recent climate-related response (-0.2 to +0.6 mm/yr), climate-driven loss from closed lakes (0.0–0.1 mm/yr), and melting of permafrost (0.0–0.005 mm/yr). In view of the significance of these terrestrial stores, it is important to assess the analogous role of climate-driven changes in ground water, soil water, and snowpack. Such an assessment is also motivated by the realization that these distributed terrestrial stores appear to be the dominant controls of sea level on the annual time scale (4–6). Although the contribution of these terms to sea-level change is expected to be negligible on the century scale, their role at interannual to decadal scales has yet to be assessed.

Global volumes of soil water and ground water are estimated to be 10¹³ to 10¹⁴ m³ (order of 0.1-m sea-level equivalent) and 10¹⁶ to 10¹⁷ m³ (100 m), respectively (7), with the smaller soil-water reservoir generally considered the more dynamic of the two. Unfortunately, available ground observations are extremely sparse, and remote-sensing technology is presently limited to snow-cover extent and its evolution with time, although measurement of snow depth using microwave sensors has been attempted.

In the absence of direct observational data, estimates can be made only by modeling. Global data from atmospheric reanalyses [e.g., from the U.S. National Centers for Environmental Prediction (8) or the European Centre for Medium-Range Weather Forecasts] could be used. However, such reanalyses, although based on atmospheric data assimilation, allow surface variables to depart substantially from reality, because errors in modeled precipitation are not directly addressed in the assimilation. Furthermore, any imposed relaxation of surface variables toward a prescribed climatology would attenuate the interannual signal.

An alternative is to use land water- and energy-balance models in a stand-alone mode, forced by observation-based estimates of surface climate. During recent years, increasingly detailed models of continental water balance have been developed. However, little effort has been devoted to their application and evaluation for simulation of interannual variability. Recently, it was demonstrated that the Land Dynamics (LaD) model (9) successfully predicts interannual variability of stream flow (10), which is the most accurately observed term in the continental water balance; the model explained about half of the interannual variance of the runoff ratio (annual runoff normalized by average annual precipitation) for a set of 44 major gaged river basins. The model has also been used to estimate mass loading for computations of crustal displacements that compared favorably with estimates derived from the Global Positioning System (11). Together, these results support use of the model for estimation of variations in terrestrial water storage. In this study, we use the LaD-modeled water balance to estimate the contributions of snowpack, soil water, and ground water to the change in sea level for the 18-year time span 1981–1998.

Methods

The LaD model is used to estimate the time-varying storage of snow, root-zone soil water, and ground water by solving water- and energy-balance equations that relate temporal change in storage to rainfall, snowfall, evapotranspiration, sublimation, snow melt, soil-water drainage, and ground-water discharge to streams. The ground-water store in the model represents the relatively shallow and dynamic unconfined saturated zone that typically regulates base flow to streams in humid regions (12); the model does not track changes of storage in deep saturated zones or in deep unsaturated zones of arid regions. Also neglected by the model are stores of surface water. The model parametrically includes effects of soil and vegetation on energy and mass transfers. In a stand-alone mode, the model is driven by spatio-temporally varying inputs of precipitation, radiation, and near-surface atmospheric state (temperature, humidity, and wind speed). Outputs include gridded time series of soil water, snow amount, and ground water, as well as water and energy fluxes (runoff, evapotranspiration, and sensible and latent heat fluxes).

The Climate Prediction Center Merged Analysis of Precipitation (CMAP) experiment (10) is a simulation of water storage on the global land mass (exclusive of Antarctica and Greenland), in which the interannual variations of water supplied to the continents are specified by the CMAP. For the present study, the original CMAP experiment was extended by 2 years for a total period of 1979–1998 inclusive. Additionally, temporal variations of near-surface air temperature were prescribed on the basis of monthly historical observations [Willmott, C. J. & Matsuura, K. (2001) Terrestrial Air Temperature and Precipitation: Monthly and Annual Time Series (1950–1999), version 1.02, http://climate.geog.udel.edu/~climate/html_pages/README.ghcn_ts2.html]; in the original CMAP experiment, a single annual cycle of temperature was applied for every year. The model outputs used here are 1° × 1° gridded monthly time series of soil water, ground water, and snow mass per unit of horizontal area. For each month of an 18-year time span (1981–1998) after a 2-yr spin-up period (1979–1980), we spatially averaged these outputs over all land, excluding Greenland and Antarctica, expressing the time series in terms of equivalent sea level. The resultant time series are estimates of the change in global mean sea level associated with climate-driven exchange of water mass between the global ocean and global snowpack, soil water, and ground water.

Results

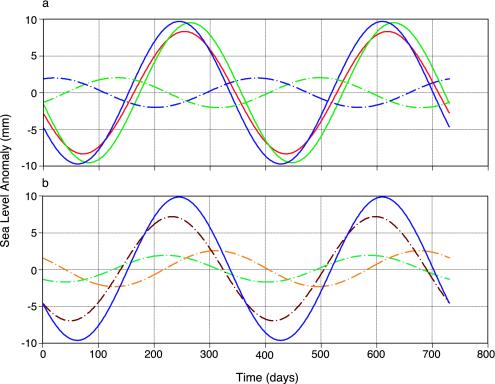
Computed storage time series are dominated by an annual signal on which is superimposed interannual variability. As a test of the model, we compared the modeled seasonal cycle with that estimated indirectly from observations and, as a primitive index of uncertainty, with corresponding continental-water results from the Interactions between Soil, Biosphere and Atmosphere (ISBA) water-balance model (13, 14). Fig. 1a compares the estimates of sea-level change caused by mass exchange with the continents. This quantity is estimated to have amplitudes of 9.7 mm (maximum on September 1) for LaD and 9.4 mm (maximum on September 21) for ISBA. The small difference in amplitude is probably fortuitous, because model parameters (for example, effective storage capacities) are not known with great accuracy. Fig. 1a also displays an observational estimate of annual sea-level change caused by mass exchange with the continents. It is based on Topex/Poseidon satellite altimetry observations (6) after correcting for thermal expansion of the oceans and subtracting the atmospheric water vapor contribution. The observation-based annual ocean-mass variation has an amplitude of 8.4 mm and a maximum on September 9. (Topex-Poseidon altimetry gives an amplitude of ≈4 mm before correcting for the steric effect. The correction approximately doubles the amplitude, without changing the phase.) The residual signals (observed minus model-derived) obtained from the LaD and ISBA models (Fig. 1a) are similar in amplitude and could reflect model errors or an unaccounted signal. The phase of the LaD residual, in contrast with that of the ISBA simulation, is consistent with the expected timing of an Antarctic mass-storage signal (6); however, the phase of the residual is probably very sensitive to possible errors in the amplitude of the modeled signal. Fig. 1b shows contributions of the three water-storage components to the annual cycle of ocean mass.

Fig. 1.

(a) Annual sea-level variation (mm) caused by continental mass exchange inferred indirectly from observations (red curve) and from modeled mass exchange with ground water, soil water, and snowpack (solid blue curve, LaD model; solid green curve, ISBA model, both expressed as equivalent sea-level change) as function of time (days). The dashed curves represent the corresponding residuals (observed minus modeled). At the annual time scale, the ocean mass can be derived from Topex/Poseidon satellite altimetry observations after removal of steric effects [density-related sea-level changes associated with thermal expansion and salinity change on the basis of the Levitus et al. climatology (15)]. This ocean-mass change is further adjusted here to remove the change caused by mass exchange with the atmosphere, which is estimated from National Centers for Environmental Prediction surface pressure fields. (Changes in global mean surface pressure are direct indications of changes in global atmospheric water content, because water is the only component of the atmosphere whose mass changes appreciably on this time scale.) Because there is no temporal overlap between the Topex/Poseidon data (1993–2001) and the ISBA data (1987–1988), we compute a mean annual cycle over all available data for each data set (including LaD data). Results for ocean mass and atmospheric water are taken from Cazenave et al. (6). To express land water mass stored on continents in terms of sea-level equivalent, we integrated unit-area water mass values, as given by the model, over the continental areas (excluding Greenland and Antarctica), then divided by water density and ocean area, and changed the sign. (b) Annual sea-level variation (mm) caused by continental mass exchange inferred from LaD-modeled mass exchange with ground water (broken light brown curve), soil water (broken green curve), and snowpack (dark brown curve), as function of time (days). Solid blue curve represents the sum of the other three curves.

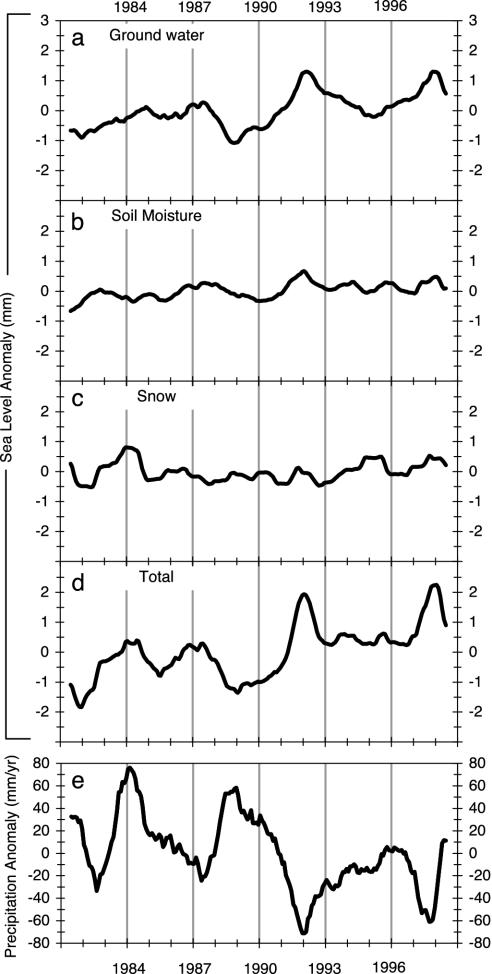
Interannual variations of all three water-storage time series from the LaD model (expressed as equivalent global mean sea-level anomalies) exhibit small positive linear trends, corresponding to 18-yr decreases in continental storage, on which are superimposed interannual fluctuations (Fig. 2 a–c). The greatest trend is associated with ground water (0.07 mm/yr), followed by soil water (0.03 mm/yr) and snow (0.015 mm/yr).

Fig. 2.

Time series of climate-driven changes in continental water mass, expressed as equivalent global sea-level anomalies (mm) for 1981–1998 [ground water (a), soil water (b), snowpack (c), sum of a–c (d)], and time series of CMAP precipitation anomaly over land (e). (Note that a positive trend in each of the first four panels corresponds to a decrease in terrestrial water storage.) For this analysis of interannual variability, we removed the total seasonal (annual and semiannual) signals from each variable and applied a 12-month running-mean smoother to the residuals.

Fig. 2d shows the equivalent sea-level time series associated with all estimated components of continental mass exchange. The positive trend (i.e., sea-level rise, or terrestrial desiccation) amounts to 0.12 mm/yr. This value is a direct estimate of the contribution to interdecadal sea-level rise associated with climate-driven changes in continental ground water, soil water, and snowpack.

For averages over all land, interannual variations in storage are controlled during most of this simulation by interannual variations of precipitation (Fig. 2e). Under a negative anomaly of precipitation, the land is generally drier than normal, hence more water is stored in the oceans. Storage anomalies track precipitation anomalies with little phase lag because residence times of water-storage anomalies on the continents are small. The reversal of this correlation for the first few years of the simulation appears to be associated with snow-storage anomalies, which are driven more by temperature than by precipitation.

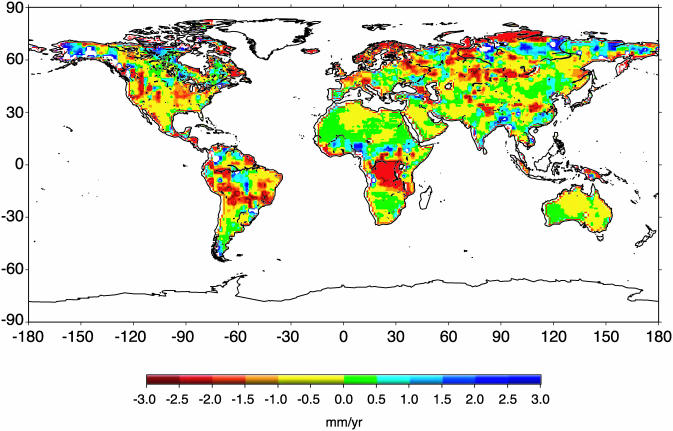
Not surprisingly, water-storage trends of the largest magnitude (and either sign) are found in the humid equatorial and mid- to high-latitude zones (Fig. 3), where means and variabilities of precipitation are greatest. Trends of minimal magnitude are found in desert zones. The overall tendency for decreasing trends during the analysis period has regional exceptions in northeastern Asia and Alaska, sub-Saharan Africa, the south-Asian monsoon region, and parts of tropical South America. This pattern corresponds closely to that of trends in precipitation (data not shown).

Fig. 3.

Geographical distribution of linear trend (1981–1998) in sum of ground water, soil water, and snowpack (mm water equivalent per yr) from the LaD model.

Discussion

The significance of the trend estimated here can be placed in the context of the observed 1.5- to 2-mm/yr rise of global mean sea level during the 20th century (2) and estimates of individual sources of sea-level change (3). For the 1981–1998 period, the ocean water density changes estimated by established methods (1) from global ocean temperature data (16) imply a steric sea-level rise of 0.72 ± 0.1 mm/yr. Our estimate of 0.12 mm/yr sea-level rise associated with mass exchange with ground water, soil water, and snow is considerably smaller than this amount but similar in magnitude to estimates of sea-level rise associated with mass exchange with ice sheets (3). Our results have errors of unknown magnitude and should be augmented by analyses with other land models and better atmospheric-forcing data sets.

The trends in ground water, soil water, and snowpack could be driven by internal variability in the hydrosphere and/or by forced climate change and so cannot be extrapolated beyond either end of the 18-yr analysis period. The controlling downtrend in precipitation during the period is not consistent with the expected global-warming precipitation signal (17) and is more likely a result of internal variability of the climate system. It seems, therefore, that the importance of this eustatic contribution to sea-level change is most significant at interannual to decadal time scales. For example, we find that the magnitude of the trend rises from 0.12 mm/yr for the period 1981–1998 to 0.18 mm/yr for 1990–1998 and to 0.25 mm/yr for 1993–1998 (the period of overlap with Topex/Poseidon observations). It is worth mentioning that the contributions to recent sea-level rise caused by mass loss from Greenland, Antarctica, and mountain glaciers have recently been revised upward (18, 19) (to 0.13 mm/yr, 0.16 mm/yr, and 0.35 mm/yr, respectively). It is unclear whether apparent acceleration of melting is associated with global warming or is at least partially another manifestation of internal variability in the water cycle.