A Comprehensive Comparison of the Continual Reassessment Method to the Standard 3 + 3 Dose Escalation Scheme in Phase I Dose-Finding Studies

Abstract

Background

An extensive literature has covered the statistical properties of the Continual Reassessment Method (CRM) and the modifications of this method. While there are some applications of CRM designs in recent Phase I trials, the standard method (SM) of escalating doses after three patients with an option for an additional three patients SM remains very popular, mainly due to its simplicity. From a practical perspective, clinicians are interested in designs that can estimate the MTD using fewer patients for a fixed number of doses, or can test more dose levels for a given sample size.

Purpose

This article compares CRM-based methods with the SM in terms of the number of patients needed to reach the MTD, total sample size required, and trial duration.

Methods

The comparisons are performed under two alternative schemes: a fixed or a varying sample approach with the implementation of a stopping rule. The stopping rule halts the trial if the confidence interval around the MTD is within a pre-specified bound. Our simulations evaluated several CRM-based methods under different scenarios by varying the number of dose levels from five to eight and the location of the true MTD.

Results

CRM and SM are comparable in terms of how fast they reach the MTD and the total sample size required when testing a limited number of dose levels (≤5), but as the number of dose levels increases, CRM reaches the MTD in fewer patients when used with a fixed sample of 20 patients. However, a sample size of 20–25 patients is not sufficient to achieve a narrow precision around the estimated toxicity rate at the MTD.

Limitations

We focused on methods with practical design features that are of interest to clinicians. However, there are several alternative CRM-based designs that are not investigated in this manuscript, and hence our results are not generalizable to other designs.

Conclusions

We show that CRM-based methods are an improvement over the SM in terms of accuracy and optimal dose allocation in almost all cases, except when the true dose is among the lower levels.

Introduction

There has been an increased interest in Bayesian Phase I designs, particularly in the oncologic community. The most prominent of these is a class of methods that are usually characterized by the acronym CRM (Continual Reassessment Method)[1]. An extensive literature [2–11] has covered the statistical properties of CRM and the modifications or extensions that followed. Many authors [6,8,12–14] have shown through simulations that their proposed modifications have improved the original CRM in terms of a particular outcome of interest. As pointed out by Eisenhauer et al. [15] the question concerning which types of designs described in the literature meet the criteria for safety, efficiency and precision in estimating the MTD still remains unresolved. We sought to evaluate the practical benefits of CRM-based methods over the standard ‘3 + 3’ dose escalation scheme in order to inform an institutional policy regarding the selection of designs for Phase I trials.

While there are some applications of CRM designs in recent Phase I trials [16–18], the standard method remains far more widely used, [19] not only because of its simplicity, but it is also well understood and accepted by clinicians. However, the standard method often underestimates the MTD, as shown by He et al. [20] resulting in selection of a dose whose toxicity rate is lower than the target rate. Clinical investigators are interested in designs that can estimate the MTD accurately while using fewer patients. In addition, for certain agents, investigators are not always certain of how many dose levels to test and where the MTD could lie. If indeed CRM reaches the MTD faster, by allowing rapid dose-escalations in sub-optimal doses, it is plausible that we could test more dose levels by skipping the lower doses without increasing the total number of patients accrued for the trial. If this is true, it offers the opportunity for a more substantial improvement over the standard method.

The performance of CRM and its sample size requirements have been examined through simulated studies under a fixed sample framework, as well as with the implementation of stopping rules [12,21,22]. The fixed sample approach assumes that the original CRM [1], under certain conditions, will converge to the true maximum tolerated dose (MTD) when the total sample size is sufficiently large (in the range of 20–25) [1,4]. Goodman et al. suggested treating patients in cohorts, with or without a fixed sample, and have compared the total sample between several CRM versions and the standard method [12]. These simulations showed that the sample size ranged from 18–20 using CRM with cohorts of 1, 2, or 3 patients, but on average the standard method required three subjects less than the CRM to test six dose levels. Previous work [9,13] used the width of the confidence interval around the dose-toxicity parameter as a stopping rule and a sample size of 24 on average was shown adequate with this stopping rule, making it similar to the fixed sample approach. Zohar and Chevret [22] extensively compared different stopping rules by varying the maximum sample at 10, 20, and 30 and confirmed that at least 20 patients are needed to reach an accurate estimate of the MTD. Similar to other studies [23,24] that have looked at sample size requirements in the context of CRM, the number of dose levels was most often held constant at six and in some cases the sample size was held fixed. As a result, it is difficult to generalize the conclusions from these studies with respect to the sample size needed among the different CRM methods in comparison to the standard method under different scenarios.

The objective of this article is to determine whether a CRM-based design should be used routinely in Phase I trials, and under which circumstances is CRM more appropriate. Which CRM design among various modified versions should we use, and is a fixed sample approach as accurate as one with a sequential stopping rule? We compared various CRM-based methods with the standard method. The methods include the original CRM; two-stage methods that combine rule-based and model-based approaches; as well as CRM that accrues patients in cohorts. We evaluated CRM-based methods using both pre-specification of the fixed sample and a stopping rule approach. We evaluated the methods under realistic scenarios that vary the location of the true MTD, covering situations where the MTD is located at the lower, middle or higher doses. Comparisons were also performed by varying the number of dose levels from five to eight. Standard endpoints are reported such as overall measures of accuracy, precision, safety, trial duration, as well as how fast the MTD is reached under the different methods and what is the total sample size needed when a stopping rule is used.

In the sections below we cover the methodological background, describe the assumptions of the simulations, present the results, and provide recommendations of which design to use in practice.

Methods

Notation: Original CRM with fixed sample size

We use the same notation as in O'Quigley [1]. The investigators choose dose levels which they believe correspond to the range of toxicity probabilities acceptable for testing. We assume pre-specified k dose levels D₁ ≤ … ≤ D_k, we denote θ as the toxicity rate at the MTD, and a as the dose-toxicity curve parameter of interest, a ε(0, ∞). Let Y_j, j = 1,…,n, be a binary random variable (0,1) where 1 denotes toxic response for the jth patient. The dose-toxicity function for E(Y_i) is given by φ(D_i, a) = [(tan h D_i + 1)/2]^a, where φ(D_i, a) denotes the probability of toxicity and is monotonic in D_i and a. After the inclusion of the jth patient and having observed whether the jth patient experiences toxicity, the posterior distribution of a is updated based on the most recent cumulative data up to and including the jth patient. Let Ω_j= [Y₁,…, Y_j-1] and f(a, Ω_;) be a nonnegative function summarizing all available information about the parameter a. The posterior density of a is given by:

$$f(a,{\Omega }_{j+1})=\frac{g\left(a\right){\Pi }_1^j\phi (D_1,y_1,a)}{{\int }_0^{\infty }g\left(u\right){\Pi }_1^j\phi (D_1,y_1,u)\text{du}}$$

where φ(D_j, y_j, a) = φ^yj(D_j, a)[1 − φ(D_j, a)]^(1−y_j⁾ is the component of the likelihood of the data observed up to patient j, and g(a) is the prior density of a. The recommended Phase II dose after the inclusion of n, a pre-specified number of patients, is the dose D_i that minimizes the euclidean distance between the target toxicity rate θ and θ'_ij, where θ'_ij = φ(D_i, μ(j)), 1 ≤ i ≤ k, and $\mu \left(j\right)={\int }_0^{\infty }af(a,{\Omega }_j)\text{d}a$ is the posterior mean for a.

CRM with stopping rule

CRM has been used within the frame of stopping rules. A stopping rule previously proposed by O'Quigley and Reiner [5] halts the trial early on the basis that continuing the trial would not lead to a change in dose recommendation with high probability. If the goal is to stop the trial earlier than accrual of 20 patients, then stopping rules based on convergence are appropriate [9]. However, we are interested in evaluating the trade-off between sample size and increase in precision around the estimated probability of toxicity at the MTD. Thus, we allow the trial to continue until the precision around this estimate is narrow enough. We followed the stopping rule proposed previously [1,9] which stops the trial once the Bayesian interval for the true parameter θ, the toxicity rate at the MTD, is fully contained in a pre-specified region R. Specifically the Bayesian interval for φ(D_j+1, μ_j) is given by ψ_j⁻,ψ_j⁺ where

$$\begin{array}{c}{\psi }_j^{-}=\psi (D_{j+1},a_j^{-}),\\ {\psi }_j^{+}=\psi (D_{j+1},a_j^{+},{\int }_{a_j^{+}}^{a_j^{-}}f\left(u\right|{\Omega }_{j+1})\text{d}u=1-\alpha ,\end{array}$$

where a_j⁺, a_j⁻ are the lower and upper confidence limits for a, respectively, calculated from the 100(1 − α)% confidence interval (CI) based on the posterior distribution. The stopping rule halts the study once the interval for θ is contained in some pre-specified range, R: (θ⁻, θ⁺) for some θ⁻ and θ⁺ chosen by the investigators.

O'Quigley [1,9] suggested the assumption of symmetry around a in order to solve the equation and obtain the 90% CI for a. In agreement with previous reports [24] our simulations showed that the posterior density of a is asymmetric, hence we extended this approach by using an asymmetric confidence interval for a by computing the highest posterior density interval [25]. The integral was estimated by an algorithm that calculated the area under the curve and solved the equation iteratively until the 90% highest posterior interval was found (shown in the Appendix).

Designs and endpoints

Designs

The original CRM as introduced by O'Quigley [1] allows skipping dose levels in the absence of dose limiting toxicities (DLT's). Skipping dose levels can potentially expose patients unnecessarily to highly toxic drug levels. Most clinicians do not feel comfortable with this risk. Thus, we ran simulations with the original CRM and confirmed that restriction in dose escalation does not affect the operating characteristics of the method (data shown in supplemental table). For the purpose of this research article, we present only CRM with constraint in dose escalation, since this method is more likely to be used in practice over the original CRM. In addition, we evaluated three CRM-based methods that are attractive to investigators due to their practical modifications that combine a rule-based and a model-based approach, and compared these with the standard method. The methods are outlined below:

Supplemental Table.

Comparison of CRM with restriction of no more than one level in dose escalation (defined in section ‘Methods’ under subsection ‘Designs and endpoints’, results also shown in Table 2), to CRM without restriction, and CRM-I as defined in section ‘Results’: Endpoint 6

	Fixed sample			Varying sample with stopping rule
	CRM with restriction	CRM w/o restriction	CRM-I with one incomplete patient	CRM with restriction	CRM w/o restriction
1. Accuracy: Percent of trials that found the true MTD
S1	63	61	61	65	67
S2	67	67	66	72	70
S3	57	57	57	58	57
S4	61	63	63	68	69
S5	55	56	56	70	70
S6	20	19	20	25	25
S7	48	48	52	64	63
S8	43	43	44	49	49
2. Optimal allocation: Percent of patients treated at the MTD (s.d.)
S1	44 (30)	43 (30)	38 (27)	47 (29)	47 (29)
S2	55 (32)	60 (32)	44 (26)	58 (30)	61 (31)
S3	54 (33)	54 (33)	37 (26)	56 (32)	54 (33)
S4	46 (30)	51 (32)	26 (20)	52 (29)	56 (31)
S5	33 (26)	39 (31)	25 (20)	41 (26)	46 (28)
S6	18 (13)	14 (12)	13 (12)	23 (17)	21 (17)
S7	36 (25)	35 (25)	40 (25)	44 (29)	45 (29)
S8	31 (23)	31 (23)	31 (20)	41 (27)	41 (27)
3. Safety: Median number of toxicities (IQR)
S1	3 (2–4)	3 (2–4)	3 (2–4)	5 (3–6)	5 (3–6)
S2	4 (3–5)	4 (3–5)	4 (3–4)	6 (4–7)	6 (4–7)
S3	5 (4–5)	5 (4–5)	4 (3–5)	7 (5–8)	7 (5–8)
S4	4 (3–4)	4 (3–5)	2 (2–3)	7 (4–10)	7 (4–10)
S5	3 (2–4)	3 (3–4)	3 (2–4)	7 (3–10)	8 (3–10)
S6	4 (4–5)	4 (4–5)	3 (2–4)	10 (6–12)	10 (6–12)
S7	6 (6–7)	7 (6–7)	6 (5–7)	11 (8–14)	11 (9–14)
S8	6 (5–6)	6 (5–6)	4 (4–5)	12 (9–14)	12 (9–14)
4. Oscillation after the nth patient	Percent of trials where Dn ≠ Dn+1			Percent of trials that used maximum n (Percent of trials that met CI criterion)
S1	13	13	17	67 (34)	67 (33)
S2	12	14	18	70 (31)	70 (31)
S3	16	16	22	77 (23)	78 (22)
S4	12	12	21	19 (83)	19 (83)
S5	20	20	27	29 (77)	31 (74)
S6	22	20	28	40 (64)	39 (65)
S7	16	14	19	22 (80)	24 (77)
S8	23	23	31	51 (53)	51 (53)
5. Median number of patients to reach the MTD (IQR)
S1	16 (9–19)	16 (8–20)	16 (9–20)	20 (9–28)	20 (9–27)
S2	15 (6–19)	14 (6–19)	15 (8–20)	19 (6–27)	19 (6–28)
S3	17 (8–20)	16 (8–19)	16 (8–20)	23 (8–29)	23 (9–29)
S4	16 (5–19)	15 (7–19)	16 (14–20)	24 (9–33)	24 (10–33)
S5	18 (10–20)	18 (9–20)	18 (12–20)	32 (11–43)	32 (11–42)
S6	18 (11–20)	18 (11–20)	18 (13–20)	34 (16–43)	35 (18–44)
S7	17 (13–20)	17 (13–20)	17 (12–20)	25 (17–29)	25 (18–30)
S8	19 (15–20)	19 (15–20)	19 (16–20)	32 (22–42)	32 (22–42)

• CRM: starts at the dose level whose toxicity rate is closest, in euclidean distance, to the target toxicity level, 6, and restricts to no more than one dose level increase at a time [1]. The method allows for more than one dose level decrease.

• E-CRM: known as extended CRM, starts at the lowest dose and uses an arbitrary starting plan for the dose allocation at the beginning of the trial until a DLT is observed. The method then switches to the CRM algorithm [14]. For example, an arbitrary starting plan assigns one patient at D₁ and D₂, two patients at D₃ and D₄, and the remaining patients at D₅ when testing five levels as long as no toxicity is observed.

• R-CRM: known as restricted, is the same as E-CRM but prevents escalation from being more than a single dose level at a time [14]. An arbitrary starting plan can assign one patient per dose if no toxicity is observed, while the method switches to CRM when a DLT is observed.

• G-CRM: referring to CRM in cohorts, starts at the lowest dose, treats patients in cohorts of three per dose level, and requires at least six patients to be treated at the MTD before the study completion [12].

• SM: the standard method as described by Korn et al. [21] treats three patients at each dose level and expands to six if there is 1/3 DLT, deescalates if there ≥2 DLT, or otherwise if no DLT's are observed the method escalates to the next dose level. The method continues to escalate if ≤1/6 experience DLT. The MTD is the dose level below the dose with ≥2 patients experiencing DLT and where there are no more than 1/6 patients with a DLT.

Endpoints

Typically reported outcomes include the percent of experimentation at the true MTD, recommendation of the true MTD out of the total number of simulated trials and median number of toxicities. We report these outcomes here, since a meaningful comparison of these methods should be in the context of accuracy and safety. However our primary comparisons are based on how many patients each method needs to reach the MTD, the total sample size required, trial duration, and the level of experimentation at the end of the trial. For the fixed sample approach, we evaluated the level of oscillation by reporting the percentage of trials where the recommended Phase II dose is different than the dose assigned to the last patient (i.e., D_n ≠ D_n+1). For the stopping rule approach we report the percentage of trials that used the maximum sample size and the proportion of trials that met the stopping rule requirement.

Simulation setting

In all examples the exponential prior g(a) = exp(−a), and the hyperbolic tangent model for the dose-toxicity curve, given by φ(D_i, a) = [(tan h D_i + 1)/2]^a were used, as recommended in the literature. Previous papers have shown that the method is robust regardless of the choice of prior and model [4,23,24]. Other authors [22,23] have shown that a sample size of 20 is enough to eliminate the bias in estimating the MTD. Thus, for consistency our article provides a comparison of the methods when the sample size is pre-defined and fixed at 20, as well as when the sample is varying and a stopping rule is implemented. The target toxicity rate is set equal to 0.25 for all simulations. Other target rates that have been examined in the literature are typically in the range of 0.2–0.3, but the performance of CRM is proven to converge to the dose associated with the target level, regardless of the value of the target, as this is considered an external tuning parameter. For the stopping rule approach, we define the region R as [0.10, 0.35]. We impose a bound on the maximum sample size to be 6 k, where k is the number of dose levels. That is, a trial will stop after reaching the maximum n, regardless if the confidence region around θ was contained in R. Our findings are based on 1000 simulations (trials) for each of the eight scenarios described below.

For trial duration, we assumed patient arrival times follow a Poisson distribution (λ), and thus interpatient arrival times follow Exponential (1/λ) The time to DLT was sampled from Uniform distribution (0,21), where 21 days is the fixed length of cycle. Patients without DLT's were followed for a minimum of one cycle of 21 days. Trial duration was calculated under four different λ rates from the Poisson distribution: 3, 2, 1.5, and 1 patient per month, which correspond to average interpatient arrival times of 10, 15, 20, 30 days, respectively.

Scenarios 1–3 (S1–S3) experiment with five dose levels, whereas Scenarios 4–8 (S4–S8) experiment with eight dose levels. Each scenario is described by two vectors: the priori toxicity rates that control the start of the trial and the true toxicity rates that correspond to each dose level (Table 1). In practice, priori toxicity rates represent the ‘best guesses’ of the probabilities of toxicity that are believed by the investigators, a priori, to correspond to each dose level (refer to [1] for standardized units of dose levels). In each scenario, the location of the MTD, i.e., the dose corresponding to the target toxicity rate (specified at 0.25) varies, but it covers situations where the true MTD is at the highest dose, middle, or lower dose. Scenarios 1–3 assume the last dose among the five is the true MTD, while the a priori toxicity rates consider D₁, D₃, and D₄ respectively. Both Scenarios 4 and 5 assume the true MTD is the last dose among eight dose levels, whereas in Scenario 6 the true MTD is between D₇ and D₈. Scenarios 7 and 8 present examples where the true MTD is among the lower and middle dose levels (D2 and D4, respectively). The arbitrary starting plans for E-CRM and R-CRM are the same across all scenarios as described in the previous section. The extended starting plan when testing eight dose levels in the event of no DLT assigns one patient at the first three doses, two patients at doses D4–D7 and the remaining patients at D8.

Table 1.

Simulation parameters: Highlighted dose corresponds to the MTD

Scenario	Parameter	Values
S1	True toxicity	0.03	0.05	0.10	0.18	0.22
	A priori toxicity rates	0.25	0.30	0.40	0.50	0.55
S2	True toxicity	0.06	0.09	0.13	0.16	0.25
	A priori toxicity rates	0.15	0.20	0.25	0.30	0.40
S3	True toxicity	0.06	0.10	0.15	0.19	0.28
	A priori toxicity rates	0.10	0.15	0.20	0.25	0.35
S4	True toxicity	0.0001	0.0025	0.02	0.06	0.09	0.12	0.16	0.25
	A priori toxicity rates	0.01	0.05	0.15	0.25	0.30	0.35	0.40	0.50
S5	True toxicity	0.035	0.04	0.06	0.08	0.11	0.15	0.19	0.24
	A priori toxicity rates	0.25	0.27	0.30	0.35	0.40	0.45	0.50	0.55
S6	True toxicity	0.0005	0.004	0.03	0.06	0.10	0.19	0.24	0.28
	A priori toxicity rates	0.001	0.01	0.05	0.10	0.15	0.25	0.30	0.35
S7	True toxicity	0.1	0.22	0.39	0.50	0.55	0.59	0.63	0.71
	A priori toxicity rates	0.01	0.05	0.15	0.25	0.30	0.35	0.40	0.50
S8	True toxicity	0.003	0.01	0.09	0.25	0.31	0.36	0.42	0.56
	A priori toxicity rates	0.0005	0.002	0.04	0.16	0.21	0.26	0.31	0.46

Results

Endpoint 1: Accuracy

Table 2 shows the results of our simulations broken down by the fixed versus the varying sample approach, for each of the eight scenarios across the various methods. The first endpoint, percent of trials that found the true MTD, represents the accuracy of the methods. There is a slight improvement in accuracy by using a varying sample over a fixed sample of 20 patients but this is also a result of a larger sample size. G-CRM has equally good accuracy as the other three CRM-based methods, which has already been shown by Goodman et al. [12]. SM found the true MTD 10–30% fewer times compared to the CRM-based methods except for S6 where all CRM-based methods selected the true MTD ∼ 17–28% of the time, which is as low as SM (18%). In S6, the true MTD is between two dose levels D₇ and D₈, but closer to D₇. All CRM-based methods mistakenly focused on D₈ which was associated with a 0.28 toxicity rate instead of D₇, whose toxicity rate was 0.24 and thus closer to the target rate of 0.25. This inability of the method to distinguish between two dose levels when they are close has been discussed previously [1,23,26].

Table 2.

Endpoints under various designs and schemes: CRM, R-CRM, E-CRM assume a fixed sample size at n = 20. Varying sample scheme follows the stopping rule in section ‘Methods’ under subsection ‘CRM with stopping rule’. G-CRM has a minimum sample of 18. IQR: Interquartile range; s.d.: Standard deviation

	Fixed sample			Varying sample with stopping rule
	CRM	R-CRM	E-CRM	CRM	R-CRM	E-CRM	G-CRM	SM
1. Accuracy: Percent of trials that found the true MTD
S1	63	63	62	65	66	66	61	39
S2	67	69	69	72	71	70	69	33
S3	57	59	60	58	57	57	63	26
S4	61	66	63	68	69	68	65	32
S5	55	57	56	70	69	70	56	23
S6	20	17	23	25	28	26	23	19
S7	48	50	50	64	61	65	48	41
S8	43	42	41	49	48	47	47	26
2. Optimal allocation: Percent of patients treated at the MTD (s.d.)
S1	44 (30)	44 (30)	38 (28)	47 (29)	47 (29)	43 (27)	20 (16)	18 (14)
S2	55 (32)	50 (30)	45 (26)	58 (30)	53 (29)	49 (27)	23 (15)	16 (13)
S3	54 (33)	46 (30)	41 (27)	56 (32)	48 (30)	43 (28)	21 (15)	13 (13)
S4	46 (30)	39 (25)	28 (18)	52 (29)	49 (28)	43 (25)	13 (11)	11 (9)
S5	33 (26)	33 (26)	25 (20)	41 (26)	43 (27)	37 (23)	13 (11)	7 (9)
S6	18 (13)	14 (11)	13 (9)	23 (17)	22 (17)	21 (16)	10 (9)	10 (9)
S7	36 (25)	38 (25)	38 (25)	44 (29)	45 (29)	46 (29)	36 (22)	35 (15)
S8	31 (23)	31 (21)	35 (21)	41 (27)	40 (26)	43 (27)	22 (14)	22 (10)
3. Safety: Median number of toxicities (IQR)
S1	3 (2–1)	3 (2–4)	3 (2–4)	5 (3–6)	5 (3–6)	5 (3–6)	2 (1–3)	2 (1–3)
S2	4 (3–5)	4 (3–5)	4 (3–4)	6 (4–7)	6 (4–7)	6 (4–7)	3 (2–4)	2 (2–3)
S3	5 (4–5)	4 (3–5)	4 (3–5)	7 (5–8)	7 (5–8)	6 (5–7)	3 (2–4)	3 (2–3)
S4	4 (3–4)	3 (2–4)	3 (2–3)	7 (4–10)	7 (4–9)	7 (4–9)	2 (2–3)	3 (2–3)
S5	3 (2–4)	3 (2–4)	3 (2–4)	7 (3–10)	7 (3–10)	7 (3–10)	3 (2–4)	3 (2–4)
S6	4 (4–5)	4 (3–4)	3 (2–4)	10 (6–12)	10 (6–11)	9 (5–11)	3 (2–4)	3 (2–4)
S7	6 (6–7)	6 (5–7)	6 (5–7)	11 (8–14)	10 (8–13)	10 (8–13)	5 (4–6)	3 (2–4)
S8	6 (5–6)	5 (4–6)	5 (4–5)	12 (9–14)	11 (9–13)	11 (9–13)	3 (3–4)	3 (2–4)
4. Oscillation after the nth patient	Percent of trials where Dn ≠ Dn+1			Percent of trials that used maximum n (Percent of trials that met CI criterion)
S1	13	13	13	67 (34)	68 (33)	67 (34)	NA	NA
S2	12	14	12	70 (31)	71 (31)	72 (31)	NA	NA
S3	16	16	17	77 (23)	78 (22)	80 (22)	NA	NA
S4	12	14	15	19 (83)	21 (81)	23 (79)	NA	NA
S5	20	20	21	29 (77)	30 (74)	30 (76)	NA	NA
S6	22	21	20	40 (64)	50 (55)	52 (53)	NA	NA
S7	16	16	16	22 (80)	22 (79)	23 (79)	NA	NA
S8	23	26	25	51 (53)	54 (49)	56 (48)	NA	NA
5. Median number of patients to reach the MTD (IQR)
S1	16 (9–19)	16 (9–19)	16 (7–19)	20 (9–28)	20 (9–27)	21 (9–28)	13 (13–18)	16 (13–16)
S2	15 (6–19)	14 (5–19)	15 (7–19)	19 (6–27)	19 (5–28)	19 (7–28)	13 (13–18)	16 (13–16)
S3	17 (8–20)	16 (5–20)	16 (7–20)	23 (8–29)	23 (8–29)	24 (8–29)	13 (13–18)	16 (13–19)
S4	16 (5–19)	15 (8–19)	16 (12–20)	24 (9–33)	25 (10–35)	25 (12–35)	22 (22–24)	25 (22–28)
S5	18 (10–20)	18 (10–20)	18 (12–20)	32 (11–43)	33 (11–42)	33 (12–13)	22 (22–24)	25 (22–28)
S6	18 (11–20)	18 (10–20)	18 (12–20)	34 (16–43)	38 (20–45)	36 (20–45)	22 (21–24)	25 (22–25)
S7	17 (13–20)	17 (13–20)	17 (13–20)	25 (17–29)	24 (17–29)	24 (17–28)	16 (10–18)	10 (10–13)
S8	19 (15–20)	19 (16–20)	19 (16–20)	32 (22–42)	35 (24–44)	34 (22–44)	18 (16–21)	16 (13–22)

Endpoint 2: Optimal allocation at MTD

The second endpoint in Table 2 presents the percent of patients treated at the MTD. CRM methods are comparable across scenarios and schemes, however there are cases (S3 and S4) where E-CRM treats 10–18% fewer patients than CRM because it escalates slower. The percent of patients treated at the MTD is consistently lower with G-CRM compared to the other three CRM-based methods because it spends time allocating patients in cohorts. All four CRM-based methods treat a much higher percentage of patients at the MTD than SM, except for S7 where the true dose is the second dose. This suggests that when the MTD is among the lowest doses, CRM-based methods spend time treating patients in higher doses before de-escalating to the correct dose level. Similarly, for situations like S6 when the target toxicity rate falls between the seventh and eighth dose, CRM-based methods treat more patients at the highest level.

Endpoint 3: Safety

Reviewing the median toxicities and interquartile ranges presented in Table 2 shows that SM results in fewer patients with toxicity than CRM but very comparable to G-CRM and the modified versions of two-stage CRM. This is expected since Moller [14] and Goodman et al. [12] proposed their modifications precisely to reduce the number of toxicities observed by the original CRM. Using CRM with a stopping rule results in more toxicities due to a larger sample (above 20 patients), as shown below in Endpoint 5. Note that in practice we can weight the distance measure used for allocation purposes so that a dose below the target is selected over a dose exceeding the target, or we can use escalation with over-dose control (EWOC) without losing efficiency as it has been shown by Babb et al. [6]. The target toxicity rate under SM varies depending on the scenario, but the method often targets doses associated with low toxicity, which implies that SM is not flexible in tuning the target threshold of acceptable toxicity.

Endpoint 4: Oscillation

The fourth endpoint shown in Table 2 presents the oscillation that occurs after the last patient (percent of trials where D_n ≠ D_n+1) under the fixed sample approach, and the percent of trials that used the maximum sample size under the varying sample scheme. This endpoint is meant to illustrate how the method is still searching for the MTD after observing the last patient. Under the fixed sample approach, the results show that as the number of dose levels increases, so does the oscillation. Although, depending on the scenario and the location of the true MTD, CRM-based methods may experiment equally regardless of the number of dose levels (the percent of oscillation for S3 is similar to the percent for S7). Scenario 8 has 23–25% oscillation, showing that CRM spends time experimenting when the true dose is in the middle level. Under the varying sample scheme, the stopping rule halts the trial if the CI requirement is met or if the maximum sample size is reached. Thus, we present the percent of trials that met the CI criterion in order to evaluate whether a maximum of 30 (five doses) or 48 (eight doses) patients is an adequate sample to reach the pre-specified precision around the MTD toxicity estimate. For S1–S3, most trials exhaust the maximum sample size without reaching the required precision. With the exception of S8, when eight levels are tested, more than half of the trials stop early because the stopping rule requirement is met. Thus, one could conclude that the precision around the toxicity estimate at the MTD is within the pre-specified region of [0.10, 0.35] more often with a sample size of 48 compared to 30 patients, despite the increase in the number of dose levels.

Endpoint 5: Sample size

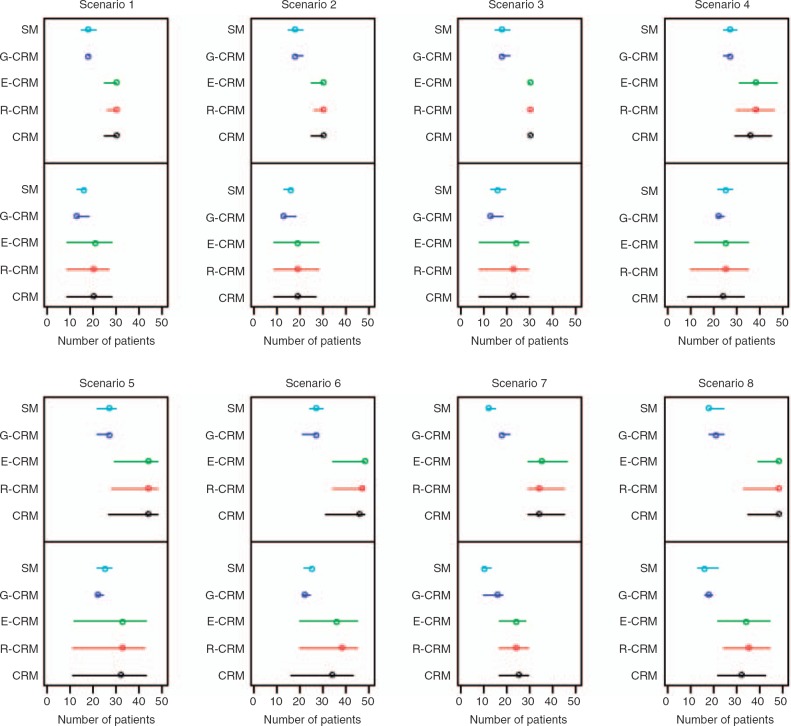
In order to assess whether various CRM-based methods reach the MTD in fewer patients compared to SM, we calculated the minimum number of patients until the CRM-based methods focused on the MTD and then remained at that dose level for the rest of the trial. For the varying sample scheme using a stopping rule, Figure 1 displays the number of patients needed to reach the MTD (lower panel) and the total sample size at the end of the trial (upper panel) under the various scenarios/methods. Note that scenarios S1–S3 test five dose levels with a maximum bound on the sample size of 30, whereas S4–S8 test eight dose levels with a maximum bound of 48. For example, in scenario S1, CRM reached the MTD at a median of 20 patients, treated all subsequent patients at the MTD, and completed the trial at a median of 30 patients. For S1, G-CRM and SM reached the MTD at a median of 13 and 16 patients, respectively, and both methods completed the trial at a median of 18 patients. The results in the figure support that CRM in cohorts and SM reach the MTD earlier and finish the trial with a smaller sample size compared to CRM-based methods with stopping rule. The number of patients that the methods require to reach the MTD under the two approaches is shown in Table 2. Simulations under both schemes show that despite the modifications in the original design, all three CRM-based methods are similar in regards to this endpoint. Using the fixed sample scheme, CRM-based methods reach the MTD at a median of 14–17 when testing five dose levels, and at a median of 15–19 when testing eight levels, which is at least as high as the number required by SM. However, in cases where the MTD is at the highest dose levels (scenarios S4–S6) the results show that the three CRM-based methods focus on the MTD earlier than G-CRM and SM.

Figure 1.

Number of patients required to reach the MTD (lower panel) and total sample size (upper panel) under five methods for each of the eight scenarios. CRM, R-CRM, and E-CRM are using the stopping rule defined in section ‘Methods’ under subsection ‘CRM with stopping rule’ with a maximum sample size bounded at 30 (5 levels) or 48 (8 levels). G-CRM and SM use the stopping rules as listed in section ‘Methods’ under subsection ‘Design and endpoints’. Circles show the median and lines indicate the interquartile range

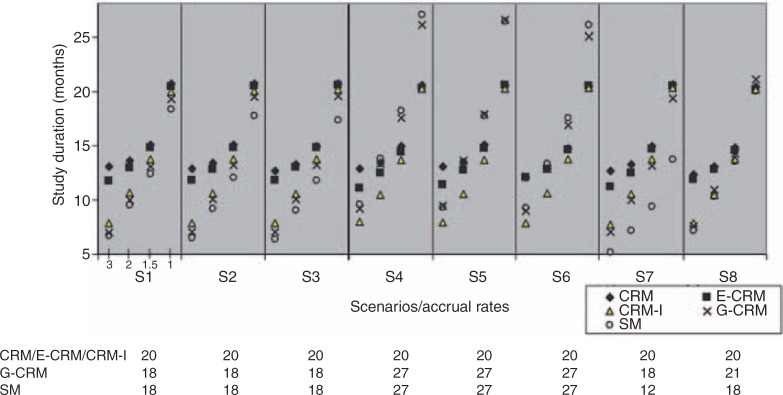
Endpoint 6: Trial duration

We report the median trial duration over 1000 simulations using the fixed sample approach, except for G-CRM and SM where the sample size varies. Since R-CRM and CRM assign one patient at a time using a fixed sample size, the trial duration of R-CRM as calculated in simulations was very close to CRM. Thus we report CRM only. We added a modified design, denoted as CRM-I, that allows for one patient with incomplete DLT information (delayed response) - a modification that allows CRM to proceed to the next patient's assignment without having observed the last patient's toxicity data. At each time point the assignment for patient j depends on data from j - 2 patients, where j ≥ 3. If patient j arrives after patient j − 1 was fully observed, the response from patient j - 1 is used. CRM-I starts at the lowest dose level and prevents escalation of more than one dose level. The results for the five designs under each of the eight scenarios and using varying accrual rates are shown in Figure 2. It is evident that when accrual rate is two or three patients/month CRM and E-CRM take on average five months longer to complete than the other three methods. As accruals become less frequent, then CRM-based methods and SM become closer in trial duration. In S4–6, as a result of a larger sample size needed to evaluate eight doses, SM and G-CRM take longer than the other CRM methods when accrual is less than two patients/month. The concept that CRM always takes longer to complete than SM because it accrues one patient at time is not correct. The longer the wait between patient accruals, the closer the two methods are in trial duration. Depending on the number of dose levels tested, CRM may have shorter trial duration than SM. CRM-I greatly decreases trial duration over CRM especially for trials when a higher accrual rate is anticipated. CRM-I performs similarly to the original CRM in accuracy and to E-CRM in terms of the other endpoints presented in this article (data shown in supplemental table). These results show that we can use CRM-I in practice with reduced trial duration without sacrificing other clinical endpoints such as accuracy and safety.

Figure 2.

Median trial duration across simulations. Each panel represents a scenario under four different accrual rates (3, 2, 1.5, or 1 patient/month). The sample sizes are shown at the bottom: CRM, E-CRM and CRM-I are using a fixed sample of 20 patients. G-CRM and SM use the stopping rules as listed in section ‘Methods’ under subsection ‘Design and endpoints’

Discussion

Is CRM a better phase I design? Under which circumstances?

Our simulations showed that CRM-based methods outperform the standard method in accurately finding the true MTD and in treating more patients at optimal dose levels, which is consistent with the literature [12,14]. This finding is supported by all examples, except when the true MTD is among the lower levels. Depending on the location of the MTD, CRM-based methods may reach the MTD in fewer patients than the standard method, especially when the MTD is among the higher levels by treating fewer patients at sub-optimal low doses. Although, CRM-based methods reach the MTD faster, this does not imply that the methods will terminate the trial early. CRM-based methods require accrual of an adequate number of patients before convergence to the true MTD. When five dose levels were tested, both CRM-based methods with pre-defined sample size and the standard method reached the MTD on average at the 16th patient and both methods needed approximately 18–20 patients to complete the trial. CRM-based methods provide an improvement over the standard method in regards to accuracy, but not in terms of sample size requirements when five dose levels are tested. However, it is important to emphasize that even in situations where the standard method completes a trial with a small number of patients the probability of selecting the wrong dose is very high [27]. Our simulations showed that CRM-based methods with a fixed sample of 20 patients can test eight dose levels with substantially increased accuracy compared to the standard method that needs an average of 27 patients. However, as the number of dose levels increase, CRM-based methods unavoidably experiment more and do not reach the MTD as quickly. The mathematical relationship between the total sample size and the number of dose levels is not yet known in the context of CRM convergence to the MTD. While this relationship remains unknown, a formal comparison of the sample size between these two designs cannot be achieved. It would be erroneous to assume that CRM-based methods need a smaller sample size than the standard method regardless of the number of dose levels tested or the location of the MTD.

Should we be using a fixed sample or a stopping rule approach?

We found that CRM with a fixed sample performs reasonably well compared to CRM with a stopping rule that ensures a narrow confidence interval around the toxicity rate at the MTD. While there are more complicated stopping rules in the literature [5,6,8,13,22–24] that have been compared and proven to stop the trial early, it was not the scope of this article to recommend a new stopping rule for halting the trial early. Instead, we allow the trial to proceed beyond 20 patients so that we can estimate the level of experimentation and precision around the toxicity estimate at the MTD. Hence, we selected a stopping rule that takes into account the confidence interval around the estimated toxicity rate at the MTD, since based on our clinical experience, investigators are interested in assessing the uncertainty around the MTD estimate. Both a fixed sample approach and a stopping rule approach resulted in similar accuracy (finding the true MTD) and optimal treatment allocation. Thus, from a practical perspective the fixed sample scheme with fewer patients is more reasonable since we achieve the dose-finding goal. It can be argued that the precision is a secondary objective of Phase I trials, but if the goal is to stop as early as possible even with accrual of 12–15 patients, then the precision around this estimate is still important. We showed that CRM-based methods require more than 36 patients (when testing eight dose levels) to achieve a narrow width around the estimated toxicity rate at the MTD. If the confidence around this estimate is prioritized highly over sample size considerations, then a stopping rule that ensures a narrow confidence around this parameter might be appropriate.

Which CRM to use in practice?

While there are many modified versions of CRM that we have not included in this review, a comprehensive comparison of each modified method with the original method across various scenarios and endpoints is needed before conclusive guidelines can be generated. For simplicity in this report, we presented versions that are of interest to investigators due to their safety features. The comparison of the original CRM to the one with restrictions in escalation to one dose level at a time showed that CRM with restrictions in dose jumps can be used without losing efficiency. E-CRM and R-CRM start from the lowest dose level and restrict dose increases at the beginning of the trial when accumulated data is limited. Their operating characteristics are comparable to the original CRM, while they are superior to the standard method. Since investigators feel more comfortable with the modified designs we presented here, we can safely use them in practice, despite their decrease in percent of patients treated at the MTD. Our examples showed a 10% decrease in the percent of patients treated at the MTD with the modified CRM designs. These numbers vary across simulated examples, but the decreases reached up to 20%, especially when treating patients in cohorts. A practical design we can safely use is CRM-I that allows for incomplete toxicity data (delayed response) for at most one patient at a time. This design shortens trial duration substantially compared to all other CRM methods investigated here, while it maintains the attractive properties of the original CRM in terms of accuracy and E-CRM in terms of optimal treatment allocation. In contrast with G-CRM which also shortens study duration, CRM-I allows patients to be treated at the most optimal doses, since it does not allocate patients in cohorts of three at suboptimal dose levels. CRM-I provides a practical improvement for a CRM-based design that combines short trial duration and increased accuracy.

A two-stage CRM design that is potentially appealing is one that accommodates information on toxicity grades by allowing rapid escalation in the presence of low grades at the beginning of the trial, before a DLT is observed. At that point, the CRM model dictates the dose escalation using all accumulated data [28]. Various versions of the first stage design exist allowing for one, two, or three patients accrued per dose level, and combining grade severity in different ways. For example, if grade 0–1 toxicity is observed, escalate to the next dose level, however, if a toxicity of grade 2 is observed remain at the same dose level. We recommend clinical expertise to guide the arbitrary starting plan of two-stage designs since this is the stage where we have not accumulated enough data and any decisions we make should be clinically-based.

Practitioners who are interested in using CRM-based methods should also know that there are extensions we have not covered here. CRM has been extended to include patient heterogeneity by including a covariate in the model and thus recommend different doses for different patients [7,29]. Also, it can accommodate two bivariate outcomes simultaneously [30,31], for example toxicity and efficacy, which is pertinent for trials of cytotoxic agents. These extensions provide additional alternatives for Phase I designs.

Conclusions

These examples illustrate that CRM-based methods improve accuracy and optimal dose allocation compared to the standard method. A fixed sample approach at n = 20 is adequate for most practical situations when testing the number of dose levels in the range of five to eight. A CRM-based method with a pre-specified sample size is easier to implement compared with the CRM that terminates based on sequential stopping rules. In the fixed sample approach, the statistician does not need to be continuously involved since the dose-allocation can be generated automatically through a webinterface. However, a fixed sample approach cannot guarantee a narrow confidence interval around the estimated toxicity rate at the MTD. In order to ensure a narrow confidence interval around this estimate, the sample size for a trial with eight dose levels needs to be increased to almost double the fixed sample of 20 patients. A Phase I trial of 35–45 patients is not always feasible, especially when the current practice is to plan Phase I trials in the range of 20–25 patients. On the other hand, underestimation of the MTD leads to patients being treated at suboptimal doses in Phase II studies and possibly Phase II doses that are not efficacious. Whether we need to increase the sample size in Phase I trials in order to increase our confidence in the estimate of the MTD is worth further study. A more accurate estimation of the MTD can lead to more successful Phase II trials.

Supplementary Materials

A supplemental table referenced in Section ‘Methods’ under subsection ‘Design and endpoints’, and in section ‘results’ is available at the end of this article.

Appendix

Algorithm for calculating the 90% confidence interval based on the area under the curve (AUC). Starting from the mode of the posterior distribution, the AUC was estimated by summing the respective rectangulars and trapezoids, after partitioning the vertical axis into M sub-intervals. That is, for each partition l, 2 ≤ l ≤ M we define the pair {(a_l⁺, a_l⁻): (f (a_l⁺) = f (a_l⁻), a_l+ < mode < a_l⁻], while the final pair a_M⁺, a_M⁻ satisfies for some M, the following:

$${\int }_{a_M^{+}}^{a_M^{-}}f\left(u\right|{\Omega }_{j+1})\text{d}u\approx (a_M^{-}-a_M^{+}\times f\left(a^{+}\right)+\sum _{I\ge 2}^M\frac{\left(f\right(a_{l-1})-f(a_1\left)\right)(a_l^{-}-a_l^{+}+a_{l-1}^{-}-a_{l-1}^{+})}{2}+\left(f\right(\text{mode}\left)\right(a_1^{-}-a_1^{+})/\text{2})\approx \text{0.90}$$